Microtubules enhance mesoscale effective diffusivity in the crowded metaphase cytoplasm

Summary

Mesoscale macromolecular complexes and organelles, tens to hundreds of nanometers in size, crowd the eukaryotic cytoplasm. It is therefore unclear how mesoscale particles remain sufficiently mobile to regulate dynamic processes, such as cell division. Here, we study mobility across dividing cells that contain densely-packed, dynamic microtubules, comprising the metaphase spindle. In dividing human cells, we tracked 40 nanometer Genetically Encoded Multimeric nanoparticles (GEMs), whose sizes are commensurate with the inter-filament spacing in metaphase spindles. Unexpectedly, the effective diffusivity of GEMs was similar inside the dense metaphase spindle and the surrounding cytoplasm. Eliminating microtubules or perturbing their polymerization dynamics decreased diffusivity by ~30%, suggesting that microtubule polymerization enhances random displacements to amplify diffusive-like motion. Our results suggest that microtubules effectively fluidize the mitotic cytoplasm to equalize mesoscale mobility across a densely-packed, dynamic, non-uniform environment, thus spatially maintaining a key biophysical parameter that impacts biochemistry, ranging from metabolism to the nucleation of cytoskeletal filaments.

Graphical Abstract

eTOC blurb

The mitotic spindle is composed of densely packed microtubules, yet mesoscale assemblies with sizes commensurate to the inter-filament spacing of the spindle need to diffuse across this structure. Carlini et al. report that metaphase microtubules help enhance the diffusive-like motion of 40 nm mesoscale particles, thereby equalizing mobility across the inhomogeneous metaphase cytoplasm.

Introduction

Intracellular obstacles to mobility can range from macromolecules, organelles and cytoskeletal filaments (Delarue et al., 2018; Janson et al., 1996; Luby-Phelps et al., 1987; Weiss et al., 2004). The effects of such obstacles on diffusion can be so prominent that mesoscale complexes, tens of nm in size, are estimated to be immobile or shown to produce subdiffusive motion in mammalian cells (Etoc et al., 2018; Janson et al., 1996; Luby-Phelps et al., 1987). The metaphase spindle can comprise 50% of the cellular volume (Good et al., 2013; Kapoor, 2017), and its interior is an example of a crowded environment, with filament densities that can exceed 100 microtubules/μm², corresponding to inter-microtubule spacings of ~30 −40 nm (Mastronarde, 1993; Nixon et al., 2015). Even macromolecules smaller than the inter-microtubule filament spacing, such as GFP (4 nm), have been observed to undergo impeded diffusion inside the spindle (Pawar et al., 2014). Larger, key macromolecules, such as the chromosomal passenger complex, the gamma-tubulin ring complex and condensins have sizes comparable to the inter-microtubule spacing (Anderson et al., 2002; Jeyaprakash et al., 2007; Samejima et al., 2015; Wieczorek et al., 2019), so we expect their diffusion to be hindered. However, fluorescence-based bulk measurements suggest that these mesoscale assemblies can remain mobile. For example, condensins and gamma tubulin ring complexes within the spindle can be exchanged with their respective cytoplasmic populations (Hallen et al., 2008; Walther et al., 2018), and the chromosomal passenger complex can readily diffuse within dividing cells (Hanley et al., 2017; Wachsmuth et al., 2015). To explain these complex dynamics, we need to map the mobility of mesoscale particles across dividing cells. However, we lack data that captures the fast, millisecond-scale dynamics of individual mesoscale particles inside and around the spindle to help address this open question.

Results

40 nm-GEMs can probe the metaphase cytoplasm

To measure mesoscale particle dynamics, we generated a stable, lentiviral HeLa cell line expressing 40 nm genetically encoded multimeric nanoparticles (GEMs) fused to the fluorescent protein, T-Sapphire (Methods), similar to a previously reported cell line (Delarue et al., 2018), and performed single particle tracking in metaphase cells. We initially characterized this cell line using two criteria. First, we measured the mitotic index and found it did not significantly differ from that measured for control HeLa cells (Fig. S1A,B). Second, we compared the fraction of cells with at least one lagging chromosome in GEMs-expressing HeLa cells with that of the control cells and found no significant difference between these two cell lines (Fig. S1C). Thus, expression of GEMs does not appear to affect the capacity of HeLa cells to divide.

Next, we examined which regions of the cytoplasm were accessible to GEMs during cell division. We identified metaphase cells and acquired high frame rate timelapse movies of the GEMs for 10 s, followed by snapshots of the DIC and SiR-DNA (a near infrared vital DNA stain) channels (Fig. 1A–C). We created maximum intensity time projections from successive time frames (time projections) of the GEMs time-lapse movies (Methods). From these time projections, we observed a relatively low signal at the metaphase plate, where the majority of chromosomes align. Conversely, the GEMs signal was relatively homogeneous throughout the imaged cytoplasm, including the region occupied by the mitotic spindle (Fig. 1D).

Figure 1: 40 nm GEMs are homogeneously distributed across metaphase HeLa cells.

(A) Metaphase GEMs-expressing HeLa cell, showing GEMs (green), (B) DNA (magenta), and (C) an overlay with the DIC channel (gray). D) Maximum intensity time projection (time projection) from a 10 s acquisition. (E) Average intensity map from the time projections of n = 12 cells. Boxes show select ROIs across the cell. (F) Distributions of intensities are quantified from select ROIs shown in (E). **** and n.s indicate p < 0.0001 and p > 0.05, respectively. Solid black circles represent median and black line extrema are the 25th and 75th percentiles of distributions. G) Example distribution of particle intensities from a single metaphase HeLa cell, acquired from a 5 s movie. Red line shows a fit to a Gaussian function (mean: 3,806 ± 1 AU, SD: 23 ± 1 AU). H) Distribution of imaged particles-per-cell for n=20 metaphase cells. Scale bars: 5μm. Also see Fig. S1.

To quantify the signal from multiple cells, we generated an average intensity map using time projection images of GEMs. These images were aligned to one another along their metaphase plate (see Methods). As there was cell-to-cell variation in diameters, we plotted average intensity values at positions rescaled according to the cell radius (see Methods). The resulting intensity map indicated that the signal of GEMs was relatively constant across the metaphase cytoplasm (Fig. 1E), and approximately 2-fold lower at the metaphase plate. Indeed, insets of this intensity map from regions of interest (ROI) proximal and distal to the metaphase plate had similar average intensities, which varied by < 1 %. These were significantly different from the intensities at the metaphase plate (Fig. 1F). We also confirmed that GEMs were distributed across the metaphase cytoplasm, without any detectable accumulation at one particular location, by analyzing circular intensity profiles (Fig. S1D,E). Finally, we labelled cells with the microtubule stain, SiR-Tubulin and directly examined the co-localization of the spindle and the positions of GEMs (Fig. S1F,G). These data indicate that, with the exception of being excluded from chromatin, there is no bias, revealed by our measurements, as to where GEMs distribute across the metaphase cytoplasm.

We examined whether GEMs remained as single, well-separated particles across the metaphase cytoplasm, as this determines the feasibility of performing single particle tracking experiments. First, we measured distributions of particle intensity, a proxy for particle size, and found they were Gaussian in nature (Fig. 1G). These unimodal distributions suggest that GEMs do not cluster within metaphase cells, as particle clustering is typically associated with tailed distributions (Liu et al., 2017). Second, we imaged cells with sparse distributions of particles (Fig. 1H), corresponding to ~2–20 particles per frame and an average minimum particle separation of ~ 2 μm. As this separation is greater than the average particle displacement between consecutive frames (Methods), it prevents multiple particles from being associated with a single trajectory.

Together, these results demonstrate that GEMs can be used to probe the metaphase cytoplasm, with a particle size previously challenging to study.

The effective diffusivity of 40 nm-GEMs increases during metaphase relative to interphase

To examine cytoplasmic diffusibility by single-particle tracking experiments, we initially determined the timescale over which these measurements were possible. To do this, we imaged cells at 100 Hz, localized the centroids of GEMs and traced these localizations over the 5 s timelapse to create trajectories (Methods). We plotted these trajectories and color-coded them according to time relative to the start of imaging. This means that trajectories with longer lifetimes contain multiple, colored segments (Fig. S2A). Qualitatively, individual trajectories persisted in the imaging plane for < 1 s. Frequency distributions of trajectory lifetimes indicate an average lifetime of 150 ms (15 frames) (Fig. S2B). These lifetimes are limited by the amount of time a particle remains in the imaging plane, as previously reported (Delarue et al., 2018). To quantify cytoplasmic diffusibility using particle trajectories, we performed a mean squared displacement (MSD) analysis over 100 ms time intervals from datasets acquires over 5 s. We measured the average time and ensemble-averaged diffusivity using particles from multiple cells and the diffusivity of individual particles (Methods).

We first compared the average diffusivity of GEMs in metaphase with that of interphase cells. To quantify the time and ensemble-averaged diffusivity, we generated average MSD versus time delay plots from multiple metaphase cells. We performed a linear fit on this MSD trace to extract the 2-dimensional (2D) effective diffusivity (D_eff) (Methods). According to the fit, D_eff was 0.70 ± 0.03 μm²/s during metaphase (Fig. 2A, n=2162 trajectories, 20 cells). We performed the same analysis in interphase cells and found D_eff was 0.52 ± 0.02 μm²/s (Fig. 2B, n=2124 trajectories, 13 cells), similar to previously reported values (Delarue et al., 2018). These results indicate that average mesoscale diffusivity increases by ~ 35% during metaphase relative to interphase.

Figure 2: Effective Diffusivity of GEMs Is Similar Within and Outside the Metaphase Spindle.

A) Mean squared displacement (MSD) of GEMs versus time delay during metaphase for n=2162 trajectories from 20 cells. Black circles are average data from individual cells, connected by black lines. Red line is linear fit (slope: 2.794 with 95% confidence interval [2.732, 2.856]). B) MSD versus time delay during interphase for N = 2124 trajectories from 13 cells; black circles are average data from individual cells, connected by black lines. Red line is linear fit (slope: 2.095 with 95% confidence interval [2.024, 2.167]). C) DIC image of cell with distances r and R outlined, showing distance from cell center to trajectory’s centroid (r) and the radius of the cell (R). Trajectories in zone 1 (r/R<0.5, green) and zone 2 (r/R>0.5, magenta) are plotted. D) Distributions of D_eff from zone 1 (green) and 2 (magenta); n=640 trajectories per zone from 20 cells (n.s, p=0.2261). E) Probability distribution of 1-dimensional particle displacements (10 ms time delay) in Zone 1. Red line is best fit to a Gaussian, (n=25 568 displacements from 20 cells). F) Probability distribution of 1-dimensional particle displacements (10 ms delays) in Zone 2. Red line is best fit to a Gaussian, (n=59 470 displacements from 20 cells). Error is standard deviation on α₂ obtained from random sampling, with replacement. Scale bar: 5 μm. Also see Fig. S2.

To analyze the diffusivity of individual particles, we performed linear fits on MSD versus time delay plots for each particle and extracted D_eff. Using these data, we generated a distribution of D_eff for all metaphase cells imaged. We found a median diffusivity of 0.75 ± 0.15 μm²/s, very similar to the time and ensemble averaged value (n=2145 trajectories, 20 cells) (Fig. S2C). We repeated this per-particle analysis in interphase cells and confirmed there was a statistically significant ~ 35% increase in the median D_eff during metaphase (Fig. S2C, Methods).

The effective diffusivity of 20 and 40 nm-GEMs in similar within and around the metaphase spindle

Next, we examined whether proximity to the metaphase spindle affected particle diffusivity. To do this, we grouped trajectories according to their distance, r from the cell center, normalized to the cell radius, R (n=2145 trajectories). Using DIC images, we could estimate the boundary of the metaphase spindle and outline the cell edge. Typically, points along the spindle boundary were positioned at a distance from the cell center corresponding to ~R/2 (Figure 2C). With these size estimates, we defined two zones, which represent trajectories “close” to the metaphase plate (zone 1, r/R<0.5) and those “far” from it (zone 2, r/R>0.5) (Fig. 2C). To analyze whether zones 1 and 2 corresponded to regions inside and outside of the spindle respectively, we labeled cells with the microtubule probe, SiR-Tubulin, and found that points along the spindle boundary were positioned at a distance corresponding to ~R/2 from the cell center (Figure S2D). Distributions of effective diffusivities in these two zones indicated there was no statistically significant difference; these populations had nearly matching median values (Fig. 2D, corresponding to median diffusivities of 0.78 μm²/s (outside) and 0.75 μm²/s (inside), p>0.05). We further examined this result by tracking GEMs in SiR-Tubulin labeled metaphase cells. We found no statistically significant difference in the effective diffusivities inside compared with outside the spindle-labeled region (Fig. S2E).

Next, we examined whether cytoplasmic diffusibility is similar within and around the metaphase spindle for smaller particles. We tracked GEMs that are 20 nm in diameter in metaphase cells and measured similar effective diffusivities in zones 1 and 2 of metaphase cells, demonstrating this effect holds on smaller length scales (Fig. S2E). We note that the median diffusivity of 20 nm GEMs is almost double that of 40 nm GEMs in the metaphase cytoplasm, corresponding to a median diffusivity of 1.37 μm²/s; these values are in relatively good agreement with previous diffusion measurements using comparably-sized dextrans in metaphase cells (Weiss et al., 2004).

Collectively, these results suggest that the distributions of mesoscale effective diffusivity are similar within and around the metaphase spindle.

40 nm-GEMs exhibit non-Gaussian dynamics across the metaphase cytoplasm

To examine the anomalous nature of trajectories, we measured particle displacements proximal and distal to the metaphase plate. We characterized these distributions by computing the 1-dimensional non-Gaussian parameter, α₂, which distinguishes thermally driven diffusion in a simple fluid (α₂ = 0) from anomalous diffusion (α₂ ≠ 0) (Wang et al., 2009). A value of α₂ > 0 indicates that there is an increased frequency of large displacements relative to a normal distribution. This regime (α₂>0) has been reported for dynamics ranging from active transport to changes in confinement (Ahmed and Saif, 2014; Nagel et al., 2020; Parry et al., 2014; Wang et al., 2009).

To start, we focused on the shortest time delay measured and separated trajectories according to their normalized distance from the cell center as before (Fig. 2C; zone 1: r/R<0.5; zone 2: r/R>0.5). We found α₂ values of 0.22 ± 0.02 (zone 1, n=n=25 568 displacements) and 0.23 ± 0.02 (zone 2, n=59 470 displacements), indicating there are deviations from a Gaussian distribution both proximal and far from the metaphase plate (Fig. 2E,F). Next, we examined α₂ at time delays up to 90 ms and found that this parameter becomes greater in the spindle-containing region relative to the surrounding cytoplasm (Fig. S2F,G). Finally, we computed α₂ in directions parallel and perpendicular to the spindle’s long axis, both in zones 1 and 2. We found α₂ was moderately greater in directions parallel to the spindle’s long axis. This difference was subtle, but statistically significant (Fig. S2F,H). Combined, these results suggest that there is an increased frequency of larger particle displacements relative to the expectation from thermally-driven diffusion. While this effect is apparent across the metaphase cytoplasm, it is measurably greater in the spindle-containing region and in directions parallel to the spindle’s long axis.

Depolymerization of metaphase microtubules reduces the mobility of 40 nm-GEMs

To examine the effect of microtubules on particle motion, we used nocodazole (33 μM, Methods). Fixed images of immunostained cells indicated that nocodazole treatment depolymerized microtubules in dividing cells (Fig. S3A). Chromatin masses were distributed over a greater area compared with control metaphase cells, consistent with previous findings (Jordan et al., 1992) (Fig. S3A). We tracked GEMs at 100 Hz for 5 s in nocodazole-treated cells and quantified particle diffusivity over a 100 ms time interval (Fig. 3A). We found that in nocodazole-treated cells, the effective diffusivity decreased relative to control metaphase cells (Fig. 3B, D_eff = 0.53 ± 0.01 μm²/s, n=2145 trajectories, 17 cells). Comparing the distributions of particle diffusivity indicated there was a ~30% decrease in the median of the nocodazole-treated diffusivity distribution (Fig. S3C, nocodazole-treated: 0.52 μm²/s, control cells: 0.75 μm²/s, n=1400 trajectories per condition, p<0.0001), consistent with measurements acquired in interphase cells (Delarue et al., 2018). After nocodazole washout, we tracked GEMs and found a distribution of effective diffusivity from individual particles that showed no statistical difference to that acquired from particle trajectories in untreated cells (Fig. 3C, Methods). We also measured the non-Gaussian parameter and found that, on short timescales (10–30 ms), α₂ remained greater in nocodazole-treated cells compared with untreated metaphase cells (Fig. 3D, S3E). Together, these results suggest that, in the absence of microtubules, mesoscale particle diffusivity decreases and is increasingly anomalous compared with control metaphase cells.

Figure 3: The Effective Diffusivity of 40 nm-GEMs Decreases in Nocodazole-Treated Metaphase Cells.

A) Nocodazole-treated (33 μM) metaphase HeLa cell expressing GEMs, showing GEMs (green), DNA (magenta), the DIC channel (grey) and an overlay. B) Mean squared displacement (MSD) of GEMs versus time delay in nocodazole-treated (33 μM) metaphase HeLa cells for n=1004 trajectories from 17 cells. Black circles are average data from individual cells, connected by black lines. Red line is linear fit (slope: 2.100 with 95% confidence bounds: [2.057, 2.143]). C) Distributions of effective diffusivity in metaphase cells after nocodazole washout (noco washout) compared to control conditions (ctrl). n=417 trajectories per condition from 6 (noco washout) and 10 (ctrl) cells. D) Probability distribution of 1-dimensional particle displacements (10 ms delay) in nocodazole-treated cells. Red line is best fit to a Gaussian (n= 28 567 displacements from 17 cells). Scale bars: 5μm. Also see Fig. S3,4

The effective diffusivity of 40 nm-GEMs is similar in monopolar and control bipolar metaphase spindles

To examine the effect of spindle organization on particle motion, we generated monopolar spindles by inhibiting the mitotic kinesin Eg5 using monastrol (Kapoor et al., 2000; Mayer, 1999) (Methods, Fig. S3F). We tracked GEMs at 100 Hz for 5 s and measured the distributions of effective diffusivity over a 100 ms time interval for hundreds of trajectories (Fig. S3F, S3G). We found no statistically significant difference between the diffusivities in monopolar spindles compared with control, bipolar spindles (Fig. S3H, p=0.06, n=711 tracks per condition). We also measured the non-Gaussian parameter at time delays ranging from 10–90 ms and found no measurable difference between monopolar and control bipolar spindles until 70 ms (Fig. S3I,J n=17 756 steps, 15 cells). Together, these results suggest that bipolar spindle organization alone does not account for the increased particle mobility we observe during metaphase.

Stabilization of metaphase microtubules reduces the mobility of 40 nm-GEMs

To examine the effect of microtubule polymerization dynamics on particle motion in dividing cells, we used Taxol (10 nM, Methods). We imaged the end-binding protein EB3, which tracks the ends of growing microtubules, in GEMs-expressing HeLa cells. We found a significant reduction in the intensity of EB3 comets, consistent with suppression of microtubule polymerization dynamics due to Taxol (Fig. S3K). In line with previous reports (Kelling et al., 2003; Yvon et al., 1999), we observed a subset of spindles in Taxol-treated cells that were disrupted. We therefore classified Taxol-treated metaphase cells based on whether or not the spindle remained bipolar, with most chromosomes congressed to the metaphase plate (Fig. 4A). We focused on this bipolar population to directly compare our results to control metaphase cells with bipolar spindles. We quantified effective particle diffusivity over a 100 ms time interval and found this value reduced relative to control cells (Fig. 4B, S3L 0.55 ± 0.05 μm²/s, n= 1384 trajectories, 17 cells). By comparing the distributions of effective diffusivity from individual trajectories, we found the median diffusivity in Taxol-treated cells with a bipolar organization was reduced by ~ 36% (Fig. S3M, Taxol-treated cells: 0.53 μm²/s, control cells: 0.82 μm²/s n=1009 trajectories per condition, p<0.0001). A statistically significant decrease in the median diffusivity was also observed in non-bipolar Taxol-treated spindles, albeit to a lesser degree (Fig. S3M). We also measured the non-Gaussian parameter and found that α₂ remained greater in Taxol-treated bipolar cells compared with control metaphase cells (Fig. 4D, S3N). Combined, these results indicate that suppressing microtubule polymerization dynamics reduces the effective diffusivity of GEMs and results in stronger deviations from thermally driven motion in a simple fluid relative to control metaphase cells.

Figure 4: The Effective Diffusivity of 40 nm-GEMs Decreases in Taxol-Treated Metaphase Cells.

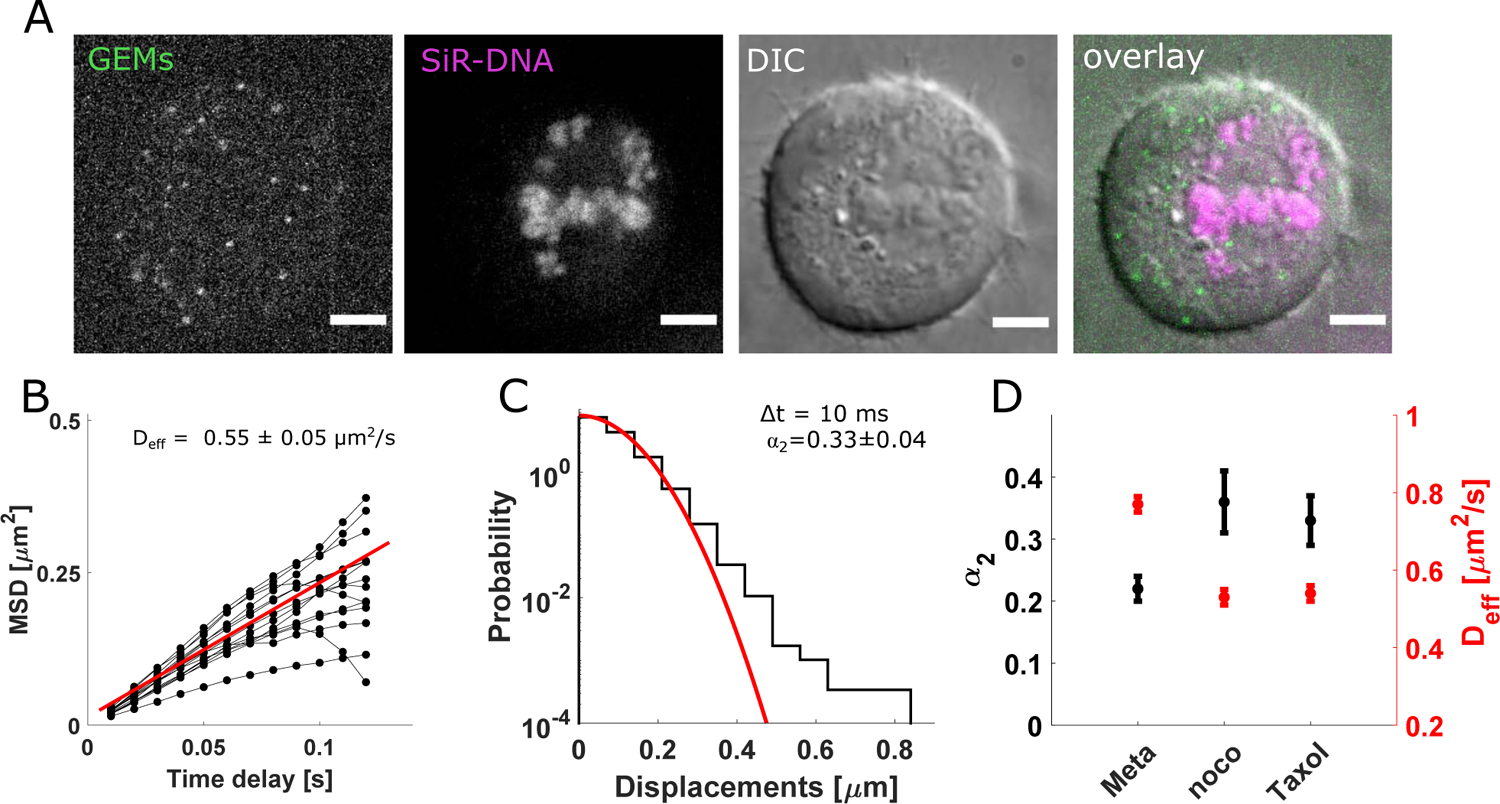
A) Taxol-treated (10 nM) metaphase HeLa cell expressing GEMs, showing GEMs (green), DNA (magenta), the DIC channel (grey) and an overlay. B) Mean squared displacement (MSD) of GEMs versus time delay in Taxol-treated (10 nM) metaphase HeLa cells with a bipolar-like organization for n=1384 trajectories from 18 cells. Black circles are average data from individual cells, connected by black lines. Red line is linear fit (slope: 2.200 with 95% confidence bounds: [1.998, 2.405]). C) Probability distribution of 1-dimensional particle displacements (10 ms delay) in Taxol-treated (10 nM) metaphase cells with a bipolar-like organization. Red line is best fit to a Gaussian (n= 41 908 displacements from 17 cells). D) Non-Gaussian parameter α₂ (black) and D_eff (red) from 3 experimental conditions tested. Error bars are standard deviation and central values are mean from random sampling with replacement. n= 20 (meta), 17 (noco) and 17 (Taxol) cells. Scale bars: 5μm. Also see Fig. S3,4.

Directionality of 40 nm-GEMs is reduced after depolymerization or stabilization of metaphase microtubules

Our analyses revealed that nocodazole- and Taxol-treated metaphase showed significant changes in particle mobility compared with control metaphase cells (Fig. 4D). Thus, we further examined individual trajectories to identify how they differed from those in untreated cells. To directly examine the space explored by GEMs in treated and untreated metaphase cells, we computed each trajectory’s radius of gyration (R_g) as previously described (Elliott et al., 2011; Notelaers et al., 2014). We found a statistically significant difference between the distributions of R_g in control versus nocodazole- and Taxol-treated cells (Fig. S3D, M bottom panel) confirming that trajectories in nocodazole and Taxol-treated cells explore less cytoplasmic space.

We next examined the anomalous motion of GEMs by calculating relative angles between successive displacements in a single trajectory as previously outlined (Fig. S4A) (Burov et al., 2013). In untreated cells, we found a higher frequency of shallow (< 30°) angles than what is to be expected from normal diffusion (Fig. S4B). These shallow angles tended to be relatively aligned with the spindle’s long axis (Fig. S4C,D). In nocodazole- and Taxol-treated metaphase cells, we measured a decrease in the frequency of shallow angles (< 30°) and an increase in that of large angles (> 100°) relative to untreated cells (Methods, Fig. S4E,F). These data indicate that, in nocodazole- and Taxol- treated cells, trajectories lose their directionality on these short timescale (10 ms). Together, these results are consistent with the hypothesis that spindle microtubules help drive the motion of mesoscale complexes during metaphase.

Discussion

Our measurements indicate that microtubules enhance the diffusivity of GEMs during metaphase. We focused on 40 nm particles, representing an important length scale during metaphase, as it is comparable to both the spacing between spindle microtubules and the size of several key macromolecules (Carmena et al., 2012; Kollman et al., 2011; Walther et al., 2018). Further, we stress that this result is distinct from microtubule-based transport, where these filaments provide tracks along which motor proteins move cytoplasmic cargo in specific directions. Instead, our results suggest that microtubule polymerization dynamics enhance the magnitude of random cytoplasmic fluctuations, thereby increasing diffusive-like motion.

How might microtubules increase macromolecular diffusivity? Tens of thousands of microtubules can collectively polymerize at speeds of up to 1 μm/s during metaphase (Yamashita et al., 2015). A macromolecule that stochastically encounters the proximity of a growing microtubule, can thus be subjected to a force resulting from polymerization. It is therefore feasible to suspect that this effect can, on average, increase the size of molecular displacements to enhance the magnitude of diffusive-like motion during metaphase. Further, it has been shown that microtubules undergo significant lateral bending fluctuations as they polymerize in living cells (Brangwynne et al., 2007). It is thus possible that these local fluctuations can agitate the cytoplasm and, in turn, amplify molecular displacements. An alternative possibility is that the increase in metaphase diffusivity is a result of incoherent motor protein activity, as previously demonstrated in interphase cells (Brangwynne et al., 2008; Fakhri et al., 2014; Guo et al., 2014). While motor protein activity may be contributing to the enhanced diffusivity we measure in metaphase, we do not expect this to be a major source of the random fluctuations we have analyzed. Indeed, motor-protein driven fluctuations are dominant on timescales longer than those measured here (Fakhri et al., 2014; Guo et al., 2014), suggesting that such fluctuations are not the main source of the increased diffusivity we calculate.

We note it is possible that microtubule-independent mechanisms can contribute to the enhanced mobility we measure in metaphase cells. For instance, clusters of actin filaments polymerize and revolve around the cell cortex at angular velocities, corresponding to ~0.02 rad/s (Mitsushima et al., 2010). This could effectively ‘stir’ the cytoplasm and contribute to the increased mobility we measure during metaphase. Experiments combining active microrheology and chemical perturbations are needed to further dissect the origin of these random cytoplasmic forces that enhance metaphase cytoplasmic diffusibility (Almonacid et al., 2015; Guo et al., 2014; Mittasch et al., 2018).

Regardless of the origin, enhanced metaphase mobility can serve to ensure that mesoscale complexes are not trapped within the dense network of microtubules during cell division. Instead, microtubule-driven cytoplasmic fluctuations can mitigate the effects of hindered diffusion due to the dense network of filaments. Further, enhanced macromolecular mobility during cell division can limit the lifetimes of phase-separated compartments, which have been implicated in microtubule nucleation and organization during mitosis and meiosis (Jiang et al., 2015; So et al., 2019). Preserving an average diffusivity across a cell can help maintain internal biochemistry, even when there are clear heterogeneities in internal cellular architecture.

STAR METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Tarun M. Kapoor (kapoor@rockefeller.edu)

Materials Availability

The 40 nm-GEM expressing HeLa cell line generated for this study is available upon request from the lead contact with no restriction.

Data and Code Availability

Full datasets are available upon request from the lead contact with no restriction. Analysis scripts are available on github: https://github.com/CarliniLina/TrackAnalysis.git

EXPERIMENTAL MODELS AND SUBJECT DETAILS

Generation of cell line

HeLa cells were provided by the lab of Dr. Dafna Bar-Sagi at NYU Langone Medical Center and originally obtained and authenticated by short tandem repeat from the American Type Culture Collection as described previously (Ramirez et al., 2019). HeLa cell lines are derived from a female patient. Cells tested negative for mycoplasma at least every 3 months by PCR. HeLa cells were cultured in DMEM (LifeTechnologies) supplemented with 10% FBS (Sigma Aldrich) and incubated at 5% CO₂ at 37°C. Stable 40-nm GEM HeLa cell lines were created by lentiviral transduction with pLH1337-CMV-PfV-Sapphire-IRES-DsRed-WPRE (Delarue et al., 2018). In order to transduce these cell lines, 50,000 cells were plated in 2 mL of media in 6 well plates. The next day, media was removed and replaced with media containing 8 μg/mL polybrene. Between 1–20 μL of concentrated virus was added to the well and then the media was replaced after 24 hours. 40 nm-GEM expressing HeLa cells were maintained at 37°C under 5% CO₂, split every 2–3 days and kept in culture for a maximum of 10 passages. Cells were maintained in DMEM containing high glucose, L-glutamine and pyruvate (LifeTechnologies), supplemented with 10% Fetal Bovine Serum (FBS) (Sigma Aldrich).

METHODS DETAILS

Spinning disk confocal imaging and labelling

Cells were cultured on 22 mm glass coverslips (Fisher Scientific) 16–24 hrs before imaging. 20 min prior to imaging, cells were labelled with 200 nM SiR-DNA (Cytoskeleton) for 10 min or 50 nM SiR-Tubulin for 15 min, then washed twice with 1X PBS and once with Leibovitz L-15 medium (Gibco), supplemented with 10% FBS (Sigma Aldrich). Cells were mounted in a custom chamber and imaged at 37°C in Leibovitz, supplemented with 10% FBS. Imaging was performed on a Nikon Eclipse Ti2-E equipped with a Yokogawa W1 confocal scanning unit and 100X objective (Plan Apo, 1.45 NA). The GEMs and SiR-DNA channels were excited with a 100 mW 488 nm (Coherent) and 75 mW 640 nm (Coherent) laser respectively. Both lasers were transmitted to the sample using a custom Yokogawa quad notch filter (405-480-561-640) and fluorescence was filtered using an ET 520/40m (Chroma Technology) and ET 670/50m (Chroma Technology) for the GEMs and SiR-DNA channel respectively. Fluorescence was directed onto a Prime 95B sCMOS camera (Photometrics). For single particle tracking experiments, the GEMs channel was imaged continuously with a 10 ms camera integration time for a total of typically 5 s. Prior to imaging the GEMs channel, a snapshot of the SiR-DNA and DIC channels were acquired with a 100 ms camera integration time. All fluorescence images in figures display intensities linearly rescaled to image intensity maximum to enhance contrast.

Chemical inhibitor treatments

For nocodazole experiments, 33 μM of nocodazole (Sigma-Aldrich) was added to cells in Leibovitz L-15 medium (Thermo Fisher), supplemented with 10% Fetal Bovine Serum (FBS) (Sigma Aldrich). Immediately after addition of the drug, metaphase cells were identified on the microscope by SiR-DNA staining and stage positions were stored. 30–40 min after addition of the drug, a snapshot of the SiR-DNA and DIC channels were acquired (100 ms integration time), followed by a continuous acquisition of the GEMs channel for 5s (10 ms integration time). For nocodazole washout experiments, the drug was washed out 30 min after its addition. Cells were washed once with 1 X PBS and imaged in Leibovitz L-15 medium (Thermo Fisher), supplemented with 10% FBS (Sigma Aldrich).

For Taxol experiments, 10 nM of Taxol (Sigma) was added to cells in DMEM (Gibco) supplemented with 10% FBS (Sigma Aldrich) for 4 hrs. Imaging was performed in Leibovitz L-15 medium (Thermo Fisher), supplemented with 10% FBS (Sigma Aldrich) and 10 nM Taxol for up to 5 hrs (total) after the start of incubation with Taxol. For monastrol experiments, 10 μM of monastrol (Cayman) was added to cells for 4 hrs. Imaging was performed in Leibovitz L-15 medium (Thermo Fisher), supplemented with 10% FBS (Sigma Aldrich) and 10 μM monastrol for up to 5 hrs (total) after the start of incubation with monastrol.

Immunostaining

Cells were plated on 5 mm glass coverslips (Fisher, # 1.5) 24 hrs before fixation. Cells were fixed for 10 min in −20°C in methanol. Following this, cells were washed three times with 1X PBS (RT) and blocked for 2 hrs in 10% FBS (in 1X PBS). After blocking, cells were washed three times in 1X PBS and then stained with FITC-DM1α (1:500, Millipore Sigma) for 1 hr. Following antibody staining, cells were washed three times with 1X PBS. In the last wash, DAPI was added to 1X PBS at 0.5 μg/mL. Glass coverslips containing fixed cells were mounted on cover slides (Thermo Scientific) using 90% glycerol (Sigma-Aldrich), 0.5% n-propyl gallate (Sigma-Aldrich) and 20 nM Tris (Sigma-Aldrich) pH 8.0.

Transient transfections

For experiments where transient transfections were performed (Figures S2E, S4K), cells were plated on 22 mm glass coverslips (Fisher Scientific) 24 hrs before imaging and immediately transfected with 400 ng of plasmid (EB3-tdTomato, addgene plasmid #50708 OR pLH1194-pcDNA3.1-AqLS-Sapphire for expression of 20 nm-GEMs) and 1.2 μL of Fugene HD (promega) in opti-MEM (Gibco).

QUANTIFICATION AND STATISTICAL ANALYSIS

Single-particle localization and tracking

GEMs were localized in TrackMate (Tinevez et al., 2017). Particle signal was enhanced using a LoG (Laplacian of Gaussian) and median filter with an estimated diameter of 4 pixels (or 440 nm). The quality threshold was set to 2 to eliminate spurious, typically dim (SNR<2), localizations. Single particle tracking was performed using the simple LAP tracker adapted from (Jaqaman et al., 2008), and implemented into TrackMate. Localizations were assigned to the same trajectory if they are present in consecutive frames and have traversed a maximum distance r, typically 8 pixels (880 nm). This maximum distance, r was adjusted according to particle density of the dataset to ensure that the distribution of particle displacements did not overlap with the distribution of nearest neighbor distances.

Generation of time projection map

To generate the average time projection map in Fig. 1E, time projection images of individual cells were normalized to their maximum intensity and rotated to ensure the axis corresponding to the metaphase plate (spindle’s short axis) was aligned to the horizontal axis of the image. Next, aligned images were translated to ensure all cell centers were co-localized. For each image, a list of points was generated, containing the cell’s normalized polar coordinates (i.e. normalized radius and angle between 0–360 degrees relative to the horizontal image axis) and corresponding normalized intensity value. Using MATLAB’s meshgrid function, an image grid was generated, where the value at each unit of the grid corresponded to the average normalized intensity at its location.

Mean squared displacement (MSD) analysis

The MSD versus time delay plot was generated for individual trajectories using the msdanalyzer (Tarantino et al., 2014). To extract the effective diffusivity for individual trajectories, we used trajectories with a minimum of 10 points (on the MSD vs τ plot) and fit the MSD versus time delay plot using the linear relationship, MSD(τ) = 2dD_effτ+c, where τ is the time delay, d is the dimension (d=2) and c is a constant. For trajectories made up of more than 10 points, only the first 10 points of the MSD versus time delay plot were used for fitting. To calculate the ensemble average effective diffusivity (Figures 2 A, B, 4B), we generated average MSD versus time delay plots for all cell data and performed a linear fit as above. As a complementary measurement to the non-Gaussian parameter, we calculated the anomalous exponent, γ according to: MSD(τ) = Cτ^γ, where C is a constant. To fit, ensemble average MSD versus time delay plots (from multiple cells) were used with time delays τ ranging between 10–500 ms. All curve fitting was performed in MATLAB using the curve fitting tool. A maximum time delay of 500 ms was chosen to obtain a more robust fit to a power law. In Taxol-treated metaphase cells, we measured more strongly confined motion (γ < 1) relative to control cells (Table S1). This higher proportion of confined particles across this 500 ms timescale may account for the increased non-Gaussian parameter we measured for all time delays in Taxol-treated cells. Explicitly, a population consisting of confined and unconfined particles could yield a non-Gaussian distribution of displacements.

Particle displacement calculation

Particle displacements at a time delay were calculated according to: $\widehat{d}(t;\tau )=\widehat{x}\left(t+\tau \right)-\widehat{x}(t)$, where $\widehat{x}(t)$ is a vector representing particle localizations at time t. All displacements were pooled to generate distributions of particle displacements.

Directional change calculation

Subsequent localizations, separated by time delay τ =10 ms, in a given trajectory were paired to make up vectors, $\widehat{v}(t;\tau )$, according to: $\widehat{v}(t;\tau )=\widehat{x}(t+\tau )-\widehat{x}(t)$, where $\widehat{x}(t)$ is a vector representing particle localizations at time t. The angle between subsequent vectors was calculated according to:

$$\text{cos}\theta (t;\tau )=\frac{\widehat{v}(t;\tau )\cdot \widehat{v}(t+\tau ;\tau )}{\left|\widehat{v}(t;\tau )\right|\left|\widehat{v}(t+\tau ;\tau )\right|}.$$

See Fig. S4G for schematic showing θ.

Non-Gaussian parameter calculation

The 1-D non-Gaussian parameter (α₂) was computed for a given time delay (τ) as:

$${\alpha }_2(\tau )=\frac{\langle \Delta r{(\tau )}^4\rangle }{3<\Delta r{(\tau )}^2{>}^2}-1,$$

where Δr is the particle displacement, or step size, and <> denotes an average over the distribution. For analyses where α₂ was computed for directions parallel or perpendicular to the spindle’s long axis (Fig. S3B), a transformation was initially defined to ensure that the by the chromatin signal (or metaphase plate) was oriented horizontally (x-direction). This transformation, defined by a rotation and translation, was next applied to the trajectories. This ensured that all displacements had components parallel (y) and perpendicular (x) to the spindle long axis. We note that this parameter cannot specify the type of particle motion, but instead indicates whether a displacement distribution contains an increased or decreased proportion of large steps relative to a normal distribution with the same variance. For example, the increased α₂ we measure along the spindle’s long axis and within the spindle could reflect an increased proportion of large displacements due to the growth of microtubules in this region (Fig. S2F–H); this is consistent with previous measurements, indicating that GFP and dextrans are more mobile along the spindle’s long axis compared to its short axis (Pawar et al., 2014). We also measure increases in the non-Gaussian parameter in Taxol- and nocodazole-treated cells (Fig. 3,4, S3). This result could reflect the increase in the proportion of confined (or slower diffusing) particles, consistent with independent measurements (Fig. S3,4). Mixing displacement distributions from confined and unconfined particles could result in non-Gaussian distributions of displacements.

Radii of gyration calculation

Each trajectory’s radius of gyration (R_g) was computed as previously described (Elliott et al., 2011; Notelaers et al., 2014). Briefly, an ellipse which covers the spatial extent of each trajectory over its lifetime was computed using the trajectory’s gyration tensor, $\widehat{T}.\widehat{T}$ is calculated according to:

$$\left[\begin{array}{cc}\frac{1}{N}{\sum }_{i=1}^N{\left(x_i-\langle x\rangle \right)}^2& \frac{1}{N}{\sum }_{i=1}^N\left(x_i-\langle x\rangle \right)\left(y_i-\langle y\rangle \right)\\ \frac{1}{N}{\sum }_{i=1}^N\left(x_i-\langle x\rangle \right)\left(y_i-\langle y\rangle \right)& \frac{1}{N}{\sum }_{i=1}^N{\left(y_i-\langle y\rangle \right)}^2\end{array}\right],$$

where N is the number of localizations in a trajectory and <x> (<y>) is the average position in x (y) over the full trajectory and i is the localization index. The eigenvalues of the gyration tensor represent the principal axes of an ellipse with magnitudes R_a (major axis) and R_b (minor axis).R_g was then computed according to: R_g² = R_a² + R_b².

Statistics

Non-normality of distributions was examined by the Kolmogorov-Smirnov test built into MATLAB. As non-normality was confirmed by this test, we used the non-parametric Kruskal-Wallis test in MATLAB. A p-value <0.05 was considered significant and denoted by ‘*’. Values of p<0.01, p<0.001 and p<0.0001 were denoted by ‘**’, ‘***’ and ‘****’ respectively. See figure legends for statistical details (exact values of N, definition of dispersion measures and center values). When directly comparing distributions of diffusivity, statistics were identical between the two distributions. To do this, values were randomly selected from the population with larger statistics. We also ensured this did not significantly alter p-value results by running the Kruskal-Wallis test with distributions of unequal statistics. When bootstrapping (random sampling with replacement) was performed, 10 000 iterations were used.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Mouse monoclonal DM1alpha-FITC	Sigma-Aldrich	Cat#F2168
Chemicals, Peptides, and Recombinant Proteins
Nocodazole	Sigma-Aldrich	Cat# 31430-18-9
Monastrol	Cayman	Cat# 329689-23-8
Taxol	Sigma-Aldrich	Cat# 33069-62-4
SiR-Tubulin	Cytoskeleton	Cat# CY-SC002
SiR-DNA	Cytoskeleton	Cat# CY-SC007
DAPI	Sigma-Aldrich	Cat# 28718-90-3
Fetal bovine serum (FBS)	Sigma-Aldrich	Cat# F7678
DMSO molecular biology grade	Sigma-Aldrich	Cat#41639
DPBS (No Calcium, No Magnesium)	VWR international	Cat# 14190–250
Leibovitz’s L-15 medium	Thermo Fisher	Cat# 11415064
DMEM	Life Technologies	Cat# 11995–073
Fugene HD	Promega	Cat# E2311
Opti-MEM	Gibco	Cat# 31-985-062
n-propyl gallate	Fisher Scientific	Cat# 121-79-9
glycerol	Fisher Scientific	Cat# G33500
Tris	Fisher Scientific	Cat#BP1521
MeOH	Thermo Fisher	Cat#A412500
Experimental Models: Cell Lines
40 nm-GEM expressing HeLa	This paper	N/A
HeLa cells	(Ramirez et al., 2019)	ATCC CCL-2
Recombinant DNA
EB3-tdTomato	(Merriam et al., 2013)	Addgene plasmid # 50708
pLH1194-pcDNA3.1-AqLS-Sapphire	(Delarue et al., 2018)	N/A
pLH1337-CMV-PfV-Sapphire-IRES-DsRed-WPRE	(Delarue et al., 2018)	N/A
Software and Algorithms
MATLAB 2018b	Mathworks (2018)	https://www.mathworks.com/products/matlab.html
FIJI (FIJI is just imageJ)	(Schindelin et al., 2012)	https://fiji.sc/
Trackmate for ImageJ	(Tinevez et al., 2017)	https://imagej.net/TrackMate
MSDanalyzer	(Tarantino et al., 2014)	https://tinevez.github.io/msdanalyzer/
Post-tracking analysis	This study	https://github.com/CarliniLina/TrackAnalysis.git

Highlights.

• Tracking of 40 nm nanoparticles is performed at 100 Hz across dividing cells

• Diffusivity (D_eff) is similar inside and around the dense metaphase spindle

• Depolymerizing metaphase microtubules leads to a decrease in D_eff

• Perturbing metaphase microtubule polymerization dynamics leads to a decrease in D_eff