Validation of Free Energy Methods in AMBER

Abstract

Herein we provide high precision validation tests of the latest GPU-accelerated free energy code in AMBER. We demonstrate that consistent free energy results are obtained in both the gas phase and in solution. We first show, in the context of thermodynamic integration (TI), that results are invariant with respect to “split” (e.g., stepwise decharge-vdW-recharge) versus “unified” protocols. This brought to light a subtle inconsistency in previous versions of AMBER that was traced to the improper treatment of 1-4 vdW and electrostatic interactions involving atoms across the softcore boundary. We illustrate that, under the assumption that the ensembles produced by different legs of the alchemical transformation between molecules “A” and “B” in the gas phase and aqueous phase are very small, the inconsistency on the relative hydration free energy ΔΔG_hydr[A → B] = ΔG_(aq)[A → B] − ΔG_(gas)[A → B] is minimal. However, for general cases where the ensembles are shown to be substantially different, as expected in ligand-protein binding applications, these errors can be large. Finally, we demonstrate that results for relative hydration free energy simulations are independent of TI or multistate Bennett’s acceptance ratio (MBAR) analysis, invariant to the specific choice of the softcore region, and agree with results derived from absolute hydration free energy values.

Graphical Abstract

Alchemical free energy simulations are widely used for many computational biophysics and drug discovery applications.^1–3 The recent development of GPU-accelerated free energy methods^4–7 have enabled free energy simulations to be performed with sufficient precision to rigorously stress test implementations for consistency, reproducibility and reliability. This, along with the development of rich datasets of solvation,⁸ absolute⁹ and relative ligand binding free energies^10–12 for drug discovery,^13,14 is vitally important to ensure the predictive capability of these methods, particularly for computational lead optimization where candidate ligands may differ in their relative binding affinity by less than 0.5 kcal/mol.

Recently, a study by Loeffler and co-workers¹⁵ compared the reproducibility of free energy calculations across different widely used molecular simulation software packages. In this work, it was brought to light that some calculations using AMBER16 did not produce internally consistent results. Herein we establish rigorous validation of free energy methods in the updated version of AMBER using the same data set of molecules and transformations (chosen in part to avoid complex sampling and allow high precision to be achieved) and extending the scope of analysis. We illustrate the source of reported inconsistent behavior in AMBER16, and demonstrate consistency of results to less than 0.1 kcal/mol with AMBER18 (and also the most recent AMBER20 release¹⁶). It is the hope that the benchmarks and protocols reported here will be instrumental to a broad community for the validation and practical application of other free energy methods and simulation software.

We first examine the test set of molecules illustrated by Loeffler et al.,¹⁵ and using their procedures, demonstrate that inconsistencies in “split” versus “unified” protocols observed with versions of AMBER prior to AMBER18 (designated pA18) no longer exist in AMBER18 with patch updates (designated A18*) and the most recent AMBER20 release.¹⁶ For the unified protocol, both electrostatic (Ele) and van der Waals (vdW) interactions are scaled simultaneously using softcore potentials from real atoms that are transformed into dummy atoms (or vice versa). The unified protocol is also sometimes referred to as a “single-step” or “one-step” transformation. Different from the unified protocol, are so-called “split”, or alternatively “multi-step”, “stepwise” or “decoupled” procedures.¹⁷ In these procedures, all or parts of the Ele and vdW transformations are decoupled, and performed as separate steps. The split protocol that is described by Loeffler et al. ¹⁵ is a 2-step procedure used in the present work to provide a direct comparison. Later in the paper, we adopt a 3-step “decharge-vdW-recharge” split protocol, whereby the atoms in the softcore region (those atoms that will transform into dummy atoms) are first decharged. Next, these decharged atoms undergo a vdW transformation using softcore potentials, and last, the atoms are recharged to the final state. Herein, we use the terms “unified” and “split” so as to be consistent with those used in the Loeffler et al.¹⁵ work, although in subsequent work we prefer the terms “concerted” and “stepwise”.

In the discussion that follows, we separate the atoms involved in the alchemical transformation into two regions: the softcore region, and the common core region. The common core atoms are those that transform from a “real atom” in the initial state to another real atom in the final state, and in intermediate λ states, interact with other (non-softcore) atoms via normal van der Waals (vdW) and electrostatic (Ele) interactions. The softcore atoms, on the other hand, are those selected to interact with other atoms (including the common core atoms) via a softcore potential¹⁸ in intermediate λ states. Often the atoms of the softcore region are transformed from “real atoms” in the pure state to “dummy atoms” in the final state. A discussion of the requirements that the dummy atoms reproduce the ensemble and potential of mean force of the real state has been discussed extensively by Boresch and Karplus^19,20 and Roux and co-workers.^21,22

All calculations presented here were performed with the latest update version of the AMBER18 GPU code, pmemd.cuda (simulation details are provided in the Supporting Information). This latest updated version has been modified from the original AMBER18 release⁶ by us to fix several problems we uncovered, including the treatment of 1-4 vdW and electrostatic interactions involving atoms in the “softcore” region. Flags have been added that enable reproduction of free energy simulation results from previous GPU and CPU versions of pmemd. The main differences between pA18 and A18* is in the treatment of interactions between atoms of the softcore and common core region is summarized in the Supporting Information (Table S1). Of particular note is that in pA18, there 1-4 vdW and Ele terms across the softcore boundary are present at full strength (i.e., not scaled by λ, and thus wrong) whereas A18* these interactions are correctly scaled by λ. This difference affects both sampling, thermodynamic derivatives and end states.

In the analysis below, we will examine the absolute hydration free energy, ΔG_hydr, of a molecule “A” defined as

$$\Delta G_{\mathit{hydr}}[A]=G_{(\mathit{aq})}[A]-G_{(\mathit{gas})}[A]$$ (1)

and the relative hydration free energy between molecules “A” and “B”

$$\Delta \Delta G_{\mathit{hydr}}[A\to B]=\Delta G_{\mathit{hydr}}[B]-\Delta G_{\mathit{hydr}}[A]=\Delta G_{(\mathit{aq})}[A\to B]-\Delta G_{(\mathit{gas})}[A\to B]$$ (2)

where ΔG_(aq)[A → B] = G_(aq)[B] − G_(aq)[A] and ΔG_(gas)[A → B] = G_(gas)[B] − G_(gas)[A]. In the discussion that follows, we will compute absolute and relative free energy values using a TI formulation,²³ as well as a thermodynamic perturbation (TP) formulation²⁴ with Bennett’s acceptance ratio²⁵ analysis and its multistate generalization.²⁶ In order to facilitate comparison of the relative hydration free energy values obtained from direct alchemical transformations to differences in absolute hydration free energy values computed independently, we will generate benchmark data for the latter using a split protocol and analyzed using BAR²⁵ (see Supporting Information, Table S2), as we find this to be generally the most robust protocol for the data set considered here.

Comparison of past and current versions of AMBER for hydration free energies

Following the procedures described by Loeffler et al.,¹⁵ we examine a set of 9 alchemical free energy transformations to obtain relative hydration free energy values, and analyzed the degree to which ΔG_(aq) and ΔG_(gas) values agree using unified and split protocols. The results are summarized in Fig. 1 (details are provided in Supporting Information, Tables S3 and S4). Whereas the pAl8 results show very poor correlation (R² ~ 0.3 − 0.6) and large variation (σ ~ 5.8 kcal/mol), the A18* results are in very close agreement (R² ~ 1.0, σ ~ 0.02 kcal/mol).

Figure 1:

Comparison of ΔG_(aq) and ΔG_(gas) values (designated generically as ΔG on the axis labels) using unified and split protocols for nine transformations tabulated in Tables S3 and S4. a) Simulations using pre-AMBER18 (pA18) with values listed in Table S3, and b) current updated AMBER18 (A18*) with values listed in Table S4.

While the values for ΔG_(aq) and ΔG_(gas) obtained with pAl8 clearly are inconsistent and in error, the overall ΔΔG_hydr values are in much closer agreement (Tables S3 and S4). This is due to the fact that, for the small and conformationally restricted molecules considered here and by Loeffler et al.,¹⁵ the ensembles generated in the gas phase and in solution are quite similar. As a consequence, the contributions from the 1-4 vdW and electrostatic terms between the softcore and common core atoms in the aqueous and gas phases largely cancel one another.

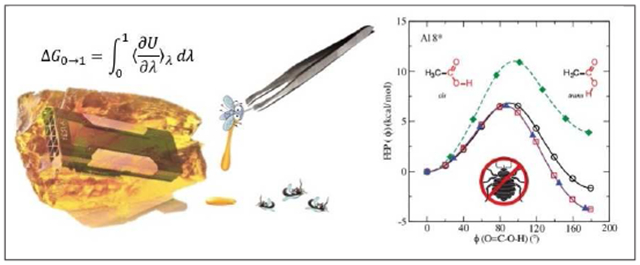
As a specific example, consider the relative hydration free energy between acetic acid and acetaldehyde. Acetic acid is well known to have a different orientation of the titratable proton in the gas and aqueous phases.²⁷ In the gas phase, the proton makes an internal 1-4 hydrogen bond with the opposite carboxylic acid oxygen (a roughly 0°, cis configuration about the O=C-O-H torsion angle). In solution, this proton prefers to occupy a roughly 180°, trans configuration, which has an enhanced dipole moment (here, note that our reference to cis and trans is with reference to the O=C-O-H torsion angle, and not the R-C-O-H torsion angle).

Figure 2 shows the free energy profiles (computed using umbrella sampling simulations, see Supporting Information for details) along the O=C-O-H torsion angle coordinate for pAl8 and A18* in both the “real state” (λ=0) and the “dummy state” (λ=1). The profiles for the real states (λ=0) are identical between pA18 and A18*, with the cis configuration being favored by 3.8 kcal/mol in the gas phase, and the trans configuration being favored by 1.6 kcal/mol in aqueous solution. In both cases, there is a significant barrier (over 5 kcal/mol) separating the cis and trans configurations. Unlike the real state, the free energy profiles for the dummy (λ=1) states are markedly different between pA18 and A18*. We expect the dummy states in the gas phase and in solution to be identical, as there is no interaction of the acetic acid with the surroundings for λ=1. We further expect that the free energy profiles of the λ=1 state differ from that of the real λ=0 state in the gas phase, as the internal energy should have 1-4 vdW and electrostatic terms between the softcore and common core regions that are λ-dependent (i.e., scaled by λ). Whereas this is indeed the case for A18*, it is not the case for pA18. In the case of pA18, the profiles of the dummy state exactly match those of the real state in the gas phase. This derives from the fact that pA18 does not scale the 1-4 vdW and electrostatic interactions between the softcore and common core regions (Supporting Information, Table S1), and thus has the same energy and forces as the real state in the gas phase.

Figure 2:

Free energy profiles (FEPs) for acetic acid along O=C-O-H torsion angle (ϕ) in the gas phase and in solution for both real (λ=0) and dummy (λ=1) states. a) FEPs computed using pA18. b) FEPs computed using A18*. Torsion angle (ϕ) values of 0° represent cis proton configuration, and 180° represent trans proton configuration.

Sampling the proper O=C-O-H torsion angle distributions, whether in the real state or the dummy state, is challenging.²⁷ Here, we adopt a procedure for rigorously taking into account the appropriate predicted distributions as determined by the computed FEPs in Fig. 2b (see Supporting Information for details). When sampling of these distributions is accounted for, it is clear that pA18 produces qualitatively incorrect ΔΔG_hydr values for both the unified and split protocols, whereas A18* have ΔΔG_hydr values with either protocol that are in agreement with one another, and with the reference values derived from absolute hydration free energy calculations. While this benchmark demonstration was for the relative hydration free energy of two simple molecules, the issue is even more relevant for the calculation of relative binding free energies of more complex ligands when the conformational ensemble of the ligand in solution changes upon binding to the protein.¹³

Comparison of relative and absolute hydration free energies with TI and MBAR

As the free energy is a state function, free energy changes are formally independent of the pathway chosen to connect states, as would be affected by the specific transformation protocol and choice of softcore region, and also independent of the thermodynamic integration or perturbation formalism used for analysis. In practice, however, these choices often have a profound effect on the amount of sampling required to achieve a target degree of statistical precision. To show consistency of the free energy methods, we compare precise benchmark results derived from absolute hydration free energy calculations with those for relative hydration free energy values using both unified and split protocols, two different softcore regions, and using alternatively a TI²³ and TP²⁴+MBAR^25,26 formalism. In the previous sections, results were shown for transformations where the softcore region was determined in accord with the procedures used by Loeffler et al.,¹⁵ with the strategy to minimize the number of unpaired atoms as the softcore region and maximize the common substructure (i.e., the number of common core atoms). Alternately, we consider a second choice of softcore atoms based on grouping softcore atoms into chemical functional groups. We designate these choices of the softcore region as “softcore region 1” and “softcore region 2”, respectively.

Detailed comparison of results for different softcore regions with both TI and TP+MBAR are provided in the Supporting Information (Figure S2, and Tables S6,S7). Overall, all of the relative hydration free energy values agree closely with the reference values obtained from the absolute hydration free energies. It should be noted that, formally, care should be taken that the bonded terms connecting the softcore atoms to the common core region obey certain constraints and conditions^19–22 in order that the ensembles generated in the state that contains “dummy atoms” reproduce the same potential of mean force on the real atoms as the real system without the dummy atoms. We considered these terms in an explicit correction step by eliminating all but a subset of bonded terms obeying the theoretical constraints. In all cases, the magnitude of this contribution was found to be well below the sampling precision (typically less than 0.1 kcal/mol), and hence the corrections are not statistically significant.

Comparison of the results using different softcore regions suggest that the softcore region 2 leads to slightly smaller average estimated errors (0.02-0.03 kcal/mol) relative to softcore region 1 (0.04-0.11 kcal/mol). The latter range is dominated by the methanol→ethane transformation, which has two of the H atoms on ethane as the softcore region 1. During the transformation, the negative charge of the methanol O atom causes H atoms of the TIP3P water molecules, which lack Lennard-Jones repulsive terms, to closely approach the softcore H atoms of the ethane molecule. This results in a sharp spike in the thermodynamic derivative that leads to numerical integration errors (see Supporting Information, Figure S3). The problem persists with use of the split protocol since the charges of the ethane H atoms (0.031 e) are already almost decharged, making the unified and split procedures almost identical. The same transformation using softcore region 2 has the -CH₃ group in ethane and the -OH group in methanol as the softcore regions. Using this functional group approach, there are no softcore transformations involving H atoms that do not also consider at the same time the heavy atoms to which they are covalently attached.

Excluding the methanol→ethane transformation (softcore region 1) outlier above, overall the statistical precision for softcore region 2 is still higher (smaller statistical errors) than for softcore region 1 using either unified or split protocols (Tables S6 and S7 of Supporting Information). This arises from smaller fluctuations of the quantities being averaged to obtain the thermodynamic estimates using the functional group softcore approach with the present data set. Results derived from TI and TP+MBAR are quite similar (typically less than 0.05 kcal/mol), with the greatest deviation occurring for the outlier mentioned above.

CONCLUSION

Herein we provide a comparison of the consistency of alchemical transformations of relative and absolute hydration free energies in updated AMBER18 (and recently released AMBER20). We demonstrate that free energy results are internally consistent to typically 0.1 kcal/mol or better, independent of unified versus split protocol, choice of softcore region, and TI versus TP+MBAR analysis. We further illustrate the need for proper treatment of λ-dependence of 1-4 van der Waals and electrostatic interactions between the softcore and common core atoms for general cases. The benchmark data provided herein will be valuable for the testing of new methods and implementations of tools for conducting and analyzing alchemical free energy simulations.

Table 1:

Comparison of relative hydration free energy values (kcal/mol) for methanol→ethane and acetic acid→acetaldehyde transformations calculated by split and unified protocols in pre-AMBER18 (pA18) and updated AMBER18 (A18*)^a

		ΔGaq		ΔGgas		ΔΔGhydr
Transformation	AMBER Version	Unified	Split	Unified	Split	Unified	Split	Δ Absb
methanol→ethane	pA18	2.21(04)	2.85(04)	−3.99(03)	−3.35(03)	6.20(04)	6.20(04)	6.23(03)
	A18*	3.04(04)	3.03(04)	−3.16(03)	−3.16(03)	6.20(04)	6.19(04)	6.23(03)
acetic acid→acetaldehyde	pA18	−9.15(04)	32.83(04)	−15.64(04)	26.41(04)	6.49(05)	6.42(05)	4.80(06)
	A18*	38.65(03)	38.63(03)	33.83(03)	33.83(03)	4.82(04)	4.80(04)	4.80(06)

^aThe hydration free energy values were obtained by unified and split protocols using softcore region 2 and analyzed using the TI method. Standard errors are shown in parentheses (multiplied by 10²). Relative hydration free energy values were obtained by differences of absolute hydration free energies between the real end state molecules. The absolute hydration free energies were obtained with the split protocol and analyzed by BAR.