Using quantum chemistry to estimate chemical shifts in biomolecules

Abstract

An automated fragmentation quantum mechanics/molecular mechanics approach (AFNMR) has shown promising results in chemical shift calculations for biomolecules. Sample results for ubiquitin, and an RNA hairpin and helix are presented, and used to recent directions in quantum calculations. Trends in chemical shift are stable with regards to change in density functional or basis sets, and the use of the small “pcSseg-0” basis, which was optimized for chemical shift prediction,[1] opens the way to more extensive conformational averaging, which can often be necessary, even for fairly well-defined structures.

1. Introduction

Nuclear magnetic resonance (NMR) spectroscopy plays an important role in the determination of three dimensional structural ensembles of macromolecules. In principle, but not so much in practice, chemical shifts could provide important information here: they provide sensitive local probes at almost every location, and (in the common case of fast exchange) are averaged in a simple additive way over the molecule’s conformational ensemble. As an electronic structure property, they report on a large number environmental factors, such as the conformation of neighboring residues, hydrogen bonding, ring-current effects, and long-range electrostatics [2–4]. A robust understanding of the connection between structure and chemical shifts could help in characterizing protein and nucleic acid structure and dynamics.

One obvious, and well-studied, approach seeks to train predictors using the large number of observed shifts collected in the BioMagResBank,[5] associating these values in some way with the structures that serve as input to the calculations.[6–12] One limitation here is that the (conformationally-averaged) structures that give rise to observed shifts are almost never known at the level of detail and precision that one might like. This can be addressed to some extent by using quantum chemical calculations in place of, or in addition to, observed shifts as input to the training procedure.[13, 14] This eliminates uncertainty about the connection between the structure and the computed chemical shift, but at the cost of losing the effects of conformational averaging that is encoded in observed shifts. A third approach, analyzed here, tries to estimate shifts directly from assumed ensembles of input structures, using established quantum chemical procedures to compute the shifts. This clearly requires procedures that are sufficiently accurate, affordable and automated to allow practical calculations to be carried out.

NMR chemical shifts describe the electronic response of a molecule to magnetic fields arising from the spectrometer and from nuclear magnetic moments. Methods and computer codes to carry out such calculations at various levels of theory are well-established.[15] Density functional theory provides a computationally straightforward way to incorporate some important effects beyond the Hartree-Fock approximation, in a manner efficient enough to be applied to molecules or fragments containing one to two hundred atoms. Since proteins and nucleic acids are too big for routine application of quantum chemical methods, fragmentation approaches that divide the system into (generally overlapping) fragments are attractive, particularly for local properties like chemical shifts. This paper gives an short overview of some recent results using one such method (“AFNMR”), setting the stage for what may be a new generation of studies that use quantum chemistry directly to interpret biomolecular chemical shifts.

2. The automated fragmentation (AFNMR) method

The AFNMR model [16–18] takes the entire protein and solvent effect into consideration, while limiting the size of the quantum region, as described in Fig. 1. Overlapping fragments are used to break the larger problem into pieces, and the electrostatic effects of the solvent and the remaining parts of the biomolecule are computed using a Poisson-Boltzmann procedure implemented in the MEAD package.[19, 20] This uses a three-dielectric model, with ε = 1 for the quantum region, ε = 4 for the remainder of the biomolecule, and ε = 78 for the solvent region. Fitting these to point charges surrounding the molecule allows for easy incorporation into most quantum chemical programs. The AFNMR code creates input files for Gaussian,[21] ORCA,[22] QChem[23] and deMon;[24] once the quantum calculations are complete, it parses their outputs, assembling results for the entire molecule in a convenient format. Further details are given elsewhere.[17] This implementation is not unique, and similar results have been reported by others.[25–29] The automatic fragmentation method used here was first made available for general use in 2015,[17] and has been applied to a fair number of problems in proteins and nucleic acids.[30–38] The code is available at https://github.com/dacase/afnmr.

Figure 1:

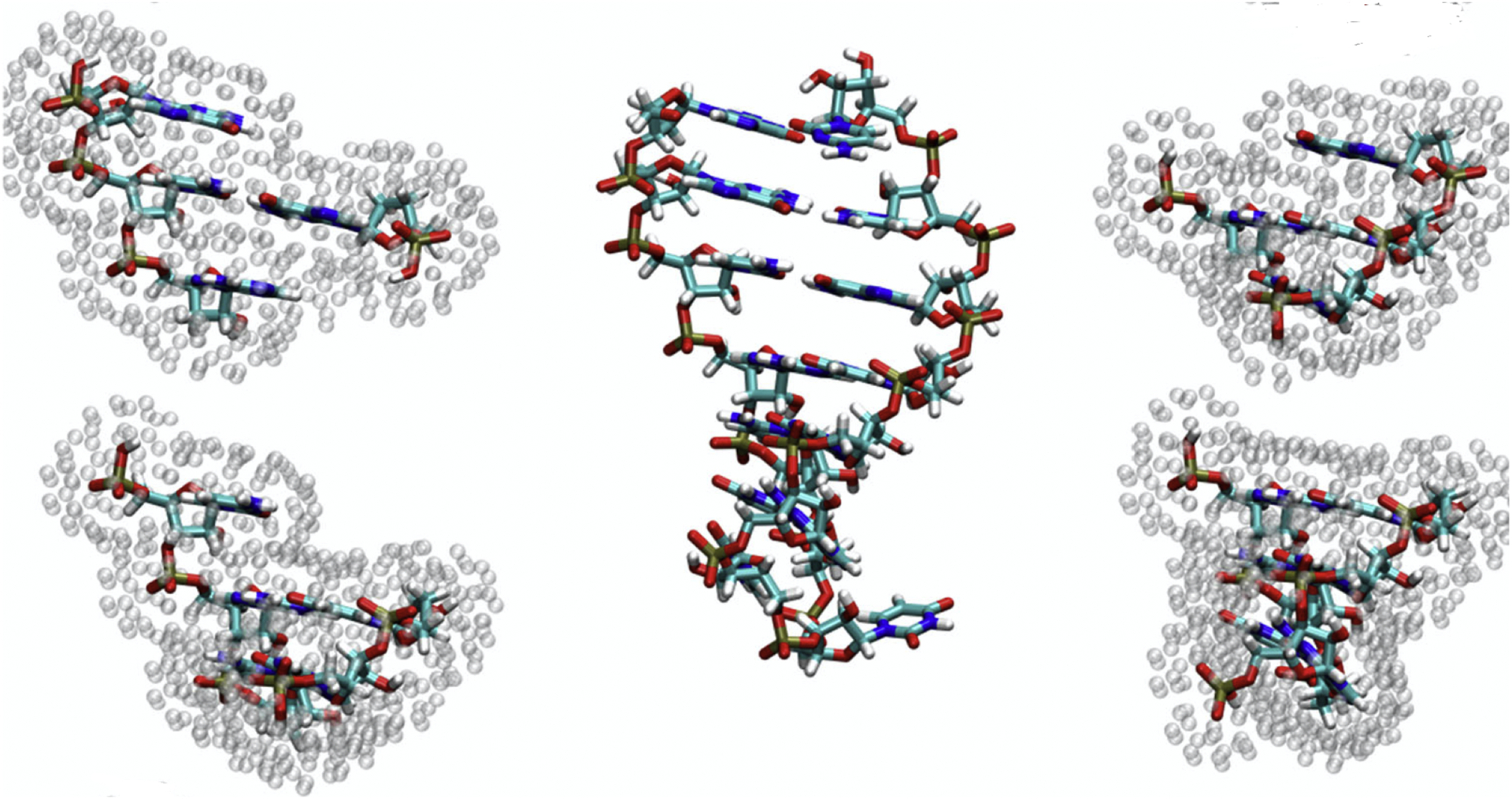
AFNMR model for an RNA hairpin. The solute (RNA) molecule is illustrated in the center. A local fragment is constructed centered on each nucleotide (or amino acid for proteins); four such fragments are illustrated at on the left and right. The atoms shown for each fragment form the quantum region, and point charges surrounding each fragment are used to represent the electrostatic effects arising from the remaining RNA atoms (which result from Amber charges embedded in the dielectric of ε = 4), and effects of solvent (represented by a dielectric ε = 78 and a Debye-Huckel ionic strength taken as 0.1M by default).

3. Some illustrative results

In the limited space available here, I will discuss some results from three systems where NMR solution structures have been generated from conventional restraints in combination with a large number of residual dipolar couplings. The first is an RNA hairpin closed by a UUCG tetraloop (PDB ID 2koc);[39–41] the second is a helix from the ψ⁷⁴⁶ element in E. coli (PDB ID 2gbh);[42–44] and the third the monomeric form of ubiquitin (PDB ID 1d3z).[45, 46] Results are chosen to illustrate particular issues that arise in the calculations, rather than for how informative they are with respect to the structures themselves. Unless otherwise noted, all calculations used the OLYP functional[47] and the psSseg-n basis sets.[1].

3.1. A UUCG RNA hairpin

This 14-nucleotide UUCG hairpin (PDB ID 2koc[39] has long served as a paradigm of a small RNA structure. In addition to a large number of NMR restraints, the chemical shift list is quite complete, and includes shifts for protons bonded to nitrogen and oxygen as well as to carbon. We reported some results for this system in the original AFNMR paper;[17] since then, we have generally moved to using the pcSseg-n basis sets optimized for chemical shielding calculations.[1] The smallest of these sets (called pcSseg-0) is at the double-zeta level with no polarization functions; the next larger (pcSseg-1) is at the [2s,1p] level for hydrogen, and the [3s,3p,1d] level for first-row atoms. Fig. 2 shows that trends in shifts, which are of primary importance in biomolecular studies, are nearly the same with the two basis sets. The main exception is for protons bonded to nitrogen or oxygen (HO2’, H41/H42, H61/H62, H1, H3), which have smaller shifts in the smaller basis set. Even here, trends for a given type of proton are nearly the same. Calculations for single structures of 2koc (taken from the deposited NMR set) at the pcSseg-2 level are nearly identical to those at the pcSseg-1 level (results not shown, but similar calculations on ubiquitin are discussed below.)

Figure 2:

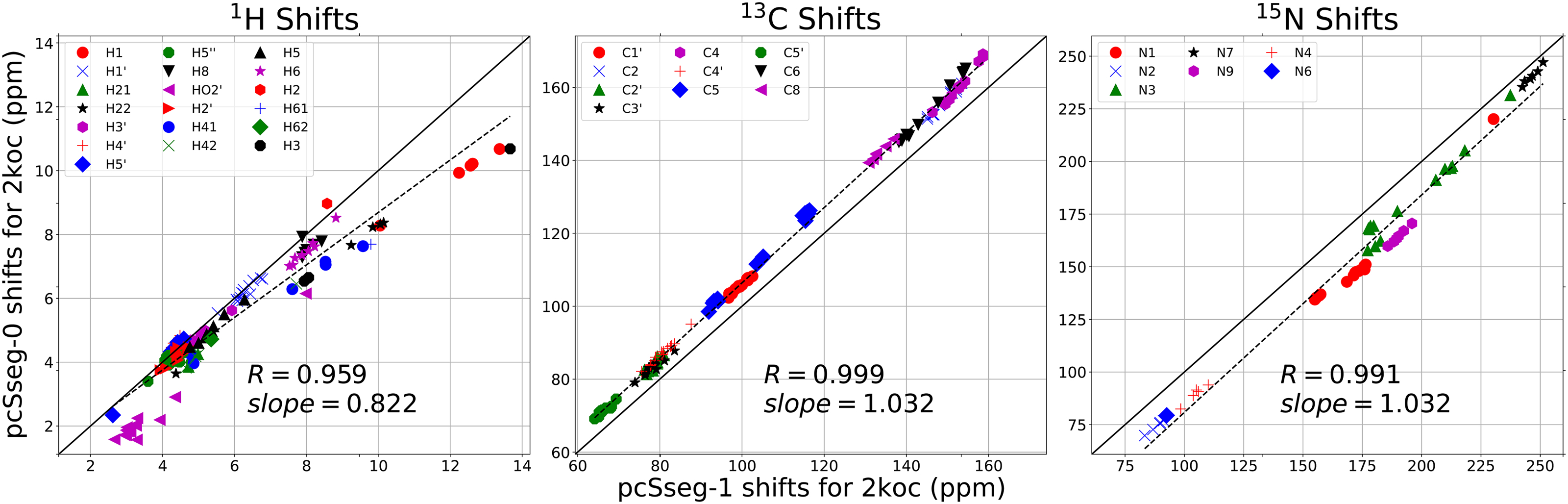
Average shifts in the 10 NMR structures from pdb ID 2koc. Calculations carried out with the deMon 5.0 code, using the OLYP functional and either the pcSseg-0 or pcSseg-1 basis sets.

The pcSseg-0 basis is about 5 times faster than pcSseg-1 using the deMon program, with the average fragment requiring 14 minutes on a single core of an Intel E5-2695 CPU. Since the fragment calculations are independent, all 14 fragments for a given conformation can be computed at the same time on a single CPU. This allows one to analyze 100 RNA conformations per day on a single CPU, allowing for much more extensive sampling than has been the case in the past. The smaller basis is also less prone to convergence failures, whereas about 1% of fragments analyzed at the pcSseg-1 level failed to converge, requiring hand intervention to tweak SCF convergence parameters.

Fig.3 compares computed and experimental shifts at the pcSseg-1 level. Even with the larger basis, results for protons bonded to nitrogen and oxygen are not well-predicted. It is known that the continuum electrostatic model for solvent does not faithfully capture the effects of hydrogen bonds to solvent molecules,[3, 48], and explicit solvent molecules are probably required for these protons. The use of explicit water molecules introduces a new set of challenges for conformational modeling; one approach is discussed in Section 3.3, below.

Figure 3:

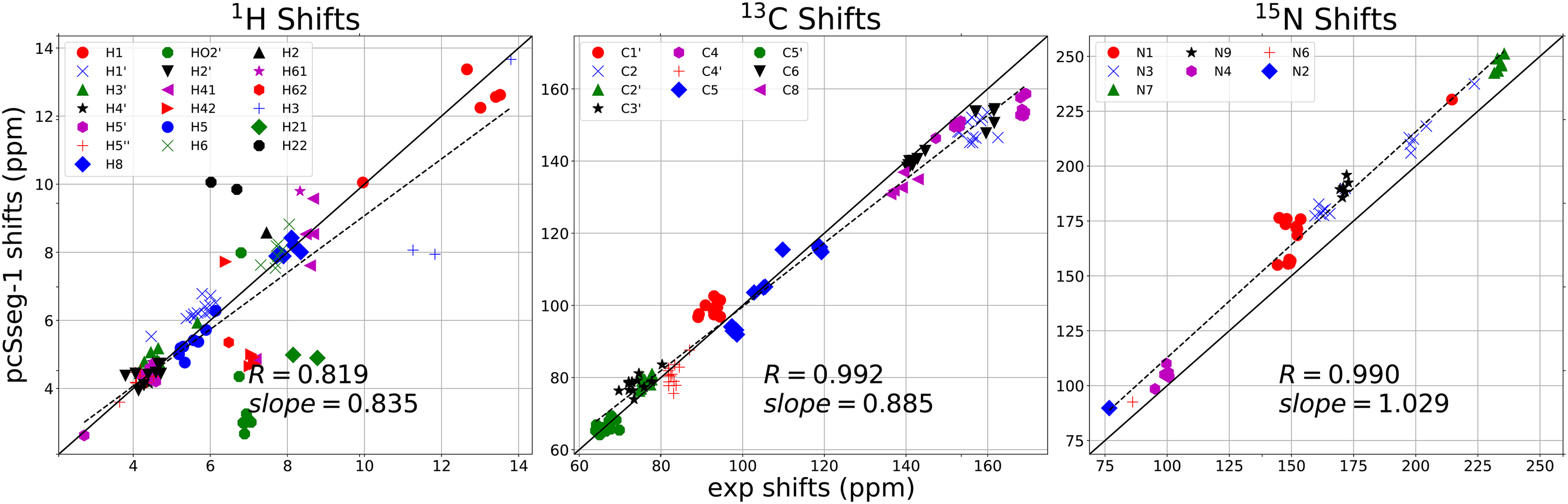
Average shifts in the 10 NMR structures from pdb ID 2koc. Calculations carried out at the OLYP/pcSseg-1 level; experimental shifts from BMRB entry bmr5705.

3.2. Ubiquitin

Like the UUCG hairpin, the ubiquitin monomer has long served as a paradigm of a folded globular protein that can be characterized by NMR.[45, 46, 49, 50] Here I give some information about how results depend upon the method used, using an early set of NMR structures (PDB ID 1d3z[45]) as a reference point. Fig. 4 shows the trends seen for pcSseg-0 calculations; here only protons bonded to carbon are considered. Both overall trends, and those for particular types of atom, are reasonably well reproduced. Of perhaps greater interest are results reported in Table 1, illustrating the dependence on method for estimates of backbone 15N shifts, which generally has a large shift dispersion in folded proteins. Empirical methods like sparta+[9] and shiftx+,[10] trained on observed shifts of globular proteins, have a smaller mean error than do the AFNMR results, but this is partially achieved by using slopes near 0.9 that somewhat limit the range of the predictions. The quantum results shown here are generally consistent with other studies: using a more expensive basis set or a hybrid functional such as B3LYP[51] gives remarkable similar results when trends across the entire protein are considered.

Figure 4:

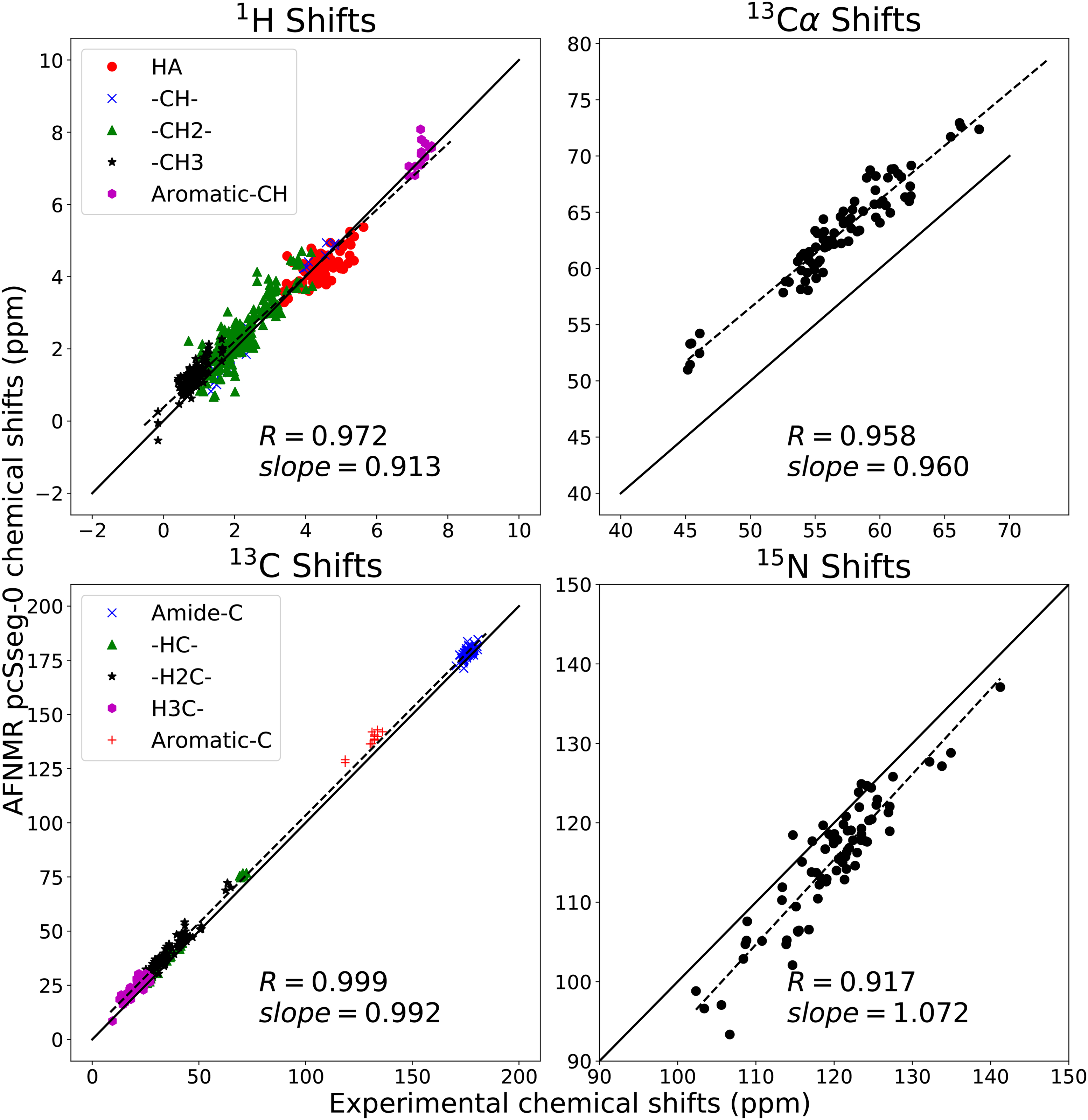
Calculated vs. observed shifts for ubiquitin. Calculated values are the average shift for the ten models in PDB ID 1d3z, at the OLYP/pcSseg-0 level. Observed shifts are from BMRB entry bmr17769. Solid line is y = x ; dashed line is a least-squares best-fit line,whose slope is shown. R is the Pearson correlation coefficient.

Table 1:

Performance of various predictors for the 15N shifts in ubiquitin, using the first model from pdb ID 1d3z as the input structure. Comparisons are made to the observed shifts from BMRB entry bmr17769. R is the Pearson correlation coefficient, slope is the slope of the best fit line (shown as dashed line in Fig. 4), and RMSE is the root-mean-square difference between calculated and observed shifts.

Method	R	slope	RMSE
sparta+[9]	0.969	0.919	1.61
shiftx+[10]	0.953	0.892	1.98
OLYP/pcSseg-O	0.908	1.069	3.41
OLYP/pcSseg-1	0.916	0.982	3.33
OLYP/pcSseg-2	0.915	1.067	3.25
B3LYP/pcSseg-1	0.897	1.156	4.05

3.3. RNA helix 35-ψ⁷⁴⁶

The 24-nt stem-loop corresponding to the Helix 35ψ from the 23S ribosomal RNA (pdb ID 2gbh[42]) has a 16nt helical step that is characterized by 17 residual-dipolar couplings per nucleotide, surpassing any other structure reported to date. Its structure is also informed by an extensive set of distance and torsional angle restraints. Importantly, it has recently been shown that unconstrained molecular dynamics simulations recapitulate NMR data to a high degree,[44] providing a new avenue for studying the effects of conformational averaging on chemical shifts.

The need for, and effects of, conformational averaging can be especially noticeable when individual conformations are drawn from a molecular dynamics simulation. Fig. 5 illustrates this for ¹³C shifts for this 16-nucleotide helix. The left panel shows typical results for a single conformation; each type of carbon (see, e.g. C1’ or C4’) tends to have nearly the same experimental shift at each position, but computed shifts are spread out over about 20 ppm due to instantaneous differences in local conformations. By the time one has averaged 10 (data not shown) or 20 conformations (right panel), the computed shifts have converged to the same average at each nucleotide in good agreement with the observed shifts. Future work will look at the more flexible loop region not analyzed here.

Figure 5:

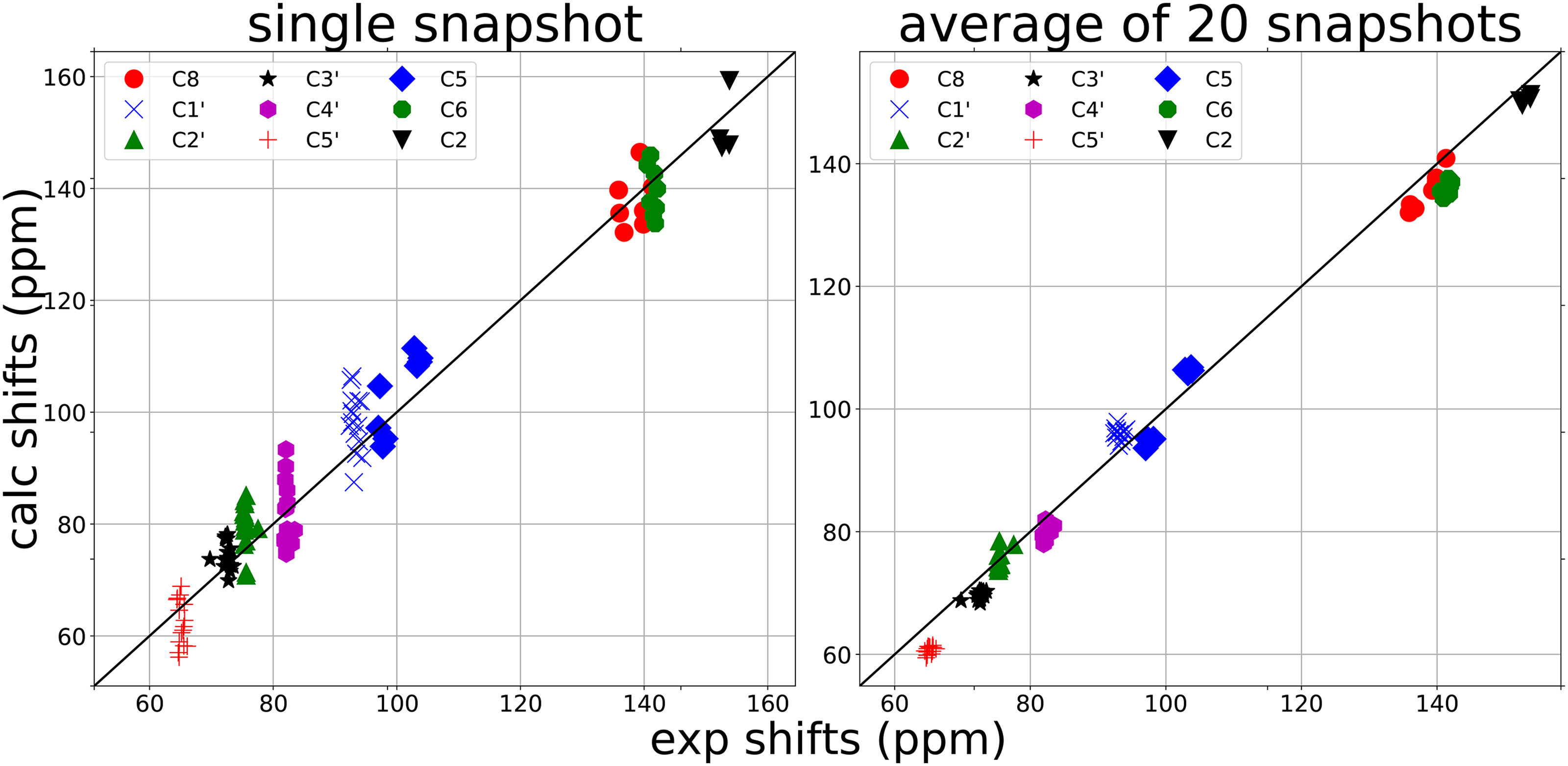
Effects of conformational averaging on the ¹³C shifts in 2gbh. Snapshots (including solvent waters and ions) are taken from Ref. [44]. Calculated shifts at the OLYP/pcSseg-0 level are shown for a single snapshot (left) and for the average over 20 snapshots spaced 0.5 nsec apart (right). Experimental shifts from Ref. [43].

4. Conclusions

The connections between chemical shift and structure in proteins and nucleic acids is a very broad subject. The direct application of quantum chemical methods avoids the need to connect structures to observed shifts in the training of a predictive algorithm, and should be able to reflect in an unbiased (if still approximate) way, the dependence of shift on structure, whether one is dealing with very local conformational changes or more global ones. Dealing with conformational variability is likely to be a key component of getting more accurate results, and also opens the possibility of using shifts to help generate (or to cross-validate) ensembles generated from other sorts of data. The results outlined here show some progress toward an automated and affordable scheme, but it may be that fewer or smaller fragments are required, or that alternative methods for creating and analyzing them can be used. The methods described here can also be used to analyze the anisotropy of shielding tensors,[30, 34] which introduces an additional set of challenges and opportunities.

Highlights.

• An automated fragmentation quantum mechanics/molecular mechanics approach (AFNMR) has shown promising results in chemical shift calculations for biomolecules. Sample results for ubiquitin, and an RNA hairpin and helix are presented, and used to recent directions in quantum calculations. Trends in chemical shift are stable with regards to change in density functional or basis sets, and the use of the small “pcSseg-0” basis, which was optimized for chemical shift prediction, opens the way to more extensive conformational averaging, which can often be necessary, even for fairly well-defined structures.