Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jun 3;60(11):5395–5406. doi: 10.1021/acs.jcim.0c00456

Toward Automated Free Energy Calculation with Accelerated Enveloping Distribution Sampling (A-EDS)

Jan Walther Perthold 1, Dražen Petrov 1, Chris Oostenbrink 1,*
PMCID: PMC7686955  PMID: 32492343

Abstract

graphic file with name ci0c00456_0005.jpg

Free-energy perturbation (FEP) methods are commonly used in drug design to calculate relative binding free energies of different ligands to a common host protein. Alchemical ligand transformations are usually performed in multiple steps which need to be chosen carefully to ensure sufficient phase-space overlap between neighboring states. With one-step or single-step FEP techniques, a single reference state is designed that samples phase-space not only representative of a full transformation but also ideally resembles multiple ligand end states and hence allows for efficient multistate perturbations. Enveloping distribution sampling (EDS) is one example for such a method in which the reference state is created by a mathematical combination of the different ligand end states based on solid statistical mechanics. We have recently proposed a novel approach to EDS which enables efficient barrier crossing between the different end states, termed accelerated EDS (A-EDS). In this work, we further simplify the parametrization of the A-EDS reference state and demonstrate the automated calculation of multiple free-energy differences between different ligands from a single simulation in three different well-described drug design model systems.

Introduction

With the paradigm shift from the rigid lock-and-key hypothesis of receptor–ligand recognition to more dynamic conceptions of molecular interactions involving structural ensembles rather than single conformations and recent advances in computer technology, molecular dynamics (MD) simulations are being used more and more in the field of drug design. Specifically, MD-based methods to efficiently calculate relative drug–target binding free energies are commonly used.1 Calculations involving transformations of one ligand into other ligands via unphysical pathways are often referred to as “alchemical” changes. If such transformations are conducted when the ligand is bound to the receptor and when free in solution, free-energy differences obtained from these transformations can be translated into relative binding free energies using thermodynamic cycles.2 A plethora of methods is available to perform alchemical transformations;3 however, free-energy perturbation (FEP) approaches involving many unphysical intermediate states are most commonly applied.1,4 Recently, FEP-based methods have been shown to allow for the calculation of relative ligand binding free energies with remarkable accuracy on large scales.5−7 FEP approaches are based on Zwanzig’s equation described more than six decades ago,8 which relates the free-energy differences between two states, ΔF2,1, to the exponential average of the energy difference given by their Hamiltonians 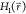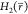Inline graphic and Inline graphic, obtained from an ensemble of the positions 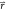Inline graphic of one of the states (R is the ideal gas constant and T is the temperature):

graphic file with name ci0c00456_m004.jpg 1

Zwanzig’s equation only gives unbiased free-energy estimates if there is sufficient overlap in the phase-space that is sampled by both states, which is the reason for the introduction of unphysical intermediate states in practice. However, it is intriguing to think about possibilities to design a single reference state which does not only allow for single-step perturbations, but also for the accurate representation of multiple end states simultaneously, thereby greatly enhancing the efficiency of the FEP approach. 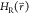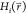One-step perturbation (OSP) methods make use of empirically tuned reference-state Hamiltonians Inline graphic which often involve “soft” atoms to accurately represent multiple end states.9−14 However, OSP approaches suffer from limited transferability of the designed Hamiltonians, i.e. a different perturbation might require empirical reparametrization of the reference-state Hamiltonian.15 Moreover, the soft-core approach does not work very well for larger changes in the charge distributions16,17 and additional end state simulations are often needed to calculate correct contributions of the electrostatic potential energy to the free-energy differences.18−20 A different approach to elegantly calculate a reference Hamiltonian is enveloping distribution sampling (EDS).21 Here, n different Boltzmann-weighted end-state Hamiltonians 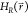Inline graphic are combined in the reference Hamiltonian Inline graphic, the partition function of which is now the sum of the partition functions of the end states. Additionally, to ensure equal sampling of the end states, constant free-energy offset parameters ΔFiR are added:21−24

graphic file with name ci0c00456_m008.jpg 2

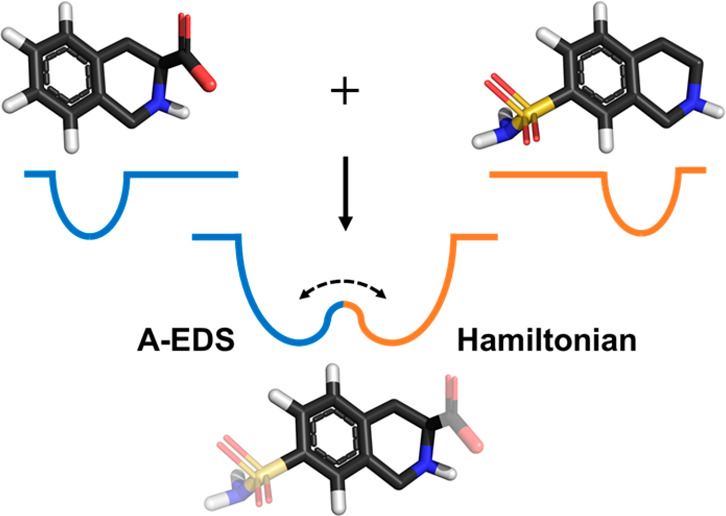
Here, we call the offset parameters ΔFiRfree-energy offset parameters, because they correspond to the relative free-energies of the end states if all states are sampled with equal probability. However, eq 2 was found to result in high energy-barriers, preventing efficient sampling of the minima of all end states. An additional smoothening parameter s was proposed to smoothen the energy landscape of the reference Hamiltonian.22,25−29 However, for the small values of s that are often used, the energy minima of the reference Hamiltonian no longer correspond to the energy minima of the original end states, reducing the phase-space overlap and further complicating the search for the optimal values of s and ΔFi.28,30−34 A computationally expensive approach to bypass this problem uses replica-exchange simulations, in which multiple replicas are performed at different values of s.35,36

We have very recently proposed an alternative EDS formulation in which the EDS reference-state Hamiltonian given in eq 2 is smoothed with a harmonic potential energy function, similar to the accelerated MD approach proposed by McCammon and co-workers.37,38 Our accelerated EDS (A-EDS) approach notably preserves local energy minima and the energy landscape around them, while simultaneously decreasing the energy barriers between the end states. Moreover, it allows for intuitive and potentially automated tuning of the EDS reference-state Hamiltonian parameters by setting an anticipated value for the maximum energy barrier between the ends-states as the only search parameter.39

In this work, we propose an improved algorithm for the A-EDS Hamiltonian parameter search which further simplifies the construction of the reference-state Hamiltonian. With our updated search scheme, it is no longer necessary to give a certain value for the anticipated maximum energy barrier between the end states. The search for the optimal acceleration parameters is instead based on a given acceleration factor. This acceleration factor is translated to the probability of reaching the maximum transition-state energy E‡, estimated from the average energy and energy fluctuation of each end state. Hence, the user specifies the likelihood of a state transition as search parameter and does not need to have any knowledge about the structure and magnitudes of the energy landscape of the nonaccelerated EDS Hamiltonian before the simulation. Additionally, we improved the fully automated search for the free-energy offset parameters ΔFiR by considering the deformation (flattening) of the original end-state Hamiltonians upon acceleration and by using a memory relaxation time for their calculation, which allows for faster adjustment of the parameters.

To demonstrate the applicability of our proposed method to automatically calculate multiple free-energy differences from a single simulation, three protein–ligand systems were chosen. All three systems are already established in the literature and the drug–target interactions were examined both using experimental and computational methods:

  • 1

    glutamate receptor A2 (GRA2) allosteric modulators14,39

  • 2

    trypsin (TRP) inhibitors19,40−47

  • 3

    phenylethanolamine N-methyltransferase (PNMT) inhibitors32,35,36,48

Notably, systems 2 and 3 both include net-charge changes in the ligand sets, which were previously considered too challenging for multistate EDS approaches.35,36

Theory

A-EDS Hamiltonian

In A-EDS the reference Hamiltonian 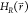Inline graphic given in eq 2 is smoothened by an approach that is similar to Gaussian accelerated MD (GAMD),38 which is a variant of the general accelerated MD approach.37 A harmonic potential energy term is added to the EDS reference Hamiltonian, pulling the energy landscape down to a minimum energy value Emin. The continuous accelerated EDS (A-EDS) reference Hamiltonian 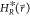Inline graphic is defined as

graphic file with name ci0c00456_m011.jpg 3

Where, Emin and Emax are tunable parameters, in addition to the ΔFiR in eq 2. Effectively, 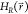Inline graphic is only modified in the region between Emin and Emax. The A-EDS functional form preserves the energy landscape around local energy minima.

A-EDS Parameter Search

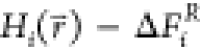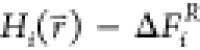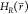In our earlier work, we have proposed an intuitive parameter search,39 which is simplified further in the current work. During a parameter-search simulation, the end state i which is currently being sampled in a simulation of the EDS reference state is defined as the state with the lowest energy Inline graphic. 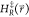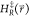We monitor the average value of Inline graphic while the state is sampled, denoted as E̅i, as well as the value of Inline graphic when a new state is sampled, indicative of the barrier height and denoted as Inline graphic. 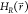From the values of Inline graphic we compute E̅max‡ as the average of the maximum transition energy between states within a state round-trip (we define a round-trip as having visited all states at least once). With these properties we define the maximum energy barrier ΔEmax between the end states in the unmodified EDS reference Hamiltonian Inline graphic:

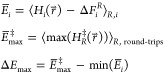graphic file with name ci0c00456_m019.jpg 4

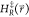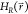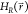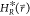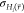Inline graphic is the value of Inline graphic when a new state is sampled. The unmodified EDS Hamiltonian Inline graphic can now be accelerated by setting Emin and Emax such that the maximum energy barrier between the states, ΔEmax, is reduced to the target value ΔEmax* in Inline graphic. 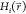The target value ΔEmax is set to a user-defined multiple z of the standard deviation, Inline graphic, of the energy Inline graphic of the state with the lowest average energy E̅i. 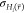Like for the average end state energies E̅i, all Inline graphic are only calculated while the respective state is sampled. By setting the acceleration as sigma-level z, the minimum probability of reaching the maximum transition-energy, Pmin (E̅max‡), becomes for Gaussian end state energy distributions:

graphic file with name ci0c00456_m027.jpg 5

where erf() is the error function. Hence, the probability of reaching the maximum transitions-energy is decreased exponentially with increasing sigma-level z.

The value of ΔEmax* that is obtained in this way, is subsequently used to determine Emin and Emax in eq 3. Emax simply corresponds to E̅max, and Emin is calculated as

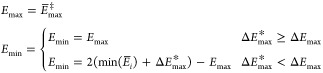graphic file with name ci0c00456_m028.jpg 6

If the resulting value of Emin is less than min(E̅i), it is adjusted to

graphic file with name ci0c00456_m029.jpg 7

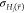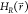The proposed optimization scheme for the acceleration parameters of the A-EDS Hamiltonian is used in a nonequilibrium parameter-search simulation in which the user only specifies the desired maximum barrier height ΔEmax* as sigma-level z which gives a multiple of Inline graphic of the end state with the lowest average energy. No initial values for Emin and Emax have to be set, as they are adjusted while the reference state explores the energy landscape. To enable sampling of all states in the beginning of the search simulation, the value of Emax is set to the maximum transition energy Emax of the unmodified Hamiltonian Inline graphic as the system explores the energy landscape until all states have been visited at least once. After all states have been visited at least once, Emax is calculated as described above.

In addition to the A-EDS parameters Emin and Emax, the free-energy offset parameters ΔFiR are optimized simultaneously during the parameter-search simulation. The free-energy offset parameter of the first state is arbitrarily set to zero and the other free-energy offset parameters are calculated relative to the first state by simply using the perturbation formula, eq 1:

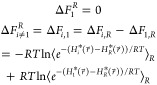graphic file with name ci0c00456_m032.jpg 8

Note that in contrast to the previously suggested approach,39 we here consider the accelerated end-state Hamiltonians 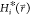Inline graphic instead of the unmodified end-state Hamiltonians to account for deformation (flattening) of the original energy landscapes:

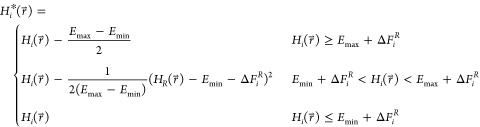graphic file with name ci0c00456_m034.jpg 9

To allow for faster adjustment of the free-energy offset parameters ΔFiR during the parameter-search simulation, we implemented a memory relaxation time τ for the exponential averages of the energy differences in analogy to time-averaged distance restraining functions.49 Accordingly, the exponential energy differences with a characteristic memory decay time τ read (t is the simulation time and Δt the time-step):

graphic file with name ci0c00456_m035.jpg 10

Additionally, we increase τ linearly over the course of the simulation from a value τA to a value τB (ttot is the total simulation time of the nonequilibrium parameter search):

graphic file with name ci0c00456_m036.jpg 11

In systems in which the free energy offset parameters ΔFiR are very large, τA can be set to a small value in beginning of the parameter-search simulation to allow for rapid adjustment of all ΔFi, while more statistics are used upon convergence toward the end of the parameter-search simulation. Using this approach, the free energy offset parameters ΔFiR fluctuate around their optimal values which ensure equal sampling of all end states.

After the nonequilibrium parameter-search simulation, the values of Emin, Emax, and ΔFiR are fixed and an equilibrium simulation is performed to determine the final free energy differences between the states.

Methods

Simulation Settings

All MD simulations were performed using the GROMOS MD++ 1.5.0 simulation engine50 to which the A-EDS functionality was added. All systems were simulated in NVT ensembles at 300 K using Nosé–Hoover chains51 to ensure canonical energy distributions with 5 coupled thermostats and relaxation times of 0.1 ps. The solute and solvent degrees of freedom were coupled to different heat-baths. The equations of motion were solved using a leapfrog integration scheme52 with a time-step of 2 fs. Covalent bond lengths of solute molecules were constrained using the SHAKE53 algorithm, and covalent bond lengths and angles of solvent water molecules were constrained using the SETTLE54 algorithm. The center-of-mass motions of the systems were removed every 10 000 steps. Neighbor searching was performed every 10 fs using a group-based cutoff scheme within a cutoff sphere of 1.4 nm. For the calculation of nonbonded interactions, a twin-range cutoff scheme was employed. Within a cutoff of 0.8 nm, nonbonded interactions were calculated every step. Between 0.8 and 1.4 nm, nonbonded interactions were evaluated every 10 fs and held constant between the updates. For the calculation of electrostatic interactions, a reaction-field contribution55 with a relative dielectric permittivity of 6156 beyond the cutoff sphere was added. For parametrization and preparation of the drug-target model systems, the reader is referred to previous literature.14,19,36 For the PNMT ligands, small updates were made to the parameters. These involved the introduction of explicit aromatic hydrogens and the more precise definition of integer-charged charge groups. The updated molecular building blocks are available in the Supporting Information. It is noted that for PNMT ligands and TRP ligands additional weak distance restraints with force constants of 250 kJ·mol–1·nm–2 were introduced to prevent the reference-state ligands from leaving the binding site during the sampling of end states with unfavorable binding affinity. The additional protein–ligand distance restraint definitions for these systems is given in Tables S1 and S2 in the Supporting Information.

Perturbation Topology Setup

For each of the protein systems, multiple end states were considered in the multistate A-EDS calculations, as shown in Figure 1. For GRA2, 16 distinct states were used, which is more than the five end states used in our previous work.39 For TRP, eight end states were used, including the protonated (state 2) and deprotonated (state 8) carboxylic acid. For PNMT, ten different states were considered, including state 2, which bears a different net-charge from all the other ligands. To combine the different ligand end states given in Figure 1 into a single reference state, a single-topology approach was chosen. This was also shown to work best in ref (32), while a dual topology approach was used in refs (35) and (36).

Figure 1.

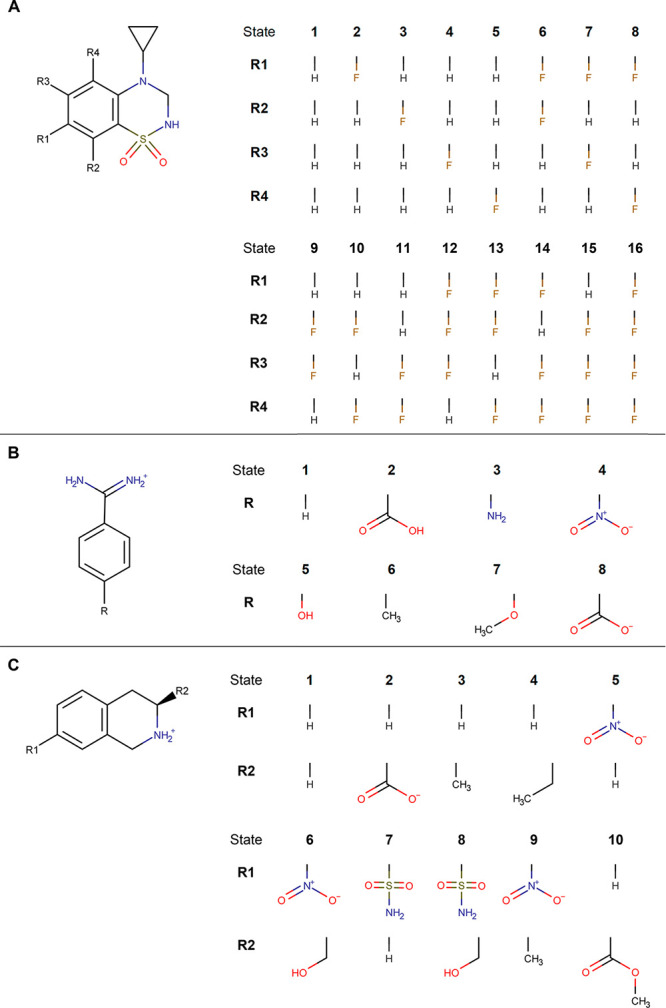
Figure 1

Open in a new tab

Different ligand end states for which relative binding free energies were calculated. Different benzothiadiazine dioxide ligands of system GRA2 (A), different benzamidine ligands of system TRP (B), and the different tetrahydroisoquinoline ligands of system PNMT (C) are shown with their corresponding end state numbering.

To simplify the complex setup of such molecules, a recently developed automated approach was used for systems TRP and PNMT, based on maximal common substructure (MCS) search for a pair of molecules. The search involves an iterative procedure in which in each step a pair of atoms, each belonging to one of the compounds, is added to the current common substructure (current solution). Upon adding a pair of atoms, common parts of molecular topologies are checked for mismatching parameters of bonded interactions. As the search was primarily aimed at maximizing the number of common atoms, while keeping all bonded interactions unperturbed, only added pairs without any mismatched parameters of bonded interactions were taken into account. To create a perturbation topology from the resulting MCS, atom pairs from the solution common substructure were merged into single atoms with interaction parameters assigned to their respective end-state parameters, while the remaining atoms from both topologies not belonging to the solution common substructure were assigned as noninteracting dummy atoms transforming into interacting atoms (end-state parameters) and the other way around.

To generate a combined multistate single topology from a set of multiple compounds (n topologies), MCS search (as described above) was performed n – 1 times. An initial MCS search was performed on two arbitrarily chosen compounds from the set, producing a first perturbation topology (representative of the first two end states). Each of the following (n – 2) MCS searches were performed on the resulting perturbation topology from the previous MSC step and one of the remaining compounds (topologies) from the set, appending an additional end state in each of the iterations and finally producing the multistate single topology.

A-EDS Parameter-Search Simulations

For the calculation of the A-EDS acceleration parameters, nonequilibrium A-EDS parameter-search simulations were first performed for the unbound ligands in water with three different acceleration σ-levels, 1σ, 2σ, and 3σ, to calculate the anticipated maximum energy barrier between the end states, ΔEmax* (i.e., z = 1, 2, and 3). In these simulations, A-EDS parameters Emax, Emin, and all free-energy offset parameters ΔFi were determined simultaneously, with an increase in the memory relaxation time for the calculation of the free-energy offset parameters ΔFiR from τA = 1 ps to τB = 100 ps within the parameter-search simulation time of 10 ns. For the parameter-search simulations of the ligands bound to the proteins, A-EDS parameters Emax and Emin previously determined for the ligands in water for the three different acceleration levels were used and held fixed throughout the parameter search. Only the free-energy offset parameters ΔFi were optimized during these parameter-search simulations, with the same relaxation time parameters as used for the ligands in water. For the PNMT system the parameter-search simulations were prolonged to 100 ns with a relaxation time τB of 1000 ps because only few state transitions were observed during the first 10 ns (see Table S3 in the Supporting Information) and free-energy offset parameters converged more slowly (see Figure 2). Since the free-energy offset parameters fluctuate around their optimal values during the parameter-search simulations, the values used for the subsequent equilibrium simulations were calculated by averaging over the free-energy offset parameter trajectories of the parameter-search simulations. For systems GRA2 and TRP, the first 5 ns of the simulations were discarded for the averaging as nonequilibrated region. For system PNMT, the first 10 ns of the simulations were discarded for the averaging as nonequilibrated region.

Figure 2.

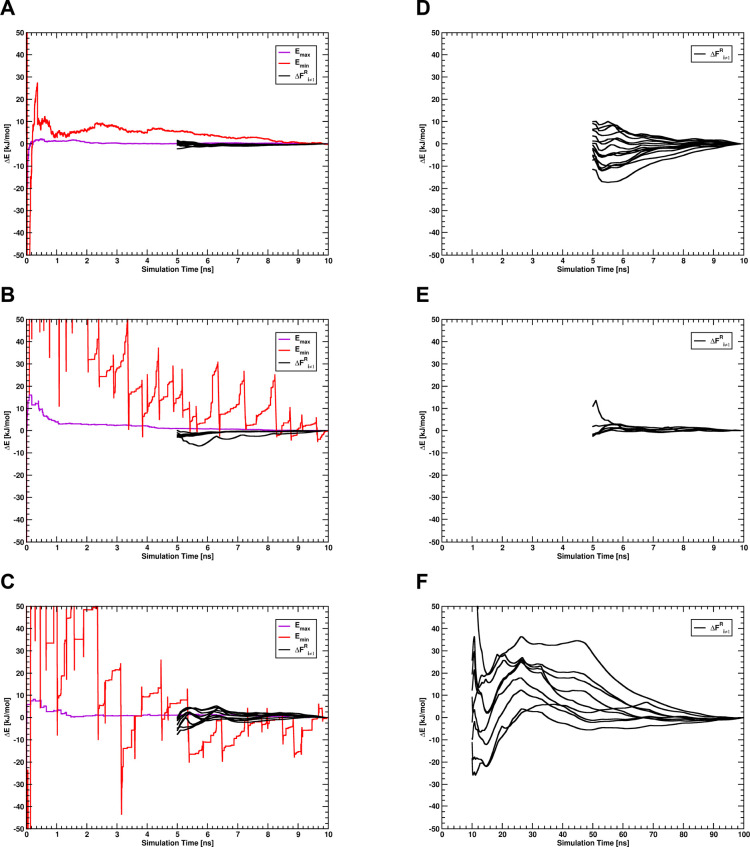
Figure 2

Open in a new tab

Convergence of the A-EDS acceleration parameters Emax and Emin and the free-energy offset parameters ΔFi≠1R relative to their final values for the A-EDS parameter-search simulation with an acceleration σ-level of 2σ, for the unbound ligands in water of system GRA2 (A), TRP (B), and PNMT (C), and for the ligands bound to the protein of system GRA2 (D), TRP (E), and PNMT (F). The convergence of the free-energy offset parameters ΔFi≠1 is shown as a forward cumulative average over the free-energy offset trajectory with the first 5 ns discarded as the nonequilibrated region. Note that in panels B and C the A-EDS parameter Emin (red solid line) falls off the plot in the beginning of the trajectory.

A-EDS Equilibrium Sampling Simulations

A-EDS equilibrium simulations for the calculation of relative binding free energies were started from the last snapshots of the parameter-search simulations in water and for the ligands bound to the proteins, respectively. The A-EDS parameters determined during the parameter-search simulations were held fixed and sampling was performed for another 10 ns in water and for 100 ns (systems GRA2 and TRP) or 200 ns (system PNMT) for the protein systems.

Results and Discussion

A-EDS Parameter-Search Simulations

To determine the A-EDS acceleration parameters Emax and Emin, and the free-energy offset parameters ΔFiR, parameter-search simulations were performed for 10 ns for the ligands solvated in water. The resulting acceleration parameters are given in Table 1 for all systems. Depending on the chosen acceleration level the resulting A-EDS parameter Emin, controlling the range over which the energy landscape is flattened, varies greatly. The parameters Emax, which correspond to the maximum energy barrier between the states, are comparably independent of the chosen acceleration level. The convergence of all parameters for all ligand systems in water for an acceleration σ-level of 2σ are given in Figure 2A–C, and for the other acceleration levels in the Supporting Information, Figure S1 and S2. Parameters mostly are converged or only change little with simulation time. The greatest fluctuation occurs for the acceleration parameter Emin, which can be explained by the dependence of this parameter on the slower-converging energy fluctuation estimate for each end state. However, this fluctuation does not have a big influence on the calculated free-energy offset parameters ΔFi.

Table 1. A-EDS Acceleration Parameter-Search Results Obtained from the Simulations of the Unbound Ligands in Water for the Three Different Acceleration σ-Levelsa.

system parameter 1σ 2σ 3σ
GRA2 Emax 158.5 97.2 93.6
ΔEmax* (i.e., z·σ) 19.2 27.0 34.5
Emax 119.2 94.7 81.4
Emin –535.0 –150.6 –44.1
TRP ΔEmax 391.4 472.2 486.2
ΔEmax* (i.e., z·σ) 132.1 209.5 240.2
Emax 33.7 36.1 36.5
Emin –546.1 –496.1 –455.6
PNMT ΔEmax 300.8 506.9 538.4
ΔEmax* (i.e., z·σ) 35.6 216.5 261.6
Emax 30.6 32.9 31.0
Emin –1240.8 –560.4 –523.2
Open in a new tab
a

ΔEmax and ΔEmax* are determined from the simulation and define the values of Emax and Emin. Energy units are kilojoules per mole.

The data in Table 1 nicely demonstrates how the selected acceleration level determines the values of Emin and Emax. Setting the acceleration level to 1σ implies requesting a large number of transitions between the states. Accordingly, the acceleration is strongest, leading to the largest range of acceleration (difference Emax – Emin is largest). In contrast, setting the acceleration level to 3σ allows for fewer transitions, higher energy barriers and hence to a reduced range of acceleration. As the fluctuations in the energy basins are system dependent, the resulting values of Emax – Emin differ considerably between the different cases.

To calculate the free-energy offset parameters ΔFiR for the end states of the ligands bound to the proteins, A-EDS acceleration parameters Emax and Emin were held fixed during the parameter-search simulation in the protein systems, as convergence of these parameters was very slow in preliminary simulations, given the generally complicated and possibly non-Gaussian energy landscapes of host–guest systems, where the EDS region is not surrounded by a homogeneous and fast-relaxing medium, but by the protein environment. In our previous work, we determined that the free-energy differences are quite robust with respect to the exact choice of Emin and Emax.39 Therefore, the acceleration parameters for each acceleration level were set to the values determined during the parameter-search simulations in water. The convergence of the free-energy offset parameters for all systems with an acceleration σ-level of 2σ is shown in Figure 2D–F and for the other acceleration levels in the Supporting Information, Figure S1 and S2. For systems GRA2 and PNMT, parameter-search simulations in the protein with an acceleration level of 1σ (very strong acceleration) became unstable. In particular, the SHAKE algorithm failed at maintaining the bond-length constraints, indicative of the occurrence of large forces due to too strong acceleration. Subsequent simulations in the protein using this acceleration level were not performed for these systems. Moreover, for system PNMT, the convergence of the free-energy offset parameters ΔFi was slower than for the other systems, and the parameter search was extended to 100 ns. All final free-energy offset parameters ΔFiR are given in the Supporting Information, Tables S7–S9. The free-energy offset values can depend strongly on the chosen acceleration level, as the flattening of the energy landscape contributes to the free-energy differences between the accelerated end states (eq 9) that are combined to the single reference state in the simulation.

A-EDS Equilibrium Simulations

To calculate relative binding free energies for the ligands, A-EDS equilibrium simulations were performed both in water and in the protein-bound state for all systems with the A-EDS parameters determined for each acceleration level in the parameter-search simulations. The free-energy differences between the ligands in each state were calculated from the free-energy difference of each state to the A-EDS reference state obtained from Zwanzig’s equation (eq 1). The effects of any distance restraints added in the simulations (Tables S1, S2) on the free energy were removed in this stage, by adding the restraining energies to the reference state Hamiltonians.

For system GRA2, all calculated free-energy differences for the unbound ligands were very similar for all three acceleration levels (Table 2) and converged very rapidly (Figure S3A–C in the Supporting Information). However, for the bound ligands, different results were obtained for acceleration levels of 2σ and 3σ, despite apparent convergence of the calculated free energy values (Figure S3D, E in the Supporting Information). Simulations with an acceleration level of 1σ were not performed in the protein, as simulations became unstable during the parameter-search simulation with this acceleration level. Analysis of the sampled states and state transitions in these equilibrium simulations revealed that for an acceleration level of 3σ, many states were not sampled adequately and state transitions to these states occurred only rarely (Table 5 and Figure S6 in the Supporting Information).

Table 2. Relative Free-Energy Differences ΔFi≠1,1 between the Ligand End States for the Three Different Acceleration σ-Levels for System GRA2a.

  ΔFi≠1,1 unbound ligand
 ΔFi≠1,1 two bound ligands
 calculated ΔΔFi≠1,1
  1σ 2σ 3σ 1σ 2σ 3σ 1σ 2σ 3σ
ΔF2,1 –111.2 ± 0.3 –111.0 ± 0.2 –110.8 ± 0.1 n.a. –224.4 ± 1.6 –231.4 ± 1.2 n.a. –2.4 ± 1.7 –9.8 ± 1.0
ΔF3,1 22.6 ± 0.2 22.5 ± 0.2 22.4 ± 0.1 n.a. 45.5 ± 1.5 39.6 ± 1.4 n.a. 0.5 ± 1.5 –5.3 ± 1.2
ΔF4,1 8.9 ± 0.2 8.6 ± 0.1 8.7 ± 0.1 n.a. 7.3 ± 1.7 24.8 ± 2.3 n.a. –9.9 ± 1.7 7.5 ± 2.1
ΔF5,1 –53.6 ± 0.3 –54.3 ± 0.2 –54.4 ± 0.1 n.a. –116.5 ± 1.5 –118.0 ± 0.6 n.a. –7.8 ± 1.6 –9.3 ± 0.4
ΔF6,1 –90.6 ± 0.3 –90.9 ± 0.2 –90.7 ± 0.1 n.a. –187.5 ± 1.6 –197.0 ± 1.3 n.a. –5.6 ± 1.6 –15.6 ± 1.1
ΔF7,1 –104.3 ± 0.2 –104.8 ± 0.2 –104.5 ± 0.1 n.a. –218.1 ± 1.7 –207.1 ± 1.8 n.a. –8.6 ± 1.7 2.0 ± 1.6
ΔF8,1 –135.0 ± 0.2 –135.7 ± 0.2 –135.8 ± 0.1 n.a. –289.5 ± 1.6 –292.5 ± 1.3 n.a. –18.1 ± 1.6 –20.9 ± 1.1
ΔF9,1 60.3 ± 0.3 60.5 ± 0.2 60.5 ± 0.1 n.a. 108.8 ± 1.5 124.8 ± 1.9 n.a. –12.2 ± 1.6 3.9 ± 1.7
ΔF10,1 –73.0 ± 0.3 –73.4 ± 0.2 –73.3 ± 0.1 n.a. –162.6 ± 1.5 –160.0 ± 1.4 n.a. –15.8 ± 1.6 –13.3 ± 1.2
ΔF11,1 –47.8 ± 0.3 –48.0 ± 0.2 –48.2 ± 0.1 n.a. –117.2 ± 1.5 –94.3 ± 1.4 n.a. –21.1 ± 1.6 2.1 ± 1.2
ΔF12,1 –55.3 ± 0.4 –54.9 ± 0.2 –54.8 ± 0.2 n.a. –123.3 ± 1.6 –113.1 ± 1.9 n.a. –13.5 ± 1.6 –3.6 ± 1.5
ΔF13,1 –156.0 ± 0.3 –157.0 ± 0.2 –156.9 ± 0.1 n.a. –340.2 ± 1.6 –338.5 ± 1.5 n.a. –26.2 ± 1.7 –24.8 ± 1.3
ΔF14,1 –130.8 ± 0.3 –131.6 ± 0.2 –131.6 ± 0.1 n.a. –286.9 ± 1.6 –270.5 ± 1.7 n.a. –23.7 ± 1.6 –7.4 ± 1.5
ΔF15,1 –38.0 ± 0.5 –37.7 ± 0.2 –37.7 ± 0.1 n.a. –102.3 ± 1.7 –79.1 ± 2.5 n.a. –27.0 ± 1.7 –3.7 ± 2.3
ΔF16,1 –123.1 ± 0.4 –123.2 ± 0.2 –123.3 ± 0.2 n.a. –277.7 ± 2.1 –260.3 ± 2.4 n.a. –31.2 ± 2.1 –13.6 ± 2.0
Open in a new tab
a

Energy units are kilojoules per mole. n.a. = not available.

Table 5. Number of Unique Visits of All Ligand End States and of the Ligand End State with the Longest Average Residence Time in Water for the Three Different Acceleration σ-Levels in the Equilibrium A-EDS Simulations.

  unbound ligands
 bound ligands
system 1σ 2σ 3σ 1σ 2σ 3σ
GRA2-all 113081 121863 129663 n.a.a 78277 14396
GRA2-1 7084 6366 6802 n.a. 2636 21
TRP-all 97020 99912 83688 249119 198880 75610
TRP-8 1328 427 128 2821 1446 15
PNMT-all 31382 18133 17138 n.a. 18741 10678
PNMT-2 5004 135 48 n.a. 11 2
Open in a new tab
a

n.a. = not available.

For system TRP, the calculated free-energy differences for all ligands in the unbound state were again similar for all three acceleration levels. However, for the bound ligands more different values were obtained, especially for the acceleration level of 3σ compared to 1σ or 2σ (Table 3). For 3σ, convergence of the calculated values was slower both in water and in the protein (Figure S4 in the Supporting Information) and much less state transition was observed (Table 5 and Figure S7 in the Supporting Information).

Table 3. Relative Free-Energy Differences ΔFi≠1,1 between the Ligand End States for the Three Different Acceleration σ-Levels for System TRPa.

  ΔFi≠1,1 unbound ligand
 ΔFi≠1,1 bound ligand
 calculated ΔΔFi≠1,1
  1σ 2σ 3σ 1σ 2σ 3σ 1σ 2σ 2σ
ΔF2,1 –160.2 ± 0.8 –163.4 ± 1.2 –161.4 ± 0.8 –150.6 ± 1.5 –148.5 ± 1.2 –160.6 ± 1.3 9.6 ± 1.7 14.9 ± 1.7 0.8 ± 1.5
ΔF3,1 –143.8 ± 0.9 –142.5 ± 0.3 –146.2 ± 1.7 –139.1 ± 0.8 –136.6 ± 0.6 –136.0 ± 0.8 4.7 ± 1.2 5.9 ± 0.7 10.2 ± 1.9
ΔF4,1 70.7 ± 0.3 70.3 ± 0.3 71.0 ± 0.3 68.6 ± 0.3 66.6 ± 0.5 63.3 ± 1.4 –2.1 ± 0.4 –3.7 ± 0.6 –7.7 ± 1.4
ΔF5,1 –171.5 ± 2.5 –166.2 ± 1.0 –166.0 ± 0.9 –158.9 ± 1.2 –161.5 ± 2.1 –158.3 ± 2.5 12.6 ± 2.8 4.7 ± 2.3 7.7 ± 2.7
ΔF6,1 –25.2 ± 0.1 –25.1 ± 0.1 –25.3 ± 0.3 –24.1 ± 0.9 –25.4 ± 1.3 –19.6 ± 0.9 1.1 ± 0.9 –0.3 ± 1.3 5.7 ± 0.9
ΔF7,1 –97.1 ± 0.5 –97.7 ± 0.8 –97.1 ± 0.6 –89.8 ± 0.6 –90.7 ± 0.6 –84.7 ± 1.0 7.3 ± 0.8 7.0 ± 1.0 12.4 ± 1.2
ΔF8,1 –427.4 ± 0.6 –425.8 ± 1.0 –430.6 ± 1.4 –402.6 ± 0.6 –401.1 ± 1.6 –395.6 ± 1.9 24.8 ± 0.8 24.7 ± 1.9 35.0 ± 2.4
Open in a new tab
a

Energy units are kilojoules per mole.

For system PNMT, the acceleration level of 1σ (very strong acceleration) lead to partially different calculated free-energy differences between the ligand end states in water compared to the other acceleration levels (Table 4). The difference was especially pronounced for the end state involving a charge-change (ligand 2), but also present for ligands 7 and 8, which have a large sulfonamide group at the R1 position. Possibly, the strong acceleration parameters determined for 1σ lead to overflattening of the energy landscape, which prohibits proper sampling of the most important regions of phase-space for these end states. For the ligands bound to the protein, sometimes different free-energy differences between the states were obtained for acceleration levels of 2σ and 3σ.

Table 4. Relative Free-Energy Differences ΔFi≠1,1 between the Ligand End States for the Three Different Acceleration σ-Levels for System PNMTa.

  ΔFi≠1,1 unbound ligand
 ΔFi≠1,1 bound ligand
 calculated ΔΔFi≠1,1
  1σ 2σ 3σ 1σ 2σ 3σ 1σ 2σ 3σ
ΔF2,1 –376.3 ± 1.7 –439.3 ± 1.4 –440.8 ± 2.3 n.a. –216.9 ± 2.8 –217.6 ± 2.8 n.a. 222.4 ± 3.1 223.2 ± 3.6
ΔF3,1 5.6 ± 0.2 5.8 ± 0.3 6.1 ± 0.3 n.a. 0.8 ± 2.6 4.2 ± 1.6 n.a. –5.0 ± 2.6 –1.9 ± 1.6
ΔF4,1 8.7 ± 0.3 7.6 ± 0.3 8.4 ± 0.3 n.a. –6.4 ± 2.9 4.7 ± 1.6 n.a. –14.0 ± 2.9 –3.7 ± 1.6
ΔF5,1 7.8 ± 0.4 7.9 ± 0.3 8.1 ± 0.3 n.a. –2.0 ± 2.5 –2.4 ± 1.4 n.a. –9.9 ± 2.5 –10.5 ± 1.4
ΔF6,1 –24.5 ± 0.9 –29.1 ± 0.8 –30.0 ± 0.9 n.a. –50.8 ± 2.2 –35 ± 1.5 n.a. –21.7 ± 2.3 –5.0 ± 1.7
ΔF7,1 –448.4 ± 0.9 –463.0 ± 1.7 –461.3 ± 1.3 n.a. –465.4 ± 1.9 –475.8 ± 1.5 n.a. –2.4 ± 2.5 –14.5 ± 2.0
ΔF8,1 –482.1 ± 1.0 –498.0 ± 1.1 –501.0 ± 1.2 n.a. –526.7 ± 2.0 –510.6 ± 1.3 n.a. –28.7 ± 2.3 –9.6 ± 1.8
ΔF9,1 13.9 ± 0.4 13.9 ± 0.3 13.8 ± 0.5 n.a. –0.5 ± 2.1 5.6 ± 1.5 n.a. –14.4 ± 2.1 –8.2 ± 1.6
ΔF10,1 –161.9 ± 1.3 –163.1 ± 0.6 –163.8 ± 0.5 n.a. –173.2 ± 2.8 –167.3 ± 2.6 n.a. –10.1 ± 2.9 –3.5 ± 2.6
Open in a new tab
a

Energy units are kilojoules per mole. n.a. = not available.

Except for the differences described above, the calculated free-energy differences between the end-states are independent of the chosen acceleration level. Notably, they do differ significantly from the corresponding free-energy offset parameters ΔFiR (Tables S7–S9 in the Supporting Information), as the offset parameters describe the free-energy differences between the accelerated end states in the reference state (eq 9), while the free-energy differences of the end states, ΔFi≠1,1, are calculated for the original (i.e., nonaccelerated) Hamiltonians.

Table 5 collects the total number of unique visits of the individual states for all simulations. The state with the longest average residence time (the fewest transitions) is also listed, to give a lower bound to these values. It is most relevant to focus on the compounds that are sampled least to judge if the sampling is sufficient. A large number of unique samples is necessary to ensure proper sampling of each of the states. For the compounds in water, the total number of unique visits of all compounds is relatively independent of the acceleration level. Only for PNMT, with the largest differences between states, we observe a significantly lower value at 2σ and 3σ. The differences are more pronounced for the states that are sampled least, with a clearer drop of the number of visits for TRP and PNMT. In system GRA2, the ligands are arguably the most similar and there is no large difference observed. In the protein-bound states, the number of unique visits is much lower throughout, especially considering that the simulations are a factor 10 (GRA2, TRP) or 20 (PNMT) longer than the ones of the ligands in water. This is representative of the fact that the sampling is much more complex in a protein environment. During the parameter search for GRA2 and PNMT, the simulations at 1σ became unstable, suggesting a too strong acceleration. On the other hand, the number of unique visits at 3σ drops down considerably, suggesting that this acceleration level, which is most conservative and therefore possibly preferred, should only be used in conjunction with longer simulation times.

Comparison to Experiment and Other Methods

The binding free energies in Tables 2–4 are reported relative to the arbitrarily chosen first compound of the set. To compare results for the computed relative binding free energies independent of an arbitrary selection, an estimate of the binding free energy of the A-EDS reference state (average difference of the relative binding free energies to the experimental binding free energies) was used to calculate ligand binding free energies which can directly be compared to experimentally determined values; i.e., the relative binding free energy values were shifted by the average deviation to the experimental binding free energies to account for the binding free energy of the reference state.19,57 This corresponds to a single fitting parameter to compare relative binding free energies to the experimental values. Tables S3–S5 report the individual binding affinities. The overall performance is summarized by computing the root-mean-square error (RMSE) with respect to the experimental values (Table 6).

Table 6. Root-Mean-Square Errors (kJ·mol–1) Relative to the Experimental Values with Error Estimates Calculated by Leave-One-Out Cross Validationa.

  GRA2 TRP PNMT
A-EDS 1σ n.a. 6.1 ± 0.1 n.a.
A-EDS 2σ 6.3 ± 0.2 6.0 ± 0.1 8.8 ± 0.1
A-EDS 3σ 6.0 ± 0.3 8.5 ± 0.2 3.8 ± 0.1
EDS 2.2b n.a. 5.2e/4.9f
TI 3.9c 6.6d 3.7
OSP 1.9c 2.8d n.a.
Open in a new tab
a

The individual values are reported in Tables S3–S5 in the Supporting Information. n.a. = not available.

b

A-EDS with fixed ΔEmax*; ref (39).

c

Reference (14).

d

Reference (19).

e

EDS with s-parameter; ref (32).

f

RE-EDS; ref (36).

For the GRA2 ligands, both simulations with acceleration levels of 2σ and 3σ performed similarly in terms of agreement with the experimental data, with RMSEs of about 6 kJ/mol. A-EDS simulations previously performed using a fixed set energy barrier39 using only the five ligands for which experimental data was available showed a lower RMSE of 2.2 kJ/mol. The RMSE of the calculations in this work to the previously reported A-EDS calculations was 9.0 and 6.6 kJ/mol for acceleration levels of 2σ and 3σ, respectively. The acceleration level in the previous simulations was between the acceleration for 2σ and 3σ used here. Furthermore, the previous simulations were significantly shorter (11 ns vs 110 ns for parameter search and equilibrium simulations in the protein system). However, the total number of visits to the five first end states lies between 927 (state 2) and 6982 (state 3) and is slightly better comparable to what we observed previously (51 to 2548 unique visits). Obviously, the longer simulation time is largely offset by the larger amount of states that needs to be sampled. The discrepancies between the two sets of simulations can rather be explained due to larger drifts in the overall conformation that are sampled. In system GRA2, two benzothiadiazine dioxide ligands are binding simultaneously to the protein–protein interface of the GRA2 dimer. At the acceleration level of 2σ, the distance between the centers of mass of the aromatic rings of the two ligands in the active site moved from initially 0.55 nm to an average value of 0.62 nm. Furthermore, the side chain of Ser108 was seen to change conformation, leading to a different environment of fluorine substituents (Figure 3).

Figure 3.

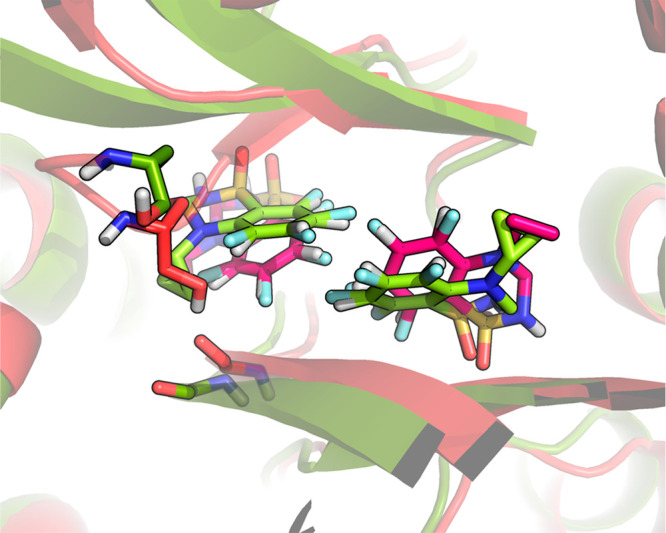
Figure 3

Open in a new tab

Different conformations of the side chain of Ser108 hydrogen-bonding to the carbonyl oxygen of Phe105 in system GRA2 at the end of A-EDS equilibrium simulations of the ligand end states bound to the protein, for an acceleration level of 2σ (red, GRA2 ligands in magenta) and 3σ (green, GRA2 ligands in light green). Also note the shift in ligand positions at an acceleration level of 2σ. The positions of the ligands in the simulation at 3σ largely correspond to the ones observed in the initial X-ray structure.

Previously reported calculations using the same force-field but using the thermodynamic integration (TI) or the OSP approach yielded better agreement with experiment, with RMSE values of 3.9 and 1.9 kJ/mol, respectively.14 These simulations were likely also too short to observe the conformational changes in the active site described above. The calculations using the TI method amounted to a total simulation time of about 50 ns, while the previous simulations with the OSP method was based on 20 ns of simulation time.

For the TRP systems, calculated binding free energies were in better agreement with experimental data for acceleration levels of 1σ and 2σ than with an acceleration level of 3σ (Table S4 in the Supporting Information), possibly caused by insufficient state transitions for the given simulation time with 3σ. Moreover, simulations with 1σ and 2σ performed slightly better than previous calculations employing the same force-field and TI; however, a previously reported method employing OSP and the third-power fitting (TPF) approach for electrostatic interactions performed better than the A-EDS simulations.19 Except for compound 2, where the TI calculations overestimated the binding affinity, the values obtained for A-EDS with 2σ agree closely to the TI data with a root-mean-square difference of 2.9 kJ/mol. The total simulation of the A-EDS simulation for each acceleration level was 130 ns, compared to 245 ns for the previously reported TI method and 52 ns for the previously reported OSP/TPF method.

For the PNMT ligands, the free-energy values computed with an acceleration of 3σ fit experimental values much better than those computed with an acceleration of 2σ (see also Table S5 in the Supporting Information). However, more state transitions occurred, as expected, for an acceleration level of 2σ (Table 5 and Figure S8 in the Supporting Information). Visual inspection of the trajectories revealed that for the simulation with acceleration parameters determined for 2σ, the S-adenosyl-l-methionine (SAM) cofactor in the PNMT enzyme was in a different conformation, thereby changing the direct environment for the PNMT ligands bound to the protein (see Figure 4), explaining differences in calculated affinities of the end state for this simulation. A-EDS simulations with an acceleration level of 3σ performed similar in terms of comparison to experiment as previously reported values obtained with the same force-field and TI48 and better than other EDS-based methods.32,36 It is, moreover, noted that in the A-EDS simulations performed in this work ligand 2, to which the perturbation includes a net-charge change of the molecule, was included in the reference state, while it was omitted in previously reported EDS calculations. While the number of visits is very limited for this state (Table 5) and the binding affinities are quite different from the TI values (Table S5), the A-EDS approach is able to include this state and correctly predicts it to be a nonbinder. For each A-EDS acceleration level a total simulation time of 320 ns was used, while for the simulations employing TI sampling was done for ∼1.5 μs, and for the most recently reported approach employing EDS (RE-EDS) sampling was done for ∼670 ns.

Figure 4.

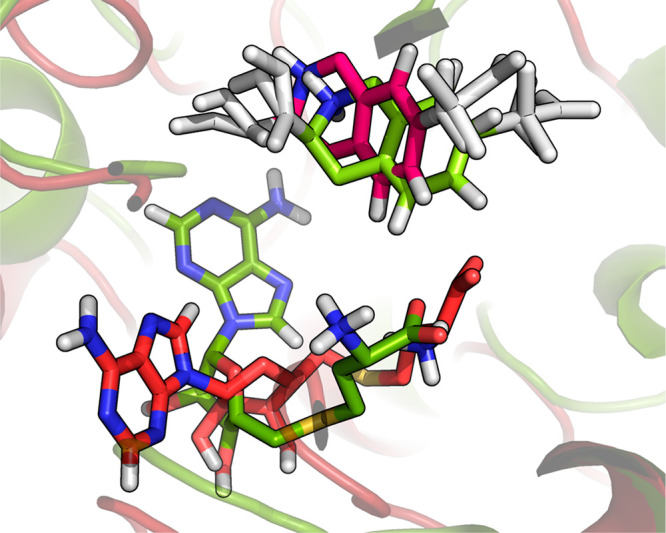
Figure 4

Open in a new tab

Different conformations of the S-adenosyl-l-methionine (SAM) cofactor in system PNMT at the end of A-EDS equilibrium simulations of the ligand end states bound to the protein, for an acceleration level of 2σ (red, PNMT ligand in magenta) and 3σ (green, PNMT ligand in light green).

For all systems, either simulations with acceleration parameters of 2σ or 3σ lead to the best agreement of the calculated binding free energies with experimental values. For system TRP, very little state transitions occurred with an acceleration level of 3σ, leading to undersampling and less good agreement with experimental values. For systems GRA2 and PNMT (2σ) conformations were sampled that differ from the experimentally determined structures, possibly explaining less good agreement with experimental values for these simulations. This highlights a so-far unexplored challenge for longer simulations sampling many different states. Due to the sampling of unphysical reference states and the inclusion of compounds with low affinity, the active site conformation may diverge to irrelevant conformations. Possibly adding further slight restraints on the active site conformations could already be sufficient to avoid this behavior.58 Simulations with an acceleration level of 3σ might perform generally better if enough simulation time is generated, as the energy landscape is less flattened and important energy minima are more pronounced.

Conclusion

In this work, we presented a novel automated parameter search scheme for A-EDS. The search scheme only requires a single chosen input-parameter, the anticipated acceleration level for flattening of the energy barriers between the EDS end states (σ-level). All other required parameters for equilibrium A-EDS simulations (A-EDS acceleration parameters Emax and Emin, and the free-energy offset parameters ΔFi≠1R) are determined using this search scheme in a nonequilibrium parameter-search simulation prior to the A-EDS equilibrium simulation. We demonstrated the applicability of this scheme with three well-established protein–ligand model systems and showed that using this method, free-energy differences between multiple ligands can be computed from a single simulation in an automated way. The full automation of the parameter-search simulations represents an important step forward compared to previously described multistate EDS simulations. All ligand end states were sampled, including ligands to which the perturbation involves net-charge changes. We tested three different acceleration levels for the parameter-search simulations and conclude that in general it is better to choose a more conservative acceleration level, as important energy minima might be lost otherwise. However, a more conservative choice of acceleration levels requires longer simulation times, and in practice, both the importance of energy minima and available simulation time have to be considered when choosing the acceleration level. A remaining challenge is the occurrence of conformational changes in the protein–ligand systems due to unfavorable ligand end states and the unphysical nature of the EDS reference state. EDS ligands that are strongly accelerated and incorporate unfavorable end-states need to be restrained to the protein to prevent them from leaving the binding site and to sample irrelevant binding modes.

Acknowledgments

The authors thank Sereina Riniker and Dominik Sidler for making the input data of the PNMT system available. J.W.P. is a recipient of a DOC Fellowship of the Austrian Academy of Sciences (ÖAW) at the Institute for Molecular Modeling and Simulation at the University of Natural Resources and Life Sciences, Vienna (Grant No. 24987). The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.0c00456.

  • Definition of the protein–ligand distance restraints for systems TRP and PNMT; calculated and experimentally determined binding affinities of all the compounds and systems; convergence of the A-EDS parameters during the parameter-search simulations for acceleration levels of 1σ and 3σ; convergence of the calculated relative free-energy differences ΔFi≠1,1 between the ligand end states relative to their final values from the equilibrium A-EDS simulations for all systems; ligand end state time series in the equilibrium A-EDS simulations for all systems; number of transitions between end states during the first 10 ns of the A-EDS parameter-search simulations with the ligand reference state bound to the protein; A-EDS free-energy offset parameter search results for the three different acceleration σ-levels for all systems (PDF)

  • GROMOS building block definitions for the different PNMT ligands used in this work (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ci0c00456_si_001.pdf (1.3MB, pdf)
ci0c00456_si_002.zip (3.6KB, zip)

References

  1. De Vivo M.; Masetti M.; Bottegoni G.; Cavalli A. Role of Molecular Dynamics and Related Methods in Drug Discovery. J. Med. Chem. 2016, 59, 4035–4061. 10.1021/acs.jmedchem.5b01684. [DOI] [PubMed] [Google Scholar]
  2. Tembre B. L.; Mc Cammon J. A. Ligand-receptor interactions. Comput. Chem. 1984, 8, 281–283. 10.1016/0097-8485(84)85020-2. [DOI] [Google Scholar]
  3. Hansen N.; van Gunsteren W. F. Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theory Comput. 2014, 10, 2632–2647. 10.1021/ct500161f. [DOI] [PubMed] [Google Scholar]
  4. Jorgensen W. L.; Thomas L. L. Perspective on Free-Energy Perturbation Calculations for Chemical Equilibria. J. Chem. Theory Comput. 2008, 4, 869–876. 10.1021/ct800011m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Christ C. D.; Fox T. Accuracy assessment and automation of free energy calculations for drug design. J. Chem. Inf. Model. 2014, 54, 108–120. 10.1021/ci4004199. [DOI] [PubMed] [Google Scholar]
  6. Mikulskis P.; Genheden S.; Ryde U. A large-scale test of free-energy simulation estimates of protein-ligand binding affinities. J. Chem. Inf. Model. 2014, 54, 2794–2806. 10.1021/ci5004027. [DOI] [PubMed] [Google Scholar]
  7. Wang L.; Wu Y.; Deng Y.; Kim B.; Pierce L.; Krilov G.; Lupyan D.; Robinson S.; Dahlgren M. K.; Greenwood J.; Romero D. L.; Masse C.; Knight J. L.; Steinbrecher T.; Beuming T.; Damm W.; Harder E.; Sherman W.; Brewer M.; Wester R.; Murcko M.; Frye L.; Farid R.; Lin T.; Mobley D. L.; Jorgensen W. L.; Berne B. J.; Friesner R. A.; Abel R. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 2015, 137, 2695–2703. 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
  8. Zwanzig R. W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
  9. Mark A. E.; Xu Y.; Liu H.; van Gunsteren W. F. Rapid non-empirical approaches for estimating relative binding free energies. Acta Biochim Pol 1995, 42, 525–535. 10.18388/abp.1995_4906. [DOI] [PubMed] [Google Scholar]
  10. Liu H.; Mark A. E.; van Gunsteren W. F. Estimating the Relative Free Energy of Different Molecular States with Respect to a Single Reference State. J. Phys. Chem. 1996, 100, 9485–9494. 10.1021/jp9605212. [DOI] [Google Scholar]
  11. Oostenbrink B. C.; Pitera J. W.; van Lipzig M. M. H.; Meerman J. H. N.; van Gunsteren W. F. Simulations of the Estrogen Receptor Ligand-Binding Domain: Affinity of Natural Ligands and Xenoestrogens. J. Med. Chem. 2000, 43, 4594–4605. 10.1021/jm001045d. [DOI] [PubMed] [Google Scholar]
  12. Oostenbrink C. Free energy calculations from one-step perturbations. Methods Mol. Biol. 2012, 819, 487–499. 10.1007/978-1-61779-465-0_28. [DOI] [PubMed] [Google Scholar]
  13. Raman E. P.; Vanommeslaeghe K.; Mackerell A. D. Jr. Site-Specific Fragment Identification Guided by Single-Step Free Energy Perturbation Calculations. J. Chem. Theory Comput. 2012, 8, 3513–3525. 10.1021/ct300088r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Norholm A. B.; Francotte P.; Goffin E.; Botez I.; Danober L.; Lestage P.; Pirotte B.; Kastrup J. S.; Olsen L.; Oostenbrink C. Thermodynamic characterization of new positive allosteric modulators binding to the glutamate receptor A2 ligand-binding domain: combining experimental and computational methods unravels differences in driving forces. J. Chem. Inf. Model. 2014, 54, 3404–3416. 10.1021/ci500559b. [DOI] [PubMed] [Google Scholar]
  15. Graf M. M.; Zhixiong L.; Bren U.; Haltrich D.; van Gunsteren W. F.; Oostenbrink C. Pyranose dehydrogenase ligand promiscuity: a generalized approach to simulate monosaccharide solvation, binding, and product formation. PLoS Comput. Biol. 2014, 10, e1003995 10.1371/journal.pcbi.1003995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Pitera J. W.; van Gunsteren W. F. One-Step Perturbation Methods for Solvation Free Energies of Polar Solutes. J. Phys. Chem. B 2001, 105, 11264–11274. 10.1021/jp012003j. [DOI] [Google Scholar]
  17. Oostenbrink C.; van Gunsteren W. F. Single-step perturbations to calculate free energy differences from unphysical reference states: limits on size, flexibility, and character. J. Comput. Chem. 2003, 24, 1730–1739. 10.1002/jcc.10304. [DOI] [PubMed] [Google Scholar]
  18. Oostenbrink C. Efficient free energy calculations on small molecule host-guest systems - a combined linear interaction energy/one-step perturbation approach. J. Comput. Chem. 2009, 30, 212–221. 10.1002/jcc.21116. [DOI] [PubMed] [Google Scholar]
  19. de Ruiter A.; Oostenbrink C. Efficient and Accurate Free Energy Calculations on Trypsin Inhibitors. J. Chem. Theory Comput. 2012, 8, 3686–3695. 10.1021/ct200750p. [DOI] [PubMed] [Google Scholar]
  20. Jandova Z.; Fast D.; Setz M.; Pechlaner M.; Oostenbrink C. Saturation Mutagenesis by Efficient Free-Energy Calculation. J. Chem. Theory Comput. 2018, 14, 894–904. 10.1021/acs.jctc.7b01099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Christ C. D.; van Gunsteren W. F. Enveloping distribution sampling: a method to calculate free energy differences from a single simulation. J. Chem. Phys. 2007, 126, 184110. 10.1063/1.2730508. [DOI] [PubMed] [Google Scholar]
  22. Han K.-K. A new Monte Carlo method for estimating free energy and chemical potential. Phys. Lett. A 1992, 165, 28–32. 10.1016/0375-9601(92)91048-V. [DOI] [Google Scholar]
  23. Wu D.; Kofke D. A. Phase-space overlap measures. II. Design and implementation of staging methods for free-energy calculations. J. Chem. Phys. 2005, 123, 084109. 10.1063/1.2011391. [DOI] [PubMed] [Google Scholar]
  24. Chen Y. G.; Hummer G. Slow conformational dynamics and unfolding of the calmodulin C-terminal domain. J. Am. Chem. Soc. 2007, 129, 2414–2415. 10.1021/ja067791a. [DOI] [PubMed] [Google Scholar]
  25. Bennett C. H. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J. Comput. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
  26. Han K. K. Multiensemble sampling: An alternative efficient Monte Carlo technique. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1996, 54, 6906–6910. 10.1103/PhysRevE.54.6906. [DOI] [PubMed] [Google Scholar]
  27. Lu N.; Wu D.; Woolf T. B.; Kofke D. A. Using overlap and funnel sampling to obtain accurate free energies from nonequilibrium work measurements. Phys. Rev. E 2004, 69, 057702. 10.1103/PhysRevE.69.057702. [DOI] [PubMed] [Google Scholar]
  28. Christ C. D.; van Gunsteren W. F. Multiple free energies from a single simulation: extending enveloping distribution sampling to nonoverlapping phase-space distributions. J. Chem. Phys. 2008, 128, 174112. 10.1063/1.2913050. [DOI] [PubMed] [Google Scholar]
  29. Reinhardt M.; Grubmüller H. Determining Free Energy Differences Through Non-Linear Morphing. J. Chem. Theory Comput. 2020, 16, 3504. 10.1021/acs.jctc.0c00106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Christ C. D.; van Gunsteren W. F. Simple, Efficient, and Reliable Computation of Multiple Free Energy Differences from a Single Simulation: A Reference Hamiltonian Parameter Update Scheme for Enveloping Distribution Sampling (EDS). J. Chem. Theory Comput. 2009, 5, 276–286. 10.1021/ct800424v. [DOI] [PubMed] [Google Scholar]
  31. Christ C. D.; Van Gunsteren W. F. Comparison of three enveloping distribution sampling Hamiltonians for the estimation of multiple free energy differences from a single simulation. J. Comput. Chem. 2009, 30, 1664–1679. 10.1002/jcc.21325. [DOI] [PubMed] [Google Scholar]
  32. Riniker S.; Christ C. D.; Hansen N.; Mark A. E.; Nair P. C.; van Gunsteren W. F. Comparison of enveloping distribution sampling and thermodynamic integration to calculate binding free energies of phenylethanolamine N-methyltransferase inhibitors. J. Chem. Phys. 2011, 135, 024105. 10.1063/1.3604534. [DOI] [PubMed] [Google Scholar]
  33. Hansen N.; Dolenc J.; Knecht M.; Riniker S.; van Gunsteren W. F. Assessment of enveloping distribution sampling to calculate relative free enthalpies of binding for eight netropsin-DNA duplex complexes in aqueous solution. J. Comput. Chem. 2012, 33, 640–651. 10.1002/jcc.22879. [DOI] [PubMed] [Google Scholar]
  34. Maurer M.; Hansen N.; Oostenbrink C. Comparison of free-energy methods using a tripeptide-water model system. J. Comput. Chem. 2018, 39, 2226–2242. 10.1002/jcc.25537. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sidler D.; Schwaninger A.; Riniker S. Replica exchange enveloping distribution sampling (RE-EDS): A robust method to estimate multiple free-energy differences from a single simulation. J. Chem. Phys. 2016, 145, 154114. 10.1063/1.4964781. [DOI] [PubMed] [Google Scholar]
  36. Sidler D.; Cristofol-Clough M.; Riniker S. Efficient Round-Trip Time Optimization for Replica-Exchange Enveloping Distribution Sampling (RE-EDS). J. Chem. Theory Comput. 2017, 13, 3020–3030. 10.1021/acs.jctc.7b00286. [DOI] [PubMed] [Google Scholar]
  37. Hamelberg D.; Mongan J.; McCammon J. A. Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–29. 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
  38. Miao Y.; Feher V. A.; McCammon J. A. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. 10.1021/acs.jctc.5b00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Perthold J. W.; Oostenbrink C. Accelerated Enveloping Distribution Sampling: Enabling Sampling of Multiple End States while Preserving Local Energy Minima. J. Phys. Chem. B 2018, 122, 5030–5037. 10.1021/acs.jpcb.8b02725. [DOI] [PubMed] [Google Scholar]
  40. Kollman P. Free energy calculations: Applications to chemical and biochemical phenomena. Chem. Rev. 1993, 93, 2395–2417. 10.1021/cr00023a004. [DOI] [Google Scholar]
  41. Åqvist J. Calculation of absolute binding free energies for charged ligands and effects of long-range electrostatic interactions. J. Comput. Chem. 1996, 17, 1587–1597. . [DOI] [Google Scholar]
  42. Essex J. W.; Severance D. L.; Tirado-Rives J.; Jorgensen W. L. Monte Carlo Simulations for Proteins: Binding Affinities for Trypsin-Benzamidine Complexes via Free-Energy Perturbations. J. Phys. Chem. B 1997, 101, 9663–9669. 10.1021/jp971990m. [DOI] [Google Scholar]
  43. Wang W.; Wang J.; Kollman P. A. What determines the van der Waals coefficient β in the LIE (linear interaction energy) method to estimate binding free energies using molecular dynamics simulations?. Proteins: Struct., Funct., Genet. 1999, 34, 395–402. . [DOI] [PubMed] [Google Scholar]
  44. Brandsdal B. O.; Smalas A. O.; Aqvist J. Electrostatic effects play a central role in cold adaptation of trypsin. FEBS Lett. 2001, 499, 171–175. 10.1016/S0014-5793(01)02552-2. [DOI] [PubMed] [Google Scholar]
  45. Brandsdal B. O.; Aqvist J.; Smalas A. O. Computational analysis of binding of P1 variants to trypsin. Protein Sci. 2001, 10, 1584–1595. 10.1110/ps.940101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Leiros H. K.; Brandsdal B. O.; Andersen O. A.; Os V.; Leiros I.; Helland R.; Otlewski J.; Willassen N. P.; Smalas A. O. Trypsin specificity as elucidated by LIE calculations, X-ray structures, and association constant measurements. Protein Sci. 2004, 13, 1056–1070. 10.1110/ps.03498604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Jiao D.; Golubkov P. A.; Darden T. A.; Ren P. Calculation of protein-ligand binding free energy by using a polarizable potential. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 6290–6295. 10.1073/pnas.0711686105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Nair P. C.; Malde A. K.; Mark A. E. Using Theory to Reconcile Experiment: The Structural and Thermodynamic Basis of Ligand Recognition by Phenylethanolamine N-Methyltransferase (PNMT). J. Chem. Theory Comput. 2011, 7, 1458–1468. 10.1021/ct1007229. [DOI] [PubMed] [Google Scholar]
  49. Torda A. E.; Scheek R. M.; van Gunsteren W. F. Time-dependent distance restraints in molecular dynamics simulations. Chem. Phys. Lett. 1989, 157, 289–294. 10.1016/0009-2614(89)87249-5. [DOI] [Google Scholar]
  50. Schmid N.; Christ C. D.; Christen M.; Eichenberger A. P.; van Gunsteren W. F. Architecture, implementation and parallelisation of the GROMOS software for biomolecular simulation. Comput. Phys. Commun. 2012, 183, 890–903. 10.1016/j.cpc.2011.12.014. [DOI] [Google Scholar]
  51. Martyna G. J.; Klein M. L.; Tuckerman M. Nosé–Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. 10.1063/1.463940. [DOI] [Google Scholar]
  52. Hockney R. W.The Potential Calculation and some Applications; Academic Press Inc.: New York, 1970; p 77 p. [Google Scholar]
  53. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  54. Miyamoto S.; Kollman P. A. Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
  55. Tironi I.; Sperb R.; Smith P.; van Gunsteren W. F. A Generalized Reaction Field Method for Molecular Dynamics Simulation. J. Chem. Phys. 1995, 102, 5451. 10.1063/1.469273. [DOI] [Google Scholar]
  56. Heinz T. N.; van Gunsteren W. F.; Hünenberger P. H. Comparison of Four Methods to Compute the Dielectric Permittivity of Liquids from Molecular Dynamics Simulations. J. Chem. Phys. 2001, 115, 1125–1136. 10.1063/1.1379764. [DOI] [Google Scholar]
  57. Oostenbrink C.; van Gunsteren W. F. Free energies of binding of polychlorinated biphenyls to the estrogen receptor from a single simulation. Proteins: Struct., Funct., Genet. 2004, 54, 237–246. 10.1002/prot.10558. [DOI] [PubMed] [Google Scholar]
  58. Menzer W. M.; Xie B.; Minh D. D. L. On Restraints in End-Point Protein-Ligand Binding Free Energy Calculations. J. Comput. Chem. 2020, 41, 573–586. 10.1002/jcc.26119. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci0c00456_si_001.pdf (1.3MB, pdf)
ci0c00456_si_002.zip (3.6KB, zip)

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES