Abstract
The purpose of this study was to identify the optimal tracer kinetic model from dynamic contrast-enhanced T1‐weighted magnetic resonance imaging (DCE-MRI) data and evaluate whether parameters estimated from the optimal model predict tumor aggressiveness determined from histopathology in patients with papillary thyroid carcinoma (PTC) prior to surgery. In this prospective study, 18 PTC patients underwent pretreatment DCE-MRI on a 3T MR scanner prior to thyroidectomy. This study was approved by the institutional review board and informed consent was obtained from all patients. The two-compartment exchange model (2CXM), compartmental tissue uptake model (CTUM), extended Tofts model (ETM), and standard Tofts model (TM) were compared on a voxel-wise basis to determine the optimal model using the corrected Akaike information criterion (AICc) for PTC. The optimal model is the one with the lowest AICc. Statistical analysis included paired and unpaired t-tests and a one-way Analysis of variance. Bonferroni correction was applied for multiple comparisons. Receiver operating characteristic (ROC) curves were generated from the optimal model parameters to differentiate PTC with and without aggressive features, and AUC’s were compared. ETM performed the best with the lowest AICc and highest weights (0.44) among the four models. ETM was preferred in 44% of all 3419 voxels. The ETM estimates of Ktrans in PTCs with aggressive feature extrathyroidal extension (ETE) were significantly higher than those without ETE (0.78±0.29 vs. 0.34±0.18 min−1, P=0.005). From ROC analysis, cut-off values of Ktrans, ve, and vp which discriminated between PTCs with and without ETE were determined at 0.45 min−1, 0.28, and 0.014, respectively. The sensitivities and specificities were 86% and 82% (Ktrans), 71% and 82% (ve), and 86% and 55% (vp). Their respective AUC’s were 0.90, 0.71, and 0.71. We conclude the ETM Ktrans has shown potential to classify tumors with and without aggressive ETE in patients with PTC.
Keywords: dynamic contrast-enhanced magnetic resonance imaging, tracer kinetic model, papillary thyroid cancer, aggressiveness, perfusion, permeability and Akaike information criterion
Introduction:
Intrathyroidal well-differentiated papillary thyroid carcinoma (PTC) is usually an indolent malignant tumor with a low recurrence rate (<3–4%) and a high disease-specific survival rate (> 99%) 1. Traditional treatment of PTC includes a total thyroidectomy, often with radioactive iodine remnant ablation 2. However, this aggressive treatment approach has been questioned by recent studies which demonstrate that very low-risk thyroid cancer patients may not require immediate thyroid surgery and approaches with an active surveillance may be safely employed 3. Therefore, initial management recommendations are very highly dependent on preoperative studies that are designed to evaluate the presence of PTC with aggressive features, including extrathyroidal extension (ETE), tall cell variant, distant metastases, regional metastases, and vascular and/or tumor capsular invasion. For example, minimal ETE is characterized by involvement of the perithyroid soft tissue or sternothyroid muscle, and significant ETE is characterized by invasion into larynx, trachea, esophagus, recurrent or subcutaneous soft tissue. Although fine-needle aspiration (FNA) cytology is the most widely used and cost-effective method for preoperative evaluation of thyroid nodules 4, it provides minimal information about tumor aggressiveness 5. Currently, tumor aggressiveness is based on surgical histological analysis which is only available after surgical resection of the thyroid gland 6. Thus, there remains a pressing need for non-invasive tests to identify patients with histologically aggressive tumors so that the initial surgical procedures can be more appropriately tailored to tumor risk.
Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is a noninvasive technique that allows estimation of the parameters reflecting physiological characteristics of tumor vasculature 7,8. The DCE technique involves the serial acquisition of T1-weighted (T1w) images before, during, and after the injection of low molecular weight gadolinium-labeled contrast agent (CA). With a proper choice of tracer kinetic model, the time course of DCE data can be analyzed to estimate the plasma flow (Fp), permeability-surface area product (PS), and volume fractions of the blood plasma (vp), and extracellular extravascular space [EES] (ve) 9,10. The most general two-compartment exchange model (2CXM: Fp, PS, ve, and vp) reduces to simpler models under special approximations, including the compartmental tissue uptake model (CTUM), extended Tofts model (ETM), and standard Tofts model (TM). Donaldson et al., reported that 2CXM generated a significantly superior fit as compared to ETM in all 30 cervical tumor patients 11. The three parameter CTUM (ie, Fp, PS, and vp) assumes negligible reflux of the CA from the EES to the vascular space. The CTUM estimates of Fp and PS have shown promise for early assessment of tumor response to radiation therapy in cervical cancer 12. The standard TM was initially purposed for weakly vascularized tissue was later extended in order to account for highly perfused tissues by introducing the parameter vp. TM and ETM estimate the physiological parameter, Ktrans (ie, volume transfer constant of CA from vascular space into EES) in tumor tissue which characterizes either Fp in flow-limited (PS >> Fp), PS in permeability limited (PS << Fp) conditions, or a combination of both Fp and PS in the mixed flow-permeability condition 13. As a measure of vessel permeability, Ktrans, has shown promise in characterizing tumor aggressiveness in breast and prostate cancers 14,15.
Model selection techniques identify the model that fits the sample of time varying data more closely (referred to as the ‘best model’) among a set of candidate models in DCE-MRI studies. The best tracer kinetic model requires accounting not only for goodness of fit, but also the number of fit parameters 16. While applying a model selection technique to DCE data, temporal resolution, duration of dynamic acquisition, tumor underlying physiology, and stability of complex models need to be considered 17. Previous clinical DCE studies in oncology have understood this importance and employed the F-Statistic (F-test) 11,18, chi-square 19, corrected Akaike information criteria (AICc) 19–22, and Bayesian information criteria 12,19 to select a model that provides the best fit to DCE data. The resulting quantitative tumor physiological parameters obtained from an optimal model have clinical importance for the use of oncologic imaging biomarkers in clinics 8.
Prior semi-quantitative DCE-MRI analyses exhibited promising ability to differentiate benign and malignant thyroid nodules, but the information provided is too limited to stratify tumors based on the histopathological markers of aggressiveness before surgery 23,24. There is a lack of literature in quantitative analysis of DCE data to non-invasively assess tumor aggressiveness in PTC. Previous studies have reported that typical DCE data samples in a tumor can provide three 18, or at most four 11,22 parameters, depending on the temporal resolution and underlying tumor physiology. To the best of our knowledge, there is no study that employed the model selection technique to assess tumor microvasculature and aggressiveness in patients with PTC.
The purpose of the present prospective study is two-fold. First, we apply a model selection technique to identify the optimal tracer kinetic model among the 2CXM, CTUM, ETM, and TM that provides the best fit to PTC DCE data, using the AICc on a voxel-wise basis. Secondly, we evaluate whether the parameters generated from the optimal model can characterize tumor aggressiveness as determined from the surgical histopathology analysis in PTCs prior to surgery.
Materials and Methods:
Calculation of R1 from SPGR DCE Data
The signal intensity of a voxel measured from a spoiled gradient recalled echo (SPGR) T1w acquisition is given by 18
| [1] |
where S (t) = signal intensity at time t, M0 = magnetization of the protons, θ = flip angle, TR=repetition time, and TE=echo time. R1 (t) (R1[t]=1/T1[t] = time course of longitudinal relaxation rate, and R2*(t) (R2*[t]=1/T*2[t]) = time course of transverse relaxation rate.
R1 (t) derived from Equation [1] can be expressed as follows:
| [2] |
For R1(t) calculation, the effects of R2* (R2*= 1/T2*) can be minimized with short TE (ie, , when TE << T2*).
Quantitative DCE-T1w data analysis assumes a linear relationship between the change in R1(t) (i.e., ΔR1[t]) and the concentration of CA in tissue after intravenous administration 13:
| [3] |
where = time course of CA concentration in tissue (mM), = longitudinal relaxivity of the CA (mM−1S−1).
Concentration-Time Equations
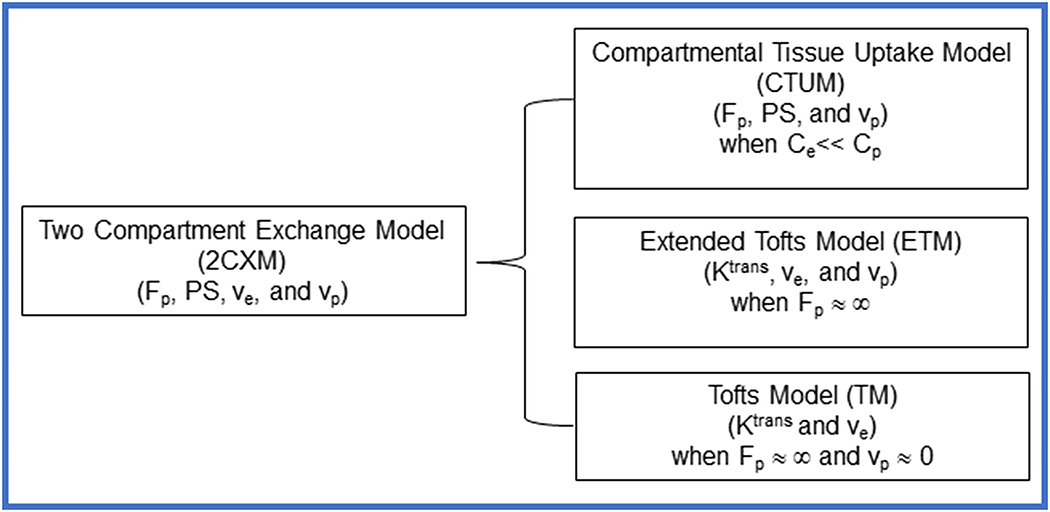
The 2CXM assumes two well-mixed compartments (blood plasma and EES space) where CA can diffuse back and forth between these two compartments. The parameters derived from the hierarchy of models, 2CXM (Fp [min−1], PS [min−1], ve, and vp), CTUM (Fp, PS, and vp), ETM (Ktrans [min−1], ve, and vp), TM (Ktrans and ve) used in this study are summarized in Figure 1. The observable Ct(t) equations used for these tracer kinetic models are described below 25.
Figure 1.
Summary of the four hierarchical tracer kinetic models and their corresponding parameters. Generalized 2CXM model under specific approximations reduces to CTUM, ETM, and TM25.
For the general 2CXM, Ct(t), is a biexponential function, expressed as 25:
| [4] |
where Cp(t) = time course of the plasma concentration of the CA (mM), which is also called the arterial input function (AIF), Fp = plasma flow (min−1) and ⨂ denotes convolution operation. and are given in Appendix 1.
The Ct (t) for the CTUM derived from a 2CXM by assuming Ce(t) << Cp (t) is given by 25
| [5] |
where E is the first extraction fraction, E = and Tp is the mean plasma transit time, .
The Ct(t) for ETM, which incorporates the contribution of vascular space, is given by 13:
| [6] |
where (min−1) is the rate constant of CA transport from EES to vascular space.
The Ct(t), for TM is given by 13:
| [7] |
Patients
Between January 2011 and March 2015, twenty patients (n=20) evaluated for thyroidectomy were enrolled due to thyroid nodule FNA after demonstrating either PTC or suspicion for thyroid cancer. Our institutional review board approved this Health Insurance Portability and Accountability Act (HIPAA)-compliant prospective study in which the patients underwent research MRI prior to thyroid surgery.
MRI Data Acquisition
MRI scans were performed on a 3.0 T MR scanner (Discovery MR 750, GE Healthcare, Milwaukee, WI) with a neurovascular phased-array coil before surgery. Preceding the DCE-MRI, anatomical scans, including T1w and T2-weighted (T2w) MRI scans covering the entire thyroid gland, were performed. DCE-MRI images were acquired using a 3D T1w SPGR pulse sequence with a flip angle of 15° and other imaging parameters as follows: repetition time (TR)/echo time (TE) = 5.7/1.7 ms, acquisition matrix=256×128 that was zero-filled to 256×256 during image reconstruction, field of view = 20–24 cm, slice thickness=5 mm, and 6–8 slices covering the tumor region, which yielded images with a temporal resolution ranging from 4.4 to 5.8 s. A total of 50 dynamic volumes were acquired in ~ 5 minutes. A bolus of 0.1 mmol/kg Gd-based CA, used in clinical practice, was delivered through an antecubital vein catheter at 2 cc/s, followed by a 20-ml saline flush using an MR-compatible programmable power injector (Spectris; Medrad, Indianola, PA, USA). Prior to the dynamic imaging acquisitions, precontrast T1w images were acquired for T1 mapping using the same 3D T1w SPGR sequence parameters with multiple flip angles of 5°, 15°, and 30°.
Tracer Kinetic Model Selection
The corrected Akaike’s Information Criterion (AICc) gives a measure of the goodness- of- fit of a model that can be used to compare two or more models by incorporating the number of variable parameters in the model, and is given by 26
| [8] |
where N = number of measurement data points, k = number of parameters (2 for TM, 3 for ETM, 3 for CTUM, and 4 for 2CXM) and SSE is the sum of squares of the residual. AICc accounts for a small number of observations, when N/k <40. The best tracer kinetic model from a set of candidate’s models is the model with the lowest AICc. The ΔAICc and Akaike weights which are derived from the AICc are other representations to rank the model.
The Akaike weights (wm) represents the ratio of for each model relative to the sum of value of all potential candidate models and is calculated as follows 26
| [9] |
where wm is the weight for the mth model, is the difference in AICcm value between m and the best model (i.e., the model with the lowest AICc), and R is the total number of candidate models. The wm represents as estimates of the relative probability of a given model for a given data.
Image Analysis
Regions of interest (ROIs) were manually drawn on T1w DCE images of each PTC patient using ImageJ 27. The ROI was assessed by a neuroradiologist with more than 10 years of experience, based on the enhancing region and radiological and clinical information, including ultrasound reports. ROIs were placed on thyroid glands while avoiding observed cystic, hemorrhagic, or calcified portions, and were used to calculate tumor volume. AIFs were extracted from the carotid artery in each patient, using manually-drawn ROI’s on the T1w DCE image as described elsewhere 28. Literature value of the blood precontrast longitudinal relaxation (T10) was set to 1660 ms 29. Blood CA concentration was converted to plasma concentrations using a literature value for a hematocrit of 0.45. The longitudinal relaxivity of CA is assumed to be a constant at a given field strength (r1=4.0 mM−1s−1). The tumor ROI volume in each patient was calculated from the dynamic T1w images.
The signal data were extracted on a voxel-by-voxel basis within the tumor ROIs across all the image slices containing sections of the tumour. Precontrast T1 maps were generated by fitting the variable flip angle data to Equation [1] for each voxel within the ROI 30. The tissue CA concentration- time course data fitted with the 2CXM (Eqn. [4]), CTUM (Eqn. [5]), ETM (Eqn. [6]), and TM (Eqn. [7]) provides estimate of all the parameters (ie, Fp, PS, Ktrans, ve, and vp) and respective AICc value in each voxel. The fitting procedures generated the parametric maps of Fp, PS, Ktrans, ve, vp, and AICc. Model-fitting employed a non-linear least squares algorithm that minimizes the sum of squared errors (SSE) between model fit and data. A multiple start scheme (~10 times in this study) was used in the optimization procedure. For each time, the start value of each parameter was the random value chosen between the lower and upper bound of the parameter set. Estimates of tracer kinetic model metrics values were bounded as follows: Fp ∈ [0, 5] (min−1), PS ∈ [0, 5] (min−1), Ktrans ∈ [0, 5] (min−1), ve, and vp ∈ [0, 1]. Non-convergent voxels, voxels converged to nonphysical value, and voxels where the monoexponential was preferred over the bi-exponential model were excluded from the analysis. The ETM estimates of Ktrans were compared with the 2CXM/CTUM constructed Ktrans, which is the product of the plasm flow, Fp, and the first-pass extraction fraction, E, and is given by 25.
The model with the lowest AICc value was identified and the ΔAICcm and Akaike weight (wm) were calculated for each model in each voxel. Voxels value of each parameter (ie, Fp, PS, Ktrans, ve, vp) and AICc over the whole tumor ROI were averaged for each model in each patient. Summary statistics for the parameters and respective AICc of each model were reported as mean±standard deviation (SD). The percentage of voxels with the lowest AICc was expressed as the ratio of the number of voxels with the lowest AICc to the total number of voxels from all ROIs for each model in each individual patient. The vascular parameters obtained from the best model were used to characterize tumor with and without aggressiveness, which was determined from the surgical histopathology analysis. The best model approach is th one with the lowest AICc and highest Akaike weight (wm) among the candidates model 21. All DCE data analysis were performed using in-house-developed software entitled MRI-QAMPER (MRI Quantitative Analysis of Multi-Parametric Evaluation Routines) written in MATLAB (Mathworks, Natick, USA).
Histopathologic examination
Surgical specimens of the PTC were taken after radical thyroidectomy or lobectomy under the supervision of a pathologist with more than 10 years of experience. The details of the pathology have been described previously by Lu, et al. 31. Paraffin-embedded tissue blocks were obtained for each surgically resected specimen by sectioning each tumor and staining the sections with hematoxylin and eosin. The pathologist reviewed the hematoxylin and eosin section of each tumor and evaluated tumor aggressiveness using established criteria 32,33. The 6 histopathologic features that were evaluated were ETE, tall cell variant, necrosis, vascular and/or tumor capsular invasion, regional metastases, and distant metastases. A tumor with the presence of any one of these features was deemed aggressive.
Statistical Analysis
The differences in mean values were assessed using a two-tailed paired t-test for three parameters, Fp, PS, and Ktrans. One-way analysis of variance (ANOVA) was performed for ve, vp, and AICc to test the significant difference among the model’s estimate. Bonferroni’s correction was performed to account for multiple comparisons of Fp, PS, Ktrans, ve, vp, and AICc. The parameters value estimated from optimal tracer kinetic model were then compared for PTC patients with and without features of tumor aggressiveness (the 6 features mentioned above) using a two-tailed unpaired two-sample t-test. For the parameters which were comparable or common between four models, Pearson correlation coefficients were calculated to examine the distribution difference of those parameters between different models. A P value <0.05 was considered statistically significant and adjusted significant P value after Bonferroni’s correction was 0.008.
Receiver operating characteristic (ROC) analysis was performed to assess the ability of a parameter to differentiate between tumors with and without aggressive features. This analysis was conducted for individual and combinations of parameters obtained from the optimal model. Best cut-off points were obtained using Youden’s index 34, and sensitivities and specificities were calculated. AUCs were estimated using the trapezoidal rule. For the optimal model, additional analysis was performed to compare the AUCs for the full model, estimated using all parameters, and the univariate model, for each parameter separately 35. All statistical analyses were performed in the R statistical computing environment 36.
Results:
T1w DCE data were acquired from all twenty (n=20) patients diagnosed with papillary thyroid cancer (PTC). From these 20, two patients were excluded from the analysis due to poor contrast-to-noise ratio. Subsequently, 18 PTC patients (mean age=44 years, age: 26–78 years, Male/Female: 6/12) comprised this prospective clinical trial. As summarized in Table 1, all 18 patients had PTC diagnosed from surgical pathology analysis, including 7 patients with ETE, 6 patients with tall cell variant, 3 patients with vascular and/or capsular invasion, and 12 patients with locoregional metastases. From T1w DCE images, the mean volume of tumor ROIs in 18 PTC patients was 0.84 ± 0.63 cm3 (range = 0.10 to 1.92 cm3).
Table 1.
Patient characteristics
| Characteristic | n (%) |
|---|---|
| Age at diagnosis (years) | 44 ± 15 years (range 26–78 years) |
| Sex | |
| Female | 12 (67%) |
| Male | 6 (33%) |
| Fine-needle aspiration cytology | |
| Papillary thyroid cancer | 15 (83%) |
| Suspicious for papillary thyroid cancer | 3 (17%) |
| Histology | |
| Classic papillary thyroid cancer (cPTC) | 9 (50%) |
| Follicular variant papillary thyroid cancer (fvPTC) | 2 (11%) |
| Diffuse sclerosing PTC (dsPTC) | 1 (6%) |
| Tall cell variant PTC (tPTC) | 3 (17%) |
| Multifocal (cPTC+tPTC) | 3 (17%) |
| Size of papillary carcinoma | 15.2 ± 6.81 mm (range 5–28 mm) |
| Aggressive features based on pathology | |
| Tall cell | 6 (33%) |
| Extrathyroidal extension | 7 (39%) |
| Necrosis | 0 (0%) |
| Vascular and/or tumor capsular invasion | 3 (17%) |
| Regional metastases | 12 (67%) |
| Distant metastases | 0 (0%) |
| Pathology T | |
| T1a | 6 (33%) |
| T1b | 5 (22%) |
| T2 | 0 (0%) |
| T3 | 7 (39%) |
| Pathology N | |
| N0 | 6 (33%) |
| N1a | 5 (28%) |
| N1b | 7 (39%) |
| Clinical M | |
| M0 | 18 (100%) |
| M1 | 0 (0%) |
| AJCC Stage | |
| I | 14 (78%) |
| II | 0 (0%) |
| III | 2 (11%) |
| IVA | 2 (11%) |
Tracer Kinetic Model selection
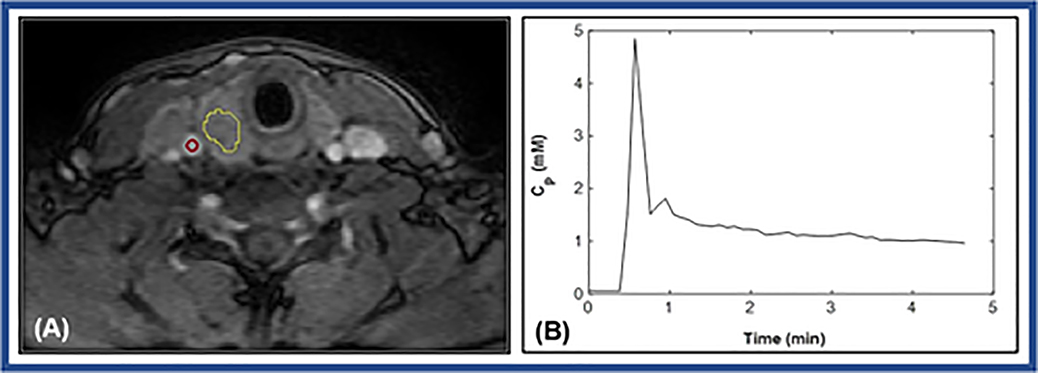
Figure 2(A) shows a representative PTC patient (36 years, female) with aggressive ETE features. The tumor ROI (delineated with yellow contour) and carotid artery ROI (red circle) are shown overlaid on the precontrast T1w image. An example AIF curve [Cp(t)] as obtained from this patient is illustrated in Figure 2(B).
Figure 2.
(A). Representative T1weighted image within dynamic scan at the postcontrast phase obtained from a papillary thyroid cancer patient with extrathyroidal extension (36 years, female). Regions of interest (ROIs) were drawn on a tumor (yellow curve line) and on a carotid artery (red circle). (B). Plot of the representative time course of plasma contrast agent (CA) concentration [Cp (t)] extracted from the ROI (red circle) within carotid.
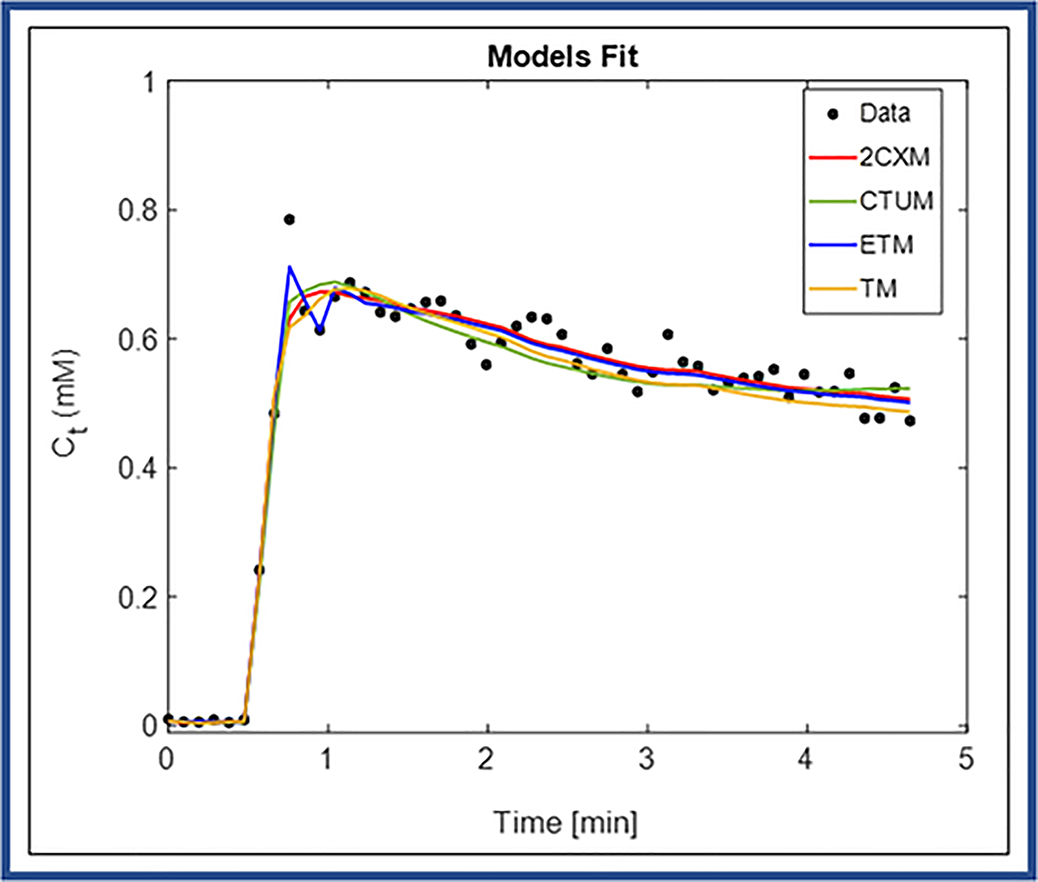
Figure 3 shows an example of tissue CA concentration- time course [Ct(t)] data obtained from one enhancing voxel from within the tumor ROI (Figure 2(A)) fitted with 2CXM, CTUM, ETM, and TM. The ETM exhibited the best model yielding the lowest AICc for this representative data (AICc = −531.09, wETM ≈ 1.0) as compared to the other three models (ie, 2CXM=−276.66, CTUM=−509.78, and TM=−341.35). For a representative voxel, the parameter values obtained from four models were as follows: 2CXM: Fp = 1.04 (min−1), PS = 0.98 (min−1) ve = 0.27, and vp = 0.25; CTUM: Fp = 0.42 (min−1), PS = 0.02 (min−1), and vp = 0.18; ETM: Ktrans = 0.69 (min−1), ve = 0.35, and vp = 0.015, and TM: Ktrans = 0.80 (min−1), ve = 0.35.
Figure 3.
Plot of the time course of tissue CA concentration data [Ct (t)] for one enhancing pixel obtained from a ROI (yellow curve line) within tumor. Data are shown in circles (black), best fit to two compartment exchange model (2CXM) in red, compartmental uptake model (CTUM) in blue, extended Tofts model (ETM) in green, and Tofts model (TM) in orange.
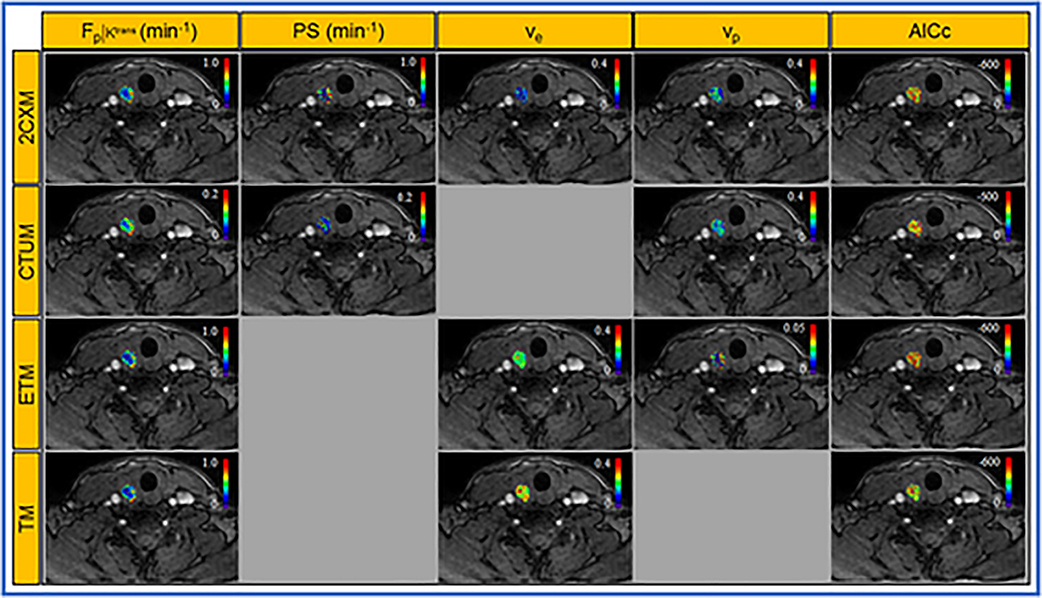
Figure 4 displays the parametric maps generated from 2CXM, CTUM, ETM, and TM, overlaid on the representative patient’s precontrast T1w image.
Figure 4.
Parametric estimates of four models map overlaid on the precontrast T1w image from a representative PTC patient with extrathyroidal extension (ETE) (female, 36 years).Two compartment exchange model (2CXM) parameters: plasma flow (Fp [min−1 ]), permeability-surface area product (PS [min−1]), and volume fractions of the extravascular extracelluar space (ve) vascular space (vp), compartmental model parameters: Fp [min−1 ], PS [min−1], and vp, extended Tofts model parameters: volume transfer constant (Ktrans [min−1 ]), ve, and vp, standard Tofts model parameters: Ktrans [min−1] and ve, and the corrected Akaike information criterion (AICc), an estimator of the relative quality of statistical models (top to bottom panels).
Table 2 summarizes whole-tumor ROI parameters values (mean±SD) estimated with the 2CXM, CTUM, ETM, and TM, for the 18 PTC patients in the study. There was a statistically significant difference between the mean value of Fp and PS obtained from 2CXM and CTUM (P<0.0001 for both Fp and PS, paired t- test).The analysis of one way ANOVA revealed significant difference among the ve value of 2CXM, ETM, and TM (ANOVA, P<0.011) and vp value of 2CXM, ETM, and CTUM (ANOVA, P<0.0001). TM and ETM estimate of mean Ktrans values were significantly lower than those mean values of Fp and PS derived from 2CXM (P<0.0001 for both Fp and PS) whereas CTUM estimates of Fp and PS were significantly lower than those of Ktrans obtained with the TM and ETM (P<0.0001 for both Fp and PS). Mean vp value estimated from 2CXM and CTUM were about 4 and 8 times greater than that of mean vp values obtained from ETM (P<0.0001). The mean Ktrans values obtained from TM and ETM were statistically significantly different (P<0.003). After Bonferroni correction, the parameters Fp, PS, Ktrans, and vp still showed significant differences (P<0.008). A significant difference was found between the ETM estimates of Ktrans values and Ktrans value constructed from the 2CXM/CTUM (P<0.001 for both 2CXM and CTUM). Mean Ktrans values constructed from the 2CXM and CTUM (P=0.001) were significantly different (P<0.001), indicating a major difference between these two model’s assumptions. The mean transit time (MTT) values calculated from the 2CXM and CTUM were 5.73±3.36 sec and 36.25±9.74 sec, respectively.
Table 2.
Summary of parameter values obtained for the four models from ROIs in 18 PTC patients*
| Model | Fp (min−1) | PS (min−1) | Ktrans (min−1) | ve | vp |
|---|---|---|---|---|---|
| 2CXM | 0.77 ± 0.48 | 0.79 ± 0.45 | 0.17 ± 0.09 | 0.12 ± 0.05 | |
| CTUM | 0.33 ± 0.21 | 0.07 ± 0.05 | 0.23 ± 0.11 | ||
| ETM | 0.51 ± 0.31 | 0.25 ± 0.10 | 0.028 ± 0.026 | ||
| TM | 0.62 ± 0.39 | 0.28 ± 0.12 | |||
| p value | <0.0001 | <0.0001 | <0.0001 | 0.0001a <0.001b 0.001c |
0.001d 0.0001e 0.0001f |
The reported values are mean ± standard deviation
The parameters vp and ve are dimensionless fractional volumes for plasma space and extracellular extravascular space, respectively.
ve obtained with two compartment exchange model (2CXM) compared with the extended Tofts model (ETM), and Tofts model (TM) and ETM compared and TM compared (ANOVA)
vp obtained with extended 2CXM compared with compartmental uptake model (CTUM) and ETM and CTUM compared with ETM (ANOVA)
The common or comparable parameters obtained from four models were tested for correlation. The mean Ktrans values estimated with ETM showed significant correlation with the mean values of Fp obtained from 2CXM (r=0.91, P<0.0001) and CTUM (r=0.95, P<0.0001). Mean values of Ktrans and 2CXM PS showed significant correlation (r=0.93 P<0.0001) whereas with CTUM derived PS showed a weak negative correlation (r = −0.44 for ETM, P >0.05). Mean values of ve obtained from 2CXM and ETM were significantly correlated (r=0.90, P<0.0001). No correlation was observed between vp estimated with the 2CXM and ETM (r = 0.08, P>0.05) and CTUM and ETM (r=0.02, P>0.05). A significant correlation was observed between vp obtained with the 2CXM and CTUM (r = 0.65, P=0.003). The estimates of Fp and PS by 2CXM were highly correlated (r= 0.97, P=0.05) whereas CTUM, which ignore the back flux, estimates of Fp and PS were negatively correlated (r= −0.40, P =.011).
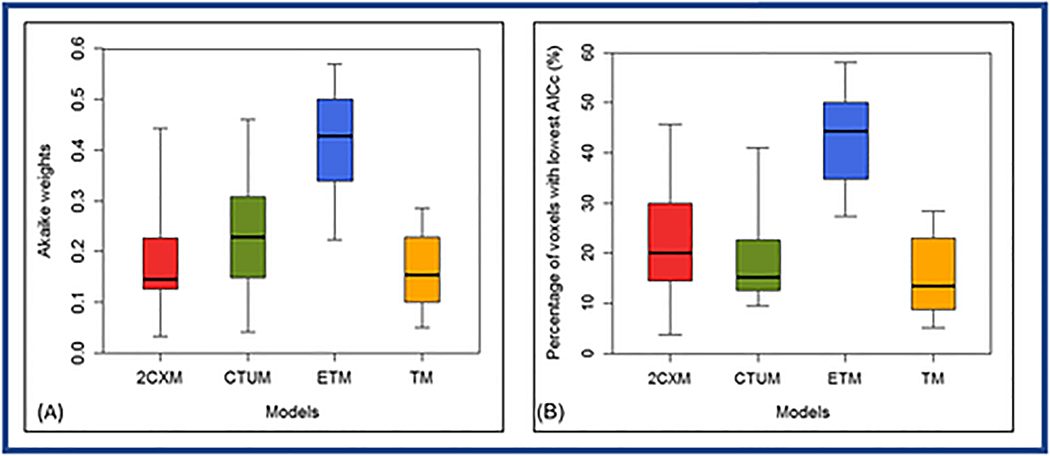
Table 3 shows the AICc and Akaike weights (wm) for the 2CXM, CTUM, ETM, and TM from the 18 PTC patients. ETM showed the lowest mean AICc (−408.20±63.98) and the highest mean Akaike weights (wETM = 0.44±0.08) among the four competing models. ETM model was shown to be optimal in 14 out of 18 PTC patients based on the lowest AICc. For the remaining four patients, the preferred models were 2CXM (n=1) or CTUM (n=3).
Table 3.
Summary of mean values of AICc and Akaike weights (wi) for the four models from the voxel basis of PTC ROIs.
| Model | 2CXM | CTUM | ETM | TM |
|---|---|---|---|---|
| AICc | −362.48±80.20 | −378.24±83.81 | −408.18±63.98 | −352.49±79.14 |
| wm | 0.18 ± 0.10 | 0.22±0.11 | 0.44±0.08 | 0.16±0.12 |
The reported values are mean ± standard deviation
ETM showed the greatest percentage of voxels with lowest AICc in 44% of a total 3419 voxels among the four competing models. Box-and-whisker plot showing the distribution of the percentage of voxel with the lowest AICc in 18 PTC patients (Figure 5). There was statistically significant difference in means of the lowest AICc (ANOVA, P<0.05) and percentage of voxel with the lowest AICc among four competing models (ANOVA, P<0.0001).
Figure 5.
Box-and-whisker plot comparing the Akaike weights (A) and percentage of voxels (B) with the lowest Akaike information Criterion AICc within the region of interest (ROI) for the two-compartment exchange model (2CXM), compartmental tissue uptake model (CTUM), extended Tofts model (ETM), and Tofts model (TM), from 18 papillary thyroid cancer patients. Each box plot shows minimum, first quartile, median (black line), third quartile, and maximum values. ETM estimated percentage of voxels with the lowest AICc were significantly different from 2CXM, CTUM, and TM (ANOVA, P<0.0001).
Tumor aggressiveness
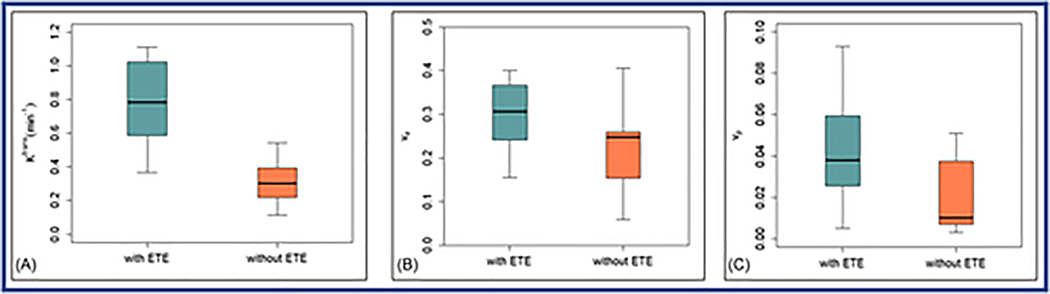
Of the 6 tumor aggressive features, ETE is the only one shown to stratify PTC patients with parameters obtained from the best fitting ETM model (as demonstrated in the previous section). The mean volumes of tumor ROIs showed a difference that is not statistically significant between with tumors with and without ETE in patients with PTC (1.04±0.70 vs.0.71±0.58 cm3, P=0.3). Table 4 shows the comparisons of mean values estimated from ETM in PTC patients with aggressive ETE features (n=7) and without ETE (n=11). ETM mean Ktrans values from PTC patients S1with ETE were significantly higher than those without (Ktrans: 0.78±0.30 vs. 0.34±0.18 min−1, P=0.005, unpaired t-test). Mean ve mean values between PTCs with and without ETE were not significantly different (ve: 0.30±0.09 vs. 0.21±0.10, P=0.12). Mean values of vp in PTC with ETE were slightly but not significantly higher than those of without ETE (0.039±0.034 vs. 0.025±0.019, P=0.11). The 2CXM, CTUM, and, TM estimated parameters value for the tumors with and without ETE are provided in Table S1.
Table 4.
Summary of mean parameter values obtained from the extended Tofts model (ETM) and total tumor volume for patients with extrathyroidal extension (ETE) and without extrathyroidal extension.
| Group | Ktrans(min−1) | ve | vp |
|---|---|---|---|
| With ETE (n = 7) | 0.78 ± 0.28 | 0.30 ± 0.09 | 0.039 ± 0.034 |
| Without ETE (n = 11) | 0.34 ± 0.18 | 0.22 ± 0.10 | 0.025 ± 0.019 |
| p value | 0.005 | 0.12 | 0.11 |
The parameters vp and ve are dimensionless fractional volumes for plasma space and extracelluar extravascular space, respectively.
The reported values are mean ± standard deviation
In Figure 5, the box and whisker plots comparing the mean values of Ktrans, ve, and vp obtained with ETM from PTCs with and without the aggressive feature of ETE.
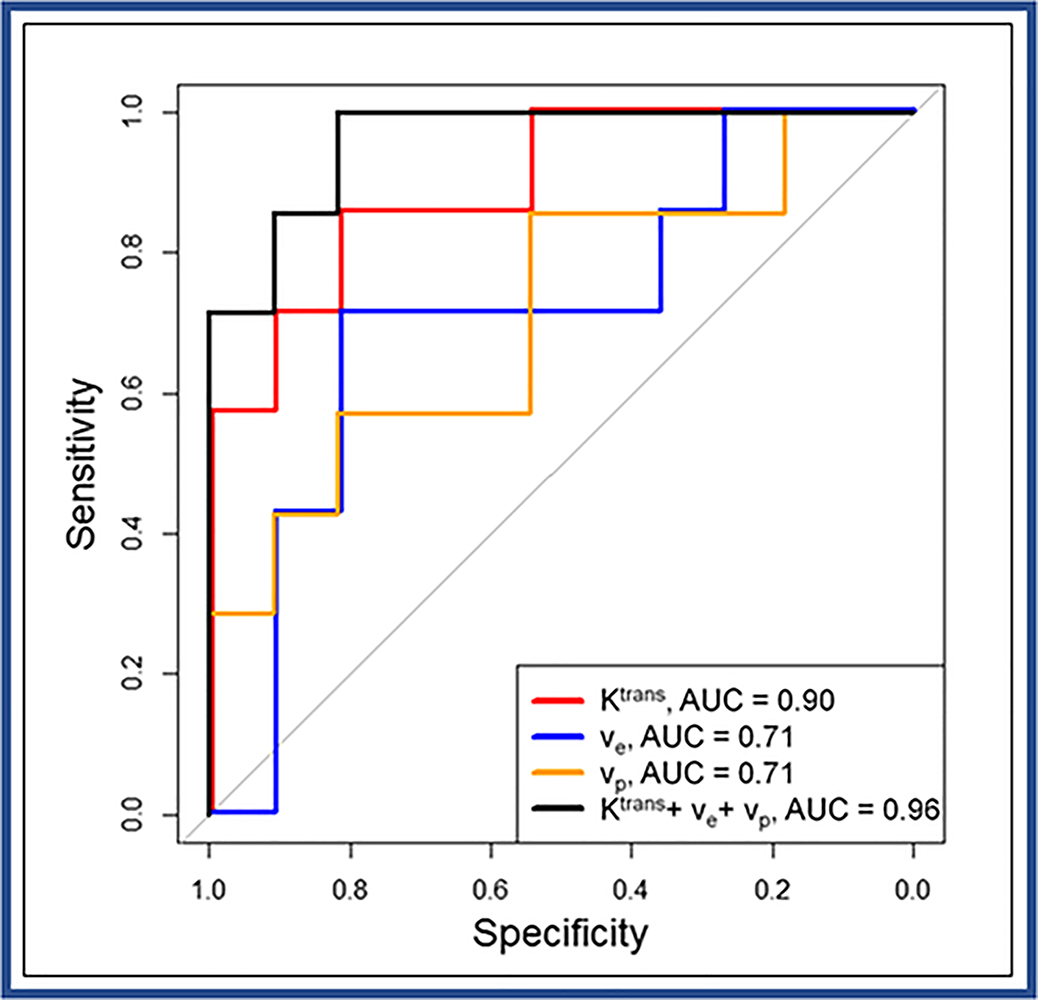
For the ETM model, the cut-off values of Ktrans, ve, and vp that discriminate between PTCs with and without ETE were determined to be 0.45 min−1, 0.28, and 0.014 with sensitivities and specificities of 86% and 82%, 71% and 82%, and 86% and 55%, respectively. Additionally, AUC for these parameters is reported to be 0.90, 0.71, and 0.71, respectively (Figure 5). The combination of Ktrans, ve, and vp reached a significant AUC 0.96 as compared with the univariate models using each parameter separately (all p-values <0.001), with sensitivity and specificity values of 100% and 82%, respectively. ROC analyses for all four models including tumor volume are shown in Table S2. ROC curves for the tumor volume alone and the parameters obtained with ETM including tumor volume are displayed in the supplemental Figure S1A and S1B, respectively.
Discussion
Our study is the first to employ the model selection strategy to identify the optimal tracer kinetic model from 2CXM, CTUM, ETM, and TM in 18 PTC patients. The most preferred optimal model was ETM, 78% of the patients. The voxel-by-voxel analysis of PTC DCE data indicated that different regions in a tumor were categorized into different tracer kinetic models that best described the measured signal time curves. Furthermore, the ETM estimates of Ktrans values could significantly differentiate between the tumors with and without aggressive features of ETE. The parameters ve and vp values of tumors with ETE were markedly higher than tumors without aggressive features. Multivariate ROC analysis performed using the parameters obtained with ETM (i.e., Ktrans, ve, and vp) performed significantly better than individual metrics alone and tumor volume in discriminating between PTC tumors with and without aggressive ETE.
Identifying an appropriate tracer kinetic model is always a challenging task for analyzing DCE data 37. AICc model selection relies on the goodness of fit of the regression model but imposes an extra penalty for additional parameters in a given set of models. Use of the AICc has greater benefits for suppressing the issue of overfitting and a higher probability for selecting the optimal model 38. AICc has been shown to be particularly strong in evaluating optimal models with finite sample sizes 39. The model with the highest Akaike weight show the evidence in favor of model being the best but does not guarantee improved parameter estimates 21.
Ktrans, a marker of vessel permeability, has three physiologic interpretations, depending on the cases 13. Under the mixed flow-permeability limited regime, (constructed from 2CXM/CTUM). While Ktrans ≈ PS, if PS ≪ Fp and Ktrans ≈ Fp, if PS ≫ Fp. In untreated extracranial tumors (ie, where extraction fraction during the first pass of the contrast agent is high), Ktrans approximates to plasma flow 8. Whereas in some a largely intact blood-brain barrier brain tumor (ie, where first extraction fraction is low), Ktrans approximates to the PS. The mixed flow-permeability conditions occur most commonly in tumors, so neither flow nor permeability predominate 8,25. The differential results in ETM estimate Ktrans and the 2CXM and CTUM/CTUM Ktrans indicate that parametric estimation of Ktrans essentially depend on the precise model assumed for the capillary bed and temporal resolution used in DCE data acquisition 10,22. A major difference between 2CXM and CTUM is consideration of or ignoring the back flux from EES to vascular space, respectively. The 2CXM and CTUM are used for a high temporal resolution DCE data (~ 2–3 sec), typically shorter than the contrast agent’s arrival time in EES. Ledsam et al. applied the 2CXM to low temporal resolution data and found large standard deviations for 2CXM estimates of Fp, PS, and vp and large errors for ve 40. In the present study, plasma MTT obtained with the 2CXM was 5.65 sec on average (ranging from ~2 to 14 sec). As the temporal resolution of this PTC DCE dataset (~4 to 6 sec) is comparable to the plasma MTT of the tumors studied, such that the ETM assumption is most likely to be valid and have minimal effects on the ETM estimates of Ktrans 41,42.
Donaldson et al. reported that the 2CXM modeling consistently found Fp greater than PS, and Ktrans was highly correlated with Fp in comparison to PS in tumour-averaged enhancement curve from a high temporal Cervical DCE data11. In the present study, ETM estimates of Ktrans was highly correlated with Fp from both CXM and CTUM whereas with that of PS was variable. The weak correlation between ETM estimates of Ktrans and CTUM estimates PS could be due to ignoring back flux from the EES into the blood plasma space. Previous studies have reported the difficulty in getting properly converge 2CXM values 40,43. The complex models are sensitive to noise and normally require image data with a high temporal resolution. The overfitting issue can be minimized with multiple starting scheme, proper selection of constraints on parameter ranges, convergence tolerances, and an improvement in temporal resolution and improving SNR 17. Thus, it should be used with caution. We note here that the estimates of equivalent parameters values in some models are apparently large (ie 2CXM/CTUM estimates of PS and 2CXM/CTUM and ETM estimates of vp etc.). This discrepancy could be related to major difference in model assumption and the temporal resolution of DCE data. The extensive analysis of model sensitivity and stability on the parametric estimates is beyond the scope of this investigation.
To study the reliability of the parametric estimates in PTC, we employed model selection strategies as used in prior DCE-T1 studies 11,12,18,19,22. Our results are in agreement with previous studies implicating that each voxel fits better to specific models due to underlying tumors physiology. Each model is optimal in different regions of the tumors. It can be inferred that tumor physiology in PTC is overall best described by ETM for given DCE data. The choice of optimal model depends on several aspects, for instance, location of tumors (ie, brain or extracranial tumors) and DCE acquisition protocols. DCE data fitting is affected by both temporal resolution, spatial resolution, and available signal noise ratio (S/N), which consequently affect estimation of the model parameter values 41,42.Discrepancy in estimated parameters may also arise due to the selection of AIF from an artery supplying blood to the tumor and assumptions from compartmental constraints, and precontrast T1 values (i.e., T10). In clinical practice due to low CA concentration and short echo time, T2* effects are assumed to be negligible. The choice of flip angle can influence the DCE, particularly at higher magnetic field strengths. The water exchange effects can be minimized with a larger flip angle and shorter recovery time. An extensive examination of how each of these factors affects model selection results is beyond the scope of this study.
Previous studies discriminated malignant thyroid nodules from normal tissue using semi-quantitative analysis 24. The semi-quantitative parameters, such as time to peak, area under the Ct(t) curve, and signal enhancement ratio are less specific to assess the tumor aggressiveness in patients with PTC. In contrast, parameters estimated from the tracer kinetic models are surrogate biomarkers of tumor permeability and vascularity 15,44,45. In the present study, higher Ktrans and vp values were obtained for the tumors with ETE compared to without ETE, indicating an overall difference in tumor aggressiveness. It has been reported that increased vp is a signature of tumor aggressiveness 46. The parameter Ktrans correlated with the ETE defined at pathology. ETE is associated with tumors extending outside of the thyroid capsule with invasion into the surrounding structure 47. Significant ETE has been identified as carrying a higher risk for local recurrence 48 and is used to ascertain risk in several staging systems, including TNM (tumor, node, and metastasis) 49, AGES (age, grade, ETE, and size) 50, AMES (age, metastasis, ETE, and size) 51, and MACIS (metastasis, age, completeness of resection, invasion, and size) 52. Because an active surveillance management approach or an initial partial thyroidectomy is best reserved for patients with intrathyroidal PTC, the ability to predict the presence of ETE is essential. Ultrasound (US) is used as a diagnostic tool of thyroid nodules, and its evaluation cannot always be relied on for deep anatomical structure 53. Additionally, routine neck US cannot reliably exclude minimal ETE 53,54. Therefore, the parameters obtained from tracer kinetic modeling of DCE data may complement the standard preoperative US for evaluating tumor aggressiveness in patients with PTC before surgery.
The present study has several limitations. The sample size of patients is small, warranting future studies with a larger cohort to verify the discriminative power of the optimal model to identify and differentiate tumor aggressiveness in PTC patients. A source of systematic error could be associated with AIF due to modest temporal resolution.
Conclusions
The appropriate model selection is key for the most accurate analysis of the time course of DCE-T1 data in patients with PTC. In the present study, ETM exhibited the best model (lowest AICc) among the whole set of candidate models with an Akaike weight of 0.44. ETM displayed the greatest percentage of voxels with the lowest AICc compared to 2CXM, CTUM, and TM. This indicates that the ETM provides the best overall fit to the time course of tissue CA concentration data under the conditions of the experiment. We conclude that parameter Ktrans obtained with the ETM is sufficient to discriminate aggressive features of ETE. These initial results are promising for stratifying the PTC patients according to aggressiveness before surgery. Future clinical studies validating our initial results in a larger patient cohort are needed. DCE- MRI studies, along with clinical variables and US imaging data, can help clinicians develop a personalized management approach, in advising either immediate surgery or active surveillance.
Supplementary Material
Figure 6:
Box-and-whisker plots comparing the mean values of quantitative metrics for (A). Ktrans (min−1), (B). ve, and (C). vp estimated with the extended Tofts model from those papillary thyroid carcinoma (PTC) patients with extrathyroidal extension (ETE) and without extrathyroidal extension. Each box plot shows minimum, first quartile, median (black line), third quartile, and maximum values. Ktrans values between PTC patients with ETE and without ETE were significantly different (P=0.005).
Figure 7.
Receiver operating characteristic (ROC) curves for Ktrans (red line), ve (blue line), and vp (green line) obtained with the extended Tofts model, and multivariate analysis using a combination of Ktrans, ve, and vp (black line) to discriminate papillary thyroid carcinoma patients with and without extrathyroidal extension (ETE). (Note: AUC = area under ROC curve).
Acknowledgments
The authors would like to thank the MRI technologists for their great efforts in helping to perform the MRI examinations and Mr. Christian Czmielewski for his helpful contribution to patient enrollment and data management. We thank Ms. Eve LoCastro for editing the manuscript.
Supported by NIH grant R21CA176660-01A1, NIH U01 CA211205 and in part through the NIH/NCI Cancer Center Support Grant P30 CA008748 and P50 CA172012
List of Abbreviations:
- AICc
Corrected Akaike Information Criterion
- AIF
Arterial Input Function
- ANOVA
Analysis of variance
- AUC
Area Under the Curve
- AW
Akaike Weights
- CA
Contrast Agent
- 2CXM
Two-compartment Exchange Model
- CTM
Compartmental Tissue Uptake Model
- DCE-MRI
Dynamic Contrast Enhanced Magnetic Resonance Imaging
- EES
Extravascular Extracellular Space
- ETE
Extra Thyroidal Extension
- ETM
Extended Tofts Model
- FNA
Fine-Needle Aspiration
- H&E
Hematoxylin and Eosin
- MTT
Mean Plasma Transit Time
- PS
Permeability Surface Area
- PTC
Papillary Thyroid Carcinoma
- ROIs
Regions of Interest
- ROC
Receiver Operating Characteristics
- SPGR
Spoiled Gradient Recalled Echo
- SSE
Sum of Squared Errors
- TM
Tofts Model
APPENDIX 1
Equations for the 2CXM described in Equation [6] are given by 25:
| [A1] |
| [A2] |
| [A3] |
where E is the extraction fraction of the plasma compartment in the 2CXM (i.e., )
References
- 1.Hay ID. Management of patients with low-risk papillary thyroid carcinoma. Endocr Pract. 2007;13(5):521–533. [DOI] [PubMed] [Google Scholar]
- 2.Vaisman F, Momesso D, Bulzico DA, et al. Thyroid Lobectomy Is Associated with Excellent Clinical Outcomes in Properly Selected Differentiated Thyroid Cancer Patients with Primary Tumors Greater Than 1 cm. J Thyroid Res. 2013;2013:398194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tuttle RM, Sabra MM. Selective use of RAI for ablation and adjuvant therapy after total thyroidectomy for differentiated thyroid cancer: a practical approach to clinical decision making. Oral Oncol. 2013;49(7):676–683. [DOI] [PubMed] [Google Scholar]
- 4.Cooper DS, Doherty GM, Haugen BR, et al. Revised American Thyroid Association Management Guidelines for Patients with Thyroid Nodules and Differentiated Thyroid Cancer. Thyroid. 2009;19(11):1167–1214. [DOI] [PubMed] [Google Scholar]
- 5.Baloch ZW, LiVolsi VA, Asa SL, et al. Diagnostic terminology and morphologic criteria for cytologic diagnosis of thyroid lesions: a synopsis of the National Cancer Institute Thyroid Fine-Needle Aspiration State of the Science Conference. Diagn Cytopathol. 2008;36(6):425–437. [DOI] [PubMed] [Google Scholar]
- 6.Miller B, Burkey S, Lindberg G, Snyder WH, Nwariaku FE. Prevalence of malignancy within cytologically indeterminate thyroid nodules. Am J Surg. 2004;188(5):459–462. [DOI] [PubMed] [Google Scholar]
- 7.Tofts PS, Berkowitz B, Schnall MD. Quantitative analysis of dynamic Gd-DTPA enhancement in breast tumors using a permeability model. Magn Reson Med. 1995;33:564–568. [DOI] [PubMed] [Google Scholar]
- 8.Padhani AR. Dynamic contrast-enhanced MRI in clinical oncology: current status and future directions. J Magn Reson Imaging. 2002;16(4):407–422. [DOI] [PubMed] [Google Scholar]
- 9.Brix G, Kiessling F, Lucht R, et al. Microcirculation and microvasculature in breast tumors: pharmacokinetic analysis of dynamic MR image series. Magn Reson Med. 2004;52(2):420–429. [DOI] [PubMed] [Google Scholar]
- 10.Sourbron S, Ingrisch M, Siefert A, Reiser M, Herrmann K. Quantification of cerebral blood flow, cerebral blood volume, and blood-brain-barrier leakage with DCE-MRI. Magn Reson Med. 2009;62(1):205–217. [DOI] [PubMed] [Google Scholar]
- 11.Donaldson SB, West CM, Davidson SE, et al. A comparison of tracer kinetic models for T1-weighted dynamic contrast-enhanced MRI: application in carcinoma of the cervix. Magn Reson Med. 2010;63(3):691–700. [DOI] [PubMed] [Google Scholar]
- 12.Duan C, Kallehauge JF, Bretthorst GL, Tanderup K, Ackerman JJ, Garbow JR. Are complex DCE-MRI models supported by clinical data? Magn Reson Med. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tofts PS, Brix G, Buckley DL, et al. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10(3):223–232. [DOI] [PubMed] [Google Scholar]
- 14.Hotker AM, Mazaheri Y, Aras O, et al. Assessment of Prostate Cancer Aggressiveness by Use of the Combination of Quantitative DWI and Dynamic Contrast-Enhanced MRI. Am J Roentgenol. 2016;206(4):756–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Margolis NE, Moy L, Sigmund EE, et al. Assessment of Aggressiveness of Breast Cancer Using Simultaneous 18F-FDG-PET and DCE-MRI: Preliminary Observation. Clin Nucl Med. 2016;41(8):e355–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Glatting G, Kletting P, Reske SN, Hohl K, Ring C. Choosing the optimal fit function: comparison of the Akaike information criterion and the F-test. Med Phys. 2007;34(11):4285–4292. [DOI] [PubMed] [Google Scholar]
- 17.Luypaert R, Sourbron S, Makkat S, de Mey J. Error estimation for perfusion parameters obtained using the two-compartment exchange model in dynamic contrast-enhanced MRI: a simulation study. Phys Med Biol. 2010;55(21):6431–6443. [DOI] [PubMed] [Google Scholar]
- 18.Bagher-Ebadian H, Jain R, Nejad-Davarani SP, et al. Model selection for DCE-T1 studies in glioblastoma. Magn Reson Med. 2012;68(1):241–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li X, Welch EB, Chakravarthy AB, et al. Statistical comparison of dynamic contrast-enhanced MRI pharmacokinetic models in human breast cancer. Magn Reson Med. 2012;68(1):261–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brix G, Zwick S, Kiessling F, Griebel J. Pharmacokinetic analysis of tissue microcirculation using nested models: multimodel inference and parameter identifiability. Med Phys. 2009;36(7):2923–2933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Luypaert R, Ingrisch M, Sourbron S, de Mey J. The Akaike information criterion in DCE-MRI: does it improve the haemodynamic parameter estimates? Phys Med Biol. 2012;57(11):3609–3628. [DOI] [PubMed] [Google Scholar]
- 22.Kallehauge JF, Tanderup K, Duan C, et al. Tracer kinetic model selection for dynamic contrast-enhanced magnetic resonance imaging of locally advanced cervical cancer. Acta Oncologica. 2014;53(8):1064–1072. [DOI] [PubMed] [Google Scholar]
- 23.Nakahara H, Noguchi S, Murakami N, et al. Gadolinium-enhanced MR imaging of thyroid and parathyroid masses. Radiology. 1997;202(3):765–772. [DOI] [PubMed] [Google Scholar]
- 24.Yuan Y, Yue XH, Tao XF. The diagnostic value of dynamic contrast-enhanced MRI for thyroid tumors. Eur J Radiol. 2012;81(11):3313–3318. [DOI] [PubMed] [Google Scholar]
- 25.Sourbron SP, Buckley DL. On the scope and interpretation of the Tofts models for DCE-MRI. Magn Reson Med. 2011;66(3):735–745. [DOI] [PubMed] [Google Scholar]
- 26.Burnham KP, Anderson DR. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociological Methods & Research, Vol 33, No 2 (2004), pp 261–304. 2004;33(2):261–304. [Google Scholar]
- 27.ImageJ [computer program]. Bethesda, Maryland, USA: U. S. National Institutes of Health; 1997–2016. [Google Scholar]
- 28.Shukla-Dave A, Lee N, Stambuk H, et al. Average arterial input function for quantitative dynamic contrast enhanced magnetic resonance imaging of neck nodal metastases. BMC medical physics. 2009;9:4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sharma P, Socolow J, Patel S, Pettigrew RI, Oshinski JN. Effect of Gd-DTPA-BMA on blood and myocardial T1 at 1.5T and 3T in humans. J Magn Reson Imaging. 2006;23(3):323–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Deoni SC, Rutt BK, Peters TM. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magn Reson Med. 2003;49(3):515–526. [DOI] [PubMed] [Google Scholar]
- 31.Lu YG, Moreira AL, Hatzoglou V, et al. Using Diffusion-Weighted MRI to Predict Aggressive Histological Features in Papillary Thyroid Carcinoma: A Novel Tool for Pre-Operative Risk Stratification in Thyroid Cancer. Thyroid. 2015;25(6):672–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ganly I, Ibrahimpasic T, Rivera M, et al. Prognostic implications of papillary thyroid carcinoma with tall-cell features. Thyroid. 2014;24(4):662–670. [DOI] [PubMed] [Google Scholar]
- 33.Ghossein R, Ganly I, Biagini A, Robenshtok E, Rivera M, Tuttle RM. Prognostic factors in papillary microcarcinoma with emphasis on histologic subtyping: a clinicopathologic study of 148 cases. Thyroid. 2014;24(2):245–253. [DOI] [PubMed] [Google Scholar]
- 34.Youden WJ. Index for rating diagnostic tests. Cancer. 1950;3(1):32–35. [DOI] [PubMed] [Google Scholar]
- 35.Heller G, Seshan VE, Moskowitz CS, Gonen M. Inference for the difference in the area under the ROC curve derived from nested binary regression models. Biostatistics. 2017;18(2):260–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.R: A Language and Environment for Statistical Computing [computer program]. Vienna, Austria: R Foundation for Statistical Computing; 2010. [Google Scholar]
- 37.Ewing JR, Bagher-Ebadian H. Model selection in measures of vascular parameters using dynamic contrast-enhanced MRI: experimental and clinical applications. NMR Biomed. 2013;26(8):1028–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shibata R Information criteria for statistical model selection. Electron Comm Jpn 3. 2002;85(4):32–38. [Google Scholar]
- 39.Akpa OM, Unuabonah EI. Small-Sample Corrected Akaike Information Criterion: An appropriate statistical tool for ranking of adsorption isotherm models. Desalination. 2011;272(1–3):20–26. [Google Scholar]
- 40.Ledsam JR, Hodgson R, Moots RJ, Sourbron SP. Modeling DCE-MRI at low temporal resolution: a case study on rheumatoid arthritis. J Magn Reson Imaging. 2013;38(6):1554–1563. [DOI] [PubMed] [Google Scholar]
- 41.Kershaw LE, Cheng HL. Temporal resolution and SNR requirements for accurate DCE-MRI data analysis using the AATH model. Magn Reson Med. 2010;64(6):1772–1780. [DOI] [PubMed] [Google Scholar]
- 42.Henderson E, Rutt BK, Lee TY. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magn Reson Imaging. 1998;16(9):1057–1073. [DOI] [PubMed] [Google Scholar]
- 43.Larsson HB, Courivaud F, Rostrup E, Hansen AE. Measurement of brain perfusion, blood volume, and blood-brain barrier permeability, using dynamic contrast-enhanced T(1)-weighted MRI at 3 tesla. Magn Reson Med. 2009;62(5):1270–1281. [DOI] [PubMed] [Google Scholar]
- 44.Dijkhoff RAP, Beets-Tan RGH, Lambregts DMJ, Beets GL, Maas M. Value of DCE-MRI for staging and response evaluation in rectal cancer: A systematic review. Eur J Radiol. 2017;95:155–168. [DOI] [PubMed] [Google Scholar]
- 45.Vos EK, Litjens GJ, Kobus T, et al. Assessment of prostate cancer aggressiveness using dynamic contrast-enhanced magnetic resonance imaging at 3 T. Eur Urol. 2013;64(3):448–455. [DOI] [PubMed] [Google Scholar]
- 46.Brem S, Cotran R, Folkman J. Tumor angiogenesis: a quantitative method for histologic grading. Journal of the National Cancer Institute. 1972;48(2):347–356. [PubMed] [Google Scholar]
- 47.Hu A, Clark J, Payne RJ, Eski S, Walfish PG, Freeman JL. Extrathyroidal extension in well-differentiated thyroid cancer: macroscopic vs microscopic as a predictor of outcome. Arch Otolaryngol Head Neck Surg. 2007;133(7):644–649. [DOI] [PubMed] [Google Scholar]
- 48.Cushing SL, Palme CE, Audet N, Eski S, Walfish PG, Freeman JL. Prognostic factors in well-differentiated thyroid carcinoma. Laryngoscope. 2004;114(12):2110–2115. [DOI] [PubMed] [Google Scholar]
- 49.Shaha AR. TNM classification of thyroid carcinoma. World J Surg. 2007;31(5):879–887. [DOI] [PubMed] [Google Scholar]
- 50.Hay ID, Bergstralh EJ, Goellner JR, et al. Predicting Outcome in Papillary Thyroid-Carcinoma - Development of a Reliable Prognostic Scoring System in a Cohort of 1779 Patients Surgically Treated at One Institution during 1940 through 1989. Surgery. 1993;114(6):1050–1058. [PubMed] [Google Scholar]
- 51.Cady B, Rossi R. An expanded view of risk-group definition in differentiated thyroid carcinoma. Surgery. 1988;104(6):947–953. [PubMed] [Google Scholar]
- 52.Hay ID, Grant CS, Taylor WF, McConahey WM. Ipsilateral lobectomy versus bilateral lobar resection in papillary thyroid carcinoma: a retrospective analysis of surgical outcome using a novel prognostic scoring system. Surgery. 1987;102(6):1088–1095. [PubMed] [Google Scholar]
- 53.Gweon HM, Son EJ, Youk JH, Kim JA, Park CS. Preoperative assessment of extrathyroidal extension of papillary thyroid carcinoma: comparison of 2- and 3-dimensional sonography. J Ultrasound Med. 2014;33(5):819–825. [DOI] [PubMed] [Google Scholar]
- 54.Lee JH, Jang HS, Kim JG, et al. Prediction of pathologic staging with magnetic resonance imaging after preoperative chemoradiotherapy in rectal cancer: pooled analysis of KROG 10–01 and 11–02. Radiotherapy and oncology : journal of the European Society for Therapeutic Radiology and Oncology. 2014;113(1):18–23. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.