Abstract
The anatomy and physiology of monosynaptic connections in rodent hippocampal CA1 have been extensively studied in recent decades. Yet, the resulting knowledge remains disparate and difficult to reconcile. Here, we present a data‐driven approach to integrate the current state‐of‐the‐art knowledge on the synaptic anatomy and physiology of rodent hippocampal CA1, including axo‐dendritic innervation patterns, number of synapses per connection, quantal conductances, neurotransmitter release probability, and short‐term plasticity into a single coherent resource. First, we undertook an extensive literature review of paired recordings of hippocampal neurons and compiled experimental data on their synaptic anatomy and physiology. The data collected in this manner is sparse and inhomogeneous due to the diversity of experimental techniques used by different groups, which necessitates the need for an integrative framework to unify these data. To this end, we extended a previously developed workflow for the neocortex to constrain a unifying in silico reconstruction of the synaptic physiology of CA1 connections. Our work identifies gaps in the existing knowledge and provides a complementary resource toward a more complete quantification of synaptic anatomy and physiology in the rodent hippocampal CA1 region.
Keywords: CA1, data integration, hippocampus, in silico modeling, synapse
1. INTRODUCTION
The hippocampal formation, notably the CA1 region, is one of the most exhaustively studied regions in the mammalian brain and is thought to play a role, for example, in the acquisition of memory, recognition of place and language (Bliss & Collingridge, 2013; Buzsáki, 1989). Neuronal microcircuits in the hippocampal CA1 region process and store information through a myriad of cell‐type‐specific monosynaptic connections.
Previous studies have shown that hippocampal cell types are connected through multiple synaptic contacts, which are positioned across distinct axo‐dendritic domains with a wide diversity in their physiology. Despite the wealth of data, we lack an integrative framework to reconcile the diversity of synaptic physiology, and therefore, identify knowledge gaps. There have been several noteworthy attempts to integrate knowledge on the cellular and synaptic components of hippocampal CA1 microcircuitry, which have provided a solid foundation to bring together anatomical properties and kinetic parameters of cell‐type‐specific connections—including the number of synapses per connection, connection probabilities, neurotransmitter release probabilities, and amplitudes of synaptic responses (Bezaire & Soltesz, 2013; Moradi & Ascoli, 2020; Wheeler et al., 2015). As a complementary endeavor, we extended a previously developed framework to reconstruct neocortical microcircuitry at the cellular and synaptic levels of detail (Markram et al., 2015), by integrating disparate data on the physiology of short‐term dynamics of depression and facilitation of cell‐type‐specific synaptic transmission in hippocampal CA1. Using this framework, we identified and extrapolated organizing principles to predict missing knowledge for a repertoire of connection types, for example, the short‐term dynamics and peak conductance of synaptic connections between inhibitory interneurons (Klausberger & Somogyi, 2008; Pelkey et al., 2017), which remain largely uncharacterized, and could, therefore, require high‐throughput strategies that employ multiple whole‐cell patch‐clamp recordings to surmount the relatively low yield obtained through conventional paired recordings (Espinoza, Guzman, Zhang, & Jonas, 2018; Jiang et al., 2015; Perin, Berger, & Markram, 2011).
We accounted for the dynamic and probabilistic nature of synaptic transmission by fitting experimental traces using a stochastic generalization of the Tsodyks–Markram (TM) short‐term plasticity (STP) model (Fuhrmann, Segev, Markram, & Tsodyks, 2002; Markram, Wang, & Tsodyks, 1998; Tsodyks & Markram, 1997), and also considered temperature and extracellular calcium concentration ([Ca2+]o) differences, which were adjusted using Q10 and Hill scaling factors, respectively.
Measuring peak quantal conductances directly at individual synaptic contacts remains very difficult, if not impossible with current experimental techniques. While theoretically, the peak synaptic conductance can be calculated from voltage‐clamp recordings by simply dividing the peak postsynaptic current (PSC) by the liquid junction potential (LJP)‐corrected driving force, this approach does not take into account the space‐clamp artifact (Gulyás, Freund, & Káli, 2016; Spruston, Jaffe, Williams, & Johnston, 1993; Williams & Mitchell, 2008). We have recently demonstrated that space‐clamp corrected peak synaptic conductances in neocortical connections are at least twofold to threefold higher than estimated previously (Markram et al., 2015). As a connection is formed by several synaptic contacts, each subject to a different space‐clamp effect, a purely theoretical correction is challenging. We, therefore, used an alternative approach, where we calibrated peak synaptic conductances in the in silico model of connected pairs such that the resulting postsynaptic potential (PSP) amplitudes match in vitro recordings. This yielded an estimate of peak synaptic conductance since other factors affecting the PSP amplitude—such as number and location of synapses, release probability and reversal potential, depression, facilitation, and synaptic conductance rise and decay time constant—were independently validated beforehand.
The resulting models for a subset of hippocampal connection types were applied predictively to the remaining uncharacterized connection types by clustering them into nine groups based on synapse types and neuronal biomarkers and applying the estimated parameters within each group. Curated and predicted parameters presented here should serve as a resource to researchers aiming to model hippocampal synapses at any level, while the detailed methodology intends to give a guideline to utilize such a framework to integrate data from other brain regions or species.
2. METHODS
2.1. Circuit building and synapse anatomy
A detailed model of the rat hippocampal CA1 area was built by adapting a previously described pipeline for reconstructing neocortical microcircuitry (Markram et al., 2015). In brief, detailed axo‐dendritic morphological reconstructions and electrophysiological traces obtained from the dorsal part of hippocampal CA1 were used to build single cell‐type‐specific computational models (Migliore et al., 2018) (see Supplementary Methods). The resulting single‐cell models were assembled in an atlas‐based volume corresponding to the dimensions of the hippocampal CA1 region (Ropireddy, Bachus, & Ascoli, 2012), cell‐densities and proportions, which yielded a tissue model consisting about 400,000 cells, ~90% pyramidal cells (PCs), and ~10% interneurons comprising 11 distinct morphology types (m‐types; see Supplementary Methods and Supplementary Figure S1) (Bezaire & Soltesz, 2013). Structural appositions between axons and dendrites were detected based on touch distance criteria and subsequently pruned to yield a functional connectome through an algorithmic process, which was constrained with experimentally reported bouton density, number of synapses per connections, and connection probability (Reimann, King, Muller, Ramaswamy, & Markram, 2015). A previous study suggests targeted innervation of interneurons from PCs (Takács, Klausberger, Somogyi, Freund, & Gulyás, 2012). Therefore, to recreate this tendency, touch distances from PCs to interneurons were set to 6 μm as against 1 μm for connections between PCs. Furthermore, touch distances of 6 μm for connections between all interneurons and 1 μm for connections between interneurons and PCs were assumed. In this manner, the number and location of synapses for each cell‐types specific connection were derived in a data‐driven manner. When reproducing paired recordings in silico (see below), monosynaptically connected pairs of neurons were sampled from this reconstructed circuit based on their intersomatic distance as sampling criterion.
2.2. Dendritic features of single cell models
Detailed, multicompartmental morphoelectrical models with 3D reconstructed dendrites from Migliore et al. (2018) were used in the present study (see Supplementary Methods and Supplementary Figure S1). The attenuation of synaptic responses along the dendrites with varying diameters was validated against experimental data from Magee and Cook (2000) using the HippoUnit framework (see Supplementary Methods). To this end, excitatory PSC (EPSC) like currents were injected into the apical trunk of PCs with varying distance from the soma and PSPs were simultaneously measured at the local site of the injection and in the soma.
2.3. Model of postsynaptic conductance and current
Synaptic conductances were modeled with biexponential kinetics:
| (1) |
where (nS) is the peak synaptic conductance and τrise and τdecay (ms) are PSC rise and decay time constants, respectively. The normalization constant ensures that synapses reach their peak conductance at tp = (τdecayτrise)/((τdecay − τrise)log(τdecay/τrise)) (ms). (Equation (1) is modified below to take stochastic release of multiple vesicles into account.) AMPAR and GABAR synaptic currents are then computed as:
| (2) |
where Vm (mV) is the membrane potential and Erev (mV) is the reversal potential of the given synapse. NMDAR currents depend also on Mg2+ block:
| (3) |
where mg(Vm) is the LJP‐corrected (see below) Jahr–Stevens nonlinearity (Jahr & Stevens, 1990):
| (4) |
where (mM) is the extracellular magnesium concentration and c1 = 0.062 (1/mV) and c2 = 2.62 (mM) are constants (the difference from the original Jahr and Stevens (1990) constant is because the authors did not correct for the LJP offset of ~5 mV). PC‐to‐PC NMDAR rise and decay time constants are Q10 corrected (see below) (Q10 = 2.2 ms for rise and 1.7 ms for decay time constants (Hestrin, Sah, & Nicoll, 1990; Korinek, Sedlacek, Cais, Dittert, & Vyklicky, 2010)) values from Andrasfalvy and Magee (2001): τrise = 3.9 ms and τdecay = 148.5 ms. All, but the CCK+ interneuron excitatory afferents have the same NMDAR time constants as the PC‐to‐PC ones, while the PC to CCK+ interneuron NMDAR conductance decays with a slower time constant: τdecay = 298.75 ms (Cornford et al., 2019; Le Roux, Cabezas, Böhm, & Poncer, 2013; Matta et al., 2013). Peak NMDAR conductance (nS) is calculated from the AMPAR one by multiplying it with NMDAR/AMPAR peak conductance ratio. PC‐to‐PC NMDAR/AMPAR peak conductance ratio = 1.22 was taken from Groc, Gustafsson, and Hanse (2002) and Myme, Sugino, Turrigiano, and Nelson (2003).
PC to CCK+ interneuron NMDAR/AMPAR ratio was set to 0.86, as against 0.28 for PC to other interneurons (Le Roux et al., 2013; Matta et al., 2013). Synaptic currents are individually delayed based on axonal path length and conduction velocity of 300 μm/ms (Stuart, Schiller, & Sakmann, 1997) and an additional 0.1 ms delay of neurotransmitter release (Ramaswamy et al., 2012).
2.4. STP parameter fitting
STP of synapse dynamics was fit by the TM model (Markram et al., 1998; Tsodyks & Markram, 1997). The model assumes that each synapse has a pool of available neurotransmitter resources (R) that is utilized by a presynaptic action potential (AP) with a release probability (U). The utilization of resources leads to postsynaptic conductance that is proportional to the amount utilized. R decreases and U increases after an AP and both R and U recover between spikes to a steady‐state (SS) value. The speed of recovery is parameterized by time constants D and F (ms) that together determine the short‐term dynamics of the synapse. This is described by the following differential equations:
| (5) |
| (6) |
where USE is the utilization of synaptic efficacy or absolute release probability (also known as the release probability in the absence of facilitation), δ(t) is the Dirac delta function and tspike indicates the timing of a presynaptic spike. Each AP in a train elicits an ASEU(tspike)R(tspike) amplitude PSC, where ASE is the absolute synaptic efficacy. R = 1 and U = USE are assumed before the first spike.
The USE, D, F, and ASE free parameters of the model were fit to amplitudes of experimentally recorded trains of PSCs. In the case of Losonczy, Zhang, Shigemoto, Somogyi, and Nusser (2002), amplitudes were already extracted by the authors, while in the case of Kohus et al. (2016) custom‐written Python routines were used to extract them from the averaged postsynaptic traces. Fitting the 10 + 1 recovery spikes was done by using a multiobjective genetic algorithm from BluePyOpt (Van Geit et al., 2016). For Kohus et al. (2016), different frequency stimulations (10, 20, and 40 Hz) were fit together for better generalization. Thus, the optimized error function contained 3 (frequencies) × 11 (peak amplitudes) points. For the event‐based version of the equations above, see Maass and Markram (2002) and Supplementary Methods. The Python source code fitting amplitudes from multiple frequencies is available on GitHub under /BluePyOpt/examples.
2.5. Stochastic TM model with multivesicular release
For the simulation of synapses, the canonical TM model (introduced above and used for fitting experimental traces) was modified to include stochastic release of multiple vesicles, and connected to the model of postsynaptic conductance described above. To take multivesicular release (MVR) into account in the postsynaptic conductance model, the classical “quantal model” of Del Castillo and Katz (1954) was used. In this model, synapses are assumed to be composed of NRRP (size of the readily releasable pool) release sites, each of which has a probability of release U (see deterministic TM model above) and contributes a 1/NRRP quanta to the postsynaptic response (Barros‐Zulaica et al., 2019; Loebel et al., 2009; Markram et al., 2015; Ramaswamy et al., 2012, 2015). Unlike in the deterministic TM model above, individual quanta were assumed to be released in an all‐or‐none fashion with probability U(t) (Fuhrmann et al., 2002). Vesicle availability is also an all‐or‐none process where only available vesicles can be released. To this end, synaptic vesicles were implemented as two‐state (available: 1 and unavailable: 0) Markov processes. After release, the state is set to unavailable and the probability of staying in the unavailable state at time t was described as a survival process, with the time constant D. The state transitions are described by the following set of equations:
| (7) |
The above‐described model converges to the canonical TM model in the limit (number of trials →∞). In this formalism, a presynaptic AP releases only a fraction Nr ≤ NRRP fraction of vesicles, which follows a Bernoulli distribution. Equation (1) is thus updated as follows:
| (8) |
| (9) |
| (10) |
where r and d are the rising and decaying components of the postsynaptic conductance, respectively. The implementation of the above described stochastic synapse model is available at the open‐access NMC portal (Ramaswamy et al., 2015).
These changes to the canonical TM model introduce variability of the postsynaptic traces, where the magnitude of the variability depends on the additional NRRP parameter (Barros‐Zulaica et al., 2019; Loebel et al., 2009). In vitro this variability is typically assessed by the coefficient of variation (CV, SD/mean) of the peak PSC (or PSP) amplitudes. Therefore, the NRRP was calibrated to match the CVs of the first PSCs extracted from the raw traces of Kohus et al. (2016). For a better comparison, artificial membrane noise was added to the simulated traces (see Barros‐Zulaica et al. (2019) and Supplementary Methods).
2.6. Calibrating peak synaptic conductances through in silico paired recordings
Paired recordings were replicated in silico as follows: First, pairs were selected from the circuit based on pathway specific distance criteria used by experimentalist (100 μm3 for cells in the same layer and 200 μm3 for cell pairs from different layers). Second, postsynaptic cells were current clamped to match the LJP‐corrected (see below) SS potential specified in the experiments. It is important to note, that in the case of PCs sodium channels were blocked (in silico TTX application) when clamping above −58 mV to avoid spontaneous firing of the cell models (see Migliore et al. (2018), figure 5), whereas sodium channels were not blocked in in vitro experiments. Next, the presynaptic cell was stimulated by somatic current injection, which resulted in a PSP recorded in the soma of the postsynaptic neuron. This protocol was repeated for 50 monosynaptic connections of the same pre‐post combination with 35 repetitions for each neuron pair. Finally, the mean PSP amplitude was compared against experimentally data and the peak conductance value was calibrated using the formula:
| (11) |
where PSPexp (mV) and PSPmodel (mV) are the experimental and modeled PSPs amplitudes respectively and df = ∣ Erev − VSS ∣ (mV) is the driving force. For all the experiments we aimed to reproduce, Erev = − 8.5 mV was calculated for excitatory connections, while Erev = − 73 mV for inhibitory connections (Moradi & Ascoli, 2020). All simulations were run using the NEURON simulator as a core engine (Hines & Carnevale, 1997) with the Blue Brain Project's collection of hoc and NMODL (Hines & Carnevale, 2000) templates for parallel execution on supercomputers (Hines, Eichner, & Schürmann, 2008; Hines, Markram, & Schürmann, 2008). The default temperature in all simulations was set to 34°C and the integration time step to 0.025 ms.
2.7. Correcting for calcium ion concentration, temperature, and LJP
Before integrating published parameters from different sources into the in silico synapse model, they were corrected for differences in experimental protocols. This included scalings for [Ca2+]o levels different from 2 mM, temperatures different from 34°C and the correction of holding and SS potentials by the theoretical LJP.
Levels of [Ca2+]o impact the neurotransmitter release probability. The corresponding in silico correction was applied by scaling the absolute release probability USE parameter (see above) of the synapses, using the Hill isotherm with n = 4 (Hill, 1910). The Hill equation below describes the nonlinear increase in release probability as a function of increasing [Ca2+]o:
| (12) |
where USEmax is the maximum value of the release probability (≤1) at high [Ca2+]o and K1/2 is the [Ca2+]o at which USE is one‐half of USEmax. USEmax and K1/2 parameters can be fit to data points (e.g., an indicator of release probability—the ratio between PSP amplitudes) measured at different [Ca2+]os. K1/2 values were taken from Rozov, Burnashev, Sakmann, and Neher (2001), 2.79 (mM) for steep and 1.09 (mM) for shallow calcium dependence and were shown to generalize well for other characterized pathways of the neocortex (see Markram et al. (2015), supplementary figure S11). In the absence of hippocampus specific data, we followed the approach of Markram et al. (2015) and assumed a steep dependence in PC to PC and PC to distal dendrite targeting inhibitory (O‐LM) cells, and a shallow dependence between PC to proximal targeting cells (PVBC (PV+ basket cell), CCKBC (CCK+ basket cell), and axo‐axonic cell). For experimentally uncharacterized pathways, an intermediate calcium dependence was used, as the average of the steep and shallow ones. This intermediate curve was in agreement with the few relevant data points for specific hippocampal synaptic connections (Price, Scott, Rusakov, & Capogna, 2008; Tyan et al., 2014). The temperature dependence of kinetic parameters such as rise and decay time constants was corrected by dividing them with Q10 scaling factors:
| (13) |
where τ is the time constant, Q10 is an empirically determined, receptor‐specific parameter, Tsim = 34 °C is the temperature used in the simulations, while Texp < Tsim is the temperature of the experiment. The Q10 correction was only needed for the NMDA current between connected PCs (see above) because all other kinetic values that we used were recorded at near physiological temperature (~34 °C).
Holding and SS potentials were corrected by the theoretical LJP (Neher, 1992). These potentials arise from the differences in solutions in the pipette and bath and are in 2–12 mV range for the standard solutions. Theoretical LJPs, calculated from the reported pipette and bath solutions were obtained from Moradi and Ascoli (2020).
2.8. Statistical analysis
R values for validating matching experimental and model values are Pearson correlations. Data are presented as mean ± SD to yield comparable values to the experimental ones. USE, D, F distributions from two different sources (e.g., found in the literature vs. fitted here) are said to be comparable if the mean of the second distributions is not further away than one‐half of the SD of the first distribution.
3. RESULTS
3.1. Literature curation
First, we undertook an extensive literature review of paired recording experiments, and compiled data on the various parameters (Figure 1, Step 1; Tables 1 and 2 for the data inclusion and exclusion criteria, and a list of data and modeling assumptions, respectively; see also Supplementary Table S1 for voltage‐clamp data from rat hippocampal CA1, and S2 for current‐clamp recordings). The data collected in this manner is sparse and inhomogeneous, due to the disparate experimental conditions used by different groups and were, therefore, corrected for various aspects (Figure 1, Step 2). For example, [Ca2+]o is known to affect release probability and, therefore, an additional Hill scaling had to be considered while parameterizing STP models (see Section 2.7). Rise and decay time constants of synaptic currents are influenced by temperature differences but can be corrected with Q10 factors (see Section 2.7). For electrophysiological recordings, patch pipettes have become the method of choice over sharp electrodes, which necessitates applying an LJP correction for voltage traces (see Section 2.7).
FIGURE 1.
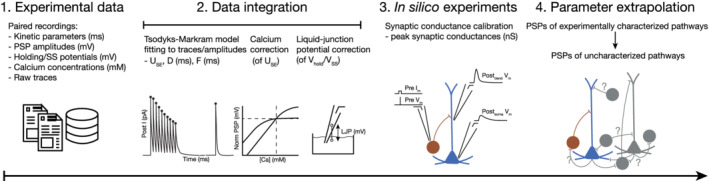
In silico data integration pipeline. (1) 51 peer‐reviewed papers, spanning 21 years were used to compile data on various parameters of connected neurons in rat CA1 including connection probability, number of synapses per connections, axo‐dendritic innervation profile, kinetics, STP profiles, calcium and temperature sensitivity. (2) Parameters were integrated into a common framework and experimental paradigm, including temperature, [Ca2+]o and liquid junction potential (LJP) corrections. TM models of STP were fit to publicly available raw traces. (3) In silico paired recordings were run to correctly adjust the unitary peak conductance of connections with experimentally characterized postsynaptic potential (PSP) amplitudes. (4) The resulting parameters were averaged within each of the nine classes of synapses and used predictively to describe experimentally uncharacterized pathways [Color figure can be viewed at wileyonlinelibrary.com]
TABLE 1.
Data inclusion and exclusion criteria
| Data inclusion criteria | |
| 1 | For the characterization of number of the synapses per connections, we used published values from anatomical studies employing electron and light microscopy; in rat CA1 slices. |
| 2 | For the validation of our axo‐dendritic innervation patterns, we used figures from published studies with biocytin‐filled pairs; under light microscopy; in rat CA1 slices. |
| 3 | For the characterization of synaptic physiology, we prioritized data from: Paired recordings from identified m‐types; in rat CA1 slices; at 2 mM [Ca2+]o; and 34°C; with reported holding/SS potential; and reported LJP or recording solutions. |
| 4 | For the parametrization the decay time constant of single PSCs, we used published decay time constant fits (independent of the model, e.g., single vs. biexponential fit). |
| 5 | For fitting the TM model, we used average raw PSC traces as well as published peak PSC amplitudes; with 10 spikes at different frequencies plus a recovery spike. |
| 6 | For the validation of the TM model, we used published fits from the neocortex (Markram et al., 2015) in order to compare USE, D, F values of the corresponding pathways. |
| 7 | For the estimation of the NRRP, we used raw PSC traces (all trials) to estimate the CV of the first peak PSC amplitude as well as published NRRP estimates. |
| 8 | For the calibration of peak synaptic conductance amplitudes, we used published peak PSP amplitudes (see Supplementary Table S2). |
| 9 | For the validation of the peak synaptic conductances, we used single‐receptor conductance and receptor number estimates. |
| Data exclusion criteria | |
| 10 | In the case of multiple reports of a single parameter or reference data, we prioritized publications which were already used for other parameters and excluded the others (see, e.g., (Pawelzik, Hughes, & Thomson, 2002) in Supplementary Table S2). |
| 11 | When we had access to individual PSP amplitudes beyond the usually reported mean ± SD, we excluded outliers and used the updated mean ± SD as target PSP amplitude (see Supplementary Table S5). |
TABLE 2.
List of assumptions. All the assumptions that were made to arrive at model parameters from a sparse set of raw data and published values
| 1 | We assume that after all the listed correction in this paper, all parameters coming from different sources can be used together to parameterize the synapse models. |
| 2 | When using data from Kohus et al. (2016), we assumed that CCK+ DTIs (dendrite‐targeting interneurons) are SCA cells in SR. Furthermore, we assumed that synaptic currents measured in mouse CA3 are representative of similar pathways in rat CA1. |
| 3 | In the lack of representative data and our lack of neurogliaform cells, we assumed that all inhibitory synapses are mediated purely by GABAA receptors. |
| 4 | For calculating release probabilities at different [Ca2+]o, we assumed that Hill functions parameterized with cortical data generalize well for hippocampal connections. |
| 5 |
For modeling synaptic currents, we assumed that all CA1 synapses can be described with biexponential conductances, with vesicle release kinetics governed by the stochastic TM model. When modeling dendritic PSC decays, we assumed a single exponential function, parametrized with a time constant extracted from somatic recording. |
| 6 | In the process of calibrating synaptic peak conductances, we simulated only the synapses mediating the given connection and thus we assume that the background activity does not matter. |
| 7 | Some of the biggest assumptions are inherited from the network model: In this work, we assumed that the published electrical models of single cells (Migliore et al., 2018) capture the behavior of different neurons in rat CA1. (The fact that unlike experimentalists, we cannot clamp PC models to potentials above −58 mV without blocking sodium channels seems to violate this assumption.) We also assumed that the cell composition and cell density within each layer are homogeneous and the constrained connectivity reflects the connectivity of rat CA1. |
| 8 | Kinetic parameters for a given pathway are drawn from a distribution, but since (almost) all experimental data used to derive these parameters are representative for a given connection and not for individual synapses per se, we use the same parameters for all synapses mediating a single connection. |
| 9 |
The biggest assumption is that one can extrapolate parameters from experimentally characterized pathways, to fill in missing values. When generalizing our parameters for similar, experimentally uncharacterized pathways we group CA1 interneurons based on only one chemical marker. However, cells express many of these and the markers overlap (see hippocampome.org (Wheeler et al., 2015)). By PV+ cells we mean: SP_PVBCs, SP_BS cells, and SP_AA cells. By CCK+ cells we mean: SP_CCKBCs, SR_SCA cells and SLM_PPA cells. The only interneurons in our NOS+ class are SP_Ivy cells. (Neurogliaform cells would belong here as well.) We assume all neurons in SO: SO_OLM cells, SO_BS cells, SO_Tri cells, and SO_BP cells to be SOM+. |
| 10 |
A usually unspoken, implicit assumption on communication between neurons is used here as well, namely, we model only glutamatergic and GABAergic synapses between presynaptic axons and postsynaptic somata and dendrites. Thus, we leave out cotransmission and neuromodulators acting on different receptors, retrograde messengers, any kind of gap junctions and any axonal receptors. |
3.2. Synaptic model parameters
We integrated the collected and corrected data into a model of synaptic transmission that includes STP and stochastic neurotransmitter release. We found that for some connection types the parameters of this model could be fully determined by employing in silico paired recordings (Figure 1, Step 3). Yet, for the majority of connection types parameters had to be extrapolated (Figure 1, Step 4). We use “synapse” to refer to a single anatomical synaptic contact and “connection” to indicate the collection of all synaptic contacts between a given presynaptic and postsynaptic neuron, comprising one or more synapses.
The underlying synapse model consisted of several parts, each with their associated parameters, which we determined in a six‐step procedure: We modeled synaptic connections with biexponential conductances requiring 8 parameters. Three parameters (Erev, τrise, τdecay) were directly obtained from the literature (see Supplementary Table S1 for AMPAR and GABAR rise and decay time constants, methods for NMDAR time constants, and Supplementary Table S2 for reversal potentials (Moradi & Ascoli, 2020)). In particular, for the τdecay (Supplementary Table S1) with the exception of Maccaferri, Roberts, Szucs, Cottingham, and Somogyi (2000) who used either single or weighted biexponential fits, none of the other studies we considered explicitly reported how τdecay was extracted. Therefore, we extrapolated single exponential fits τdecay of all pathways, which were measured through somatic voltage‐clamp recordings. We used these measurements directly as dendritic PSC time constants without any correction for attenuation (Table 2). STP was modeled with the TM model, which added three parameters USE, D, F) to a synaptic connection type. They were fit in conjunction to the experimentally observed STP behavior (Figure 2, Step 4; see Section 2.4). Stochastic synaptic transmission was modeled by extending the TM model to include quantal release from multiple sites. This added another parameter (NRRP) that was fit to the observed variability of PSC amplitudes of experimental traces in terms of their CV (SD/mean; Figure 2, Step 5; see Section 2.5). Finally, the mean amplitude of PSPs depended on three of the parameters and thus could be fit to the peak synaptic conductance () only after the other two parameters had been determined (Figure 2, Step 6).
FIGURE 2.
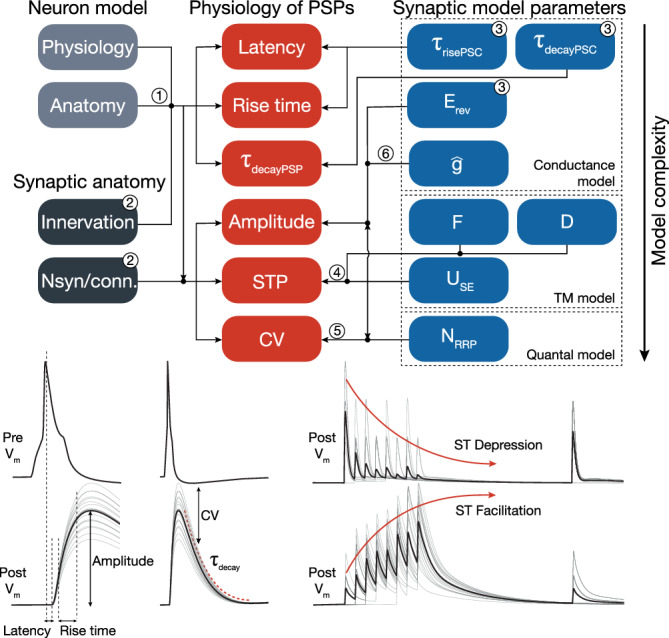
In silico synapse model and parameter fitting: Properties of the network (left) and the parameters synapse model (right) determine certain features of the emergent postsynaptic potentials (PSPs) (middle). (These PSP features are schematized at the bottom of the figure. Individual trials are shown in gray and their average postsynaptic voltage trace in black.) These dependencies between properties/parameters and PSP features (indicated by arrows, and dots where they join and continue as a single arrow) were used to fit the synapse model parameters to data in six steps. Left: Parts of the network model that affect these features such as biophysical and anatomical neuron models via dendritic attenuation (1) as well as dendritic innervation and the number of synapses per connection (2) are independently validated. Top right: Parameters of the model of postsynaptic conductance are taken from averaged experimental PSC traces (3). Middle right: The TM model of STP adds three parameters that are fit to observed STP behavior (4). Bottom right: The model of stochastic quantal release adds another parameter fit to the observed CV of PSP amplitudes (5). In the last step, peak synaptic conductances are calibrated to match PSP amplitudes from data (6). Numbers on arrows indicate that the given parameter was validated against—or fitted to data, while numbers on boxes indicate that the parameters were taken from literature and directly plugged in into the model [Color figure can be viewed at wileyonlinelibrary.com]
In addition to the parameters of synaptic models, the physiology of PSPs is also dependent on several anatomical parameters, which result from the single‐cell and tissue modeling workflow (see Section 2.2; Supplementary Figure S1). To ensure the accuracy of the fitted synaptic parameters we independently validated aspects of the modeled anatomy (Figure 2, Steps 1 and 2). In the following sections, we present the results of the anatomical validations, followed by the results of the various fits of synaptic parameters.
3.3. Validation of synaptic anatomy and dendritic attenuation
The anatomical properties of synaptic connections such as number of synapses per connection and axo‐dendritic innervation patterns, along with the dendritic properties of single cell models were validated against experimental data (Figure 3). Pairs of synaptically connected neurons were sampled from a dense tissue‐level reconstruction of the rat hippocampal CA1 region (see Section 2.1, Supplementary Figure S1, Figures 3a and 4a). The number of synapses per connection for the handful of experimentally characterized pathways (Ali, 2011; Biró, Holderith, & Nusser, 2005; Buhl, Halasy, & Somogyi, 1994; Buhl, Han, et al., 1994; Deuchars & Thomson, 1996; Földy, Lee, Morgan, & Soltesz, 2010; Maccaferri et al., 2000; Sik, Penttonen, Ylinen, & Buzsáki, 1995; Vida, Halasy, Szinyei, Somogyi, & Buhl, 1998) was consistent with biological data (r = 0.98; Figure 3b and Supplementary Table S3). The mean number of synapses per connection for the in silico pathways that have been experimentally characterized are as follows: Excitatory to excitatory (E‐E): 1.26 ± 0.6; inhibitory to excitatory (I‐E): 8.2 ± 2.1; excitatory to inhibitory (E‐I); only connections between PC to O‐LM cells): 2.8 ± 1.2; inhibitory‐inhibitory (I‐I): 2.8 ± 0.2 (Supplementary Table S3). A systematic, quantitative characterization of axo‐dendritic innervation profiles for hippocampal CA1 synaptic connections is largely lacking. Therefore, although we derived many predictions of axo‐dendritic innervation profiles from in silico synaptic pathways, these could, however, only be validated based on anecdotal evidence (Figures 3a and 4a). In addition, we sampled neuron pairs at intersomatic distances of 0–200 μm to predict their connection probability and number of synapses per connection (Figure 3c,d). The upper bound of 200 μm ensured that we obtained a sufficient number (100 ≤ n ≤ 5, 000) of pairs for all connections, even where the pre–post neurons were in different layers, for example, Schaffer collateral‐associated and OLM cells to PC connections. Although the perforant path‐associated cell to PC connections occur in our model, they were excluded in these analyses since their somata are farther apart than the general 200 μm distance criteria chosen for these predictions.
FIGURE 3.
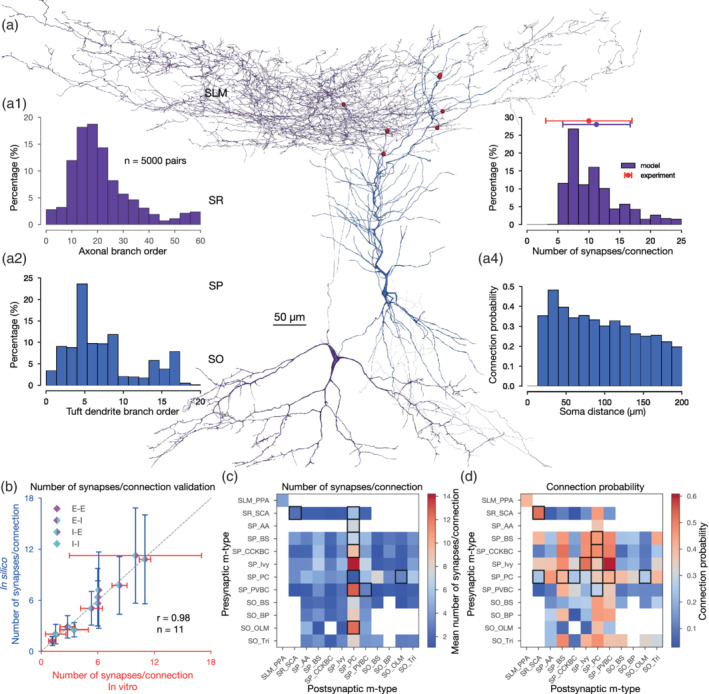
In silico synapse anatomy. (a) A representative in silico O‐LM (purple) to PC (blue) pair, with synapses visualized in red. 3D morphologies were reconstructed with the Neurolucida software by the members of the Thomson/Mercer lab (Migliore et al., 2018). (a1) Branch order distribution (n = 5, 000 connections) of the presynaptic (O‐LM) axons. (a2) Branch order distribution of the postsynaptic (PC) tuft dendrites. (a3) Distribution of the number of synapses per connection of the in silico O‐LM to PC pathway. In vitro experimental data is indicated in red. (a4) Distance‐dependent connection probability of the in silico O‐LM to PC pathway. (b) Validation of the number of synapses per connection against experimental data. (E: excitatory, I: inhibitory, e.g.,: I‐E: inhibitory to excitatory pathways.) Dashed gray line represents perfect correlation between experimental and model values. (c) Predicted mean number of synapses per connections for all pathways in the full‐scale CA1 network model. Only connections with ≤200 μm intersomatic distance were used to calculate the average. Averages were calculated from 100 ≤ n ≤ 5, 000 pairs. White boxes represent connections that are not present in the circuit model due to the lack of axo‐dendritic overlap (given the ≤200 μm intersomatic distance sampling criteria). Experimentally measured values (same as on its left) are highlighted with black rectangles. Layer abbreviations: SR, stratum radiatum; SP, stratum pyramidale; SO, stratum oriens. M‐type abbreviations: AA, axo‐axonic cell; BP, back‐projecting cell; BS, bistratified cell; CCKBC, CCK+ basket cell; Ivy, ivy cell; OLM, oriens‐lacunosum moleculare cell; PC, pyramidal cell; PVBC, PV+ basket cell; PPA, performant path‐associated cell; SCA, Schaffer collateral‐associated cell; Tri, trilaminar cell (see Supplementary Methods). (d) Predicted mean connection probability (within 200 μm intersomatic distance) for all pathways in the CA1 network model. M‐type abbreviations, white boxes, black rectangles, and number of pairs are as in (c) [Color figure can be viewed at wileyonlinelibrary.com]
FIGURE 4.
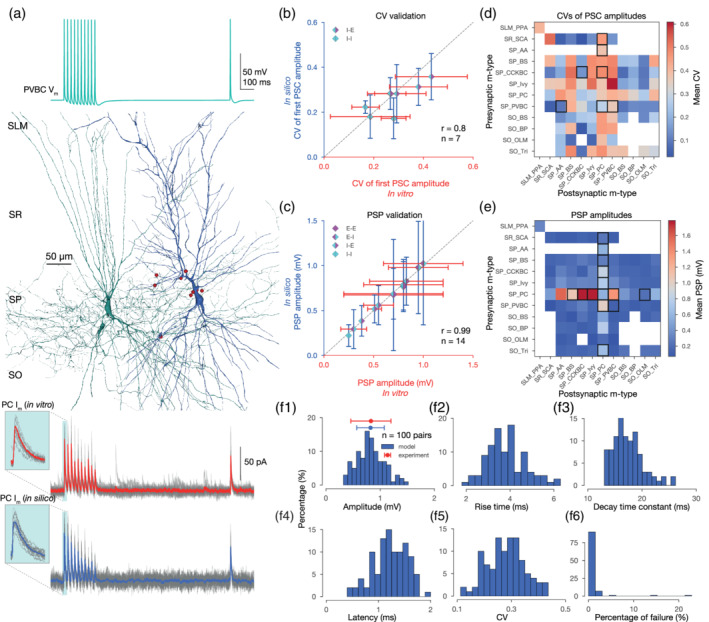
In silico synapse physiology. (a) In silico paired recording experiment with the STP protocol used in Kohus et al. (2016). Presynaptic (PVBC) voltage trace is shown on top. In silico PVBC (green) to PC (blue) pair, with synapses visualized in red in the middle. 3D morphologies were reconstructed with the Neurolucida software by the members of the Thomson/Mercer lab (Migliore et al., 2018). Postsynaptic (PC) experimental traces recorded in vitro (in gray) and their mean in red, as well as model traces recorded in silico (in gray) and their mean in blue, are presented at the bottom panel. Insets show the variance of the first IPSCs. (b) Validation of the CV of the first PSC amplitudes (excluding failures) against experimental data. (E: excitatory, I: inhibitory, e.g.,: I‐E: inhibitory to excitatory pathways.) Dashed gray line represents perfect correlation between experimental and model values. (c) Validation of the postsynaptic potential (PSP) amplitudes against experimental data. (d) Predicted CVs of first PSC amplitudes (excluding failures) for all pathways in the CA1 network model after synapse parameter generalization. As in Figure 3c, only connections with ≤200 μm intersomatic distance were used to calculate the average postsynaptic response from n = 20 pairs with 35 repetitions for each pair. Postsynaptic cells were held at −65 mV in in silico voltage‐clamp mode. M‐type abbreviations, white boxes, and black rectangles are as in Figure 3c. (e) Predicted PSP amplitudes for all pathways in the CA1 network model after synapse parameter generalization. Then, 20 pairs with 35 repetitions for every possible connection. Postsynaptic cells were held at −65 mV steady‐state potential in in silico current‐clamp mode. Consistent with Gulyás et al. (1993), PC to interneurons are the strongest. M‐type abbreviations, white boxes, black rectangles and number of pairs are as in (d). (f) Properties of postsynaptic (PC) IPSPs from 100 PVBC to PC pairs with 35 repetitions each. (f1) Distribution of in silico PSP amplitudes. In vitro experimental data from Pawelzik et al. (2002) is indicated in red. (f2) Distribution of in silico PSP 10–90% rise times. (10–90% rise time constants of PSCs are fixed to 0.2 ms in the model, but the PSP rise times wary.) (f3) Distribution of in silico PSP decay time constants (single exponential fit). (f4) Distribution of in silico PSP latencies. (f5) Distribution of the CVs of the first in silico PSP amplitudes (excluding failures). (f6) Distribution in silico failures (0 measurable PSP amplitude from 35 repetitions) [Color figure can be viewed at wileyonlinelibrary.com]
Finally, we also validated the dendritic attenuation profile of PSPs in single neuron models of PCs, which were also found to be consistent with experimental data (Magee & Cook, 2000) (τmodel = 235.2, τexp = 155.6, Supplementary Figure S2).
3.4. STP of synapses
The synaptic physiology of hippocampal CA1 connections expresses a rich diversity of STP profiles in response to presynaptic AP trains at different stimulus frequencies (Ali, Bannister, & Thomson, 1999; Ali, Deuchars, Pawelzik, & Thomson, 1998; Ali & Thomson, 1998; Éltes, Kirizs, Nusser, & Holderith, 2017; Kohus et al., 2016; Losonczy et al., 2002; Pouille & Scanziani, 2004). However, to the best of our knowledge, only Losonczy et al. (2002) reported TM model parameters for CA1 pathways and used an additional recovery spike elicited about 500–100 ms after the last spike in the train, which is crucial to characterize frequency‐dependent STP profiles of depression and facilitation (Gupta, Wang, & Markram, 2000). Published STP parameters from Losonczy et al. (2002) were used for PC to BC pathways, after refitting a subset of their data, and ensuring their consistency with our resulting USE, D, F values (see Section 2). The dataset from Kohus et al. (2016) were obtained in the mouse CA3 region at 1.6 mM [Ca2+]o, which differs from the rest of the datasets we considered, we nevertheless made use of this resource due to the availability of their raw data, which was subsequently used in our procedure of fitting TM model parameters (see Section 2.4; Table 1 for data inclusion and exclusion criteria; Table 2 for a list of data and modeling assumptions). The resulting TM model parameters following the fitting procedure were consistent with those in the source dataset (Kohus et al., 2016). In addition, we were able to match the CVs of the first PSC amplitudes (r = 0.8; Figure 4b, Supplementary Table S4), by calibrating NRRP (see Loebel et al. (2009); Barros‐Zulaica et al. (2019) and Section 2.5) with the resulting values of NRRP in a biologically plausible range. An elegant study demonstrated that under experimental conditions to induce high neurotransmitter release probability (high Mg/Ca) CCKBC to PC connections in CA3 are characterized by MVR (with NRRP = 5 − 7 vesicles) (Biró, Holderith, & Nusser, 2006). However, univesicular release (UVR, NRRP = 1) is more prevalent under physiological conditions (Biró et al., 2006). The in silico CV of CCKBC to PC PSCs with NRRP = 1 compared well against experimental data obtained under physiological conditions. In the cases of synaptic connections from PVBC to PC and PVBC, a value larger than 1 (NRRP = 6) vesicles were required (see Section 2.5; Figure 4b). For pathways not present in the Kohus et al.'s (2016) dataset, the NRRP could not be calibrated and was thus assumed. The assumption of MVR with NRRP = 2 vesicles at each excitatory to excitatory connections was used in this study (Barros‐Zulaica et al., 2019; Christie & Jahr, 2006; Conti & Lisman, 2003; Tong & Jahr, 1994), while UVR was assumed at all other noncalibrated pathways (see Gulyás et al. (1993); Biró et al. (2005) suggesting UVR for certain PC to interneuron connections).
Based on the literature and our model fitting, we identified several rules to group STP profiles. The mapping of STP profiles for all pathways is as follows: PC to O‐LM cells (Ali & Thomson, 1998; Biró et al., 2005; Losonczy et al., 2002; Pouille & Scanziani, 2004) and other interneurons in stratum oriens (Éltes et al., 2017) E1 (excitatory facilitating). PC to PC (Deuchars & Thomson, 1996), PC to all SOM interneurons (Ali et al., 1998; Losonczy et al., 2002; Pouille & Scanziani, 2004) E2 (excitatory depressing). CCK+ interneurons to CCK+ interneurons (Ali, 2007, 2011; Kohus et al., 2016) I1 (inhibitory facilitating), PV+ and SOM+ interneurons to PC (Ali et al., 1998, 1999; Bartos et al., 2002; Buhl, Cobb, Halasy, & Somogyi, 1995; Daw, Tricoire, Erdelyi, Szabo, & McBain, 2009; Kohus et al., 2016; Maccaferri et al., 2000; Pawelzik et al., 2002) as well as interneurons to interneurons (except the CCK+ ones) (Bartos et al., 2002; Daw et al., 2009; Elfant, Pal, Emptage, & Capogna, 2008; Karayannis et al., 2010; Kohus et al., 2016; Price et al., 2005) I2 (inhibitory depressing). CCK+ and NOS+ (only Ivy cells, since we lack NGF morphologies) to PC (Fuentealba et al., 2008; Kohus et al., 2016; Price et al., 2008) I3 (inhibitory pseudo linear). The parameters of the groups and the resulting dynamics are summarized in Table 3 and Figure 5.
TABLE 3.
Parameters and generalization to nine classes
| Pre | Post |
|
τdecay | USE | D | F | NRRP | |
|---|---|---|---|---|---|---|---|---|
| PC to PC (E2) | ||||||||
| PC | PC | 0.6 ± 0.1 | 3 ± 0.2 | 0.5 ± 0.02a | 671 ± 17a | 17 ± 5a | 2 | |
| PC to SOM+ (E1) | ||||||||
| PC | OLM | 0.8 ± 0.05 | 1.7 ± 0.14 a | 0.09 ± 0.12 a | 138 ± 211 a | 670 ± 830 a | 1 | |
| PC | SOM+ | 0.8 ± 0.05 | 1.7 ± 0.14 a | 0.09 ± 0.12 a | 138 ± 211 a | 670 ± 830 a | 1 | |
| PC to SOM− (E2) | ||||||||
| PC | PVBC | 2 ± 0.05 | 4.12 ± 0.5 | 0.23 ± 0.09 | 410 ± 190 | 10 ± 11 | 1 | |
| PC | CCKBC | 3.5 ± 0.4 | 4.12 ± 0.5 | 0.23 ± 0.09 | 410 ± 190 | 10 ± 11 | 1 | |
| PC | BS | 1.65 ± 0.1 | 4.12 ± 0.5 | 0.23 ± 0.09 | 410 ± 190 | 10 ± 11 | 1 | |
| PC | Ivy | 2.3 ± 0.4 | 4.12 ± 0.5 | 0.5 ± 0.022 | 671 ± 17a | 17 ± 5a | 1 | |
| PC | SOM− | 2.35 ± 0.7 | 4.12 ± 0.5 | 0.23 ± 0.09 | 410 ± 190 | 10 ± 11 | 1 | |
| PV+ to PC (I2) | ||||||||
| PVBC | PC | 2.15 ± 0.2 | 5.94 ± 0.5 | 0.16 ± 0.02 | 965 ± 185 | 8.6 ± 4.3 | 6 | |
| AA | PC | 2.4 ± 0.1 | 11.2 ± 0.9 | 0.1 ± 0.01 | 1,278 ± 760 | 10 ± 6.7 | 1 | |
| BS | PC | 1.6 ± 0.1 | 16.1 ± 1.1 | 0.13 ± 0.03 | 1,122 ± 156 | 9.3 ± 0.7 | 1 | |
| PV+ | PC | 2 ± 0.35 | 11.1 ± 4.1 | 0.13 ± 0.03 | 1,122 ± 156 | 9.3 ± 0.7 | 1 | |
| CCK+ to PC (I3) | ||||||||
| CCKBC | PC | 1.8 ± 0.3 | 9.35 ± 1 | 0.16 ± 0.04 | 153 ± 120 | 12 ± 3.5 | 1 | |
| SCA | PC | 2.15 ± 0.3 | 8.3 ± 0.44 | 0.15 ± 0.03 | 185 ± 32 | 14 ± 5.8 | 1 | |
| CCK+ | PC | 2 ± 0.15 | 8.8 ± 0.25 | 0.16 ± 0.01 | 168 ± 15 | 13 ± 0.5 | 1 | |
| SOM+ to PC (I2) | ||||||||
| Tri | PC | 1.4 ± 0.3 | 7.75 ± 0.9 | 0.3 ± 0.08 a | 1,250 ± 520 a | 2 ± 4 a | 1 | |
| SOM+ | PC | 1.4 ± 0.3 | 8.3 ± 2.2 a | 0.3 ± 0.08 a | 1,250 ± 520 a | 2 ± 4 a | 1 | |
| NOS+ to PC (I3) | ||||||||
| Ivy | PC | 0.48 ± 0.05 | 16± 2.5 | 0.32 ± 0.14a | 144 ± 80a | 62 ± 31a | 1 | |
| CCK− to CCK− (I2) | ||||||||
| PVBC | PVBC | 4.5 ± 0.3 | 2.67 ± 0.13 | 0.26 ± 0.05 | 930 ± 360 | 1.6 ± 0.6 | 6 | |
| PVBC | AA | 4.5 ± 0.3 | 2.67 ± 0.13 | 0.24 ± 0.15 | 1,730 ± 530 | 3.5 ± 1.5 | 1 | |
| CCK− | CCK− | 4.5 ± 0.3 | 2.67 ± 0.13 | 0.26 ± 0.05 | 930 ± 360 | 1.6 ± 0.6 | 1 | |
| CCK+ to CCK+ (I1) | ||||||||
| CCKBC | CCKBC | 4.5 ± 0.3 | 4.5 ± 0.55 | 0.11 ± 0.03 | 115 ± 110 | 1,542 ± 700 | 1 | |
| CCK+ | CCK+ | 4.5 ± 0.3 | 4.5 ± 0.55 | 0.11 ± 0.03 | 115 ± 110 | 1,542 ± 700 | 1 | |
Note: Synapse parameters either taken from the literature (τdecay (ms)), fitted directly to data (USE, D (ms), F (ms)), calibrated in silico ( (nS), NRRP) or taken from the somatosensory cortex ((Markram et al., 2015) marked with superscript “a”). Values in the τdecay column which neither appear in Supplementary Table S1 (summarizing rat PSCs) nor are taken from the somatosensory cortex, are from mouse recordings (Daw et al., 2009; Lee et al., 2014). Average class parameters are marked in bold and are used predictively for the remaining pathways belonging to the same class. For cells belonging into the same class, see Table 2, Assumption 9. M‐type abbreviations are as in Figure 3c. [Correction added on 12 October 2020, after first online publication: Values in the above table were updated.]
FIGURE 5.
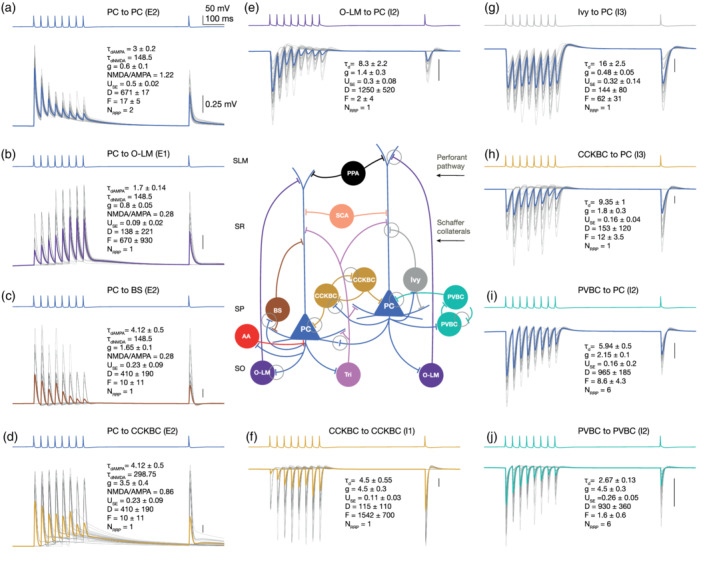
Summary of synapse diversity in the CA1 network model. Panels represent exemplar in silico pairs from the nine generalized pathways (two for PC to SOM− interneurons). Presynaptic voltage traces are shown in the upper traces of each panel (a–j), while the postsynaptic potentials elicited in 35 trials (in gray) and the average of these trials are superimposed in the lower traces of each panel. Postsynaptic cells were held at −65 mV steady‐state potential in in silico current‐clamp mode. Physical dimensions are as follows: decay time constant τd and D, F depression and facilitation time constants: ms, peak synaptic conductance : nS, while the absolute release probability USE and NMDA/AMPA conductance ratios are dimensionless. (a) PC to PC (E2). (b) PC to O‐LM cell (E1). (c) PC to (SP) bistratified cell (E2). (d) PC to CCKBC (E2). (e) O‐LM cell to PC (I2). (f) CCKBC to CCKBC (I1). (g) Ivy cell to PC (I3). (h) CCKBC to PC (I3). (i) PVBC to PC (I2). (j) PVBC to PVBC (I2). Vertical scale bars on each panel represent 0.25 mV. Connectivity in the schematic CA1 microcircuit in the middle is simplified for clarity (e.g., most of the interneuron to interneuron connections are missing). Simplified synapses of the pathways shown in the panels around are indicated with gray circles. M‐type abbreviations are as in Figure 3c [Color figure can be viewed at wileyonlinelibrary.com]
Neurotransmitter release probability and the STP profile are not only sensitive to the recording temperature and the developmental age but also [Ca2+]o (Guzman, Schlögl, Frotscher, & Jonas, 2016; Rozov et al., 2001; Williams & Atkinson, 2007). Therefore, we modeled [Ca2+]o sensitivity with a highly nonlinear scaling of USE (absolute release probability) values (see Section 2.7). As an exemplar result of this additional modeling detail, the PC‐to‐PC pathway exhibits an E3 (excitatory pseudolinear) STP profile characterized by low PSP amplitudes with high trial‐by‐trial variability and failures at in vivo like [Ca2+]o levels (1.1–1.3 mM) compared to the in vitro levels (2–2.5 mM) E2 (excitatory depressing) profile (Supplementary Figure S2b). USE values are scaled by a Hill isotherm (see Section 2.7) parameterized with data from PSP amplitudes in neocortex (Markram et al. (2015), supplementary figure S11), which is an indirect measure of the release probability. Here, we have shown that applying this Hill isotherm directly to the USE values indeed results in the same scaling profile of PSP amplitudes in the case of PC‐to‐PC connection (Supplementary Figure S3a).
3.5. Calibration of peak synaptic conductances to match PSP amplitudes
There is a dearth of studies characterizing both the PSC and PSP amplitudes for the same connections in rat hippocampal CA1 (compare Supplementary Tables S1 and S2). Therefore, we only used PSP amplitudes that were measured experimentally to calibrate the in silico peak synaptic conductances in order to match the in vitro PSPs (Ali et al., 1998; Ali & Thomson, 1998; Cobb et al., 1997; Deuchars & Thomson, 1996; Fuentealba et al., 2008; Pawelzik et al., 2002; Pawelzik, Bannister, Deuchars, Ilia, & Thomson, 1999) (see Figure 3d and Table 3). Having parameterized all relevant anatomical and physiological synaptic properties including the number of synapses per connections, axo‐dendritic innervation patterns, PSC rise and decay time constants, STP parameters, NRRP, NMDA/AMPA peak conductance ratio, and reversal potential, we undertook in silico paired recordings by following a sequence of steps. A connected pair of neurons within a pathway specific intersomatic distance (usually ~100 μm) for a given pathway was sampled from the hippocampal CA1 model, the postsynaptic neuron was current clamped to a pathway‐specific SS potential (see Supplementary Table S2), an AP was elicited in the presynaptic neuron, which caused a postsynaptic response, measured in the soma. After repeating this sequence for multiple pairs of the same pathway (n = 50) with many trials (n = 35), we derived the peak synaptic conductance value that yielded the reference mean experimental PSP amplitude (see Section 2.6). Next, we repeated the same protocol on a set of 50 randomly selected pairs with the calibrated peak conductance values as a validation of our approach (r = 0.99; Figure 4c and Supplementary Table S5).
As an independent external validation of the peak conductances, we compared them against sparse published data estimating single‐receptor conductance and receptor numbers in excitatory synapses on PCs. Hippocampal CA1 PCs receive most of their inputs from CA3 PCs through the Schaffer collaterals (Megías, Emri, Freund, & Gulyás, 2001; Takács et al., 2012), whereas in this study we only considered intrinsic connections—for example, excitatory connections between local CA1 PCs—and not long‐range extrinsic projections. Thus, single‐receptor conductances and receptor number estimates from the Schaffer collateral synapses were assumed to generalize for the intrinsic PC‐to‐PC connections. Using nonstationary fluctuation analysis on EPSCs recorded in outside‐out dendritic membrane patches, (Spruston, Jonas, & Sakmann, 1995) estimated peak single‐receptor conductances of 10.2 pS and 43.5 pS for AMPARs and NMDARs, respectively. Based on these numbers, our calibrated values resulting in a peak AMPAR conductance of 0.6 ± 0.1 nS is the net result of ~59 AMPARs per synaptic contact. Based on an experimentally measured NMDAR/AMPAR peak conductance ratio of 1.22 (Myme et al., 2003), we predict that there are about ~18 NMDARs constituting a single synaptic contact between CA1 PCs. Our in silico predictions are consistent with experimental studies that estimate ~58–70 AMPA and ~5–30 NMDA receptors (Jonas, Major, & Sakmann, 1993; Matsuzaki et al., 2001; Nusser et al., 1998; Spruston et al., 1995). Taken together, these experimental datasets enable an independent validation of the calibrated peak conductance of PC‐to‐PC connections in CA1. In addition, we also predict an average GABA peak conductance of 2 ± 1 nS at a single inhibitory synaptic contact comprising ~100 GABAergic receptors, which is also in good agreement with previous estimates (Mody & Pearce, 2004).
3.6. Parameter extrapolation
By integrating all the synaptic parameters and performing paired recordings in silico, we procured a dataset of 16 pathways (Table 3). The number of theoretically possible pathways (based on 12 m‐types) in our CA1 circuit model is 144; however, only 102 of these are biologically viable based on the extent of axo‐dendritic overlap (Figure 3c,d). Therefore, the parameters of the remaining 90% of the pathways had to be extrapolated. We generalized the anatomical properties of synapses (number of synapses per connection, connection probability, bouton density, innervation profile) obtained from the fraction of characterized to the remainder of uncharacterized pathways as shown previously (Markram et al., 2015; Reimann et al., 2015). However, for STP profiles of hippocampal connections obtained from studies that reported measurements of paired‐pulse ratios, but did not provide the raw experimental traces with ≥2 presynaptic spikes (Ali & Thomson, 1998; Deuchars & Thomson, 1996; Fuentealba et al., 2008), we applied analogous parameters from the somatosensory cortex (Markram et al., 2015). We performed a prior consistency check of the parameter ranges for similar connection types—perisomatic inhibitory (BCs) to PC, and inhibitory to inhibitory—that have been experimentally characterized in both somatosensory cortex and hippocampus and found them to be comparable. Therefore, our rationale to generalize four sets of USE, D, F values from the somatosensory cortex to the hippocampus (Table 3) could be justified. Thereafter, we approximated the missing parameters with averaged values across specific connection types that were grouped according to neurochemical markers that appear to have similar STP parameters and peak conductances (Table 3). For example, it is known that excitatory synapses on distal dendrite targeting interneurons, which predominantly express SOM—such as PC to O‐LM connections—are mostly facilitating, and on the contrary inhibitory synapses from SOM+ neurons to PCs are strongly depressing (Ali & Thomson, 1998). This exercise resulted in nine synaptic classes, covering all connection types in the CA1 region (Table 3 and Figure 5). Most of these classes contain few experimentally characterized examples, especially between inhibitory interneurons (Table 3). We have previously shown that averaging STP parameters and peak conductances within synaptic classes is a valid method to extrapolate missing values (Markram et al., 2015; Ramaswamy et al., 2015).
With the integrated and calibrated, but mostly generalized set of parameters (, τdecay, USE, D, F parameters of STP and NRRP; Figure 2) for all pathways in the CA1 model we predicted the CVs of the first PSCs (Figure 4d) and the first PSP amplitudes (Figure 4e), based on previously published cell models (Migliore et al., 2018) and statistically derived connectivity. In addition, we performed in silico paired recordings in all possible pre‐post combination of m‐type‐specific pathways (n = 102 biologically viable pathways) to generate detailed predictions of the physiological properties of synaptic transmission including PSP amplitudes, 10–90% rise times, decay time constants, latencies, CV of first PSP amplitude, and percentage of failures (Figure 4f). Although these predictions could provide preliminary insights into the organizing principles of synaptic transmission in hippocampal CA1—in particular, inhibitory pathways, which remain mostly uncharacterized—they require further validation through targeted experiments, for example, employing state‐of‐the‐art multiple whole‐cell patch‐clamp recordings (Espinoza et al., 2018; Guzman et al., 2016; Perin et al., 2011).
4. DISCUSSION
Recent advances in high‐performance computing have enabled biologically detailed, data‐driven reconstructions and large‐scale simulations of brain regions (Bezaire, Raikov, Burk, Vyas, & Soltesz, 2016; Bezaire & Soltesz, 2013; Markram et al., 2015; Wheeler et al., 2015). Here, we demonstrate that a data‐driven workflow grounded in biological first‐principles, which was used to reconstruct a biologically detailed model of rat neocortical tissue digitally, can be extended to model other brain regions such as the hippocampal CA1, to reconcile disparate cellular and synaptic data, and to extrapolate from the sparse set of experimentally obtained parameters to predict those of synaptic connections not yet characterized experimentally. In this study, we chose a previous implementation of the phenomenological TM model of STP, which is based on the quantal model of neurotransmitter release. The approach was able not only to extract relevant parameters from raw experimental traces, but scaled well to simulate dynamic transmission (Markram et al., 2015; Ramaswamy et al., 2012, 2015). In addition, this version of the TM model also enabled us to simulate trial‐to‐trial fluctuations to recreate, validate, and predict a broad spectrum of synaptic properties for cell‐type‐specific hippocampal connections including amplitudes, rise and decay times, latency, variability, and response failures (Figure 4f). It is known that [Ca2+]o regulates the neurotransmitter release probability, and therefore, the amplitudes of PSPs. In this study, we adapted the existing data‐driven digital reconstruction workflow to reconcile differences in synaptic dynamics that were characterized at different [Ca2+]o levels. Therefore, we scaled the neurotransmitter release probabilities for all pathways that were characterized at 1.6–2 mM [Ca2+]o (Kohus et al., 2016; Losonczy et al., 2002; Markram et al., 2015) before calibrating peak conductances to match PSP amplitudes that were measured at 2.5 mM [Ca2+]o, which is more representative of baseline values for hippocampal slice experiments (Ali et al., 1998; Ali & Thomson, 1998; Deuchars & Thomson, 1996; Fuentealba et al., 2008; Pawelzik et al., 1999, 2002).
In the continuing spirit of bringing together, hippocampal synaptic electrophysiology from published literature a recent complementary study leveraged text‐mining techniques to extract the properties of synaptic connections in hippocampal CA1, including PSP amplitudes and peak conductances (Moradi & Ascoli, 2020). The authors have also open‐sourced their collection of papers and parameters alongside useful cloud‐based tools to calculate reversal potentials and LJPs, of which we took advantage for this paper. However, our approach to data integration from literature demonstrates that synaptic properties reported in the literature such as peak conductances should not be interpreted at face value but require further corrections to account for inadequate space‐clamp errors, which could severely underestimate their value by twofold to threefold (Markram et al., 2015). Furthermore, when integrating data from whole‐cell patch‐clamp recordings, the interaction between the extracellular bath and intracellular pipette solutions, and their influence on the kinetics of ion channel mechanisms used in the in silico single‐cell models becomes paramount.
The results we report, to the best of our knowledge, constitute a comprehensive resource, not only for the anatomy but also for the physiology of synaptic connections in the rat hippocampal CA1 region. Consolidation of the state of the literature not only facilitates building detailed models but also highlights knowledge gaps and could help in prioritizing the identification of missing data on CA1 connections, such as PC to interneurons, and between interneurons, which could form diverse presynaptic–postsynaptic combinations of potential CA1 connection types that are crucial in regulating hippocampal oscillations (Klausberger & Somogyi, 2008; Pelkey et al., 2017). Our modeling approach predicts relatively high connection probabilities for interneuron to interneuron connections, and low IPSP amplitudes (see Figures 3d and 4e). However, these predictions need further experimental validation, probably through multiple patch‐clamp recordings, which have enabled high‐throughput mapping of inhibitory circuits not only in the neocortex (Jiang et al., 2015), but also in the dentate gyrus of the hippocampal formation (Espinoza et al., 2018). Indeed, the parameter set presented here should be considered a first draft, with many assumptions and limitations. For example, we assume somatically measured PSC decay time constants for dendritic synapses without any correction for attenuation, use USE, D, F values obtained in CA3, generalize NMDA/AMPA peak ratios characterized between PCs to all other excitatory pathways, and do not model GABAB receptors. We plan to refine these assumptions systematically in future versions of our model and overcome limitations by integrating new experimental data when available (see Table 1 for all data inclusion criteria and Table 2 for all explicit limitations). The presence of blockers such as TTX, QX314, cesium, and gluconate among many others, alter the kinetics of dendritic ion channels, which are active in the subthreshold regime, and thus, are key factors in governing the attenuation of PSPs in active dendrites. However, in our study, the core experimental dataset that was used to calibrate the peak synaptic conductances (Supplementary Tables S2 and S5) were derived exclusively from sharp‐electrode recordings where the intracellular medium is devoid of any of the above blockers, and therefore, the subthreshold regime of the single‐cell models are not unduly influenced. Indeed, the effects of blockers on the subthreshold regime will not only become important for future refinements of single‐cell models but also when more experimental data from whole‐cell patch clamp recordings are available.
By detailing all the integration steps in this study, we had two main objectives. First, we aimed to demonstrate that published parameters should not be taken at face value without rigorously checking their consistency within any modeling framework and the necessity of being abreast of the state‐of‐the‐art experimental techniques. Second, we attempted to emphasize the fact that a growing diversity of experimental standards combined with published literature that provides access to only processed data sets but not raw experimental traces could lead to an inconsistent picture of a fundamental mechanism such as synaptic transmission. The bottom‐up modeling framework presented as a resource in this article could facilitate the integration of disparate datasets and provide a platform within which a community‐driven consensus of the synaptic organization of the hippocampal formation could develop.
CONFLICT OF INTEREST
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
AUTHOR CONTRIBUTIONS
Srikanth Ramaswamy, András Ecker, and Eilif Muller conceptualized the study. Srikanth Ramaswamy supervised the study. Joanne Falck and Sigrun Lange reconstructed single cells in Neurolucida. Audrey Mercer and Alex M. Thomson provided experimental datasets. Sára Sáray, Szabolcs Káli, and Michele Migliore optimized and validated single cell models. Armando Romani built the CA1 circuit with inputs from all authors. András Ecker performed literature curation, simulations, analyses, and generated the figures with inputs from Szabolcs Káli, Michael W. Reimann, and Srikanth Ramaswamy. András Ecker, Michael W. Reimann, and Srikanth Ramaswamy wrote the manuscript with inputs from all authors.
Supporting information
Appendix S1: Supporting information
ACKNOWLEDGMENTS
The authors would like to thank Drs Giuseppe Chindemi, Natali Barros‐Zulaica, Julian M. L. Budd, Rodrigo Perin, and Zoltán Nusser for fruitful discussions as well as Werner van Geit, Michael Gevaert, Arseniy Povolotsky, Shailesh Appukuttan, Cyrille Favreau, and Marwan Abdellah for technical assistance. This study was supported by funding to the Blue Brain Project, a research center of the École Polytechnique Fédérale de Lausanne, from the Swiss Government's ETH Board of the Swiss Federal Institutes of Technology. Funding was also provided by the Human Brain Project through the European Union Seventh Framework Program (FP7/2007‐2013) under grant agreement no. 604102 (HBP) and from the European Union's Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreements No. 720270 (Human Brain Project SGA1) and No. 785907 (Human Brain Project SGA2). The Blue Brain 5 supercomputer (HPE SGI 8600 system) is financed by ETH Board Funding to the Blue Brain Project as a National Research Infrastructure and hosted at the Swiss National Supercomputing Center (CSCS) in Lugano. Paired recordings and reconstructions from Alex Thomson's lab were also supported by the Medical Research Council, the Wellcome Trust and Novartis Pharma. Sára Sáray was also supported by the ÚNKP‐19‐3‐III New National Excellence Program of the Ministry for Innovation and Technology, the European Union, cofinanced by the European Social Fund (EFOP‐3.6.3‐VEKOP‐16‐2017‐00002).
Ecker A, Romani A, Sáray S, et al. Data‐driven integration of hippocampal CA1 synaptic physiology in silico . Hippocampus. 2020;30:1129–1145. 10.1002/hipo.23220
Funding information École Polytechnique Fédérale de Lausanne; ETH Board Funding; European Union Seventh Framework Program, Grant/Award Numbers: 604102, FP7/2007‐2013; European Union's Horizon 2020 Framework Programme for Research and Innovation, Grant/Award Numbers: 785907, 720270; ÚNKP‐19‐3‐III New National Excellence Program; European Social Fund, Grant/Award Number: EFOP‐3.6.3‐VEKOP‐16‐2017‐00002
Contributor Information
András Ecker, Email: andras.ecker@epfl.ch.
Srikanth Ramaswamy, Email: srikanth.ramaswamy@epfl.ch.
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available on request from the corresponding author.
REFERENCES
- Ali, A. B. (2007). Presynaptic inhibition of GABAA receptor‐mediated unitary IPSPs by cannabinoid receptors at synapses between CCK‐positive interneurons in rat hippocampus. Journal of Neurophysiology, 98, 861–869. [DOI] [PubMed] [Google Scholar]
- Ali, A. B. (2011). CB1 modulation of temporally distinct synaptic facilitation among local circuit interneurons mediated by N‐type calcium channels in CA1. Journal of Physiology, 105, 1051–1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ali, A. B. , Bannister, A. P. , & Thomson, A. M. (1999). IPSPs elicited in CA1 pyramidal cells by putative basket cells in slices of adult rat hippocampus. European Journal of Neuroscience, 11, 1741–1753. [DOI] [PubMed] [Google Scholar]
- Ali, A. B. , Deuchars, J. , Pawelzik, H. , & Thomson, A. M. (1998). CA1 pyramidal to basket and bistratified cell EPSPs: Dual intracellular recordings in rat hippocampal slices. Journal of Physiology, 507, 201–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ali, A. B. , & Thomson, A. M. (1998). Facilitating pyramid to horizontal oriens‐alveus interneurone inputs: Dual intracellular recordings in slices of rat hippocampus. Journal of Physiology, 507, 185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrasfalvy, B. K. , & Magee, J. C. (2001). Distance‐dependent increase in AMPA receptor number in the dendrites of adult hippocampal CA1 pyramidal neurons. The Journal of Neuroscience, 21, 9151–9159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barros‐Zulaica, N. , Rahmon, J. , Chindemi, G. , Perin, R. , Markram, H. , Muller, E. , & Ramaswamy, S. (2019). Estimating the readily‐releasable vesicle pool size at synaptic connections in a neocortical microcircuit. Frontiers in Synaptic Neuroscience, 11, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos, M. , Vida, I. , Frotscher, M. , Meyer, A. , Monyer, H. , Geiger, J. R. P. , & Jonas, P. (2002). Fast synaptic inhibition promotes synchronized gamma oscillations in hippocampal interneuron networks. PNAS, 99, 13222–13227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezaire, M. J. , Raikov, I. , Burk, K. , Vyas, D. , & Soltesz, I. (2016). Interneuronal mechanisms of hippocampal theta oscillations in a full‐scale model of the rodent CA1 circuit. eLife, 5, 1–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezaire, M. J. , & Soltesz, I. (2013). Quantitative assessment of CA1 local circuits: Knowledge base for interneuron‐pyramidal cell connectivity. Hippocampus, 23, 751–785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biró, A. A. , Holderith, N. B. , & Nusser, Z. (2005). Quantal size is independent of the release probability at hippocampal excitatory synapses. Journal of Neuroscience, 25, 223–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biró, A. A. , Holderith, N. B. , & Nusser, Z. (2006). Release probability‐dependent scaling of the postsynaptic responses at single hippocampal GABAergic synapses. The Journal of Neuroscience, 26, 12487–12496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bliss, T. V. P. , & Collingridge, G. L. (2013). Expression of NMDA receptor‐dependent LTP in the hippocampus: Bridging the divide. Molecular Brain, 6, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buhl, E. H. , Cobb, S. R. , Halasy, K. , & Somogyi, P. (1995). Properties of unitary IPSPs evoked by anatomically identified basket cells in the rat hippocampus. European Journal of Neuroscience, 7, 1989–2004. [DOI] [PubMed] [Google Scholar]
- Buhl, E. H. , Halasy, K. , & Somogyi, P. (1994). Diverse sources of hippocampal unitary inhibitory postsynaptic potentials and the number of synaptic release sites. Nature, 368, 823–828. [DOI] [PubMed] [Google Scholar]
- Buhl, E. H. , Han, Z.‐S. , Lörinczi, Z. , Stezhka, V. V. , Karnup, S. V. , & Somogyi, P. (1994). Physiological properties of anatomically identified AxoAxonic in the rat hippocampus. Journal of Neurophysiology, 71, 1289–1307. [DOI] [PubMed] [Google Scholar]
- Buzsáki, G. (1989). Two‐stage model of memory trace formation: A role for “noisy” brain states. Neuroscience, 31, 551–570. [DOI] [PubMed] [Google Scholar]
- Christie, J. M. , & Jahr, C. E. (2006). Multivesicular release at Schaffer collateral‐CA1 hippocampal synapses. Journal of Neuroscience, 26, 210–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cobb, S. R. , Halasy, K. , Vida, I. , Nyíri, G. , Tamás, G. , Buhl, E. H. , & Somogyi, P. (1997). Synaptic effects of identified interneurons innervating both interneurons and pyramidal cells in the rat hippocampus. Neuroscience, 79, 629–648. [DOI] [PubMed] [Google Scholar]
- Conti, R. , & Lisman, J. (2003). The high variance of AMPA receptor‐and NMDA receptor‐mediated responses at single hippocampal synapses: Evidence for multiquantal release. PNAS, 100, 4885–4890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornford, J. , Mercier, M. S. , Leite, M. , Magloire, V. , Häusser, M. , & Kullmann, D. M. (2019). Dendritic NMDA receptors in parvalbumin neurons enable strong and stable neuronal assemblies. eLife, 8, 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw, M. I. , Tricoire, L. , Erdelyi, F. , Szabo, G. , & McBain, C. J. (2009). Asynchronous transmitter release from cholecystokinin‐containing inhibitory interneurons is widespread and target‐cell independent. Journal of Neuroscience, 29, 11112–11122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Castillo, J. , & Katz, B. (1954). Quantal components of the end‐plate potential. The Journal of Physiology, 124, 560–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deuchars, J. , & Thomson, A. M. (1996). CA1 pyramid‐pyramid connections in rat hippocampus in vitro: Dual intracellular recordings with biocytin filling. Neuroscience, 74, 1009–1018. [DOI] [PubMed] [Google Scholar]
- Elfant, D. , Pal, B. Z. , Emptage, N. , & Capogna, M. (2008). Specific inhibitory synapses shift the balance from feedforward to feedback inhibition of hippocampal CA1 pyramidal cells. European Journal of Neuroscience, 27, 104–113. [DOI] [PubMed] [Google Scholar]
- Éltes, T. , Kirizs, T. , Nusser, Z. , & Holderith, N. (2017). Target cell type‐dependent differences in Ca2+ channel function underlie distinct release probabilities at hippocampal glutamatergic terminals. The Journal of Neuroscience, 37, 1910–1924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Espinoza, C. , Guzman, S. J. , Zhang, X. , & Jonas, P. (2018). Parvalbumin + interneurons obey unique connectivity rules and establish a powerful lateral‐inhibition microcircuit in dentate gyrus. Nature Communications, 9, 4605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Földy, C. , Lee, S. , Morgan, R. J. , & Soltesz, I. (2010). Regulation of fast‐spiking basket cell synapses by the chloride channel ClC‐2. Nature Neuroscience, 13, 1047–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuentealba, P. , Begum, R. , Capogna, M. , Jinno, S. , Márton, L. F. , Csicsvari, J. , … Klausberger, T. (2008). Ivy cells: A population of nitric‐oxide‐producing, slow‐spiking GABAergic neurons and their involvement in hippocampal network activity. Neuron, 57, 917–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuhrmann, G. , Segev, I. , Markram, H. , & Tsodyks, M. (2002). Coding of temporal information by activity‐dependent synapses. Journal of Neurophysiology, 87, 140–148. [DOI] [PubMed] [Google Scholar]
- Groc, L. , Gustafsson, B. , & Hanse, E. (2002). Spontaneous unitary synaptic activity in CA1 pyramidal neurons during early postnatal development: Constant contribution of AMPA and NMDA receptors. The Journal of Neuroscience, 22, 5552–5562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulyás, A. , Miles, R. , Sik, A. , Toth, K. , Tamamaki, N. , & Freund, T. (1993). Hippocampal pyramidal cells excite inhibitory neurons through a single release site. Nature, 366, 683–687. [DOI] [PubMed] [Google Scholar]
- Gulyás, A. I. , Freund, T. F. , & Káli, S. (2016). The effects of realistic synaptic distribution and 3D geometry on signal integration and extracellular field generation of hippocampal pyramidal cells and inhibitory neurons. Frontiers in Neural Circuits, 10, 1–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta, A. , Wang, Y. , & Markram, H. (2000). Organizing principles for a diversity of GABAergic interneurons and synapses in the neocortex. Science, 287, 273–278. [DOI] [PubMed] [Google Scholar]
- Guzman, S. J. , Schlögl, A. , Frotscher, M. , & Jonas, P. (2016). Synaptic mechanisms of pattern completion in the hippocampal CA3 network. Science, 353, 1117–1123. [DOI] [PubMed] [Google Scholar]
- Hestrin, S. , Sah, P. , & Nicoll, R. A. (1990). Mechanisms generating the time course of dual component excitatory synaptic currents recorded in hippocampal slices. Neuron, 5, 247–253. [DOI] [PubMed] [Google Scholar]
- Hill, A. V. (1910). The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. Journal of Physiology, 40, 4–7. [Google Scholar]
- Hines, M. L. , & Carnevale, N. T. (1997). The NEURON simulation environment. Neural Computation, 9, 1179–1209. [DOI] [PubMed] [Google Scholar]
- Hines, M. L. , & Carnevale, N. T. (2000). Expanding NEURON's repertoire of mechanisms with NMODL. Neural Computation, 12, 995–1007. [DOI] [PubMed] [Google Scholar]
- Hines, M. L. , Eichner, H. , & Schürmann, F. (2008). Neuron splitting in compute‐bound parallel network simulations enables runtime scaling with twice as many processors. Journal of Computational Neuroscience, 25, 203–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines, M. L. , Markram, H. , & Schürmann, F. (2008). Fully implicit parallel simulation of single neurons. Journal of Computational Neuroscience, 25, 439–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahr, C. E. , & Stevens, C. F. (1990). Voltage dependence of NMDA‐activated macroscopic conductances predicted by single‐channel kinetics. The Journal of Neuroscience, 10, 3178–3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang, X. , Shen, S. , Cadwell, C. R. , Berens, P. , Sinz, F. , Ecker, A. S. , … Tolias, A. S. (2015). Principles of connectivity among morphologically defined cell types in adult neocortex. Science, 350, aac9462–aac9462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonas, P. , Major, G. , & Sakmann, B. (1993). Quantal components of unitary EPSCs at the mossy fibre synapse on CA3 pyramidal cells of rat hippocampus. The Journal of Physiology, 472, 615–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karayannis, T. , Elfant, D. , Huerta‐Ocampo, I. , Teki, S. , Scott, R. S. , Rusakov, D. A. , … Capogna, M. (2010). Slow GABA transient and receptor desensitization shape synaptic responses evoked by hippocampal neurogliaform cells. The Journal of Neuroscience, 30, 9898–9909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klausberger, T. , & Somogyi, P. (2008). Neuronal diversity and temporal dynamics: The unity of hippocampal circuit operations. Science, 321, 53–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohus, Z. , Káli, S. , Schlingloff, D. , Papp, O. , Rovira‐Esteban, L. , Freund, T. F. , … Gulyás, A. I. (2016). Properties and dynamics of inhibitory synaptic communication within the CA3 microcircuits of pyramidal cells and interneurons expressing parvalbumin or cholecystokinin. The Journal of Physiology, 594, 3745–3774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korinek, M. , Sedlacek, M. , Cais, O. , Dittert, I. , & Vyklicky, L. (2010). Temperature dependence of N‐methyl‐d‐aspartate receptor channels and N‐methyl‐d‐aspartate receptor excitatory postsynaptic currents. Neuroscience, 165, 736–748. [DOI] [PubMed] [Google Scholar]
- Le Roux, N. , Cabezas, C. , Böhm, U. L. , & Poncer, J. C. (2013). Input‐specific learning rules at excitatory synapses onto hippocampal parvalbumin‐expressing interneurons. Journal of Physiology, 591, 1809–1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, S. , Marchionni, I. , Bezaire, M. , Varga, C. , Danielson, N. , Lovett‐Barron, M. , … Soltesz, I. (2014). Parvalbumin‐positive basket cells differentiate among hippocampal pyramidal cells. Neuron, 82, 1129–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loebel, A. , Silberberg, G. , Helbig, D. , Markram, H. , Tsodyks, M. , & Richardson, M. J. E. (2009). Multiquantal release underlies the distribution of synaptic efficacies in the neocortex. Frontiers in Cellular Neuroscience, 3, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Losonczy, A. , Zhang, L. , Shigemoto, R. , Somogyi, P. , & Nusser, Z. (2002). Cell type dependence and variability in the short‐term plasticity of EPSCs in identified mouse hippocampal interneurones. The Journal of Physiology, 542, 193–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maass, W. , & Markram, H. (2002). Synapses as dynamic memory buffers. Neural Networks, 15, 155–161. [DOI] [PubMed] [Google Scholar]
- Maccaferri, G. , Roberts, J. D. B. , Szucs, P. , Cottingham, C. A. , & Somogyi, P. (2000). Cell surface domain specific postsynaptic currents evoked by identified GABAergic neurones in rat hippocampus in vitro. Journal of Physiology, 524, 91–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee, J. C. , & Cook, E. P. (2000). Somatic EPSP amplitude is independent of synapse location in hippocampal pyramidal neurons. Nature Neuroscience, 3, 895–903. [DOI] [PubMed] [Google Scholar]
- Markram, H. , Muller, E. , Ramaswamy, S. , Reimann, M. W. , Abdellah, M. , Sanchez, C. A. , … Schürmann, F. (2015). Reconstruction and simulation of neocortical microcircuitry. Cell, 163, 456–492. [DOI] [PubMed] [Google Scholar]
- Markram, H. , Wang, Y. , & Tsodyks, M. (1998). Differential signaling via the same axon of neocortical pyramidal neurons. PNAS, 95, 5323–5328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki, M. , Ellis‐Davies, G. C. R. , Nemoto, T. , Miyashita, Y. , Iino, M. , & Kasai, H. (2001). Dendritic spine geometry is critical for AMPA receptor expression in hippocampal CA1 pyramidal neurons. Nature Neuroscience, 4, 1086–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matta, J. A. , Pelkey, K. A. , Craig, M. T. , Chittajallu, R. , Jeffries, B. W. , & McBain, C. J. (2013). Developmental origin dictates interneuron AMPA and NMDA receptor subunit composition and plasticity. Nature Neuroscience, 16, 1032–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Megías, M. , Emri, Z. , Freund, T. F. , & Gulyás, A. I. (2001). Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience, 102, 527–540. [DOI] [PubMed] [Google Scholar]
- Migliore, R. , Lupascu, C. A. , Bologna, L. L. , Romani, A. , Courcol, J.‐D. , Antonel, S. , … Migliore, M. (2018). The physiological variability of channel density in hippocampal CA1 pyramidal cells and interneurons explored using a unified data‐driven modeling workflow. PLoS Computational Biology, 14, e1006423–e1006423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mody, I. , & Pearce, R. A. (2004). Diversity of inhibitory neurotransmission through GABA A receptors. Trends in Neurosciences, 27, 569–575. [DOI] [PubMed] [Google Scholar]
- Moradi, K. , & Ascoli, G. A. (2020). A comprehensive knowledge base of synaptic electrophysiology in the rodent hippocampal formation. Hippocampus, 30(4), 314–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myme, C. I. O. , Sugino, K. , Turrigiano, G. G. , & Nelson, S. B. (2003). The NMDA‐to‐AMPA ratio at synapses onto layer 2/3 pyramidal neurons is conserved across prefrontal and visual cortices. Journal of Neurophysiology, 90, 771–779. [DOI] [PubMed] [Google Scholar]
- Neher, E. (1992). Correction for liquid junction potentials in patch clamp experiments. Methods in Enzymology, 207, 123–131. [DOI] [PubMed] [Google Scholar]
- Nusser, Z. , Lujan, R. , Laube, G. , Roberts, J. D. B. , Molnar, E. , & Somogyi, P. (1998). Cell type and pathway dependence of synaptic AMPA receptor number and variability in the hippocampus. Neuron, 21, 545–559. [DOI] [PubMed] [Google Scholar]
- Pawelzik, H. , Bannister, A. P. , Deuchars, J. , Ilia, M. , & Thomson, A. M. (1999). Modulation of bistratified cell IPSPs and basket cell IPSPs by pentobarbitone sodium, diazepam and Zn2+: Dual recordings in slices of adult rat hippocampus. European Journal of Neuroscience, 11, 3552–3564. [DOI] [PubMed] [Google Scholar]
- Pawelzik, H. , Hughes, D. I. , & Thomson, A. M. (2002). Physiological and morphological diversity of immunocytochemically defined parvalbumin‐ and cholecystokinin‐positive interneurones in CA1 of the adult rat hippocampus. Journal of Comparative Neurology, 443, 346–367. [DOI] [PubMed] [Google Scholar]
- Pelkey, K. A. , Chittajallu, R. , Craig, M. T. , Tricoire, L. , Wester, J. C. , & McBain, C. J. (2017). Hippocampal GABAergic inhibitory interneurons. Physiological Reviews, 97, 1619–1747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perin, R. , Berger, T. K. , & Markram, H. (2011). A synaptic organizing principle for cortical neuronal groups. PNAS, 108, 5419–5424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouille, F. , & Scanziani, M. (2004). Routing of spike series by dynamic circuits in the hippocampus. Nature, 429, 717–723. [DOI] [PubMed] [Google Scholar]
- Price, C. J. , Cauli, B. , Kovács, E. R. , Kukik, Á. , Lambolez, B. , Shigemeto, R. , & Capogna, M. (2005). Neurogliaform neurons form a novel inhibitory network in the hippocampal CA1 area. Journal of Neuroscience, 25, 6775–6786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price, C. J. , Scott, R. , Rusakov, D. A. , & Capogna, M. (2008). GABAB receptor modulation of feedforward inhibition through hippocampal neurogliaform cells. The Journal of Neuroscience, 28, 6974–6982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramaswamy, S. , Courcol, J.‐D. , Abdellah, M. , Adaszewski, S. R. , Antille, N. , Arsever, S. , … Markram, H. (2015). The neocortical microcircuit collaboration portal: A resource for rat somatosensory cortex. Frontiers in Neural Circuits, 9, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramaswamy, S. , Hill, S. L. , King, J. G. , Schürmann, F. , Wang, Y. , & Markram, H. (2012). Intrinsic morphological diversity of thick‐tufted layer 5 pyramidal neurons ensures robust and invariant properties of in silico synaptic connections. Journal of Physiology, 590, 737–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reimann, M. W. , King, J. G. , Muller, E. B. , Ramaswamy, S. , & Markram, H. (2015). An algorithm to predict the connectome of neural microcircuits. Frontiers in Computational Neuroscience, 9, 120–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ropireddy, D. , Bachus, S. E. , & Ascoli, G. A. (2012). Non‐homogeneous stereological properties of the rat hippocampus from high‐resolution 3D serial reconstruction of thin histological sections. Neuroscience, 15, 91–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rozov, A. , Burnashev, N. , Sakmann, B. , & Neher, E. (2001). Transmitter release modulation by intracellular Ca2+buffers in facilitating and depressing nerve terminals of pyramidal cells in layer 2/3 of the rat neocortex indicates a target cell‐specific difference in presynaptic calcium dynamics. Journal of Physiology, 531, 807–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sik, A. , Penttonen, M. , Ylinen, A. , & Buzsáki, G. (1995). Hippocampal CA1 interneurons: An in vivo intracellular labeling study. Journal of Neuroscience, 10, 6651–6665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston, N. , Jaffe, D. B. , Williams, S. H. , & Johnston, D. (1993). Voltage‐ and space‐clamp errors associated with the measurement of electrotonically remote synaptic events. Journal of Neurophysiology, 70, 781–802. [DOI] [PubMed] [Google Scholar]
- Spruston, N. , Jonas, P. , & Sakmann, B. (1995). Dendritic glutamate receptor channels in rat hippocampal CA3 and CAl pyramidal neurons. Journal of Physiology, 482, 325–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart, G. , Schiller, J. , & Sakmann, B. (1997). Action potential initiation and propagation in rat neocortical pyramidal neurons. The Journal of Physiology, 505(Pt 3), 617–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takács, V. T. , Klausberger, T. , Somogyi, P. , Freund, T. F. , & Gulyás, A. I. (2012). Extrinsic and local glutamatergic inputs of the rat hippocampal CA1 area differentially innervate pyramidal cells and interneurons. Hippocampus, 22, 1379–1391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong, G. , & Jahr, C. E. (1994). Multivesicular release from excitatory synapses of cultured hippocampal neurons. Neuron, 12, 51–59. [DOI] [PubMed] [Google Scholar]
- Tsodyks, M. , & Markram, H. (1997). The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. PNAS, 94, 719–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyan, L. , Chamberland, S. , Magnin, E. , Camiré, O. , Francavilla, R. , Suzanne David, L. , … Topolnik, L. (2014). Dendritic inhibition provided by interneuron‐specific cells controls the firing rate and timing of the hippocampal feedback inhibitory circuitry. Journal of Neuroscience, 34, 4534–4547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Geit, W. , Gevaert, M. , Chindemi, G. , Rössert, C. , Courcol, J.‐D. , Muller, E. , … Markram, H. (2016). BluePyOpt: Leveraging open source software and cloud infrastructure to optimise model parameters in neuroscience. Frontiers in Neuroinformatics, 10, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vida, I. , Halasy, K. , Szinyei, C. , Somogyi, P. , & Buhl, E. H. (1998). Unitary IPSPs evoked by interneurons at the stratum radiatum—Stratum lacunosum‐moleculare border in the CA1. Journal of Physiology, 506, 755–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler, D. W. , White, C. M. , Rees, C. L. , Komendantov, A. O. , Hamilton, D. J. , & Ascoli, G. A. (2015). Hippocampome.org: A knowledge base of neuron types in the rodent hippocampus. eLife, 4, 1–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams, S. R. , & Atkinson, S. E. (2007). Pathway‐specific use‐dependent dynamics of excitatory synaptic transmission in rat intracortical circuits. Journal of Physiology, 585, 759–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams, S. R. , & Mitchell, S. J. (2008). Direct measurement of somatic voltage clamp errors in central neurons. Nature Neuroscience, 11, 790–798. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supporting information
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.


