Abstract
Function magnetic resonance imaging (fMRI) data are typically contaminated by noise introduced by head motion, physiological noise, and thermal noise. To mitigate noise artifact in fMRI data, a variety of denoising methods have been developed by removing noise factors derived from the whole time series of fMRI data and therefore are not applicable to real-time fMRI data analysis. In the present study, we develop a generally applicable, deep learning based fMRI denoising method to generate noise-free realistic individual fMRI volumes (time points). Particularly, we develop a fully data-driven 3D convolutional encapsulated Long Short-Term Memory (3DConv-LSTM) approach to generate noise-free fMRI volumes regularized by an adversarial network that makes the generated fMRI volumes more realistic by fooling a critic network. The 3DConv-LSTM model also integrates a gate-controlled self-attention model to memorize short-term dependency and historical information within a memory pool. We have evaluated our method based on both task and resting state fMRI data. Both qualitative and quantitative results have demonstrated that the proposed method outperformed state-of-the-art alternative deep learning methods.
Keywords: Adversarial regularizer, fMRI denoising, 3D convolutional LSTM, Gate-controlled self-attention
1. Introduction
Head motion, physiological noise, and thermal noise are main sources of noise in functional magnetic resonance imaging (fMRI) data [1, 2]. To mitigate noise artifact in fMRI data analysis, a variety of methods have been developed. Particularly, the combination of global signal regression (GSR) and motion censoring [3] has achieved promising performance to reduce head motion related noise [3–5]. However, such an approach reduces motion artifact in fMRI data analysis at a risk of losing fMRI volumes and even entire participants from analyses because of insufficient data remain after scrubbing. Filtering based methods are widely used to remove cardiac and respiratory noise fluctuations with the record of the spectrum or physiological wave functions [6, 7]. However, such methods may also affect the BOLD signal at the same frequency.
Data driven methods built upon principal component analysis (PCA) [8, 9] or independent component analysis (ICA) [10, 11] have achieved promising performance in fMRI data denoising. Deep learning methods have also been developed for denoising fMRI data [12–14], including a convolutional neural network (CNN) method for noise component identification after ICA decomposition [12], a Long Short-Term Memory (LSTM) method for denoising task-based fMRI data [13], and a deep convolutional generative adversarial network to reconstruct lost BOLD signal in resting state fMRI (rsfMRI) data [14]. However, these methods are not generally applicable in that they could only work on ICA component data, task fMRI data, or one-dimension BOLD signals.
In order to overcome limitation of the existing fMRI denoising methods, we develop a 3D convolutional LSTM method to generate noise-free fMRI volumes. Particularly, our method consists of an encoder network, a decoder network, and a critic network. The encoder network is built upon 3D convolutional encapsulated LSTM (3DConv-LSTM) structures to generate spatiotemporal data, in conjunction with the decoder network. The critic network together with an adversarial regularizer encourages the generated spatiotemporal data to be realistic by fooling the critic network which is trained to predict a mixing factor of different time points, similar to Generative Adversarial Networks (GANs) [15, 16]. We have evaluated our method in two different experiments. The first experiment with task fMRI data of the Human Connectome Project (HCP) [17] has demonstrated that our method could accurately generate fMRI volumes without altering brain activation patterns. The second experiment with rsfMRI data from ABIDE data [18] has demonstrated that our method could directly generate noise-free fMRI data by learning from supervision information generated by ICA-AROMA [11]. Different from ICA-AROMA method that identifies and removes noisy independent components, our method directly predicts noise-free individual time points. All these experimental results have demonstrated that our method is generally applicable to both task and resting state fMRI data and could achieve promising fMRI denoising performance.
2. Methods
In order to generate realistic fMRI data by learning from spatiotemporal fMRI data, an adversarial regularization together with 3D convolutional LSTM module is implemented. Assuming we have a 4D fMRI data with M × N × V voxels and T time points, we learn a data reconstruction model by adopting a 3D convolutional LSTM encoder to obtain latent factors for individual time point at time t, where θ denotes parameters of the encoder. The latent factor is then passed through a decoder to generate a time point . A critic network together with an adversarial regularizer is adopted to encourage the generated fMRI data to be realistic by fooling the critic network which is trained to predict a mixing factor of different time points. The overall algorithm and the 3D Convolutional LSTM encoder/decoder are illustrated in Fig. 1.
Fig. 1.
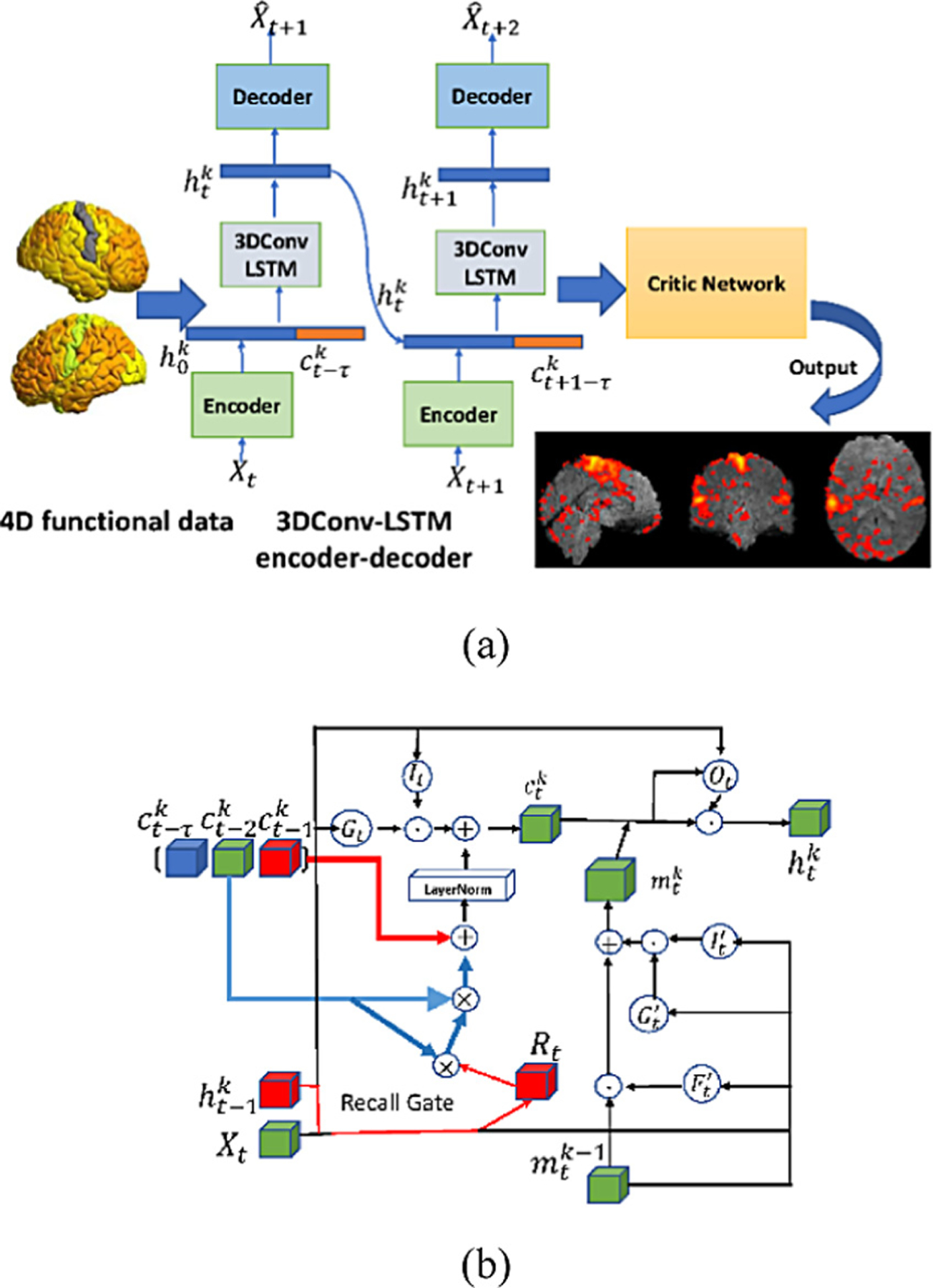
Flowchart of the proposed method, including a 3DConv-LSTM encapsulated encoder-decoder and a critic network with adversarial regularizer. (a) the overall framework; (b) the 3DConv-LSTM encoder.
The encoder network and decoder network are trained simultaneously to minimize the cost function:
| (1) |
where and Xt are predicted frame point and ground truth at time t. We will give more details about critic network in Sect. 2.2.
2.1. 3D Convolutional LSTM Structure (3DConv-LSTM)
The proposed 3D convolutional LSTM encoder is illustrated in Fig. 1(b), where the red arrow shows the flow of short-term memory and the blue arrow shows the flow of long-term information. The input to the 3DConv-LSTM encoder is denoted by Xt, the hidden state from the previous time stamp , the memory state from previous time stamp , and previous layer spatio-temporal memory . In order to capture the long-term time point relationship, we adopt a new memory RECALL mechanism [19], defined as:
| (2) |
where σ is the sigmoid function, denotes the 3D convolutional operation, ʘ is the Hadamard product, Rt is the recall gate, is the memory states, τ denotes the number of memory states that are included along the temporal interval, · denotes the matrix product of Rt and , and wxr, whr, wxi, whi, wxg, and whg are model parameters to be optimized. The Recall function controls the temporal interactions to learn temporally distant states of the spatiotemporal information. The input gate It and the input modulation Gt, similar to a standard LSTM, are used to encode and that connect short term changes between different time points. The output hidden states are defined as:
| (3) |
where w1×1×1 is the 1 × 1 × 1 convolutions. , and .are gate structures of the spatiotemporal memory.Ot is the output gate.
2.2. Adversarial Regularizer for Critic Network
In order to generate fMRI time points that are realistic, indistinguishable from the real data, and semantically smooth across time points, we adopted a critic network , similar to Generative Adversarial Networks (GANs) [15, 16], to regularize a mixture of two data points, i.e. , where and , are two latent factors at t1 and t2 (t1 < t2) respectively, and α ∈ [0, 1] is a mixing coefficient.
The critic network is trained to predict the mixing coefficient α of . We constrain α ∈ [0, 0.5] to resolve the ambiguity between α and 1 – α. Taken together, the 3DConv-LSTM is behaving like the generative process with the control of α to generate a realistic time point from and . The critic network works as a discriminator to distinguish the mixture coefficient α of latent factors and . Particularly, the critic network is trained to minimize:
| (4) |
where denotes the critic network, , and γ is a scalar hyperparameter. The second term constrains the critic network to yield an output of 0 if the input is Xt. By generating an interpolation between Xt and g∅(fθ (Xt), the second term also encourages the critic network to generate realistic data even if the decoder output is poor.
The encoder-decoder network loss is finally defined as
| (5) |
where the scalar parameter λ controls the weight of regularization term. Similar to train a GAN, θ and ∅ are optimized by minimizing Lf,g and is optimized by minimizing Ld.
3. Experimental Results
We evaluated our method on both task and resting state fMRI data and compared it with state-of-the-art alternatives, including a 3DConv-LSTM and an implementation of GANs. Particularly, the 3DConv-LSTM method was the encoder and decoder part of the proposed method without the critic network and adversarial regularizer, and the GAN was a combination of the critic network and a 3D autoencoder without the LSTM structure. The encoder consisted of two 3 × 3 × 3 convolutional layers followed by 2 × 2 × 2 max pooling layer. The convolution layer was zero-padded so that the input and output of the convolutional layer are of the same size. The decoder after the 3DConv-LSTM layer consisted of two 3 × 3 × 3 deconvolutional layers, followed by 2 × 2 × 2 × nearest neighbor upsampling. Models are trained with batch size 1 on a NVIDIA tesla P100 GPU with 12 GB memory. All the methods were implemented using TensorFlow and trained with ADAM optimizer based on the same training and validation data and tested on the same testing data.
3.1. Generation of Task fMRI Data
The proposed method was evaluated on task fMRI data of the HCP to generate realistic fMRI volumes so that they could replace noisy time points of fMRI scans instead of censoring. Particularly, 490 subjects of motor task fMRI were used in this experiment. The motor task consists of 6 events, left foot (LF), left hand (LH), right foot (RF), right hand (RH), tongue (T) and additionally 1 cue event (CUE) prior to each movement event. Each subject’s motor task fMRI scan consists of 284 time points. We randomly selected 350 subjects as training data, 50 subjects for validation, and the remaining 90 subjects for testing. For each testing subject, we split the whole time series into clips of 40 time points without overlapping and the trained deep learning models were used to generate fMRI data at 20 randomly selected time points based on the other time points within each clip.
We used structural similarity index measure (SSIM), peak signal-to-noise ratio (PSNR) and mean squared error (MSE) [19] to quantitatively measure difference between the real fMRI data and those generated by the deep learning models under comparison on the testing data. As summarized in Table 1, the average measures of all testing time points have demonstrated that our method obtained substantially better performance than both the GAN and 3DConv-LSTM methods.
Table 1.
Quantitative performance measures obtained on the motor task fMRI data by the deep learning models under comparison (mean ± standard deviation).
| Model | PSNR | SSIM | MSE |
|---|---|---|---|
| GAN | 36.722 ± 0.5744 | 0.970 ± 0.0031 | 25.796 ± 1.3058 |
| 3DConv-LSTM | 39.084 ± 0.3957 | 0.989 ± 0.0014 | 11.036 ± 0.7625 |
| Proposed method | 42.545 ± 0.1136 | 0.992 ± 0.0003 | 5.818 ± 0.3243 |
Representative fMRI data generated by the deep learning models under comparison along with the real fMRI data are show in Fig. 2. Representative real motor task fMRI data (a) and those generated by the deep learning methods under comparison, including GANs (b), 3DConv-LSTM (c), and our method (d), demonstrating that our method could generate fMRI time points visually more similar to the real data than the alternative methods under comparison. Figure 3 shows brain activation results obtained from real fMRI data and fMRI data generated by the deep learning methods under comparison. The activation results were thresholded at a p value 0.05 (uncorrected, two tailed). These results further demonstrated that the fMRI data generated by our method did not alter the brain activation patterns in that the activation map of fMRI data generated by our method was almost identical to that of the real fMRI data.
Fig. 2.
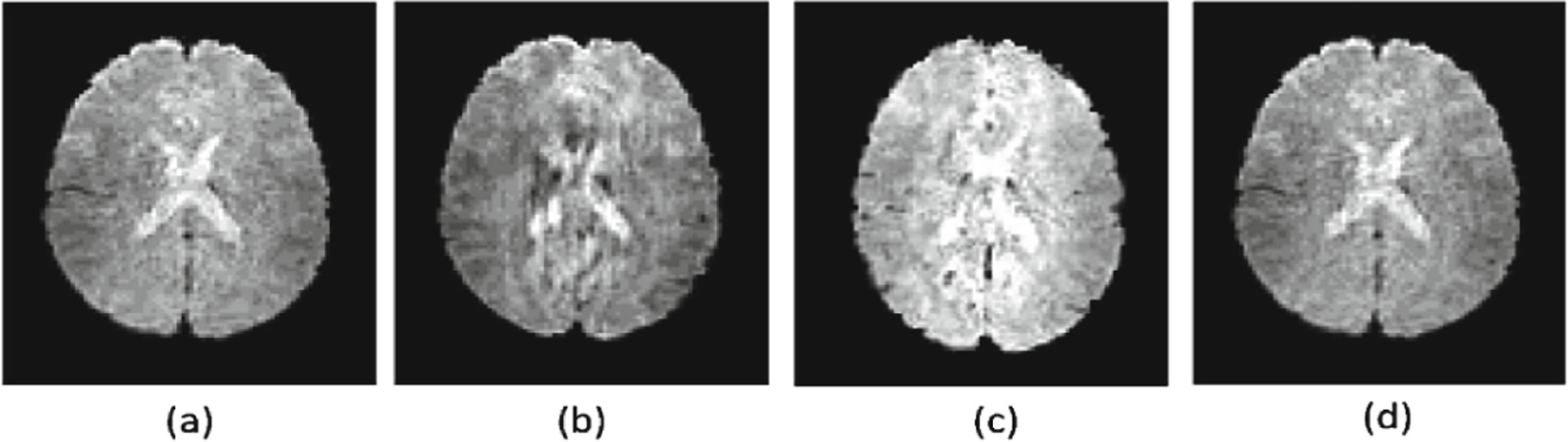
Representative real motor task fMRI data (a) and those generated by the deep learning methods under comparison, including GANs (b), 3DConv-LSTM (c), and our method (d).
Fig. 3.
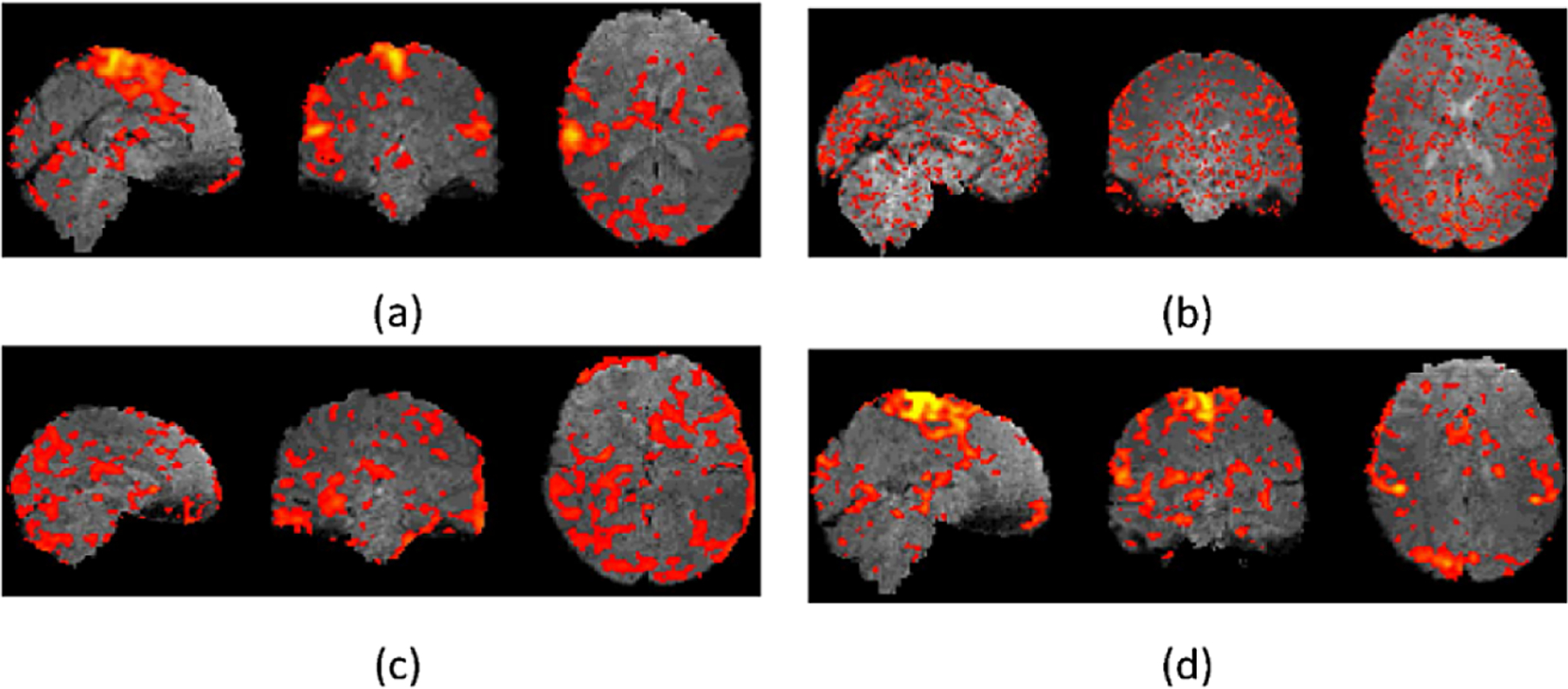
Representative Activation maps for motor task fMRI. (a) and those generated by the deep learning methods under comparison, including GANs (b), 3DConv-LSTM (c), and our method (d).
3.2. Generation of Resting State fMRI Data
The proposed method was evaluated on resting state fMRI data of the ABIDE study to generate noise-free fMRI data from raw fMRI scans. Particularly, we used rsfMRI data of 55 subjects from KKI site as training (80%) and validation (20%) data and rsfMRI of 38 subjects from Caltech site as testing data. All the training and testing data were preprocessed using fMRIPrep pipelines [20], and noise of the preprocessed rsfMRI data were removed using ICA-AROMA to generate noise-free data [11]. Based on the training data, the deep learning methods under comparison were used to train deep learning models to generate noise-free data from the preprocessed rsfMRI data with the noise-free data as supervision information. The deep learning models were finally applied to the preprocessed data of the testing dataset to generate noise-free data that were compared with those generated using ICA-AROMA.
The differences between noise-free data generated by ICA-AROMA and the deep learning models were quantitatively measured using SSIM, PSNR and MSE [19]. As summarized in Table 2, the average performance measures of all testing time points have demonstrated that our method obtained substantially better performance than both the GAN and 3DConv-LSTM methods. Consistent with the results summarized in Table 1, the 3DConv-LSTM method obtained better performance than the GAN method, and our method obtained the overall best performance.
Table 2.
Quantitative performance measures obtained on the rsfMRI data by the deep learning models under comparison (mean ± standard deviation).
| Model | PSNR | SSIM | MSE |
|---|---|---|---|
| GANs | 28.162 ± 0.8161 | 0.927 ± 0.0067 | 68.323 ± 7.5052 |
| 3DConv-LSTM | 32.382 ± 0.1789 | 0.950 ± 0.0026 | 59.735 ± 6.8117 |
| Proposed method | 33.697 ± 0.0097 | 0.958 ± 0.0001 | 55.746 ± 3.8986 |
We further evaluated the noise-free rsfMRI data generated by ICA-AROMA and the deep learning models using ICA. Particularly, MELODIC of FSL with its default parameters was used to compute independent components of different sets of the noise-free rsfMRI data. Figure 4 shows representative independent components computed from noise-free fMRI data generated by different methods. Compared with those computed from noise-free data generated by the GAN and 3DCOv-LSTM methods, the component computed from noise-free data generated by our method was visually closer to the component computed from the data generated by ICA-AROMA, indicating that our method generated fMRI data more similar to the supervision information.
Fig. 4.
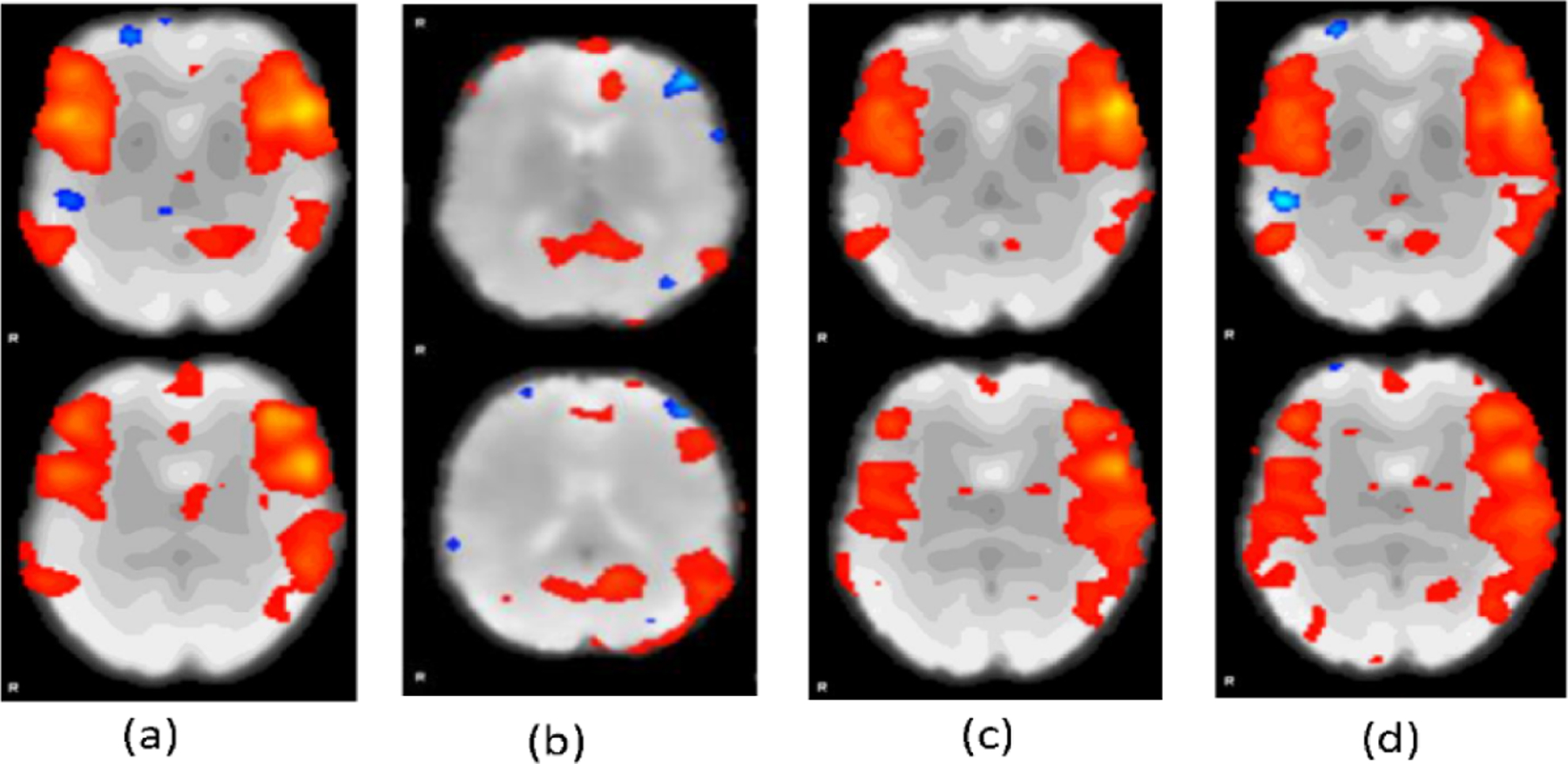
Representative independent components computed from noise-free data generated by ICA-AROMA (a), GAN (b), 3DConv-LSTM (c), and our method (d), respectively.
4. Discussion and Conclusions
We develop a deep learning method to generate realistic fMRI data for denoising fMRI data in this study. Our method is built upon encapsulated 3D convolutional LSTM networks and an adversarial regularizing procedure implemented by a critic network. Particularly, the encapsulated 3D convolutional LSTM networks facilitate effective learning of spatiotemporal relation of fMRI data across different time points, and the critic network enhances generation of realistic fMRI data. Moreover, our method is generally applicable to both task and resting-state fMRI data. Experimental results have demonstrated that our method obtained better performance in terms of data generation/reconstruction than state-of-the-art alternative deep learning methods on both task and resting state fMRI data from different datasets, including HCP and ABIDE. Different from existing fMRI denoising methods that typically remove noise based on whole time series of individual subjects, our method could be used to remove noise of individual time points of fMRI data and therefore could be used to carry out real-time fMRI data analysis in conjunction deep brain decoding methods [21–23].
Acknowledgement.
Research reported in this study was partially supported by the National Institutes of Health under award number [R01MH120811 and R01EB022573]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- 1.Caballero-Gaudes C, Reynolds RC: Methods for cleaning the BOLD fMRI signal. Neuroimage 154, 128–149 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Murphy K, Birn RM, Bandettini PA: Resting-state fMRI confounds and cleanup. Neuroimage 80, 349–359 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, Petersen SE: Methods to detect, characterize, and remove motion artifact in resting state fMRI. Neuroimage 84, 320–341 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ciric R, et al. : Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity. Neuroimage 154, 174–187 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Raut RV, Mitra A, Snyder AZ, Raichle ME: On time delay estimation and sampling error in resting-state fMRI. Neuroimage 194, 211–227 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Birn RM, Smith MA, Jones TB, Bandettini PA: The respiration response function: the temporal dynamics of fMRI signal fluctuations related to changes in respiration. Neuroimage 40, 644–654 (2008) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tijssen RH, Jenkinson M, Brooks JC, Jezzard P, Miller KL: Optimizing RetroICor and RetroKCor corrections for multi-shot 3D FMRI acquisitions. NeuroImage 84, 394–405 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Behzadi Y, Restom K, Liau J, Liu TT: A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. Neuroimage 37, 90–101 (2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kay K, Rokem A, Winawer J, Dougherty R, Wandell B: GLMdenoise: a fast, automated technique for denoising task-based fMRI data. Front. Neurosci 7, 247 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM: Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90, 449–468 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pruim RH, Mennes M, van Rooij D, Llera A, Buitelaar JK, Beckmann CF: ICA-AROMA: a robust ICA-based strategy for removing motion artifacts from fMRI data. Neuroimage 112, 267–277 (2015) [DOI] [PubMed] [Google Scholar]
- 12.Kam T-E, et al. : A deep learning framework for noise component detection from resting-state functional MRI In: Shen D, Liu T, Peters Terry M., Staib Lawrence H., Essert C, Zhou S, Yap P-T, Khan A (eds.) MICCAI 2019. LNCS, vol. 11766, pp. 754–762. Springer, Cham: (2019). 10.1007/978-3-030-32248-9_84 [DOI] [Google Scholar]
- 13.Yang Z, Zhuang X, Sreenivasan K, Mishra V, Curran T, Cordes D: A robust deep neural network for denoising task-based fMRI data: An application to working memory and episodic memory. Med. Image Anal 60, 101622 (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yan Y, et al. : Reconstructing lost BOLD signal in individual participants using deep machine learning. bioRxiv 808089 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Goodfellow I, et al. : Generative adversarial nets. In: Advances in Neural Information Processing Systems, pp. 2672–2680 (2014)
- 16.Berthelot D, Raffel C, Roy A, Goodfellow I: Understanding and improving interpolation in autoencoders via an adversarial regularizer. arXiv preprint arXiv:1807.07543 (2018)
- 17.Glasser MF, et al. : The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Di Martino A, Yan C-G, Li Q, Denio E, Castellanos FX, Alaerts K, Anderson JS, Assaf M, Bookheimer SY, Dapretto M: The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Molecular Psychiatry 19, 659–667 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang Y, Jiang L, Yang M-H, Li L-J, Long M, Fei-Fei L: Eidetic 3D LSTM: a model for video prediction and beyond. In: International Conference on Learning Representations (2018)
- 20.Esteban O, et al. : fMRIPrep: a robust preprocessing pipeline for functional MRI. Nat. Methods 16, 111–116 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li H, Fan Y: Interpretable, highly accurate brain decoding of subtly distinct brain states from functional MRI using intrinsic functional networks and long short-term memory recurrent neural networks. NeuroImage 202, 116059 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li H, Fan Y: Identification of temporal transition of functional states using recurrent neural networks from functional MRI In: Frangi Alejandro F., Schnabel Julia A., Davatzikos C, Alberola-López C, Fichtinger G (eds.) MICCAI 2018. LNCS, vol. 11072, pp. 232–239. Springer, Cham: (2018). 10.1007/978-3-030-00931-1_27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li H, Fan Y: Brain decoding from functional MRI using long short-term memory recurrent neural networks In: Frangi AF, Schnabel JA, Davatzikos C, Alberola-López C, Fichtinger G (eds.) MICCAI 2018. LNCS, vol. 11072, pp. 320–328. Springer, Cham: (2018). 10.1007/978-3-030-00931-1_37 [DOI] [PMC free article] [PubMed] [Google Scholar]


