Cortical Observation by Synchronous Multifocal Optical Sampling Reveals Widespread Population Encoding of Actions

Isaac V Kauvar; Timothy A Machado; Elle Yuen; John Kochalka; Minseung Choi; William E Allen; Gordon Wetzstein; Karl Deisseroth

doi:10.1016/j.neuron.2020.04.023

. Author manuscript; available in PMC: 2020 Nov 25.

Published in final edited form as: Neuron. 2020 May 19;107(2):351–367.e19. doi: 10.1016/j.neuron.2020.04.023

Cortical Observation by Synchronous Multifocal Optical Sampling Reveals Widespread Population Encoding of Actions

Isaac V Kauvar ^1,^2,⁷, Timothy A Machado ^1,⁷, Elle Yuen ¹, John Kochalka ^1,³, Minseung Choi ^1,³, William E Allen ^1,^3,⁴, Gordon Wetzstein ², Karl Deisseroth ^1,^5,^6,^*

PMCID: PMC7687350 NIHMSID: NIHMS1643850 PMID: 32433908

SUMMARY

To advance the measurement of distributed neuronal population representations of targeted motor actions on single trials, we developed an optical method (COSMOS) for tracking neural activity in a largely uncharacterized spatiotemporal regime. COSMOS allowed simultaneous recording of neural dynamics at ~30 Hz from over a thousand near-cellular resolution neuronal sources spread across the entire dorsal neocortex of awake, behaving mice during a three-option lick-to-target task. We identified spatially distributed neuronal population representations spanning the dorsal cortex that precisely encoded ongoing motor actions on single trials. Neuronal correlations measured at video rate using unaveraged, whole-session data had localized spatial structure, whereas trial-averaged data exhibited widespread correlations. Separable modes of neural activity encoded history-guided motor plans, with similar population dynamics in individual areas throughout cortex. These initial experiments illustrate how COSMOS enables investigation of large-scale cortical dynamics and that information about motor actions is widely shared between areas, potentially underlying distributed computations.

In Brief

Kauvar, Machado, et al. have developed a new method, COSMOS, to simultaneously record neural dynamics at ~30 Hz from over a thousand near-cellular resolution neuronal sources spread across the entire dorsal neocortex of awake, behaving mice. With COSMOS, they observe cortex-spanning population encoding of actions during a three-option lick-to-target task.

INTRODUCTION

Cortical computations may depend on the synchronous activity of neurons distributed across many areas. Anatomical evidence includes the observation that many individual pyramidal cells send axons to functionally distinct cortical areas (Economo et al., 2018; Oh et al., 2014); for example, nearly all layer 2/3 pyramidal cells in primary visual cortex project to at least one other cortical area—often hundreds of microns away (Han et al., 2018). Physiological evidence has shown that ongoing and past sensory information relevant for decision making is widely encoded across cortex (Akrami et al., 2018; Allen et al., 2017; Gilad et al., 2018; Harvey et al., 2012; Hattori et al., 2019; Hernández et al., 2010; Makino et al., 2017; Mante et al., 2013; Mohajerani et al., 2013; Pinto et al., 2019; Vickery et al., 2011). In addition, neural activity tuned to spontaneous or undirected movements is found in many cortical areas (Musall et al., 2019; Stringer et al., 2019). In the motor system, persistent activity may be mediated by inter-hemispheric feedback in mouse motor cortex (Li et al., 2016) in addition to other long-range loops between the motor cortex and the thalamus (Guo et al., 2017; Sauerbrei et al., 2020), and the cerebellum (Chabrol et al., 2019; Gao et al., 2018). Finally, studies in primates have shown that non-motor regions of frontal cortex contain neurons that encode information related to decisions that drive specific motor actions (Campo et al., 2015; Hernández et al., 2010; Lemus et al., 2007; Ponce-Alvarez et al., 2012; Siegel et al., 2015).

Thus, while specialized computations for motor (Georgopoulos, 2015; Mountcastle, 1997) versus sensory (Hubel and Wiesel, 1968) or cognitive (Shadlen and Newsome, 1996) processes may be performed in each cortical area, the results of these computations may be propagated to dozens of other areas via direct, often monosynaptic, pathways. Prior work, often limited by technological capabilities, has primarily focused on the tuning properties of individual neurons or population encoding in individual regions, potentially missing an alternative systems-level viewpoint of how distributed populations together encode behavior (Saxena and Cunningham, 2019; Yuste, 2015). Thus, it remains unclear how widespread population activity is involved in transforming sensory stimuli and contextual information into specific actions.

A technical barrier to studying distributed encoding has been the lack of a method for simultaneously measuring fast, cortex-wide neural dynamics at or near cellular resolution. Despite recent progress in neural recording techniques, persistent limitations have underscored the need for new approaches. Large field-of-view, two-photon microscopes have enabled simultaneous recording from a few cortical areas at single-cell resolution, revealing structured large-scale correlations in neural activity but at low rates (Chen et al., 2015; Lecoq et al., 2014; Sofroniew et al., 2016; Stirman et al., 2016; Tsai et al., 2015). Widefield imaging has also revealed cortex-wide task involvement and activity patterns, albeit with low spatial resolution (Allen et al., 2017; Ferezou et al., 2007; Makino et al., 2017; Mayrhofer et al., 2019; Musall et al., 2019; Pinto et al., 2019; Wekselblatt et al., 2016). Furthermore, multi-electrode extracellular recording has revealed inter-regional correlations in spiking, information flow between a few cortical areas, and phase alignment of local field potentials across a macaque cortical hemisphere (Campo et al., 2015; Dotson et al., 2017; Feingold et al., 2012; Hernández et al., 2008; Ponce-Alvarez et al., 2012). However, despite the merits of these approaches, each is limited by one or more of several key parameters, including field of view, acquisition speed, spatial resolution, and cell-type targeting capability. We thus developed a complementary technique that leveraged multifocal widefield optics to enable high-speed, simultaneous, genetically specified recording of neural activity across the entirety of mouse dorsal cortex at near-cellular resolution. To illustrate utility of this new methodology, we devised a task requiring mice to initiate bouts of targeted licking guided by recent trial history. Imaging fast cortex-wide neural activity during this task revealed a scale-crossing interplay between localized activity and distributed population encoding on single trials.

RESULTS

A Multifocal Macroscope for Imaging the Curved Cortical Surface with High Signal-to-Noise Ratio

We sought to record the activity of neurons dispersed across the entirety of dorsal cortex at fast sampling rates. Since many mouse behaviors, such as licking, can occur at 10 Hz or faster (Boughter et al., 2007), and widely used spike-inference algorithms can only estimate firing rate information up to the data acquisition rate (Pnevmatikakis et al., 2016; Theis et al., 2016), we decided to use one-photon widefield optics with its potential for highly parallel sampling at rates >20 Hz over a large field of view, as well as genetic specificity; this combination is difficult to achieve with other approaches such as two-photon microscopy or electrophysiology (Harris et al., 2016; Weisenburger and Vaziri, 2018). Other imaging techniques either lack the desired sampling rate (Sofroniew et al., 2016; Stirman et al., 2016), spatial resolution (Allen et al., 2017; Kim et al., 2016; Makino et al., 2017; Wekselblatt et al., 2016), or field of view (Bouchard et al., 2015; Lecoq et al., 2014; Nöbauer et al., 2017; Rumyantsev et al., 2020). The approach described here, cortical observation by synchronous multifocal optical sampling (COSMOS), records in-focus projections of 1-cm × 1-cm × 1.3-mm volumes at video rate (29.4 Hz for the presented data), with high light-collection efficiency and resolution across the entire field of view.

In conjunction with this macroscope, we advanced a surgical approach enabling long-term, high-quality optical access to a large fraction of dorsal cortex (based on Kim et al., 2016; Allen et al., 2017). We used a trapezoidal window curved along a 10-mm radius (Figures 1A and S1A), and we performed the craniotomy using a robotic stereotaxic apparatus (Pak et al., 2015; Figures 1B and S1B-S1J).

We selectively drove sparse Ca²⁺ sensor expression in superficial cortico-cortical projection neurons using a Cre-dependent, tetracycline-regulated transactivator (tTA2)-amplified, GCaMP6f reporter mouse line (Ai148) crossed to a Cux2-CreER driver line (Daigle et al., 2018; Franco et al., 2012; Figure 1C). CreER allowed control over the fraction of neurons expressing GCaMP and obviated potential abnormalities from expressing GCaMP during development (Steinmetz et al., 2017). Even 1 year after window implantation, we found little evidence of filled nuclei indicative of impaired cell health (Figures 1C and S1K-S1L). By sparsely labeling only a subset of superficial cortical cells (from layers 2/3 and 4), we biased the widefield signal origin toward somatic sources from cortico-cortical neurons, instead of layer 1 neuropil (Allen et al., 2017). Post-experiment histology (Figure S1L) validated that the GCaMP6f spatial expression pattern was consistent with previous descriptions of Cux2-CreER mice (Franco et al., 2012).

The optical design for the COSMOS macroscope used a dual-focus lenslet array (Figure 1D), balancing high light throughput, long depth-of-field, ease of implementation, and resolution, with modest data processing requirements and reasonable system cost. Theoretical analysis demonstrated that, in terms of light collection, defocus, and extracted neuronal source signal-to-noise ratio (SNR) across the extent of the curved window, the COSMOS macroscope design outperformed other potential solutions (Abrahamsson et al., 2013; Brady and Marks, 2011; Cossairt et al., 2013; Hasinoff et al., 2009; Levin et al., 2009; Schechner et al., 2007; Figure S2). Empirical comparisons demonstrated that a COSMOS macroscope, with focal planes offset by ~600 μm (Figures 1E and 1F), outperformed a comparable conventional macroscope in terms of depth of field while maintaining equivalent light throughput (Figures 1G and 1H).

We captured Ca²⁺-dependent fluorescence videos with the COSMOS macroscope and extracted putative neuronal sources, taking advantage of an improved version of the constrained non-negative matrix factorization (CNMF) algorithm (Pnevmatikakis et al., 2016), which was designed specifically to handle high-background, one-photon data (CNMF-E; Zhou et al., 2018; Figure 1I; raw data in Videos S1 and S2; for atlas registration methods, see Figure 1J, STAR Methods, Figure S3, and Video S3). In contrast to the output of a conventional macroscope, high-quality sources detected by the COSMOS macroscope spanned the entire curved window, thus providing simultaneous coverage of visual, somatosensory, motor, and association areas. Furthermore, the COSMOS macroscope recovered significantly more sources than a conventional macroscope at any single aperture setting. Nearly twice as many neuronal sources were detected with the COSMOS macroscope, compared to a macroscope with equivalent light collection (aperture open to f/2 setting) and with comparable SNR (Figures 1K-1O).

Characterization of Extracted Neuronal Sources Using a Visual Stimulus Assay

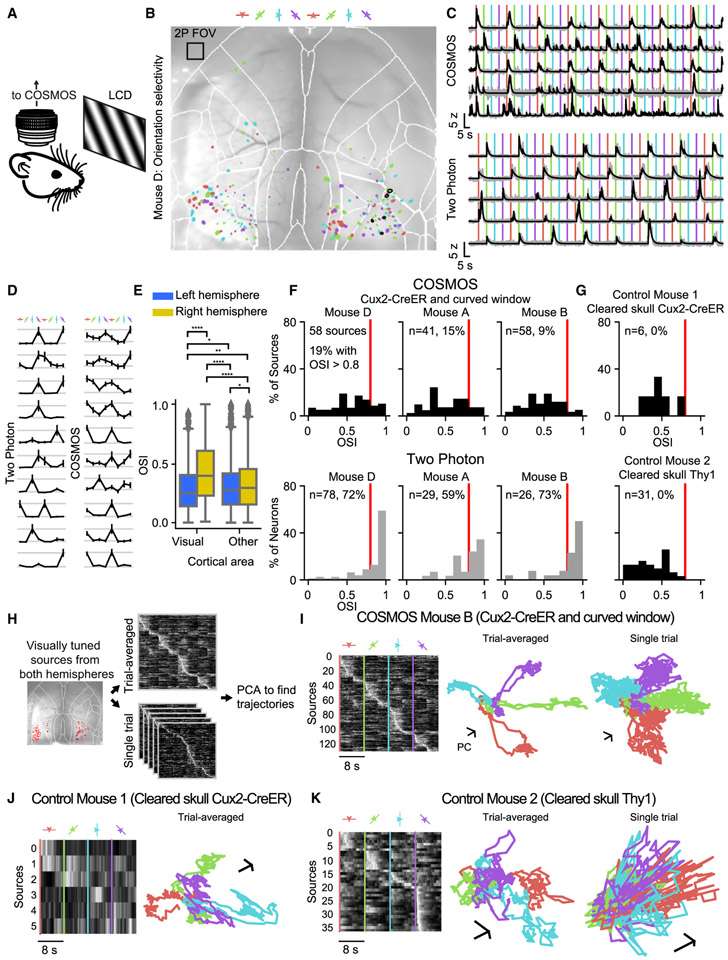
We next assessed whether the sources extracted from COSMOS data originated from single neurons or mixtures of multiple cells. We leveraged the finding that, in rodents, neurons in visual cortex tuned to differently oriented visual stimuli are spatially intermixed in a salt-and-pepper manner (Chen et al., 2013; Niell and Stryker, 2008; Ohki et al., 2005). In our data, merging of adjacent neurons into a single extracted source would, thus, diminish orientation tuning relative to sub-cellular resolution, two-photon measurements.

Using COSMOS, we measured orientation tuning in response to a drifting grating stimulus centered on the left eye (Figure 2A; the monitor provided weaker visual input to the right eye). Nearly all orientation-tuned sources were confined to the visual cortex (Figure 2B; visually responsive sources highlighted; one-way ANOVA, p < 0.01; on the superimposed atlas, the border around the visual cortex is indicated with thicker white lines). We then repeated this procedure with each mouse, using a two-photon microscope with a high-magnification objective (Nikon, 16×/0.8 NA) positioned over the right visual cortex (note much smaller size of two-photon imaging field indicated by box in Figure 2B). Both COSMOS and two-photon datasets contained sources exhibiting highly selective orientation tuning consistent with reported single-neuron responses measured with GCaMP6f in primary visual cortex (V1) (Chen et al., 2013) (Figure 2C and 2D). As expected, the average orientation selectivity index (OSI) of COSMOS sources in the right visual cortex was higher than in any other cortical region (Figure 2E; Mann-Whitney U test analyzing all visually responsive sources from 3 different mice; corrected p < 0.0001 for all comparisons versus right visual areas). Furthermore, across 3 mice, 14% of all visually responsive sources had OSIs >0.8 (Figure 2F, top row). In two-photon data from the same mice, 68% of visually responsive sources had orientation tunings >0.8 (Figure 2F, bottom row).

To further assess the COSMOS sources, we simulated mixtures of single-neuron signals obtained with two-photon data to reproduce the COSMOS OSI distributions. Across mice, the COSMOS OSI distributions could be explained by the presence of sources representing mixtures of signals from 1–15 neurons (Figure S4A). The presence of sources with OSIs >0.8 is not trivial; if we had observed zero high OSI sources, the COSMOS OSI distributions would be, instead, more consistent with mixtures of 11–19 neurons—well outside the single-neuron regime (Figure S4B; STAR Methods; importantly, though, no particular source is required to be a single neuron, and our analyses are structured accordingly).

To test the importance of the overall COSMOS preparation in achieving this key result, we performed the same procedure on conventional cleared-skull widefield preparations with two different genetically specified expression profiles: Thy1-GCaMP6s and Cux2-CreER;Ai148 (Allen et al., 2017; Makino et al., 2017; Wekselblatt et al., 2016; Figures S4C-S4H). Following identical imaging and data processing as with the earlier mice, even in the best of three Thy1-GCaMP6s mice, we found zero neurons with an OSI >0.8 (Figure 2G). Additionally, with both genotypes, fewer total sources were extracted, the spatial footprint of each source was larger, and there were fewer visually responsive sources (Figures S4C-S4F).

To further explore the improved capability of COSMOS relative to existing widefield techniques, we computed a population encoding of the visual stimuli. By applying principal-component analysis (PCA) to trial-averaged traces, we computed a low-dimensional basis for representing high-dimensional trial-averaged or single-trial neural population activity (Figure 2H). Trajectories corresponding to each visual stimulus orientation were well separated with COSMOS (Figure 2I) and trial-averaged two-photon data (compare Figures S4G and S4H) but not with conventional widefield preparations (Figures 2J and 2K). Only with COSMOS could robust trajectories of neural population dynamics be measured that encompassed synchronously recorded activity from across the full extent of the dorsal cortex.

Cortex-wide Recording during a Head-Fixed Lick-to-Target Task

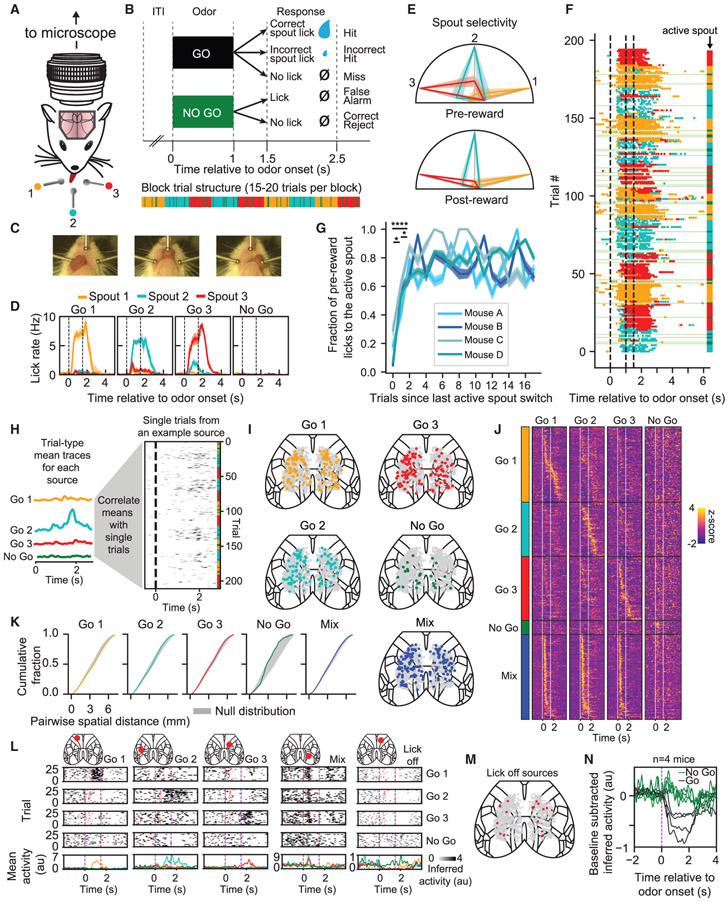
Using COSMOS, we set out to perform a proof-of-principle investigation of cortex-wide representations of targeted actions in the context of a head-fixed lick-to-target task. Mice were trained to lick one of three waterspouts in response to a single “go” odor and to take no action in response to a second “no-go” odor (Figure 3A). In this more complex variant of a previously studied task (Allen et al., 2017; Komiyama et al., 2010), sessions consisted of blocks with 15–20 trials, where a water droplet reward was available from one active spout per block (Figure 3B). The “go” odor remained constant, even as the rewarded active spout changed. Thus, no cue ever indicated which spout was active; the next reward was simply more likely to come from the spout that had delivered the previous reward 5–10 s prior to the current trial. Successful actions were, thus, history guided: they depended upon integrating experience from recent trials, as opposed to just responding to an immediate cue. Mice were rewarded if the first lick following a 0.5-s delay after odor offset was toward the active spout. Licking an inactive spout at this time yielded a penalty (a reduced-size water droplet from the active spout). Although other licks did not affect the outcome, mice tended to lick the active spout shortly after odor onset. To facilitate exploration during the first three trials of each block, a full-sized reward was dispensed from the new active spout if any spout was licked following the “go” odor.

Head-fixed mice reliably learned to lick each spout (Figure 3C; Video S4), with a bias to the active spout (Figures 3D and 3E). Furthermore, consistent with a strategy that integrates information across multiple previous trials (spanning tens of seconds), specificity of pre-reward anticipatory licking to the new active spout progressed over the first three trials of a block (Figures 3F and 3G; lick selectivity increased from trials 1 to 2, and from trials 2 to 3, of each block; corrected p < 0.05, paired t test, data pooled across sessions; n = 4 mice). Mice rarely licked on “no-go” trials (Figures 3D and 3F).

In four well-trained mice, we imaged the dorsal cortex during this task (all mice yielded >1,000 neuronal sources per session; mean = 1,195). After observing sources with reliable trial-type-related dynamics, we assigned sources to one of five task-related classes: responsive selectively for one trial type (go 1, go 2, go 3, or no go) or responsive to a mixture of trial types (mix) (Figures 3H-3J; consistent results were observed across these mice and also in a different genotype, Rasgrf2-dCre;Ai93D;CaMK2a-tTA, also targeting layer 2/3 neurons; Figures S5A and S5B). Sources from each class appeared randomly distributed across the dorsal cortex (Figures 3K and S5C; there was no consistently significant spatial pattern across mice for corrected p < 0.05, permutation test in STAR Methods; this analysis is sensitive to clusters >1 mm in diameter, Figure S5D; Hofer et al., 2005). For each task class, sources were present in all regions (Figure S5E). We also found sources across the cortex with clear encoding of each trial type (Figure 3L) and a subclass of sources with sustained activity during the pre-odor period followed by reduced activity at odor onset of the “go” trials (Figures 3M, 3N, and S5G; fraction of sources across n = 4 mice: 1.8% ± 0.4%, mean ± SD).

Correlations of Unaveraged Activity Exhibit Localized Spatial Structure

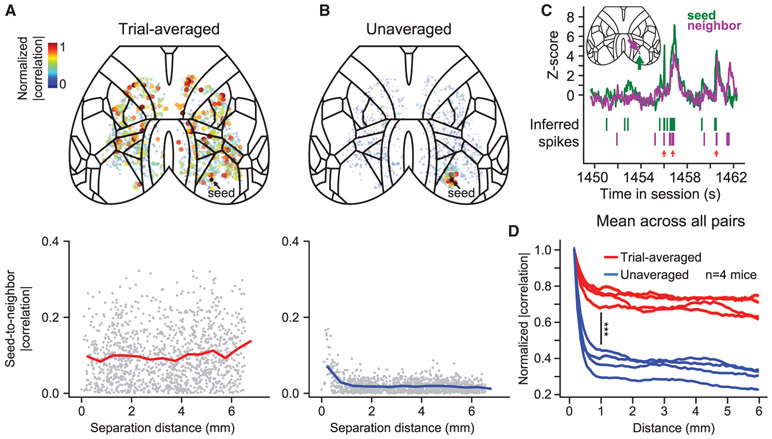
We next investigated the structure of correlated neural activity across cortex—taking advantage of the simultaneity of our large-scale data—via correlation maps, where we computed the correlation magnitude of the 29.4-Hz activity of a seed source with that of every other source (at zero lag with Gaussian-smoothed, SD = 50 ms, deconvolved spiking activity; STAR Methods). We computed this correlation map using either unaveraged traces from the whole session (i.e., the concatenated time series from all single trials after removing the variable-length intertrial interval) or concatenated trial-averaged traces (similar to Figure 3J). With trial-averaged data, sources with high correlation to the seed source were distributed widely, in support of our initial observations (Figure 4A). In contrast, with unaveraged data, we found many instances of localized correlation structure for seeds located throughout the cortex (Figures 4B and S6). This correlation did not result from a localized imaging artifact, as raw extracted fluorescence traces demonstrated that, although neighboring sources exhibited occasionally correlated firing, they had distinct activity patterns (Figure 4C). Additionally, there existed bilaterally symmetric correlations (Figure S6B). When summarizing the correlation versus distance for all pairs of sources, we observed a consistent pattern across mice (Figure 4D). For example, at a separation distance of 1 mm, unaveraged correlations were consistently lower than trial-averaged correlations (p = 0.0001, paired t test; n = 4 mice). Thus, although sources throughout the cortex exhibited similar activity when averaged according to trial type, correlations in unaveraged cortical activity showed increased dependence on spatial proximity.

Figure 4. — (A) Seeded trial-averaged activity correlations (for a single seed): top, spatial distribution; bottom, correlation versus distance to the seed (black dot).

(B) Seeded unaveraged activity correlations (format matches that in A).

(C) Example illustrating unaveraged activity correlation (locations indicated on atlas inset). Red arrows indicate time points when the seed source and its neighbor are active simultaneously.

(D) Summary across all mice of correlation analyses shown in (A) and (B). Lines for each mouse represent the mean correlation across all pairs of sources (binned and normalized). Statistic shown at 1-mm distance (***corrected p = 0.0001, paired t test; n = 4 mice).

Single-Trial Representations of Distinct Motor Actions Are Distributed across Cortex

We used the synchronous-recording capability of COSMOS to assess how populations of sources jointly encoded information about ongoing behavior on single trials. We first characterized the ability of each individual source to discriminate any of four different ongoing actions: licking to spout 1, spout 2, or spout 3 or not licking at all. We found that most of the sources detected in each mouse exhibited significant discrimination capacity (78% ± 4% of all neuronal sources for n = 4 mice), where discrimination capacity was defined for each source as corrected p < 0.05 (Kruskal-Wallis H test for whether the source time series could discriminate any of the four actions; Figure S7A). These discriminating sources were distributed across all dorsal cortical regions (Figure S7B).

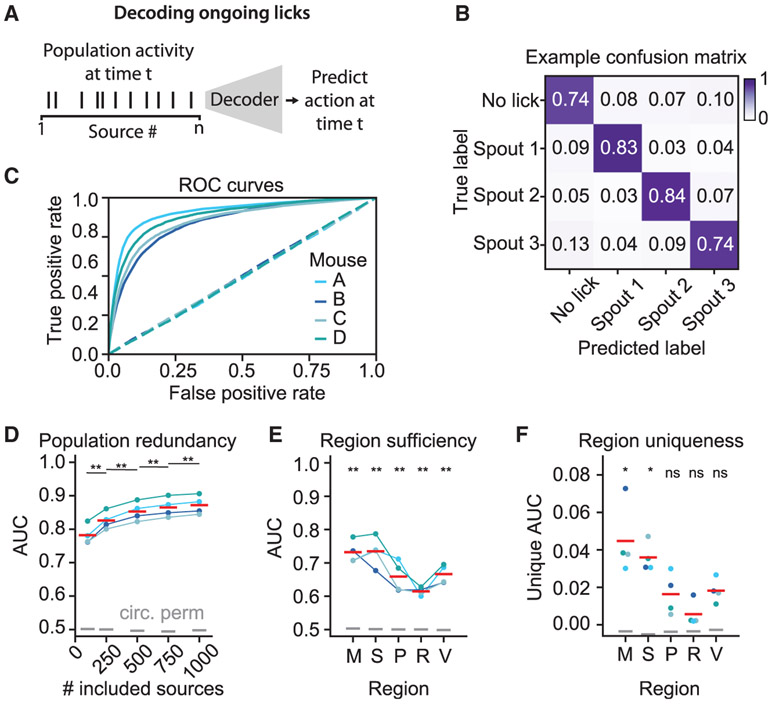
Next, we asked how cortical neurons jointly encoded information about ongoing actions. Across all four mice, a linear decoder could predict lick direction at the frame rate of our deconvolved Ca²⁺ data (29.4 Hz) with high accuracy on single-trial data (Figures 5A-5C; receiver operating characteristic [ROC] curves shown; STAR Methods). Indeed, as demonstrated in Figure S7C, we could readily decode individual lick bouts to different spouts, even when interleaved within a single trial. Thus, ongoing motor actions of the mouse are represented with high temporal fidelity by neuronal sources in the dorsal cortex.

Figure 5. — (A) Schematic for decoding ongoing licks.

(B) Row-normalized lick confusion matrix for one mouse.

(C) Receiver operating characteristic (ROC) curve for each mouse, averaged across folds. Dashed lines indicate ROC curves for shuffled data.

(D) Improvement in the area under the ROC curve (AUC) as more neural sources are included. Red lines indicate means across mice. Gray lines indicate circularly permuted control. Corrected p values from paired t test are shown for each of the sources versus the closest evaluated number of sources.

(E) Decoding using only sources from within single cortical regions (using the 75 sources per area with best discrimination ability; M, motor; S, somatosensory; p,= parietal; R, retrosplenial; V, visual). Corrected p values for two-sided t test are shown for each region versus AUC = 0.5.

(F) Unique contribution of each region to decoding accuracy, measured as 1 – AUC (without region)/AUC (with region). Corrected p values from two-sided t test are shown for each region versus AUC = 0.0.

ns denotes corrected p > 0.05; *corrected p < 0.05; **corrected p < 0.01.

Finally, we compared decoding performance when using different numbers of sources. To provide a fair comparison, only the most discriminative sources were used for decoding (according to the ordering in Figure S7A), and all decoding models had the same number of parameters. We found a monotonic increase in decoding performance as more sources were included (Figure 5D, corrected p < 0.01, paired t test comparison versus area under the ROC curve [AUC] with next closest number of sources; n = 4 mice). To further examine this phenomenon, we decoded lick events using only the 75 most discriminative sources from each region (merged across hemispheres). Each region could decode lick direction far above chance (Figure 5E, corrected p < 0.01 for all regions, t test versus AUC = 0.5; n = 4 mice). Finally, by comparing decoding using all but one region with decoding using all regions (again, using only the top 75 sources per region), we demonstrated that at least some cortical regions—somatosensory and motor, in this case—contained significant unique information that was not present in the top sources sampled from other regions (Figure 5F; corrected p < 0.05, t test versus unique AUC = 0; n = 4 mice).

History-Guided Motor Plans Are Encoded by Neuronal Populations across Cortex

In this history-guided task, the mouse must maintain information during the pre-odor intertrial interval about where it plans to lick at odor onset. To detect and localize neural representations of this information, we trained decoders using “pre-odor” denoised neural Ca²⁺ data taken from the final 2.2 s of the intertrial interval, which preceded any stimulus or licking. We could successfully predict the spout that was most licked between odor and reward onsets (the “preferred spout”) using a linear technique (partial least-squares regression [PLS]; Figure 6A). Trials containing pre-odor licks were not used for prediction (0.1%–10.3% of all recorded licks were during the pre-odor period).

Figure 6. — (A) Schematic of approach.

(B) Row-normalized confusion matrix predicting preferred spout location from pre-odor neural data (chance is 0.33).

(C) Predictions for one behavioral session (training trials and trials that contain any licks during the pre-odor period are not shown).

(D) Preferred spout neural decoding performance using data from three different time epochs. Red lines denote means across mice. Black lines and gray lines denote random shuffle and circularly permuted controls, respectively.

(E) Pre-odor neural decoding performance quantified for: motor (M), somatosensory (S), parietal (p), retrosplenial (R), and visual (V) areas. Each area-specific decoder used the 75 sources with best discrimination ability. Corrected paired t test values are shown versus both random controls in (D) and (E). Error bars in (D) and (E) show 99% bootstrapped confidence intervals over 20 model fits to different sets of training data.

(F) Pre-reward neural decoding of the spout most licked during the pre-reward period (purple) and fraction of pre-reward licks toward the active spout (cyan), shown as a function of location within a trial block. Note that both sets of lines use identical data taken from testing trials.

(G) Pre-odor behavioral decoding performance using data from both lower and upper cameras and a decoder trained on motion energy principal components derived from both the upper and lower videos (1,000 from each).

ns denotes corrected p > 0.05; *corrected p < 0.05; **corrected p < 0.01; ***corrected p < 0.001.

These PLS-based decoders exhibited above-chance performance, as exemplified in the predictions for a representative dataset (Figures 6B and 6C; four dimensions and up to 500 sources were used for training; see Figures S7D and S7E and STAR Methods for fitting details; sources were ordered by discrimination ability; Figure S7F). These decoders could predict the preferred spout using neural activity taken from the entire trial, the pre-reward period, or just the pre-odor period (Figure 6D). Performance was quantified by comparison with randomized controls with shuffled preferred spout labels. Shuffling was either performed randomly or, more conservatively, by circularly permuting the labels by random numbers of trials. Decoding was significant relative to either control (Figure 6D; corrected p < 0.01, paired t tests versus randomly shuffled; corrected p < 0.01 versus circularly permuted).

We next tested the decoding performance of different cortical regions, using only the 75 most discriminative sources from each region. We found that areas across the cortex yielded above-chance performance (Figure 6E; corrected p < 0.05, paired t tests versus random shuffle; corrected p < 0.05 for all areas but parietal versus circular permutation), including the visual cortex, even though no task elements were visible to the mouse. Decoder prediction of the true active spout was comparable to that of the preferred spout (Figure S7G; corrected p = 0.42, paired t test; n = 4 mice; only trials where the preferred and active spouts were identical were used for model training in all PLS analyses; in the test set; these labels were similar but not identical).

Additionally, we investigated how the ability to predict the preferred spout changed within each block of trials. Multiple trials were required for licking to adapt to a new active spout (Figure 6F, cyan points; comparison of trial 1 to trial 2 or 3; corrected p < 0.01, paired t test). In contrast, preferred spout decoding performance remained relatively constant over this period (Figure 6F, purple points; comparison of trial 1 to trial 2 or 3; corrected p = 0.43). However, we found a relationship between decoding and lick selectivity, with significantly greater performance on trials with >80% of pre-reward licks to a preferred spout compared with trials where <80% of licks were selective (corrected p <0.05, paired t test; n = 4 mice; Figure S7H). Thus, while we can successfully predict future actions throughout trial blocks, performance is reduced when future licking behavior is less selective. Moreover, when decoding the true active spout (instead of the preferred spout), performance with “correct go” trials where >70% of all licks were toward the active spout was significantly higher than either with “incorrect go” trials, where <70% of licks were toward the active spout, or with the error-prone second trials of each block (Figure S7I; corrected p < 0.05, paired t test).

Finally, we explored whether this ability to use neural data to predict upcoming actions might also be manifested in the visible behavior of the animal during the pre-odor period. We attempted to decode the preferred spout using only video of behavior (200-Hz video recordings of the face and body of each animal during neural data acquisition). We predicted the preferred spout using the top 1,000 principal components from each video (and then using PLS and identical training/test trials as with the neural analyses). We found that it was, indeed, possible to decode the preferred spout based on behavior (corrected p < 0.001 versus shuffle; corrected p < 0.01 versus circularly permuted labels; Figure 6G; Figures S8A-S8C). By decoding using specific regions of interest, we determined that movements of the mouth and whiskers contain information about the preferred spout during the pre-odor period, despite exclusion of all trials with detected licking to spouts during the pre-odor period (Figure S8D). Consistent with a neural representation of the upcoming spout target, distributed bodily signals well before lick onset may represent a physical readout of this neurally maintained information.

Distinct Patterns of Population Neural Activity Encode Different Motor Plans and Actions

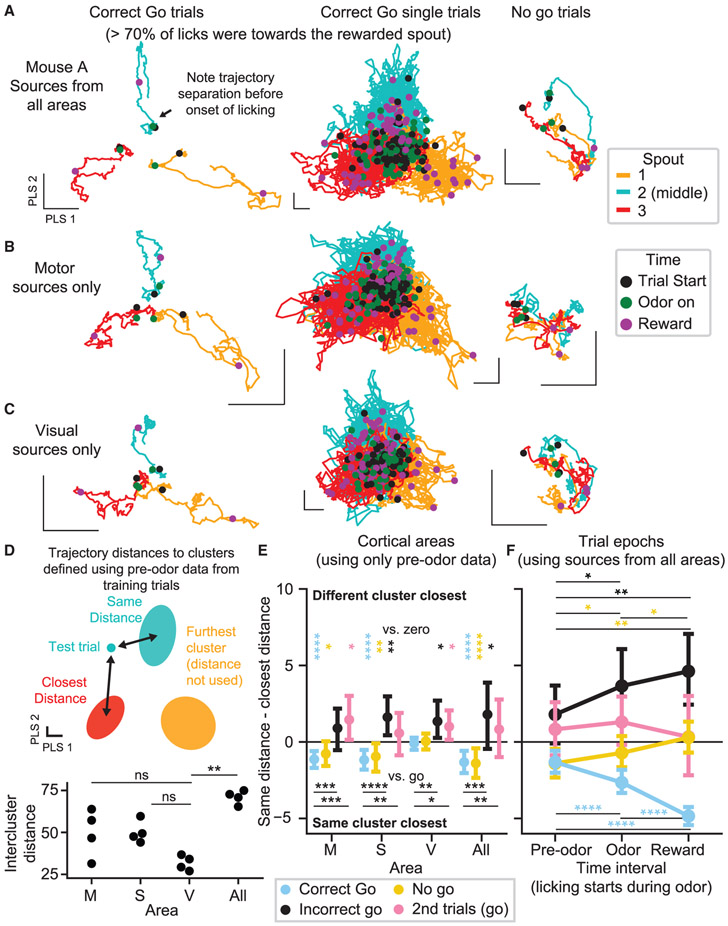
We next examined population dynamics by projecting neural activity onto the four-dimensional PLS basis that defined our decoders (which was optimized to discriminate preferred spout direction, not to explain the most variance; Figure S7J). On correct trials, trial-averaged neural trajectories were already segregated into distinct zones in state space at trial onset (black dots), before diverging further upon lick onset (using held-out “correct go” trials where >70% of all licks were toward the active spout, and, thus, the preferred and active spouts were always identical; Figure 7A, left; Video S5). This dynamical structure appeared reproducibly, albeit with greater noise, when examining held-out single-trial data (Figure 7B, middle). On “no-go” trials, which were indistinguishable from “go” trials before odor onset, we also saw clear separation of the trial types at trial start, but trajectory differences diminished as mice forewent licking. Furthermore, we observed qualitatively consistent dynamics when repeating this analysis with neuronal sources taken from only motor (Figure 7B) or only visual areas (Figure 7C).

Figure 7. — (A–C) Neural trajectories from mouse A (trial averaged in first and third columns, single-trial in second column). Basis vectors computed as in the previous figure using PLS regression on entire training trials and sources from all (A), only motor (B), or only visual (C) areas. Scale bars are arbitrary units but indicate an equivalent length in each dimension.

(D) Schematic of analysis scheme used in (E) and (F). Bottom panel shows summed intercluster Mahalanobis distance for clusters fit to data from each mouse. Corrected p values from a paired t test are shown versus visual data. M, motor; S, somatosensory; V, visual, All, all sources.

(E) Distributions of (same cluster Mahalanobis distances) – (next closest cluster distances). Data are pooled across four mice. Comparisons versus zero were computed using a Wilcoxon test. Comparisons versus “correct go” trials used a Mann-Whitney U test. 223 “correct go,” 110 “no go,” 29 “incorrect go,” and 37 second trials from 4 mice.

(F) Format matches that of (E), using sources from all areas and comparing pre-odor clusters to single-test-trial trajectories averaged over different time epochs: before odor, during odor, and after reward onset. Statistics were computed across time intervals using a Wilcoxon test. Error bars in (E) and (F) show 99% bootstrapped confidence intervals.

ns denotes corrected p > 0.05; *corrected p < 0.05; **corrected p < 0.01; ***corrected p < 0.001; ****corrected p < 0.0001. All statistical comparisons were FDR (false discovery rate) corrected, and comparisons that yielded corrected p > 0.05 are not shown in (E) and (F).

We next investigated the consistency across single trials of the pre-odor trajectory segregation. Pre-odor population activity occupied clusters in state space corresponding to the preferred spout on that trial (for all training trials used to define clusters, active and preferred spouts were identical). The separation distance between clusters was not the same in each area, with visual cortical clusters significantly closer than all-area clusters (Figure 7D, bottom; corrected p < 0.05, paired t test versus visual). We computed an index representing the distance from the average pre-odor position in state space of a given trial to the cluster corresponding to the preferred spout on that trial minus its distance to the next closest cluster (Figure 7E; see STAR Methods); negative values indicate that population activity is nearest the preferred spout cluster. We found that “correct go” and “no-go” trials had distributions centered below zero (except for the visual cortex, which was not significantly positive).

In contrast, on error trials, we would expect this trend to be weakly present—if present at all—as the trajectory could encode confusion or incorrect spout preference evident in the animal’s subsequent behavior. “Second trials” (where there was uncertainty in behavior after an active spout change; Figure 3G) highlighted data wherein mice often lick to the wrong spout—but after demonstrating awareness of the correct spout on the preceding trial (only 50% ± 38% [mean ± SD] of pre-reward licks on “second trials” were toward the active/correct spout, while 74% ± 17% of reward period licks were toward the active spout on corresponding “first trials”; 37 trials pooled over 4 mice). We found that “incorrect go” (<30% of trial licks were toward the correct spout) and “second trials” (situations with many licks to spouts besides the active/correct one) both had distributions centered above zero. The index was significantly lower for “correct go” trials than for “incorrect go” and “second trials” (corrected p < 0.05 or less, Mann-Whitney U test) across all cortical areas analyzed (consistent with Figure S7I).

We tracked this index across time by repeating the analysis using data following either odor onset or reward onset (Figure 7F; see STAR Methods). During “correct go” trials, the neural trajectories moved even further along the direction of the preferred spout cluster (corrected p < 0.001, Wilcoxon test versus pre-odor). In contrast, “incorrect go” trial trajectories moved away from the preferred spout cluster as mice licked toward incorrect spouts (corrected p < 0.05, pre-odor epoch versus odor and reward epochs). “No-go” trajectories also moved away from the preferred spout cluster as mice suppressed licking (corrected p < 0.05 for all comparisons between epochs).

Together, these findings further support the presence of a population representation of targeted action-related motor plans across the cortex. Additional analyses suggest that there is a distinction between the population representation of motor plans versus motor plan execution (Figures S8E-S8G). Finally, multi-region optogenetic inhibition revealed evidence fora potential causal role of non-motor regions in motor plan execution (Figure S9).

DISCUSSION

Here, we developed a new technique, COSMOS, for simultaneously measuring the activity of over a thousand neuronal sources spread across the entirety of the mouse dorsal cortex. We demonstrated that COSMOS is well suited for studying population dynamics across many cortical areas, with resolution enabling recovery of sources composed of ~1–15 neurons over a centimeter-scale field of view at ~30 Hz. We then used COSMOS to investigate cortical neuronal population dynamics during a three-spout lick-to-target task. We found that, although unaveraged correlations exhibit localized spatial structure, widespread populations of neurons—with no apparent mesoscale spatial structure— encode targeted motor actions and history-guided plans on single trials.

Distributed Cortical Computation

Our observations indicate that ongoing and planned motor actions are encoded in the joint firing of superficial cortico-cortical projection neurons (derived from the Cux2 lineage; Franco et al., 2012; Gil-Sanz et al., 2015) throughout the dorsal cortex. Recent work has demonstrated that many cells throughout the brain exhibit mixed-selectivity tuning, which can be driven strongly by ongoing, spontaneous movement (Allen et al., 2017; Musall et al., 2019; Stringer et al., 2019). Building upon this work, we focused on assessing the extent to which the joint activity of many neurons together could encode targeted motor behaviors, rather than seeking to explain the activity of individual neurons based on a breakdown of contributing behavioral factors. We found that, as more neuronal sources were used for training classifiers, the ability to decode ongoing lick actions improved, a hallmark of distributed codes (Rigotti et al., 2013).

We also found modes of neural activity that predicted future history-guided motor actions. Our ability to simultaneously measure the multi-unit activity of many neurons across the dorsal cortex on single trials—in addition to our specific behavioral task—may account for the fact that we found a population encoding future actions beyond the frontal cortex, unreported in previous work (Steinmetz et al., 2019). Interestingly, on trials with nonselective licking, neural decoding performance for the preferred spout (Figure S7H) and the active spout (Figure S7I) was significantly reduced. On these trials with disorganized behavior, the mouse is potentially in a distinct brain state that does not map onto the subspace defined using correct trial data.

Our results suggest that neural representations of history-guided motor plans may not be confined to cortical regions predicted to be involved in the task, at least for layer 2/3 neurons. We identified a widespread population encoding of targeted motor actions and plans, a lack of structure in the spatial distribution of trial type selective sources, and diffuse trial-averaged seeded correlations. At first glance, these results could be consistent with a non-hierarchical view of cortical computation (Hunt and Hayden, 2017)—or even with a weak version of Lashley’s “law of mass action” (Kolb and Whishaw, 1988)—but we also importantly observed localized spatial structure when analyzing cortex-wide single-trial correlations. Thus, there may be an interplay between local and global computation whereby individual neurons intermittently encode task-related information, but a reliable population code still persists (Gallego et al., 2020).

We propose two potential interpretations for our observations of widespread encoding of motor plans and actions. First, information arising across the cortex (itself predictive of future actions) may converge onto classical motor regions, as local “specialist” areas process and transmit disparate information streams that are integrated into a plan in the motor cortex. Second, an efference-copy-like plan may be generated in the motor cortex and broadcast widely, potentially as a contextual signal to aid in distributed processing or learning. In a predictive coding framework, for example, widespread motor plan encodings could contribute to a predictive signal in each region against which ongoing activity is compared (Friston, 2018; Keller and Mrsic-Flogel, 2018; Schneider et al., 2014). Distinguishing between these hypotheses will likely require the ability to simultaneously record from and inhibit large regions of cortex (Sauerbrei et al., 2020), which could be built upon COSMOS.

Our results also showed that upcoming licking can be decoded from gross body movements observed before the onset of licking. These predictive body movements could represent a consequence, rather than a cause, of our observed predictive cortical activity patterns (like a poker tell or an instance where a latent brain state manifests physically; Dolensek et al., 2020). As the mouse cannot determine which spout is active by sensing the pre-odor environment, a broadcast signal could facilitate global preparation for the upcoming targeted action. Alternatively, these subtle movements could help the mouse remember the information (like a physical mnemonic), guided by centrally derived neural activity. Distinguishing between these possibilities will require targeted manipulations, potentially by disrupting the mouse’s ability to move its body (as in Safaie et al., 2019).

Imaging Large-Scale Population Dynamics

Over the past decade, one-photon Ca²⁺ imaging—using widefield macroscopes or microendoscopic approaches—has seen renewed popularity due to comparative technical simplicity and compatibility with increasingly sensitive and bright genetically encoded Ca²⁺ sensors (Allen et al., 2017; Chen et al., 2013; Scott et al., 2018; Ziv et al., 2013). Early microendoscopic imaging in hippocampal CA1 (Ziv et al., 2013), where sparsely active neurons are stratified into a layer only 5–8 cells thick (Mizuseki et al., 2011), provided evidence that activity signals in single neurons could be resolved, but cellular resolution does not appear to hold universally across all systems. In the birdsong system, one-photon imaging data (Liberti et al., 2016) yielded results in conflict with a follow-up two-photon imaging study (Katlowitz et al., 2018) that showed significantly more stable single-neuron representations than in the earlier work.

As our results estimate that each COSMOS source is likely a mixture of 1–15 neurons (akin to multi-unit spiking activity), neuronal sources arising from COSMOS should not be treated as single units unless so validated. High-resolution two-photon or electrophysiological approaches would be better suited for questions that require true single-cell resolution, albeit over smaller fields of view. However, COSMOS data also exist in a regime complementary to previous methods, and, as demonstrated, key population analyses that work with COSMOS cannot be performed using conventional widefield imaging data.

Much work in the realm of large-scale neural population dynamics leverages dimensionality reduction techniques that estimate a neural state vector as a linear combination of the activities of individual neurons (Churchland et al., 2012). Recent work has begun to investigate the idea that major results derived from sorted individual unit recordings can be recapitulated just as well from multi-unit activity (Trautmann et al., 2019) and, likely, also COSMOS data. Indeed, as attention in systems neuroscience increasingly broadens from a focus on individual neurons to more abstract population codes (Saxena and Cunningham, 2019; Yuste, 2015), COSMOS provides a means of measuring distributed codes in genetically defined populations of neurons across cortex and for testing how cortical dynamics vary across diverse behaviors.

STAR★METHODS

RESOURCE AVAILABLILITY

Lead Contact

Further information and requests for requests for resources and reagents may be directed to and will be fulfilled by the Lead Contact, Karl Deisseroth (deissero@stanford.edu).

Materials Availability

This study did not generate new unique reagents. Information about how to build a COSMOS macroscope using publicly available parts can be found at http://clarityresourcecenter.com/.

Data and Software Availability

Pre-processed data generated during this study are available at http://clarityresourcecenter.com/. Owing to the large size of our datasets, raw data and relevant processing code will be made available upon reasonable request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All procedures were in accordance with protocols approved by the Stanford University Institutional Animal Care and Use Committee (IACUC) and guidelines of the National Institutes of Health. The investigators were not blinded to the genotypes of the animals. Both male and female mice were used, aged 6 - 12 weeks at time of surgery. Mice were group housed in plastic cages with disposable bedding on a standard light cycle until surgery, when they were split into individual cages and moved to a 12 hr reversed light cycle. Following recovery after surgery, mice were water restricted to 1 mL/day. All experiments were performed during the dark period. The mouse strains used were Tg(Thy1-GCaMP6s)GP4.3Dkim (Thy1-GCaMP6s, JAX024275), Cux2-CreERT2 (gift of S. Franco, University of Colorado), Ai148(TIT2L-GC6f-ICL-tTA2)-D (Ai148, Jax 030328) (gift of H. Zeng, Allen Institute for Brain Science), B6.Cg-Tg(Slc32a1-COP4*H134R/EYFP)8Gfng/J (VGAT-ChR2-EYFP, Jax 014548), B6;129S-Rasgrf2tm1(cre/folA)Hze/J (Rasgrf2-2A-dCre, Jax 022864), and gs7tm93.1(tetO- GCaMP6f)Hze Tg(Camk2a-tTA)1Mmay (Ai93(TITL-GCaMP6f)-D;CaMK2a-tTA, Jax 024108), all bred in a mixed C57BL6/J background. Mice homozygous for Ai148 and heterozygous for the CreER transgenes were bred to produce double transgenic mice with the genotype Cux2-CreER;Ai148.

To induce GCaMP expression in Cux2-CreER;Ai148 mice, tamoxifen (Sigma-Aldrich T5648) was administered at 0.1 mg/g. Preparation of the tamoxifen solution followed (Madisen et al., 2010). Specifically, tamoxifen was dissolved in ethanol (20 mg/1mL). Aliquots of this solution were stored indefinitely at −80 C. On the day of administration, an aliquot was thawed, diluted 1:1 in corn oil (Acros Organics, AC405430025) into microcentrifuge tubes, and then vacuum centrifuged (Eppendorf Vacufuge plus) for 45 minutes (V-AQ setting). After vacuuming, no ethanol should be visible, and the tamoxifen should be dissolved in the oil. Each mouse was weighed, and for every 10 g of mouse, 50 μL of solution was injected intraperitoneally.

To induce GCaMP expression in Rasgrf2-2A-dCre;Ai93D;CaMK2a-tTA mice, trimethoprim (Sigma-Aldrich T7883-25G) was dissolved in DMSO (Sigma-Aldrich 472301) at 10mg/mL and administered at 50 μg/g. Each mouse was weighed, and for every 10 g of mouse, 50 μL of solution was injected intraperitoneally.

METHOD DETAILS

Optical implementation details

The COSMOS macroscope uses a 50 mm f/1.2 camera lens (Nikon) as the main objective. It is mounted on a 60 mm cage cube (Thorlabs LC6W), which was modified to be able to hold a large dichroic (Semrock FF495-Di03 50mm x 75mm). It is also possible, though not optimal, to use an unmodified cage cube with a 50mm diameter dichroic. Illumination is provided by an ultra-high power 475 nm LED (Prizmatix UHP-LED-475), passed through a neutral density filter (Thorlabs NE05A, to ensure that the LED driver was never set to a low-power setting, which could cause flickering in the illumination), an excitation filter (Semrock FF02-472/30), and a 50mm f/1.2 camera lens (Nikon) as the illumination objective. An off-axis beam dump is used to capture any illumination light that passed through the dichroic. The detection path consists of an emission filter (Semrock FF01-520/35-50.8-D), followed by a multi-focal dual-lenslet array which projects two juxtaposed images onto a single sCMOS camera sensor (Photometrics Prime 95B 25mm). The approximate system cost was $40,000 USD, where the Prime 95B camera was ~$30,000. Raw images collected by the COSMOS macroscope contain sub-images from each lenslet, each focused at a different optical plane. The camera has a particularly large area sensor with a 25mm diagonal extent. The lenslet array is fabricated by mounting two modified 25mm diameter, 40mm focal length aspherized achromats (Edmund Optics #49-664) in a custom mount (fabricated by Protolabs.com, CAD file provided upon request). To maximize light throughput as well as position the optical axis of the two lenslets such that the two images fit side-by-side on the sensor, 7.09 mm was milled away from the edge of each lenslet (using the university’s crystal shop). The mount was designed to offset the vertical position and hence the focal plane of each lenslet by a specified amount - in our case 600μm. The mount was further designed to position the camera sensor at the midpoint between the working distance of each lenslet. A small green LED (1mm, Green Stuff World, Spain) was placed close to the primary objective such that it did not obstruct the image but was visible to the sensor and was synchronized to flash at the beginning of each behavioral trial. We measured the point spread function of each sub-image using a 10 μm fluorescent source; the focal planes were offset by 620 μm, close to the designed 600 μm.

There were a number of factors contributing to this final system design, which we describe here.

First, based on our simulation analyses in Figure S2, we determined that a multi-focal approach would yield the highest signal-to-noise ratio (SNR) across the target field of view. In particular, a dual-focal design best leveraged all of the light passing through the main objective, achieving a balance between increasing the total transmitted signal from each neuronal source and keeping the signal from each source compact. Although one obvious approach to increasing the depth of field of an imaging system is to simply close down the aperture, this comes at the cost of reducing the light throughput, SNR, and maximum spatial resolution of the system (Brady and Marks, 2011). Such a trade-off has spurred the development of multiplexed computational imaging approaches for extending the depth of field while maintaining high SNR. Computational imaging yields performance advantages specifically when the average signal level per pixel is lower than the variance of signal-independent noise sources, such as read noise (Cossairt et al., 2013). In particular, multiplexing approaches begin to fail when the photon noise of the signal overwhelms the signal-independent noise (Schechner et al., 2007; Wetzstein et al., 2013). As shown in Figure S2, our imaging paradigm falls within the regime where computational imaging ought to be beneficial. In particular, this is due to the bright background from autofluorescence and out-of-focus fluorescence that adds significant noise to the neuronal signal.

We thus took inspiration from a number of computational imaging techniques to develop an approach suitable for the requirements of our preparation: large field of view, microscopic resolution, high light-collection, high imaging speed, and minimal computational cost. In particular, there exist a number of potentially applicable extended depth of field (EDOF) imaging techniques, including use of a high-speed tunable lens (Liu and Hua, 2011; Wang et al., 2015), multi-focal imaging (Abrahamsson et al., 2013; Levin et al., 2009), light field microscopy (Levoy et al., 2006), and wavefront coding (Dowski and Cathey, 1995). While these techniques extend the depth of field, they require deconvolution to form a final image, which is computationally expensive and, as demonstrated later in our noise analysis, also provides a lower SNR for shot noise-limited applications such as our own. Additionally, further analyses of these techniques have demonstrated that the performance of any EDOF camera is improved if multiple focal settings are used during image capture (Brady and Marks, 2011; Hasinoff et al., 2009; Levin et al., 2009). We thus decided to pursue a multi-focal imaging approach and to design our system such that post-processing did not require a spatial deconvolution step.

Second, we found that the maximum illumination power is limited, and it was therefore essential to optimize the light throughput of the detection path in order to achieve maximum SNR. We found empirically that there was a maximum allowable illumination power density: continuous one-photon illumination intensity of around 500 mW/cm² yielded adverse effects on the mouse, including an enhanced risk of blood vessel rupture. Thus, indeterminately turning up the illumination power to increase signal is not an option, even if ultra-bright light sources exist.

Third, we require high image quality across a large, centimeter-scale field of view. When paired with the light throughput requirement, this means the optical system must have high etendue; without the use of large and extremely expensive custom optics, it is difficult to simultaneously maintain image quality and prevent light loss when passing the image through relay optics. We thus preferred designs that minimized the number of optical components in the detection path. In particular, rather than demagnifying an image onto a smaller camera sensor, we gained flexibility by using a large area sensor. Furthermore, it was also problematic to use a beamsplitter approach followed by relaying images to separate cameras, in terms of light throughput, image quality, and data acquisition complexity. Not only is a multi-camera beamsplitter approach costly and complex, but the beamsplitter approach is worse than the lenslet approach: in this setup, each image from the beamsplitter shares light that passed through the same central region of the aperture of the main objective; on the other hand, each lenslet image uses light that passed through one of two non-overlapping regions of the aperture of the main objective. Thus, for a given depth of field of each sub-image, and consequent f/# of either the lenslet or post-beamsplitter relay optics, each lenslet image will receive twice as much light as compared with the each beamsplitter image. Finally, because the lenslets themselves are physically large, we needed to be wary of aberrations (geometric and chromatic) induced by the lenslets. For microlenslets, this is less of an issue and is often ignored. The easiest, most cost-effective, and most reproducible way to fabricate high performance lenslets is to leverage the design of commercial off-the-shelf aspherized achromats. We found that with minor machined modifications to existing optics, it was possible to produce lenslets with the right physical dimensions while maintaining the high performance associated with aspheric optics. In the end, our image quality and light throughput of each lenslet image was on par with an image from a simple macroscope with equivalent aperture-size (as shown in Figure 1G, H); the multi-focal design is thus uniformly better than the conventional approach. Note that to generate Figure 1H, we manually merged the two focally offset sub-images (in Photoshop, Adobe). This was the only instance in which we ever needed to merge the image data; for all other processing, we processed each sub-image separately and then merged the extracted neural sources.

We characterize the resolution of our system in Figure S2N, and we find it to be sufficient for our application. The resolution of the system would likely be improved with smaller pixels; at the time of development, the only sCMOS camera available with a large enough sensor and fast enough framerate had 11 μm pixels, which with the magnification of our system yields pixels that sample from 13.75 μm in the specimen. However, the current resolution is likely acceptable for a number of reasons. First, cortical neuron somas are around 10-20 μm in diameter; with scattering, the point spread function of each neuronal source is further enlarged. Second, our current labeling strategy also labels dendrites, which serves to further increase the spatial spread of each source. Third, although an increased resolution could potentially help in distinguishing nearby sources, because of scattering it is unlikely that a slightly increased resolution would fundamentally change the data. Fourth, an increased resolution would lead to larger dataset sizes and consequent processing times without a concomitant increase in capability. Nevertheless, future improvements in the design will likely harness increased resolution. In particular, the most immediate improvements to the system could be achieved by using a custom primary objective with larger numerical aperture, or a camera with a larger or higher resolution sensor. Additionally, use of structured illumination is a viable route for potentially reducing the effect of scattering and for increasing the ability to discriminate between nearby sources.

Neuronal source extraction pipeline

The first step of processing raw videos collected on the COSMOS macroscope was to load the video (i.e., image stack) into memory from a remote data server, followed by cropping and then saving out to a local workstation separate image stacks for the top-focused and bottom-focused regions of interest (ROI). We applied rigid motion correction to each lenslet sub-image independently. Each ROI was motion corrected with a translation shift that was computed using the peak in the autocorrelation of a few sub-ROIs relative to the first frame in the stack. The motion correction was tested by plotting the maximum shift associated with additional test sub-ROIs, as well as manually inspecting each video, to ensure that motion throughout the video is smaller than 1 pixel in radius and that there are no large nonrigid movements. A proper surgery and rigid head fixation were adequate to maintain image stability.

Motion corrected stacks were then processed using Constrained Nonnegative Matrix Factorization for microendoscopic data, implemented in MATLAB (CNMF-E; Zhou et al., 2018). This algorithm is an improved version of the original CNMF (Pnevmatikakis et al., 2016), which has been modified primarily to incorporate better background subtraction, specifically for one-photon data. This background subtraction is very important for COSMOS data, since one-photon widefield recordings can be contaminated by large scale fluctuations in blood-flow related fluorescence modulation (Allen et al., 2017). Importantly, since we are extracting signal from sparse point sources, it is possible to separate the spatially broad background fluctuations from the more spatially compact neuronal signals–this was not the case in previous widefield preparations such as Allen et al. (2017). In particular, the CNMF-E algorithm excels at this background removal. As parameters for CNMF-E, we used a ring background model, with a 21-pixel source diameter initialization. For initializing seed pixels, we used a minimum local correlation of 0.8, and a minimum peak-to-noise ratio of 7. To analyze a 60,000-frame dataset, on a workstation with 512 GB of RAM, we can use 7 cores in parallel without running out of memory. With less available RAM, the number of parallel cores must be correspondingly scaled down. Since the algorithm is factorization based, the time for processing a dataset depends on the number of neuronal sources and the length of the video. Processing the top-focused and bottom-focused videos for a 60,000-frame dataset (equivalent to a 30-minute recording) requires about 36 hours in total. There are a number of paths to making this more efficient in the future: multiple workstations could be used to separately process the top-focused and bottom-focused videos; source extraction could be run only on the in-focus regions of the top-focused and bottom-focused stacks; and the improved background removal of CNMF-E could be applied to OnACID, an online version of the original CNMF algorithm that has demonstrated real-time processing speeds (Giovannucci et al., 2017). While all processing and analysis code for this project was written in Python, we elected to use the MATLAB implementation of CNMF-E because, as of the time when we were implementing our data analysis pipeline (in early 2018), the CNMF-E implementation in Caiman (Giovannucci et al., 2019) returned inferior results because it only initialized neural components with the full CNMF-E background model and then performed iterative update steps using a simpler background model.

Once CNMF-E has extracted neuronal sources (i.e., their spatial footprints and corresponding denoised time series) from the top-focused and bottom-focused videos, we merge the best in-focus sources from each focal plane, while ensuring that no sources were double counted by finding a classification line that spatially segmented the in-focus region of each sub-image. First, using a pair of manually selected keypoints, easily selected just once per dataset, we align the top-focused and bottom-focused coordinate systems. Then, in a semi-automated manner, we draw a separation curve for each cortical hemisphere, such that on one side of the separation curve we use sources extracted from the bottom-focused plane, and on the other side of the curve we use sources from the top-focused plane. This curve traces out the crossover in focus-quality between the two focal settings along the curved cortical surface. Due to different positioning and tilt of the headbar, these curves are not always in the same location across mice, even if the implanted glass window has identical curvature. Here, we use the radius of the source spatial footprints as a proxy for focus-quality across the field of view.

After merging sources from the top-focused and bottom-focused videos, we verify the quality of each source. First, we ensure that for each source the deconvolved trace returned by CNMF-E has a correlation of at least 0.75 with the corresponding non-deconvolved trace. The deconvolution algorithm assumes that the traces are generated by GCaMP, with a fast onset and a slow, exponential decay. Thus, any sources for which the deconvolved trace does not match the raw trace are likely not GCaMP signal. Second, we manually inspect all remaining traces, only keeping sources that are not located over blood vessels, that have radially symmetric spatial footprints, or that have a high signal-to-noise ratio. This process provides confidence that we have high-quality sources with minimal contamination. Finally, we manually align the atlas to each dataset based on the intrinsic imaging alignment assay, such that sources from all mice are situated in the same coordinate system.

Comparison of COSMOS with conventional macroscope

One mouse with good GCaMP expression and a clear window was used for this experiment. Over one hour, three independent videos each of 1800 frames were recorded at each macroscope setting: f/1.2, f/2, f/2.8, f/4, f/5.6, f/8, as well as with the detection lens replaced by the multifocal lenslet array. The mouse was awake but was sitting in a dark and quiet environment while not performing any behavioral task. The recordings for each macroscope setting were interleaved with one another throughout the session, such that recordings of the same setting were not captured sequentially, to mitigate the impact of any changes in the mouse’s behavioral state. The intensity of the excitation light at the sample remained constant throughout the experiment. In particular, changing the detection aperture setting did not alter the illumination, as the aperture was only changed on the detection lens as opposed to on the primary objective. The videos were processed using the same neuronal source extraction pipeline used throughout this paper, with identical parameter settings. During manual quality inspection and culling of the recovered sources, the operator was blinded to the macroscope setting of that video.

The COSMOS macroscope outperformed a comparable conventional macroscope in terms of depth of field while maintaining equivalent light throughput. We qualitatively compared the fidelity and depth-of-field of an image captured with a f/2 macroscope versus an image generated by merging the lenslet sub-images. Whereas a conventional macroscope offered nearly zero contrast at the lateral edges, the COSMOS macroscope provided good contrast laterally with only slightly reduced contrast medially. Light throughput of each lenslet was the same as that of a standard macroscope with the aperture set to f/2, and the light from defocused emitters was not diminished by vignetting.

The resolution of COSMOS was characterized using two approaches. The point spread function was acquired using a 10 μm precision pinhole (Thorlabs P10D) atop a fluorescent slide (Thorlabs FSK5, green). Additionally, an image was acquired of a USAF 1951 resolution chart (Thorlabs R3L3S1N) atop a fluorescent slide.

Intrinsic imaging for atlas alignment

Based on Garrett et al. (2014), Juavinett et al. (2017), and Nauhaus and Ringach (2007), a macroscope was constructed using two back-to-back 50mm f/1.2 F-mount camera lenses (Nikon), mounted using SM2 adapters (Thorlabs), and an sCMOS camera (Hamamatsu Orca Flash v4.0). A 700/10nm optical filter (Edmund Optics) was inserted between the lenses. Illumination was provided using a fiber-coupled 700nm LED (Thorlabs M700F3) that was positioned for each mouse so as to maximize coverage of the left posterior region of cortex (contralateral to the right visual field). A small green LED (1mm, Green Stuff World, Spain) was inserted after the optical filter and was synchronized to flash for 30 ms at the beginning of every trial. Mice were lightly sedated using chlorprothixene (Sigma-Aldrich C1671-1G, 2 mg of chlorprothixene powder in 10 mL of sterilized saline, administered 0.1 mL/20 g per mouse), and inhaled isoflurane at 0.5% concentration throughout the acquisition session. Mice were visually monitored during the session to ensure that they were awake.

The visual stimulus was generated using PsychoPy. Based on Zhuang et al. (2017), it consisted of a bar being swept across the monitor. The bar contained a flickering black-and-white checkerboard pattern, with spherical correction of the stimulus to stimulate in spherical visual coordinates using a planar monitor (Marshel et al., 2011). The pattern subtended 20 degrees in the direction of propagation and filled the monitor in the perpendicular dimension. The checkerboard square size was 20 degrees. Each square alternated between black and white at 6 Hz. The red channel of all displayed images was set to 0, to limit bleed-through onto the intrinsic imaging camera. To generate a map, the bar was swept across the screen in each of the four cardinal directions, crossing the screen in 10 s. A gap of 1 s was inserted between sweeps, resulting in repetition period of 11 s. Owing to the large size of our stimulus monitor, we also used a spherical warping transformation (PsychoPy function psychopy.visual.windowwarp) to simulate the effect of a spherical display using our flat monitor.

Finally, we developed a protocol for aligning a standardized atlas (Lein et al., 2007), shown in Figures 2J, S3C, and S3D, to each recorded video. We take advantage of the retinotopic sign reversal that occurs on the border between visual areas V1 and PM (Garrett et al., 2014). We use optical intrinsic imaging to record low spatial resolution neural activity in response to a drifting bar visual stimulus (Garrett et al., 2014; Juavinett et al., 2017) yielding a clear border between visual regions that can be computationally processed to define a phase map indicating the V1/PM border (Video S3). This landmark, in combination with the midline blood vessel can be used to scale and align the atlas to each mouse (Figure S3C). In Figure S3D, we provide the atlas alignment for all mice in the cohort. We used intrinsic imaging since, due to the sparsity of the cellular labeling in our Cux2-CreER mice, GCaMP imaging did not provide a spatially smooth enough signal to extract a phase map.

We performed 150 repeats of the stimulus. This number of repeats is higher than previous reports likely due to the 10x smaller pixel well capacity of our camera (5e4 electrons, compared with the 5e5 electron well depth of the Dalsa Pantera 1m60 used in Juavinett et al. (2017) and Nauhaus and Ringach (2007)), and subsequent increase in the minimum variance of photon shot noise.

The computer monitor was oriented at 60 degrees lateral to the midline of the mouse, tilted down 20 degrees, and placed 10 cm away from the right eye. Tape was placed around the around the headbar to prevent the mouse’s whisker and body from entering the imaging field of view. The mouse and microscope were covered with black cloth to occlude any external visual stimuli. Video was recorded at 20Hz with 2x2 pixel binning, with an effective pixel size of 13 μm at the sample. These acquisition parameters trade off dynamic range with dataset size. Illumination was adjusted to fill the dynamic range of the camera.

To process the video, it was first scaled down by a factor of 2 in x, y, and t dimensions. Trial start frames were extracted using the flashes from the synchronization LED. Trials of the same orientation were averaged together into an average video. In this average video, one should be able to see a bar propagating in one direction across V1 and a second bar propagating in the opposite direction across AM. A phase map was computed from this video by, for each pixel, finding the frame when the signal reached its minimum (corresponding to maximum hemodynamic absorption when the visual stimulus passes within the retinotopic field of view of that pixel). A 2D top-projection atlas was generated from the annotated Allen Brain Atlas volume, version CCFv3 (Lein et al., 2007), in MATLAB (MathWorks). The atlas was aligned to the phase map based on the location of the border between V1 and AM, and the midline. By aligning the intrinsic imaging field of view to the COSMOS field of view using landmarks along the edge of the window, the atlas could then be aligned to the COSMOS recordings.

Visual orientation selectivity assay

Sinusoidal visual gratings were presented to mice under the COSMOS macroscope using a small 15.5 cm x 8.5 cm (width x height)-sized LCD display mounted horizontally on an optical post (ThorLabs). The monitor (Raspberry Pi Touch Display) was centered 7.5 cm in front of the left eye of the mouse (at a 30° offset from perpendicular with the center of the eye). Contrast on the display was calibrated using a PR-670 SpectraScan Spectroradiometer (Photo Research). Significantly, this orientation of the monitor stretched across the midline of each animal and thus delivered some visual stimulation to both eyes. To block stray stimulation light from reaching the cranial window on the mouse, we attached a light-blocking cone that we designed to attach to the head bar of each animal (Figure S2K).

Gray sinusoidal grating stimuli were generated using PsychoPy (running on a Raspberry Pi 3 Model B). Eight stimuli (separated by 45°) were successively presented to each mouse (4 s per stimulus, with a 4 s intertrial interval). Each stimulus was presented five times, each time in the same order. The spatial frequency of the grating pattern was 0.05° and its temporal frequency was 2 Hz.

Comparison of COSMOS with two-photon imaging

The same three mice that had their visual responses characterized using drifting gratings under the COSMOS microscope were also imaged beneath a two-photon microscope (Neurolabware). Data were obtained at 30 Hz using an 8 kHz resonant scanner. We used a Nikon CFI LWD 16X water dipping objective (Thorlabs N16XLWD-PF) with clear ultrasound gel used as an immersion medium (Aquasonic, Parker Laboratories) between the surface of the cranial window and the objective itself. Following motion correction using moco (Dubbs et al., 2016), activity traces were extracted using the standard CNMF algorithm implemented the February 2018 version of Caiman (Giovannucci et al., 2019).

An identical visual stimulation system (the same model computer and display) was used with our two-photon microscope as with the COSMOS microscope. The display was calibrated to use the same contrast settings and the computer was loaded with identical stimulus code. Because the whole visual stimulation apparatus was mounted on an optical post, alignment relative to the mouse was similar in both settings.

The results from this characterization reveal that the present preparation affords an intermediate, complementary level of resolution relative to other techniques. We can access a field of view equivalent to existing widefield techniques, but with greatly improved near single-neuron-scale resolution; and we can record with reduced single-neuron detection ability compared with two-photon microscopy, but across a much larger field of view. For further thoughts about this, please see details described in the “Source Mixing Model,” described later in the methods section.

Robotic surgery protocol

Following Kim et al. (2016), we implanted a curved window over dorsal cortex. The dimensions of the window are described in Figure S1. The window was fabricated by first having glass blanks cut to the specified dimensions (TLC International) as shown in Figure S1, and then curved to the specified radius (Glaswerk).

We developed a semi-automated protocol for performing consistent large area craniotomies, which is one of the most crucial steps of the surgery. We used a computer-controlled drill and motorized stereotactic system (Neurostar GmbH, mounted on Kopf Model 900).

In Figures S1E-S1J, we show the state of the craniotomy at key steps during the surgery. In Figure S1C are the coordinates of the keypoints used for defining the drill path, as well as the approximate skull thickness at each location across mice. The keypoints (yellow) and interpolated drill positions (blue) are shown graphically in Figure S1B. In Figure S1D is a photograph of the robotic drill and the vacuum mount used for positioning the window implant (a 20-gauge needle with the sharp tip removed using a saw).

The surgical protocol is as follows:

Anesthetize mouse with isoflurane (3%, adjust to 1.5% after mouse is unconscious).
Position mouse on stereotaxic bite bar, do not engage earbars. Ensure mouse is breathing consistently and is unresponsive to toe pinch. Turn down the isoflurane to (1.5%).
Sterilize the skin and hair with an alcohol pad and cut off at least 1cm diameter circle of skin on the top of the head.
Secure mouse tightly with the ear bars. Push the skin down (i.e., with a cotton swab) while positioning the ear bars, such that the ear bars are in direct contact with the muscle, and the skin is fully out of the working area. Level the mouse.
Clean off and dry the skull completely. Use back side of cotton swab stick to pull back muscle on the posterior left and right corners.
Apply eye ointment to both eyes.
Clean the copper grounding clip connected to the Neurostar drill (i.e., with an alcohol wipe—you want to make sure there will be good conductive contact), and clip it to the skin on side of the skull and position the clip such that the clip is out of the way. Ensure there is a good connection with the moist underside of the skin. Ensure the clip is not in contact with the ear bars.
Open the Neurostar software. Tools- > Project- > New project. If you have previously used the same drilling coordinates that you will use for this surgery, you can ‘Select a template project’, and check the box ‘Keep Protocol elements’.
Use flat drill bit (Neurostar). This facilitates drilling along the curved lateral edges of the skull. A standard spherical drill bit may work, but not as well.
In the Neurostar software, open Tools- > Correct for Tilt and Scaling.
Find and set bregma for the drill (Ensure that ‘Drill’ is selected. See Neurostar documentation for navigation directions. Arrow keys and pg-up/pg-down control drill movement). Do not set lambda (this will rescale the window coordinates, which we do not want, since our window is of fixed dimensions). Ensure that midline is straight, parallel to the anterior-posterior axis of the drill. Ensure that angle of stereotax is set to 0. Ensure that anterior blood vessel (between the olfactory bulb and prefrontal cortex) is no closer than +3.25 AP. Adjust bregma if this is not the case. Ensure that −4.90AP looks reasonable at the back (i.e., it should be slightly behind the lambdoid suture).
Open drill menu. If you have never input the drill keypoint coordinates, then do so at this time (see Neurostar documentation for more detail). Press Ctrl+Shift+D so you can see details about the seed points. Turn on auto-stop.
Press F6. Turn ‘auto-speed’ on.
Go to next seed. Manually move the drill until it is touching the surface of the skull. Click ‘set surface.’ Press the ADVANCE button to advance the drill in 50 μm steps slowly until the conductance drops. Pause between each advance to ensure that the skull has time to settle. Click ‘set dura.’ Repeat. Note: The first depth should be between 300-600 μm. If autostop is not working (which sometimes happens), then there are other ways to determine whether you have drilled deeply enough. These include: observing bleeding (this means you probably drilled slightly too far); listening for the drill to not be going through bone anymore–there is a subtle but detectable difference in the sound of drilling through bone versus past the bone; and drilling to within the range of average thickness for that seed point location.
Ensure the auto cut edge-scaling is set to the second highest setting.
Inject 0.5 mL saline subcutaneously.
Press ‘autocut.’ Check for bleeding during autocutting. If there is significant bleeding at any point, pause autocutting and use Gelfoam (Pfizer) soaked in saline to stop the bleeding.
After autocut is finished, ensure that each location has been drilled through. You can right click on a point and select go-to drill depth, and then manually advance from there. The skull flap should be detached all the way around - lightly touching near each edge with a scalpel or needle should cause the skull flap to move.
When skull is detached fully, you can move the drill out of the way, to coordinates AP 35, ML 25, DV −35.
Apply a generous amount of saline to the skull. Clean away any hairs.
Inject mouse subcutaneously with 1 mL of saline.
Pull off the skull flap in one go, pulling up and away. Be sure to get a good grip using forceps and grab on the left posterior corner. In order to get a grip with the forceps, with the other hand, use a syringe filled with saline to lift up the skull flap, while simultaneously injecting saline. As a layer of saline begins to float the skull flap, grab it with the forceps and after ensuring a tight grip, pull the skull flap off in one motion. This is the most difficult and variable part of the surgery to do consistently and may take some practice. There will be bleeding. However, the blood should all be above the dura and can be cleaned with a Sugi absorption spear. The key thing to look for here is that the dura is intact and not folded over. If the dura is indeed intact, then you can spend time cleaning up the blood before implanting the window. This cleaning step can take tens of minutes, especially if you are waiting for the bleeding to stop. If the dura is not intact, then you can attempt to unfold it, however the likelihood for a successful surgery is lower.
Wash with saline. If you ever touch a Sugi spear to the brain, first ensure that is wet (dip it in saline first).
Submerge a Sugi spear in saline so that it is fully wet (dripping wet) and use that to wipe off blood on the surface of the brain. Keep the brain wet and be gentle.
When blood is clear from the brain surface, mount the window on the vacuum holder. The vacuum holder consists of a needle (16-20 gauge) with the sharp tip drilled off. The needle is connected to a vacuum tube and mounted on the robotic stereotax. Using a syringe, drip saline onto the bottom of the window so that there is saline between the window and brain, and slowly bring the window down from above (You can press F6— > Change the DV speed to something small such as 10 μm/s).
Push the window down so that all accessible parts of cortex make contact with the window. If you do not push down far enough, then a number of bad things can happen: the brain will move when the animal moves, leading to motion artifacts; there will be tissue growth between the window and brain over time; and Vetbond glue (3M) may seep under the window during the next step of the surgery. If you push down too far, however, then you may cut off blood supply through the central blood vessel. Ensure that the blood flow is not restricted (the vessels should not lose color).
When the window is held down successfully, pause for a minute to ensure that no bleeding begins. If bleeding does begin then there are two options: either remove the window, clean things up, and wait for the bleeding to stop; or raise the window slightly and inject saline under the window while using a Sugi to draw the water and blood out of the other side of the window. Once the window is in place with no bleeding, then dry the tissue/bone surrounding to the window (while ensuring that you do not dry up the water layer between the window and brain) and apply Vetbond around the edges of the window. Do not use too much Vetbond, as it will then take longer to dry. Ensure that no Vetbond is seeping under the window: if it is, then push the window down further.
Once the Vetbond has dried, apply Metabond (C&B, Parkell). At this step, it is key to ensure that there is a very good bond with the front of the skull. In particular, be sure that the bone anterior even to the olfactory bulb is visible, accessible and dry. You can additionally use a surgical blade to score the surface of the skull to provide additional surface area for bonding cement. If this bond is not good, then when the mouse is first head mounted, the head bar and window may detach.
After the cement dries, if mouse is doing okay, you can optionally attach the headbar using additional Metabond. This step can also be performed in the future (i.e., a few days later) after the mouse has had a chance to recover.
Inject mouse with saline and painkiller (buprenorphine).
Immediately after surgery, there should ideally be no big blood splotches, and in general the window should be clear. This does not guarantee that the window will remain clear, and there is a chance that window gets worse. However, sometimes if there is some blood in the window it may actually clear up. The key to at least having a chance for a good, clear window, however, is that the dura is intact and not folded over - it will be impossible to image through areas with a damaged dura, and this will not heal with time.

Animal behavior hardware

As in Allen et al. (2017), a microcontroller-based real-time behavioral system (Sanworks, Bpod State Machine r1) was used to control delivery of stimuli and water reward. Three independent waterspouts (Popper animal feeding needle, 22 gauge, 1.5” length, Lab Supply Outlaws part #01-290-2B) were arranged using a custom mount (fabricated by Protolabs.com, CAD file provided upon request), positioned at 75 degree intervals, with the tips of the spouts aligned along a circle of radius 5mm (determined by an appropriately sized drill bit). Licks were detected independently for each spout, with a lickometer built using a capacitive touch sensor (Sparkfun Tinkerkit) and a microcontroller (Arduino Uno). Water was delivered by a gravity-assisted syringe attached to the lickometer and controlled by a quiet solenoid valve (Lee Valve LHDA1231115H). For olfactory stimuli, an olfactometer was constructed using pure odorants (ethyl acetate and 2-pentanone, Sigma) diluted to 4% v/v in paraffin oil (Sigma) and pressurized with air (1 L/min). Two 3-way valves (NResearch #161T031) controlled odor delivery, with the normally open port connected to a blank vial and the normally closed port connected to an odor vial. Odor delivery was controlled by actuating solenoid valves to switch airflow away from a blank valve and to the odor valve. Odors were delivered through a Teflon tube (NResearch, #TBGM109 with #102P109-10 connectors), placed ~1 cm from the mouse’s nose.

Two cameras (Basler acA1300-200uc), one with a 25mm lens (Edmund Optics #59871), and the other with a 4.5mm lens (Edmund Optics #86900), were positioned below the mouse to monitor its tongue and whiskers and to the side to monitor the face and body, respectively. Video acquisition was performed using custom software (Python, using pypylon). A small green LED (1mm Green Stuff World, Spain) was placed in front of each camera, and was synchronized by Bpod to flash at the beginning of each trial. All valve openings were controlled with Bpod, which also recorded the time of licks to each spout.

Animal behavioral training

After waiting at least a week after surgery, mice were water restricted to 1mL/day while maintaining > 80% pre-deprivation weight. After several days of handling and habituation to head fixation, mice were trained to lick for free reward (2-3μL) from a single spout. Once mice could reliably lick for water, they were started on a shaping protocol that automatically provided water reward (2-3μL) 500 ms after the offset of either of the two odors (delivered for 1 s). Initially, mice were trained to receive water reward from the central spout in response to the odor. After succeeding at this, they progressed to a protocol where water was provided from each of the three spouts, but only from one spout on each trial. The spout from which reward was delivered remained consistent for blocks of 35-40 trials. The mice received the full reward if they licked any of the spouts during the response interval. For the next stage, a distinction was made between the two odors such that only one of the odors corresponded to a reward trial. Finally, after the mice demonstrated that they could distinguish between the “go” and “no go” odor, and that they are able to consistently obtain reward from all three spouts, they progressed to the final stage. For the final protocol, mice learned to lick only to the active spout of the current block in response to the go odor. Specifically, if the first lick during the response period (which begins 0.5 s after odor offset) was to the active spout, then the mice would receive a full reward (2-3μL) from the active spout. If the mice responded by licking to a different spout, then they would instead receive a small reward (0.25 μL) from the active spout. No reward was delivered if the mice licked during a “no go” odor. Although the mice were only required to lick to the active spout during a very specific time interval, in general they learned to lick almost exclusively to that spout starting at odor onset. We found that more complicated schemes requiring the mouse to not lick to any of the other spouts were too difficult during training and led to demotivation. The whole training process takes 2-8 weeks, with some mice learning faster than others. “No go” trials were chosen by randomly sampling from a Bernoulli distribution with a fixed ratio such that there was a 20% chance that any given trial would be “no go.”

Histology and Tissue Imaging

Animals were transcardially perfused with 4% paraformaldehyde in PBS. The brain was removed from the skull and post-fixed in 4% paraformaldehyde in PBS at 4°C overnight. Tissue sections (75 μm) were cut with a vibrating microtome (Leica).

Sections were mounted on glass slides with liquid mounting medium (Fluoromount-G with DAPI, ThermoFisher Scientific). Images were acquired either on the custom-built tandem lens macroscope described earlier or using a confocal microscope (TCS SP5, Leica).

Multi-region optogenetic inhibition

We built a system for simultaneous inhibition of multiple cortical regions. It is known that projections from S1 can drive M1 activity and drive the initiation of whisking (Sreenivasan et al., 2016). But in addition, posterior regions like retrosplenial cortex and primary sensory areas (Barthas and Kwan, 2017; Yamawaki et al., 2016; Zingg et al., 2014), also project to secondary motor cortex and may thus play an important role in producing any dynamics observed in motor areas. We therefore set out to inhibit activity from multiple areas, to avoid the possibility that uninhibited areas in cortex might compensate for the acute shutdown of a single area. VGAT-ChR2 mice were prepared with a cleared skull and headbar as in Guo et al. (2014). The positions of lambda and bregma were marked. Mice were trained to > 80% performance on the three-spout block-structured task described earlier. On successive days, different regions of cortex were inhibited. Specifically, all reachable dorsal cortical regions, just M1 and M2 motor regions, or all reachable regions except for M1 and M2 were targeted. Stimulation occurred either during the 2 s preceding odor onset (Pre-odor), or during the 1.5 s following odor onset (Peri-odor). This protocol restricted optical stimulation to the interval of time when either motor plans were maintained, or motor plan execution initiated. Stimulation turned off before the response period, during which the first lick the mouse makes is counted as the selected spout. Thus, there was never inhibition during the time when the mouse actually indicated the selected spout; there was only inhibition during the preceding period when the mouse would otherwise anticipatorily lick toward the selected spout. Optical patterning was accomplished using a digital micromirror device (DMD, Polygon400, Mightex Systems) with a large field of view macroscope (OASIS Macro, Mightex Systems). A 5W 488nm laser (Genesis, Coherent) was fiber-coupled into the DMD, after passing through a laser-mode mixer (LMX-015-0400, Mightex Systems). The field of view accessible for stimulation was about 7 mm diameter, with a power density of 0.5-1 mW/mm² after correction to ensure similar intensity across the field of view. Based on the characterizations performed in Guo et al. (2014), this power density should be adequate to achieve a significant decrease in spike rate while also providing high spatial resolution (< 1mm diameter of influence per pixel). Custom-written software was used to align the projected light pattern based on the lambda and bregma markings as imaged using an alignment camera, ensuring consistent alignment across days. The power distribution and vignetting were calibrated by recording power measurements sequentially throughout the field of view (Thorlabs S175C). A software correction was applied to correct for a nonuniform power transmission. The displayed stimulation pattern was controlled through MATLAB using HDMI and treating the DMD as an external display. A blue fiber-coupled LED (Thorlabs M470F3) was directed into the mouse’s right eye. For eye-LED control sessions, an LED was turned on in place of DMD stimulation, only during stimulation trials. For stimulation sessions, the LED was turned on for all trials during the time period within the trial corresponding to stimulation. Sessions were only included if the performance on non-stimulation trials reached a pre-defined threshold of at least 80% correct. For each stimulation pattern and for each mouse, we used data from at least two complete sessions. Within each session, two thirds of the blocks were stimulation blocks, and there was at least one non-stimulation block for each of the three possible active spouts. The ordering of blocks was randomized.

Optical design principles

In this section, we describe the analysis underlying the principles we used to design the COSMOS macroscope. As the primary metric for comparing optical designs, we use the signal-to-noise ratio (SNR) of the reconstructed neural signal. There are two primary sources of noise in the system: signal-dependent photon shot noise γ_s, and signal-independent photon shot noise γ_b. With modern sCMOS cameras, read noise and dark current can essentially be ignored. Instead, γ_b derives primarily from the background fluorescence that is incident on each pixel, composed of autofluorescence and nonspecific neuropil fluorescence, and which has a mean value and variance which is roughly independent of how the signal from each individual neuron is fluctuating. For our application, the mean value of the Poisson distributed γ_s and γ_b is in the thousands to tens of thousands (as shown in Figures S2A and S2B), and they are therefore well approximated as Gaussian distributed. To represent the noise-induced variance, we use zero-mean Gaussian random variables η_s and η_b, which have variances equal to that of γ_s and γ_b, respectively. We model image formation as

\hat{y} = a c + b + η_{s} + η_{b}

(1)

where $\hat{y} \in R^{m \times t}$ for m pixels and t time points is the sensor video; $a \in R^{m \times n}$ for n neurons is the sensor point spread function of each neuron; $c \in R^{n \times t}$ is the time course of each neuron’s signal; $b \in R^{m}$ is the background at each pixel; $η_{s} \in R^{m}$ is the zero-mean signal-dependent noise at each pixel; $η_{b} \in R^{m}$ is the zero-mean signal-independent noise at each pixel. Following Cossairt et al. (2013) and Wetzstein et al. (2013), we model signal reconstruction using least-squares inversion.

\hat{c} = a^{†} (y - b)

(2)

where a^† = (a^Ta)⁻¹a^T. As we derive in the ‘Noise analysis full derivation’ section, we can write the SNR for a single emitting neuron (i.e., n = 1) as

S N R = \frac{s i g n a l}{\sqrt{M S E}}

(3)

= \frac{c}{\sqrt{\frac{1}{n} T r a c e [a^{†} C o v (η_{s} + η_{b}) a^{† T}]}}

(4)

= \frac{\sqrt{α} c_{0}}{\sqrt{\sum_{i = 1}^{m} (a^{†} [i])^{2} (a [i] c_{0} + b_{0} [i])}}

(5)

where MSE is the mean-squared-error in the reconstructed signal; c = αc₀ is the measured value of the signal of a point emitter, where α is the scalar fraction of the full aperture that is transmissive and scalar c₀ is the peak value of the signal if the aperture were fully open; $a \in R^{m}$ represents the footprint of the emitted light incident on the sensor; a^† is the pseudo-inverse used for reconstructing c; $b_{0} \in R^{m}$ is the mean value of the background signal incident on each sensor pixel. The three main design principles presented in the main text can be extracted from Equation 5:

Background fluorescence substantially degrades SNR if greater than the signal per pixel.
SNR increases as total light transmission α increases.
SNR increases when signal photons are dense, as opposed to spread out, on the sensor. This is the case when an emitter is in focus.

In simulation, we verified the validity of these principles and explored the repercussions for various potential designs. In Figures S2C-S2E, we quantify the background, defocus blur, and recovered signal photons characteristics of the competing designs. In Figure S2F, we summarize the SNR at each position along the curved window, based on the data in Figures S2C-S2E. Although the f/1.4 and f/2 macroscope configurations perform best near their single focal plane, the dual-lenslet design performs well across the entire curved field of view. In Figure S2G we summarize the gain in improvement offered by the dual-lenslet design relative to the other approaches, in terms of the median SNR per pixel across the field of view. In conclusion, informed by this analysis, we decided to pursue the dual-lenslet, dual-focus design.

Noise analysis full derivation

In this section, we provide a full derivation of Equation 5, which was fundamental to determining the principles that guided our optical design. We additionally explore the ramifications of Equation 5. We found that for our application, optical designs which spread light out and rely on post-capture image deconvolution make SNR strictly worse and should be avoided. In particular, we demonstrate that if there is a background flux of photons incident on each pixel, then signal recovered from an emitter degrades when a fixed amount of emission light is spread across a larger number of sensor pixels. The key assumption is that the background brightness is independent of the signal from the emitter and is incident on all sensor pixels. Locally, this assumption is approximately true in the COSMOS preparation. The implication of this result is that it is better to design a system where as much signal as possible is in-focus and concentrated, rather than attempting to deconvolve or demultiplex a blurred or distributed signal.

We begin with the simple case of a background of constant mean value incident on each sensor pixel, for a single time point. Let $\hat{y} \in R^{m}$ represent the noisy, measured value of each of the m pixels, $b \in R^{m}$ represent the noiseless background value, $s \in R^{m}$ represent the noiseless signal value of a single emitter, $γ_{b} \in R^{m} \overset{i i d}{\sim} Poisson (b)$ the photon shot noise associated with b, and $γ_{s} \in R^{m} \overset{i i d}{\sim} Poisson (s)$ the photon shot noise associated with s. For high rates Poisson distributions become approximately Gaussian with a variance equal to the mean (Cossairt et al., 2013). Since our total signal is in the tens of thousands of photons, this approximation is valid and we can approximate the noise as additive but signal dependent. We thus represent the noise in our image formation model as $η_{b} \in R^{m} \overset{i i d}{\sim} N (0, b)$ the noise associated with b, and $η_{s} \in R^{m} \overset{i i d}{\sim} N (0, s)$ the noise associated with s. We can write $\hat{y}$ in terms of its underlying noiseless values and the added noise.

\hat{y} = s + b + η_{s} + η_{b}

(6)

Let’s next assume that we can factor s as the product of a spatial and temporal matrix, s = ac, where $s \in R^{m}$ , $a \in R^{m \times k}$ , and $c \in R^{k \times t}$ , with m as the number of pixels, k as the number of neurons, and t as the number of time points. Let’s also assume that a is known: that is, we know the spatial sensor footprint, or point spread function, associated with the emitter. We add two more assumptions: each column of a sums to 1, and we account for differences in aperture light transmission as c = αc₀, where 0 ≤ α ≤ 1 represents the fraction of the full aperture that is open, and c₀ represents the total signal transmitted with the aperture fully open. Let’s further assume that we know b, and define it as b = αb₀, where b₀ is the mean background per pixel with the aperture fully open. Our goal is then to recover c as the maximum likelihood estimate under the noise assumptions. According to our signal-dependent noise assumptions, Var (η_s) = ac = aαc₀ and Var (η_b) = b = αb₀. We estimate c by minimizing the squared error

\hat{c} = \min_{c} ‖ \hat{y} - a c - b ‖^{2}

(7)

If the variance was the same for each pixel, this would be the maximum likelihood estimate under Gaussian noise. Although this is explicitly not the case in our scenario, we make a simplifying assumption here that the least-squares estimate is adequate; this also aligns ultimately with the factorization-based source extraction algorithm we use on our actual data. For known $\hat{y}$ , a, and b, this is a simple least-squares problem, which is minimized using the normal equation (here, we ignore any non-negativity constraints).

\hat{c} = a^{†} (\hat{y} - b)

(8)

= a^{†} (s + η_{s} + η_{b})

(9)

= a^{†} (a c + η_{s} + η_{b})

(10)

where a^† = (a^T a)⁻¹a^T. For a single emitter, a and b are each a single column-vector, and a^Ta is a scalar. For a single time point, c is a scalar. We can reduce Equation 10:

\hat{c} = c + a^{†} (η_{s} + η_{b})

(11)

We are then ultimately interested in the signal-to-noise ratio (SNR), defined as the ratio between the signal mean and the standard deviation of the noise (i.e., the square root of the mean-square-error, or MSE). We can compute the MSE as the trace of covariance matrix of the noise in the reconstruction. Let η = η_s + η_b, where $η \in R^{m}$ , and R = a^†η is the noise propagated through the reconstruction, with $R \in R^{k}$ .

M S E = E [(R - μ_{R})^{2}]

(12)

= E [(a^{†} (η - μ_{η}))^{2}]

(13)

= \frac{1}{k} \sum (a^{†} (η - μ_{η}))^{2}

(14)

= \frac{1}{k} T r a c e (C o v (a^{†} η))

(15)

= \frac{1}{k} T r a c e (a^{†} C o v (η) a^{† T})

(16)

where Equation 16 results from Cov (Ax) = A Cov (x)A^T, which can be derived by expanding Cov(Ax, Ay) ≡ E[(A(x – μ_x))(A(y μ μ_y))^T]. We then write out a full expression for the SNR.

S N R = \frac{s i g n a l}{\sqrt{M S E}}

(17)

= \frac{c}{\sqrt{\frac{1}{k} T r a c e [a^{†} C o v (η_{s} + η_{b}) a^{† T}]}}

(18)

Here, we simplify by assuming that we are recovering the signal of a single emitter, such that k = 1. Furthermore, since we assume the noise at each pixel is independent of the noise at other pixels, the off-diagonal terms in Cov (η_s + η_b) are zero. We can therefore reduce Equation 18.

S N R = \frac{c}{\sqrt{\sum_{i = 1}^{m} (a^{†} [i])^{2} (V a r (η_{s} [i]) + V a r (η_{b} [i]))}}

(19)

= \frac{α c_{0}}{\sqrt{\sum_{i = 1}^{m} (a^{†} [i])^{2} (a [i] α c_{0} + α b_{0} [i])}}

(20)

= \frac{\sqrt{α} c_{0}}{\sqrt{\sum_{i = 1}^{m} (a^{†} [i])^{2} (a [i] c_{0} + b_{0} [i])}}

(21)

where i is used to index into each vector. We have thus derived Equation 5.

Now, with Equation 21, we can determine how SNR changes as a, b₀, and α change, where a is the spatial footprint of a single emitter, b₀ is the mean background level per pixel relative to the signal level c₀, and α is the fraction of the full aperture that is open.

To begin, we can derive an analytical expression for how the SNR changes as the emission light is spread across more sensor pixels if we use a simple representation of a. In particular, we assume that if there are n non-zero entries in a, then each non-zero entry has value 1/n, i.e., that light is distributed uniformly within the point spread function. If H = {i∣a[i] > 0}, then for i∈H, a[i] = 1/n, and $\sum_{i = 1}^{m} [a i] = \sum_{i \in H} [a i] = 1$ . Here, we deal with only a single time point, such that c = αc₀ is a scalar. It follows that only for i∈ H is s[i] > 0, and thus $\sum_{i = 1}^{m} [s i] = \sum_{i \in H} [s i] = c$ . We can then compute a^†.

a^{T} a = \sum \frac{1}{n^{2}} = \frac{1}{n}

(22)

(a^{T} a)^{- 1} = n

(23)

a^{†} = n a^{T}

(24)

Thus, a^† is the same as a, except that each non-zero entry has a value of 1 instead of 1 /n. From Equation 10, thus

\hat{c} = \sum_{i = 1}^{m} [a^{†} i] (s [i] + η_{s} [i] + η_{b} [i])

(25)

= \sum_{i \in H} [s i] + η_{s} [i] + η_{b} [i]

(26)

= c + \sum_{i \in H} [η_{s} i] + η_{b} [i]

(27)

Because η_b is composed of independent random variables, their variances add. Let’s assume that b = B₁ for scalar B. Because η_b[i] ~ Pois (B), Var(η_b[i]) = B. Thus

V a r (\sum_{i \in H} [η_{b} i]) = \sum_{i \in H} B = n B

(28)

In contrast, the variance of η_s does not depend on n,

V a r (\sum_{i \in H} [η_{s} i]) = \sum_{i \in H} [s i] = c

(29)

and thus,

V a r (\hat{c}) = n B + c

(30)

We can also directly compute SNR based on Equation 21,

S N R = \frac{\sqrt{α} c_{0}}{\sqrt{c_{0} + n B_{0}}}

(31)

The result is thus that as n, the number of sensor pixels over which the light from an emitter is spread, increases, so does the variance of the recovered signal. If the light from a single emitter is spread across more pixels, then the relative influence of the background shot noise is higher. That is, the recovered signal is noisier and the SNR degrades. Again, the implication of this result is that the best design should have high overall light transmission, but with the signal photons focused in as concentrated manner onto as few pixels as possible.

Simulation details

The following describes details of how the simulation results in Figure S2 were generated.

We estimated the level of the background signal relative to the somatic signal based on the output of CNMF-E, which estimates the background as part of the source extraction process. We captured three one-minute long videos with the aperture open to f/1.4 with 50mW illumination with a Cux2-CreER;Ai148 mouse. Using the quantum efficiency conversion factor of the Prime95b camera (0.93 across the green part of the spectrum), we estimated the number of photons incident on the sensor. The total signal per neuron was computed as the median across neurons of the maximum signal (across the video) for each neuron, multiplied by the sum across the footprint weights for each neuron. The number of pixels per neuron was computed based on the number of pixels in the footprint required to reach 90% of the total weight across the footprint. For the background, we used the reconstructed background output from CNMF-e. This provides a background image for each frame in the video. We computed the median background value for each pixel across time, and then using the pixels with values in the middle eight deciles, we computed the median background value per pixel. These results, in addition to results for other aperture settings as well as for the dual lenslet design, are shown in Figures S2A and S2B. For f/1.4, averaged across the three videos, the mean background photons per pixel was n_background = 10e3, and the total signal per source was n_emission = 13e4.

Defocus Blur

We started by comparing the simulated defocus blur across the extent of the curved glass window for each the following imaging approaches: stopping down the aperture on a conventional macroscope; a pellicle beamsplitter with two cameras; a multi-focal lenslet array; and an oscillating tunable lens. The curved geometry of the window is demonstrated in Figure S1A.

To simulate defocus blur, we began with a simple ray-optics model and modified it to include the effects of aperture-induced diffraction. We assumed 1:1 magnification. We determined the angle of the marginal ray based on the f-number, N, as

θ_{m a r g} = arctan (\frac{D ∕ 2}{f}) = arctan (\frac{1}{2 N})

(32)

The blur radius at each location along the window was determined based on the axial distance to the nearest native focal plane, z_near. For the conventional macroscope, there was one focal plane, for the bi-focal plane, there were two, and for the lenslet array, there were two focal planes.

b = ∣ z - z_{n e a r} ∣ \tan (θ_{m a r g})

(33)

For the tunable lenses, we used a slightly different approach. In order to image at 30 Hz, the tunable lenses must oscillate across the focal volume, as opposed to stepping between fixed focal planes. We modeled the effective blur radius as the average blur radius across a focal sweep from z₀ to z₁. For an axial position z between z₀ and z₁, the average radius is

r = \frac{1}{∣ z_{0} - z_{1} ∣} \int_{z_{0} - z}^{z_{1} - z} ∣ c h ∣ d h

(34)

= \frac{1}{∣ z_{0} - z_{1} ∣} \frac{1}{2} (c h^{2}) s i g n (c h) ∣_{z_{0} - z}^{z_{1} - z}

(35)

where c = tan(θ_marg).

To incorporate the effects of diffraction into this simplified model, we added a constant blur at all depths with a radius computed according to the Rayleigh resolution criterion, as

r_{d i f f r a c t i o n} = \frac{0.61 λ}{N A} = (0.61 λ) (2 N)

(36)

where we used the approximation of the numerical aperture NA in terms of the f-number N

N A = n \sin θ_{m a r g} = n \sin (arctan \frac{D}{2 f}) \approx \frac{1}{2 N}

(37)

where n ≈ 1 in air.

As is visible in Figure S2D, the maximal defocus blur is substantially smaller for larger f-numbers. However, both the mirror and lenslet designs achieve similar depth-of-field performance.

Light throughput

We next considered the detected light throughput of each design. Although a smaller aperture yields smaller defocus blur, it also throws away light. We established experimentally that with 470 nm light, a total constant excitation illumination intensity of 500 mW across the field of view, i.e., 5mW/mm², causes significant damage to the brain. As it is essential that we are able to perform long imaging sessions, to be safe we chose a maximum threshold of 50 mW illumination. With an upper limit on excitation power, it is thus of paramount importance that our light collection is efficient.

We first compared light collection simply based on the open area of the aperture. For the lenslet array, we conservatively assumed that when reconstructing neuronal traces, for each location across the window we only ever use light from one of the lenslet images, and thus the image effectively had an f-number of F/D = 40/21.9 = 1.8 where F = 40mm is the focal length of each lenslet, and D = 21.9mm is the diameter of a circular lens with the same area as a 25mm diameter lens with 7mm milled off from the edge. For the beamsplitter, to yield adequate depth-of-field we set the f-number to be f/2. For the tunable lens, we set the diameter of the aperture to be the size of the clear aperture of the tunable lens. We normalized all aperture areas based on the total area of the maximum f/1.4 aperture area. These results are shown in Figure S2C.

Overall SNR

We next constructed a measure that incorporates both light throughput and blur size, incorporating the effects of shot noise from background fluorescence. We began by computing the number of photons per sensor pixel detected from an individual emitting point source in the specimen. This is an important measurement because there is a relatively high intensity background signal in the COSMOS imaging preparation, which according to our noise analysis derivation influences the overall SNR of an optical design . This background derives primarily from diffuse and defocused neuropil fluorescence and tissue autofluorescence, which is particularly strong around the emission spectrum of GCaMP. For the purposes of this analysis, we treat the background as a mean constant intensity addition to each sensor pixel. Importantly, however, although the mean intensity is constant, there is photon shot noise that adds variance to the background. In particular, for a background of mean photon count B, the standard deviation in photon counts is $\sqrt{B}$ .

Next, we computed the number of photons per pixel from a single neuronal emitter, at each point along the curved glass window. We determined the size of the blur disc based on the blur radii shown in Figure S2D, according to a = πr². We then multiplied the blur disc by the normalized light collections of Figure S2C. Multiplying this by n_emission yielded the number of photons within the blur disc. We then normalized this by the number of pixels within the blur disc (for pixels of sidelength 11 μm). In Figure S2E, we see that the multi-focal designs lead to a substantially higher density of collected photons on average.

Now, we computed the SNR per pixel. We approximate the footprint a as Gaussian weighted across pixels within the blur disc, with a standard deviation equal the half of the number of pixels within the blur disc. Using a^† = (a^Ta)⁻¹ a^T, we computed SNR as light transmission according to Equation 21, with c = n_emission and b = n_background.

In Figure S2F, we see that while the large aperture macroscope designs offer the highest peak SNR, there are large stretches where the SNR is much lower, i.e., where everything is out of focus. The multifocal designs, however, maintain a good compromise, with fairly even performance across the field of view, as well as a higher minimum SNR than the other designs. In particular, as shown in Figure S2G, the dual-focus lenslet provides the best overall performance across the extent of the curved field of view.

QUANTIFICATION AND STATISTICAL ANALYSIS

Open source packages used

The following open source libraries were used in the statistical analyses of the data presented in this paper:

IPython (Pérez and Granger, 2007): https://ipython.org/

Numpy (Van Der Walt et al., 2011): https://www.numpy.org

Matplotlib (Hunter, 2007): https://www.matplotlib.org

Pandas (McKinney, 2010): https://pandas.pydata.org/

Scikit-learn (Pedregosa et al., 2011): https://scikit-learn.org/stable/index.html

SciPy (Oliphant, 2007): https://www.scipy.org

Seaborn (Waskom et al., 2017): http://seaborn.pydata.org

Statsmodels (Seabold and Perktold, 2010): https://www.statsmodels.org/stable/index.html

Keras (Chollet, 2015): https://keras.io

PsychoPy (Peirce, 2007): https://www.psychopy.org

Micromanager (Edelstein et al., 2014): https://www.micro-manager.org

Fiji (Schindelin et al., 2012): https://imagej.net/Welcome

Statistical analysis

The number of subjects used in each experiment was based on numbers used in previous studies. Unless otherwise specified, statistics were reported as means and SEM values. Probabilities from multiple hypothesis tests were corrected using the Benjamini-Hochberg correction (alpha = 0.05) in all cases, unless otherwise indicated.

A single session of imaging data from each mouse with the Cux2-CreER; Ai148 genotype that were fully trained on the task (defined as reaching 80% correct in at least three sessions) was included in all imaging analyses. This single session of data was chosen in each case based only on high behavioral performance. Main experimental analyses were not additionally run on any other undisclosed datasets.

For the optogenetic inhibition experiments, mice had to achieve at least 75% performance on the task in two consecutive sessions, with the eye-LED on for a subset of trials, before attempting a day with optogenetic perturbation. Then, for each optogenetic stimulation condition, data were included from each mouse where they had at least two sessions worth of data with performance during the no-stimulation blocks averaging > 80%. If more than two sessions from a given mouse and condition had no-stimulation performance greater than this threshold, the best two sessions were used.

Orientation selectivity analysis

To compute the orientation selectivity of COSMOS and two-photon data taken during visual grating presentation, we used the following definition of the orientation selectivity index (OSI):

O S I = \frac{r_{p r e f} - r_{o r t h}}{r_{p r e f} + r_{o r t h}}

where r_pref is the maximum trial-averaged fluorescence in response to any grating orientation and r_orth is the response to the 90° offset grating using the raw fluorescence traces extracted from CNMF-E. OSI histograms only show values from sources that pass a one-way ANOVA comparing the average response to the grating stimuli versus blank periods with p < 0.01. These methods are similar to those previously used in Chen et al. (2013) to characterize GCaMP6 under two-photon microscopy and yielded similar results for our two-photon data.

Source mixing model

We estimated the number of neurons underlying each extracted COSMOS source using a simple averaging model. We first computed the OSI histogram for the visual drifting grating data obtained from each of three mice taken under our two-photon microscope and, separately, under the COSMOS macroscope using the procedure described in the previous section. Next, for each mouse, we attempted to simulate the COSMOS OSI histogram by using mixtures of neurons from the two-photon data. To do this, we sampled from all of the neurons that comprised the two-photon OSI histogram 500 times, each time generating a “mixed” trace by averaging over a random number of sources. The number of sources to average over on each iteration was chosen from a uniform distribution. Once 500 sources had been generated using this approach, we then regenerated the OSI histogram for that simulation.

This process was repeated 10 times (with different random seeds) for different uniform distributions (i.e., source mixing ranges). We searched over all combinations of uniform distributions [min, max], where min ranged from 1-20 and max ranged from 1-50. Combinations where min was greater or equal to max were not used.

Finally, we computed the optimal min and max parameter to approximate the empirical COSMOS OSI histogram by computing the parameters that minimized the mean Kullback-Leibler divergence between each of the 10 models for a given parameter choice and the empirical OSI distribution.

The consistency of this observation between animals is likely related to the similar density of neurons in each animal (owing to similar tamoxifen dosing of 0.1 mg/g); these results could change under a stimulus that recruits a different fraction of the network (the visual stimuli here may drive particularly strong correlations).

Region specific analyses

After registering the Allen Brain Atlas volume, version CCFv3, to each mouse (using the procedure described the “intrinsic imaging for atlas alignment” section), we identified five groups of cortical areas that we analyzed separately at many points in the paper (motor, somatosensory, parietal, retrosplenial, and visual). Each of these areas is a “parent” node for all the “child” nodes saved in the Allen Atlas. For example, “secondary motor area” (ID = 993) has parent node ID = 500, “somatomotor areas.” All sources coming from these “somatomotor areas” are therefore analyzed when we restricted our analysis to motor. These are the parent nodes that we analyzed in the paper (that are all children of the “isocortex” node):

Motor = “somatomotor areas,” ID = 500

Somatosensory “somatosensory areas,” ID = 453

Parietal = “posterior parietal association areas,” ID = 315

Retrosplenial = “retrosplenial area” 254

Visual = “visual areas,” ID = 669

Task-related class assignment

Using deconvolved spike events smoothed with a Gaussian (s.d. = 50 ms), the mean trace was computed for each of the four trial types (go-left, go-middle, go-right, no go), for the 2.5 s interval beginning at odor onset. The mean trace was computed on a set of training trials, and then using a separate set of testing trials the squared-correlation was computed between the mean trace and each single-trial trace of the corresponding trial type. The mean correlation could be used as a proxy for the unique variance explained by each trial-type for each source. Five-fold cross-validation was used, and the overall correlation was computed as the mean of the correlation on each fold. We used a bootstrap shuffling procedure to determine the significance of the trial-type correlations for each source. Specifically, for each shuffle, a random set of 50 trials (the mean number of trials per trial type per session) was used to define a trial type, and the above five-fold cross validation procedure was performed. A total of 10,000 shuffles was run. For each source, the maximum correlation value across all shuffles was used as the threshold for determining significance (p < 0.05 with Bonferroni correction; across n = 4 mice, the fraction of sources that were assigned: 44% +/− 1.1%, mean ± s.d.). We then assigned each source with significant correlation to any of the trial types to one of 5 groups: lick-left selective, lick-middle selective, lick-right selective, “no go” selective, and lick-direction independent. Insignificant correlations were set to zero, and the correlation to each trial type was normalized by summed correlation to all trial types. Sources were assigned to a task-related class based on the relative strength of correlation to each trial type. A source was assigned to one of the selective groups if the normalized correlation to that trial type was above 0.6, and the maximum normalized correlation to any other trial type was below 0.3. A source was assigned to the ‘mixed’ group if the normalized correlation to at least three trial types was above 0.2. Sources that did not meet any of these criteria were not assigned to a class.

Spatial pattern analysis

To assess whether there was any regularity or clustering in the spatial distribution of sources within each task-class, we analyzed the spatial autocorrelation and compared it with a null distribution derived from random spatial distributions. We transformed the centroid of each source into units of mm based on the measured equivalent pixel size. Then for all sources assigned to each task-class, we computed the pairwise distance between each source and every other source. We then computed the empirical cumulative density function (CDF) of probability for each pairwise distance. To generate the null distribution, we used a shuffling procedure: the task-class labels were randomly permuted across sources, such that each task-class maintained the same total number of member sources, and the pairwise distance histogram was computed. This procedure was run for 10,000 shuffles. Using these shuffle distributions, we computed a p value for each value in the corresponding empirical CDF, based on the percentile of the measured value within the shuffle distributions. This p value was corrected for multiple comparisons using Benjamini-Hochberg FDR correction, across all values within a single session (i.e., across all trial types and discretized CDF values). Using these corrected p values, a threshold of 0.05 was used to determine whether a CDF value was significantly different from the null distribution.

We found that across five mice, each with five task classes, only 5/25 CDFs yielded any significant values, albeit with a small effect size. Furthermore, there was no consistency across mice in terms of which task class displayed significance. Our conclusion was thus that there was no consistent pattern in the spatial distribution of sources associated with each task class.

As a positive control, and to assess the sensitivity of this analysis, we simulated distributions of sources with known spatial structure. The same analysis was then applied to these simulated distributions to assess whether the structure was detectable using our shuffle-based procedure. The simulated distributions consisted of a random selection of 1/3 of the sources within a circle of specified diameter, in addition to the selection of 30 random sources distributed across the rest of the field of view. By varying the diameter, we generated simulated distributions with spatial features of different sizes. Our conclusion was that this procedure has a sensitivity to spatial features around 1mm diameter and above.

Detecting lick-off sources

Only trials where lick onset occurred 300 ms after odor onset were included. For each trial, for each source, mean activity was computed across pre- and post-lick-onset periods (each 2 s in duration). Separately for each trial type, we determined whether there was a significant decrease in activity across trials (one-sided t test, Bonferroni corrected across sources, p < 0.001). We then found sources that decreased on any “go” trial, but that did not decrease on “no go” trials. We allowed for the possibility that a source may decrease on just one trial type or on multiple trial types. The locations of these lick-off sources are plotted in the figure and showed no apparent spatial pattern or restriction that was consistent across mice. To summarize across mice, we computed the mean across trials and lick-off cells for each mouse. For visualization, we subtracted from each trace the mean activity during the first 300 ms of the baseline.

Single-trial versus trial-averaged correlations

Centroid locations were scaled to units of mm using the measured equivalent pixel size. Gaussian smoothed deconvolved spikes (s.d. = 50 ms) were used. The Spearman correlation coefficient was computed between all pairs of sources, using either the full, single-trial dataset consisting of concatenated trials from the entire session (thus excluding the variable-length part of the ITI), or using trial-averaged traces consisting of a concatenation of the average trace from each trial type (go 1, go 2, go 3, no go). The distance was also computed between each pair of sources. Each pair was only counted once. The absolute value of the correlation was used, to assess the magnitude of the correlation. Correlation magnitude values were binned based on the distance of the corresponding pair of sources, with a bin size of 100 μm. Source pairs within 150 μm of one another were excluded from the analysis. Within each bin, the mean and s.e.m. correlation values were computed. The resulting correlation versus distance curves were normalized by (i.e., divided by) the maximum value of the curve. A p value was computed for the mean correlation value at a distance of 1 mm, using a paired t test between the means for each mouse using either single-trial or trial-averaged correlations. For spatial plots related to a single seed source, the radius, colormap, and alpha value were set according to the correlation magnitude, normalized by the maximum non-self correlation value. For correlation versus distance plots related to a single seed, a bin size of 500 μm was used.

Decoding lick direction

To analyze the information represented by different subsets of neuronal sources on a single-trial basis, we used a decoding approach (Glaser et al., 2017). Specifically, we trained a classification algorithm to predict from the activity of a subset of sources whether the mouse was performing one of four actions: licking to spout #1, licking to spout #2, licking to spout #3, or not licking. The behavioral data were binned at a temporal resolution of 29.4 Hz, and prediction was performed based on the neural time points (also binned at 29.4 Hz) centered on the labeled behavioral time point. We use this centered time point because here we are explicitly not making any claims about predicting future action; rather, we are claiming that the ongoing behavior is represented by the neural activity (which may include delayed neural response to the sensory stimuli associated with the licking action). We used the unsmoothed deconvolved event output from CNMF-E as the neural data. We randomly assigned trials to training, cross-validation, and test sets with a ratio of 0.5:0.25:0.25. There were at least 180 trials per mouse, and a trial consisted of 200 time points, yielding a total of at least 36,000 data points split between the training, validation, and test sets. There were at least 1000 neuronal sources for each mouse, and 1 time point was used for each source, yielding at least 1000 parameters to be fit when decoding using all sources. We used a linear model with a softmax over 4 outputs and a categorical cross-entropy loss function, implemented using Keras. The Adam optimizer was used to train the parameters. During optimization, datapoints were weighted according to the inverse of the frequency of the corresponding class (i.e., because there are so many more “no lick” datapoints, each such data point was weighted in an accordingly decreased manner). We also investigated using more complicated networks with hidden layers as well as with nonlinear activation functions, however we found no appreciable increase in classification performance. This is potentially interesting because it either implies that information represented by the simultaneously recorded neurons can be characterized in a linear manner, or that we did not have enough data to adequately fit information stored in nonlinear interactions between neural activation states. To account for the noisiness of the neural signal and the relative paucity of training data, we regularized using cross-validation-based early stopping. Specifically, after each training epoch, the loss was computed on the cross-validation set. We then used the parameters that were set during the best epoch across 20 total epochs. Classification performance was evaluated using the test dataset, which the algorithm never saw during training. This whole process was repeated for 4 folds, such that each data point was used in a fold-test dataset once.

To account for the disparity in class sizes (there were many more datapoints where the mouse did not lick than when the mouse did lick to any of the spouts), we computed a normalized confusion matrix. Each row was normalized by the sum that row, or (True Positives + False Negatives). The diagonals of the normalized confusion matrix thus represented the True Positive Rate, (# True Positives / # Total Actual Positives).

The Receiver Operating Curve (ROC) was computed for each class in a one versus all manner, by varying the classification threshold and computing the corresponding True Positive Rate and False Positive Rate. This was performed for each class for each fold. The ROC curves were resampled such that they all had the same discretization of False Positive Rate, and then they were averaged together (this is the ‘macro’ average in the parlance of sklearn), yielding an overall ROC curve to summarize the classification for that session. Likewise, the area under the ROC curve (AUC) was computed for each fold and class, and then averaged together. We use this AUC as the measure for characterizing classification performance across different conditions.

When comparing the information contained in different subsets of neuronal sources, we took a number of steps to ensure that the comparisons were fair. First, we ordered all sources based on the extent to which they were capable of distinguishing between any of the behavioral conditions. Specifically, for each source there were around 36,000 time points of neural activity, and an associated label for each time point indicating whether the mouse was licking to spouts 1, 2, or 3 or not licking. For each source, we performed a Kruskal-Wallis H test to determine whether the distributions of neural activity during any of the four behavioral conditions were significantly different. We used the p value output from this test as a proxy for the ability of that source to distinguish the behavioral conditions. P values were adjusted for multiple comparisons using the Benjamini-Hochberg correction. Using these p values, we could rank all neuronal sources based on their ability to distinguish the behavior, as shown in Figures S7A and B. Importantly, though, for the comparisons in Figures 5D-5F, for each subset of sources included in each test condition we used the highest ranked sources, that is, the sources that contained the most decoding information according to the H test. Although not guaranteeing that we were using the best combination of sources for decoding, heuristically this approach ensures that we are not using an unfairly bad combination of sources.

Additionally, we ensured that even if different numbers of neuronal sources were included in each subset, the number of model parameters was exactly the same. To accomplish this, we performed PCA on the [sources x time] matrix and used the 75 dimensions that explained the most variance. This [75 x time] matrix was then passed into the decoding algorithm. Thus, there is no chance for the model to overfit for one subset simply based on the number of model parameters.

Decoding the preferred spout position from neural data

We used Partial Least-squares regression to simultaneously perform linear regression and dimensionality reduction (sklearn class cross_decomposition.PLSRegression, which implements the PLS2 algorithm). In contrast to the lick decoding analysis, here we used the denoised Ca²⁺ signal rather than the deconvolved spike trains. This smoother signal over time enhanced our ability to construct intelligible single-trial neural trajectories (see subsequent section “Computing low-dimensional trajectories…” for more details)—which was crucial as the same decoding model was used for both purposes. Our PLS models all used k = 4 components, which we found to be the minimum value that approximately maximized the normalized model prediction accuracy on held-out test data across all four experimental mice (as defined as the area under the ROC; see Figure S7D).

In a similar manner to the approach used in an earlier analysis, region specific analyses were performed using the 75 sources from each area with most discrimination ability for the preferred spout (in Figure 6E) or all sources from each area (in Figure 7). In order to avoid overfitting on analyses that used sources from all regions in Figure 6, we used a maximum of 500 sources for model training/evaluation, choosing first those with the lowest p values as for the region-specific analyses. The impact of using different numbers of sources can be seen in Figure S7E, using more than 500 sources appears to show reduced model prediction performance on held out test data. The preferred spout is defined as the one with the most licks in the interval of time between odor onset and reward onset.

To identify the preferred spout discrimination ability of each source, we performed a Kruskal-Wallis H-test that, for each source and time point, compared the source’s activity between trials where different spouts were active (in Figure S7F). Only time points where the maximum denoised Ca²⁺ across trials exceeded 0.1 were quantified here. In this way, sources were each assigned the lowest p value observed across all time points evaluated. All sources were then sorted by their p values such that the sources with lower p values were defined as having more discrimination ability.

We elected to use PLSRegression, a linear approach, instead of a more complex nonlinear algorithm because we wanted to fit the least complex model possible in order to aid interpretability and because a model with considerably more parameters would take more data to train. The fact that PLSRegression models simultaneously fit regression weights as well as identifying a related low-dimensional basis (that we could project single-trial neural activity into) greatly aided us in this with respect to interpretability.

Each model was fitted using 30 total training trials (10 for each active spout condition), out of the approximately 200 trials from each experimental session (meaning we used approximately 15% of each dataset for training). These 30 training trials were randomly selected from a list of all “go” trials where at least 80% of all licks on that trial at any time were toward the active spout. We also explicitly enforced that identity of the active spout matched the preferred spout on each training trial. The training data matrix ([frames * training trials] x sources) then consisted of all denoised Ca²⁺ signal time points from either the 75 sources with best discrimination ability in the region under analysis, or by using up to 500 sources for non-regional analyses. All frames on a given training trial were used for training. Trials that had licks during the “pre-odor period” were not excluded from training if they met the other requirements because training was always performed on all trial frames (including those with licks). However, these trials with pre-odor licks were always excluded when testing model performance. The target regressor vectors (([frames * training trials] x spouts) for each training trial comprised a binary indicator matrix denoting the active spout on each trial—which was constant across each frame within a trial.

Model evaluation was performed individually on all held-out trials, but specifically enforcing that all evaluated trials had zero licks during the “pre-odor period,” which was the final 2.2 s of the intertrial interval. Evaluation was specifically performed on the mean of all time points acquired from this interval of time (a vector of length equal to the number of sources). This resulted in a prediction vector of size 3 (the number of spouts). The reported prediction of the preferred spout was then defined as the spout with the highest numerical value in the prediction vector at the optimal classifier setpoint, argmax(predictions * [1-setpoint]), here the setpoint vector is three-dimensional and ‘*’ denotes element-wise multiplication. For computing model performance (AUC of the ROC), unthresholded predictions were used to compute ‘macro’ AUC values in an identical manner to that described in the previous section (“decoding lick direction”).

The only exception to the above training procedure is in Figures S8E-S8G, where models were trained and evaluated on different temporal epochs of data. Here, trials with a nonzero number of licks during the “pre-odor period” were excluded from both training and testing (versus just testing). When training on all frames from a trial (as in Figure 6 and 7), models were already exposed to licks later in every trial, so we did not remove those trials in order to leave more selective “go” trials available for training/testing.

We computed the optimal classifier setpoint by generating a ROC curve using both the true preferred spout and raw predictions on the training trials. We used this setpoint fit to training data on the held-out test data. The optimal setpoint was defined as the threshold that maximized the difference between the true positive rate and the false positive rate. The confusion matrix in Figure 6B was normalized using the same procedure as described in the “decoding lick direction” section earlier in the methods. In Figures 6D, 6E, S7G, and S7H 20 models were trained for each condition of each analysis. The resultant distributions of model performance were statistically compared to an equally large set of models trained on identical training data, but data where the active spout information was randomly permuted across trials. This permutation was done in two ways: either by randomly shuffling the correct spout labels or by circularly permuting the labels. The simple random shuffling procedure breaks the temporal autocorrelation structure of the task. Therefore, it could destroy long-timescale fluctuations resulting from making the same movement many times in a row that could persist over many seconds (and thus beyond trial boundaries).

To better control for this, and therefore more solidly test whether we are predicting upcoming actions versus simply decoding a neural state generated by repeated past actions, we used a much more conservative null model for comparison where, instead of shuffling, we circularly rotated the trial labels by a random shift of between 0 and the number of trials in the experiment. This manipulation perfectly preserves the temporal autocorrelation structure of the active spout identity over a session. However, because of the long block length, any rotations that are shorter than a block (15-20 trials) will overlap heavily with the true class labels—making this a harsher control. Statistics were therefore presented versus both the shuffle and this circular permutation control.

In Figure 6F, we interpolated between some adjacent points in the lines drawn using data from individual mice. This was done when there were gaps in the data at some trial indices that arose from excluding trials where there were a nonzero number of pre-odor licks. We performed the same analysis either using binning, or by including the currently excluded trials. In both cases, similarly statistically significant results were found.

To quantify the variance explained by a low-dimensional (k = 4) basis provided by PLS and PCA (Figure S7I), we used all sources from each area or the top 500 sources with most spout discrimination ability if pooling over all areas. Then we fit PLS and PCA models to data taken from all “go” trials where at least 80% of all licks were toward the active spout. Given the fitted PLS basis vectors, we computed the total explained variance as:

\frac{V a r (X \cdot W_{P L S})}{\sum V a r (X)}

where X is the mean centered neural data and W are the basis vectors from PLS (stored in the x_rotations_ variable in the PLSRegression model object). This value was computed for the PCA basis in a similar manner. All time points were used from each trial in this calculation.

Decoding the preferred spout position from high-speed video data

We used PLSRegression to predict the preferred spout from the pre-odor behavior of the animal measured using high-speed (200 Hz) videos taken from below the head and to the side of the body. First, we converted the movies to grayscale and computed their “motion energy” (Stringer et al., 2019) as the magnitude of the framewise difference in pixel intensities. Treating each motion energy movie as a centered data matrix $X \in R^{N \times M}$ where N is the number of pixels and M is the number of time points, we find the eigende-composition of the pixelwise covariance matrix C = M⁻¹XX^T = VΛV^T, yielding the left (spatial) eigenvectors of X and their associated eigenvalues. We then compute the right (temporal) eigenvectors as $U = Λ^{- \frac{1}{2}} V^{T} X$ , i.e., the motion energy principal components (PCs), and keep the top 1000 to use as features for prediction. We then apply the same PLS approach we used for neural decoding described above to predict the preferred spout from pre-odor motion energy PCs. To summarize each trial, we compute the average of each PC over the 2.17 s (434 frames) preceding odor onset, and train and test the PLS models on the identical sets of trials used for neural decoding, varying the number of PCs used for prediction. To assess the sufficiency of different orofacial components for decoding the active spout, we extracted data from 512-pixel regions of interest covering the nose, mouth, and whiskers and applied the same PCA+PLS decoding analysis on the top 250 PCs separately for each region.

Computing low-dimensional trajectories and analysis of condition type separability

To compute low-dimensional neural trajectories (as shown in Figure 7), we again used PLSRegression models that were trained using all time points from each training trial (as in Figure 6). But instead of predicting the preferred spout on each trial using only the “pre-odor” data, we instead projected every time point during each trial into the low dimensional basis found by PLSRegression. Parietal and retrosplenial areas had the fewest average sources across mice and also had lowest decoding performance (Figure 6E) and therefore were not analyzed individually here. Training data and testing trials were selected as described in the previous section for active spout decoding. For evaluation, all “go” trials with at least 80% of licks to the active spout, and zero pre-odor licks, were projected into the PLS basis in order to plot the dataset-averaged or single trial trajectories. These were defined as “correct go” trials. “Incorrect go” trials were defined as “go” trials where the fraction of licks to the active spout is 30% or worse. “No go” trials were subject no further requirements. “2^nd trials” simply consisted of all trials that were second in a block, discarding only those with pre-odor licks. For single region trajectories (e.g., visual only), all sources in the region selected were used, when pooling across areas, all available sources in each mouse were used.

To quantify the separation between the position of neural trajectories during the pre-odor period (as shown in Figure 7E and 7F), we first fit a PLS model to the area under analysis (in the same manner as was done to plot neural trajectories). Then, we projected each training trial into a 4-dimensional PLS basis (as described in the previous section of the methods) and computed the average position of each of these training trajectories during the pre-odor period. This defined a single point for each training trial (its “pre-odor position”). We grouped together these “pre-odor-positions” for all trials from each active spout type—defining a set of three means and covariances.

Then, for each testing trial, we computed its “pre-odor position,” “odor position,” and “reward position” and measured the Mahalanobis distance (in the full 4-dimensional space) between each point and the three different spout-specific clusters. Given these three distances between the test trial and each cluster (see cartoon in Figure 7D), we computed the statistic: “same distance” – “different distance.” Here the “same distance” is the distance between the trial and its homonymous cluster (e.g., if we are evaluating a Spout 2 trial, this is the distance between that trial and the Spout 2 cluster). The “different distance” is the distance between the trial and the closest of the other two clusters.

The “pre-odor position” was defined by averaging over the frames between trial onset and odor onset, the “odor position” averaged over frames between odor onset and reward onset, and the “reward position” averaged over a period following the reward of equal length to the odor-reward duration.

In Figure S7H the analysis was conducted in an identical manner to the analyses shown in Figure 6D and 6E, except decoding the active spout instead of the preferred spout. In addition, “incorrect go” trials were defined as those with less than 70% of total licks toward the active spout (instead of 30% or worse), and “correct go” trials were still defined as those with at least 70% of trials toward the active spout. We used a less conservative threshold for defining a trial as “incorrect” here (versus in Figure 6D and 6E) because data was required for all three active spout types to compute the AUC as we did previously.

The temporal consistency analysis (Figure S8E-S8G) was done by training 40 PLS models on sequential sets of data (each of 170 ms in duration). The key concern of this analysis was to determine how neural representations varied over time. Therefore, we used deconvolved spiking activity rather than denoised Ca²⁺ for only this PLS analysis. Training data was selected as previously described and used all available sources for decoding. But here model evaluation training was performed only on trials where the active spout identity matched the preferred spout identity (trials where this was not true were always removed from all training using PLS models). Ensuring that the preferred and active spouts always matched was done to avoid the chance that block-like structure was artifactually imposed when the mouse switched from licking one spout pre-reward to lick another post reward. The ‘macro’ AUC-ROC was reported here as in all other similar analyses.

ADDITIONAL RESOURCES

Further information about our study, as well as resources about how to use the COSMOS technique can be found at: http://clarityresourcecenter.com/.

Supplementary Material

Supplementary Video 1

Download video file^{(323.5KB, mp4)}

Supplementary Video 3

Download video file^{(1.4MB, mp4)}

Supplementary Video 4

Download video file^{(332.5KB, mp4)}

Supplementary Video 5

Download video file^{(270.1KB, mp4)}

Supplement

NIHMS1643850-supplement-Supplement.pdf^{(15.6MB, pdf)}

Supplementary Video 2

Download video file^{(13.2MB, mp4)}

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Chlorprothixene	Sigma-Aldrich	Cat# C1671-1G
Tamoxifen	Sigma-Aldrich	Cat# T5648
Corn oil	Acros Organics	Cat# AC405430025
Trimethoprim	Sigma-Aldrich	Cat# T7883-25G
DMSO	Sigma-Aldrich	Cat# 472301
Experimental Models: Organisms/Strains
Mouse: Tg(Thy1-GCaMP6s)GP4.3Dkim (Thy1-GCaMP6s)	The Jackson Laboratory	Jax Stock# 024275
Mouse: Cux2-CreERT2	Franco et al., 2012	N/A
Mouse: Ai148(TIT2L-GC6f-ICL-tTA2)-D (Ai148)	The Jackson Laboratory	Jax Stock# 030328
Mouse: VGat-ChR2-EYFP	The Jackson Laboratory	Jax Stock# 014548
Mouse: Rasgrf2-2A-dCre	The Jackson Laboratory	Jax Stock# 022864
Mouse: Ai93(TITL-GCaMP6f)-D;CaMK2a-tTA	The Jackson Laboratory	Jax Stock# 024108
Software and Algorithms
Image registration, signal extraction, and analysis tools for two-photon and one-photon imaging data.	This paper	http://github.com/deisseroth-lab/cosmos-tools
CNMF-E	Zhou et al., 2018	http://github.com/zhoupc/CNMF_E
IPython	Pérez and Granger, 2007	http://ipython.org
Numpy	Van Der Walt et al., 2011	http://numpy.org
Matplotlib	Hunter, 2007	http://matplotlib.org
Pandas	McKinney, 2010	http://pandas.pydata.org
Scikit-learn	Pedregosa et al., 2011	http://scikit-learn.org
SciPy	Oliphant, 2007	http://scipy.org
Seaborn	Waskom et al., 2017	http://seaborn.pydata.org
Statsmodels	Seabold and Perktold, 2010	http://statsmodels.org
Keras	Chollet, 2015	http://keras.io
PsychoPy	Peirce, 2007	http://psychopy.org
Micromanager	Edelstein et al., 2014	http://micro-manager.org
Fiji	Schindelin et al., 2012	http://imagej.net/Welcome

Open in a new tab

Highlights.

COSMOS enables fast, synchronous recording of cortex-spanning neural dynamics
Distributed neural activity throughout cortex encodes targeted actions
Unaveraged, but not trial-averaged, activity correlations show local structure
Population dynamics encode history-guided motor plans similarly between areas

ACKNOWLEDGMENTS

We would like to thank K. Merkle and T. Brand for custom machining, J. Marshel for visual assay assistance, S. Pak and C. Lee for administrative assistance, C. Ramakrishnan for molecular biology assistance, C. Raja and N. Pichamoorthy for animal husbandry and training assistance, S. Franco (UC Denver) for Cux2-CreER mice, and H. Zeng and J. Harris (Allen Institute for Brain Science) for Ai148 mice. We thank K. Shenoy, S. Druckman, and S. Ganguli for helpful conversations and for reading the manuscript. We thank S. Vesuna, E. Richman, A. Drinnenberg, M. Lovett-Barron, K. Ting, and members of the K.D. and G.W. laboratories for comments and advice. I.V.K. was supported by a National Science Foundation (NSF) Graduate Research Fellowship (grant DGE-114747). T.A.M. is an AP Giannini Fellow and was supported by a Stanford Dean’s Fellowship. G.W. is supported by an NSF CAREER Award (IIS 1553333), a Terman Faculty fellowship, a Sloan fellowship, DARPA, and a PE-CASE by the ARL (W911NF-19-1-0120). K.D. is supported by the DARPA Neuro-FAST program, NIMH, NIDA, NSF, the Simons Foundation, the Wiegers Family Fund, the Nancy and James Grosfeld Foundation, the H.L. Snyder Medical Foundation, and the Samuel and Betsy Reeves Fund.

Footnotes

SUPPLEMENTAL INFORMATION

Supplemental Information can be found online at https://doi.org/10.1016/j.neuron.2020.04.023.

DECLARATION OF INTERESTS

The authors have made all the designs and protocols for COSMOS freely available for nonprofit use; Stanford University is also submitting a patent application to further facilitate commercial translation.

REFERENCES

Abrahamsson S, Chen J, Hajj B, Stallinga S, Katsov AY, Wisniewski J, Mizuguchi G, Soule P, Mueller F, Dugast Darzacq C, et al. (2013). Fast multicolor 3D imaging using aberration-corrected multifocus microscopy. Nat. Methods 10, 60–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
Akrami A, Kopec CD, Diamond ME, and Brody CD (2018). Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 554, 368–372. [DOI] [PubMed] [Google Scholar]
Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Barthas F, and Kwan AC (2017). Secondary Motor Cortex: Where ‘Sensory’ Meets ‘Motor’ in the Rodent Frontal Cortex. Trends Neurosci. 40, 181–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bouchard MB, Voleti V, Mendes CS, Lacefield C, Grueber WB, Mann RS, Bruno RM, and Hillman EMC (2015). Swept confocally-aligned planar excitation (SCAPE) microscopy for high speed volumetric imaging of behaving organisms. Nat. Photonics 9, 113–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
Boughter JD Jr., Baird JP, Bryant J, St John SJ, and Heck D (2007). C57BL/6J and DBA/2J mice vary in lick rate and ingestive microstructure. Genes Brain Behav. 6, 619–627. [DOI] [PubMed] [Google Scholar]
Brady DJ, and Marks DL (2011). Coding for compressive focal tomography. Appl. Opt 50, 4436–4449. [DOI] [PubMed] [Google Scholar]
Campo AT, Martinez-Garcia M, Nácher V, Luna R, Romo R, and Deco G (2015). Task-driven intra- and interarea communications in primate cerebral cortex. Proc. Natl. Acad. Sci. U S A 112, 4761–4766. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chabrol FP, Blot A, and Mrsic-Flogel TD (2019). Cerebellar Contribution to Preparatory Activity in Motor Neocortex. Neuron 103, 506–519.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen T-W, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen JL, Margolis DJ, Stankov A, Sumanovski LT, Schneider BL, and Helmchen F (2015). Pathway-specific reorganization of projection neurons in somatosensory cortex during learning. Nat. Neurosci. 18, 1101–1108. [DOI] [PubMed] [Google Scholar]
Chollet F, et al. (2015). Keras (Keras). https://keras.io. [Google Scholar]
Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, and Shenoy KV (2012). Neural population dynamics during reaching. Nature 487, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cossairt O, Gupta M, and Nayar SK (2013). When does computational imaging improve performance? IEEE Trans. Image Process 22, 447–458. [DOI] [PubMed] [Google Scholar]
Daigle TL, Madisen L, Hage TA, Valley MT, Knoblich U, Larsen RS, Takeno MM, Huang L, Gu H, Larsen R, et al. (2018). A suite of transgenic driver and reporter mouse lines with enhanced brain-cell-type targeting and functionality. Cell 174, 465–480.e22. [DOI] [PMC free article] [PubMed] [Google Scholar]
Dolensek N, Gehrlach DA, Klein AS, and Gogolla N (2020). Facial expressions of emotion states and their neuronal correlates in mice. Science 368, 89–94. [DOI] [PubMed] [Google Scholar]
Dotson NM, Hoffman SJ, Goodell B, and Gray CM (2017). A Large-Scale Semi-Chronic Microdrive Recording System for Non-Human Primates. Neuron 96, 769–782.e2. [DOI] [PubMed] [Google Scholar]
Dowski ER Jr., and Cathey WT (1995). Extended depth of field through wave-front coding. Appl. Opt 34, 1859–1866. [DOI] [PubMed] [Google Scholar]
Dubbs A, Guevara J, and Yuste R (2016). moco: Fast motion correction for calcium imaging. Front. Neuroinform 10, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Economo MN, Viswanathan S, Tasic B, Bas E, Winnubst J, Menon V, Graybuck LT, Nguyen TN, Smith KA, Yao Z, et al. (2018). Distinct descending motor cortex pathways and their roles in movement. Nature 563, 79–84. [DOI] [PubMed] [Google Scholar]
Edelstein AD, Tsuchida MA, Amodaj N, Pinkard H, Vale RD, and Stuurman N (2014). Advanced methods of microscope control using μManager software. J. Biol. Methods 1, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
Feingold J, Desrochers TM, Fujii N, Harlan R, Tierney PL, Shimazu H, Amemori K, and Graybiel AM (2012). A system for recording neural activity chronically and simultaneously from multiple cortical and subcortical regions in nonhuman primates. J. Neurophysiol 107, 1979–1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ferezou I, Haiss F, Gentet LJ, Aronoff R, Weber B, and Petersen CCH (2007). Spatiotemporal dynamics of cortical sensorimotor integration in behaving mice. Neuron 56, 907–923. [DOI] [PubMed] [Google Scholar]
Franco SJ, Gil-Sanz C, Martinez-Garay I, Espinosa A, Harkins-Perry SR, Ramos C, and Müller U (2012). Fate-restricted neural progenitors in the mammalian cerebral cortex. Science 337, 746–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
Friston K (2018). Does predictive coding have a future? Nat. Neurosci 21, 1019–1021. [DOI] [PubMed] [Google Scholar]
Gallego JA, Perich MG, Chowdhury RH, Solla SA, and Miller LE (2020). Long-term stability of cortical population dynamics underlying consistent behavior. Nat. Neurosci 23, 260–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gao Z, Davis C, Thomas AM, Economo MN, Abrego AM, Svoboda K, De Zeeuw CI, and Li N (2018). A cortico-cerebellar loop for motor planning. Nature 563, 113–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
Garrett ME, Nauhaus I, Marshel JH, and Callaway EM (2014). Topography and areal organization of mouse visual cortex. J. Neurosci 34, 12587–12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
Georgopoulos AP (2015). Columnar organization of the motor cortex: direction of movement In Recent Advances on the Modular Organization of the Cortex, Casanova MF and Opris I, eds. (Springer Netherlands; ), pp. 127–141. [Google Scholar]
Gil-Sanz C, Espinosa A, Fregoso SP, Bluske KK, Cunningham CL, Martinez-Garay I, Zeng H, Franco SJ, and Müller U (2015). Lineage Tracing Using Cux2-Cre and Cux2-CreERT2 Mice. Neuron 86, 1091–1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gilad A, Gallero-Salas Y, Groos D, and Helmchen F (2018). Behavioral Strategy Determines Frontal or Posterior Location of Short-Term Memory in Neocortex. Neuron 99, 814–828.e7. [DOI] [PubMed] [Google Scholar]
Giovannucci A, Friedrich J, Kaufman M, Churchland A, Chklovskii D, Paninski L, and Pnevmatikakis EA (2017). OnACID: online analysis of calcium imaging data in real time In Advances in Neural Information Processing Systems 30, Guyon I, Luxburg UV, Bengio S, Wallach H, Fergus R, Vishwanathan S, and Garnett R, eds. (Neural Information Processing Systems; ), pp. 2381–2391. [Google Scholar]
Giovannucci A, Friedrich J, Gunn P, Kalfon J, Brown BL, Koay SA, Taxidis J, Najafi F, Gauthier JL, Zhou P, et al. (2019). CaImAn an open source tool for scalable calcium imaging data analysis. eLife 8, e38173. [DOI] [PMC free article] [PubMed] [Google Scholar]
Glaser JI, Chowdhury RH, Perich MG, Miller LE, and Kording KP (2017). Machine learning for neural decoding. arXiv, arXiv:1708.00909 https://arxiv.org/abs/1708.00909. [DOI] [PMC free article] [PubMed] [Google Scholar]
Guo ZV, Li N, Huber D, Ophir E, Gutnisky D, Ting JT, Feng G, and Svoboda K (2014). Flow of cortical activity underlying a tactile decision in mice. Neuron 81, 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
Guo ZV, Inagaki HK, Daie K, Druckmann S, Gerfen CR, and Svoboda K (2017). Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545, 181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
Han Y, Kebschull JM, Campbell RAA, Cowan D, Imhof F, Zador AM, and Mrsic-Flogel TD (2018). The logic of single-cell projections from visual cortex. Nature 556, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harris KD, Quiroga RQ, Freeman J, and Smith SL (2016). Improving data quality in neuronal population recordings. Nat. Neurosci 19, 1165–1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hasinoff SW, Kutulakos KN, Durand F, and Freeman WT (2009). Time-constrained photography. Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, (IEEE; ), 333–340. [Google Scholar]
Hattori R, Danskin B, Babic Z, Mlynaryk N, and Komiyama T (2019). Area-Specificity and Plasticity of History-Dependent Value Coding During Learning. Cell 177, 1858–1872.e15. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hernández A, Nácher V, Luna R, Alvarez M, Zainos A, Cordero S, Camarillo L, Vázquez Y, Lemus L, and Romo R (2008). Procedure for recording the simultaneous activity of single neurons distributed across cortical areas during sensory discrimination. Proc. Natl. Acad. Sci. USA 105, 16785–16790. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hernández A, Nácher V, Luna R, Zainos A, Lemus L, Alvarez M, Vázquez Y, Camarillo L, and Romo R (2010). Decoding a perceptual decision process across cortex. Neuron 66, 300–314. [DOI] [PubMed] [Google Scholar]
Hofer H, Carroll J, Neitz J, Neitz M, and Williams DR (2005). Organization of the human trichromatic cone mosaic. J. Neurosci 25, 9669–9679. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hubel DH, and Wiesel TN (1968). Receptive fields and functional architecture of monkey striate cortex. J. Physiol 195, 215–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hunt LT, and Hayden BY (2017). A distributed, hierarchical and recurrent framework for reward-based choice. Nat. Rev. Neurosci 18, 172–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hunter JD (2007). Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng 9, 90–95. [Google Scholar]
Juavinett AL, Nauhaus I, Garrett ME, Zhuang J, and Callaway EM (2017). Automated identification of mouse visual areas with intrinsic signal imaging. Nat. Protoc 12, 32–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
Katlowitz KA, Picardo MA, and Long MA (2018). Stable Sequential Activity Underlying the Maintenance of a Precisely Executed Skilled Behavior. Neuron 98, 1133–1140.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
Keller GB, and Mrsic-Flogel TD (2018). Predictive Processing: A Canonical Cortical Computation. Neuron 100, 424–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kim TH, Zhang Y, Lecoq J, Jung JC, Li J, Zeng H, Niell CM, and Schnitzer MJ (2016). Long-Term Optical Access to an Estimated One Million Neurons in the Live Mouse Cortex. Cell Rep. 17, 3385–3394. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kolb B, and Whishaw IQ (1988). Mass action and equipotentiality reconsidered In Brain Injury and Recovery, Finger JS, Levere TE, Almli CR, and Stein DG, eds. (Springer; ), pp. 103–116. [Google Scholar]
Komiyama T, Sato TR, O’Connor DH, Zhang Y-X, Huber D, Hooks BM, Gabitto M, and Svoboda K (2010). Learning-related fine-scale specificity imaged in motor cortex circuits of behaving mice. Nature 464, 1182–1186. [DOI] [PubMed] [Google Scholar]
Lecoq J, Savall J, Vučinić D, Grewe BF, Kim H, Li JZ, Kitch LJ, and Schnitzer MJ (2014). Visualizing mammalian brain area interactions by dualaxis two-photon calcium imaging. Nat. Neurosci 17, 1825–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lein ES, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, Boe AF, Boguski MS, Brockway KS, Byrnes EJ, et al. (2007). Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176. [DOI] [PubMed] [Google Scholar]
Lemus L, Hernández A, Luna R, Zainos A, Nácher V, and Romo R (2007). Neural correlates of a postponed decision report. Proc. Natl. Acad. Sci. U S A 104, 17174–17179. [DOI] [PMC free article] [PubMed] [Google Scholar]
Levin A, Hasinoff SW, Green P, Durand F, and Freeman WT (2009). 4D frequency analysis of computational cameras for depth of field extension. ACM Trans. Graph 28 (3), Article 97. [Google Scholar]
Levoy M, Ng R, Adams A, Footer M, and Horowitz M (2006). Light field microscopy. ACM Trans. Graph 25, 924–934. [Google Scholar]
Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
Liberti WA 3rd, Markowitz JE, Perkins LN, Liberti DC, Leman DP, Guitchounts G, Velho T, Kotton DN, Lois C, and Gardner TJ (2016). Unstable neurons underlie a stable learned behavior. Nat. Neurosci 19, 1665–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
Liu S, and Hua H (2011). Extended depth-of-field microscopic imaging with a variable focus microscope objective. Opt. Express 19, 353–362. [DOI] [PubMed] [Google Scholar]
Madisen L, Zwingman TA, Sunkin SM, Oh SW, Zariwala HA, Gu H, Ng LL, Palmiter RD, Hawrylycz MJ, Jones AR, et al. (2010). A robust and high-throughput Cre reporting and characterization system for the whole mouse brain. Nat. Neurosci 13, 133–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
Makino H, Ren C, Liu H, Kim AN, Kondapaneni N, Liu X, Kuzum D, and Komiyama T (2017). Transformation of Cortex-wide Emergent Properties during Motor Learning. Neuron 94, 880–890.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mante V, Sussillo D, Shenoy KV, and Newsome WT (2013). Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
Marshel JH, Garrett ME, Nauhaus I, and Callaway EM (2011). Functional specialization of seven mouse visual cortical areas. Neuron 72, 1040–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mayrhofer JM, El-Boustani S, Foustoukos G, Auffret M, Tamura K, and Petersen CCH (2019). Distinct Contributions of Whisker Sensory Cortex and Tongue-Jaw Motor Cortex in a Goal-Directed Sensorimotor Transformation. Neuron 103, 1034–1043.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
McKinney W (2010). Data structures for statistical computing in Python In Proceedings of the Ninth Python in Science Conference (SciPy 2010), van der Walt S and Millman J, eds. (SciPy; ), pp. 51–66. [Google Scholar]
Mizuseki K, Diba K, Pastalkova E, and Buzsáki G (2011). Hippocampal CA1 pyramidal cells form functionally distinct sublayers. Nat. Neurosci 14, 1174–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mohajerani MH, Chan AW, Mohsenvand M, LeDue J, Liu R, McVea DA, Boyd JD, Wang YT, Reimers M, and Murphy TH (2013). Spontaneous cortical activity alternates between motifs defined by regional axonal projections. Nat. Neurosci 16, 1426–1435. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mountcastle VB (1997). The columnar organization of the neocortex. Brain 120, 701–722. [DOI] [PubMed] [Google Scholar]
Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nat. Neurosci 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nauhaus I, and Ringach DL (2007). Precise alignment of micromachined electrode arrays with V1 functional maps. J. Neurophysiol 97, 3781–3789. [DOI] [PubMed] [Google Scholar]
Niell CM, and Stryker MP (2008). Highly selective receptive fields in mouse visual cortex. J. Neurosci 28, 7520–7536. [DOI] [PMC free article] [PubMed] [Google Scholar]
Nöbauer T, Skocek O, Pernía-Andrade AJ, Weilguny L, Traub FM, Molodtsov MI, and Vaziri A (2017). Video rate volumetric Ca²⁺ imaging across cortex using seeded iterative demixing (SID) microscopy. Nat. Methods 14, 811–818. [DOI] [PubMed] [Google Scholar]
Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, et al. (2014). A mesoscale connectome of the mouse brain. Nature 508, 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ohki K, Chung S, Ch’ng YH, Kara P, and Reid RC (2005). Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature 433, 597–603. [DOI] [PubMed] [Google Scholar]
Oliphant TE (2007). Python for Scientific Computing. Comput. Sci. Eng 9, 10–20. [Google Scholar]
Pak N, Siegle JH, Kinney JP, Denman DJ, Blanche TJ, and Boyden ES (2015). Closed-loop, ultraprecise, automated craniotomies. J. Neurophysiol 113, 3943–3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. (2011). Scikit-learn: Machine learning in Python. J. Mach. Learn. Res 12, 2825–2830. [Google Scholar]
Peirce JW (2007). PsychoPy–Psychophysics software in Python. J. Neurosci. Methods 162, 8–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pérez F, and Granger BE (2007). IPython: A system for interactive scientific computing. Comput. Sci. Eng 9, 21–29. [Google Scholar]
Pinto L, Rajan K, DePasquale B, Thiberge SY, Tank DW, and Brody CD (2019). Task-Dependent Changes in the Large-Scale Dynamics and Necessity of Cortical Regions. Neuron 104, 810–824.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W, et al. (2016). Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron 89, 285–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ponce-Alvarez A, Nácher V, Luna R, Riehle A, and Romo R (2012). Dynamics of cortical neuronal ensembles transit from decision making to storage for later report. J. Neurosci 32, 11956–11969. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rigotti M, Barak O, Warden MR, Wang XJ, Daw ND, Miller EK, and Fusi S (2013). The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rumyantsev OI, Lecoq JA, Hernandez O, Zhang Y, Savall J, Chrapkiewicz R, Li J, Zeng H, Ganguli S, and Schnitzer MJ (2020). Fundamental bounds on the fidelity of sensory cortical coding. Nature 580, 100–105. [DOI] [PubMed] [Google Scholar]
Safaie M, Jurado-Parras M-T, Sarno S, Louis J, Karoutchi C, Petit LF, Pasquet MO, Eloy C, and Robbe D (2019). The Embodied Nature of Well-Timed Behavior. bioRxiv. 10.1101/716274. [DOI] [Google Scholar]
Sauerbrei BA, Guo J-Z, Cohen JD, Mischiati M, Guo W, Kabra M, Verma N, Mensh B, Branson K, and Hantman AW (2020). Cortical pattern generation during dexterous movement is input-driven. Nature 577, 386–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
Saxena S, and Cunningham JP (2019). Towards the neural population doctrine. Curr. Opin. Neurobiol 55, 103–111. [DOI] [PubMed] [Google Scholar]
Schechner YY, Nayar SK, and Belhumeur PN (2007). Multiplexing for optimal lighting. IEEE Trans. Pattern Anal. Mach. Intell 29, 1339–1354. [DOI] [PubMed] [Google Scholar]
Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schneider DM, Nelson A, and Mooney R (2014). A synaptic and circuit basis for corollary discharge in the auditory cortex. Nature 513, 189–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
Scott BB, Thiberge SY, Guo C, Tervo DGR, Brody CD, Karpova AY, and Tank DW (2018). Imaging Cortical Dynamics in GCaMP Transgenic Rats with a Head-Mounted Widefield Macroscope. Neuron 100, 1045–1058.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Seabold S, and Perktold J (2010). Statsmodels: Econometric and statistical modeling with Python In Proceedings of the Ninth Python in Science Conference (SciPy 2010), van der Walt S and Millman J, eds. (SciPy; ), pp. 92–96. [Google Scholar]
Shadlen MN, and Newsome WT (1996). Motion perception: seeing and deciding. Proc. Natl. Acad. Sci. USA 93, 628–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
Siegel M, Buschman TJ, and Miller EK (2015). Cortical information flow during flexible sensorimotor decisions. Science 348, 1352–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sofroniew NJ, Flickinger D, King J, and Svoboda K (2016). A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging. eLife 5, e14472. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sreenivasan V, Esmaeili V, Kiritani T, Galan K, Crochet S, and Petersen CCH (2016). Movement Initiation Signals in Mouse Whisker Motor Cortex. Neuron 92, 1368–1382. [DOI] [PMC free article] [PubMed] [Google Scholar]
Steinmetz NA, Buetfering C, Lecoq J, Lee CR, Peters AJ, Jacobs EAK, Coen P, Ollerenshaw DR, Valley MT, de Vries SEJ, et al. (2017). Aberrant Cortical Activity in Multiple GCaMP6-Expressing Transgenic Mouse Lines. eNeuro 4, ENEURO.0207–17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Steinmetz NA, Zatka-Haas P, Carandini M, and Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stirman JN, Smith IT, Kudenov MW, and Smith SL (2016). Wide field-of-view, multi-region, two-photon imaging of neuronal activity in the mammalian brain. Nat. Biotechnol 34, 857–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255. [DOI] [PMC free article] [PubMed] [Google Scholar]
Theis L, Berens P, Froudarakis E, Reimer J, Román Rosón M, Baden T, Euler T, Tolias AS, and Bethge M (2016). Benchmarking Spike Rate Inference in Population Calcium Imaging. Neuron 90, 471–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
Trautmann EM, Stavisky SD, Lahiri S, Ames KC, Kaufman MT, O’Shea DJ, Vyas S, Sun X, Ryu SI, Ganguli S, and Shenoy KV (2019). Accurate estimation of neural population dynamics without spike sorting. Neuron 103, 292–308.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tsai PS, Mateo C, Field JJ, Schaffer CB, Anderson ME, and Kleinfeld D (2015). Ultra-large field-of-view two-photon microscopy. Opt. Express 23, 13833–13847. [DOI] [PMC free article] [PubMed] [Google Scholar]
Van Der Walt S, Colbert SC, and Varoquaux G (2011). The NumPy array: a structure for efficient numerical computation. Comput. Sci. Eng 13, 22–30. [Google Scholar]
Vickery TJ, Chun MM, and Lee D (2011). Ubiquity and specificity of reinforcement signals throughout the human brain. Neuron 72, 166–177. [DOI] [PubMed] [Google Scholar]
Wang Y-J, Shen X, Lin Y-H, and Javidi B (2015). Extended depth-of-field 3D endoscopy with synthetic aperture integral imaging using an electrically tunable focal-length liquid-crystal lens. Opt. Lett 40, 3564–3567. [DOI] [PubMed] [Google Scholar]
Waskom M, Botvinnik O, O’Kane D, Hobson P, Lukauskas S, Gemperline DC, Augspurger T, Halchenko Y, Cole JB, Warmenhoven J, et al. (2017). mwaskom/seaborn: v0.8.1. (Zenodo; ). [Google Scholar]
Weisenburger S, and Vaziri A (2018). A Guide to Emerging Technologies for Large-Scale and Whole-Brain Optical Imaging of Neuronal Activity. Annu. Rev. Neurosci 41, 431–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wekselblatt JB, Flister ED, Piscopo DM, and Niell CM (2016). Large-scale imaging of cortical dynamics during sensory perception and behavior. J. Neurophysiol 115, 2852–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wetzstein G, Ihrke I, and Heidrich W (2013). On plenoptic multiplexing and reconstruction. Int. J. Comput. Vis 101, 384–400. [Google Scholar]
Yamawaki N, Radulovic J, and Shepherd GMG (2016). A corticocortical circuit directly links retrosplenial cortex to M2 in the mouse. J. Neurosci 36, 9365–9374. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yuste R (2015). From the neuron doctrine to neural networks. Nat. Rev. Neurosci 16, 487–497. [DOI] [PubMed] [Google Scholar]
Zhou P, Resendez SL, Rodriguez-Romaguera J, Jimenez JC, Neufeld SQ, Giovannucci A, Friedrich J, Pnevmatikakis EA, Stuber GD, Hen R, et al. (2018). Efficient and accurate extraction of in vivo calcium signals from microendoscopic video data. eLife 7, e28728. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zhuang J, Ng L, Williams D, Valley M, Li Y, Garrett M, and Waters J (2017). An extended retinotopic map of mouse cortex. eLife 6, e18372. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zingg B, Hintiryan H, Gou L, Song MY, Bay M, Bienkowski MS, Foster NN, Yamashita S, Bowman I, Toga AW, and Dong HW (2014). Neural networks of the mouse neocortex. Cell 156, 1096–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ziv Y, Burns LD, Cocker ED, Hamel EO, Ghosh KK, Kitch LJ, El Gamal A, and Schnitzer MJ (2013). Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci 16, 264–266. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Video 1

Download video file^{(323.5KB, mp4)}

Supplementary Video 3

Download video file^{(1.4MB, mp4)}

Supplementary Video 4

Download video file^{(332.5KB, mp4)}

Supplementary Video 5

Download video file^{(270.1KB, mp4)}

Supplement

NIHMS1643850-supplement-Supplement.pdf^{(15.6MB, pdf)}

Supplementary Video 2

Download video file^{(13.2MB, mp4)}

Data Availability Statement

[R1] Abrahamsson S, Chen J, Hajj B, Stallinga S, Katsov AY, Wisniewski J, Mizuguchi G, Soule P, Mueller F, Dugast Darzacq C, et al. (2013). Fast multicolor 3D imaging using aberration-corrected multifocus microscopy. Nat. Methods 10, 60–63. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] Akrami A, Kopec CD, Diamond ME, and Brody CD (2018). Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 554, 368–372. [DOI] [PubMed] [Google Scholar]

[R3] Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] Barthas F, and Kwan AC (2017). Secondary Motor Cortex: Where ‘Sensory’ Meets ‘Motor’ in the Rodent Frontal Cortex. Trends Neurosci. 40, 181–193. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Bouchard MB, Voleti V, Mendes CS, Lacefield C, Grueber WB, Mann RS, Bruno RM, and Hillman EMC (2015). Swept confocally-aligned planar excitation (SCAPE) microscopy for high speed volumetric imaging of behaving organisms. Nat. Photonics 9, 113–119. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] Boughter JD Jr., Baird JP, Bryant J, St John SJ, and Heck D (2007). C57BL/6J and DBA/2J mice vary in lick rate and ingestive microstructure. Genes Brain Behav. 6, 619–627. [DOI] [PubMed] [Google Scholar]

[R7] Brady DJ, and Marks DL (2011). Coding for compressive focal tomography. Appl. Opt 50, 4436–4449. [DOI] [PubMed] [Google Scholar]

[R8] Campo AT, Martinez-Garcia M, Nácher V, Luna R, Romo R, and Deco G (2015). Task-driven intra- and interarea communications in primate cerebral cortex. Proc. Natl. Acad. Sci. U S A 112, 4761–4766. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] Chabrol FP, Blot A, and Mrsic-Flogel TD (2019). Cerebellar Contribution to Preparatory Activity in Motor Neocortex. Neuron 103, 506–519.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] Chen T-W, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, et al. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] Chen JL, Margolis DJ, Stankov A, Sumanovski LT, Schneider BL, and Helmchen F (2015). Pathway-specific reorganization of projection neurons in somatosensory cortex during learning. Nat. Neurosci. 18, 1101–1108. [DOI] [PubMed] [Google Scholar]

[R12] Chollet F, et al. (2015). Keras (Keras). https://keras.io. [Google Scholar]

[R13] Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, and Shenoy KV (2012). Neural population dynamics during reaching. Nature 487, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] Cossairt O, Gupta M, and Nayar SK (2013). When does computational imaging improve performance? IEEE Trans. Image Process 22, 447–458. [DOI] [PubMed] [Google Scholar]

[R15] Daigle TL, Madisen L, Hage TA, Valley MT, Knoblich U, Larsen RS, Takeno MM, Huang L, Gu H, Larsen R, et al. (2018). A suite of transgenic driver and reporter mouse lines with enhanced brain-cell-type targeting and functionality. Cell 174, 465–480.e22. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] Dolensek N, Gehrlach DA, Klein AS, and Gogolla N (2020). Facial expressions of emotion states and their neuronal correlates in mice. Science 368, 89–94. [DOI] [PubMed] [Google Scholar]

[R17] Dotson NM, Hoffman SJ, Goodell B, and Gray CM (2017). A Large-Scale Semi-Chronic Microdrive Recording System for Non-Human Primates. Neuron 96, 769–782.e2. [DOI] [PubMed] [Google Scholar]

[R18] Dowski ER Jr., and Cathey WT (1995). Extended depth of field through wave-front coding. Appl. Opt 34, 1859–1866. [DOI] [PubMed] [Google Scholar]

[R19] Dubbs A, Guevara J, and Yuste R (2016). moco: Fast motion correction for calcium imaging. Front. Neuroinform 10, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Economo MN, Viswanathan S, Tasic B, Bas E, Winnubst J, Menon V, Graybuck LT, Nguyen TN, Smith KA, Yao Z, et al. (2018). Distinct descending motor cortex pathways and their roles in movement. Nature 563, 79–84. [DOI] [PubMed] [Google Scholar]

[R21] Edelstein AD, Tsuchida MA, Amodaj N, Pinkard H, Vale RD, and Stuurman N (2014). Advanced methods of microscope control using μManager software. J. Biol. Methods 1, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] Feingold J, Desrochers TM, Fujii N, Harlan R, Tierney PL, Shimazu H, Amemori K, and Graybiel AM (2012). A system for recording neural activity chronically and simultaneously from multiple cortical and subcortical regions in nonhuman primates. J. Neurophysiol 107, 1979–1995. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] Ferezou I, Haiss F, Gentet LJ, Aronoff R, Weber B, and Petersen CCH (2007). Spatiotemporal dynamics of cortical sensorimotor integration in behaving mice. Neuron 56, 907–923. [DOI] [PubMed] [Google Scholar]

[R24] Franco SJ, Gil-Sanz C, Martinez-Garay I, Espinosa A, Harkins-Perry SR, Ramos C, and Müller U (2012). Fate-restricted neural progenitors in the mammalian cerebral cortex. Science 337, 746–749. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] Friston K (2018). Does predictive coding have a future? Nat. Neurosci 21, 1019–1021. [DOI] [PubMed] [Google Scholar]

[R26] Gallego JA, Perich MG, Chowdhury RH, Solla SA, and Miller LE (2020). Long-term stability of cortical population dynamics underlying consistent behavior. Nat. Neurosci 23, 260–270. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Gao Z, Davis C, Thomas AM, Economo MN, Abrego AM, Svoboda K, De Zeeuw CI, and Li N (2018). A cortico-cerebellar loop for motor planning. Nature 563, 113–116. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Garrett ME, Nauhaus I, Marshel JH, and Callaway EM (2014). Topography and areal organization of mouse visual cortex. J. Neurosci 34, 12587–12600. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Georgopoulos AP (2015). Columnar organization of the motor cortex: direction of movement In Recent Advances on the Modular Organization of the Cortex, Casanova MF and Opris I, eds. (Springer Netherlands; ), pp. 127–141. [Google Scholar]

[R30] Gil-Sanz C, Espinosa A, Fregoso SP, Bluske KK, Cunningham CL, Martinez-Garay I, Zeng H, Franco SJ, and Müller U (2015). Lineage Tracing Using Cux2-Cre and Cux2-CreERT2 Mice. Neuron 86, 1091–1099. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Gilad A, Gallero-Salas Y, Groos D, and Helmchen F (2018). Behavioral Strategy Determines Frontal or Posterior Location of Short-Term Memory in Neocortex. Neuron 99, 814–828.e7. [DOI] [PubMed] [Google Scholar]

[R32] Giovannucci A, Friedrich J, Kaufman M, Churchland A, Chklovskii D, Paninski L, and Pnevmatikakis EA (2017). OnACID: online analysis of calcium imaging data in real time In Advances in Neural Information Processing Systems 30, Guyon I, Luxburg UV, Bengio S, Wallach H, Fergus R, Vishwanathan S, and Garnett R, eds. (Neural Information Processing Systems; ), pp. 2381–2391. [Google Scholar]

[R33] Giovannucci A, Friedrich J, Gunn P, Kalfon J, Brown BL, Koay SA, Taxidis J, Najafi F, Gauthier JL, Zhou P, et al. (2019). CaImAn an open source tool for scalable calcium imaging data analysis. eLife 8, e38173. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Glaser JI, Chowdhury RH, Perich MG, Miller LE, and Kording KP (2017). Machine learning for neural decoding. arXiv, arXiv:1708.00909 https://arxiv.org/abs/1708.00909. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] Guo ZV, Li N, Huber D, Ophir E, Gutnisky D, Ting JT, Feng G, and Svoboda K (2014). Flow of cortical activity underlying a tactile decision in mice. Neuron 81, 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] Guo ZV, Inagaki HK, Daie K, Druckmann S, Gerfen CR, and Svoboda K (2017). Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545, 181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] Han Y, Kebschull JM, Campbell RAA, Cowan D, Imhof F, Zador AM, and Mrsic-Flogel TD (2018). The logic of single-cell projections from visual cortex. Nature 556, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Harris KD, Quiroga RQ, Freeman J, and Smith SL (2016). Improving data quality in neuronal population recordings. Nat. Neurosci 19, 1165–1174. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Hasinoff SW, Kutulakos KN, Durand F, and Freeman WT (2009). Time-constrained photography. Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, (IEEE; ), 333–340. [Google Scholar]

[R41] Hattori R, Danskin B, Babic Z, Mlynaryk N, and Komiyama T (2019). Area-Specificity and Plasticity of History-Dependent Value Coding During Learning. Cell 177, 1858–1872.e15. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Hernández A, Nácher V, Luna R, Alvarez M, Zainos A, Cordero S, Camarillo L, Vázquez Y, Lemus L, and Romo R (2008). Procedure for recording the simultaneous activity of single neurons distributed across cortical areas during sensory discrimination. Proc. Natl. Acad. Sci. USA 105, 16785–16790. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Hernández A, Nácher V, Luna R, Zainos A, Lemus L, Alvarez M, Vázquez Y, Camarillo L, and Romo R (2010). Decoding a perceptual decision process across cortex. Neuron 66, 300–314. [DOI] [PubMed] [Google Scholar]

[R44] Hofer H, Carroll J, Neitz J, Neitz M, and Williams DR (2005). Organization of the human trichromatic cone mosaic. J. Neurosci 25, 9669–9679. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R45] Hubel DH, and Wiesel TN (1968). Receptive fields and functional architecture of monkey striate cortex. J. Physiol 195, 215–243. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Hunt LT, and Hayden BY (2017). A distributed, hierarchical and recurrent framework for reward-based choice. Nat. Rev. Neurosci 18, 172–182. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] Hunter JD (2007). Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng 9, 90–95. [Google Scholar]

[R48] Juavinett AL, Nauhaus I, Garrett ME, Zhuang J, and Callaway EM (2017). Automated identification of mouse visual areas with intrinsic signal imaging. Nat. Protoc 12, 32–43. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Katlowitz KA, Picardo MA, and Long MA (2018). Stable Sequential Activity Underlying the Maintenance of a Precisely Executed Skilled Behavior. Neuron 98, 1133–1140.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Keller GB, and Mrsic-Flogel TD (2018). Predictive Processing: A Canonical Cortical Computation. Neuron 100, 424–435. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] Kim TH, Zhang Y, Lecoq J, Jung JC, Li J, Zeng H, Niell CM, and Schnitzer MJ (2016). Long-Term Optical Access to an Estimated One Million Neurons in the Live Mouse Cortex. Cell Rep. 17, 3385–3394. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R52] Kolb B, and Whishaw IQ (1988). Mass action and equipotentiality reconsidered In Brain Injury and Recovery, Finger JS, Levere TE, Almli CR, and Stein DG, eds. (Springer; ), pp. 103–116. [Google Scholar]

[R53] Komiyama T, Sato TR, O’Connor DH, Zhang Y-X, Huber D, Hooks BM, Gabitto M, and Svoboda K (2010). Learning-related fine-scale specificity imaged in motor cortex circuits of behaving mice. Nature 464, 1182–1186. [DOI] [PubMed] [Google Scholar]

[R54] Lecoq J, Savall J, Vučinić D, Grewe BF, Kim H, Li JZ, Kitch LJ, and Schnitzer MJ (2014). Visualizing mammalian brain area interactions by dualaxis two-photon calcium imaging. Nat. Neurosci 17, 1825–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Lein ES, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, Boe AF, Boguski MS, Brockway KS, Byrnes EJ, et al. (2007). Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176. [DOI] [PubMed] [Google Scholar]

[R56] Lemus L, Hernández A, Luna R, Zainos A, Nácher V, and Romo R (2007). Neural correlates of a postponed decision report. Proc. Natl. Acad. Sci. U S A 104, 17174–17179. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] Levin A, Hasinoff SW, Green P, Durand F, and Freeman WT (2009). 4D frequency analysis of computational cameras for depth of field extension. ACM Trans. Graph 28 (3), Article 97. [Google Scholar]

[R58] Levoy M, Ng R, Adams A, Footer M, and Horowitz M (2006). Light field microscopy. ACM Trans. Graph 25, 924–934. [Google Scholar]

[R59] Li N, Daie K, Svoboda K, and Druckmann S (2016). Robust neuronal dynamics in premotor cortex during motor planning. Nature 532, 459–464. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] Liberti WA 3rd, Markowitz JE, Perkins LN, Liberti DC, Leman DP, Guitchounts G, Velho T, Kotton DN, Lois C, and Gardner TJ (2016). Unstable neurons underlie a stable learned behavior. Nat. Neurosci 19, 1665–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] Liu S, and Hua H (2011). Extended depth-of-field microscopic imaging with a variable focus microscope objective. Opt. Express 19, 353–362. [DOI] [PubMed] [Google Scholar]

[R62] Madisen L, Zwingman TA, Sunkin SM, Oh SW, Zariwala HA, Gu H, Ng LL, Palmiter RD, Hawrylycz MJ, Jones AR, et al. (2010). A robust and high-throughput Cre reporting and characterization system for the whole mouse brain. Nat. Neurosci 13, 133–140. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] Makino H, Ren C, Liu H, Kim AN, Kondapaneni N, Liu X, Kuzum D, and Komiyama T (2017). Transformation of Cortex-wide Emergent Properties during Motor Learning. Neuron 94, 880–890.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] Mante V, Sussillo D, Shenoy KV, and Newsome WT (2013). Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Marshel JH, Garrett ME, Nauhaus I, and Callaway EM (2011). Functional specialization of seven mouse visual cortical areas. Neuron 72, 1040–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] Mayrhofer JM, El-Boustani S, Foustoukos G, Auffret M, Tamura K, and Petersen CCH (2019). Distinct Contributions of Whisker Sensory Cortex and Tongue-Jaw Motor Cortex in a Goal-Directed Sensorimotor Transformation. Neuron 103, 1034–1043.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] McKinney W (2010). Data structures for statistical computing in Python In Proceedings of the Ninth Python in Science Conference (SciPy 2010), van der Walt S and Millman J, eds. (SciPy; ), pp. 51–66. [Google Scholar]

[R68] Mizuseki K, Diba K, Pastalkova E, and Buzsáki G (2011). Hippocampal CA1 pyramidal cells form functionally distinct sublayers. Nat. Neurosci 14, 1174–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] Mohajerani MH, Chan AW, Mohsenvand M, LeDue J, Liu R, McVea DA, Boyd JD, Wang YT, Reimers M, and Murphy TH (2013). Spontaneous cortical activity alternates between motifs defined by regional axonal projections. Nat. Neurosci 16, 1426–1435. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R70] Mountcastle VB (1997). The columnar organization of the neocortex. Brain 120, 701–722. [DOI] [PubMed] [Google Scholar]

[R71] Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nat. Neurosci 22, 1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] Nauhaus I, and Ringach DL (2007). Precise alignment of micromachined electrode arrays with V1 functional maps. J. Neurophysiol 97, 3781–3789. [DOI] [PubMed] [Google Scholar]

[R73] Niell CM, and Stryker MP (2008). Highly selective receptive fields in mouse visual cortex. J. Neurosci 28, 7520–7536. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Nöbauer T, Skocek O, Pernía-Andrade AJ, Weilguny L, Traub FM, Molodtsov MI, and Vaziri A (2017). Video rate volumetric Ca²⁺ imaging across cortex using seeded iterative demixing (SID) microscopy. Nat. Methods 14, 811–818. [DOI] [PubMed] [Google Scholar]

[R75] Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, et al. (2014). A mesoscale connectome of the mouse brain. Nature 508, 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] Ohki K, Chung S, Ch’ng YH, Kara P, and Reid RC (2005). Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature 433, 597–603. [DOI] [PubMed] [Google Scholar]

[R77] Oliphant TE (2007). Python for Scientific Computing. Comput. Sci. Eng 9, 10–20. [Google Scholar]

[R78] Pak N, Siegle JH, Kinney JP, Denman DJ, Blanche TJ, and Boyden ES (2015). Closed-loop, ultraprecise, automated craniotomies. J. Neurophysiol 113, 3943–3953. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R79] Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. (2011). Scikit-learn: Machine learning in Python. J. Mach. Learn. Res 12, 2825–2830. [Google Scholar]

[R80] Peirce JW (2007). PsychoPy–Psychophysics software in Python. J. Neurosci. Methods 162, 8–13. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] Pérez F, and Granger BE (2007). IPython: A system for interactive scientific computing. Comput. Sci. Eng 9, 21–29. [Google Scholar]

[R82] Pinto L, Rajan K, DePasquale B, Thiberge SY, Tank DW, and Brody CD (2019). Task-Dependent Changes in the Large-Scale Dynamics and Necessity of Cortical Regions. Neuron 104, 810–824.e9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R83] Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W, et al. (2016). Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron 89, 285–299. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R84] Ponce-Alvarez A, Nácher V, Luna R, Riehle A, and Romo R (2012). Dynamics of cortical neuronal ensembles transit from decision making to storage for later report. J. Neurosci 32, 11956–11969. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R85] Rigotti M, Barak O, Warden MR, Wang XJ, Daw ND, Miller EK, and Fusi S (2013). The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R86] Rumyantsev OI, Lecoq JA, Hernandez O, Zhang Y, Savall J, Chrapkiewicz R, Li J, Zeng H, Ganguli S, and Schnitzer MJ (2020). Fundamental bounds on the fidelity of sensory cortical coding. Nature 580, 100–105. [DOI] [PubMed] [Google Scholar]

[R87] Safaie M, Jurado-Parras M-T, Sarno S, Louis J, Karoutchi C, Petit LF, Pasquet MO, Eloy C, and Robbe D (2019). The Embodied Nature of Well-Timed Behavior. bioRxiv. 10.1101/716274. [DOI] [Google Scholar]

[R88] Sauerbrei BA, Guo J-Z, Cohen JD, Mischiati M, Guo W, Kabra M, Verma N, Mensh B, Branson K, and Hantman AW (2020). Cortical pattern generation during dexterous movement is input-driven. Nature 577, 386–391. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R89] Saxena S, and Cunningham JP (2019). Towards the neural population doctrine. Curr. Opin. Neurobiol 55, 103–111. [DOI] [PubMed] [Google Scholar]

[R90] Schechner YY, Nayar SK, and Belhumeur PN (2007). Multiplexing for optimal lighting. IEEE Trans. Pattern Anal. Mach. Intell 29, 1339–1354. [DOI] [PubMed] [Google Scholar]

[R91] Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R92] Schneider DM, Nelson A, and Mooney R (2014). A synaptic and circuit basis for corollary discharge in the auditory cortex. Nature 513, 189–194. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R93] Scott BB, Thiberge SY, Guo C, Tervo DGR, Brody CD, Karpova AY, and Tank DW (2018). Imaging Cortical Dynamics in GCaMP Transgenic Rats with a Head-Mounted Widefield Macroscope. Neuron 100, 1045–1058.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R94] Seabold S, and Perktold J (2010). Statsmodels: Econometric and statistical modeling with Python In Proceedings of the Ninth Python in Science Conference (SciPy 2010), van der Walt S and Millman J, eds. (SciPy; ), pp. 92–96. [Google Scholar]

[R95] Shadlen MN, and Newsome WT (1996). Motion perception: seeing and deciding. Proc. Natl. Acad. Sci. USA 93, 628–633. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R96] Siegel M, Buschman TJ, and Miller EK (2015). Cortical information flow during flexible sensorimotor decisions. Science 348, 1352–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R97] Sofroniew NJ, Flickinger D, King J, and Svoboda K (2016). A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging. eLife 5, e14472. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R98] Sreenivasan V, Esmaeili V, Kiritani T, Galan K, Crochet S, and Petersen CCH (2016). Movement Initiation Signals in Mouse Whisker Motor Cortex. Neuron 92, 1368–1382. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R99] Steinmetz NA, Buetfering C, Lecoq J, Lee CR, Peters AJ, Jacobs EAK, Coen P, Ollerenshaw DR, Valley MT, de Vries SEJ, et al. (2017). Aberrant Cortical Activity in Multiple GCaMP6-Expressing Transgenic Mouse Lines. eNeuro 4, ENEURO.0207–17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R100] Steinmetz NA, Zatka-Haas P, Carandini M, and Harris KD (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R101] Stirman JN, Smith IT, Kudenov MW, and Smith SL (2016). Wide field-of-view, multi-region, two-photon imaging of neuronal activity in the mammalian brain. Nat. Biotechnol 34, 857–862. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R102] Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R103] Theis L, Berens P, Froudarakis E, Reimer J, Román Rosón M, Baden T, Euler T, Tolias AS, and Bethge M (2016). Benchmarking Spike Rate Inference in Population Calcium Imaging. Neuron 90, 471–482. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R104] Trautmann EM, Stavisky SD, Lahiri S, Ames KC, Kaufman MT, O’Shea DJ, Vyas S, Sun X, Ryu SI, Ganguli S, and Shenoy KV (2019). Accurate estimation of neural population dynamics without spike sorting. Neuron 103, 292–308.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R105] Tsai PS, Mateo C, Field JJ, Schaffer CB, Anderson ME, and Kleinfeld D (2015). Ultra-large field-of-view two-photon microscopy. Opt. Express 23, 13833–13847. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R106] Van Der Walt S, Colbert SC, and Varoquaux G (2011). The NumPy array: a structure for efficient numerical computation. Comput. Sci. Eng 13, 22–30. [Google Scholar]

[R107] Vickery TJ, Chun MM, and Lee D (2011). Ubiquity and specificity of reinforcement signals throughout the human brain. Neuron 72, 166–177. [DOI] [PubMed] [Google Scholar]

[R108] Wang Y-J, Shen X, Lin Y-H, and Javidi B (2015). Extended depth-of-field 3D endoscopy with synthetic aperture integral imaging using an electrically tunable focal-length liquid-crystal lens. Opt. Lett 40, 3564–3567. [DOI] [PubMed] [Google Scholar]

[R109] Waskom M, Botvinnik O, O’Kane D, Hobson P, Lukauskas S, Gemperline DC, Augspurger T, Halchenko Y, Cole JB, Warmenhoven J, et al. (2017). mwaskom/seaborn: v0.8.1. (Zenodo; ). [Google Scholar]

[R110] Weisenburger S, and Vaziri A (2018). A Guide to Emerging Technologies for Large-Scale and Whole-Brain Optical Imaging of Neuronal Activity. Annu. Rev. Neurosci 41, 431–452. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R111] Wekselblatt JB, Flister ED, Piscopo DM, and Niell CM (2016). Large-scale imaging of cortical dynamics during sensory perception and behavior. J. Neurophysiol 115, 2852–2866. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R112] Wetzstein G, Ihrke I, and Heidrich W (2013). On plenoptic multiplexing and reconstruction. Int. J. Comput. Vis 101, 384–400. [Google Scholar]

[R113] Yamawaki N, Radulovic J, and Shepherd GMG (2016). A corticocortical circuit directly links retrosplenial cortex to M2 in the mouse. J. Neurosci 36, 9365–9374. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R114] Yuste R (2015). From the neuron doctrine to neural networks. Nat. Rev. Neurosci 16, 487–497. [DOI] [PubMed] [Google Scholar]

[R115] Zhou P, Resendez SL, Rodriguez-Romaguera J, Jimenez JC, Neufeld SQ, Giovannucci A, Friedrich J, Pnevmatikakis EA, Stuber GD, Hen R, et al. (2018). Efficient and accurate extraction of in vivo calcium signals from microendoscopic video data. eLife 7, e28728. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R116] Zhuang J, Ng L, Williams D, Valley M, Li Y, Garrett M, and Waters J (2017). An extended retinotopic map of mouse cortex. eLife 6, e18372. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R117] Zingg B, Hintiryan H, Gou L, Song MY, Bay M, Bienkowski MS, Foster NN, Yamashita S, Bowman I, Toga AW, and Dong HW (2014). Neural networks of the mouse neocortex. Cell 156, 1096–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R118] Ziv Y, Burns LD, Cocker ED, Hamel EO, Ghosh KK, Kitch LJ, El Gamal A, and Schnitzer MJ (2013). Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci 16, 264–266. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Cortical Observation by Synchronous Multifocal Optical Sampling Reveals Widespread Population Encoding of Actions

Isaac V Kauvar

Timothy A Machado

Elle Yuen

John Kochalka

Minseung Choi

William E Allen

Gordon Wetzstein

Karl Deisseroth

SUMMARY

In Brief

INTRODUCTION

RESULTS

A Multifocal Macroscope for Imaging the Curved Cortical Surface with High Signal-to-Noise Ratio

Figure 1. COSMOS Enables Recovery of High SNR Neural Sources across the Curved Surface of Dorsal Cortex.

Characterization of Extracted Neuronal Sources Using a Visual Stimulus Assay

Figure 2. Characterization of COSMOS Sources Using Visual Stimuli.

Cortex-wide Recording during a Head-Fixed Lick-to-Target Task

Figure 3. Behavioral and Neural Correlates of Specific Targeted Motor Actions.

Correlations of Unaveraged Activity Exhibit Localized Spatial Structure

Figure 4. Unaveraged Data Exhibit More Localized Correlation Structure Than Trial-Averaged Data.

Single-Trial Representations of Distinct Motor Actions Are Distributed across Cortex

Figure 5. Representations of Distinct Motor Actions Are Distributed across Dorsal Cortex.

History-Guided Motor Plans Are Encoded by Neuronal Populations across Cortex

Figure 6. The Direction of Future Licks Is Encoded by Neurons Distributed across the Dorsal Cortex.

Distinct Patterns of Population Neural Activity Encode Different Motor Plans and Actions

Figure 7. Population Neural Activity Encodes Upcoming Lick Bouts toward Specific Spouts.

DISCUSSION

Distributed Cortical Computation

Imaging Large-Scale Population Dynamics

STAR★METHODS

RESOURCE AVAILABLILITY

Lead Contact

Materials Availability

Data and Software Availability

EXPERIMENTAL MODEL AND SUBJECT DETAILS

METHOD DETAILS

Optical implementation details

Neuronal source extraction pipeline

Comparison of COSMOS with conventional macroscope

Intrinsic imaging for atlas alignment

Visual orientation selectivity assay

Comparison of COSMOS with two-photon imaging

Robotic surgery protocol

Animal behavior hardware

Animal behavioral training

Histology and Tissue Imaging

Multi-region optogenetic inhibition

Optical design principles

Noise analysis full derivation

Simulation details

Defocus Blur

Light throughput

Overall SNR

QUANTIFICATION AND STATISTICAL ANALYSIS

Open source packages used

Statistical analysis

Orientation selectivity analysis

Source mixing model

Region specific analyses

Task-related class assignment

Spatial pattern analysis

Detecting lick-off sources

Single-trial versus trial-averaged correlations

Decoding lick direction

Decoding the preferred spout position from neural data

Decoding the preferred spout position from high-speed video data

Computing low-dimensional trajectories and analysis of condition type separability

ADDITIONAL RESOURCES

Supplementary Material

Highlights.

ACKNOWLEDGMENTS

Footnotes

REFERENCES

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK