Abstract
We report a cross-talk free simultaneous three-wavelength digital holographic microscopy setup for spectroscopic imaging of biological cells during flow. The feasibility of the proposed measurement technique is demonstrated on erythrocytes, due to their unique morphology and dependency of hemoglobin (Hb) molecule absorption on wavelength. From the spectroscopic quantitative phase profiles of cells acquired during flow in a microfluidic device, we decoupled the refractive index and the physical thickness. We then used our quantitative phase imaging results to dynamically calculate the mean cell volume (MCV), mean corpuscular Hb concentration (MCHC), mean corpuscular Hb content (MCH) and sphericity index.
1. Introduction
Flow cytometry has made significant progress during the past two decades. Biological staining can be used to obtain imaging capabilities during flow cytometry [1,2]. Staining, however, might change the cell physiology in the long run, specifically if multiple staining cycles are needed [3]. For conventional imaging flow cytometry, where the cells are imaged during flow, the resulting image is two-dimensional in nature, thus volumetric measurement of individual cells based on staining alone might have large calculation errors [4]. Interferometric phase microscopy (IPM), also called digital holographic microscopy or quantitative phase microscopy, is an imaging modality that utilizes the inherent characteristics of the interaction of electrical fields with transparent cells to accurately measure various biological parameters, such as dry mass and volume in live cells without the need for staining [5–8]. IPM records an interference of the light passing through the sample with a reference beam in order to measure the delay of light due to its interaction with the biological cell that is associated with its different refractive index (RI) in comparison to the surrounding watery medium. From a single-exposure off-axis interference pattern, one can reconstruct the optical path difference (OPD) map, which is the product of the cell RI map and physical thickness map. One of the problems in IPM lies in the coupling of these two parameters. While the OPD can be a valid indicator for certain cellular parameters, as long as the RI and the cell thickness are not decoupled, it is difficult to measure actual physical properties of the cell, such as the mean cell volume (MCV), which is frequently used to characterize erythrocytes, or red blood cells (RBCs).
There have been numerous attempts to decouple the RI and the thickness of cellular OPD maps. A recent paper [9] has categorized the decoupling techniques into three groups. The straightforward approach is to evaluate the physical thickness of cells by either approximating the cell shape to a sphere or ellipsoid, which is not applicable for RBCs, or by direct measurement by other thickness measurement methods, such as atomic force microscopy [10,11] or confocal fluorescent microscopy [12,13], which is not applicable for cell during fast flow [4,14]. Another solution is using tomographic phase microscopy (TPM) [15–18], where objects must be imaged from various viewing angles. These interferometric projections images are then processed into the cellular 3D RI and thickness distributions. However, due to the need for multiple measurements in preliminary known viewing angles and the associated computation burden, this approach is less suitable for rapidly measuring cells during flow in case that only the cell thickness is eventually required. The third approach for RI-thickness decoupling relates to solving two equations for two unknown variables. For example, to obtain the two equations, one can acquire the same cells in two surrounding mediums with two RI [13,19,20]. This approach is not suitable for cells during flow since during medium change, the cell must be stationary. A more suitable imaging approach makes use of two separate wavelengths in case that the RI of the cell or the surrounding medium is dispersive [21–23], but this approach cannot be considered as completely label-free, since it still changes the surrounding medium properties.
In multi-wavelength holography, two wavelengths or more illuminate the sample either consecutively or simultaneously, to calculate its spectral phase data. This multi-wavelength holographic imaging can be used to create a synthetic wavelength that allows imaging thicker samples by optical phase unwrapping [24–28]. Alternatively, the spectroscopic information can be used for decoupling of thickness and RI in quantitative phase imaging of biological cells. In this case, imaging the sample by two wavelengths may be sufficient for simple samples with known dispersion or dispersive medium. For RBCs, two wavelengths may not be enough and multi-wavelength illumination can be applied, without using dispersive medium. Jang et al. [8,29] have shown that the RI of RBCs cytoplasm depends on the concentration of hemoglobin (Hb), its known RI increment and the average RI of other molecules in the cell [30,31]. Thus, together with the cell physical thickness, there are three unknown variables, and thus, it requires the use of three wavelengths for solving a non-linear equation system.
Interferometric imaging of RBCS with simultaneous acquisition of three wavelengths was previously demonstrated in [8] by using three color channels of a color Bayer camera. However, cross-talk between the camera wavelength channels limits the applicable light sources and might affect the accuracy of the results. Recently, our group introduced simultaneous three wavelength IPM, capable of cross-talk free imaging of samples, which was used to obtain the three wavelength quantitative phase unwrapping metrological samples, which are thicker than is possible with a single wavelength [27].
The current manuscript presents an improved, cross-talk-free simultaneous three wavelength IPM system and adapts it, for the first time, for obtaining quantitative imaging spectroscopy during imaging flow cytometry. Based on this parallel quantitative imaging capability, we performed various volumetric measurements of RBCs during flow.
2. Methods
2.1. Optical setup
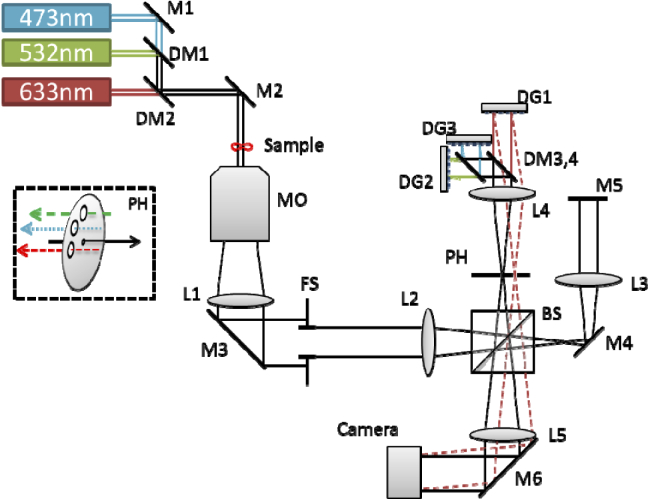
The optical design of the system used for dynamic spectroscopy of RBCs is based on our optical system used for three wavelength phase unwrapping [27], with several modifications, including using reflective diffraction gratings. As shown in Fig. 1, three separate light sources are combined by dichroic mirrors (DM) to illuminate the sample: a 473 nm laser diode (LD) (LaserGlow, LRS-0473-FPM-00050-03), a 532 diode-pumped solid state (DPSS) laser (Thorlabs, CPS532), and a 633 nm Helium-Neon (HeNe) laser (Thorlabs, HNL050L). The LD and DPSS lasers are combined by DM1 (Semrock, R488-Di02), after which both beams are combined with light originated from the HeNe laser, by DM2 (Semrock, FF593-Di03). The illumination of the sample is therefore coaxial and simultaneous in all three wavelengths. Since the LD light sources have a relatively short coherence length of hundreds of microns, the area of interference upon the sensor is too narrow due to loss of mutual coherence across the interfering beams. We therefore use, for the first time in this approach, diffraction gratings (DGs) to create the off-axis angles, as they tilt the propagation of the light but not its wavefront, enabling a uniform interference pattern across a larger field of view (FOV) [32,33].
Fig. 1.
Imaging system scheme for improved 3wl off-axis holography. M1-6: dielectric mirrors. DM1-4: dichroic mirrors. MO: microscope objective. L1-5: achromatic lenses. BS: beam splitter, FS: field stop, PH: pinhole with additional holes drilled for the back-reflecting beams. DG1-3: diffraction gratings. Back-reflected beams from DG2, DG3 are not drawn, for simplicity. The inset at the left shows a perspective view of the PH plate, spatially filtering the incoming beam (black), and allowing back-reflected light of the three wavelengths channels.
The sample plane is imaged by an apochromatic microscope objective (MO) and tube lens L1 to the image plane, where under ordinary microscopy conditions the camera sensor would be located. The image plane, set by field stop FS to avoid stray-light, is imaged through our three wavelength module on the camera sensor. In this module, beam splitter (BS) splits the beam into sample and reference arms. The sample arm consists of two consecutive 4f lens configurations (L2-L3, followed by L3-L5) for relay imaging upon the camera of all three wavelengths simultaneously. In the sample arm, the light is reflected from mirror M5, and is combined with the reference arm by the BS. In the reference arm, the pinhole plate PH is located at the Fourier plane of L2, filtering spatial data of the sample and essentially creating the reference for all three wavelengths, externally to the microscope. Lens L4 is positioned at the backend of the PH, forming the first 4f configuration for the reference arm. The reference beams are then split by a dichroic mirror DM3 (Semrock, FF593-Di03), where both shorter wavelengths are reflected to a dichroic mirror DM4 (Semrock, R488-Di02), after which each wavelength is separated. Reflective diffraction gratings DG1, DG2, and DG3 (Thorlabs, GR25-0305) are located at focal distances from L4 in order to keep the 4f lens configuration, similarly to the sample arm. These diffraction gratings are positioned at the image plane, each of them rotated at a different angle. Consequently, each diffraction grating reflects the light of its respective wavelength at a different solid angle. Lens L4 then focuses the wavelengths at three different regions on PH, as shown in Fig. 1 inset, elaborating the PH settings. One pinhole is used for low-pass spatial filtering of the beam and creating a reference beam for all three wavelengths on the coming on-axis beams. The periphery of the PH plate is cut to enable the three off-axis back-reflected reference beams to go back and recombine with the sample beams at BS, where lens L5 projects all three pairs of beams on the monochrome camera sensor (IDS, UI-3880CP-M0GL). Each wavelength creates an off-axis interference pattern on the camera sensor plane with respect to the relative angle between the sample and the reference beams. Therefore, three multiplexed interference patterns appear on the monochrome camera sensor at once, and can be acquired in a single camera exposure. These three wavelength channels are separable on the spatial frequency domain, as explained later, allowing reconstruction of the full three wavefronts, acquired simultaneously.
2.2. Three-wavelength quantitative phase profiles extraction
As mentioned above, an off-axis interference pattern is formed upon the sensor by each of the wavelengths. Each interference pattern holds information about the quantitative phase of light interacting with the sample at that wavelength. The interference of each wavelength on the sensor can be described as:
| (1) |
where Es and Er are the sample and reference electric fields, respectively, Δϕ is the phase difference, x defines the interference pattern axis, k = 2π / λ is the wavenumber, and α is the relative angle (on the respective x-axis) between the sample and reference waves. The OPD can be calculated by dividing Δϕ by k, where Δϕ is extracted separately for each wavelength, per pixel [34]. The three wavelength multiplexed hologram is shown in Fig. 2(a). The extraction of Δϕ is executed by first Fourier transforming the digital hologram of Eq. (1), filtering the corresponding cross-correlation terms, inverse Fourier transforming, followed by phase unwrapping to avoid possible 2π ambiguities [35], as shown in Fig. 2(b). Note that the off-axis angles between the three pairs of interfering beams, each pair in a different wavelength, have been chosen such that the cross-correlation terms will not overlap in the spatial frequency domain, as shown in Fig. 2(b).
Fig. 2.
(a) Raw off-axis digital hologram of RBC during flow, containing three wavelength channels, acquired in a single monochrome camera shot. (b) The spatial frequency spectrum of the multiplexed hologram shown in (a), with three pairs of separable cross-correlation terms, containing the complex wavefronts of the cells at the three wavelengths. The chosen term at each wavelength is marked by color dash-line ellipse. (c)-(e) The reconstructed OPD maps at 473 nm (c), 532 nm (d) and 633 nm (e).
Therefore, the full reconstruction of the corresponding quantitative phase maps at the three wavelength channels is possible. Such phase maps of all three wavelength channels are shown in Figs. 2(c)–2(e). The phase can be written as Δϕ = k·h·Δn, or the product of the known wavenumber, the unknowns physical thickness h and the RI difference of the cell and its surroundings Δn. We used an apochromatic microscope objective to avoid chromatic aberrations. In addition, slight corrections of wave propagation can be done on each channel after initial system calibration, as proposed by Ferraro et al. [25].
2.3. Volumetric cytometry
In the case of RBCs, Δn is a function of λ, Hb concentration C, and the RI of other cytoplasmic molecules nX, which can be described by the following equation [8,30,31]:
| (2) |
where β is a constant calibrated from prior knowledge in literature [30]. In order to solve this equation, which has three unknowns, C, nX and h, we use the optical system described earlier that supports simultaneous phase acquisition by three wavelengths. Since the unknowns are coupled to each other and form a set of nonlinear equations, an optimization process is needed [8]. The physical thickness of the RBCs is then decoupled from the RI, and a true thickness map of the cell can be processed. Shortly, since the proteins within each RBC are homogenous, their concentration should be uniform across the cell area. Therefore, in order to solve the non-linear Eq. (2) for three wavelengths, it is considered as an optimization problem, where the standard deviation of C and nX should be minimized, with the following constraints:
| (3) |
The volume and Hb concentration of each cell is then derived, enabling the calculation of advanced erythrocytic measures. First, cell volume is calculated by integrating its thickness. Cell surface area (SA) is then measured by calculating a three-dimensional mesh surface and its area, similarly to the calculation suggested by Mir et al. [6]:
| (4) |
where SAC is the calculated mesh surface area, P is the perimeter and hP is the mean optical thickness at the perimeter. Once the cellular SA is calculated, the sphericity of the erythrocyte can also be derived, as follows [36]:
| (5) |
where V is the volume of the cell. The sphericity measure is crucial since it gives an indication for the ability of the RBCs to deform and squeeze through thin capillaries [36]. Finally, the MCHC is calculated by averaging C per cell, and MCH derived by integration. Abnormal values of MCH and MCHC may indicate on various medical conditions such as anemia.
3. Results
As a proof-of-concept demonstration of our high-throughput capabilities, a cytometric flow setup was introduced to the system. RBC sample was extracted from a human donor, followed by dilution in PBS at a rate of 1:250. The diluted blood was inserted into a syringe connected to a microfluidic channel (Ibidi, µ-Slide VI 0.1), the center of which placed at the sample plane of the imaging system. Pressure applied to the syringe piston was used in order to control the flow of cells through the channel and across the imaging FOV. The actual exposure time per frame was 0.98 ms and the effective point spread function of the imaging system was 0.56 µm, corresponding to a maximal possible flow velocity of 0.57 mm/s, to avoid smearing of cells during flow. A total of 101 cells were singled out from the data for validation of the imaging technique. For each cell, the OPD map was extracted for each wavelength separately and the cellular parameters of the cells were then calculated. Equations (2) and (3) were solved by MATLAB conventional interior-point nonlinear optimization. Statistical data is then calculated for all 101 cells to dynamically extract MCV, sphericity, MCHC and MCH values.
Visualization 1 (22.2MB, mp4) shows the dynamic cell flow in the multiplexed off-axis hologram and the three extracted dynamic quantitative phase maps at the three wavelength channels. Additionally, the calculated thickness maps of the three recently analyzed cells are shown at the bottom, and are updated dynamically. It should be noted that within the framework of this proof-of-concept study, only discocytes were chosen. However, the method can be applied to any shape of erythrocyte.
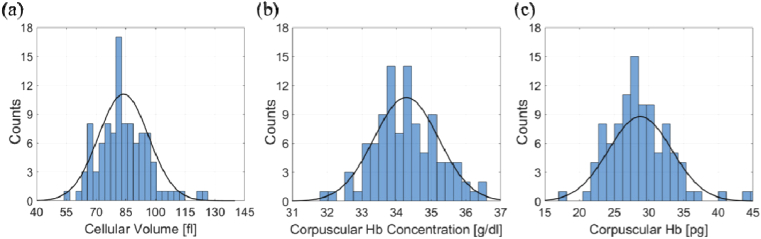
The MCV of all 101 cells was 83.8 ± 12.6 fl, which is closely within the healthy physiological range of 80-94fl [37]. The measured values of MCHC and MCH were 34.3 ± 0.90 g/dl and 28.8 ± 4.5 pg, respectively, both of which are closely within conventional normal range of 32-36 g/dl and 27-31 pg, respectively [37]. MCV, MCH and MCHC histograms are shown in Fig. 3. Solid black graphs are the data fits to normal distributions.
Fig. 3.
Dynamically measured cytological values for RBCs during flow cytometry. (a) Volume. (b) Hb concentration. (c) Hb contents. Bars represent histogram counts and solid black graph indicates the fit to normal distribution.
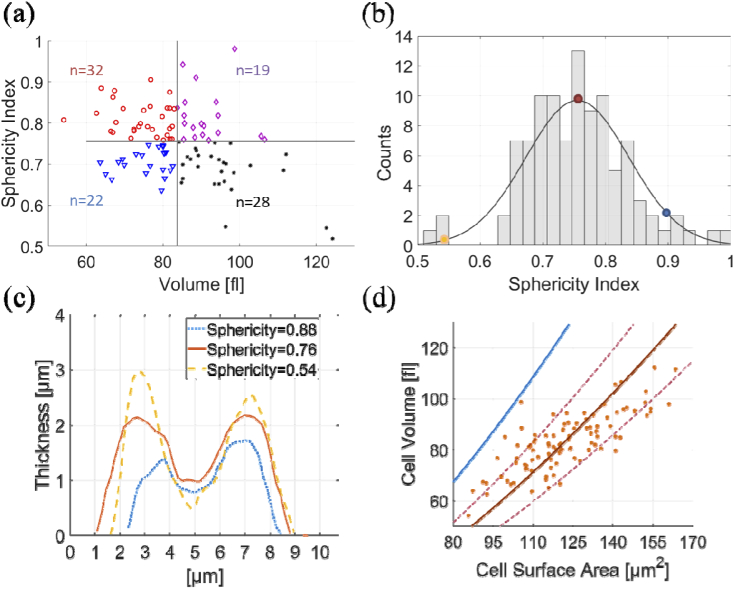
Volume histogram and MCV values are dynamically updated on the left bottom corner of Visualization 1 (22.2MB, mp4) , where each cell analyzed adds its value to the histogram. SA and sphericity measures were 124.4 ± 23.4 µm2 and 0.76 ± 0.08, respectively. Sphericity index is further analyzed in Fig. 4. The correlation between the sphericity and cellular volume illustrated in Fig. 4(a) shows that cells with greater volume tend to have a smaller sphericity index and their surface have larger gradients, limiting the cell ability to squeeze through narrow blood vessels. This can also be seen from Figs. 4(b) and 4(c), where cross-sections of three cells with distinctive sphericity values are drawn. This is with agreement to previous studies [6,36], but here we perform it dynamically on flowing cells using our three wavelength system. The correlation between the volume of the cells and their respective surface areas is shown in Fig. 4(d). The crimson solid and dashed lines depict this correlation according to Eq. (5), with mean sphericity index of 0.76 ± 0.08. The solid blue line marks the correlation of a perfect sphere volume and surface area, as reference.
Fig. 4.
Erythocytic sphericity analysis of 101 dynamically flowing cells. (a) Correlation of sphericity measure and cellular volume, quadrated by mean values. The number of cells is indicated per quadrant. (b) Sphericity measure histogram. Gray bars represent histogram values. Solid black line represents Gaussian fit. (c) Cross-sections of three instances of the individual cells indicated by orange, red and blue dots in (b). (d) Correlation of cellular volume and surface area with mean theoretical value and standard deviation boundaries marked by crimson solid and dashed lines, respectively. Solid blue line marks the correlation of a perfect sphere volume and surface area.
4. Discussion and summary
The study presented here describes dynamic quantitative cellular imaging using cross-talk free three wavelength off-axis holography, allowing dynamic acquisition of various measures of cells during flow based on their spectroscopic quantitative phase maps. In contrast to the Bayer-mosaic camera used in previous work [8], we used a monochrome sensor with spatial multiplexing of holograms, which is cross-talk free spectrally and superior in terms of field of view and resolution. Our system also provides wavelengths selection flexibility regardless of the digital camera. We used 473 nm, 532 nm and 633 nm partially coherent sources, but with a different selection of dichroic mirrors, the lasers can be easily replaced to match a different set of wavelengths as necessary. The introduction of diffraction gratings also allows for an improvement in design flexibility, as even spectrally-broader illumination sources may be chosen, allowing off-axis interferences on the entire camera sensor area. Moreover, the proposed imaging system is not limited to three wavelengths, as, in contrast to Ref. [8], the modular design enables more wavelength channels to be inserted by adding a pair of dichroic mirrors and grating, where up to six channels can be multiplexed using the same principle without loss of spatial bandwidth [38,39].
As demonstrated in this feasibility study, the presented system is capable of imaging dynamically flowing RBCs, with velocities over 0.5 mm/s and a FOV width of ∼200 µm. The transition from stationary to dynamic holographic imaging in multi-wavelength holography holds a great value for label-free imaging flow cytometry, as it enables processing a high number of cells [40–42], but it can also be used to increase the throughput for imaging stationary cells. This work demonstrated a proof-of-concept for 101 cells in imaging flow cytometry. However, the throughput can be further increased in the future by using faster flow rate and faster sensors, without changing the proposed optical module basic design, potentially reaching hundreds or thousands of cells per second. If the processing is still needed in real-time, stronger parallel computing capabilities are needed, such as using the computer graphic processing unit (GPU).
The simultaneous acquisition of data with three wavelengths increases the robustness of cytological analyses, where they can now be based on three independent measurements of the same sample, supporting each other for better assessment of these parameters. It should be noted that while MCV, MCHC, MCH and sphericity index are indeed valuable cellular parameters, we have only used them to demonstrate the immediate advantages of the system for blood analysis. However, there are numerous more applications for cytometry that can benefit from the proposed spectroscopic holography approach, including cancer diagnosis and monitoring [14]. Furthermore, another rising field where the spectroscopic IPM is expected to be very useful for is the incorporation of artificial intelligence (AI) for label-free classification of cells [42,43], where the simultaneous spectroscopic acquisition of IPM data can be translated into robust multi-layered neural networks performing the classification. In this case, various quantitative spectroscopic features can be extracted for the rapidly flowing cells, increasing classification success and the overall performance of such techniques.
Typographical corrections were made to Eq. (1), the caption of Fig. 3, and the funding section.
Funding
H2020 European Research Council10.13039/100010663 (ERC) (678316).
Disclosures
NTS and NAT: Tel Aviv University (P).
References
- 1.Givan A. L., “Principles of flow cytometry: an overview,” Methods Cell Biol. 63, 19–50 (2001). 10.1016/S0091-679X(01)63006-1 [DOI] [PubMed] [Google Scholar]
- 2.Watanabe M., Uehara Y., Yamashita N., Fujimura Y., Nishio K., Sawada T., Takeda K., Koizumi F., Koh Y., “Multicolor detection of rare tumor cells in blood using a novel flow cytometry-based system,” Cytometry, Part A 85(3), 206–213 (2014). 10.1002/cyto.a.22422 [DOI] [PubMed] [Google Scholar]
- 3.Heitzer E., Auer M., Gasch C., Pichler M., Ulz P., Hoffmann E. M., Lax S., Waldispuehl-Geigl J., Mauermann O., Lackner C., Höfler G., Eisner F., Sill H., Samonigg H., Pantel K., Riethdorf S., Bauernhofer T., Geigl J. B., Speicher M. R., “Complex tumor genomes inferred from single circulating tumor cells by array-CGH and next-generation sequencing,” Cancer Res. 73(10), 2965–2975 (2013). 10.1158/0008-5472.CAN-12-4140 [DOI] [PubMed] [Google Scholar]
- 4.Cohen Maslaton S., Barnea I., Taieb A., Shaked N. T., “Cell and nucleus refractive-index mapping by interferometric phase microscopy and rapid confocal fluorescence microscopy,” J. Biophotonics 13(9), 1 (2020). 10.1002/jbio.202000117 [DOI] [PubMed] [Google Scholar]
- 5.Rappaz B., Cano E., Colomb T., Kühn J., Depeursinge C., Simanis V., Magistretti P. J., Marquet P., “Noninvasive characterization of the fission yeast cell cycle by monitoring dry mass with digital holographic microscopy,” J. Biomed. Opt. 14(3), 034049 (2009). 10.1117/1.3147385 [DOI] [PubMed] [Google Scholar]
- 6.Mir M., Wang Z., Tangella K., Popescu G., “Diffraction phase cytometry: blood on a CD-ROM,” Opt. Express 17(4), 2579–2587 (2009). 10.1364/OE.17.002579 [DOI] [PubMed] [Google Scholar]
- 7.Girshovitz P., Shaked N. T., “Generalized cell morphological parameters based on interferometric phase microscopy and their application to cell life cycle characterization,” Biomed. Opt. Express 3(8), 1757–1773 (2012). 10.1364/BOE.3.001757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jang Y., Jang J., Park Y., “Dynamic spectroscopic phase microscopy for quantifying hemoglobin concentration and dynamic membrane fluctuation in red blood cells,” Opt. Express 20(9), 9673–9681 (2012). 10.1364/OE.20.009673 [DOI] [PubMed] [Google Scholar]
- 9.Dardikman G., Shaked N. T., “Review on methods of solving the refractive index–thickness coupling problem in digital holographic microscopy of biological cells,” Opt. Commun. 422(1), 8–16 (2018). 10.1016/j.optcom.2017.11.084 [DOI] [Google Scholar]
- 10.Cardenas N., Ingle N., Yu L., Mohanty S., “Development of a digital holographic microscopy system integrated with atomic force microscope,” in Three-Dimensional and Multidimensional Microscopy: Image Acquisition and Processing XVIII 790709 (2011). [Google Scholar]
- 11.Balberg M., Levi M., Kalinowski K., Barnea I., Mirsky S. K., Shaked N. T., “Localized measurements of physical parameters within human sperm cells obtained with wide-field interferometry,” J. Biophotonics 10(10), 1305–1314 (2017). 10.1002/jbio.201600186 [DOI] [PubMed] [Google Scholar]
- 12.Curl C. L., Bellair C. J., Harris T., Allman B. E., Harris P. J., Stewart A. G., Roberts A., Nugent K. A., Delbridge L. M. D., “Refractive index measurement in viable cells using quantitative phase-amplitude microscopy and confocal microscopy,” Cytometry, Part A 65A(1), 88–92 (2005). 10.1002/cyto.a.20134 [DOI] [PubMed] [Google Scholar]
- 13.Rappaz B., Barbul A., Emery Y., Korenstein R., Depeursinge C., Magistretti P. J., Marquet P., “Comparative study of human erythrocytes by digital holographic microscopy, confocal microscopy, and impedance volume analyzer,” Cytometry, Part A 73A(10), 895–903 (2008). 10.1002/cyto.a.20605 [DOI] [PubMed] [Google Scholar]
- 14.Dudaie M., Nissim N., Barnea I., Gerling T., Duschl C., Kirschbaum M., Shaked N. T., “Label-free discrimination and selection of cancer cells from blood during flow using holography-induced dielectrophoresis,” J. Biophotonics (2020). [DOI] [PubMed]
- 15.Kuś A., Dudek M., Kemper B., Kujawińska M., Vollmer A., “Tomographic phase microscopy of living three-dimensional cell cultures,” J. Biomed. Opt. 19(4), 046009 (2014). 10.1117/1.JBO.19.4.046009 [DOI] [PubMed] [Google Scholar]
- 16.Habaza M., Gilboa B., Roichman Y., Shaked N. T., “Tomographic phase microscopy with 180° rotation of live cells in suspension by holographic optical tweezers,” Opt. Lett. 40(8), 1881–1884 (2015). 10.1364/OL.40.001881 [DOI] [PubMed] [Google Scholar]
- 17.Dardikman G., Nygate Y. N., Barnea I., Turko N. A., Singh G., Javidi B., Shaked N. T., “Integral refractive index imaging of flowing cell nuclei using quantitative phase microscopy combined with fluorescence microscopy,” Biomed. Opt. Express 9(3), 1177–1189 (2018). 10.1364/BOE.9.001177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dardikman G., Singh G., Shaked N. T., “Four dimensional phase unwrapping of dynamic objects in digital holography,” Opt. Express 26(4), 3772–3778 (2018). 10.1364/OE.26.003772 [DOI] [PubMed] [Google Scholar]
- 19.Cardenas N., Mohanty S., “Decoupling of geometric thickness and refractive index in quantitative phase microscopy,” Opt. Lett. 38(6), 1007–1009 (2013). 10.1364/OL.38.001007 [DOI] [PubMed] [Google Scholar]
- 20.Rappaz B., Marquet P., Cuche E., Emery Y., Depeursinge C., Magistretti P. J., “Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy,” Opt. Express 13(23), 9361–9373 (2005). 10.1364/OPEX.13.009361 [DOI] [PubMed] [Google Scholar]
- 21.Boss D., Kühn J., Jourdain P., Depeursinge C., Magistretti P. J., Marquet P., “Measurement of absolute cell volume, osmotic membrane water permeability, and refractive index of transmembrane water and solute flux by digital holographic microscopy,” J. Biomed. Opt. 18(3), 036007 (2013). 10.1117/1.JBO.18.3.036007 [DOI] [PubMed] [Google Scholar]
- 22.Jafarfard M. R., Moon S., Tayebi B., Kim D. Y., “Dual-wavelength diffraction phase microscopy for simultaneous measurement of refractive index and thickness,” Opt. Lett. 39(10), 2908–2911 (2014). 10.1364/OL.39.002908 [DOI] [PubMed] [Google Scholar]
- 23.Xin Z. D., Xu Y. Y., Ji Y., Jin W. F., Zheng H. R., Zhang L., Wang Y. W., “The homogeneous and dual-medium cell’s refractive index decoupling method and entropy tomographic imaging,” in High Power Lasers, High Energy Lasers, and Silicon-Based Photonic Integration, 101520T (2016). [Google Scholar]
- 24.Kühn J., Colomb T., Montfort F., Charrière F., Emery Y., Cuche E., Marquet P., Depeursinge C., “Real-time dual-wavelength digital holographic microscopy with a single hologram acquisition,” Opt. Express 15(12), 7231–7242 (2007). 10.1364/OE.15.007231 [DOI] [PubMed] [Google Scholar]
- 25.Ferraro P., Miccio L., Grilli S., Paturzo M., De Nicola S., Finizio A., Osellame R., Laporta P., “Quantitative Phase Microscopy of microstructures with extended measurement range and correction of chromatic aberrations by multiwavelength digital holography,” Opt. Express 15(22), 14591–14600 (2007). 10.1364/OE.15.014591 [DOI] [PubMed] [Google Scholar]
- 26.Mann C. J., Bingham P. R., Paquit V. C., Tobin K. W., “Quantitative phase imaging by three-wavelength digital holography,” Opt. Express 16(13), 9753–9764 (2008). 10.1364/OE.16.009753 [DOI] [PubMed] [Google Scholar]
- 27.Turko N. A., Eravuchira P. J., Barnea I., Shaked N. T., “Simultaneous three-wavelength unwrapping using external digital holographic multiplexing module,” Opt. Lett. 43(9), 1943–1946 (2018). 10.1364/OL.43.001943 [DOI] [PubMed] [Google Scholar]
- 28.Yamagiwa M., Minamikawa T., Trovato C., Ogawa T., Ibrahim D. G. A., Kawahito Y., Oe R., Shibuya K., Mizuno T., Abraham E., Mizutani Y., Iwata T., Yamamoto H., Minoshima K., Yasui T., “Multi cascade-linked synthetic wavelength digital holography using an optical-comb-referenced frequency synthesizer,” Opt. Express 26(20), 26292–26306 (2018). 10.1364/OE.26.026292 [DOI] [PubMed] [Google Scholar]
- 29.Park Y., Yamauchi T., Choi W., Dasari R., Feld M. S., “Spectroscopic phase microscopy for quantifying hemoglobin concentrations in intact red blood cells,” Opt. Lett. 34(23), 3668–3670 (2009). 10.1364/OL.34.003668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Friebel M., Meinke M., “Model function to calculate the refractive index of native hemoglobin in the wavelength range of 250-1100 nm dependent on concentration,” Appl. Opt. 45(12), 2838–2842 (2006). 10.1364/AO.45.002838 [DOI] [PubMed] [Google Scholar]
- 31.Zhernovaya O., Sydoruk O., Tuchin V., Douplik A., “The refractive index of human hemoglobin in the visible range,” Phys. Med. Biol. 56(13), 4013–4021 (2011). 10.1088/0031-9155/56/13/017 [DOI] [PubMed] [Google Scholar]
- 32.Popescu G., Ikeda T., Dasari R. R., Feld M. S., “Diffraction phase microscopy for quantifying cell structure and dynamics,” Opt. Lett. 31(6), 775–777 (2006). 10.1364/OL.31.000775 [DOI] [PubMed] [Google Scholar]
- 33.Bhaduri B., Pham H., Mir M., Popescu G., “Diffraction phase microscopy with white light,” Opt. Lett. 37(6), 1094–1096 (2012). 10.1364/OL.37.001094 [DOI] [PubMed] [Google Scholar]
- 34.Cuche E., Bevilacqua F., Depeursinge C., “Digital holography for quantitative phase-contrast imaging,” Opt. Lett. 24(5), 291–293 (1999). 10.1364/OL.24.000291 [DOI] [PubMed] [Google Scholar]
- 35.Dennis M. D. P., Ghiglia C., Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software (Wiley, 1998). [Google Scholar]
- 36.Canham P. B., Burton A. C., “Distribution of size and shape in populations of normal human red cells,” Circ. Res. 22(3), 405–422 (1968). 10.1161/01.RES.22.3.405 [DOI] [PubMed] [Google Scholar]
- 37.Walker H. K., Hall W. D., Hurst J. W., Clinical Methods: The History, Physical, and Laboratory Examinations, 3rd ed. (Butterworths, 1990), Ch. 152. [PubMed] [Google Scholar]
- 38.Rubin M., Dardikman G., Mirsky S. K., Turko N. A., Shaked N. T., “Six-pack off-axis holography,” Opt. Lett. 42(22), 4611–4614 (2017). 10.1364/OL.42.004611 [DOI] [PubMed] [Google Scholar]
- 39.Mirsky S. K., Shaked N. T., “First experimental realization of six-pack holography and its application to dynamic synthetic aperture superresolution,” Opt. Express 27(19), 26708–26720 (2019). 10.1364/OE.27.026708 [DOI] [PubMed] [Google Scholar]
- 40.Merola F., Memmolo P., Miccio L., Savoia R., Mugnano M., Fontana A., D’Ippolito G., Sardo A., Iolascon A., Gambale A., Ferraro P., “Tomographic flow cytometry by digital holography,” Light: Sci. Appl. 6(4), e16241 (2017). 10.1038/lsa.2016.241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lee K. C. M., Wang M., Cheah K. S. E., Chan G. C. F., So H. K. H., Wong K. K. Y., Tsia K. K., “Quantitative phase imaging flow cytometry for ultra-large-scale single-cell biophysical phenotyping,” Cytometry, Part A 95(5), 510–520 (2019). 10.1002/cyto.a.23765 [DOI] [PubMed] [Google Scholar]
- 42.Li Y., Mahjoubfar A., Chen C. L., Niazi K. R., Pei L., Jalali B., “Deep cytometry: deep learning with real-time inference in cell sorting and flow cytometry,” Sci. Rep. 9(1), 11088 (2019). 10.1038/s41598-019-47193-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rubin M., Stein O., Turko N. A., Nygate Y., Roitshtain D., Karako L., Barnea I., Giryes R., Shaked N. T., “TOP-GAN: dtain-free cancer cell classification using deep learning with a small training set,” Med. Image Anal. 57, 176–185 (2019). 10.1016/j.media.2019.06.014 [DOI] [PubMed] [Google Scholar]