Optical coherence tomography-based tissue dynamics imaging for longitudinal and drug response evaluation of tumor spheroids

Abstract

We present optical coherence tomography (OCT)-based tissue dynamics imaging method to visualize and quantify tissue dynamics such as subcellular motion based on statistical analysis of rapid-time-sequence OCT signals at the same location. The analyses include logarithmic intensity variance (LIV) method and two types of OCT correlation decay speed analysis (OCDS). LIV is sensitive to the magnitude of the signal fluctuations, while OCDSs including early- and late-OCDS (OCDS_e and OCDS_l, respectively) are sensitive to the fast and slow tissue dynamics, respectively. These methods were able to visualize and quantify the longitudinal necrotic process of a human breast adenocarcinoma spheroid and its anti-cancer drug response. Additionally, the effects of the number of OCT signals and the total acquisition time on dynamics imaging are examined. Small number of OCT signals, e.g., five or nine suffice for dynamics imaging when the total acquisition time is suitably long.

1. Introduction

Cancer is one of the most deadly diseases worldwide [1,2]. Cancers can be caused by abnormal mutations and by the proliferation of any cell type in the human body, so there are more than one hundred specific types of cancer, which then vary from patient to patient [3]. Cancer survival rates can be increased by early detection and optimal selection of the anticancer agent used. Therefore, there is an indispensable requirement for effective and fast cancer detection and drug selection methods for individual patients.

Ex vivo cultures of tumor cells would be useful in selection of the optimal anticancer agent. Tumor cells including human cancer cells can be cultured as a multicellular spheroids [4,5] and these spheroids can then be used to investigate the drug responses of these tumor cells [6,7].

Although the drug response of the tumor spheroid can be evaluated based on its morphology [8], this process can take from days to weeks after application of the drug [9–11]. If a more sensitive modality was available to see the drug response, the drug selection process could then be conducted within a few hours or days and this would increase the cancer survival rate.

Fluorescence microscopy with appropriate markers is used widely for cell viability evaluation, and is one of the standard modalities used for drug response evaluation [12–14]. However, there are three issues with fluorescence microscopy. First, the procedure requires markers. Therefore, this modality is invasive and this prevents its use in longitudinal evaluation. Second, the fluorescence signal is not fully quantitative, which means that it can be used for image observation but it is not suitable for objective quantification of the drug response. Third, its imaging penetration is limited to within a few hundreds of micrometers.

To overcome the first and second issues, we aim to evaluate the tissue dynamics. Tissue dynamics, such as subcellular motion, are sensitive indicators of both cell and tissue viability. Therefore, if we can measure the tissue dynamics, such measurements may be useful in drug response investigations [15,16].

Subcellular motion, which is the main source of tissue dynamics, can be observed directly via a super-resolution microscopy [17–19]. It is a label-free procedure, and quantitative image analysis is potentially applicable, but the imaging penetration of this method is only on the micrometer scale. Therefore, there is still a need for a high-penetration label-free imaging modality that meets all three requirements of label-free, quantitative, and high-penetration.

Optical coherence tomography (OCT) is a noninvasive, high resolution, and three-dimensional (3-D) imaging modality that has a high penetration depth range of approximately 1-3 mm [20]. Although the widely used clinical OCT is not really a microscopic modality because its lateral resolution is configured to a few tens of micrometers, there is a microscopic version of OCT, which is referred to as optical coherence microscopy (OCM). OCM offers higher lateral resolution than OCT and can visualize the cellular and subcellular characteristics of tissues [21,22]. Conventional OCT, and thus also OCM, are label-free processes with high imaging penetration. However, conventional OCT is only sensitive to tissue structure and has no sensitivity to the tissue dynamics.

Several extensions are available that can make OCT sensitive to more than the tissue structure, including OCT angiography (OCTA) for flow imaging [23–25], polarization-sensitive OCT for tissue ultrastructure investigations [26,27], optical coherence elastography for mechanical properties investigations [28–30], and also their integration [31]. Among these extensions, OCTA, in its widest sense, visualizes the fast dynamics of tissues, such as their flow. The majority of recent OCTA implementations have used signal decorrelation and variance [32–34]. Intensity or precise phase analysis was used to investigate the dynamics of retinal photoreceptors [35–39]. Time-frequency analysis of the OCT signal, which is known as dynamic OCT, is another promising technique for tissue dynamics visualization, that is mainly sensitive to tissue metabolism properties such as adenosine triphosphate (ATP) consumption. Dynamic OCT has also been used for retinal dynamics imaging [40,41]. Dynamic OCT was originally performed with time-domain full-field OCT [42–44], and a high-speed spectral-domain OCT-based dynamic OCT imaging was also demonstrated recently [45]. For tumor spheroid investigations, speckle decorrelation was used to assess cell death in the tumor spheroids [46]. OCT signal attenuation was also used to assess the necrotic changes in spheroids [22], although this approach only used the static property of the OCT signal.

This paper demonstrates three OCT-based methods for subjective observation and objective quantification of the tissue dynamics of tumor spheroids. The first is “logarithmic OCT intensity variance (LIV),” which is essentially the time variance of a rapidly acquired sequence of OCT signals. The other two methods are two variations of the “OCT correlation decay speed (OCDS),” which is used to assess the temporal rate of intensity alteration. Both the LIV and OCDS methods only use the intensity of the OCT signal, so the OCT/OCM device is not necessarily phase sensitive. In addition, these methods are implemented using a standard speed (50,000-A-line/s) scanning swept-source OCT. These methods are thus portable to most of the standard OCT systems.

The utility of these methods is investigated by performing two studies. The first study involved hourly visualization and quantification of human breast adenocarcinoma (MCF7 cell line) spheroid dynamics. This study is intended to validate the applicability of these noninvasive methods for longitudinal evaluation of tumor spheroids. The second study is a cross-sectional study used to assess the drug responses of the MCF7 spheroids, where the spheroids are exposed to an anti-cancer agent (paclitaxel) at several concentrations and the results are compared with those obtained from fluorescence microscopy.

2. OCT based tissue dynamics imaging

2.1. OCT device and data acquisition protocol

A Jones-matrix-based multi-functional swept-source OCT is used to implement the tissue dynamics imaging [31,47]. The light source is a microelectromechanical systems (MEMS)-based swept-source with a center wavelength of 1.3 µm and a scan speed of 50 kHz. The probe power incident on the sample is 14 mW and the system sensitivity is 104 dB. The axial resolution in tissue is 14 µm, while the depth pixel separation in tissue is 7.24 µm. The lateral resolution (1/$e^2$-width) is 19 µm, while the lateral pixel separation is 1.95 µm. The complete system specification is published elsewhere [31]. Although this system is capable of polarization-sensitive tomography measurements, only polarization-insensitive OCT, which is the average intensity of four OCT images from four polarization channels, is used.

For the tissue dynamics imaging, 350 sequential cross-sectional frames (B-scans) are captured in 4.48 s at the same location in the sample. The frame covers a 1-mm lateral field. A single frame consists of 512 depth-scans (A-lines), and the frame acquisition time is 10.24 ms. The frames are repeatedly acquired every 12.8 ms.

2.2. Time-sequence-signal analyses

To visualize and quantify the tissue dynamics, we compute three quantities from the temporal sequence of the OCT signal. The first quantity is the LIV, which is described in Section 2.2.1. The other two quantities are two variations of OCDS that are described in Section 2.2.2.

2.2.1. Logarithmic intensity variance (LIV)

The first quantity computed for tissue dynamics imaging is the LIV, which is a measure of the signal fluctuation magnitude over the total acquisition time period, which is 4.48 s in the present case. The LIV is based on a model in which the OCT signal intensity $I(x,z,t_i)$ is expressed by the static component $I_S(x,z)$ and the dynamic component $I_D(x,z,t_i)$ as

$$I(x,z,t_i)=I_D(x,z,t_i)I_S(x,z),$$ (1)

where $x$ and $z$ are the lateral and depth positions, respectively. $t_i$ is the sampling time point of the $i$-th frame where $i$ = 0, 1, 2, $\cdots$, $N-1$, and $N$ is the number of frames, which is 350 in this case.

To separate the dynamic component from the static component, we convert the measured OCT intensity into a logarithmic (dB-) scale as

$$I_{dB}(x,z,t_i)\equiv 10\log I(x,z,t_i)=10\log I_D(x,z,t_i)+10\log I_S(x,z),$$ (2)

where the base of the logarithm is 10. Finally, the LIV is computed as the time variance of $I_{dB}$ as

$$\begin{array}{rl}\mathrm{L}\mathrm{I}\mathrm{V}(x,z)=& \frac{1}{N}\sum _{i=0}^{N-1}{[I_{dB}(x,z,t_i)-{⟨I_{dB}(x,z)⟩}_{t_i}]}^2\\ =& \frac{1}{N}\sum _{i=0}^{N-1}{[10\log I_D(x,z,t_i)-{⟨10\log I_D(x,z)⟩}_{t_i}]}^2,\end{array}$$ (3)

where ${⟨⟩}_{t_i}$ is the average over $t_i$.

As is evident from the equation, the LIV is only sensitive to the dynamic component of the OCT signal and is unaffected by the magnitude of the static component. It is also notable that the LIV is only sensitive to the magnitude of the OCT signal fluctuation and not sensitive to the temporal rate, i.e., the speed, of the dynamics.

2.2.2. OCT correlation decay speed (OCDS)

The second type of the dynamics quantities is OCDS, which is the temporal decorrelation rate (speed) of OCT intensity signal. The first step required to compute the OCDS is to compute the autocorrelation of the OCT signal ${\rho }_A$ over time as

$${\rho }_A({\tau }_j,x,z)=\frac{\mathrm{C}\mathrm{o}\mathrm{v}[I_{dB}(x,z,t_i),I_{dB}(x,z,t_i+{\tau }_j)]}{\mathrm{V}\mathrm{a}\mathrm{r}[I_{dB}(x,z,t_i)]\mathrm{V}\mathrm{a}\mathrm{r}[I_{dB}(x,z,t_i+{\tau }_j)]},$$ (4)

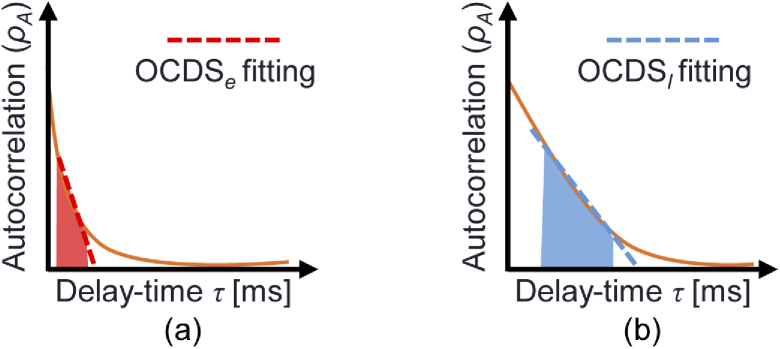
where the numerator is the covariance of $I_{dB}(x,z,t_i)$ and $I_{dB}(x,z,t_i+{\tau }_j)$ and $\mathrm{V}\mathrm{a}\mathrm{r}[]$ represents the variance. $t_i$ is the sampling time point of the $i$-th frame where $i$ = 0, 1, 2, $\cdots$, $N-1$, and $N$ is the number of frames. ${\tau }_j$ is a discrete variable that represents the time delay defined as $j\mathrm{\Delta }t$ where $j$ is an integer variable. $\mathrm{\Delta }t$ is the repeating time of sequential frame acquisition, which is 12.8 ms in this case. For the numerical computations, the covariance and the variance were computed within the overlapped time region between $I_{dB}(x,z,t_i)$ and $I_{dB}(x,z,t_i+{\tau }_j)$. Therefore, $\mathrm{V}\mathrm{a}\mathrm{r}[I_{dB}(x,z,t_i)]$ is not the same as $\mathrm{V}\mathrm{a}\mathrm{r}[I_{dB}(x,z,t_i+{\tau }_j)]$. The OCDS is then defined as the slope of ${\rho }_A({\tau }_j)$ within a specific range of ${\tau }_j$, where the slope is computed via a linear regression. In our implementation, two types of OCDS are computed within two delay-time (${\tau }_j$) ranges, as depicted schematically in Fig. 1. The “early OCDS”, denoted by ${\mathrm{OCDS}}_e$, is defined as the slope in the short delay region [red region and red dashed line in Fig. 1(a)], while the “late OCDS” (${\mathrm{OCDS}}_l$) is computed over the larger delay region [blue region and line in Fig. 1(b)]. In our particular case, the ${\mathrm{OCDS}}_e$ is defined in the range ${\tau }_j$ = [12.8, 64] ms ($j=[1,5]$), while the ${\mathrm{OCDS}}_l$ is defined in the range ${\tau }_j$ = [64, 627.2] ms ($j=[5,49]$). The delay-time point ${\tau }_j=0$ ($j=0$) is not included for the slope analysis, because ${\rho }_A$ at ${\tau }_j=0$ is not affected by the measurement noise and always has a value of unity, while ${\rho }_A$ for ${\tau }_j\le \mathrm{\Delta }t$, i.e., $j\le 1$, is constantly slightly down-estimated because of the effects of noises.

Fig. 1.

Schematics representing the definitions of the OCDSs. The curves in each figure represent the autocorrelations in which the fast (a) and slow (b) dynamics are dominant. ${\mathrm{OCDS}}_e$ and ${\mathrm{OCDS}}_l$ are defined at the red and blue regions, respectively. In the present case, these regions are [12.8, 64] ms for ${\mathrm{OCDS}}_e$ and [64, 627.2] ms for ${\mathrm{OCDS}}_l$. The red and blue lines represent the slope for the ${\mathrm{OCDS}}_e$ and the ${\mathrm{OCDS}}_l$, respectively.

The ${\mathrm{OCDS}}_e$ becomes larger than the ${\mathrm{OCDS}}_l$ if the dynamics are fast [Fig. 1(a)], while the two OCDSs have similar values if the dynamics are slow [Fig. 1(b)]. Note also that the OCDS is sensitive to the temporal rate (speed) of the signal dynamics, while the LIV is only sensitive to the magnitude of the signal dynamics.

In our implementation, Eq. (4) is implemented using fast Fourier transform (FFT), as described in the Appendix of Ref. [48], for fast computation. And it is computed for each pixel of a cross-sectional image in order to form the images of OCDS${\mathrm{OCDS}}_e$ and ${\mathrm{OCDS}}_l$.

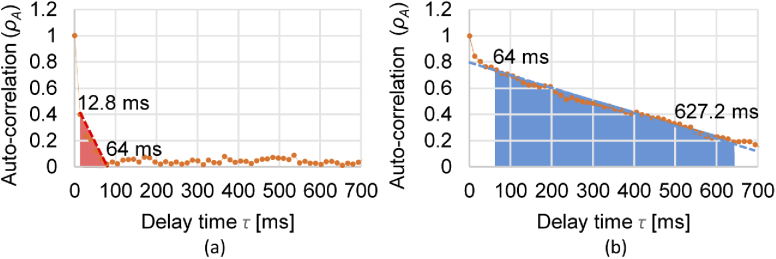
Figure 2 shows two examples of experimentally obtained autocorrelation profiles with a tumor spheroid sample that will be described later in Section 4.1. Figure 2(a) is an example obtained in a region with fast dynamics. Here ${\rho }_A$ rapidly decays and becomes almost zero at 64-ms delay time. The ${\mathrm{OCDS}}_e$’s slope computation range, [12.8, 64 ms] (red-colored range), was selected to account for this fast dynamics. Figure 2(b) shows another example measured at a region with slow dynamics. The ${\mathrm{OCDS}}_l$’s slope computation range, [64, 627.2 ms] (blue-colored range), was selected to account for this slow dynamics.

Fig. 2.

Experimentally obtained autocorrelation decay profiles of a tumor spheroid sample described in Section 4.1. The curves represent the autocorrelation decay of fast (a) and slow (b) dynamics tissue regions. The ${\mathrm{OCDS}}_e$ and ${\mathrm{OCDS}}_l$ computation ranges are highlighted as red and blue regions in (a) and (b), respectively.

2.3. Pseudo-color dynamics image formation

A pseudo-color image is created by combining one of the tissue dynamics images (i.e. the LIV, ${\mathrm{OCDS}}_e$, or ${\mathrm{OCDS}}_l$) with the OCT intensity image. In this image, the color hue, i.e., the H channel of the HSV (hue, stauration, value) color representation, is defined by the dynamics quantity, while the pixel brightness (the V channel) is defined using the OCT intensity. The color saturation (the S channel) is set at 1 for all pixels. As shown in the color bars in the result figures, high-dynamics region appears in green, while the low-dynamics region is red. This image is created to assimilate the fluorescence microscopy image, which will be described in Section 3.2.

3. Validation method: tumor spheroid evaluation

3.1. Sample and study protocols

Two studies involving human breast adenocarcinoma (MCF7 cell line) spheroids were performed to evaluate the proposed tissue dynamics imaging methods.

Study 1 involves longitudinal hourly imaging of the tumor spheroids for up to 28 hours and was organized to validate the utility of dynamics imaging for noninvasive longitudinal studies. Human breast adenocarcinoma cells (MCF7 cell line) were used. For each well of a ultra-low attachment plate with 6 wells, 5,000 MCF7 cells were seeded for 15 days to reach spheroid size around 500 µm. The culture environment was attached with a ${\mathrm{CO}}_2$ supply. The cell culture medium contained EMEM/F12 (1:1) (Invitrogen, Waltham, MA) with a 2% B-27 supplement (Invitrogen), 2-ng/mL bFGF (Wako, Osaka, Japan), 2-ng/mL EGF (Sigma-Aldrich, St.Louis, MO), 100 U/mL penicillin G, and 0.1 mg/mL streptomycin sulfate (Wako). Tumor spheroids with diameters in approximate range from 200 to 300 µm were formed after 15 days. These spheroids were extracted from the cultivation environment and were then kept in the same culture medium without ${\mathrm{CO}}_2$ being supplied. The first OCT imaging was performed 30 minutes after the extraction and hourly imaging was performed up to 28 hours after the first imaging. During imaging, the samples were kept at a room temperature of approximately ${22}^{\circ }$C and were also kept in the culture medium without ${\mathrm{CO}}_2$ supply.

Study 2 involves cross-sectional investigation of multiple spheroids under several concentrations of the anti-cancer agent (paclitaxel, which is also known by the trade name Taxol), which was preformed to validate the utility of the dynamics imaging as a tool for drug-response testing. In this study, 10,000 of MCF7 cells were seeded in each of four wells in the ultralow attachment plate with 96 wells for 4 days to reach spheroid size around 500 µm. The different growing speed of the spheroid in comparison to the Study 1 is due to the different number of initially seeded cells. The samples were then cultured in the same environment used in the longitudinal study descibed above. After four days, paclitaxel at concentrations of 5, 50, and 500 nM was applied to three of the four wells, while one well was maintained as a control sample without paclitaxel. After one day of drug application, a cell-permeant dye (calcein acetoxymethyl; Calcein-AM) and a fluorescent intercalating agent (propidium iodide; PI) were applied and incubated with spheroids at ${37}^{\circ }$C for 3 hours, and fluorescence microscope imaging was then performed to serve as a reference standard. OCT imaging was performed after around 30 minutes of fluorescence imaging. During OCT imaging, the samples were kept in the same medium but ${\mathrm{CO}}_2$ was again not supplied.

3.2. Fluorescence microscopy

Fluorescence microscopic imaging was performed to act as a reference standard for the spheroid drug response study (second study). A THUNDER imaging system (Leica Micro-systems, Wetzler, Germany) was used for this imaging study. A microscopic objective with a numerical aperature (NA) of 0.12 was used. The image acquisition process of a scientific complementary metal-oxide semiconductor (sCMOS) camera was synchronized with the flashing of a light-emitting diode (LED) lighthouse to avoid photo bleaching.

For spheroid imaging, two fluorescence solutions were applied. The first was calcein acetoxymethyl (Calcein-AM) which mainly stains the living cells and gives a green fluorescence. The second was propidium iodide (PI) which mainly contrasts the dead cells with red fluorescence.

4. Results

4.1. Study 1: longitudinal evaluation of human breast adenocarcinoma spheroids

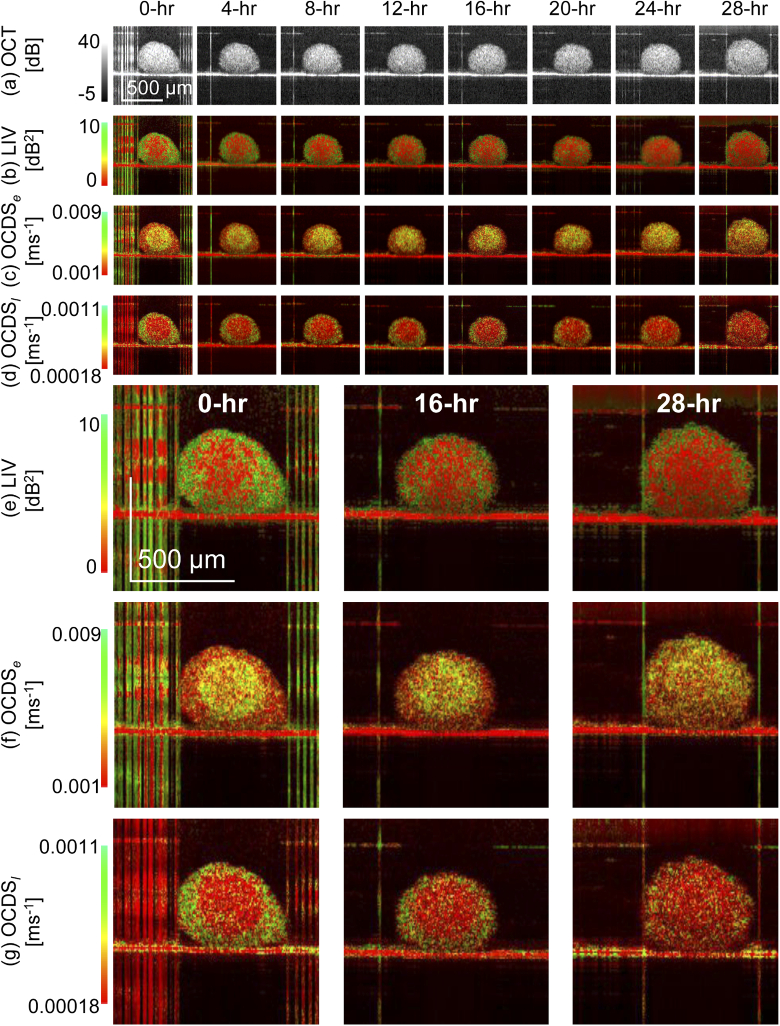
Figure 3 summarizes the longitudinal time course imaging of MCF7 spheroid. The first row shows the time course images of the OCT B-scans. The vertical lines in some of the images are artifacts caused by specular reflection from the glass surface of a petri dish. Although the spheroid size changes slightly over time, this change would be due to slight changes in the scan location because of the floating action of the spheroid. Therefore, this would not be a significant finding.

Fig. 3.

Longitudinal dynamics visualization of an MCF7 spheroid. The first to fourth rows show time-course images of (a) OCT intensity , (b) LIV , (c) ${\mathrm{OCDS}}_e$, and (d) ${\mathrm{OCDS}}_l$. The fifth, sixth, and seventh rows show magnified images of (e) LIV , (f) ${\mathrm{OCDS}}_e$ , and (g) ${\mathrm{OCDS}}_l$, respectively at the 0-, 16-, and 28-hour time points.

The second to fourth rows show the time course cross-sectional images of the LIV, ${\mathrm{OCDS}}_e$, and ${\mathrm{OCDS}}_l$, while the fifth to seventh rows show magnified images of the LIV, ${\mathrm{OCDS}}_e$, and ${\mathrm{OCDS}}_l$, respectively, at the time points of 0, 16, and 28 hours.

The LIV images (second row) showed that, at the early time points, the OCT signal fluctuation magnitude is large (green) at the periphery, while that in the internal region is low (red). At the later time points, the high LIV at the periphery faded. It is known that the necrosis of large spheroids starts at their center because of the lack of nutrient supply [49–51]. This finding in the LIV is consistent with this necrotic process of the spheroids.

The ${\mathrm{OCDS}}_e$ images (third row) show that at the early time points, the center region of the spheroid shows fast dynamics (green), while the peripheral region does not show these dynamics. At the later time points, the entire region of the spheroid exhibits fast dynamics (green). It was previously reported that the necrotic process in the spheroid exhibited fast decorrelation of the OCT signal [46]. This is consistent with the present finding here.

The ${\mathrm{OCDS}}_l$ images are shown in the fourth row and represents the correlation decay at long delay times ($\tau$ = [64, 627.2] ms, as described in Section 2.2.2). These images show the opposite contrast to that of the ${\mathrm{OCDS}}_e$. Specifically, at the 0-hour time point, the peripheral region shows significant correlation decay (green), while it becomes dim at the later time points. At all time points, the center region appears in red, i.e., it does not show any significant correlation decay. This would be because the correlation already decayed at an early delay time as it was indicated by the green color in the ${\mathrm{OCDS}}_e$ images.

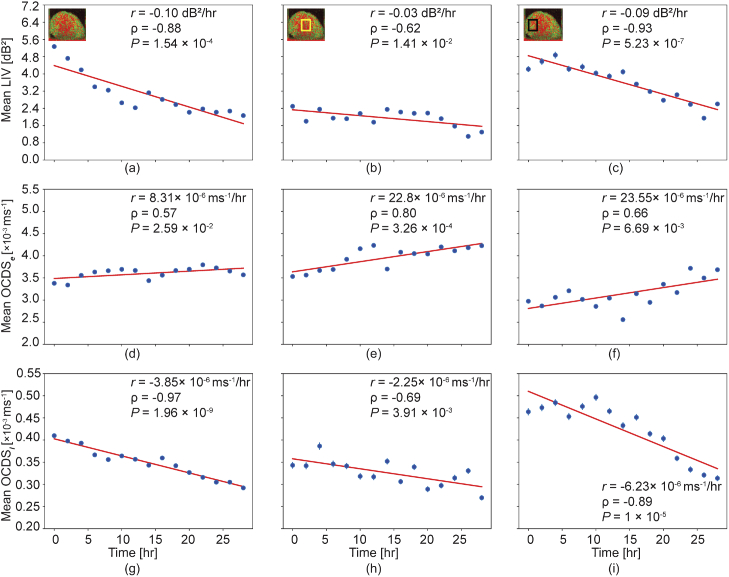
The hourly alterations in the tissue dynamics can be observed more quantitatively by plotting the mean values of the dynamics signal over time, as shown in Fig. 4. Here, the first to third rows represent the mean values of the LIV, ${\mathrm{OCDS}}_e$, and ${\mathrm{OCDS}}_l$, respectively. These means were computed over the entire spheroid region for the first column, at the center region [as indicated by the box in the inset of Fig. 4(b)] for the second column, and at the periphery region [as shown by the box in the inset of Fig. 4(c)]. All the LIV results (first row) show that mean LIV values decrease over time. This behavior is more pronounced at the periphery than at the center. This difference may occur because the center cells were already necrotic at the early time points, while the peripheral tissues were still alive at the early time point and gradually dying over time.

Fig. 4.

Time course plots of the mean LIV (first row), ${\mathrm{OCDS}}_e$ (second row), and ${\mathrm{OCDS}}_l$ (third row). The means of each quantity were computed over the entire spheroid region (first column), at the center region (second column), and at the periphery region (third column). The mean computation regions are indicated in the insets of (b) and (c). $r$ is the slope that was obtained by linear regression. $\rho$ is Pearson’s correlation coefficient between the values and the time. $P$ is the P-value of the correlation analysis.

The ${\mathrm{OCDS}}_e$ plots (second row) show a gradual increase. Farhat et al. reported that this fast decorrelation is associated with the necrotic process [46]. Therefore, this gradual increase in the ${\mathrm{OCDS}}_e$ may indicate that the necrotic process became more intense over time. Notably, even at 0 hour, the mean ${\mathrm{OCDS}}_e$ was higher than 3.5 $\times {10}^{-3}$ ${\mathrm{ms}}^{-1}$ [Fig. 4(e)] in the center region. This suggests that the necrotic process was intense at the early time points. In contrast, in the peripheral region, the mean ${\mathrm{OCDS}}_e$ was 3.0 $\times {10}^{-3}$ ${\mathrm{ms}}^{-1}$ at the early time point and reached more than 3.5 $\times {10}^{-3}$ ${\mathrm{ms}}^{-1}$ at the late time points [Fig. 4(f)]. This may indicate that the necrotic process became more intense, reaching the same height as that at the early time point of the center region, after 28 hours.

The ${\mathrm{OCDS}}_l$ plots (third row) show similar tendencies to those of the LIV. This may indicate that the dynamics observed using the LIV were slow process.

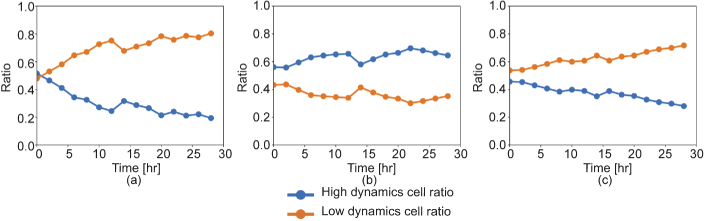
Figure 5 shows the area ratios of the high- and low- dynamic areas over the entire spheroid area computed from (a) LIV, (b) ${\mathrm{OCDS}}_e$ , and (c) ${\mathrm{OCDS}}_l$. These areas are defined as numbers of pixels that have higher or lower values than the cutoff values. And its area ratio is defined as the number of these pixels divided by the total number of pixels in the tissue.

Fig. 5.

Time course alteration of the ratios of the high- (blue line) or low- (orange line) dynamics areas over the entire spheroid area. These plots were obtained from (a) LIV , (b) ${\mathrm{OCDS}}_e$ , and (c) ${\mathrm{OCDS}}_l$.

The cutoff values were selected empirically by checking the values of each dynamics parameter at the necrotic region of the spheroid. They were 3 ${\mathrm{dB}}^2$ for the LIV, 3 $\times {10}^{-3}$ ${\mathrm{ms}}^{-1}$ for the ${\mathrm{OCDS}}_e$, and 0.4 $\times {10}^{-3}$ ${\mathrm{ms}}^{-1}$ for the ${\mathrm{OCDS}}_l$. The low-dynamic area ratios of the LIV and the ${\mathrm{OCDS}}_l$ increase over time, which may indicate that the dead cell region increases in size. In contrast, the ${\mathrm{OCDS}}_e$ shows a more constant time profile. Assuming that the ${\mathrm{OCDS}}_e$ is sensitive to the necrotic process, this result can be interpreted as showing that the area of the active necrotic process remains rather constant. Namely, during the measurement period, the necrotic process starts in some regions but finishes at certain other regions.

4.2. Study 2: cross-sectional drug response evaluation

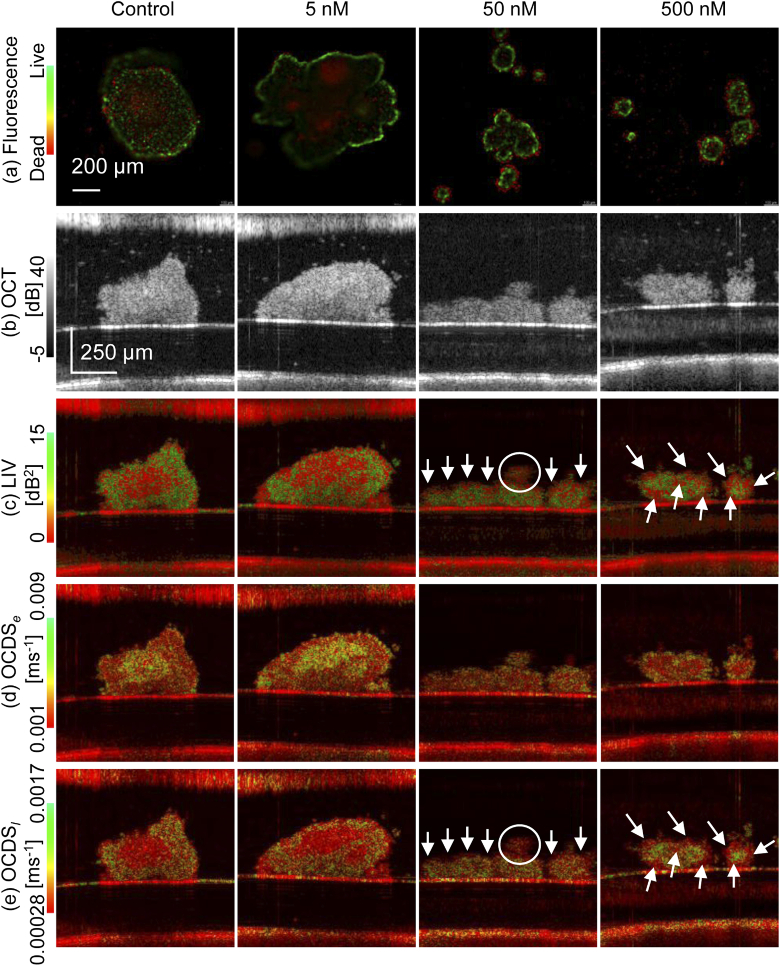
Figure 6 summarizes the results of the second study. The rows in the figure represent the fluorescence, OCT, LIV, ${\mathrm{OCDS}}_e$, and ${\mathrm{OCDS}}_l$ from top to bottom, while the columns correspond to the Paclitaxel concentrations 0 nM (control), 5 nM, 50 nM and 500 nM from left to right. It should be noted here that the fluorescence images are en face images, while the OCT and dynamics images are all depth cross-section images. The control images show similar appearances to those at the early time point of Study 1, where the peripheral region of the spheroid exhibits a high LIV, i.e., large magnitude of OCT signal fluctuation and slow decay of the correlation, i.e., low ${\mathrm{OCDS}}_e$ and high ${\mathrm{OCDS}}_l$. These appearances indicates that the cells at the periphery are still alive, while those within the central region are in the necrotic process. The fluorescence image is consistent with these findings of dynamics images because the peripheral cells exhibit green fluorescence and the center cells exhibit red fluorescence.

Fig. 6.

Drug response of MCF7 spheroids. The first to fifth rows represent the results from (a) fluorescence microscopy, (b) the OCT intensity image, (c) the LIV, (d) the ${\mathrm{OCDS}}_e$, and (e) the ${\mathrm{OCDS}}_l$. The fluorescence microscopy images are en face images, while the other images are all cross-sectional images. The columns represent the paclitaxel concentrations as 0 nM (control), 5 nM, 50 nM, and 500 nM from left to right.

The spheroid with 5 nM Paclitaxel (second column) show similar appearance with the control except that the red appearance in the fluorescence image forms large clusters. This fluorescence finding is consistent with dynamics images. The LIV image shows a moderate clustering appearance of low dynamics (red) within the spheroid. This is seen more obviously in the ${\mathrm{OCDS}}_e$ image, where clusters of fast correlation decay (colored yellow to green) are shown clearly.

The dynamics images of the 50- and 500-nM cases show opposite contrasts to the control and 5-nM cases. Specifically, the external parts of the spheroid show low LIV (red), high ${\mathrm{OCDS}}_e$ (green), and low ${\mathrm{OCDS}}_l$ (red) as depicted by the white arrows and circle, while the internal parts exhibit high LIV (green), low ${\mathrm{OCDS}}_e$ (red), and high ${\mathrm{OCDS}}_l$ (green). Because we believe that the combination of low LIV and high ${\mathrm{OCDS}}_e$ are indicators of the necrotic process, these appearances can be interpreted as the necrotic process occurring at the outer part of the spheroid. And it might be due to the high concentrations of paclitaxel. Consistent appearances can be found in the fluorescence images, where the outer and inner parts of the spheroid exhibit red and green fluorescence, respectively. It is also notable that the dynamics images of the 500 nM case show clearer contrast than those of the 50 nM case. For example, the 500-nM LIV shows a tessellated appearance of red and green as highlighted by the white arrows, while such an appearance is not evident in the 50-nM case. The 500-nM ${\mathrm{OCDS}}_e$ and ${\mathrm{OCDS}}_l$ show higher contrast between the outer and inner parts than that of 50-nM. Although these differences can be found in the dynamics OCT images, they are not evident in the fluorescence images.

5. Discussion

5.1. OCT-based dynamics imaging and fluorescence imaging

Although fluorescence imaging is a gold standard imaging modality, the OCT-based dynamics imaging procedure proposed here has three advantages. First, dynamics imaging is both label-free and noninvasive. This enables longitudinal studies to be performed for days, as demonstrated by Study 1.

Second, the penetration of dynamics imaging is deeper than that of the fluorescence microscope. For instance, while the former is approximately a few millimeters, the latter is only a few hundred micrometers. This enabled full depth imaging of the spheroids in both Studies 1 and 2. In contrast, because of the limited penetration, the fluorescence images in Study 2 (Fig. 6) showed high fluorescence at the surfaces of the spheroids, while the fluorescence signal in the internal areas was either dim or absent. Because thick cultured tissues such as large spheroids and organoids are closer to in vivo tissues than thin cultivated tissues such as monolayer cell cultures [52–54], high imaging penetration is important for ex vivo tissue investigations.

Third, OCT-based dynamics imaging is more quantitative and more objective than fluorescence imaging. For example, the fluorescence signal strength is only a relative value in an image and thus it cannot be compared among multiple images. In addition, the limited penetration issue mentioned above even prevents intra-image comparison of the signal intensities. Penetration of the fluorescence solutions and photo-bleaching [55] may also impede signal quantification. In contrast, the signal values of the dynamics images are absolute quantities, so they can be compared among the images. This quantitative nature of the dynamics signal enabled the objective time-course analysis to be performed in Study 1 (Fig. 4).

However, fluorescence imaging also offers a major advantage when compared with the OCT-based dynamics imaging. Fluorescence imaging can be highly specific to tissues, cell types, molecules, and particular gene expressions by introducing several probes and markers.

So the combination of OCT-based dynamics imaging and fluorescence imaging will broaden the scope of the cultured tissue investigation.

5.2. Multiple contrast investigations of samples

We have presented three types of OCT-based tissue dynamics quantities, including the LIV, ${\mathrm{OCDS}}_e$, and ${\mathrm{OCDS}}_l$, which are each sensitive to different aspects of the dynamics. The LIV is sensitive to the magnitude of the OCT signal fluctuations and is insensitive to the temporal rate (speed) of the dynamics. The ${\mathrm{OCDS}}_e$ is sensitive to both of fast and slow dynamics of the tissue, while the ${\mathrm{OCDS}}_l$ is sensitive only to the slow dynamics of the tissue. These quantities are thus complementary to each other.

In addition to these dynamics quantities, we also can compute other OCT-based contrasts from the same raw OCT data with the dynamics images. For example, the attenuation coefficient [56,57] is known to be sensitive to the necrotic change of the spheroids [22]. The Jones matrix OCT system used in this study can potentially provide the birefringence [47] and polarization-randomness contrast, such as the degree-of-polarization uniformity [58–60]. Therefore, OCT and JM-OCT can provide several types of images including the three types of dynamics images, using a single acquisition process.

These multiple contrasts can be used to perform multi-dimensional analysis such as contrast synthesis [61,62] and multi-parameter tissue segmentation [31,63]. These analyses will enhance the image contrast and will also provide sensitive and accurate tissue/cell-type classification.

5.3. Frame number dependence of the dynamics imaging sensitivity

The current OCT-based dynamics imaging method used 350 frames at a single location on the sample. The acquisition time of this method of 4.48 s is short enough for a single cross-sectional imaging but prevents volumetric imaging, which requires measurement of 100 or more locations.

Here, we investigate the minimum number of frames required for dynamics imaging using the LIV for future extension of the proposed method to volumetric imaging. This investigation consists of two studies. The first study is an objective evaluation of the dynamics imaging sensitivity versus number of frames used to compute the dynamics image. The second study is a subjective image quality evaluation of images generated using several different numbers of frames and acquisition time-length configurations.

5.3.1. Required number of frames and acquisition time duration

The first study examines the sensitivity of dynamics imaging, which is defined by the standard deviation of the dynamics image signal within a local region. This is defined as the sensitivity because it is the minimum contrast that can be defined or distinguished in the image. In other words, two tissues can be distinguished if the dynamics signal value difference is greater than the sensitivity.

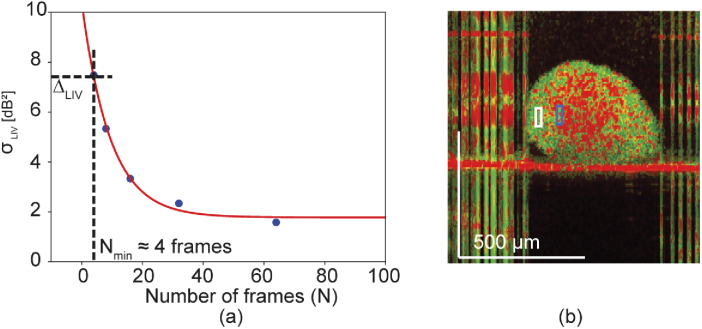
The sensitivities (i.e. the standard deviations of the dynamics signal) of the LIV (${\sigma }_{\mathrm{L}\mathrm{I}\mathrm{V}}$) were computed using the data sets of Study 1 (0-hour time point) at the peripheral region of the spheroid, and were plotted as a function of the number of frames in Fig. 7(a). Here, limited number of frames, such as 4, 8, 16, 32, and 64, were extracted from the original data set used in Section 4.1 and the dynamics signals were then computed from the extracted frames. These frames were spaced equally in time and the time separations of the first and last frames were large enough as 4.45, 5.73, 6.14, 6.34, and 6.45 s for 4, 8, 16, 32, and 64 frames, respectively. For each different number of frames, the LIV was computed from several different frame sets of the same time sequence of OCT images, and the standard deviation among them, i.e., the sensitivity, was computed. Here, we only analyze the LIV because of the difficulty involved in defining the ${\mathrm{OCDS}}_e$ and ${\mathrm{OCDS}}_l$ with non-standard numbers of frames.

Fig. 7.

(a) Sensitivity curve of the LIV as a function of the number of frames. The sensitivity is defined here as the ensemble standard deviation of the LIV values obtained within the same region in the sample. (b) Two regions of a spheroid (white and blue boxes) in which the difference of the mean LIV values was computed. Comparison of the difference with the sensitivity curve shown in (a) shows that four frames are required to distinguish the blue and white box regions shown in (b).

Figure 7(a) shows the sensitivity curve of the LIV as a function of the number of frames. For smaller numbers of frames, e.g., less than 20, the sensitivity improves (decreases) significantly as the number of frames increases. In contrast, the sensitivity becomes less sensitive to the number of frames as the number of frames increases.

To show an example of the required number of frames, we estimate the minimum number of frames required here to distinguish the two regions indicated by the two boxes in Fig. 7(b). The mean LIV values for these white and blue boxes are 12.19 ${\mathrm{dB}}^2$ and 4.77 ${\mathrm{dB}}^2$, respectively. The difference between these values is 7.42 ${\mathrm{dB}}^2$, and this is the required sensitivity. Comparison of this value with the sensitivity curve in Fig. 7(a) shows that the minimum number of frames required to distinguish these two regions is four. This is significantly smaller than the number of frames (350) used in the current method. This therefore suggests that dynamics imaging can be performed using smaller numbers of frames, meaning that it is potentially applicable to volumetric imaging with a realistic acquisition time.

5.3.2. Effect of total measurement time

Because the tissue dynamics that we observed included very slow tissue dynamics, the appearance of the dynamics images would be affected not only by the number of frames but also by the total acquisition time window, i.e., by the time separation between the first and last frames. Here, we evaluated this effect qualitatively by comparing the dynamics images computed using several configurations of the number of frames and acquisition time windows. The numbers of frames were configured as 5, 9, 17, 33 and 65, which were chosen to split the acquisition time window into 4, 8, 16, 32, 64 time-regions. The acquisition time windows were 0.82, 1.64, 3.28, 4.48, and 6.55 s. The longest time window is defined as an acquisition time of sequential 512 frames. 3.28, 1.64, and 0.82 s were the 1/2, 1/4, and 1/8 of the longest time window. 4.48 s was included in this analysis because it is the time window used in the studies presented in Sections 3 and 4. Dynamics images were computed for all combinations of the number of frames and the acquisition time window. It should be noted here that all images were generated from the same OCT data set, so the acquisition time window does not represent the real acquisition time in the experiment; instead it represents the time duration in which the frames were extracted. This analysis was performed only for the LIV because of the same reason with the sensitivity analysis, i.e., the difficulty in the definition of the ${\mathrm{OCDS}}_e$ and OCDS${\mathrm{OCDS}}_l$ when using non-standard numbers of frames.

The LIV images obtained with all numbers of frames and all time windows are summarized in Figs. 8. Both the number of frames and the acquisition time window affect the image quality significantly. However, the acquisition time window has a more significant impact because, for example, the images with the 0.82-s time window do not show sufficient contrast, even for 65 frames. In contrast, for longer acquisition times such as 4.48 s and 6.55 s, the small number of frames such as nine frames gave sufficient contrast similar to that obtained with 65 frames. Furthermore, the image obtained from only five frames also somehow gives acceptable contrast. This small number of required frames is consistent with the findings of the sensitivity analysis (Section 5.3.1). In contrast to the small number of frames required, a long acquisition time window is desired. This difference can be explained by the fact that measured tissue and OCT signal dynamics contain very slow dynamics, i.e., longer than a few seconds.

Fig. 8.

LIV computed using different numbers of frames and different acquisition time windows. Each column represents LIV images computed from 5, 9, 17, 33, and 65 frames (left to right). Each row represents the maximum time separation from the first frame to the last frame, i.e., the total acquisition time window. This window ranges from 0.82 (shortest, top) to the 6.55 s (longest, bottom).

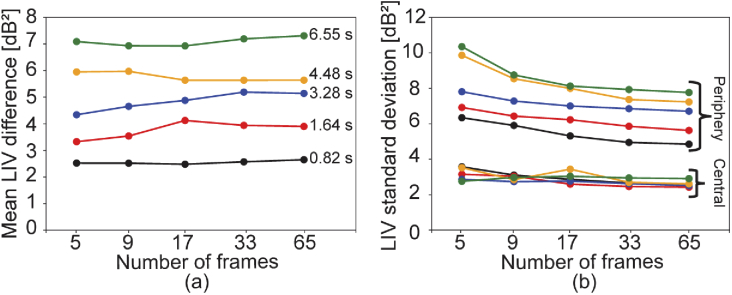
These findings can be confirmed by quantitative plots shown in Fig. 9. Figure 9(a) shows the difference of mean LIVs between two regions of interest shown by blue and yellow boxes in Fig. 8. In this figure, the mean LIV differences are plotted against the number of frames, and each series of data represents each time window of 0.82 s (black), 1.64 s (red), 3.28 s (blue), 4.48 s (yellow) , and 6.55 s (green). As we can see, the LIV difference is rather independent from the number of frames. On the other hand, it strongly depends on the time window, i.e., the mean LIV difference becomes larger as the time window becomes larger. It might be because the tissue contains very slow dynamics, longer than a few seconds.

Fig. 9.

(a) The mean LIV signal differences between the periphery and central regions of interest. Each series represents each acquisition time window. (b) The standard deviations of LIV in the same regions of interest. The colors of the series in (b) indicates the acquisition time window in the same manner with (a).

In comparison to the mean LIV difference, the standard deviations of LIV show the dependency on the number of frames as shown in Fig. 9(b). Here the color of the series indicates the time window in the same manner with Fig. 9(a). The standard deviations are high with the small number of frames, such as 5, and it becomes stable as the number of frames becomes large, such as 17. This data suggests that the small number of frames such as 17 are enough for the LIV imaging.

6. Conclusion

We introduced OCT-based dynamics imaging methods and examined the utility of the proposed methods for tumor spheroid evaluation. Owing to the label-free and noninvasive nature of the dynamics imaging method, longitudinal study of a human breast cancer spheroid was enabled. This study revealed the time-course of the necrotic changes in the spheroid for up to 28 hours. Both subjective observation and objective quantification were enabled in this longitudinal analysis. Another cross-sectional study showed that the dynamics imaging modality can also be used for drug response evaluation of the tumor spheroids. Good consistency was found between the dynamic images obtained in this study and standard reference images, i.e., fluorescence microscopy images. From these results, we conclude that OCT-based tissue dynamics imaging can be a useful tool for spheroid investigation and it can complement fluorescence imaging.

The impact of the imaging parameters on the quality of the OCT-based dynamics images was also investigated. This investigation revealed that the number of frames required for the tissue dynamics imaging can be as small as a few frames, i.e., less than 10 frames. This suggests that volumetric OCT-based dynamics imaging with standard speed OCT could be performed within a practical acquisition time, e.g., a few tens of seconds. Volumetric dynamics imaging would further complement the current standard modalities for spheroid evaluation.

Funding

Japan Society for the Promotion of Science10.13039/501100001691 (15K13371, 18H01893, 18J13841, 18K19961); Japan Science and Technology Agency10.13039/501100002241 (JPMJMI18G8).

Disclosures

Abd El-Sadek, Miyazawa, Mukherjee: Yokogawa Electric Corp. (F), Sky Technology (F), Nikon (F), Kao Corp. (F), Topcon (F), Tomey Corp (F). Makita, Yasuno: Yokogawa Electric Corp. (F), Sky Technology (F), Nikon (F), Kao Corp. (F), Topcon (F), Tomey Corp (F, P). Shen, Fukuda, Yamashita, Oka, Matsusaka, Kano: None. Oshika: Topcon (F), Tomey Corp (F).