Abstract
Scaffold-based bone tissue engineering aims to develop 3D scaffolds that mimic the extracellular matrix to regenerate bone defects and damages. In this paper, we provide a laser speckle analysis to characterize the highly porous scaffold. The experimental procedure includes in situ acquisition of speckle patterns of the bone scaffold at different times under preserved environmental conditions, and follow-up statistical post-processing toward examining its internal activity. The activity and overall viscoelastic properties of scaffolds are expressed via several statistical parameters, and the variations in the computed parameters are attributed to time-varying activity of the samples during their internal substructure migration.
1. Introduction
Bone is a basic element of the human skeleton supporting and protecting various vital organs within it [1–3]. It undergoes continuous renovation during our lifetime and is made of four types of cells: osteoblasts, osteoclasts, osteocytes, and bone lining cells, which regulate bone homeostasis dynamically [4,5]. Creating tissue constructs that can be replaced by the bone in both structure and function has received intensive attention [6]. A bone graft or scaffold, while providing all the necessary environmental cues found in natural bone, should mimic the structure and mechano-chemical properties of the natural bone extracellular matrix. This is where bone tissue engineering becomes important. Different methods use various synthetic or natural, biodegradable or non-biodegradable materials in the fabrication of bone scaffolds [7,8]. The scaffold, after implantation, should elicit a desirable local or systemic response to the host, whilst undesirable effects may also reduce healing or cause rejection by the body [9–11]. A successfully fabricated scaffold must possess few aspects: (1) degrades over time while providing the necessary structural support, (2) eventually allows the original cells to replace the implanted scaffold, (3) degraded parts must be non-toxic and able to exit the body without interference with other organs [12,13], (4) has a high porosity ensuring cellular penetration and adequate diffusion of nutrients to cells within the construct [14,15], (5) has similar mechanical properties to the implementation site [16–18].
Materials used for scaffolds in bone tissue engineering are categorized into four classes: ceramic, composite, polymeric, and metallic scaffolds [10]. Polymeric materials provide more controllability on the physiochemical characteristics of scaffolds, such as porosity, solubility, biocompatibility, enzymatic reactions, and allergic response. The other materials come along with serious drawbacks: ceramics suffer of disadvantages such as brittleness, low fracture strength, difficulty to fabricate, and high density. Biocompatibility of composite materials are often insufficient, and even though metallic scaffolds have high mechanical strength, they are non-biodegradable [7,10,19]. The superiority of polymeric materials and their excellent mechanical properties have led to consideration of synthetic polymers for scaffolds [20]. Materials such as collagen, gelatin, alginate, hyaluronic acid, chitin, and chitosan (CS) are examples of naturally derived polymers [21]. Among these materials, CS has gained great significance in the field of scaffold fabrication. This is because CS possesses several important properties, such as biodegradability, biocompatibility, bioadhesivity, solubility, and non-toxicity to humans [22–24]. The degradation of scaffolds has been studied under different conditions to understand the pertinence of external effects or constituents on their activity. For example, the degradation behavior of the scaffold has been investigated inside micro-channels and static or shaking incubators to understand the role of the shear stress in the changes of scaffolds, in terms of weight loss, water uptake, pH value, porosity, morphology [25]. In this research, we also use CS materials, according to the aforementioned properties to fabricate the scaffolds.
The common polymer characterization methods normally include measurement of water uptake, mass loss, porosity change, etc. [26,27] or complementary imaging either in macro-scales, such as macromorphology that provides very low resolution and low magnification images [26], or in high-resolution scales, such as scanning electron microscopy (SEM) [28,29]. They have their own limitations. SEM, for example, although being high resolution and suitable for 3D imaging, is expensive, and must be housed in an area free of any possible electric, magnetic, or vibration interference. In SEM, sample preparation is required, which can result in artifacts and errors and might be damaging, and the method can be applied only to solid inorganic samples, small enough to fit inside the vacuum chamber. Atomic force microscopy (AFM), in comparison to SEM, is free of special sample treatment, expensive vacuum environment, and high maintenance and can be higher in resolution and can be also used for liquids [30,31]. However, its scanning speed is slow, proximity of its tip can be destructive to the sample, and it also unable to work for dynamic specimens. Other studies by placing the scaffolds under different conditions have been pursued to understand their degradation and the effect of external constituents and stimuli, e.g., inside micro-channels and by applying external movement to investigate the role of the shear stress in the changes of scaffolds [25,32]. Here, by the use of dynamic speckle pattern analysis we interrogate the activities on the surface structure of the scaffolds. Speckle light patterns are high-contrast, fine-scale granular patterns that are the result of the interference of a large number of dephased but coherent monochromatic light waves propagating in with different directions [33]. Such kind of interference can be formed through different processes, such as scattering of laser light from a rough surface or mode-mixing in a multimode fiber [34]. Despite the intrinsic randomness of these patterns, the analysis of the speckle patterns may find interesting usefulnesses, and the methodologies based on speckle patterns have been considered as versatile tools to purposively investigate numerous physical, chemical and biological phenomena [35,36]. In the case of speckle patterns that are obtained through the scattering of laser light from a rough surface, each point on the illuminated area acts as a source of secondary waves and contains information about the surface. Therefore, throughout the image recording device, overall information about the surface will be present.
Dynamic speckle patterns occur when an illuminated surface includes any kind of activity. Based on the origins and characteristics of dynamic speckles the knowledge about the inner dynamics of the phenomena may be increased. The more inner dynamics of the samples are known, a better insight can be obtained in controlled experiments and simulations to assess how these dynamics show up in the speckle evolution. Several types of research have been carried out involving the dynamic speckle analysis: monitoring and investigation of blood flow [37–39], seed health [40], fruit ripeness [41], paper crumpling [42], tissue viscoelastic properties evaluation [43,44], adhesive drying [45], and parasite motility [46] are among the applications, to name a few. The advantage of the presented methodology over the common polymer characterization techniques includes possibility of dynamic and live acquisition of information about the samples. It is a nondestructive and noncontact method and provides spatiotemporal information integration. In addition, this technique is free of phototoxic effects on the sample since a very low laser power is used to illuminate the samples. Dynamic speckle analysis can be applied in the same manner for all the classes of materials that are used in bone tissue engineering, i.e., ceramic, composite, polymeric, and metallic scaffolds. Here we focused on polymeric materials for their excellent mechanical properties. The method can be used for long period studies even for days, providing that the environmental conditions for the samples are preserved.
The application of the dynamic speckle analysis method on the CS scaffold is addressed in this paper. In Section 2 the experimental procedure and the theoretical background on the statistical analysis of dynamic speckle patterns are described. In Section 3 the experimental results are presented and the analysis results are discussed. The paper is concluded in Section 4.
2. Materials and methods
2.1. Sample preparation
Several methodologies exist to provide porous scaffolds [47]. Freeze-casting is one of the most common ones since it is environmentally and economically friendly [48]. The samples in this study are prepared with the Freeze-casting method. CS (Acros Chemical Co.) has deacetylation degree of 85% and molecular weight of 100000-300000. CS is dissolved in 1wt acetic acid (Merck Inc.) by stirring for 24 h at room temperature to prepare 2wt CS solutions. This solution is then poured into the self-made plastic molds and is kept frozen at -20 °C (24 hours), followed by freeze-drying for 24 h to achieve the porous structure of 3D CS scaffolds. The prepared scaffolds are immersed in 1 NaOH (Merck Inc.) for 2 h to remove any residual acetic acid, and further washed several times with sterile water to reach pH=7.0 level. The CS samples are lyophilized again overnight in a freeze dryer until getting dried. Finally, scaffolds of 10 mm in diameter and 3 mm in thickness are fabricated.
2.2. Experimental procedure
The experimental procedure for recording dynamic speckle patterns is shown schematically in Fig. 1(a). The laser beam (He-Ne Laser, 632.8 nm, 5 mW) passes through a spatial filter (SF), which filters out the unwanted spatial frequencies in the Fourier space through placing a pinhole in the lens focal plane. The emerging beam is highly divergent and by the use of another lens () it is collimated to provide a uniform beam profile. The collimated beam is directed through mirror M into the sample (S) to illuminate it. The speckle pattern is created and recorded on a digital camera (DCC1545M, Thorlabs, 8-bit dynamic range, 5.2 m pixel pitch) by a collecting lens (). has focal length of 10 cm and of 2. The camera is set to record 700700 pixels in its central area with the exposure time of 0.20 ms. The He-Ne laser possesses sufficient coherency and stability. The laser is switched on at least half an hour before the experiment to ensure intensity stability, which is of high importance in speckle analysis. The laser is kept on during the experiments and by using a laser shutter (Sh), without touching the elements of the setup, the beam is blocked. When required, the laser shutter is removed and the data is acquired. The uniformity of the beam is checked by placing a mirror in the place of the sample and collecting the reflected light by the camera for about a minute.
Fig. 1.
(a) Experimental setup for dynamic speckle acquisition; Sh: shutter, SF: spatial filter, L1: collimating lens, M: mirror, L2: collecting lens. (b) A SEM image of a porous bone scaffold sample. (c) A picture of overall scaffold sample.
The sample is placed in a dish including phosphate buffered saline (PBS) solution. PBS closely mimics the pH, osmolarity, and ion concentrations of the human body. Therefore, PBS solution with a pH of 7.4 in C is used here to simulate the condition of a healthy human body [49,50]. In order to fix the scaffold in the sample dish we pinned it using a couple of thin rods which are supported by magnets from the bottom of the dish. The sample dish has a lid to prevent evaporation of PBS during the experiment. The dish is placed inside a container filled up of liquid paraffin, which is heated by a feedback-controlled plate heater to create a thermal equilibrium and maintain the sample temperature at 37 C. The closed chamber is not in direct contact with air. However, the experiments were performed inside an isolated room for the reason of controlled temperature and humidity, and these parameters of the lab were controlled and live monitored. The humidity level was adjusted to 45%5%. The setup is built on a pneumatic optical table and the laboratory is based on the ground level. Therefore, the vibrational noises are highly damped out. In Fig. 1(b) an SEM image of a typical porous bone scaffold sample is shown. In Fig. 1(c) a picture of the overall sample along with its dimensions is shown, which also demonstrates that the sample is not transparent, and a reflective-mode speckle pattern analysis setup suits its investigation.
Once the laser intensity is stabilized and the sample chamber reached a fixed thermal condition, the sample is shone by the laser beam of uniform intensity. Different parts of the fabricated scaffold sample are prepared and kept inside the PBS solution. The scattered laser beam from the samples is collected and form the speckle patterns. The time evolution of the samples are rather slow, therefore, each experiment for a sample lasts for several hours. The camera is programmed to acquire 100 successive speckle patterns at 25 fps in every 30 min. We record the process of speckle pattern dynamics for several samples for 5 h. For quantitative assessment we consider examination and pattern post-processing of at least 5 samples. The protocol of the experiment is preserved for different samples.
To assure clean data and negligible effect of the noises, such as contaminations in the optical elements, we also conduct control experiments. However, for control experiments, in order to preserve the experimental conditions, and to avoid inclusion of unknown noise sources we do not remove the sample or replace it with a reference one. Instead, since only a part of the sample area is occupied by the scaffold sample, an empty area in the vicinity of the sample, which is also observed by the detector is taken as a reference surface. Then we conduct the speckle analysis procedure on it. The results of a typical control experiment is presented in Supplement 1 (2.1MB, pdf) , Fig. S1.
2.3. Numerical processing
The characterization procedure through dynamic speckle analysis provides a useful description of the surface properties of the sample under study. The activity of the sample, especially in bio-materials, may be revealed through different analysis results. The essence of the present work is to characterize the activity of the bone scaffold as a function of time. This is done by numerically processing the recorded speckle patterns and calculating multiple statistical parameters that are defined in this section. Dynamic laser speckle occurs when an object in dynamic activity is illuminated by a laser light. Therefore, the high spatial and temporal coherence of the laser illumination enables maintaining the speckle pattern stable when the scatterers do not move. As a result, the activity observed by the dynamic laser speckle in biomaterials can be attributed to their internal features, such as growth and cell division, cytoplasmic movement and biochemical reactions, as well as water-related activities [51–56]. Endogenous motions may also be used as a source of deformation, which provides optical mapping of the viscoelastic properties within the biological tissue [56,57]. These motions can be influenced by several factors ranging from the mechanical properties of the extracellular matrix surrounding it to some chemokinetic responses [58]. In biodegradable scaffolds the degradation measurement which can be in terms of mass loss, porosity change, body distortion, etc. is related to the structure of scaffolds [19]. We name the aforementioned structural variations as “internal activities”.
The time history speckle pattern (THSP) is a 2D matrix that represents the time evolution of a set of points, often called image datapack points, in successive speckle patterns. Therefore, a line of a THSP matrix represents this set of points in a speckle pattern during the pattern acquisition and the columns represent the time evolution. The set of points is randomly chosen from the initial pattern in order to reconstruct the first column of THSP. From the successive patterns, the corresponding points are taken to build the other columns of the THSP matrix. THSP provides an immediate graphical sign of the sample activity level; Higher THSP line variations correspond to samples of higher dynamicity [59].
THSP concept is the base of further numerical outcomes, such as auto-correlation (AC), inertia moment (IM), the absolute value of the differences (AVD), co-occurence matrix (COM), etc [59]. Furthermore, several parameters without using the THSP, such as contrast, homogeneity, and roughness parameters (skewness, kurtosis, etc.) may also be evaluated [7]. Here, we consider and define parameters from both aforementioned sets. COM is an intermediary matrix, still graphical, for evaluation of the dispersion of consecutive pixels in a THSP of points monitoring through speckle patterns. It represents a transition histogram of intensities:
| (1) |
IM is a numerical activity indicator and statistical outcome defined as:
| (2) |
where the normalization is for reduction of the inhomogeneities effect in the analyzed images, and is performed in a way to make the sum of values in each line of the COM equal to 1. The name “inertia moment” is taken from the mechanical analogue of this operation.
Autocorrelation (AC) is an important factor to derive the mean square displacements (MSD), which implies statistical data diffusion in samples and is meaningful especially in biological samples [44]. Typically, the speckle intensity temporal autocorrelation curve, AC, is obtained by measuring the correlation between pixel intensities analyzed in the first speckle frame with subsequent frames, over the imaging duration or image sequence [60].
The correlation is calculated between the pixels of THSP in the instant , THSP, and the pixels in the instant , THSP:
| (3) |
where indicates mean calculation. In the context of diffusing wave spectroscopy, it is shown that the AC of the speckle pattern can be quantitatively related to the embedded scatterers in a solid matrix, such as the present specimen we use [61]. The fluctuations in either their refractive index or local density, or, more generally, in any arbitrary deformation of them may cause changes in their intensity ACs [62]. The AC function of TSHPs, similar to the AC of intensity patterns function, is directly related to the MSD of the scatterers between the instant and the instant [63]:
| (4) |
where is the wave vector of the incident light and is a coefficient that depends on the polarization state of light. Therefore, from the AC curve, MSD, i.e., of contributing scatterers of the samples that produce the speckle patterns may be retrieved. Equation (4) is the approximated expression for the case of moderately scattering samples with light absorption. The general expression is discussed in detail in [62]. Technically, MSDs are obtained from the fitted curves to the experimental data points.
Furthermore, statistical processing on the speckle intensity patterns can result in roughness parameters, i.e. different moments of the deviation from the mean values of the intensities throughout the patterns. Average roughness () represents the average variation of intensities to mean value of data and root mean square () represents the standard deviation of the distribution:
| (5) |
| (6) |
where and are the horizontal and vertical sizes of the speckle patterns, and count the pixel numbers, and is the intensity throughout the speckle patterns. These metrics can be used to provide a general estimate of the distribution roughness.
Similarly, Skewness, , and Kurtosis, , are other common roughness parameters to evaluate the samples:
| (7) |
| (8) |
According to the definition of , being the third moment of the deviation from the mean value, it is a measure of the degree of symmetry of the distribution of intensities. Negative skew indicates a predominance of valleys, i.e. low intensities, while positive skew indicates a “peaky” distribution. = 0 indicates a surface with symmetric intensity distribution, and () indicates the presence of extreme peaks (valleys) on the pattern [64]. Kurtosis, , is a parameter that measures the sharpness of the distribution throughout the pattern. For a perfectly random distribution of intensities with a Gaussian probability density function . Kurtosis is related to the width of the intensity distribution. values smaller than 3.0, however, indicate broader distributions corresponding to the speckle patterns described as gradually varying, free of extreme peaks or valley features in the intensity distributions. Values greater than 3.0 indicate the presence of inordinately high peaks or deep valleys. Due to the inclusion of negative values of deviations to mean value, we choose and examine skewness as the representer to the speckle pattern roughness analysis. There are, of course, multiple parameters to retrieve further information regarding the samples through their statistical analysis. For example, there are some parameters that include the distribution of differentiations on the distributions, which provide complementary information on the roughness of the function [64].
It is remarkable that the roughness parameters of the “intensity” distribution throughout the speckle field are calculated and assumed to resemble the roughness of the sample surface. These sets of parameters are inherently different as the former set is associated with the intensity fluctuations and the latter to the height fluctuations throughout the sample surface. However, it is the rough surface that produce the speckle patten when illuminated with the laser beam due to the scattering of light rays. Similar trends of the two different sets parameters for various samples have been already studied and reported [65,66].
3. Results and discussion
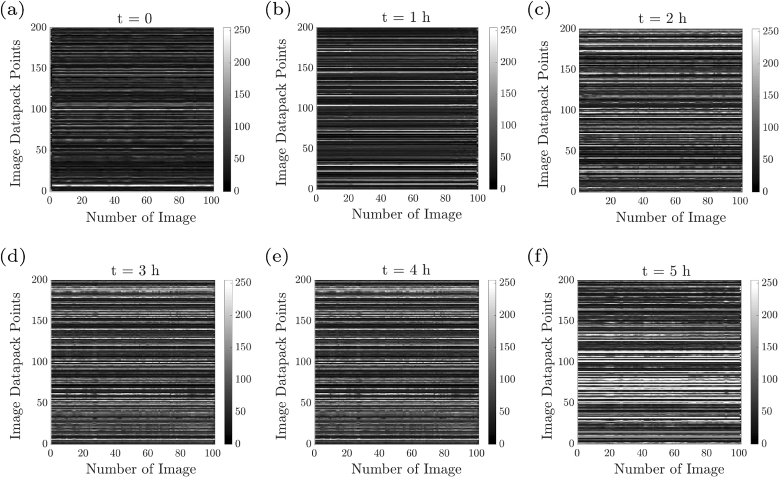
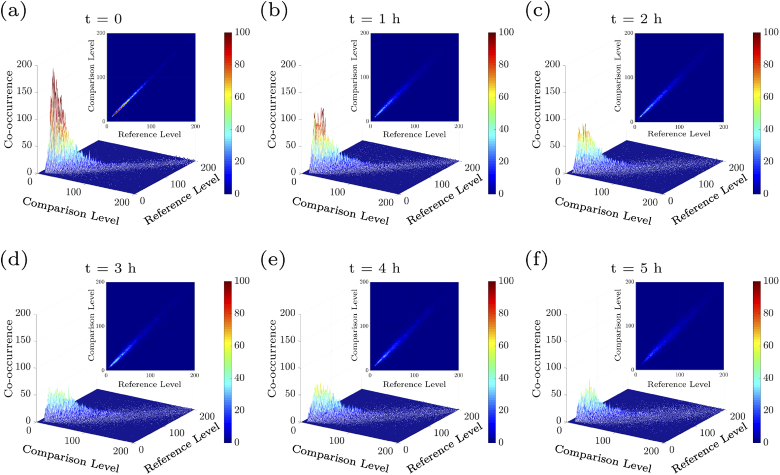
Figures 2(a)–2(f) show the THSP matrices for a typical scaffold sample at the beginning of the experiment and after 1 to 5 h after the experiment starts. THSPs are built by putting the intensity of 200 random pixels throughout a collection of 100 speckle patterns together. Therefore, big fluctuations in the intensity of the points will be the result of the high internal activity of scaffolds. Recognizable bright horizontal lines appearing-disappearing as well as the appearance of discontinued lines in the THSPs as time goes indicate a growing activity of the scaffold during 5 h of sample examination. In very high activity cases the THSP pattern turns into an ordinary speckle pattern, in which the bright lines cannot be recognized and the structure resembles a random light field. Further, for better understanding the changes in the activities, we calculated the associated COM matrices of the samples at the aforementioned time intervals. Figure 3(a-f) shows the resulted 3D plot and 2D map of COM matrix of the THSPs of scaffold’s time evolution (depicted in Fig. 2), at every 1 h after the experiment starts. Reference level and comparison level show intensity levels of and in Eq. (1), respectively. From Fig. 3 two points may be remarked: (1) it is observed that the points are spread further away the principal diagonal of COM and the matrix resembles a cloud as time passes, and (2) the number of points with very high COM values decrease in longer times. According to the definition of COM and THSP, higher activities are associated with more frequent and bigger departures from the diagonal per unit time. Therefore, the distributions around its principal diagonal are related to homogeneous samples while the appearance of nonzero elements far from the diagonal represent strong fluctuations in the sample. Usually, COM values are normalized and is called “modified co-occurrence matrix” [67] in order to represent the transition probability matrix between intensity values in the THSP. Therefore, the number of points with high COM values does not provide additional information about the sample.
Fig. 2.
Time history speckle pattern (THSP), formed by tracking 200 random points throughout a collection of 100 speckle patterns of scaffold (image datapack points). The results at (a) the beginning of the experiment, and (b) t=1 h, (c) t=2 h, (d) t=3 h, (e) t=4 h, and (f) t=5 h after the experiment starts, are shown.
Fig. 3.
(a-f) 3D plot and 2D map of COM matrix of the associated THSPs in Fig. 2 at every one hour after the experiment starts. Reference level and comparison level show intensity levels of and in Eq. (1), respectively.
To provide a more quantitative assessment of the spread of the COM values around the principal diagonal as an activity indicator for the scaffold samples, we computed the IM values of several samples as a function of time. Figure 4 shows the average IM value of the 5 samples at every 30 min. The definition of IM is based on summation on the squared row distance to the principal diagonal of THSP and hence it is the right quantitative representer to the “cloudiness”, e.g. amount of data spreading of COM distribution around its principal diagonal. Figure 4 shows increasing of IM values and the increasing activity of the scaffold samples as time passes during the experiment. The error bars correspond to the averaging over five IM values associated with the five samples. The increase of the IM can be attributed to the scaffold activity during its internal substructure migration. However, the increase does not follow a single linear behavior during the whole experiment. Instead, it seems in the longer times after the experiment onsets there is only a flatter upward change as a function of time. Moreover, the error bars also experience a slight increase during the experiment.
Fig. 4.
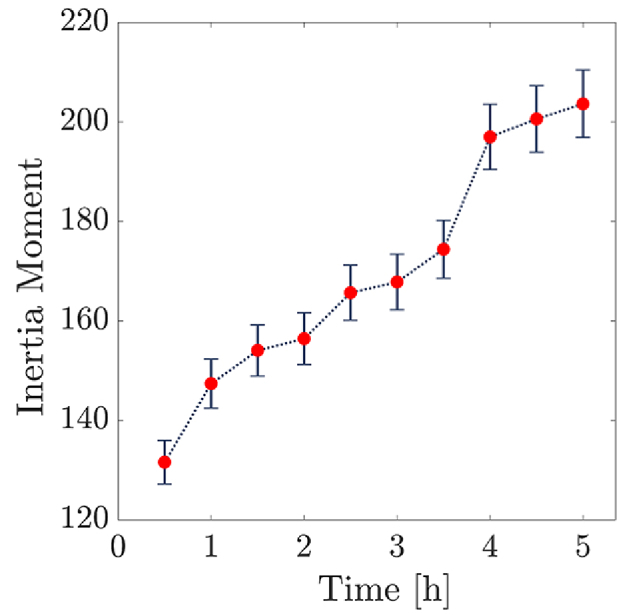
Average inertia moment over the scaffold samples’ THSPs as a function of time.
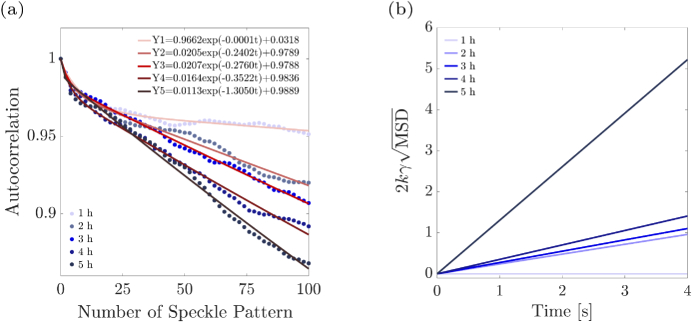
The fact that the scatterers in the bone scaffold can also move during morphogenesis [62], enables us to consider rheology related indicators [44]. Typically, the speckle intensity temporal autocorrelation curve is obtained by measuring the correlation between pixel intensities in the first speckle frame with subsequent frames over the acquisition duration, i.e. the constructed THSPs. Figure 5(a) demonstrates the AC variations as a function of time, for the 100 speckle patterns acquired every 1 h. Different bluish colors depict different evaluation times. Then to each set of calculated AC values we fit an exponential function, according to Eq. (4). The fitted functions are depicted by reddish lines for different evaluation times and the resulted fitting parameters are shown in the legend of Fig. 5(a) (Y1 to Y5). According to Eq. (4), we expect a linear variation vs. time for . Due to this, in Fig. 5(b), the sketched fitted curves are linear as a function of time. We sketched them for 4 seconds as the 100 patterns are acquired for 4 seconds. It shows that the scatterers in the samples get away from each other as time passes, which is another indicator of increasing activities of the samples.
Fig. 5.
(a) Autocorrelation as a function of time for 100 speckle patterns and best fitting functions. (b) as a function of time extracted from the AC curves.
Furthermore, we examined the roughness parameter for the samples. These parameters provide overall information about the surface structure. For porous structures such as bone scaffold studied here the roughness information is important. Figure 6 demonstrates the variations of the skewness parameter. Each data point is obtained by taking an average over the skewness values of 100 speckle patterns, associated with each sample. The error bars correspond to the averaging over the five skewness mean values, and those mean skewness values, themselves, are taken from averaging over the 100 associated speckle patterns for each sample. The variation of skewness shows that the surfaces of the samples get rougher in longer times due to the internal activities happening in the samples. However, similar to Fig. 4, the increase in the values of skewness in the initial stages is higher than the final stages. In Supplement 1 (2.1MB, pdf) , Fig. S4, we have also presented the similar examination of average roughness, root mean square, and kurtosis parameters.
Fig. 6.
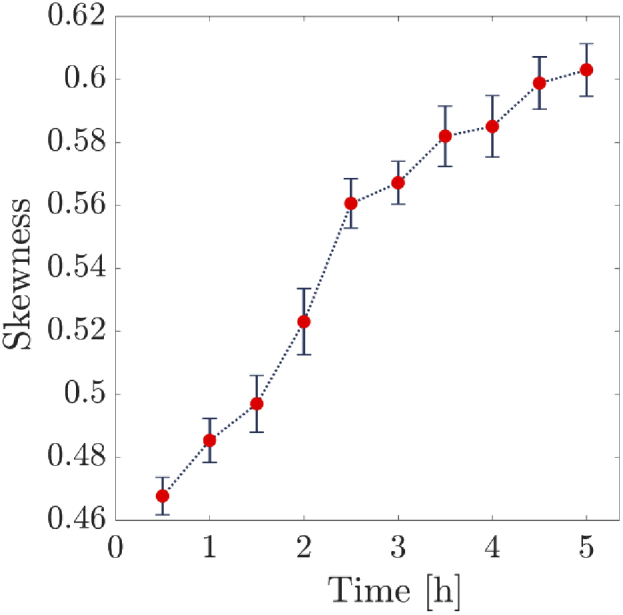
Average skewness of 100 speckle patterns of scaffold surface as a function of time.
The internal activities of bone scaffolds which are revealed by several parameters out of the analysis of speckle patterns are attributed to the interactions between the scaffold material and PBS solution that cause the degradation in long times. These effects can be also studied in microscopic and submicroscopic scales by several imaging technologies. Remarkably, the degradation rate of scaffolds can be measured by porosity change, surface wrinkling, body distortion, and pore size change. i.e., water uptake increases over time in the scaffold. However, the present methodology shows the collective effects and includes both the internal mobilities and the frequent fluctuations of the scaffold matrix.
4. Conclusion
This paper presents an investigation of the scaffold morphology that includes its surface characteristics and internal structure. The investigation is based on a dynamic speckle pattern analysis. We show that scaffold dynamics can be measured by calculating several statistical and morphological parameters. The results show that the internal activities of bone scaffolds are increased by time, which is attributed to the interactions between the scaffold material and PBS solution that cause degradation in long times.
Acknowledgments
The authors would like to thank Hamideh Aghahoseini for the preparation of the samples, and Mohammad-Reza Yaftian for his assistance in performing the experiments.
Disclosures
The authors declare no conflicts of interest.
See Supplement 1 (2.1MB, pdf) for supporting content.
References
- 1.Brotto M., Johnson M. L., “Endocrine crosstalk between muscle and bone,” Curr. Osteoporos. Reports 12(2), 135–141 (2014). 10.1007/s11914-014-0209-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kang H.-W., Lee S. J., Ko I. K., Kengla C., Yoo J. J., Atala A., “A 3d bioprinting system to produce human-scale tissue constructs with structural integrity,” Nat. Biotechnol. 34(3), 312–319 (2016). 10.1038/nbt.3413 [DOI] [PubMed] [Google Scholar]
- 3.Rao S. H., Harini B., Shadamarshan R. P. K., Balagangadharan K., Selvamurugan N., “Natural and synthetic polymers/bioceramics/bioactive compounds-mediated cell signalling in bone tissue engineering,” Int. J. Biol. Macromol. 110, 88–96 (2018). 10.1016/j.ijbiomac.2017.09.029 [DOI] [PubMed] [Google Scholar]
- 4.Mohamed A. M., “An overview of bone cells and their regulating factors of differentiation,” The Malaysian Journal of Medical Sciences: MJMS 15(1), 4 (2008). [PMC free article] [PubMed] [Google Scholar]
- 5.Nakamura H., “Morphology, function, and differentiation of bone cells,” J. Hard Tissue Biol. 16(1), 15–22 (2007). 10.2485/jhtb.16.15 [DOI] [Google Scholar]
- 6.Patrick C. W., Mikos A. G., McIntire L. V., Frontiers in Tissue Engineering (Elsevier, 1998). [Google Scholar]
- 7.Dhandayuthapani B., Yoshida Y., Maekawa T., Kumar D. S., “Polymeric scaffolds in tissue engineering application: a review,” Int. J. Polym. Sci. 2011, 1–19 (2011). 10.1155/2011/290602 [DOI] [Google Scholar]
- 8.Khan A. F., Afzal A., Chaudhary A. A., Saleem M., Shahzadi L., Jamal A., Yar M., Habib A., ur Rehman I., “Synthesis of highly porous composite scaffolds for trabecular bone repair applications,” Sci. Adv. Mater. 7(6), 1177–1186 (2015). 10.1166/sam.2015.2246 [DOI] [Google Scholar]
- 9.Mallick S., Tripathi S., Srivastava P., “Advancement in scaffolds for bone tissue engineering: a review,” IOSR J Pharm Biol Sci 10(1), 37–54 (2015). 10.9790/3008-10143754 [DOI] [Google Scholar]
- 10.Velasco M. A., Narváez-Tovar C. A., Garzón-Alvarado D. A., “Design, materials, and mechanobiology of biodegradable scaffolds for bone tissue engineering,” BioMed Res. Int. 2015, 1–21 (2015). 10.1155/2015/729076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cortizo M. S., Belluzo M. S., “Biodegradable polymers for bone tissue engineering,” in Industrial Applications of Renewable Biomass Products, (Springer, 2017), pp. 47–74. [Google Scholar]
- 12.Niranjan R., Koushik C., Saravanan S., Moorthi A., Vairamani M., Selvamurugan N., “A novel injectable temperature-sensitive zinc doped chitosan/β-glycerophosphate hydrogel for bone tissue engineering,” Int. J. Biol. Macromol. 54, 24–29 (2013). 10.1016/j.ijbiomac.2012.11.026 [DOI] [PubMed] [Google Scholar]
- 13.Loh Q. L., Choong C., “Three-dimensional scaffolds for tissue engineering applications: role of porosity and pore size,” Tissue Eng. Part B: Rev. 19(6), 485–502 (2013). 10.1089/ten.teb.2012.0437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wheelton A., Mace J., Khan W. S, Anand S., “Biomaterials and fabrication to optimise scaffold properties for musculoskeletal tissue engineering,” Curr. Stem Cell Res. & Ther. 11(7), 578–584 (2016). 10.2174/1574888X11666160614101037 [DOI] [PubMed] [Google Scholar]
- 15.Balagangadharan K., Chandran S. V., Arumugam B., Saravanan S., Venkatasubbu G. D., Selvamurugan N., “Chitosan/nano-hydroxyapatite/nano-zirconium dioxide scaffolds with mir-590-5p for bone regeneration,” Int. J. Biol. Macromol. 111, 953–958 (2018). 10.1016/j.ijbiomac.2018.01.122 [DOI] [PubMed] [Google Scholar]
- 16.Saravanan S., Leena R., Selvamurugan N., “Chitosan based biocomposite scaffolds for bone tissue engineering,” Int. J. Biol. Macromol. 93, 1354–1365 (2016). 10.1016/j.ijbiomac.2016.01.112 [DOI] [PubMed] [Google Scholar]
- 17.Prasadh S., Wong R. C. W., “Unraveling the mechanical strength of biomaterials used as a bone scaffold in oral and maxillofacial defects,” Oral Sci. Int. 15(2), 48–55 (2018). 10.1016/S1348-8643(18)30005-3 [DOI] [Google Scholar]
- 18.Sughanthy A., Ansari M., Siva A., Ansari M., “A review on bone scaffold fabrication methods,” Int. Res. J. Eng. Technol 2(6), 1232–1238 (2015). [Google Scholar]
- 19.Chocholata P., Kulda V., Babuska V., “Fabrication of scaffolds for bone-tissue regeneration,” Materials 12(4), 568 (2019). 10.3390/ma12040568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ghassemi T., Shahroodi A., Ebrahimzadeh M. H., Mousavian A., Movaffagh J., Moradi A., “Current concepts in scaffolding for bone tissue engineering,” Arch. Bone Jt. Surg. 6(2), 90 (2018). 10.22038/ABJS.2018.26340.1713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Soundarya S. P., Menon A. H., Chandran S. V., Selvamurugan N., “Bone tissue engineering: Scaffold preparation using chitosan and other biomaterials with different design and fabrication techniques,” Int. J. Biol. Macromol. 119, 1228–1239 (2018). 10.1016/j.ijbiomac.2018.08.056 [DOI] [PubMed] [Google Scholar]
- 22.Ferreira A. M., Gentile P., Chiono V., Ciardelli G., “Collagen for bone tissue regeneration,” Acta Biomater. 8(9), 3191–3200 (2012). 10.1016/j.actbio.2012.06.014 [DOI] [PubMed] [Google Scholar]
- 23.LogithKumar R., KeshavNarayan A., Dhivya S., Chawla A., Saravanan S., Selvamurugan N., “A review of chitosan and its derivatives in bone tissue engineering,” Carbohydr. Polym. 151, 172–188 (2016). 10.1016/j.carbpol.2016.05.049 [DOI] [PubMed] [Google Scholar]
- 24.Balagangadharan K., Dhivya S., Selvamurugan N., “Chitosan based nanofibers in bone tissue engineering,” Int. J. Biol. Macromol. 104, 1372–1382 (2017). 10.1016/j.ijbiomac.2016.12.046 [DOI] [PubMed] [Google Scholar]
- 25.Ma C., Zhang H., Yang S., Yin R., Yao X., Zhang W., “Comparison of the degradation behavior of plga scaffolds in micro-channel, shaking, and static conditions,” Biomicrofluidics 12(3), 034106 (2018). 10.1063/1.5021394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Campbell D., Pethrick R. A., White J. R., Polymer Characterization: Physical Techniques (CRC Press, 2000). [Google Scholar]
- 27.Bismarck A., Aranberri-Askargorta I., Springer J., Lampke T., Wielage B., Stamboulis A., Shenderovich I., Limbach H.-H., “Surface characterization of flax, hemp and cellulose fibers; surface properties and the water uptake behavior,” Polym. Compos. 23(5), 872–894 (2002). 10.1002/pc.10485 [DOI] [Google Scholar]
- 28.Santana B. P., Nedel F., Perelló Ferrúa C., e Silva R. M., da Silva A. F., Demarco F. F., Lenin Villarreal Carreño N., “Comparing different methods to fix and to dehydrate cells on alginate hydrogel scaffolds using scanning electron microscopy,” Microsc. Res. Tech. 78(7), 553–561 (2015). 10.1002/jemt.22508 [DOI] [PubMed] [Google Scholar]
- 29.Kovacs J. Z., Andresen K., Pauls J. R., Garcia C. P., Schossig M., Schulte K., Bauhofer W., “Analyzing the quality of carbon nanotube dispersions in polymers using scanning electron microscopy,” Carbon 45(6), 1279–1288 (2007). 10.1016/j.carbon.2007.01.012 [DOI] [Google Scholar]
- 30.Bellitto V., Atomic Force Microscopy: Imaging, Measuring and Manipulating Surfaces at the Atomic Scale (BoD–Books on Demand, 2012). [Google Scholar]
- 31.Khulbe K. C., Feng C., Matsuura T., Synthetic Polymeric Membranes: Characterization by Atomic Force Microscopy (Springer Science & Business Media, 2007). [Google Scholar]
- 32.Dawson A., Dyer C., Macfie J., Davies J., Karsai L., Greenman J., Jacobsen M., “A microfluidic chip based model for the study of full thickness human intestinal tissue using dual flow,” Biomicrofluidics 10(6), 064101 (2016). 10.1063/1.4964813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bouchaud J.-P., Georges A., “Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications,” Phys. Rep. 195(4-5), 127–293 (1990). 10.1016/0370-1573(90)90099-N [DOI] [Google Scholar]
- 34.Goodman J. W., Speckle Phenomena in Optics: Theory and Applications (Roberts and Company Publishers, 2007). [Google Scholar]
- 35.a. Aizu Y., Asakura T., “Bio-speckle phenomena and their application to the evaluation of blood flow,” Opt. Laser Technol. 23(4), 205–219 (1991). 10.1016/0030-3992(91)90085-3 [DOI] [Google Scholar]
- 36.Fujisawa N., Aiura S., Ohkubo M., Shimizu T., “Temperature measurement of dilute hydrogen flame by digital laser-speckle technique,” J. Visualization 12(1), 57–64 (2009). 10.1007/BF03181943 [DOI] [Google Scholar]
- 37.Fujii H., Asakura T., Nohira K., Shintomi Y., Ohura T., “Blood flow observed by time-varying laser speckle,” Opt. Lett. 10(3), 104–106 (1985). 10.1364/OL.10.000104 [DOI] [PubMed] [Google Scholar]
- 38.Fujii H., Nohira K., Yamamoto Y., Ikawa H., Ohura T., “Evaluation of blood flow by laser speckle image sensing. part 1,” Appl. Opt. 26(24), 5321–5325 (1987). 10.1364/AO.26.005321 [DOI] [PubMed] [Google Scholar]
- 39.Fujii H., “Visualisation of retinal blood flow by laser speckle flowgraphy,” Med. Biol. Eng. Comput. 32(3), 302–304 (1994). 10.1007/BF02512526 [DOI] [PubMed] [Google Scholar]
- 40.Rabal H. J., Braga Jr R. A., Dynamic Laser Speckle and Applications (CRC Press, 2008). [Google Scholar]
- 41.Braga R. A., Dal Fabbro I. M., Borem F. M., Rabelo G., Arizaga R., Rabal H. J., Trivi M., “Assessment of seed viability by laser speckle techniques,” Biosyst. Eng. 86(3), 287–294 (2003). 10.1016/j.biosystemseng.2003.08.005 [DOI] [Google Scholar]
- 42.Rad V. F., Ramírez-Miquet E. E., Cabrera H., Habibi M., Moradi A.-R., “Speckle pattern analysis of crumpled papers,” Appl. Opt. 58(24), 6549–6554 (2019). 10.1364/AO.58.006549 [DOI] [PubMed] [Google Scholar]
- 43.Hajjarian Z., Nia H. T., Ahn S., Grodzinsky A. J., Jain R. K., Nadkarni S. K., “Laser speckle rheology for evaluating the viscoelastic properties of hydrogel scaffolds,” Sci. Rep. 6(1), 37949 (2016). 10.1038/srep37949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hajjarian Z., Nadkarni S. K., “Tutorial on laser speckle rheology: technology, applications, and opportunities,” J. Biomed. Opt. 25(05), 1 (2020). 10.1117/1.JBO.25.5.050801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ansari M. Z., Nirala A. K., “Following the drying process of fevicol (adhesive) by dynamic speckle measurement,” J. Opt. 45(4), 357–363 (2016). 10.1007/s12596-015-0298-x [DOI] [Google Scholar]
- 46.Pomarico J., Di Rocco H., Alvarez L., Lanusse C., Mottier L., Saumell C., Arizaga R., Rabal H., Trivi M., “Speckle interferometry applied to pharmacodynamic studies: evaluation of parasite motility,” Eur. Biophys. J. 33(8), 694–699 (2004). 10.1007/s00249-004-0413-4 [DOI] [PubMed] [Google Scholar]
- 47.Chen G., Ushida T., Tateishi T., “Development of biodegradable porous scaffolds for tissue engineering,” Mater. Sci. Eng., C 17(1-2), 63–69 (2001). 10.1016/S0928-4931(01)00338-1 [DOI] [Google Scholar]
- 48.Deville S., Saiz E., Tomsia A. P., “Freeze casting of hydroxyapatite scaffolds for bone tissue engineering,” Biomaterials 27(32), 5480–5489 (2006). 10.1016/j.biomaterials.2006.06.028 [DOI] [PubMed] [Google Scholar]
- 49.Handzlik P., Fitzner K., “Corrosion resistance of ti and ti–pd alloy in phosphate buffered saline solutions with and without h2o2 addition,” Trans. Nonferrous Met. Soc. China 23(3), 866–875 (2013). 10.1016/S1003-6326(13)62541-8 [DOI] [Google Scholar]
- 50.Du S., Kendall K., Toloueinia P., Mehrabadi Y., Gupta G., Newton J., “Aggregation and adhesion of gold nanoparticles in phosphate buffered saline,” J. Nanopart. Res. 14(3), 758 (2012). 10.1007/s11051-012-0758-z [DOI] [Google Scholar]
- 51.Braga R. A., Dupuy L., Pasqual M., Cardoso R., “Live biospeckle laser imaging of root tissues,” Eur. Biophys. J. 38(5), 679–686 (2009). 10.1007/s00249-009-0426-0 [DOI] [PubMed] [Google Scholar]
- 52.Cardoso R., Braga R., “Enhancement of the robustness on dynamic speckle laser numerical analysis,” Opt. Lasers Eng. 63, 19–24 (2014). 10.1016/j.optlaseng.2014.06.004 [DOI] [Google Scholar]
- 53.Grassi H. C., García L. C., Lobo-Sulbarán M. L., Velásquez A., Andrades-Grassi F. A., Cabrera H., Andrades-Grassi J. E., Andrades E. D., “Quantitative laser biospeckle method for the evaluation of the activity of trypanosoma cruzi using vdrl plates and digital analysis,” PLoS Neglected Trop. Dis. 10(12), e0005169 (2016). 10.1371/journal.pntd.0005169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ramírez-Miquet E. E., Cabrera H., Grassi H. C., d. J. Andrades E., Otero I., Rodríguez D., Darias J. G., “Digital imaging information technology for biospeckle activity assessment relative to bacteria and parasites,” Lasers Med. Sci. 32(6), 1375–1386 (2017). 10.1007/s10103-017-2256-0 [DOI] [PubMed] [Google Scholar]
- 55.Zdunek A., Adamiak A., Pieczywek P. M., Kurenda A., “The biospeckle method for the investigation of agricultural crops: A review,” Opt. Lasers Eng. 52, 276–285 (2014). 10.1016/j.optlaseng.2013.06.017 [DOI] [Google Scholar]
- 56.Vladimirov A., Baharev A., Malygin A., Mikhailova J., Novoselova I., Yakin D., “Applicaton of speckle dynamics for studies of cell metabolism,” in Optical Methods for Inspection, Characterization, and Imaging of Biomaterials II, vol. 9529 (International Society for Optics and Photonics, 2015), p. 95291F. [Google Scholar]
- 57.Braga R. A., González-Peña R. J., Viana D. C., Rivera F. P., “Dynamic laser speckle analyzed considering inhomogeneities in the biological sample,” J. Biomed. Opt. 22(4), 045010 (2017). 10.1117/1.JBO.22.4.045010 [DOI] [PubMed] [Google Scholar]
- 58.Chung S., Sudo R., Mack P. J., Wan C.-R., Vickerman V., Kamm R. D., “Cell migration into scaffolds under co-culture conditions in a microfluidic platform,” Lab Chip 9(2), 269–275 (2009). 10.1039/B807585A [DOI] [PubMed] [Google Scholar]
- 59.Braga R., Silva W., Sáfadi T., Nobre C., “Time history speckle pattern under statistical view,” Opt. Commun. 281(9), 2443–2448 (2008). 10.1016/j.optcom.2007.12.069 [DOI] [Google Scholar]
- 60.Xu Z., Joenathan C., Khorana B. M., “Temporal and spatial properties of the time-varying speckles of botanical specimens,” Opt. Eng. 34(5), 1487–1503 (1995). 10.1117/12.199878 [DOI] [Google Scholar]
- 61.Bicout D., Maynard R., “Diffusing wave spectroscopy in inhomogeneous flows,” Phys. A 199(3-4), 387–411 (1993). 10.1016/0378-4371(93)90056-A [DOI] [Google Scholar]
- 62.Nagazi M.-Y., Brambilla G., Meunier G., Marguerès P., Périé J.-N., Cipelletti L., “Space-resolved diffusing wave spectroscopy measurements of the macroscopic deformation and the microscopic dynamics in tensile strain tests,” Opt. Lasers Eng. 88, 5–12 (2017). 10.1016/j.optlaseng.2016.07.006 [DOI] [Google Scholar]
- 63.Hajjarian Z., Nadkarni S. K., “Evaluating the viscoelastic properties of tissue from laser speckle fluctuations,” Sci. Rep. 2(1), 316 (2012). 10.1038/srep00316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Gadelmawla E., Koura M., Maksoud T., Elewa I., Soliman H., “Roughness parameters,” J. Mater. Process. Technol. 123(1), 133–145 (2002). 10.1016/S0924-0136(02)00060-2 [DOI] [Google Scholar]
- 65.Peregrina-Barreto H., Perez-Corona E., Rangel-Magdaleno J., Ramos-Garcia R., Chiu R., Ramirez-San-Juan J. C., “Use of kurtosis for locating deep blood vessels in raw speckle imaging using a homogeneity representation,” J. Biomed. Opt. 22(6), 066004 (2017). 10.1117/1.JBO.22.6.066004 [DOI] [PubMed] [Google Scholar]
- 66.Petrov N. V., Pavlov P. V., Malov A. N., “Numerical simulation of optical vortex propagation and reflection by the methods of scalar diffraction theory,” Quantum Electron. 43(6), 582–587 (2013). 10.1070/QE2013v043n06ABEH015190 [DOI] [Google Scholar]
- 67.Arizaga R., Trivi M., Rabal H., “Speckle time evolution characterization by the co-occurrence matrix analysis,” Opt. Laser Technol. 31(2), 163–169 (1999). 10.1016/S0030-3992(99)00033-X [DOI] [Google Scholar]