Abstract
Photoacoustic (PA) technology has been used extensively on vessel imaging due to its capability of identifying molecular specificities and achieving high optical-diffraction-limited lateral resolution down to the cellular level. Vessel images carry essential medical information that provides guidelines for a professional diagnosis. Modern image processing techniques provide a decent contribution to vessel segmentation. However, these methods suffer from under or over-segmentation. Thus, we demonstrate both the results of adopting a fully convolutional network and U-net, and propose a hybrid network consisting of both applied on PA vessel images. Comparison results indicate that the hybrid network can significantly increase the segmentation accuracy and robustness.
1. Introduction
Photoacoustic (PA) imaging involves in applying a nanosecond pulsed laser to biological tissues and retrieving induced pressure waves. Acoustic waves are emitted by the process of laser absorption, abrupt rise in temperature and transient thermoelastic expansion. An ultrasonic detector is placed to collect data and reconstruct the target image. It has been shown that the unique optical absorption of substances provide quantification functionalities to endogenous nonfluorescent chromophores (hemoglobin, melanin, lipids and collagen etc.) and contribute to deepening the understanding of pathological knowledge of biological tissues [1,2]. Among various PA imaging categories, optical-resolution photoacoustic microscopy (OR-PAM) stands out due to the high optical-diffraction-limited lateral resolution at a cellular level of micrometers [3]. This non-invasive imaging technique performs significantly well with simultaneous high contrast and high spatial resolutions in vascular biology, ophthalmology, thyroid cancer and breast cancer detection [1,4,5].
Vessel segmentation is an essential task for biomedical imaging analyzing. Thus, it is challenging to provide reliable and accurate vessel segmentation on PA imaging. Boink et al. [6] demonstrated good segmentation accuracy on the blood vessels acquired from photoacoustic computed tomography (PACT). OR-PAM features high spatial resolution and simple imaging reconstruction [3], and thus has found broad applications in vascular imaging. To date, many efforts focus on the segmentation to the blood vessels captured by the OR-PAM system.
Among various image processing tasks, image segmentation has been widely discussed in medical image processing fields (i.e. Skin surface detection [7], surgical vessel guidance [8], and vessel filtering [9] etc.). Further research and articles have proven that various image processing techniques are suitable for vascular segmentation and structural information extraction. Among these, adaptive thresholding based on pixel intensities is one of the simplest approaches, but the low morphological sensitivity to blood vessels often leads to over-segmentation [10]. Feature descriptors such as Hessian matrix have been extensively used in vascular segmentation [11–13] to extract image details and preserve morphological information. However, traditional hessian feature maps suffer from blurriness of small vessels when the Gaussian scale is not chosen with care [5]. Multiscale hessian filter proposed by Frangi et al. demonstrated the advantage of considering all possible aspect ratios [5]. In addition, iterative algorithms such as region growing (RG), and K-Mean clustering have been frequently used in a wide range of image processing fields [14–16]. Diyar et al. demonstrated breast cancer segmentation results based on region growing techniques [17] and Yang et al. presented the segmentation enhancement on OR-PAM for quantitative microvascular imaging [18]. However, it is generally acknowledged that PA images suffer from imaging distortions and noise, which significantly affect the segmenting quality.
Deep learning (DL) has been extensively used in recent years due to development in hardware (GPUs) as well as novel algorithms. Highly accurate segmentation approaches supported by deep learning methods can overcome the aforementioned difficulties. Such rapid development reinforced the growing field of various image processing tasks such as 3D tomography of red cells [19], image classification and segmentation [20]. These tasks demand the use of DL methods and require the capability of handling 2D images. Specifically, Convolutional neural network (CNN) inherits from DL neural networks and has shown its feasibility and superiority when tackling segmentation problems [21]. A recent survey conducted by Yang et al. [22] indicated that deep learning has been widely used in PA imaging fields such as PA image reconstruction [23], quantitative imaging [24], PA image detection [25] & classification [26], PA-assisted intervention [27] and PA segmentation [26]. Apart from the examples mentioned in this survey, other relevant work also provides evidence indicating that deep learning methods applied on medical imaging are feasible and contributing. Zhao et al. introduced an image deblurring deep learning network for optical microscopic systems [28] and motion correction for OR-PAM [29]. However, it was discovered that deep learning models were not widely applied to PA images for vessel segmentation. Thus, relevant research on medical image segmentation based on DL methods have been studied. For instance, Zhang et al. [30] proposed a CNN method for segmenting brain tissues on magnetic resonance imaging (MRI) and Li et al. [31] proposed a CNN model for liver tumor segmentation on computed tomography (CT) images. However, the fully connected layers which appear before the classification node has a lack of consistency with the spatial context [32]. Surprisingly, these difficulties can be solved by using a fully convolutional net (FCN) [33] or U-net [34]. Furthermore, Milletari et al. [35] demonstrated an FCN solution for 3D MRI image segmentation and Li et al. [36] demonstrated that U-net can perform well with liver tumor segmentation on CT volumes.
Hence, in this paper, FCN and U-net were separately applied in PA imaging for vascular segmentation, and a hybrid network consisting of both which are combined via a voting scheme on PA vascular images. The results are qualitatively compared and evaluated on Dice Coefficients, Intersection of Union (IoU), sensitivity and accuracy. The following sections will examine the proposed hybrid network, simulation results and conclusions. An open-source Python code for the simulation of our proposed system can be found in the following linkhttps://github.com/szgy66/Vessel-Segmentation-of-photoacoustic-imaging. Manual annotations of capillaries vary from individuals due to the complex structure. Therefore, the proposed models were not trained for the capillaries segmentation.
2. Method
2.1. Data description
The in vivo vascular images were acquired from the ear of a Swiss Webster mouse using an OR-PAM system that incorporates a surface plasmon resonance sensor as the ultrasonic detector [37,38]. The maximum-amplitude-projection (MAP) image (Fig. 4) was reconstructed by projecting the maximum amplitude of each PA A-line at the depth direction. The system’s lateral resolution was estimated at 4.5m, enabling the visualization of capillaries in addition to major blood vessels (Fig. 4). Our surface plasmon resonance sensor can respond ultrasounds with broad bandwidth, determining the depth resolution of the OR-PAM system at 7.6m [38]. It took around 10 minutes for capturing a vascular image consisting of 512 512 pixels. All experimental animal procedures were performed in compliance with laboratory animal protocols approved by the Animal Studies Committee of the Shenzhen University. With the OR-PAM system, 38 images were obtained while 5 images were discarded due to the presence of either noise, breakpoints or discontinuous, which affects later tests. Due to the insufficient number of images presented by the PA system, data augmentation methods such as cropping, flipping and mapping were applied to the PA images to tackle model overfitting and low training accuracy. Furthermore, the dataset images were cropped into pixels of to accelerate the training process. The final dataset consists of 177 images where 10 of them were randomly selected as testing set and the remaining images were randomly placed into either the training set (133 images) or the validation set (34 images) with ratios of 80% and 20% respectively. In addition, all dataset images were manually annotated by Labelmel, which is a graphical interface image annotation software developed by Massachusetts Institute of Technology that can be found in the following link:https://github.com/CSAILVision/LabelMeAnnotationToo.
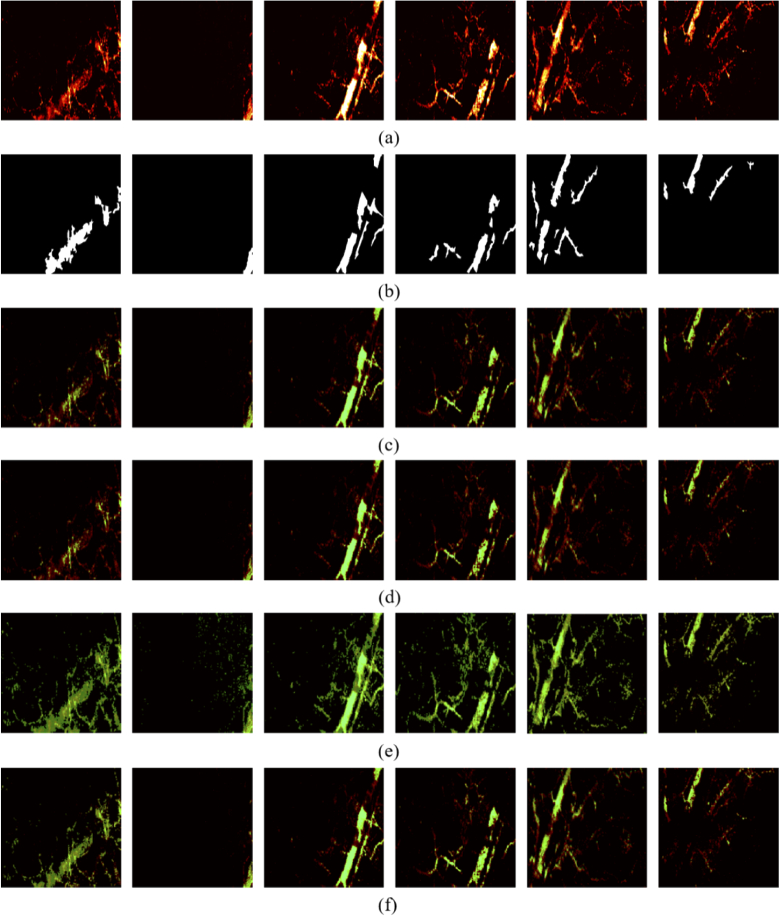
Fig. 4.
Visualization of traditional image segmentation results. (a) Testing images; (b) Manual labels; (c) Threshold segmentation; (d) Region growing; (e) Maximum entropy; (f) K-means clustering.
2.2. Traditional methods
Most existing PA image processing technologies are based on traditional optimization algorithms. In this paper, we mainly discuss four methods (threshold segmentation, region growing, Maximum entropy and K-means clustering) as well as three deep learning approaches (FCN, U-net and Hy-Net).
The threshold segmentation method is to select an appropriate threshold pixel intensity as the dividing line. Thus, a clear classification between the foreground and background can be observed [39]. The two main drawbacks of using thresholding as the segmenting methods are the high sensitivity of threshold selection and lack of considering morphological information.
Region growing (RG) is the process of aggregating pixels or sub-regions into larger regions according to pre-defined criteria [40]. The basic idea is to start from a group of seed points which are manually chosen as the initial points. The seed points can be either a single pixel or a small area. The first step is to combine adjacent pixels or areas with similar properties together and form a new grown seed point. The following step is to repeat the above process until the region has converged (No additional seed points can be found). It can be clearly seen that the key issue with RG is the choice of initial growth point cannot be empirically determined.
Information entropy, as shown in Eq. (1), is used to describe the degree of information uncertainty. The essence of the principle of maximum entropy is that the probability of the occurrence of an event in the system satisfies all known constraints, without making assumptions about any unknown information, in other words treating the unknown as equal probabilities. In the maximum entropy image segmentation [41], the total entropy of the images under all the segmentation thresholds is calculated to find the maximum entropy, and the segmentation threshold corresponding to the maximum entropy is used as the final threshold. The pixels in the image whose gray level is greater than this threshold are classified as the foreground, otherwise classified as the background.
| (1) |
K-means clustering is an iterative algorithm, which can be mainly divided into the following 4 steps: a) a set of randomly selected initial centroids of K classes; b) label each sample according to the distance between them and each cluster center; c) calculate and update the new centroids of each class; d) Repeat steps b), and c) until centroids convergence occur.
2.3. Deep learning methods
Convolutional Neural Networks (CNN) are powerful visual models that produce a hierarchical structure of features. The application of CNN in semantic segmentation has exceeded the most advanced level. Although past models, such as GoogleNet [42], VGG [43] and AlexNet [44], have demonstrated superior performance, none of them achieved an end-to-end training due to the existence of fully connected layers before the network output and a consistent dimension of label size. Furthermore, the fully connected layers of the network expand the extracted features into a one-dimensional vector, thus discarding the spatial information of the feature map extracted from each map. On the contrast, by replacing the fully connected layers with convolutional layers, the spatial information can be preserved with the use of a Fully Convolutional Network (FCN) which avoids the pre-processing and post-processing of images.
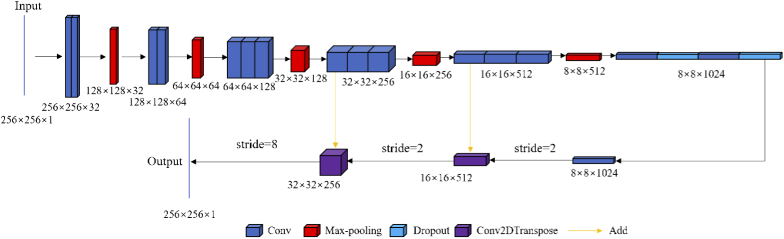
Hence, an FCN model has been introduced in this paper, where the convolutional kernel size has been uniformly set to with a step size of 2. The number of channels and the image size corresponding to each convolution process is written below with the corresponding blocks in Fig. 1. Two up-sampling operations with a step size of 2 and a single operation with a step size of 8 have been performed in the deconvolution process.
Fig. 1.
The structure of FCN.
Each convolution block except for the last layer of the network has been appended with a nonlinear correction unit ReLu. Jun et al. [45] demonstrated that no significant difference can be observed when selecting between up-sampling and ConvTranspose. Hence, up-sampling has been adopted in this network to reduce the number of training parameters. In the meantime, we use two convolution operations and a dropout block to prevent overfitting during the conversion process from convolution to deconvolution. This network implementation was based on an existing FCN method [33].
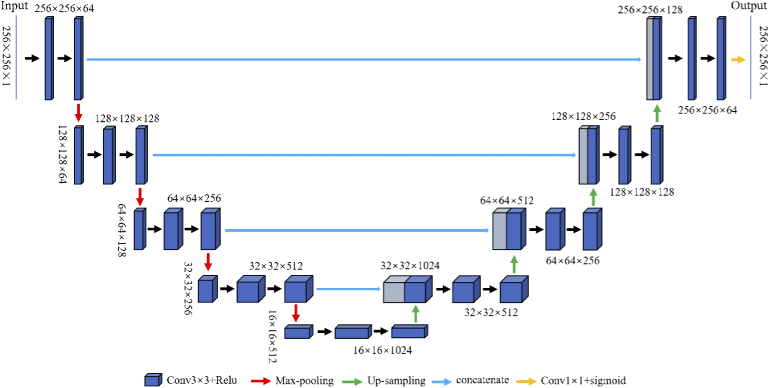
U-net is a model developed based on FCN which demonstrates strong robustness and a wide application field in both academia and industry. Although both networks consist of fully convolutional layers, a subtle difference can be found in the concatenation layer, where it combines the low-level features of the encoding part of the network with the high-level features of the decoding part. This effectively avoids feature-loss caused by the pooling layers in the network. In this paper, the U-net introduced consists of convolution kernels with size , four down-sampling and up-sampling steps with a step size of 2. The corresponding image size and number of channels are written above the blocks in Fig. 2. In this network, the additional layers were replaced by concatenation layers to fuse the low-level features with the high-level features, and the channel capacities were expanded instead of simply adding the corresponding pixels.
Fig. 2.
The structure of U-net.
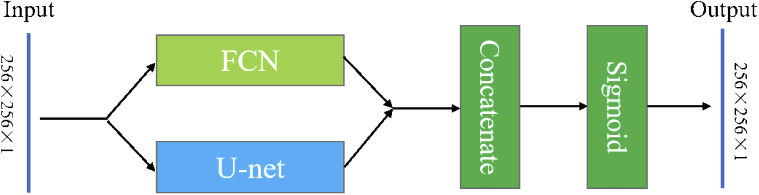
Furthermore, a hybrid deep learning network Hy-Net as shown in Fig. 3 was proposed based on both FCN and U-net as previously mentioned. The Hy-Net combines the results from FCN [33] and U-net [34] with a concatenation block followed by a activation (sigmoid) block.
Fig. 3.
The structure of Hy-Net.
The final probability map, in other words, the network output, is processed by the sigmoid function as expressed in Equation (2). A default threshold has been empirically set to 0.5 indicating that map entries greater than 0.5 are classified as foreground while the remaining entries are considered as the background. Although a default parameter has been used, other values were tested but limited promotion was observed. However, cases of over or under segmentation still exist despite the high segmentation accuracy achieved.
| (2) |
2.4. Evaluation methods
The following four metrics (Dice Coefficient(DC), Intersection over Union(IoU), Sensitivity(Sen) and Accuracy(Acc)) were applied to each test experiment to quantify the performance of our experiments on various segmentation methods. We abbreviate the variables with TP (True Positive), FP (False Positive), TN (True Negative), FN (False Negative) as shown in Table 1. In addition, GT (Ground Truth) and SR (Segmentation Result) were defined to represent our manual segmentation standard and the result of our network output, respectively. Related calculation formulas for the various metrics are shown in Table 2.
Table 1. Definition of TP, FP, TN, FN.
| P(Positive) | N(Negative) | |
|---|---|---|
| T(True) | TP | FP |
| F(False) | FN | TN |
Table 2. Expressions of different evaluation metrics.
| Evaluation metrics | Formulation |
|---|---|
| DC | |
| IoU | |
| Sen | |
| Acc |
2.5. Implementation
The proposed method was implemented in Python 3 by utilizing the public Keras [46,47] front-end package with TensorFlow [48] package as the backend. The learning rate is set constantly to 0.0001 during the training process. We use Adam to optimize the cross-entropy loss function, and the minimum batch size is set to 2. The total number of training epochs is 50. The training time of FCN, U-net and Hy-Net elapsed about 3.052, 5.525 and 6.426 hours respectively on an Intel Xeon Platinum 8158 CPU @3.00GHz 2.99 GHz with 256GB RAM. In the test phase, the prediction of 10 images took about 14s.
3. Result and discussion
3.1. Traditional methods
Four traditional non-deep learning methods are compared in terms of DC, IoU, Sen and Acc as shown in Table 3. A pixel intensity threshold value of 100 has been chosen for the thresholding method and this resulted in a segmentation accuracy of 97.40%. However, the remaining 3 metrics produced were worse and resulted in mean values of 70.98%, 56.09% and 61.64%, respectively.
Table 3. Performance comparison of four evaluation methods.
| Methods | DC(%) | IoU(%) | Sen(%) | Acc(%) |
|---|---|---|---|---|
| Threshold segmentation | ||||
| Region Growing | ||||
| Maximum entropy | ||||
| K-Means clustering |
As mentioned previously, RG requires a selection of initial seed points. Hence, the image pixels were sorted in ascending order in terms of pixel curvature. Pixels with the smallest curvature were determined as the initial seed points. This selection method ensures that the algorithm starts from the smoothest area in the image, thus, reducing the number of divisions taken. The threshold value (the maximum density distance among the 8 pixels around the centroid) was set to 0.8. The RG based method resulted in an evaluation score of 64.30%, 49.70%, 51.96%, and 97.26% for DC, IoU, Sen and acc, respectively.
The maximum entropy method achieved 50.77%, 35.33%, 95.95% and 91.02% for DC, IoU, Sen and Acc respectively.
The K-mean clustering segmentation was implemented in MATLAB by utilizing the imsegkmeans function and resulted in 75.21%, 60.93%, 70.92% and 97.59% for DC, IoU, Sen and Acc respectively. In the meantime, visual comparison results are provided in Fig. 4 to better illustrate the major segmentation difference among various mentioned methods. The original test image, as shown in Fig. 4(a), was presented in RGB channels and represent the raw data captured by the PA imaging system. The ground truth were manually annotated as shown in Fig. 4(b). The segmentation results processed by traditional methods (Fig. 4(c)-(f)) were presented in light green and overlaid with the test image to conveniently observe the overlapping sections.
A few observations and conclusions can be made from Fig. 4. It is clearly seen from columns 3,4 and 5 that traditional methods perform well on bright images with clear contour boundaries. However, these methods perform badly on images with unclear boundaries (columns 1,2 and 6). Hence, it can be concluded that the four mentioned traditional segmentation approaches have a lack of robustness and insufficient generalization.
3.2. Proposed method
Significant improvements in the four evaluation indicators can be observed (Table 4) on the three deep learning methods. Among the deep learning methods, FCN has the worst performance, followed by U-net, whereas Hy-Net has the best. Specifically, U-net outperforms FCN by 13.71%, 17.97%, 13.37%, and 1.46%; Hy-Net model outperforms FCN by 15.34%, 20.05%, 18.62% and 1.55%; Hy-Net outperforms U-net by 1.63%, 2.08%, 5.25% and 0.09%.
Table 4. Performance comparison of the FCN, U-net and Hy-Net.
| Methods | DC(%) | IoU(%) | Sen(%) | Acc(%) |
|---|---|---|---|---|
| FCN | ||||
| U-net | ||||
| Hy-Net | 83.51± 0.11 | 72.15± 0.18 | 88.94± 0.09 | 97.98± 0.02 |
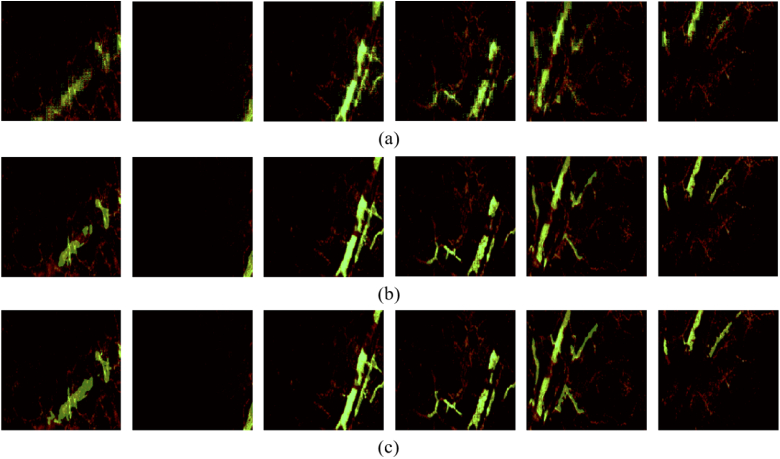
Meanwhile, the visualization results shown in Fig. 5 concludes that the Hy-Net is capable of gaining a high degree of overlapping with the label in both large and small vessel. The segmentation results of the network are represented in green and therefore overlaid on the original image for better comparison.
Fig. 5.
Visualization of DL image segmentation results. (a) FCN; (b) U-net; (c) Hy-Net.
Traditional methods, on the one hand, as mentioned previously, either focus on global or local features which do not consider the information of the image space and leads to sub-optimal segmentation solutions. On the other hand, deep learning methods have demonstrated accurate segmentation results for PA blood vessel images and a significant improvement can be seen when compared with traditional methods. Such improvement can be attributed to the use of convolutional kernels (feature descriptors) and the parameter sharing feature of these kernels, which exploits the overall characteristics of the target image.
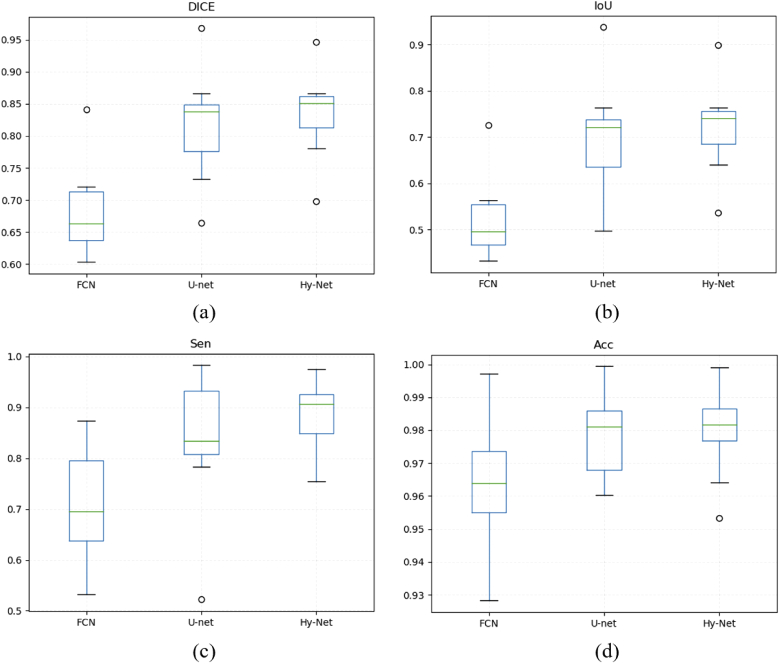
To further analyse the performance of various methods in a statistical manner, a box plot comparison is presented in Fig. 6. The minimum performance values of FCN in terms of DC, IoU, Sen and Acc are 60.31%, 43.17%, 53.23%, 92.82% and the maximum values are 84.07%, 72.52%, 87.43%, 99.71%. The minimum performance values of U-net in terms of DC, IoU, Sen, Acc are 66.38%, 49.68%, 52.20%, 96.03% and the maximum values are 96.77%, 93.75%, 98.29%, 99.94%. The minimum performance values of Hy-Net in terms of DC, IoU, Sen, Acc are 69.83%, 53.65%, 75.47%, 95.32% and the maximum values are 94.67%, 89.87%, 97.49%, 99.90%. The median DICE between the FCN, U-net and Hy-Net are 66.32%, 83.79% and 85.13%, the median IoU between three deep learning methods are 49.61%, 72.10% and 74.11%, the median Sen are 69.57%, 83.36% and 90.62%, and the median Acc are 96.38%, 98.11% and 98.18% respectively.
Fig. 6.
Comparison between the FCN, U-net, and Hy-Net for test images using (a) Dice similarity coefficient; (b) IoU; (c) Sensitivity; (d) Accuracy.
As shown by the quantification and visualization results (Table 4, Fig. 4, Fig. 5), it can be seen that Hy-Net outperforms FCN and U-net and demonstrates good stability and robustness. The main manifestation is that FCN and U-net are both under-segmented. This phenomenon can be further explained by the following two aspects.
-
1.
FCN and U-net both suffer from characteristic limitations of models regardless of different hyperparameter tuning, increasing iterations, or increasing training set size.
-
2.
Hy-Net optimizes the results of the two models by combining the feature output of both FCN and U-net, which effectively avoids the uniqueness of the output from a single model.
Despite of gaining outstanding results from the Hy-Net model, manual annotations do not follow a uniform standard and fluctuates the segmentation accuracy. A visualization of the three worst test images along with the under-segmented (highlighted in red) and the over-segmented (highlighted in blue) results are depicted in Fig. 7 to illustrate the encountered issue. Two main reasons can be concluded from Fig. 7. 1) The over-segmented regions recognized by the model were actual blood vessels but mislabeled by human. 2) The high uncertainty when choosing the binarization thresholds could lead to under or over-segmentations. In this paper, a set of thresholds were tested, and the following configurations (FCN:80, U-net:100, Hy-Net 150) resulted in the best results.
Fig. 7.
Visualization of over- and under- segmentation. (a) Testing images; (b) manual masks; (c) FCN; (d) U-net; (e) Hy-Net.
Considering the one-sidedness of a single probability map, the final thresholding value decision could be sensitive when converting from grayscale to binary, which possibly affects the overall segmentation accuracy severely. Therefore, the combined network output, which is decided by two probability maps, form a final complementarity mask. It can be seen from Table 5 that FCN is much smaller than U-Net in terms of parameters count and memory usage.
Table 5. The summary of required GPU memory for FCN, U-Net and Hy-Net.
| FCN | U-net | Hy-Net | |
|---|---|---|---|
| Number of params | M | M | M |
| Memory of params | MB | MB | M |
4. Conclusion and further works
In this paper, we proposed a deep learning network (Hy-Net) for blood vessel segmentation on PA images. From the results obtained from our experiments, it can be concluded that our method achieve higher accuracy and robustness when compared with traditional methods(thresholding, region growing, maximum entropy and K-Means cluster), and furthermore, the Hy-Net outperforms both FCN and U-net significantly supported by the four evaluation indicators.
The promising results provide motivations for our future work and we are mainly committed to the following four aspects: 1) Annotate our images with the Double-blind method to avoid personal subjective opinions instead of single-person operation; 2) Focus on smaller tissue structures provided by photoacoustic images; 3) Investigate the practicability of applying deep learning models on other photoacoustic images and conduct photoacoustic image segmentations on mice or even human tissues; 4) Exploit and propose other deep learning networks that provide high segmentation accuracy; Propose a novel network for the capillaries segmentation.; 6) Focus on model optimization and parameter simplification to reduce the number of parameters and conduct studies on the microvessel segmentation via transfer learning.
Funding
National Natural Science Foundation of China10.13039/501100001809 (61875130, 11774256); Science, Technology and Innovation Commission of Shenzhen Municipality10.13039/501100010877 (KQJSCX20180328093810594, KQTD2017033011044403); Natural Science Foundation of Guangdong Province10.13039/501100003453 (2016A030312010); Shenzhen University10.13039/501100009019 (No. 860-000002110434).
Disclosures
The authors declare no conflicts of interest.
References
- 1.Wang L. V., “Multiscale photoacoustic microscopy and computed tomography,” Nat. Photonics 3(9), 503–509 (2009). 10.1038/nphoton.2009.157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhou Y., Li M., Liu W., Sankin G., Luo J., Zhong P., Yao J., “Thermal memory based photoacoustic imaging of temperature,” Optica 6(2), 198–205 (2019). 10.1364/OPTICA.6.000198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hu S., Wang L., “Optical-resolution photoacoustic microscopy: Auscultation of biological systems at the cellular level,” Biophys. J. 105(4), 841–847 (2013). 10.1016/j.bpj.2013.07.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Xu M., Wang L. V., “Photoacoustic imaging in biomedicine,” Rev. Sci. Instrum. 77(4), 041101 (2006). 10.1063/1.2195024 [DOI] [Google Scholar]
- 5.Liu T., Sun M., Feng N., Wu Z., Shen Y., “Multiscale hessian filter-based segmentation and quantification method for photoacoustic microangiography,” Chin. Opt. Lett. 13(9), 91701–91706 (2015). 10.3788/COL201513.091701 [DOI] [Google Scholar]
- 6.Boink Y. E., Manohar S., Brune C., “A partially-learned algorithm for joint photo-acoustic reconstruction and segmentation,” IEEE Trans. Med. Imaging 39(1), 129–139 (2020). 10.1109/TMI.2019.2922026 [DOI] [PubMed] [Google Scholar]
- 7.Attia A. B. E., Balasundaram G., Moothanchery M., Dinish U., Bi R., Ntziachristos V., Olivo M., “A review of clinical photoacoustic imaging: Current and future trends,” Photoacoustics 16, 100144 (2019). 10.1016/j.pacs.2019.100144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gandhi N., Allard M., Kim S., Kazanzides P., Bell M. A. L., “Photoacoustic-based approach to surgical guidance performed with and without a da Vinci robot,” J. Biomed. Opt. 22(12), 1–12 (2017). 10.1117/1.JBO.22.12.121606 [DOI] [Google Scholar]
- 9.Oruganti T., Laufer J. G., Treeby B. E., “Vessel filtering of photoacoustic images,” in Photons Plus Ultrasound: Imaging and Sensing 2013, vol. 8581 Oraevsky A. A., Wang L. V., eds., International Society for Optics and Photonics (SPIE, 2013), pp. 319–328. [Google Scholar]
- 10.Zhang J., Yan C.-H., Chui C.-K., Ong S.-H., “Fast segmentation of bone in ct images using 3d adaptive thresholding,” Comput. Biol. Med. 40(2), 231–236 (2010). 10.1016/j.compbiomed.2009.11.020 [DOI] [PubMed] [Google Scholar]
- 11.Shah S. A. A., Tang T. B., Faye I., Laude A., “Blood vessel segmentation in color fundus images based on regional and hessian features,” Graefe’s Arch. Clin. Exp. Ophthalmol. 255(8), 1525–1533 (2017). 10.1007/s00417-017-3677-y [DOI] [PubMed] [Google Scholar]
- 12.Salem N. M., Salem S. A., Nandi A. K., “Segmentation of retinal blood vessels based on analysis of the hessian matrix and clustering algorithm,” in 2007 15th European Signal Processing Conference, (2015). [Google Scholar]
- 13.Zhao H., Wang G., Lin R., Gong X., Song L., Li T., Wang W., Zhang K., Qian X., Zhang H., Li L., Liu Z., Liu C., “Three-dimensional hessian matrix-based quantitative vascular imaging of rat iris with optical-resolution photoacoustic microscopy in vivo,” J. Biomed. Opt. 23(4), 046006 (2018). 10.1117/1.JBO.23.4.046006 [DOI] [PubMed] [Google Scholar]
- 14.Justice R. K., “Medical image segmentation using 3d seeded region growing,” Proceedings of SPIE - The International Society for Optical Engineering 3034, 1 (1997). [Google Scholar]
- 15.Chen C. W., Luo J., Parker K. J., “Image segmentation via adaptive k-mean clustering and knowledge-based morphological operations with biomedical applications,” IEEE Trans. on Image Process. 7(12), 1673–1683 (1998). 10.1109/83.730379 [DOI] [PubMed] [Google Scholar]
- 16.Ng H. P., Ong S. H., Foong K. W. C., Goh P. S., Nowinski W. L., “Medical image segmentation using k-means clustering and improved watershed algorithm,” in 2006 IEEE Southwest Symposium on Image Analysis and Interpretation, (2006), pp. 61–65. [Google Scholar]
- 17.Zeebaree D. Q., Haron H., Abdulazeez A. M., Zebari D. A., “Machine learning and region growing for breast cancer segmentation,” in 2019 International Conference on Advanced Science and Engineering (ICOASE), (2019). [Google Scholar]
- 18.Yang Z., Chen J., Yao J., Lin R., Meng J., Liu C., Yang J., Li X., Wang L., Song L., “Multi-parametric quantitative microvascular imaging with optical-resolution photoacoustic microscopy in vivo,” Opt. Express 22(2), 1500–1511 (2014). 10.1364/OE.22.001500 [DOI] [PubMed] [Google Scholar]
- 19.Lim J., Ayoub A. B., Psaltis D., “Three-dimensional tomography of red blood cells using deep learning,” Adv. Photonics 2(2), 026001 (2020). 10.1117/1.AP.2.2.026001 [DOI] [Google Scholar]
- 20.Xu Y., Jia Z., Ai Y., Zhang F., Lai M., Chang E. I., “Deep convolutional activation features for large scale brain tumor histopathology image classification and segmentation,” in 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), (2015), pp. 947–951. [Google Scholar]
- 21.Kayalibay B., Jensen G., van der Smagt P., “Cnn-based segmentation of medical imaging data,” arXiv preprint arXiv:1701.03056 (2017).
- 22.Yang C., Lan H., Gao F., Gao F., “Deep learning for photoacoustic imaging: a survey,” arXiv preprint arXiv:2008.04221 (2020).
- 23.Antholzer S., Haltmeier M., Schwab J., “Deep learning for photoacoustic tomography from sparse data,” Inverse Probl. Sci. Eng. 27(7), 987–1005 (2019). PMID: 31057659. 10.1080/17415977.2018.1518444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cai C., Deng K., Ma C., Luo J., “End-to-end deep neural network for optical inversion in quantitative photoacoustic imaging,” Opt. Lett. 43(12), 2752–2755 (2018). 10.1364/OL.43.002752 [DOI] [PubMed] [Google Scholar]
- 25.Jnawali K., Chinni B., Dogra V., Rao N., “Transfer learning for automatic cancer tissue detection using multispectral photoacoustic imaging,” in Medical Imaging 2019: Computer-Aided Diagnosis, vol. 10950 Mori K., Hahn H. K., eds., International Society for Optics and Photonics (SPIE, 2019), pp. 982–987. [Google Scholar]
- 26.Zhang J., Chen B., Zhou M., Lan H., Gao F., “Photoacoustic image classification and segmentation of breast cancer: A feasibility study,” IEEE Access 7, 5457–5466 (2019). 10.1109/ACCESS.2018.2888910 [DOI] [Google Scholar]
- 27.Allman D., Assis F., Chrispin J., Lediju Bell M. A., “Deep learning to detect catheter tips in vivo during photoacoustic-guided catheter interventions : Invited presentation,” in 2019 53rd Annual Conference on Information Sciences and Systems (CISS), (2019), pp. 1–3. [Google Scholar]
- 28.Zhao H., Ke Z., Chen N., Wang S., Li K., Wang L., Gong X., Zheng W., Song L., Liu Z., Liang D., Liu C., “A new deep learning method for image deblurring in optical microscopic systems,” J. Biophotonics 13(3), e201960147 (2020). 10.1002/jbio.201960147 [DOI] [PubMed] [Google Scholar]
- 29.Zhao H., Chen N., Li T., Zhang J., Lin R., Gong X., Song L., Liu Z., Liu C., “Motion correction in optical resolution photoacoustic microscopy,” IEEE Trans. Med. Imaging 38(9), 2139–2150 (2019). 10.1109/TMI.2019.2893021 [DOI] [PubMed] [Google Scholar]
- 30.Zhang W., Li R., Deng H., Wang L., Lin W., Ji S., Shen D., “Deep convolutional neural networks for multi-modality isointense infant brain image segmentation,” NeuroImage 108, 214–224 (2015). 10.1016/j.neuroimage.2014.12.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hu W. L. J., “Automatic segmentation of liver tumor in ct images with deep convolutional neural networks,” JCC 3(11), 146–151 (2015). 10.4236/jcc.2015.311023 [DOI] [Google Scholar]
- 32.Liu X., Bi L., Xu Y., Feng D., Kim J., Xu X., “Robust deep learning method for choroidal vessel segmentation on swept source optical coherence tomography images,” Biomed. Opt. Express 10(4), 1601–1612 (2019). 10.1364/BOE.10.001601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Long J., Shelhamer E., Darrell T., “Fully convolutional networks for semantic segmentation,” IEEE Transactions on Pattern Analysis & Machine Intelligence (2017). [DOI] [PubMed]
- 34.Ronneberger O., Fischer P., Brox T., “U-net: Convolutional networks for biomedical image segmentation,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, Navab N., Hornegger J., Wells W. M., Frangi A. F., eds. (Springer International Publishing, 2015), pp. 234–241. [Google Scholar]
- 35.Milletari F., Navab N., Ahmadi S., “V-net: Fully convolutional neural networks for volumetric medical image segmentation,” in 2016 Fourth International Conference on 3D Vision (3DV), (2016), pp. 565–571. [Google Scholar]
- 36.Li X., Chen H., Qi X., Dou Q., Fu C., Heng P., “H-denseunet: Hybrid densely connected unet for liver and tumor segmentation from ct volumes,” IEEE Trans. Med. Imaging 37(12), 2663–2674 (2018). 10.1109/TMI.2018.2845918 [DOI] [PubMed] [Google Scholar]
- 37.Song W., Guo G., Wang J., Zhu Y., Zhang C., Fang H., Min C., Zhu S., Yuan X., “In vivo reflection-mode photoacoustic microscopy enhanced by plasmonic sensing with an acoustic cavity,” ACS Sens. 4(10), 2697–2705 (2019). 10.1021/acssensors.9b01126 [DOI] [PubMed] [Google Scholar]
- 38.Song W., Peng L., Guo G., Yang F., Zhu Y., Zhang C., Min C., Fang H., Zhu S., Yuan X., “Isometrically resolved photoacoustic microscopy based on broadband surface plasmon resonance ultrasound sensing,” ACS Appl. Mater. Interfaces 11(30), 27378–27385 (2019). 10.1021/acsami.9b03164 [DOI] [PubMed] [Google Scholar]
- 39.Wang R., Li C., Wang J., Wei X., Li Y., Zhu Y., Zhang S., “Threshold segmentation algorithm for automatic extraction of cerebral vessels from brain magnetic resonance angiography images,” J. Neurosci. Methods 241, 30–36 (2015). 10.1016/j.jneumeth.2014.12.003 [DOI] [PubMed] [Google Scholar]
- 40.Qian Zhao Y., Hong Wang X., Fang Wang X., Shih F. Y., “Retinal vessels segmentation based on level set and region growing,” Pattern Recognition 47(7), 2437–2446 (2014). 10.1016/j.patcog.2014.01.006 [DOI] [Google Scholar]
- 41.Kapur J., Sahoo P., Wong A., “A new method for gray-level picture thresholding using the entropy of the histogram,” Computer Vision, Graphics, and Image Processing 29(3), 273–285 (1985). 10.1016/0734-189X(85)90125-2 [DOI] [Google Scholar]
- 42.Szegedy C., Liu W., Jia Y., Sermanet P., Reed S., Anguelov D., Erhan D., Vanhoucke V., Rabinovich A., “Going deeper with convolutions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2015). [Google Scholar]
- 43.Simonyan K., Zisserman A., “Very deep convolutional networks for large-scale image recognition,” arXiv preprint arXiv:1409.1556 (2014).
- 44.Krizhevsky A., Sutskever I., Hinton G. E., “Imagenet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems 25, Pereira F., Burges C. J. C., Bottou L., Weinberger K. Q., eds. (Curran Associates, Inc., 2012), pp. 1097–1105. [Google Scholar]
- 45.Jun T. J., Kweon J., Kim Y.-H., Kim D., “T-net: Nested encoder–decoder architecture for the main vessel segmentation in coronary angiography,” Neural Networks 128, 216–233 (2020). 10.1016/j.neunet.2020.05.002 [DOI] [PubMed] [Google Scholar]
- 46.Wang X., Yang L. T., Feng J., Chen X., Deen M. J., “A tensor-based big service framework for enhanced living environments,” IEEE Cloud Comput. 3(6), 36–43 (2016). 10.1109/MCC.2016.130 [DOI] [Google Scholar]
- 47.Chollet F., Deep Learning with Python & Keras (Manning Publications Co, 2018). [Google Scholar]
- 48.Abadi M., Agarwal A., Barham P., Brevdo E., Chen Z., Citro C., Corrado G. S., Davis A., Dean J., Devin M., Ghemawat S., Goodfellow I., Harp A., Irving G., Isard M., Jia Y., Jozefowicz R., Kaiser L., Kudlur M., Levenberg J., Mane D., Monga R., Moore S., Murray D., Olah C., Schuster M., Shlens J., Steiner B., Sutskever I., Talwar K., Tucker P., Vanhoucke V., Vasudevan V., Viegas F., Vinyals O., Warden P., Wattenberg M., Wicke M., Yu Y., Zheng X., “Tensorflow: Large-scale machine learning on heterogeneous distributed systems,” arXiv preprint arXiv:1603.04467 (2016).