Abstract
We propose the signal quality index (SQI) algorithm as a novel tool for quantitatively assessing the functional near infrared spectroscopy (fNIRS) signal quality in a numeric scale from 1 (very low quality) to 5 (very high quality). The algorithm comprises two preprocessing steps followed by three consecutive rating stages. The results on a dataset annotated by independent fNIRS experts showed SQI performed significantly better (p<0.05) than PHOEBE (placing headgear optodes efficiently before experimentation) and SCI (scalp coupling index), two existing algorithms, in both quantitatively rating and binary classifying the fNIRS signal quality. Employment of the proposed algorithm to estimate the signal quality before processing the fNIRS signals increases certainty in the interpretations.
1. Introduction
Functional near-infrared spectroscopy (fNIRS) neuroimaging technique makes it possible to non-invasively investigate brain activity in both experimental and clinical settings [1–12]. In order to guarantee a reliable estimation of the functional hemodynamics in the brain cortex, the initial task of a researcher is to collect signals with a good quality. A poor signal quality may lead to wrong interpretations of the collected data and to consequent findings of false positives and false negatives in the analysis. False positives and false negatives in fNIRS functional experiments are changes in O2Hb and HHb concentrations over a certain brain area that can be caused by task related systemic activity and/or extracerebral hemodynamics, but could be mistakenly interpreted as increased neural activity (false positives) in that brain area, or could mask the neuronally induced hemodynamic response (false negatives) [13].
To the best of our knowledge, there are no standardized criteria for quantitatively assessing fNIRS signal quality unlike, for example, in electroencephalography (EEG), where the impedance of the electrodes with the human scalp can be assessed to infer good scalp contact. These impedances are usually measured and reported, providing researchers with a reference metric for conducting proper set-up and contributing to a standardized assessment of EEG signal quality over the entire research community [14]. In the case of fNIRS, however, it is currently up to the researcher’s expertise and subjective judgment to deem a signal good enough, which makes it difficult to have reliable and reproducible studies. In addition, researchers new to the field of fNIRS are often faced with the issue that they lack the experience to judge the quality of the signals, leading to recordings of poor or inconsistent quality data. Therefore, it is necessary to have an objective measure that quantifies fNIRS signal quality independently of the researcher's experience and subjective judgment.
A high quality fNIRS signal is characterized by the presence of a strong cardiac component, which is the main indicator of a good optode-scalp coupling and can be employed for the assessment of fNIRS signal quality. The reason behind this is that in fNIRS, emitted near infrared light travels through superficial and cerebral layers. When the light passes through these layers, intrinsic and extrinsic factors affect the absorption and scattering of the transmitted light. The intrinsic factors are hemodynamics caused by systemic artefacts in the cerebral and extracerebral compartments, as well as the functional brain hemodynamics in the cerebral compartment [10,15]. The heartbeat is one of such systemic artefacts, present in both compartments [10,13]. Hence, its presence in fNIRS signals indicates that enough light has reached the brain and that most of the absorption and scattering are caused by intrinsic factors. This is not the case when extrinsic factors excessively limit the amount of light reaching the brain, causing a decrease in the optode-scalp coupling and compromising fNIRS signal quality. Examples of extrinsic factors are looseness of the optodes, scalp and skull thickness, skin properties, and hair density and color in the cases where hair is present [16].
With the purpose of assessing the strength of the scalp-optode coupling and the presence of a clear heartbeat in fNIRS signals, two algorithms have been proposed for distinguishing between good and bad quality fNIRS signals: SCI (Scalp Coupling Index, [17]) and PHOEBE (Placing Headgear Optodes Efficiently Before Experimentation, [18]). SCI and PHOEBE, though, are not designed to discern low and high quality signals from medium quality signals. Instead, they are designed to binary discriminate between good and bad quality signals. Such a distinction is sharp and does not consider the different levels of signal quality that a good quality signal may have. For challenging cases in which the amount of light reaching the brain is strongly limited due to unavoidable extrinsic factors, the best quality signal that can be achieved will not have the characteristics of a high quality signal achieved for a less challenging case. Being aware of these differences in the signal quality of the collected data and reporting them is important for subsequent analysis and interpretations. While for photoplethysmography (PPG), an optical modality sharing the same principles as fNIRS, several signal quality measures have been proposed [19,20], for fNIRS no efforts have been conducted so far to rate fNIRS signal quality in more than two levels. Here, we propose an algorithm for quantitatively rating the fNIRS signal quality based on the strength of the optodes coupling with the scalp, providing the fNIRS research community with an objective estimate of fNIRS signal quality and eliminating the researchers’ subjective bias. In this study, the proposed Signal Quality Index (SQI) algorithm is compared with the SCI and PHOEBE algorithms in quantitative rating as well as binary classification of the fNIRS signal quality.
2. Materials and methods
2.1. Data collection and annotation
We assembled two sets of data from previously recorded, unpublished data: a training dataset, to develop and fit the parameters of the algorithm; and a validation dataset, to provide an unbiased evaluation of the performance of the algorithm on an unseen set of data.
2.1.1. Training dataset
The training dataset used in this study consisted of fNIRS recordings of adult healthy volunteers collected with the following devices using OxySoft software (Artinis Medical Systems B.V., Elst, The Netherlands): OctaMon, Brite 23, Brite 24, and OxyMon (all by Artinis Medical Systems B.V., Elst, The Netherlands). The transmitters for all of these devices emit light at two different wavelengths in the near infrared spectrum. This dataset consisted of 158 10-second signal segments of optical densities and HHb and O2Hb concentration changes, which were sampled at 50 Hz. The dataset contains two optical density signals per signal segment, corresponding to the two wavelengths used by each device. The data was collected from 14 participants. The signal segments were sampled from arbitrary channels of the dataset. Source detector distances ranged from 3 to 3.5 cm, and the brain areas measured were prefrontal cortex, temporal cortex and parietal cortex.
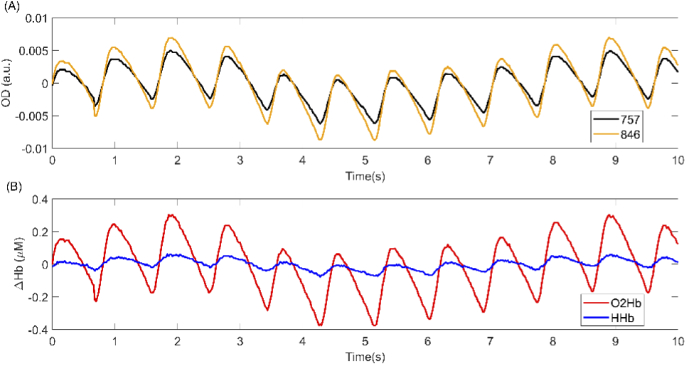
Seven independent fNIRS experts (annotators A-G) working at Artinis Medical Systems B.V. rated all 158 signal segments on the presence of motion artefacts and overall signal quality. Presence of motion artefacts was assessed as a “Yes/No” question. Signal quality was rated on an ordinal scale ranging from 1 (very low quality) to 5 (very high quality). We chose these 5 levels of quality because it is the scale most often used by fNIRS experts working at Artinis Medical Systems B.V. (the annotators) for discriminating between different levels of fNIRS signal quality. For each signal segment, both the changes in optical densities and the corresponding changes in O2Hb and HHb concentrations were shown to the annotator. The signal segments were presented to the annotators in randomized order. Figure 1 and Fig. 2 show, respectively, an example of a signal segment rated as having very low and very high signal quality by all annotators.
Fig. 1.
A sample signal segment having a very low quality. This signal segment was rated as having very low quality by all annotators in the training phase. (A) Orange and black curves represent the detrended optical density signals for the wavelengths 850 and 760 nm, respectively. (B) Red and blue curves represent the detrended changes in O2Hb and HHb concentrations, respectively.
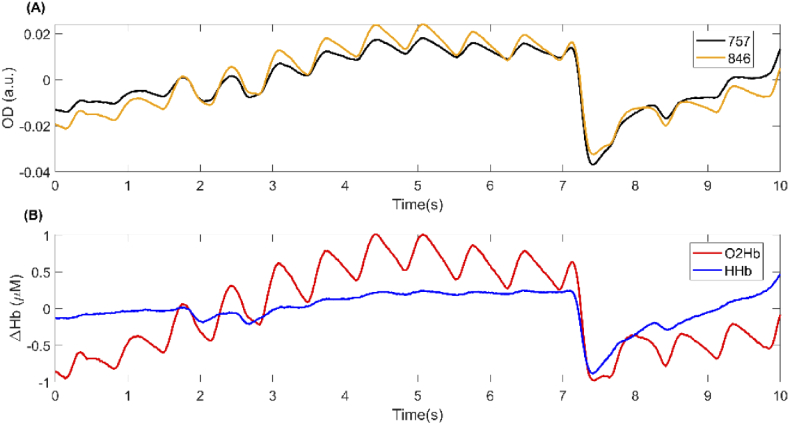
Fig. 2.
A sample signal segment having a very high quality. This signal segment was rated as having very high quality by all annotators in the training phase. (A) Orange and black curves represent the detrended optical density signals for the wavelengths 846 and 757 nm, respectively. (B) Red and blue curves represent the detrended changes in O2Hb and HHb concentrations, respectively.
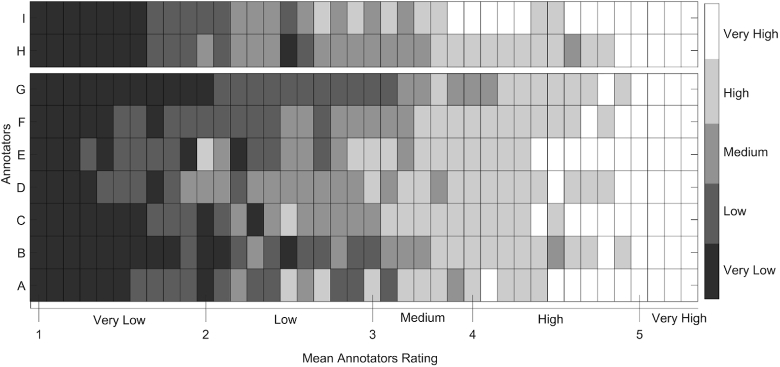
Signal segments containing motion artefacts according to at least half of the annotators were excluded, leaving a total of 123 signal segments. The resulting dataset includes a similar number of signal segments for each of the five different signal quality levels. Figure 3 shows the ratings given by the annotators for each of the 123 signal segments. Generally, very low (1) and very high (5) rated signal segments received similar ratings across annotators, while there was less agreement across the annotators ratings for signal segments that were rated from low (2) to high quality (4). We used the mean annotators rating as the reference rating for the quality of the fNIRS signal segments in the training phase (see section 2.3.1).
Fig. 3.
The ratings given by the annotators for each of the signal segments included in the training dataset. The x-axis represents the mean annotators rating for each of the signal segments from very low to very high signal quality. The y-axis shows the ratings of the seven annotators A-G. The colorbar on the right represents the ordinal rating scale considered by the annotators: 1 (Very Low), 2 (Low), 3 (Medium), 4 (High), and 5 (Very High). The signal segments were sorted in ascending order based on their mean annotators rating.
2.1.2. Validation dataset
For the validation phase, a new set of data was assembled, which comprised fNIRS recordings of adult healthy volunteers collected with the same devices as the training dataset, using OxySoft software (Artinis Medical Systems B.V., Elst, The Netherlands): OctaMon, Brite 23, Brite 24, and OxyMon (all by Artinis Medical Systems B.V., Elst, The Netherlands). This dataset consisted of 40 10-second signal segments of optical densities, which were sampled at 50 Hz (as the data in the training dataset). The data was collected from 4 participants, 3 of which were also included in the training dataset. The signal segments were sampled from arbitrary channels of the dataset. Source detector distances ranged from 3 to 3.5 cm, and the brain areas measured were prefrontal cortex, temporal cortex and parietal cortex.
The validation dataset was rated by the same annotators as in the training dataset, and two additional fNIRS experts working at Artinis Medical Systems B.V., each with more than 10 years of experience in the field of fNIRS. The validation set was free of motion artefacts, and hence the annotators were only asked to rate the signal quality on an ordinal scale ranging from 1 (very low quality) to 5 (very high quality). For the rating, the signal segments were presented to the annotators in the same manner as was done for the training dataset. Figure 4 shows the ratings given by the annotators for each of the 40 signal segments. Although there was less agreement between the annotators ratings for the signal segments that were annotated as having low (2) and medium (3) quality; very low (1), high (4), and very high (5) rated signal segments received similar ratings across annotators. The mean of the annotators ratings was considered as the reference rating for the quality of the fNIRS signal segments in the validation phase (see section 2.3.2).
Fig. 4.
The ratings given by the annotators for each of the signal segments included in the validation dataset. The x-axis represents the mean annotators rating for each of the signal segments from very low to very high signal quality. The y-axis shows the ratings of the nine annotators: the seven annotators that rated the training dataset (A-G) and the two additional annotators I-H. The colorbar on the right represents the ordinal rating scale considered by the annotators: 1 (Very Low), 2 (Low), 3 (Medium), 4 (High), and 5 (Very High). The signal segments were sorted in ascending order based on their mean annotators ratings.
2.2. SQI algorithm workflow
The here developed Signal Quality Index (SQI) algorithm comprises two preprocessing steps (see section 2.2.1) followed by three consecutive rating stages: 1) identifying very low quality signals, 2) identifying very high quality signals and 3) signal quality rating. Rating stage one and two hereby serve as heuristics to identify signal segments with clear characteristics of very low quality signals or very high quality signals, respectively, early on. In the third stage, a signal segment could still be rated as having very low or very high quality, but could also receive a rating in between.
The workflow of the SQI algorithm per signal segment is as follows (see Fig. 5). After signal preprocessing (see section 2.2.1), the signal segment enters rating stage one (for more details, see Materials and Methods, section Rating stage one: identifying very low quality signals), where it is identified as a very low quality signal or otherwise enters rating stage two. If the signal segment is identified as a very low quality signal in rating stage one, it is rated with the lowest rating (i.e. 1) and does not go through the subsequent stages of the algorithm. Similarly, in rating stage two (for more details, see Materials and Methods, section Rating stage two: identifying very high quality signals) the signal segment is identified as a very high quality signal or not. If the signal segment is identified as a very high quality signal, it is rated with the highest rating (i.e. 5) and does not enter the signal quality rating stage. If instead the signal segment is not identified as a very high quality signal in rating stage two, then it enters the signal quality rating stage. In this third stage (for more details, see Materials and Methods, section Rating stage three: signal quality rating), a rating between 1 (very low quality) and 5 (very high quality) is assigned to the signal segment.
Fig. 5.
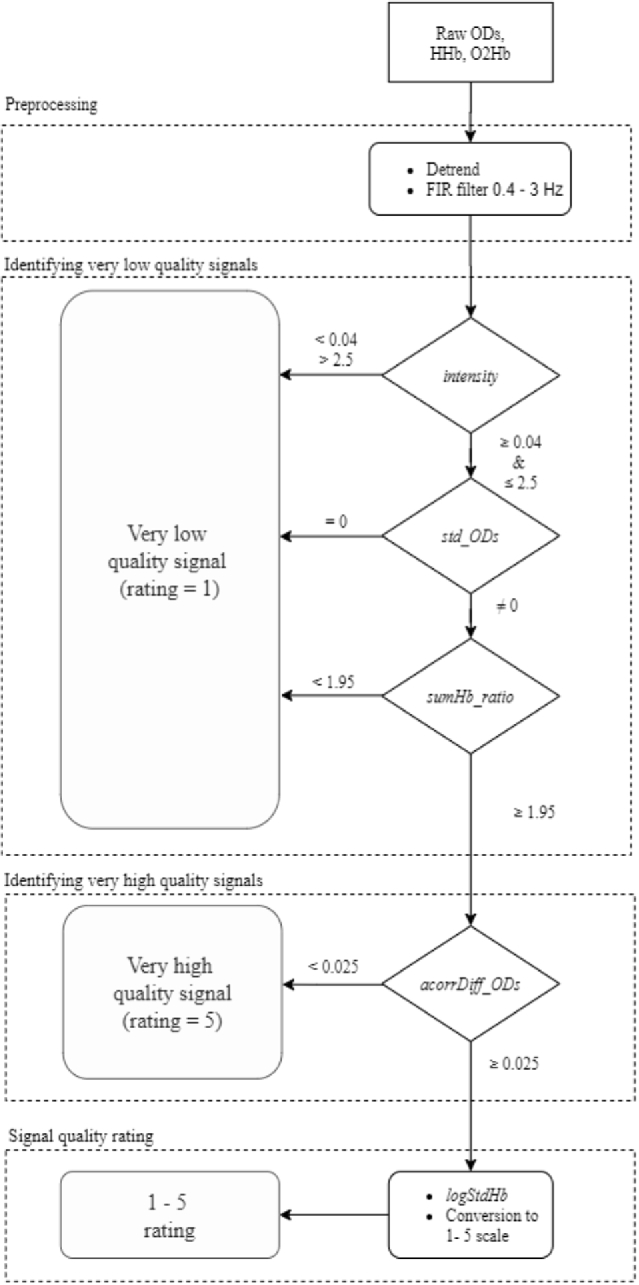
Flowchart of the rating process implemented by the SQI algorithm. The SQI algorithm comprises two preprocessing steps followed by three consecutive rating stages: 1) identifying very low quality signals, 2) identifying very high quality signals, and 3) signal quality rating. A 10-second signal segment is input into the algorithm in the form of raw optical densities and HHb and O2Hb concentration changes. After signal preprocessing (see section 2.2.1 for details), the signal segment enters rating stage one, in which it is evaluated by three consecutive features (see Materials and Methods, section Rating stage one: identifying very low quality signals): absolute light intensity (abbreviated as intensity) assesses whether the intensity of the measured light is within a certain range, standard deviation of the ODs per wavelength (std_ODs) detects whether one or both optical density signal segments are flat, and ratio of oxygenated and deoxygenated hemoglobin summation (sumHb_ratio) assesses the difference in amplitude between O2Hb and HHb. If any of these features exceeds the thresholds for the signal segment, it is identified as a very low quality signal, obtaining the lowest rating (i.e. 1), and does not go through the subsequent stages of the algorithm. Otherwise, it enters rating stage two. In this stage, the feature standard deviation of the difference between optical density signals autocorrelation (acorrDiff_ODs) evaluates whether the two optical densities in the signal segment have similar amplitude and shape. If the value obtained for this feature is lower than the threshold, the signal segment is identified as a very high quality signal, it is rated with the highest rating (i.e. 5), and does not enter the signal quality rating stage. Otherwise, it enters the signal quality rating stage. In this stage, the signal segment is evaluated by the feature logarithm of the ratio between the standard deviation of O2Hb and HHb (logStdHb). This feature characterizes the relative presence of the heartbeat in O2Hb and HHb signals. The raw value obtained for this feature is then converted to assign a rating between 1 (very low quality) and 5 (very high quality).
2.2.1. Preprocessing
First, the received light intensities digitized with 16-bit resolution were converted to optical densities (OD). The optical densities were then converted into oxygenated hemoglobin (O2Hb) and deoxygenated hemoglobin (HHb) changes in concentration by applying the modified Beer-Lambert law [21]. In the following, we processed the OD values as well as O2Hb and HHb, as each of them was required for different features. Two preprocessing steps were applied to ODs, O2Hb and HHb. Firstly, HHb, O2Hb and OD signal segments were detrended by subtracting the least-squares fit of a straight line to the data. Secondly, these signal segments were band-pass filtered using a zero-phase forward Hamming-windowed sinc FIR filter of order 208 with cutoff frequencies (−6 dB) of 0.4 Hz and 3 Hz. The transition width of the filter was of 0.8 Hz, with a passband between 0.8-2.6 Hz, and a stopband (−53 dB) between 3.4 - 25 Hz. The filter order was estimated based on the normalized transition width for the Hamming window [22]. This band-pass filter was implemented using ft_preproc_bandpassfilter function in the FieldTrip toolbox [23], commit 62c9a0d on master branch. In order to avoid edge artefacts, prior to filtering, the signal segments were zero-padded with a sample length corresponding to two seconds of data both in the beginning and end of the signal segment.
2.2.2. SQI features
2.2.2.1. Rating stage one: identifying very low quality signals
We used three different features for assessing whether a signal segment is identified as a very low quality signal in this stage:
-
•
Absolute light intensity (abbreviated as intensity): this feature represents the intensity of the measured light, which should be within a certain range in order to guarantee a linear response from the system and a sufficient signal-to-noise ratio. Bright ambient light, low pigmentation in skin and hair, or lack of hair can saturate the detector, while too little or no light could indicate that there is too much light absorption, e.g. by hair between the scalp and the optodes. We use a thresholding of the raw light intensity, as has previously been used in [16,24]. Lower (too much light) and upper thresholds (too little light) were respectively set to 0.04 OD and 2.5 OD. If the signal segment exceeded these thresholds, it was identified as a very low quality signal.
-
•
Standard deviation of the ODs per wavelength (std_ODs): this feature detects whether one or both optical density signal segments are flat, and thus have a standard deviation of zero, indicating a poor coupling with the scalp. This feature was calculated as the standard deviation of the optical density over the whole 10-second length of the signal segment. If the signal segment obtained a value of zero for either wavelength, it was identified as a very low quality signal. The feature std_ODs was constrained to be equal to zero rather than being evaluated by a higher threshold, because empirical evaluation showed that values different than zero were not discriminative.
-
•Ratio of oxygenated and deoxygenated hemoglobin summation (sumHb_ratio): high quality fNIRS signals are characterized by a clear heartbeat for O2Hb signals, with a smaller and attenuated one for HHb signals (see Fig. 2). This difference makes the sum of the absolute values of the O2Hb signals greater than that of the HHb signals. In contrast, for very low quality fNIRS signals, the opposite happens. Feature sumHb_ratio, considers this difference by computing the ratio between the sum over samples of the absolute value of O2Hb and the sum over samples of the absolute value of HHb for the 10-second signal segment (Eq. (1), where |x| represents the absolute value of x). Low values for this feature indicate very low signal quality due to the prominence of HHb signal amplitude over that of O2Hb. The threshold for this feature was empirically derived from the training dataset and set to 1.95. If the signal segment obtained a value lower than this threshold, it was identified as a very low quality signal.
(1)
2.2.2.2. Rating stage two: identifying very high quality signals
In this stage, we used one feature for assessing whether a signal segment is identified as a very high quality signal:
-
•Standard deviation of the difference between optical density signals autocorrelation (acorrDiff_ODs): for very high quality signals, the autocorrelation for the two optical densities of a signal segment have similar amplitude and shape. Hence, the standard deviation of the difference between them is low. This feature was calculated by Eq. (2), where OD1acorr and OD2acorr are the autocorrelations of the optical densities measured for each wavelength, and std() is the standard deviation.
(2)
A threshold of 0.025 was used, as empirically derived from the training dataset. If the signal segment obtained a value below this threshold, it was identified as a very high quality signal.
2.2.2.3. Rating stage three: signal quality rating
In this stage, we used one feature for rating the signal segment between 1 (very low quality) and 5 (very high quality).
-
•Logarithm of the ratio between the standard deviation of O2Hb and HHb (logStdHb): the natural logarithm of the ratio of the standard deviation of the 10-second O2Hb and HHb time series was computed by Eq. (3). Its output value was used to quantitatively rate the quality of the signal segment in an adimensional magnitude. High quality fNIRS signals are characterized by a strong clear heartbeat as the strongest signal component. For high quality signals, the magnitude of the heartbeat is higher in the O2Hb signal than in HHb. Therefore, the standard deviation of O2Hb is higher than the standard deviation of HHb for high quality fNIRS signals. Consequently, the higher the signal quality, the higher the ratio between them, which adopts an exponential trend. This trend is made linear by means of the natural logarithm implemented in this feature.
(3)
2.3. Performance assessment
We assessed the performance of the SQI algorithm in two different phases: training phase and validation phase. All computation and analysis in this study were done using MATLAB R2019b (MathWorks, Natick, Massachusetts), on an ASUS workstation with Intel Core-i7-8565U @ 1.99 GHz CPU and 16 GB RAM.
2.3.1. Training phase
First, we assessed the correctness of each of the features of the SQI algorithm on the training dataset. Next, we assessed the performance of the SQI algorithm with respect to the mean annotators rating.
2.3.1.1. Features correctness assessment
In order to assess and compare the correctness of the different features included in rating stage one (identifying very low quality signals) and rating stage two (identifying very high quality signals) of the algorithm on the training dataset, we computed the following quantitative metrics: precision in correct identifications, number of signal segments identified as very low quality signals (for features in rating stage one) and number of signal segments identified as very high quality signals (for the feature in rating stage two), correct and incorrect decisions. For rating stage one of the algorithm, the identified signal segments for which the mean annotators ratings were below or equal to 2 (low quality) were classified as correct decisions, and otherwise classified as incorrect decisions. Similarly, for rating stage two of the algorithm, the identified signal segments for which the mean annotators ratings were above or equal to 4 (high quality) were classified as correct decisions, and otherwise classified as incorrect decisions.
For evaluating the correctness of the rating feature logStdHb in the third stage of the algorithm, we used Pearson’s correlation coefficient between the raw feature values and the mean annotators ratings for all 123 signal segments in the training dataset. To test for the significance of the correlation, we considered a significance level α=5% and computed the p-value using a Student’s t distribution as implemented in Matlab's corr function. We applied the Benjamini-Hochberg method [25] to correct for multiple comparisons.
2.3.1.2. Algorithm performance assessment
We assessed the performance of the SQI algorithm in 1) quantitative rating the signal quality, 2) binary classification of the signal quality (good or bad signal quality). We compared the performance of the SQI algorithm with the performance of two existing algorithms used for binary assessing fNIRS signal quality: SCI [17] and PHOEBE [18].
SCI quantifies the similarity of the cardiac component in both optical densities to determine the strength of the coupling between the scalp and the optodes. The algorithm computes the zero-lag cross-correlation between both optical density signal segments as a quantitative measure of the signal-to-noise ratio of the signal segment [17]. According to the original implementation of the SCI algorithm, signal segments with a zero-lag cross-correlation value above 0.75 are considered high quality signals. The PHOEBE algorithm evaluates the similarity of both optical density signal segments by means of the SCI metric, as well as the spectral power of their cross-correlation to determine the strength of the cardiac component. According to the original implementation of the PHOEBE algorithm, signal segments with a spectral value above 0.1 are considered high quality signals. Both SCI and PHOEBE were computed as implemented by the main author of the original papers [26].
2.3.1.2.1. Quantitative rating performance
A regression analysis was performed to obtain the linear models that convert the raw values of the rating feature in the signal quality rating stage of SQI to the 1 - 5 scale that the annotators used for rating. The linear model was built by computing a least squares regression between the mean annotators ratings and the raw values of the rating feature logStdHb on the training data to obtain the slope and intercept. This regression was carried out only on the signal segments that were not identified in rating stage one or two, and that hence entered rating stage three in the SQI algorithm workflow. The slope and intercept were then used to convert the raw value of the rating feature logStdHb to a rating on the 1-5 scale. In order to compare the performance of SCI and PHOEBE with the proposed algorithm, the raw values of the rating features used in SCI and PHOEBE were also converted into a 1-5 scale in the same manner. In this conversion, we considered the zero-lag cross-correlation between the two optical density signals and the peak spectral power of the cross-correlation as the rating features used in SCI and PHOEBE, respectively (see Materials and Methods, section Algorithm performance assessment). The ratings obtained for each of the algorithms in a 1-5 scale will be hereon referred to as estimated ratings.
Moreover, Bland Altman limits of agreement (BLA) [27] were computed between the mean annotators ratings and the estimated ratings introduced in this section for each of the evaluated algorithms SQI, SCI, and PHOEBE. Bland Altman limits of agreement were computed by calculating 1.96 times the standard deviation of the error, representing the range in which 95% of the differences between the mean annotators ratings and estimated ratings fell. Three quantitative measures were calculated to further compare the performance of the evaluated algorithms: mean of error (ME), standard deviation of error (StdE), and coefficient of determination (r2) assessed by Pearson’s correlation coefficient. To test for the significance of the correlation, we considered a significance level α=5% and computed the p-value using a Student’s t distribution as implemented in Matlab's corr function. In addition to the three quantitative measures, the computation time using our reference implementation in MATLAB R2019b (MathWorks, Natick, Massachusetts) for a single signal segment was measured five times and then averaged to compare the time required for each of the algorithms to obtain the estimated rating.
2.3.1.2.2. Binary classification performance
To conduct a binary classification for the proposed SQI algorithm, signal segments identified in rating stage one (identifying very low quality signals) were classified as “bad quality” signals; while those identified in rating stage two (identifying very high quality signals) were classified as “good quality” signals. For the signal segments that entered rating stage three, a threshold for the raw value of the feature logStdHb was empirically derived on the training dataset. This threshold value was set to 1.478. Signal segments with a value equal or higher than this threshold were classified as “good quality” signals. They were otherwise classified as “bad quality” signals. For SCI and PHOEBE, we used the thresholds proposed in the original papers (see [17,18]): a zero-lag cross-correlation value of 0.75 and a peak spectral power of 0.1. For both algorithms, signal segments with values equal or higher than the considered thresholds were classified as “good quality” signals. They were otherwise classified as “bad quality” signals.
To assess the binary classification performance of the algorithms, the mean annotators ratings were binarized by thresholding at a value of 3.5. Signal segments rated lower than this threshold were labeled as “bad quality” signals, while those rated equal to or higher than this threshold were labeled as “good quality” signals. Accuracy, sensitivity, specificity, precision, and F1-Score were computed as performance measures in the binary classification of the signal quality. We applied McNemar’s binomial test [28] with a significance level α=5% to assess whether the classification accuracies obtained for the different algorithms were significantly different from each other. We applied the Benjamini-Hochberg method [25] to correct for multiple comparisons.
2.3.2. Validation phase
In the validation phase, the performance of the SQI algorithm was assessed in the validation dataset in the same manner as performance was assessed in the training dataset. For the quantitative rating, this assessment included computing the estimated ratings of the SCI and PHOEBE algorithms for the validation dataset to allow a comparison with their performance. For this, the feature values of SCI and PHOEBE were converted to a continuous scale from 1 (very low quality) to 5 (very high quality) using the linear models fitted in the training phase (see Materials and Methods, section Quantitative rating performance). For the binary classification, we proceeded as explained in Materials and Methods, section Binary classification performance.
3. Result
3.1. Training phase
3.1.1. Features correctness assessment
The here proposed fNIRS signal quality algorithm, SQI, assesses the quality of fNIRS signal segments in three consecutive rating stages: 1) identifying very low quality signals, 2) identifying very high quality signals and 3) signal quality rating (see section 2.2 for more details). Here, we assess the correctness of these features.
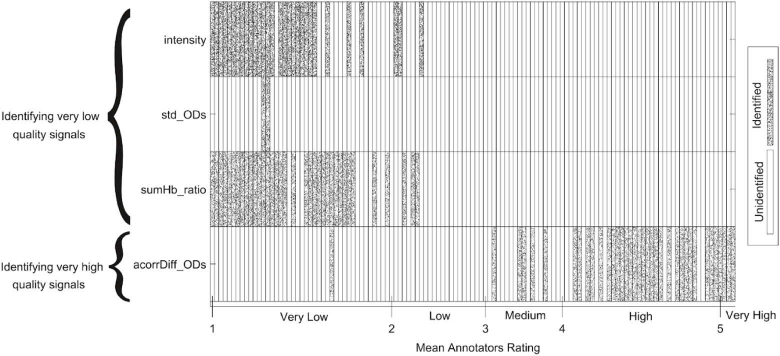
In rating stage one (identifying very low quality signals), the algorithm identifies very low quality signal segments based on three features: the absolute light intensity (abbreviated as intensity), the standard deviation of the ODs per wavelength (std_ODs), and the ratio of oxygenated and deoxygenated hemoglobin summation (sumHb_ratio). For each of these features, we applied an empirically derived threshold to identify signal segments having very low quality. Figure 6 shows the identification of each signal segment by these features. Each signal segment identified as a very low quality signal had a mean annotators rating indicating a low or very low signal quality. This means none of these features incorrectly identified medium, high, or very high quality signal segments as very low quality signals. Although the feature std_ODs correctly identified signal segments with very low quality, its identification completely coincided with the identification of the features intensity and sumHb_ratio. Moreover, the number of identified signal segments is lower than that of the other two features in this stage. Nonetheless, we decided to include this feature in the algorithm because of two reasons. Firstly, it is an intuitive feature that identifies signal segments having at least one optical density signal as a flatline, which is a clear sign of a very low quality signal. Secondly, it potentially avoids misclassification of signal segments in subsequent stages of the algorithm (see Appendix 1 for more details).
Fig. 6.
Signal segments identified during rating stage one (identifying very low quality signals) and two (identifying very high quality signals) of the SQI algorithm. The y-axis shows the three features included in rating stage one at the top, and the feature included in rating stage two at the bottom. The features in rating stage one are: the absolute light intensity (abbreviated as intensity), the standard deviation of the ODs per wavelength (std_ODs), and the ratio of oxygenated and deoxygenated hemoglobin summation (sumHb_ratio). The feature in rating stage two is the standard deviation of the difference between optical density signals autocorrelation (acorrDiff_ODs). The x-axis represents the mean annotators rating for each of the 123 signal segments. The signal segments were sorted in ascending order based on their mean annotators ratings. Cells in the plot filled with a speckle pattern represent the signal segments that were identified as either very low or very high quality signals in the respective rating stage by the feature. Cells left blank represent the signal segments that were not identified by the features in rating stage one and two.
In rating stage two (identifying very high quality signals), the algorithm identifies very high quality signal segments based on one feature: the standard deviation of the difference between optical density signals autocorrelation (acorrDiff_ODs). We applied an empirically derived threshold to identify signal segments with clear characteristics of very high quality signals. Figure 6 shows the output of the feature acorrDiff_ODs and its threshold. Note that we show all 123 signal segments, although the signal segments identified as very low quality signals in rating stage one would not enter rating stage two in the SQI algorithm. The figure shows that most of the signal segments identified as very high quality signals had mean annotators ratings of 4 (high quality) or higher. However, some medium quality signal segments as well as one very low quality signal segment were incorrectly identified as very high quality signals in this stage. As can be seen in Fig. 6, this very low quality signal segment was identified as a very low quality signal by feature sumHb_ratio in rating stage one. This means that in the SQI algorithm workflow, it would not enter rating stage two and would hence not be incorrectly classified by the algorithm.
Quantitative metrics evaluating the correctness of the features in rating stage one and two are reported in Table 1 (for more details, see Materials and Methods, section Features correctness assessment). Regarding the features included in rating stage one, the features intensity and sumHb_ratio identified a greater number of signal segments as very low quality signals than the feature std_ODs. Both features achieved a high precision in the identification (both above 94%). The feature std_ODs identified less signal segments as having very low quality than the other two features, though with 100% precision. In rating stage two, feature acorrDiff_ODs identified 37 signal segments as very high quality signals with a precision of 83.78%.
Table 1. Quantitative metrics for correctness assessment of the proposed features identifying very low (intensity, std_ODs, and sumHb_ratio) and very high (acorrDiff_ODs) quality signal segments in rating stage one and two of the SQI algorithm, respectively.
| Feature | Precision (%) | Number of identified signal segments a | Number of correct decisions | Number of incorrect decisions |
|---|---|---|---|---|
| intensity | 96.67 | 30 | 29 | 1 |
| std_ODs | 100 | 2 | 2 | 0 |
| sumHb_ratio | 94.44 | 36 | 34 | 2 |
| acorrDiff_ODs | 83.78 | 37 | 31 | 6 |
Number of signal segments identified as very low quality signals (for features in rating stage one) and number of signal segments identified as very high quality signals (for the feature in rating stage two).
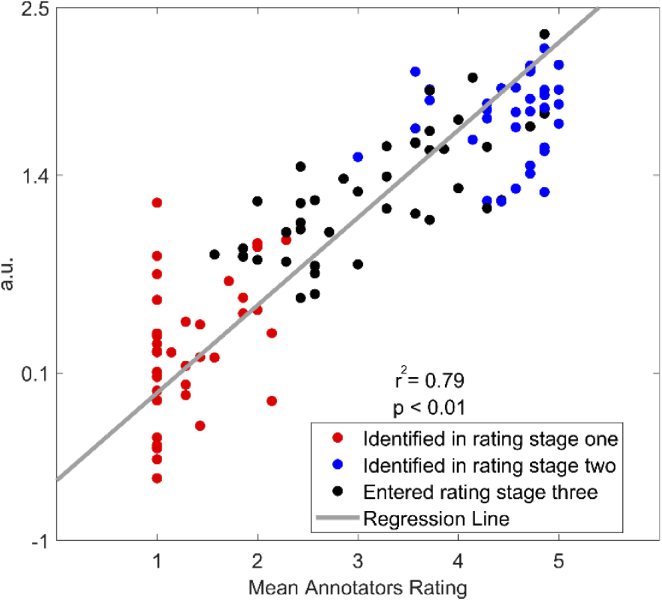
In rating stage three (signal quality rating), using the feature logStdHb (the logarithm of the ratio between the standard deviation of O2Hb and HHb), the SQI algorithm rates the signal quality for those signal segments which have not been identified in rating stage one and two. Figure 7 shows a scatter plot of this feature for all 123 signal segments, revealing a significant positive linear relationship (r2 = 0.79, p-value < 0.05) between the raw values of the feature logStdHb and their mean annotators ratings. Signal segments that were identified by features in rating stage one and two are shown in red (very low quality) and blue (very high quality), respectively.
Fig. 7.
Scatter plot of the feature logStdHb in rating stage three (signal quality rating) of the SQI algorithm. Raw values (y-axis) obtained for the feature logStdHb (logarithm of the ratio between the standard deviation of O2Hb and HHb) with respect to the mean annotators ratings (x-axis) for each of the signal segments are depicted. Each dot represents one of the 123 signal segments included in the training dataset. Red dots represent signal segments that were identified as very low quality signals in rating stage one. Blue dots represent signal segments that were identified as very high quality signals in rating stage two. Black dots represent signal segments that were not identified as very low or very high quality signals in rating stage one and two and consequently entered rating stage three. The gray line represents the regression line obtained between the raw values for the feature logStdHb and the mean annotators ratings.
3.1.2. Algorithm performance assessment
3.1.2.1. Quantitative rating performance
The raw values of the rating features were converted to a continuous scale from 1 to 5 (for more details, see Materials and Methods, section Quantitative rating performance) in order to evaluate the performance of SQI, SCI and PHOEBE algorithms in quantitatively rating fNIRS signal quality. We refer to these as estimated ratings.
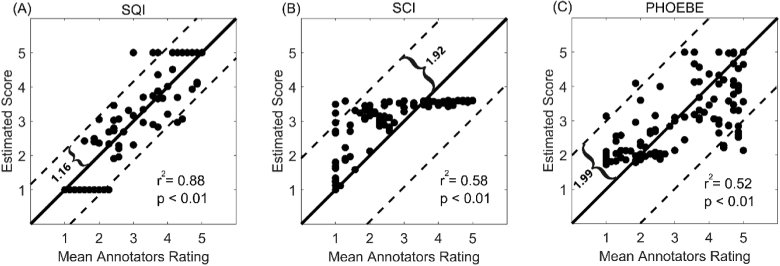
Figure 8 illustrates the scatter plots comparing the estimated ratings with the mean annotators ratings for SQI, SCI and PHOEBE algorithms. The proposed algorithm exhibits a better fit to the mean annotators ratings than PHOEBE and SCI, although a significant positive correlation can be observed for the three algorithms (p < 0.05). While SQI explains 88% (p-value < 0.05) of the variance, PHOEBE and SCI explain 52% and 58% (p-value < 0.05) of the variance, respectively. Data points in the scatter plots for the PHOEBE and SCI algorithms are more sparsely distributed around the y = x line than for SQI. This is reflected by the higher Bland Altman limits of agreement obtained for PHOEBE (BLA=1.99) and SCI (BLA=1.92) with respect to SQI (BLA=1.16). Quantitative measures showing the similarity between the mean annotators ratings and estimated ratings for each of the algorithms are reported in Table 2. SQI had a lower standard deviation of error than SCI and PHOEBE. The mean of error of all considered algorithms was below 0.07. The computation time took the longest (53.11 ms) for the SQI algorithm, whereas for SCI and PHOEBE this time was approximately 20% and 60% of the SQI computation time, respectively.
Fig. 8.
Scatter plots for the estimated rating after the regression to a 1-5 continuous scale. The scatter plots show the estimated ratings (y axis) for each of the signal segments with respect to the mean annotators ratings (x axis). Each dot represents one of the 123 signal segments included in the training dataset. The full and dashed lines are, respectively, the y = x line and the Bland Altman limits of agreement. From left to right, the figure shows the scatter plots for: SQI (A), SCI (B) and PHOEBE (C).
Table 2. Quantitative measures for comparing the performance of the considered algorithms in quantitatively rating the fNIRS signal quality on the training dataset.
| Method | ME a | StdE b | r2 | p-value of correlation c | Computation Time d (ms) |
|---|---|---|---|---|---|
| SCI | 0.06 | 0.98 | 0.58 | <0.01 | 10.77 |
| PHOEBE | −0.004 | 1.01 | 0.52 | <0.01 | 31.42 |
| SQI | 0.04 | 0.59 | 0.88 | <0.01 | 53.11 |
Mean of error.
Standard deviation of error.
P-values were corrected for multiple comparisons applying the Benjamini-Hochberg method.
The computation time was calculated for a single signal segment using our reference implementation in MATLAB R2019b (MathWorks, Natick, Massachusetts) without considering the time to compute the linear regression.
3.1.2.2. Binary classification performance
We compared the binary classification performance of the three considered algorithms in classifying the signal segments into “bad quality” and “good quality” signals. To assign these binary labels to the training dataset, the mean annotators ratings were thresholded using a threshold value of 3.5. The binary classification of fNIRS signal quality performed by the considered algorithms was conducted as explained in Materials and Methods, section Binary classification performance.
The binary classification performance results on the training dataset are reported in Table 3. The SQI, PHOEBE and SCI algorithms performed with an accuracy equal or higher than 65%, which is above chance level (50%). All three algorithms showed a high specificity and precision (above 92%), with SCI obtaining the highest for both measures. SQI showed the highest sensitivity (sensitivity = 92.86%) of all three algorithms, with PHOEBE and SCI showing a high (sensitivity = 78.57%) and low (sensitivity = 38.57%) sensitivity, respectively. The results of the statistical comparison of the binary performance of all algorithms against each other (see Table 4) exhibit that all three algorithms performed significantly differently from each other.
Table 3. Performance measures for comparing the performance of the considered algorithms in binary classification of the fNIRS signal quality on the training dataset.
| Method | Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | F1-score (%) |
|---|---|---|---|---|---|
| SCI | 65.04 | 38.57 | 100 | 100 | 55.67 |
| PHOEBE | 84.55 | 78.57 | 92.45 | 93.22 | 85.27 |
| SQI | 92.68 | 92.86 | 92.45 | 94.20 | 93.53 |
Table 4. Z-scores and p-values calculated by applying McNemar’s binomial test to compare the classification accuracies between each pair of algorithms with respect to the binarized mean annotators ratings on the training dataset. P-values were corrected for multiple comparisons applying the Benjamini-Hochberg method.
| SCI | PHOEBE | SQI | |
|---|---|---|---|
| SCI | - | z(123) = −4.15, p < 0.01 | z(123) = −5.21, p < 0.01 |
| PHOEBE | z(123) = −4.15, p < 0.01 | - | z(123) = −1.82, p < 0.05 |
| SQI | z(123) = −5.21, p < 0.01 | z(123) = −1.82, p < 0.05 | - |
3.2. Validation phase
We further assessed the performance of the SQI algorithm on the validation dataset in i) quantitative rating fNIRS signal quality and ii) binary classification of fNIRS signal quality. In both cases, we compared its performance with the performance of SCI and PHOEBE algorithms.
3.2.1. Quantitative rating performance
For all three algorithms, the raw values of the rating features were converted to the continuous scale from 1 to 5 (estimated rating) by using the linear models fitted on the training dataset. Quantitative measures showing the similarity between the mean annotators ratings and the estimated ratings for each of the algorithms are reported in Table 5. These results are consistent with the results obtained for the training dataset. While SQI explained 85% (p-value < 0.05) of the variance, PHOEBE and SCI only explained 43% and 65% (p-value < 0.05), respectively. In addition, SQI showed a lower standard deviation of error than both SCI and PHOEBE algorithms. The mean of error (ME) for SQI was lower than 0.1 and was the lowest of all three algorithms.
Table 5. Quantitative measures for comparing the performance of the considered algorithms in quantitatively rating the fNIRS signal quality on the validation dataset.
| Method | ME a | StdE b | r2 | p-value of correlation c |
|---|---|---|---|---|
| SCI | −0.15 | 0.80 | 0.65 | <0.01 |
| PHOEBE | 0.44 | 1.01 | 0.43 | <0.01 |
| SQI | −0.09 | 0.60 | 0.85 | <0.01 |
Mean of error.
Standard deviation of error.
P-values were corrected for multiple comparisons applying the Benjamini-Hochberg method.
3.2.2. Binary classification performance
We compared the binary classification performance of the three considered algorithms on the validation dataset in classifying the signal segments into “bad quality” and “good quality” signals. We binarized the output of the three considered algorithms as well as the mean annotators ratings as detailed in Materials and Methods, section Binary classification performance. The threshold used for the logStdHb feature in rating stage three of the SQI algorithm was the same as empirically derived in the training phase. The thresholds used for PHOEBE and SCI were those suggested in the original papers (see [17,18]). The binary classification performance results are reported in Table 6. All considered algorithms performed with an accuracy equal or higher than 65%, which is above chance level (50%). However, the accuracy for the SQI algorithm (accuracy = 95%) was 30% higher than SCI (accuracy = 65%) and 20% higher than PHOEBE (accuracy = 75%). Although both PHOEBE and SCI obtained a 100% for both specificity and precision, they obtained low sensitivity values: 39.13% SCI and 56.52% PHOEBE. This shows that, despite correctly classifying all good quality signals, they did not perform well at classifying bad quality signals. This is reflected in the lower accuracy and F1-score obtained for both algorithms compared to SQI. Conversely, the SQI algorithm showed high values for the three metrics (specificity = 94.12%, precision = 95.65%, sensitivity = 95.65%). We conducted a binomial test to determine whether the differences in performance of the considered algorithms were significant. The results for this test are reported in Table 7. The SQI algorithm performed significantly differently (p-value < 0.05) from SCI and PHOEBE at binary classifying fNIRS signals quality, while SCI and PHOEBE did not perform significantly differently from each other. Furthermore, since 3 out of the total of 4 participants included in the validation dataset were also common to the training dataset (see section 2.1.2), in Appendix 2 we analyzed whether they introduced any bias in the classification.
Table 6. Performance measures for comparing the performance of the considered algorithms in binary classification of the fNIRS signal quality on the validation dataset.
| Method | Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | F1-score (%) |
|---|---|---|---|---|---|
| SCI | 65 | 39.13 | 100 | 100 | 56.25 |
| PHOEBE | 75 | 56.52 | 100 | 100 | 72.22 |
| SQI | 95 | 95.65 | 94.12 | 95.65 | 95.65 |
Table 7. Z-scores and p-values calculated by applying McNemar’s binomial test to compare the classification accuracies between each pair of algorithms with respect to the binarized mean annotators ratings on the validation dataset. P-values were corrected for multiple comparisons applying the Benjamini-Hochberg method.
| SCI | PHOEBE | SQI | |
|---|---|---|---|
| SCI | - | z(40) = -1.53, p > 0.05 | z(40) = −2.76, p < 0.01 |
| PHOEBE | z(40) = −1.53, p > 0.05 | - | z(40) = −1.99, p < 0.05 |
| SQI | z(40) = −2.76, p < 0.01 | z(40) = −1.99, p < 0.05 | - |
4. Discussion
In this study, we developed a novel algorithm, Signal Quality Index (SQI), capable of quantitatively assessing the quality of fNIRS signals in a numeric scale from 1 (very low quality) to 5 (very high quality). To the best of our knowledge, the SQI algorithm is the first algorithm to quantitatively rate fNIRS signal quality in more than two quality levels. Current existing algorithms, like SCI [17] and PHOEBE [18], offer only a sharp distinction between two quality levels of good and bad signal quality. We found that, despite higher computation time, the SQI algorithm showed a significantly better performance (p < 0.05) in quantitatively rating the fNIRS signal quality than PHOEBE and SCI (see Tables 2 and 5). SQI numerically showed a greater positive correlation (r2 = 0.85, p < 0.05) between the estimated ratings and the mean annotators ratings than PHOEBE (r2 = 0.43, p < 0.05) and SCI (r2 = 0.65, p < 0.05). Furthermore, we found that SQI showed a significantly better performance in binary classification of the fNIRS signal quality (p < 0.05) than PHOEBE and SCI, in terms of accuracy, sensitivity, and F1-score (see Tables 3 and 6).
The novelty of the here developed SQI algorithm is that, rather than using a single metric for directly rating the signal quality as SCI does, or a combination of two metrics as done by the PHOEBE algorithm, the SQI algorithm is composed of three different rating stages: identifying very low quality signals (rating stage one), identifying very high quality signals (rating stage two), signal quality rating (rating stage three). Each of these stages includes one or more features, which were selected in order to translate current heuristics in visual assessment of fNIRS signal quality into a numeric rating. The performance of the features in rating stage one and two on the training dataset (see Table 1) showed that they are well suited for identifying very low and very high quality signals with high precision (>80%). The performance results of the feature logStdHb in rating stage three demonstrated that it is well suitable for fNIRS signal quality rating. This claim is supported by the significant positive linear relationship (r2 = 0.79, p-value < 0.05) observed between the raw values of this feature and the mean annotators ratings (See Fig. 7). Furthermore, including rating stage one and two in the algorithm improves its performance, since the features in these stages identify very low and very high quality signal segments that would otherwise be incorrectly rated by the feature logStdHb in rating stage three. This shows the efficacy of including three rating stages in the SQI algorithm workflow, outperforming the state-of-the-art algorithms SCI and PHOEBE.
In this study, the SCI and PHOEBE algorithms used for comparison were implemented as done by their authors (see [26]). We used the thresholds proposed in the original papers [17,18] for binary classification. Though beyond the scope of this study, these thresholds could be optimized on the training dataset to improve their performance. Further studies could be conducted to evaluate the performance sensitivity of the SQI, SCI, and PHOEBE algorithms to different thresholds.
Binary approaches for signal quality assessment, such as SCI and PHOEBE, provide a sharp distinction between “bad” and “good” quality signals. Conversely, three or more levels of signal quality rating allow for the discrimination of “bad” and “good” quality signals into different levels of quality. In some experiments, recording “good” quality signals is very hard to achieve, e.g. when the signals are recorded from subjects or brain areas with a high density of dark hair. In such cases, although the signal might show a weak pulsatile heart beat component because a great part of the transmitted light is absorbed by hair, the quality of such signal segments might still be considered sufficient for certain types of analysis. In a binary approach, these signal segments would either be classified as “bad” or “good” quality signals, depending on the sensitivity of the classifier. In a three or more levels signal quality approach, however, an intermediate quality rating for such signal segments allows the researcher to decide whether the achieved level of quality is sufficient for the analysis. Furthermore, the five-level scale provided in the SQI algorithm makes it possible to decrease the resolution of rating to either a three-level scale or a binary one, which is not possible for the other way around. Therefore, depending on the type of analysis that is to be conducted, the researcher can convert this five-level scale to fewer levels.
Although the results we obtained for the SQI algorithm are promising for both offline and online applications, further improvements are possible. We did not include a stage identifying and rating signal segments affected by motion, since it was beyond the scope of this study. Therefore, in the current work, the analysis of the algorithm performance was limited to data free of motion artifacts. However, motion artifacts are an important source of noise in fNIRS signals. These artifacts, often caused by head and body movements, are unavoidable especially in challenging subject groups like infants and in rehabilitation research and sport science, which often deal with subjects in motion [29–32]. Subject movement causes motion between the optodes and the scalp, leading to rapid shifts in the optical coupling. These rapid shifts take the form of transient spikes in fNIRS signals, and have a scale and frequency composition that are distinct from the background fNIRS signal [32].
The features included in the SQI algorithm use heuristics about meaningful physiological components and characteristics of fNIRS signals, therefore the presence of motion artifacts might affect the performance of the algorithm. We included a section in Appendix 3 where we compared the performance of the considered algorithms on a motion-corrupted dataset. We found that none of the algorithms performed well in quantitatively rating fNIRS signal quality. Therefore, to improve the performance of the SQI algorithm in the presence of motion, future research should consider the effects of motion on fNIRS signal quality and include a stage for motion artefact recognition [29,31].
In addition, both the training and validation of the SQI algorithm were conducted in a set of data collected from healthy young adults. Because functional and systemic-related hemodynamics depend on age [33,34], further studies could be conducted to assess the SQI algorithm in a more extensive dataset, comprising data from infants and elderly people as well as from subjects with cardiac abnormalities.
In this study, we introduced an algorithm, SQI, which is capable of quantitatively rating and binary classifying fNIRS signal quality and outperforms current state-of-the-art algorithms. It can be used as an offline tool for identifying and rejecting channels and trials with a poor signal quality, as well as for online assessment of fNIRS signal quality during set-up and data acquisition. The SQI algorithm was designed to run over 10-second sliding windows. When applying the algorithm to either offline or online data, the user can compute the SQI values for every 10 seconds of data. This allows for an estimation of the varying signal quality of long recordings over time, making it possible to drop trials with poor signal quality rather than the channels themselves. We believe that the widespread use of this algorithm for reporting signal quality ratings for each of the measured channels would ensure that experiments are carried out in proper conditions for collecting actual hemodynamic information and reducing artefacts. Therefore, whether a novice or an experienced researcher conducts an experiment would no longer be an issue for guaranteeing the collection of good quality fNIRS data. The source code for the SQI algorithm is available at https://github.com/Artinis-Medical-Systems-B-V/SignalQualityIndex. The algorithm will be implemented in Artinis’ fNIRS software OxySoft 3.3.
5. Conclusion
In this study we have developed an algorithm, signal quality index (SQI), to quantitatively assess NIRS signal quality in a numeric scale from 1 (very low quality) to 5 (very high quality). The results demonstrate the adequacy of the proposed algorithm for both binary and quantitatively rating the NIRS signal quality. The SQI algorithm performed better than SCI and PHOEBE, existing algorithms in the literature. The promising results obtained in this study suggest that the SQI algorithm could be exploited in different applications: from offline use after recording the signals to online use during recording or optodes setup.
Acknowledgements
The authors would like to thank Dr. Roemer van der Meij and Liucija Svinkunaite for their contribution to an early version of the algorithm, as well as the fNIRS experts working at Artinis Medical Systems B.V., who participated in annotating the quality of the fNIRS signal segments.
Appendix 1
Although the feature std_ODs correctly identified signal segments with very low quality, its identification completely coincided with the identification of the features intensity and sumHb_ratio. Moreover, the number of identified signal segments is very low compared with the number of signal segments identified by the other two features in this stage. Nonetheless, we decided to include this feature in the algorithm because of two reasons. Firstly, it is an intuitive feature that identifies signal segments having at least one optical density (OD) signal as a flatline, which is a clear sign of a very low quality signal. Secondly, it potentially avoids misclassification of signal segments in subsequent stages of the algorithm.
Misclassification of such signal segments could arise in cases where the amplitude of the flatline OD signal is within the permitted range for feature intensity in rating stage one. The signal segment would not be rated by this feature as a very low quality signal and would then be evaluated by feature sumHb_ratio. This feature could fail at identifying the signal segment as a very low quality signal because of using concentration changes in O2Hb (Δ[O2Hb]) and HHb (Δ[HHb]) signals, obtained from OD signals by means of the Modified Beer-Lambert Law (Eq. (4)). For illustrative purposes, we replaced in Eq. (4) the values for the molar extinction coefficients of each chromophore for two sample wavelengths used by the devices (1 = 850 nm, 2 = 760 nm), the source detector distance (d = 3 cm), and the differential pathlength factor (DPF = 6). This is simplified in Eq. (5). The resulting HHb and O2Hb signals are a linear combination of both OD signals, as shown in Eq. (6) and (7), respectively.
| (4) |
| (5) |
| (6) |
| (7) |
Feature sumHb_ratio of rating stage one considers a scale ratio between HHb and O2Hb signals. If one of the OD signals is a flat line of constant amplitude, i.e. it has a zero standard deviation, the resulting O2Hb and HHb signals will be a factor of the OD signal having a non-zero standard deviation plus a constant value introduced by the OD signal with a zero standard deviation (see Eq. (6)). This constant value is removed from the O2Hb and HHb signals in the preprocessing stage. Depending on which of the OD signals is a flat line, the ratio between the filtered O2Hb and HHb signals will be either greater or lower than one. In the case in which this ratio is lower than one, the signal segment will be correctly identified as a very low quality signal by feature sumHb_ratio. In the opposite case, however, it would enter subsequent stages of the algorithm, which could result in its misclassification. Therefore, considering that the computation time of the standard deviation is low, including the feature std_ODs is necessary to guarantee a better performance of the SQI algorithm.
In the present study, the two signal segments having a standard deviation of zero were correctly identified as very low quality signals by feature intensity, because they had null amplitudes. They were also correctly identified by the feature sumHb_ratio, because they are examples of the case where the ratio between O2Hb and HHb signals is lower than one. However, as explained above, this is not necessarily always the case.
Appendix 2
We checked whether the three participants common to the training and validation datasets introduced any bias in the classification. In order to do so, we split the validation dataset into two sets: one with only the common participants (set A) and the other with only the additional participant not present in the training dataset (set B). We compared the binary classification performance of the algorithms for each of these sets (see Table 8). We found that the performances of the algorithms were consistent for both sets of data and thus conclude that there was no bias in the classification.
Table 8. Accuracy for comparing the performance of the considered algorithms in binary classification of the fNIRS signal quality on two sets of the validation dataset: one with the participants common to both training and validation datasets (set A) and the other with only the additional participant not present in the training dataset (set B).
| Method | Accuracy (%) for set A | Accuracy (%) for set B |
|---|---|---|
| SCI | 63.3 | 70 |
| PHOEBE | 76 | 70 |
| SQI | 96.7 | 90 |
Appendix 3
We further assessed the performance of the SQI algorithm on a validation dataset contaminated with motion artifacts, in both quantitatively rating and binary classifying fNIRS signal quality. We compared the performance of the SQI algorithm with the performance of SCI and PHOEBE. The dataset used comprised 35 10-second signal segments, which had been excluded in the training phase as signal segments containing motion (see section 2.1.1). Figure 9 shows one of the signal segments rated as having motion artifacts by all annotators in the training phase.
Fig. 9.
A sample signal segment contaminated with motion artifacts. This signal segment was rated as containing motion artifacts by all annotators in the training phase. (A) Orange and black curves represent the detrended optical density signals for the wavelengths 846 and 757 nm, respectively. (B) Red and blue curves represent the detrended changes in O2Hb and HHb concentrations, respectively.
Quantitative rating performance
For each of the three algorithms, estimated ratings in the 1-5 scale were obtained for the motion corrupted validation dataset by applying the linear models fitted on the training dataset (see Materials and Methods, section Quantitative rating performance). Quantitative measures showing the similarity between the mean annotators ratings and the estimated ratings are reported in Table 9. While PHOEBE explained 31% (p-value < 0.01) of the variance, SQI and SCI explained 20% and 11% (p-value < 0.05) of the variance, respectively. SCI and PHOEBE had a lower standard deviation of error than SQI. The mean of error of all considered algorithms was below 0.9, and was higher for SCI than for SQI and PHOEBE.
Table 9. Quantitative measures for comparing the performance of the considered algorithms in quantitatively rating the fNIRS signal quality on the motion-corrupted validation dataset.
| Method | ME a | StdE b | r2 | p-value of correlation c |
|---|---|---|---|---|
| SCI | 0.87 | 1.06 | 0.11 | <0.05 |
| PHOEBE | −0.18 | 0.91 | 0.31 | <0.01 |
| SQI | 0.03 | 1.39 | 0.20 | <0.01 |
Mean of error.
Standard deviation of error.
P-values were corrected for multiple comparisons applying the Benjamini-Hochberg method.
Binary classification performance
For the three considered algorithms, we compared the binary classification performance on the motion corrupted validation dataset as explained in Materials and Methods, section Binary classification performance. The binary classification performance results are reported in Table 10. Both SQI and PHOEBE algorithms performed with an accuracy higher than chance level (50%), while SCI performance was below chance level. Although SCI showed the highest specificity and precision (100%), its sensitivity and F1-score were very low, and were the lowest of the three algorithms.
Table 10. Performance measures for comparing the performance of the considered algorithms in binary classification of the fNIRS signal quality on the motion-corrupted validation dataset.
| Method | Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | F1-score (%) |
|---|---|---|---|---|---|
| SCI | 28.57 | 7.41 | 100 | 100 | 13.79 |
| PHOEBE | 80 | 92.59 | 37.50 | 83.33 | 87.72 |
| SQI | 65.71 | 74.07 | 37.50 | 80 | 76.92 |
The results of the statistical comparison of the binary performance of all algorithms against each other are reported in Table 11. These results show that SQI and PHOEBE did not perform significantly differently from each other (p-value > 0.05). However, both algorithms performed significantly differently (p-value < 0.01) from SCI at binary classifying fNIRS signals quality.
Table 11. Z-scores and p-values calculated by applying McNemar’s binomial test to compare the classification accuracies between each pair of algorithms with respect to the binarized mean annotators ratings on the motion-corrupted validation dataset. P-values were corrected for multiple comparisons applying the Benjamini-Hochberg method.
| SCI | PHOEBE | SQI | |
|---|---|---|---|
| SCI | - | z(35) = −2.94, p < 0.01 | z(35) = −2.33, p < 0.01 |
| PHOEBE | z(35) = −2.94, p < 0.01 | - | z(35) = −1.47, p > 0.05 |
| SQI | z(35) = −2.33, p < 0.01 | z(35) = −1.47, p > 0.05 | - |
Funding
European Regional Development Fund10.13039/501100008530 (PROJ-00872); Horizon 2020 Framework Programme10.13039/100010661 (No. 813234, No. 813843).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Chance B., Zhuang Z., UnAh C., Alter C., Lipton L., “Cognition-activated low-frequency modulation of light absorption in human brain,” Proc. Natl. Acad. Sci. U. S. A. 90(8), 3770–3774 (1993). 10.1073/pnas.90.8.3770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hakimi N., Setarehdan S. K., “Stress assessment by means of heart rate derived from functional near-infrared spectroscopy,” J. Biomed. Opt. 23(11), 1 (2018). 10.1117/1.JBO.23.11.115001 [DOI] [PubMed] [Google Scholar]
- 3.Pinti P., Tachtsidis I., Hamilton A., Hirsch J., Aichelburg C., Gilbert S., Burgess P. W., “The present and future use of functional near-infrared spectroscopy (fNIRS) for cognitive neuroscience,” Ann. N. Y. Acad. Sci. 1464(1), 5–29(2020). 10.1111/nyas.13948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ehlis A. C., Schneider S., Dresler T., Fallgatter A. J., “Application of functional near-infrared spectroscopy in psychiatry,” NeuroImage 85, 478–488 (2014). 10.1016/j.neuroimage.2013.03.067 [DOI] [PubMed] [Google Scholar]
- 5.Villringer A., Planck J., Hock C., Schleinkofer L., Dirnagl U., “Near infrared spectroscopy (NIRS): A new tool to study hemodynamic changes during activation of brain function in human adults,” Neurosci. Lett. 154(1-2), 101–104 (1993). 10.1016/0304-3940(93)90181-J [DOI] [PubMed] [Google Scholar]
- 6.Ferrari Q. a., “A Mini-Review on Functional Near-Infrared Spectroscopy (fNIRS): Where Do We Stand, and Where Should We Go?” Photonics 6(3), 87 (2019). 10.3390/photonics6030087 [DOI] [Google Scholar]
- 7.Hakimi N., Jodeiri A., Mirbagheri M., Setarehdan S. K., “Proposing a convolutional neural network for stress assessment by means of derived heart rate from functional near infrared spectroscopy,” Comput. Biol. Med. 121, 103810 (2020). 10.1016/j.compbiomed.2020.103810 [DOI] [PubMed] [Google Scholar]
- 8.Boas D. A., Gaudette T., Strangman G., Cheng X., Marota J. J. A., Mandeville J. B., “The accuracy of near infrared spectroscopy and imaging during focal changes in cerebral hemodynamics,” Neuroimage 13(1), 76–90 (2001). 10.1006/nimg.2000.0674 [DOI] [PubMed] [Google Scholar]
- 9.Colier W. N. J. M., Quaresima V., Oeseburg B., Ferrari M., “Human motor cortex oxygenation changes induced by cyclic coupled movements of hand and foot,” Exp. Brain Res. 129(3), 0457–0461 (1999). 10.1007/s002210050913 [DOI] [PubMed] [Google Scholar]
- 10.Scholkmann F., Kleiser S., Metz A. J., Zimmermann R., Pavia J. M., Wolf U., Wolf M., “A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology,” NeuroImage 85, 6–27 (2014). 10.1016/j.neuroimage.2013.05.004 [DOI] [PubMed] [Google Scholar]
- 11.Hoshi Y., Tamura M., “Detection of dynamic changes in cerebral oxygenation coupled to neuronal function during mental work in man,” Neurosci. Lett. 150(1), 5–8 (1993). 10.1016/0304-3940(93)90094-2 [DOI] [PubMed] [Google Scholar]
- 12.Kato T., Kamei A., Takashima S., Ozaki T., “Human visual cortical function during photic stimulation monitoring by means of near-infrared spectroscopy,” J. Cereb. Blood Flow Metab. 13(3), 516–520 (1993). 10.1038/jcbfm.1993.66 [DOI] [PubMed] [Google Scholar]
- 13.Tachtsidis I., Scholkmann F., “False positives and false negatives in functional near-infrared spectroscopy: issues, challenges, and the way forward,” Neurophotonics 3(3), 031405 (2016). 10.1117/1.NPh.3.3.031405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Huigen E., Peper A., Grimbergen C. A., “Investigation into the origin of the noise of surface electrodes,” Med. Biol. Eng. Comput. 40(3), 332–338 (2002). 10.1007/BF02344216 [DOI] [PubMed] [Google Scholar]
- 15.Caldwell M., Scholkmann F., Wolf U., Wolf M., Elwell C., Tachtsidis I., “Modelling confounding effects from extracerebral contamination and systemic factors on functional near-infrared spectroscopy,” NeuroImage 143, 91–105 (2016). 10.1016/j.neuroimage.2016.08.058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Orihuela-Espina F., Leff D. R., James D. R. C., Darzi A. W., Yang G. Z., “Quality control and assurance in functional near infrared spectroscopy (fNIRS) experimentation,” Phys. Med. Biol. 55(13), 3701–3724 (2010). 10.1088/0031-9155/55/13/009 [DOI] [PubMed] [Google Scholar]
- 17.Pollonini L., Olds C., Abaya H., Bortfeld H., Beauchamp M. S., Oghalai J. S., “Auditory cortex activation to natural speech and simulated cochlear implant speech measured with functional near-infrared spectroscopy,” Hear. Res. 309, 84–93 (2014). 10.1016/j.heares.2013.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pollonini L., Bortfeld H., Oghalai J. S., “PHOEBE: a method for real time mapping of optodes-scalp coupling in functional near-infrared spectroscopy,” Biomed. Opt. Express 7(12), 5104 (2016). 10.1364/BOE.7.005104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Elgendi M., “Optimal signal quality index for photoplethysmogram signals,” Bioengineering 3(4), 21 (2016). 10.3390/bioengineering3040021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sukor J. A., Redmond S. J., Lovell N. H., “Signal quality measures for pulse oximetry through waveform morphology analysis,” Physiol. Meas. 32(3), 369–384 (2011). 10.1088/0967-3334/32/3/008 [DOI] [PubMed] [Google Scholar]
- 21.Delpy D. T., Cope M., Van Der Zee P., Arridge S., Wray S., Wyatt J., “Estimation of optical pathlength through tissue from direct time of flight measurement,” Phys. Med. Biol. 33(12), 1433–1442 (1988). 10.1088/0031-9155/33/12/008 [DOI] [PubMed] [Google Scholar]
- 22.Ifeachor E. C., Jervis B. W., Digital Signal Processing: A Practical Approach. Prentice Hall, Upper Saddle River, NJ, 2002. [Google Scholar]
- 23.Oostenveld R., Fries P., Maris E., Schoffelen J. M., “FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data,” Comput. Intell. Neurosci. 2011, 1–9 (2011). 10.1155/2011/156869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huppert T. J., Diamond S. G., Franceschini M. A., Boas D. A., “HomER: A review of time-series analysis methods for near-infrared spectroscopy of the brain,” Appl. Opt. 48(10), D280–D298 (2009). 10.1364/AO.48.00D280 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Benjamini Y., Hochberg Y., “Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing,” J. R. Stat. Soc. Ser. B 57(1), 289–300 (1995). 10.1111/j.2517-6161.1995.tb02031.x [DOI] [Google Scholar]
- 26.[26] Pollonini L., Perry J., “PHOEBE (2020), Github repository,” 2020. [Online]. Available: https://bitbucket.org/lpollonini/phoebe/wiki/Home. [Accessed: 01-Sep-2020].
- 27.Altman D. G., Bland J. M., “Measurement in Medicine: the Analysis of Method Comparison Studies †,” Am Stat. 32(3), 307–317 (1983). 10.2307/2987937 [DOI] [Google Scholar]
- 28.Dietterich T. G., “Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms,” Neural Comput. 10(7), 1895–1923 (1998). 10.1162/089976698300017197 [DOI] [PubMed] [Google Scholar]
- 29.Brigadoi S., Ceccherini L., Cutini S., Scarpa F., Scatturin P., Selb J., Gagnon L., Boas D. A., Cooper R. J., “Motion artifacts in functional near-infrared spectroscopy: A comparison of motion correction techniques applied to real cognitive data,” NeuroImage 85(0 1), 181–191 (2014). 10.1016/j.neuroimage.2013.04.082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pfeifer M. D., Scholkmann F., Labruyère R., “Signal Processing in Functional Near-Infrared Spectroscopy (fNIRS): Methodological Differences Lead to Different Statistical Results,” Front. Hum. Neurosci. 11, 641 (2018). 10.3389/fnhum.2017.00641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Scholkmann F., Spichtig S., Muehlemann T., Wolf M., “How to detect and reduce movement artifacts in near-infrared imaging using moving standard deviation and spline interpolation,” Physiol. Meas. 31(5), 649–662 (2010). 10.1088/0967-3334/31/5/004 [DOI] [PubMed] [Google Scholar]
- 32.Cooper R. J., Selb J., Gagnon L., Phillip D., Schytz H. W., Iversen H. K., Ashina M., Boas D. A., “A Systematic Comparison of Motion Artifact Correction Techniques for Functional Near-Infrared Spectroscopy,” Front. Neurosci. 6, 147 (2012). 10.3389/fnins.2012.00147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Peng T., Ainslie P. N., Cotter J. D., Murrell C., Thomas K., Williams M. J. A., George K., Shave R., Rowley A. B., Payne S. J., “The effects of age on the spontaneous low-frequency oscillations in cerebral and systemic cardiovascular dynamics,” Physiol. Meas. 29(9), 1055–1069 (2008). 10.1088/0967-3334/29/9/005 [DOI] [PubMed] [Google Scholar]
- 35.Safonova L. P., Michalos A., Wolf U., Wolf M., Hueber D. M., Choi J. H., Gupta R., Polzonetti C., Mantulin W. W., Gratton E., “Age-correlated changes in cerebral hemodynamics assessed by near-infrared spectroscopy,” Arch. Gerontol. Geriatr. 39(3), 207–225 (2004). 10.1016/j.archger.2004.03.007 [DOI] [PubMed] [Google Scholar]