Diffuse optical tomography to measure functional changes during motor tasks: a motor imagery study

Abstract

The present work shows the spatial reliability of the diffuse optical tomography (DOT) system in a group of healthy subjects during a motor imagery task. Prior to imagery task performance, the subjects executed a motor task based on the finger to thumb opposition for motor training, and to corroborate the DOT spatial localization during the motor execution. DOT technology and data treatment allows us to distinguish oxy- and deoxyhemoglobin at the cerebral gyri level unlike the cerebral activations provided by fMRI series that were processed using different approaches. Here we show the DOT reliability showing functional activations at the cerebral gyri level during motor execution and motor imagery, which provide subtler cerebral activations than the motor execution. These results will allow the use of the DOT system as a monitoring device in a brain computer interface.

1. Introduction

Optical imaging techniques such as functional near infrared spectroscopy (fNIRS) can measure changes in oxyhemoglobin (HbO) and deoxyhemoglobin (HbR) at a much higher sampling rate than functional magnetic resonance imaging (fMRI) and uses low cost instruments compared to other neuroimaging techniques such as fMRI or magnetoencephalography (MEG). Additionally, optical imaging does not need a contrast agent but positron emission tomography (PET) [1] or x-ray computed tomography [2] sometimes require limited doses of contrast agent which could induce anaphylactic reactions in some people.

These circumstances have strengthened the development of optical imaging techniques in research, diagnosis and prognostic studies. The most significant improvements in optical imaging occurred when image reconstruction techniques were proposed in the 1990s using diffusive photons [3,4]. Diffuse optical tomography (DOT) is an fNIRS approach that transforms the detected light intensity from different measuring distances on the surface of the head into depth information providing three dimensional images of cerebral activations [5]. DOT uses the multidistance approach with the aim of increasing spatial resolution and positional accuracy of optical brain imaging [6]. DOT uses at least two wavelengths in a range of 650-950 nm travelling to and from the DOT system via light-emitting diodes (LEDs) or laser light to measure the absorbed quantity of NIR light from biological tissue by measuring diffusely scattered light. The NIR light is applied on the subject’s head combined as source-detector pairs to detect changes in the optical density produced by hemodynamic changes in the brain, known as optical channels. The changes in NIR light attenuation between a source and a detector located on the scalp are transformed into changes in the concentration of HbO and HbR by applying the modified Beer-Lambert law [7].

Optical measurements can play a role in determining brain physiology, especially when investigating the relationship between neural activity and hemodynamic changes known as neurovascular coupling [8]. fNIRS has been used in a wide variety of applications in neuroimaging studies to measure functional changes associated to a motor stimulus or motor paradigm. In these cases, the cerebral activation amplitudes are higher than the amplitudes given by other paradigms e.g. in cognitive paradigms, the cerebral activations are not always reproducible and spatial localizations are not well known as opposed to the motor paradigms which are used in new method applications such as image reconstruction algorithms [9], filtering procedures [10] or corroboration of simulated models [11].

In the motor context, the scientific community has wondered whether the same brain area networks are recruited during motor imagery and motor execution. Consequently, many studies have identified a consistent premotor, parietal, and somatosensory network of brain areas [12,13,14,15]. For example, the primary sensorimotor cortex (SMC), the premotor cortex and supplementary motor area (SMA) are activated during simple finger movements [16,17,18]. Moreover, similar motor cerebral activation loci are generated during the motor imagery task to those generated during the motor movements [19,20]. All these studies have been developed using a wide range of neuroimaging techniques such as fMRI or PET. The present work shows how a motor execution paradigm based on the finger to thumb opposition task was used to evaluate the DOT method sensitivity and reliability when measuring cerebral functional changes, and ability to distinguish hemodynamic changes at the gyri level [21]. The cerebral activation maps provided by DOT data processing [22] were compared to the cerebral activation maps generated by two fMRI processing methods: the standard General Linear Model (GLM) [23] as well as a more recent method called slice-based fMRI [24]. If the whole DOT set covering continuous-wave system and DOT data processing are accurate, it is possible to measure functional changes generated during the motor imagery whose amplitudes are subtler than motor execution, helping to corroborate the reliability of DOT, as used in the present work.

2. Material and methods

2.1. Subjects and training period

Eight healthy right-handed volunteers who had no history of neurological disease participated in the present study. Written informed consent was explained and signed prior to experiment. The study was approved by the local ethics committee (Universidad de La Laguna) and was conducted in accordance with the Declaration of Helsinki.

Neural mechanisms of motor imagery overlap with the mechanisms of motor execution. To avoid confounding motor execution and imaginary activity which activate the same cerebral network, the study was structured in two motor paradigms: motor execution based on finger tapping and motor imagery. In addition, motor imagery needs a greater task time to ensure which the subject performed the task. During the experimental procedure all participants were monitored with the DOT and fMRI devices.

Prior to the functional studies, the participants were trained for five minutes by the researcher. The participants performed both the motor execution and motor imagery trainings to familiarize themselves with the protocol. The participants were seated, with their hands placed in front of them on a table. After an initial resting period of 20s, the participants were instructed to perform both tasks that were presented randomly. The motor execution task consisted of performing movements between the index finger and the thumb with the right hand at a frequency of 2 Hz (with a white cross flickering at 2 Hz in the middle of the screen) for 27 seconds. The motor imagery task consisted of imagining the same action as in the motor execution task and abstaining from any movement during 30s, purely to perceive sensations associated with a movement such as the contraction and relaxation of the arm muscle. Both motor trainings were repeated 3 times.

2.2. Experimental design for the motor execution

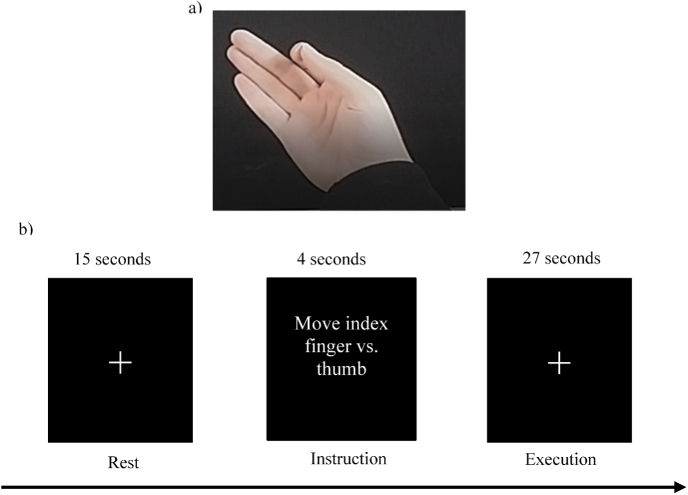
A block design was developed where the participants began with a 15s resting period which consisted of the observation of a static white cross in the center of the screen. The instruction, e.g., “Move index finger vs. thumb” in the mother-tongue of the participant (Spanish) appeared 4s before each task block, which started when the statement disappeared. The execution condition consisted of the opposition movement between the index finger and the thumb for 27s, at a frequency determined by a visual cue (a white cross flashing at 2 Hz in the middle of the screen), which was executed by the participants with their right hand, as is shown in the Fig. 1.

Fig. 1.

a) Depiction of the opposition movement between the index finger and thumb with the right hand. b) Scheme of the block design with the time of each condition. A total of 6 blocks were conducted with both fMRI and DOT devices. The top row indicates the time of each block. The bottom row indicates each condition.

2.3. Experimental design for the motor imagery

The bibliography widely describes two motor imagery approaches: the visual motor imagery, when the participants only visualize the movements and the kinesthetic motor imagery (KMI), where the participants feel the movements, without executing them in either case [25,26]. KMI was used in the present work.

A block design was developed in which the participants began with a 20s rest period which consisted of the observation of a static white cross in the center of the screen for 20s. The instruction, e.g., “Imagery” in the mother-tongue of the participant (Spanish) appeared 6s before each task block, which started when the statement disappeared. The motor imagery condition consisted of imagining the same action as the motor execution task and abstaining from any movement, which was performed by the participants for 30s while a dark screen appeared, as shown in the Fig. 2.

Fig. 2.

Schematic block design of the paradigm, including the time of each condition. A total of 6 blocks were conducted with both fMRI and DOT devices. The top row indicates the time of each block. The bottom row indicates each condition.

A dummy time of 20s to stabilize the physiological fluctuations and to ensure tissue steady-state magnetization in fMRI was presented prior to both the motor execution and imagery paradigms. The paradigms were displayed on the screen using Presentation software (Neurobehavioral Systems, Inc., Albany, California). A total of six task blocks for each condition, motor execution and imagery, were performed with both DOT and fMRI devices with a random order of the instructions.

2.4. Data acquisition in MRI

Functional magnetic resonance images were acquired from a 3.0 T Signa Excite HD scanner (General Electric Healthcare). T1-weighted volume was acquired for precise anatomical localization (TR = 6 ms, TE = 1 ms, flip angle = 12°, matrix size = 256 × 256 pixels, 0.98 × 0.98 mm in plane resolution, spacing between slices = 1 mm, slice thickness = 1 mm, inter-slice gap = 0). The anatomical slices covered the whole brain and were acquired parallel to the anterior-posterior commissure. Two sequences of 230 and 190 T2-weighted echo-planar imaging (EPI) volumes were acquired during the motor execution and the motor imagery paradigms, respectively. The parameters for both EPI sequences consisted of: 36 axial slices covered the whole head; field of view 25.6 mm, slice thickness 4 mm, inter-slice gap 1 mm, 64 × 64 matrix, flip angle 90°, repetition time (TR) = 2 sec, echo time (TE) = 22.1 ms.

2.5. Data analysis in MRI

fMRI volumes were preprocessed in Statistical Parametric Mapping (SPM12, The Wellcome Trust Centre for Neuroimaging, University College London) by applying realignment to improve motion artifacts, slice timing correction, registration with structural image (T1), and fit into standard anatomical space (Montreal Neurological Institute, MNI). An isotropic smoothing kernel of 2-mm full-width half-maximum was applied to the EPI images to suppress noise and effects due to residual differences in functional and gyral anatomy and high-pass filter with 64s cut-off period was used to remove low frequency noise corresponding to breathing and pulse.

A general linear model (GLM) was constructed in SPM12 for each paradigm. The design matrix consisted of two regressors with onsets for rest blocks and onsets for task blocks (execution or imagery blocks), according to the paradigm performed. The regressors were convolved with the canonical hemodynamic response function (HRF). After estimation, a fixed effects model analysis was performed to generate t-contrast images comparing motor execution > rest and motor imagery > rest. The fixed model analysis does not allow for any overall conclusions for the population, but it is adequate for this sample, because the goal of the present work is to compare both neuroimaging techniques during the performance of the motor paradigms.

One disadvantage of the previously described method in fMRI data analysis is that, it relies on an expected shape of the blood-oxygen-level dependent (BOLD) signal, which may lead to reduced signal detection [27]. Other techniques such as Finite Impulse Response (FIR) based modeling [28], Independent Component Analysis (ICA) [29], and Slice-Based fMRI [24] have been proposed to overcome this problem by detecting signal changes in a data-driven manner. Here, the Slice-Based approach was used to detect BOLD signal changes during the motor task and compare them to those detected by the DOT technique.

2.6. Optical data acquisition

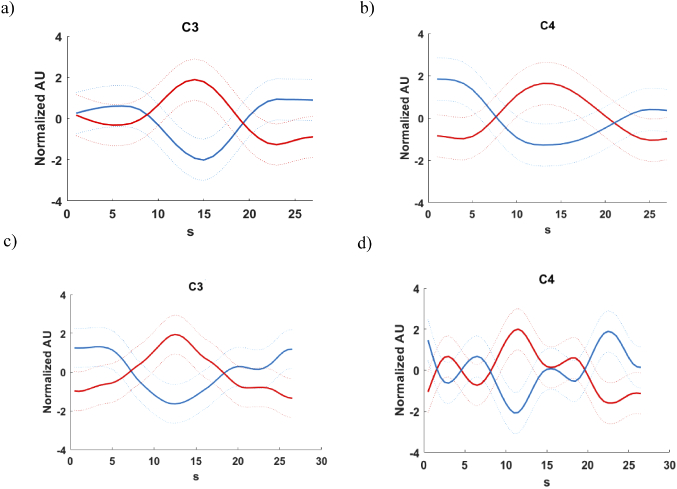
A DYNOT 232 instrument (NIRx Medizintechnik GmbH Berlin, Germany) was used to acquire the DOT data. The system performs continuous-wave measurements using two frequency encoded laser sources at 760 and 830 nm with a sampling rate of 1.8 Hz in a time multiplexed scanning fashion. The equipment provides a high dynamic measurement range needed for diffuse tomography multidistance measurements. NIR light travelled to and from the DOT device via optical fibers (optodes). In the present study, 32 optical fibers were used to measure hemodynamic changes in each cerebral hemisphere (left & right sides). The optical fibers acted as detectors and 16 of them acted as source (colocalization), thereby providing 496 optical channels for each cerebral side. The optodes were arranged in a rectangular grid of 4 × 8 at a distance of 1 cm between them, covering each cerebral hemisphere. Both cerebral hemispheres join in the Cz position, which was used as reference to place the center of grid and cover both the C3 and the C4 positions referring to the EEG 10-20 system [30]. These positions allowed recordings of hemodynamic changes over the SMC, SMA and premotor cortex. As an example, average time series for HbO and HbR calculated from optical channels placed in C3 and C4 during task execution, are shown in Fig. 3.

Fig. 3.

Representation of the time series for HbO (red lines) and HbR (blue lines) recorded in a) C3 and b) C4 positions during the motor execution task for a subject. Time series for HbO and HbR recorded in c) C3 and d) C4 positions during the motor imagery task. Axial axis shows the normalized arbitrary unit (A.U). Horizontal axis shows the average time during task execution (s).

2.7. Data quality

The signals measured by DOT contain fluctuations originating from the physiology itself such as cardiac pulsation or respiratory movement, which contaminate the hemodynamic signals and may induce spatial and temporal changes [31]. A bayesian filter that modeled and removed physiological data from raw DOT signals was used to remove physiological noise [32].

Moreover, electromyographic recordings (EMG) were made during two conditions: motor imagery and finger opposition movement. Positive electrodes were placed over the first dorsal interosseous, the negative electrodes were placed near the wrist and the ground was in the center of the dorsal part of the palm of the hand. The EMG and the physiological data were recorded continuously at 4 KHz using AD Instrument ML870/P PowerLab16/30 as the measurement system.

2.8. Forward model and Image reconstruction

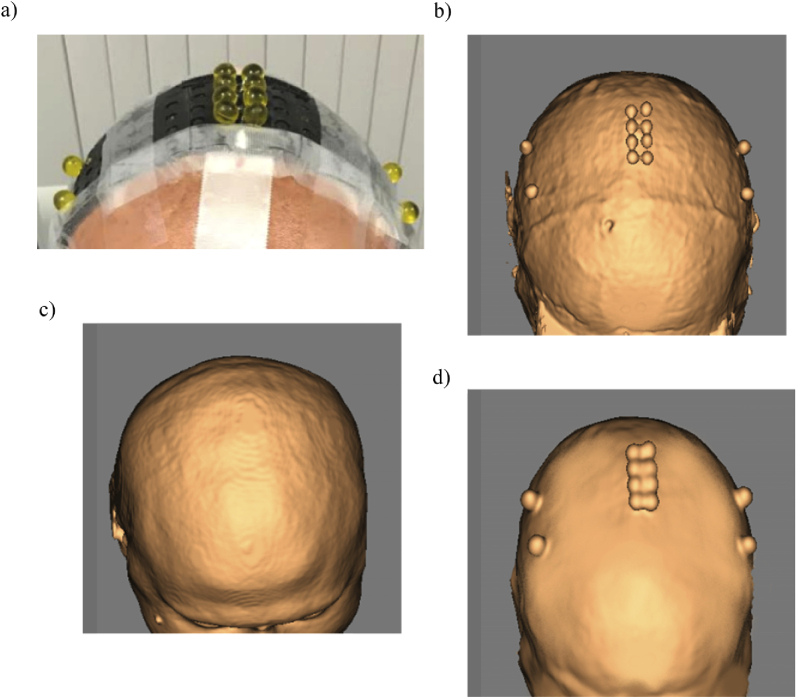
Prior to the DOT measurements, the optical fiber grid was positioned on each subject to mark the four corners of the grid array used in each cerebral side. The corners were marked with vitamin E capsules, which provide a contrast in T1 images. The use of a pre-calculated finite-element mesh (FEM) over a generic head model requires a translocation of the marked corners from the subject’s anatomy to the anatomic MR scans of the generic head model on which the FEM is based. This translocation was performed using an SPM spatial normalization tool, which computes an affine and a nonlinear transformation between two volumes to warp both images and fit them into a template. The positions of 32 optical fibers placed on the head were interpolated between the coordinates of the four corners marked and assigned to the FEMs. Figure 4.

Fig. 4.

a) Representation of the four corners marked with vitamin E covering each cerebral hemisphere. b) Subject’s anatomical scans with the four corners marked on the head surface in a real space. c) MRI scans of the generic head model on which the FEM is based. d) Subject’s MRI scans warped into the space of the generic head model.

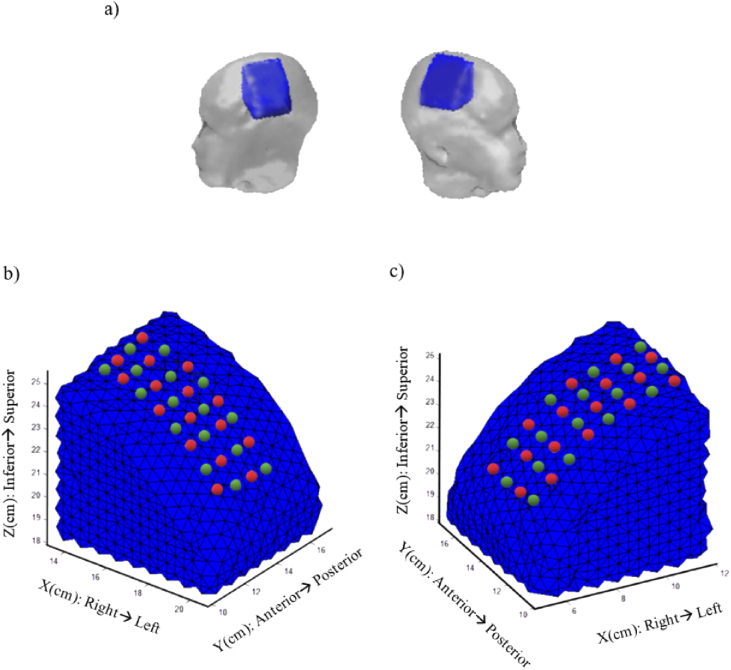
The BrainModeler tool from NIRx NAVI imaging was used, which contains FEMs [33] to describe a homogeneous distribution of optical properties ($\mu$a = 0.06 cm⁻¹, $\mu s^{\mathrm{\prime }}$ = 10 cm⁻¹). The source-detector pair localization on the head’s surface and inner optical properties are defined as the forward model. The forward model describes the changes measured in boundary data that are caused by small changes of absorption within the tissue for each channel-node combination. Two sub-meshes that best approximate to the areas of the measurements here depending on the translocate positions of the fibers grid were selected for each cerebral hemisphere. The submesh selected which covered the left hemisphere contained 4518 nodes and 19573 tetrahedrons and thus, its dimensions were 7.65 cm (width) x 7.05 cm (height) x 7.20 cm (thickness). The submesh which covered the right cerebral hemisphere contained 4211 nodes and 18049 tetrahedrons and thus, its dimensions were 7.33 cm (width) x 7.08 cm (height) x 7.10 cm (thickness), as is shown in Fig. 5.

Fig. 5.

Finite model element mesh selection. a) Atlas with an FEM (blue) covering both cerebral sides. Localizations of optical fibers (circles) on the boundary. Red dots correspond to sources (16) and all of them (32) act as receptors for b) left side and c) right side.

A weight matrix J is obtained as result of the relationship between the selected node-numbers of the submesh and optical channels measured by the combination of source-detector pairs located on the head surface. The weight matrix J containing information on each DOT voxel of the signal collected (optical properties, $\mathrm{\Delta }\mu$) from all source-detector combinations on the surface of the medium $\mathrm{\Delta }y$ necessary for the reconstruction of DOT images:

$$\mathrm{\Delta }y=J\mathrm{\Delta }\mu$$

The normalized difference method [34] was used to reconstruct DOT volumes. The method relates measurements on the head´s surface with changes in the interior optical properties of the medium used, compared to a reference medium, using the perturbation approach [35]. The absorption changes at two wavelengths led to reconstructed images of relative HbO and HbR concentrations using extinction coefficients for both wavelengths [36]. The rebuilding of the DOT images requires inverting the weight matrix $\text{J}$ resulting in an ill-posed problem formulated as an inverse problem, because NIR light is highly attenuated with an increasing depth. The weight matrix is inverted using a truncate singular value decomposition (tSVD) algorithm. The truncated number of singular values explains the dimensionality of the matrix that was determined by the minimum description length (MDL) as a selection criterion. A total of 826 and 657 DOT volumes series were reconstructed for the motor execution and imagery paradigms, respectively. The DOT volumes were rebuilt with a size of 64 × 64 × 64 voxels, in Nifti format for each hemoglobin state (HbO & HbR), in each cerebral hemisphere.

2.9. DOT statistics using canonical SPM12

A new approach to treating DOT volumes as if they were fMRI volumes, using the canonical SPM 12 software to obtain cerebral activation maps as is performed with fMRI images [22] was used in the present work. DOT volumes were filtered to improve the signal to noise ratio, using a high pass filter based on a discrete cosine transform, with a 64s cut-off period. The design matrix consisted of two regressors with onsets for rest blocks and onsets for task blocks (motor execution or motor imagery). The regressors were convolved with the canonical HRF functions. The convolutions were reversed to visualize negative response corresponding to the HbR signal. After estimation, cerebral activation maps were generated by applying a fixed effects model analysis. Two contrasts were computed for each paradigm: motor execution > rest and motor imagery > rest.

2.10. Region of interest and Spatial Conjunction

The aim of the present work is to study the motor areas and surroundings using the multi-distance approach in DOT system and the fMRI recordings for comparative purposes. Thus, only the motor areas corresponding to the selected sub-meshes without extra-cerebral layers (masked) are represented.

In addition, a spatial conjunction analysis was computed to test the level of overlapping between both modalities. Conjunction analysis is a method which controls the false positive (type I) error for conjunction inference. The use of this method in a typical data analysis is very straightforward. To test for common activations across subjects or tasks, one simply creates the intersection of the statistical maps thresholder at a specified alpha rate, e.g., 0.05 FWE-corrected, from Random Field Theory or permutation [37].

3. Results

3.1. t-contrast maps in the motor execution paradigm (individual analysis)

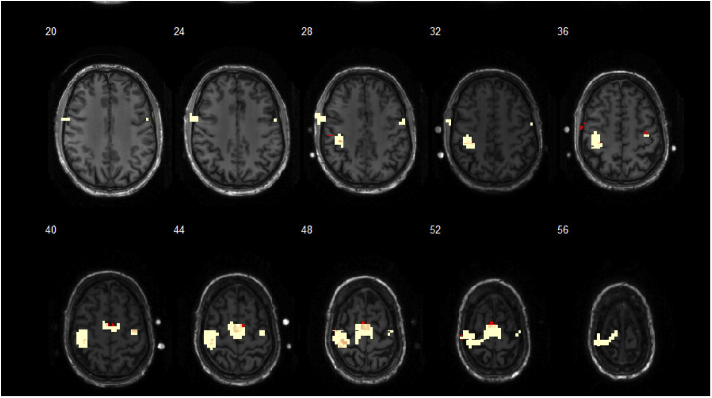
Motor paradigms are widely used in the development of methods or data analysis because the spatial localization of cerebral activity is well known. Based on the aforementioned, assuming that fMRI results are valid and knowing that the DOT technique is still not fully developed [38], a prior analysis of the spatial distribution of the cerebral activity generated by both BOLD and HbO signals onto motor regions of a healthy subject was performed to see which technique is better for locating activation in this type of paradigm. Therefore, individual t-contrast maps were generated by SPM12 for the motor execution > rest contrast, as shown in Fig. 6.

Fig. 6.

t-contrast maps of brain activation for the motor execution > rest contrast measured by DOT and fMRI devices. All results were mapped onto an individual space (subject’s anatomy image). Threshold p<0.001 corrected FDR at voxel level for BOLD signal (yellow) and HbO signal (red) onto the bilateral motor regions are shown. Note the fiducial marks on both cerebral sides to localize the position of the optical fiber grid.

Individual t-contrast maps show the cerebral activations were located in the SMC, premotor and SMA areas for both BOLD and HbO signals during the motor execution. DOT and fMRI results were analyzed using a spatial conjunction analysis to test the level of overlapping between measured signals, Table 1.

Table 1. Representation of the number of common voxels for the BOLD-HbO combination by anatomical area for one individual subject.

t-contrast	Hemisphere	Peak coordinates.			No. common voxels
		x	y	z
T:3.9, p < 0.001	Left	−33	10	29	41
T:3.9, p < 0.001	Left	−45	18	30	10
T:2.36, p < 0.001	Right	6.5	29	41	20

The individual results show a greater number of common voxels (BOLD-HbO) in the left side than in the right side. In addition, the localization of cerebral activations (loci) represented by the t-maps for both DOT and fMRI measurements show the same spatial distribution.

3.2. t-contrast maps in the motor execution paradigm (group analysis)

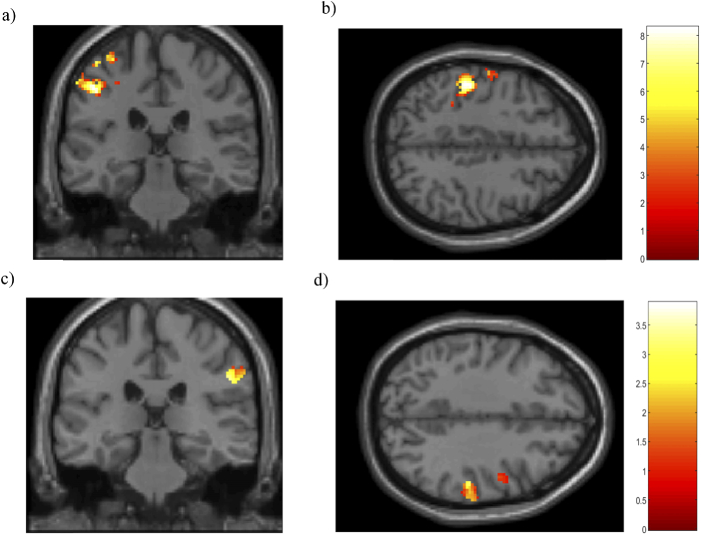
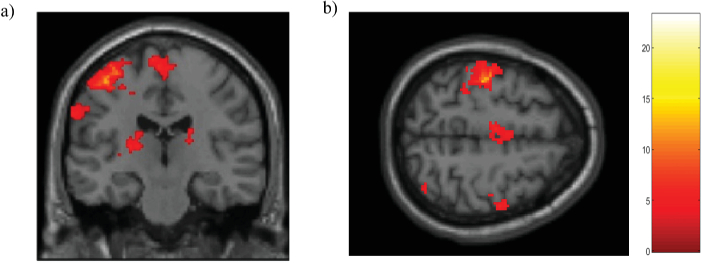
t-contrast maps in the group analysis for DOT and fMRI series were displayed using XjView 8.1. By the use of pre-computed FEM, the t-contrast maps were shown for each cerebral hemisphere in the MNI space. Figure 7 shows the t-contrast maps for the HbO signal in coronal and axial views on the left side (T: 4.7; p<0.001) and on the right side (T: 1.9; p<0.05).

Fig. 7.

t-contrast maps of cerebral activation for the motor execution > rest contrast measured by the DOT device in a subject group (N=8) in the left hemisphere in a) coronal and b) axial view. t-contrast maps of the right hemisphere in c) coronal and d) axial view. All results were mapped onto a standard space (MNI). Threshold p-value corrected FDR at the voxel level for HbO signal. Color bar depicts the HbO signal changes.

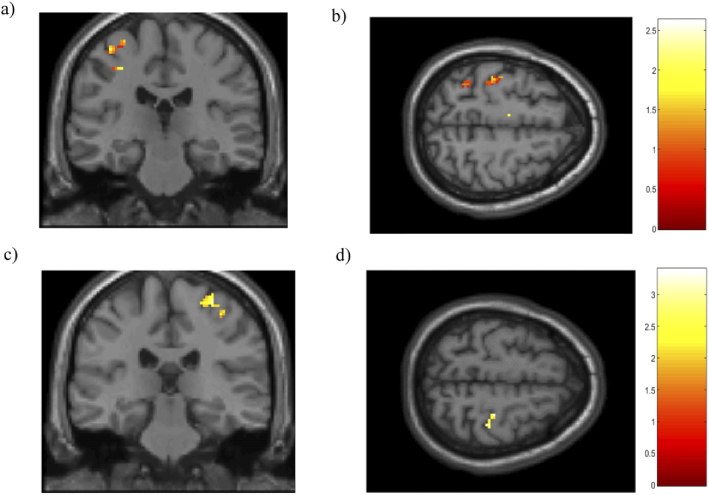
Figure 8 shows the t-contrast maps for the HbR signal in coronal and axial views of the left side (T: 4.7; p<0.001) and of the right side (T: 1.9; p<0.05).

Fig. 8.

t-contrast maps of cerebral activation for the motor execution > rest contrast measured by the DOT device in a subject group (N=8) in the left hemisphere in a) coronal and b) axial view. t-contrast maps of the right hemisphere in c) coronal and d) axial view. All results were mapped onto a standard space (MNI). Threshold p-value corrected FDR at the voxel level for HbR signal. Color bar depicts the HbR signal changes.

Figure 9 shows the t-contrast maps for the BOLD signal (T: 4.7; p<0.001) in coronal and axial views.

Fig. 9.

t-contrast maps of cerebral activation for the motor execution > rest contrast measured by the fMRI device in a subject group (N=8) in a) coronal and b) axial view. All results were mapped onto a standard space (MNI). Threshold p<0.001 corrected FDR at the voxel level for BOLD signal. Color bar depicts the BOLD signal changes.

Maps of cerebral activations generated by DOT and fMRI measurements were analyzed using a spatial conjunction analysis [37] to analyze common regions in the subjects’ group. Table 2.

Table 2. Representation of the number of common voxels by anatomical area according to HbO-BOLD and HbR-BOLD.

Anatomical region	Peak MNI co-ordinate			No. of common voxels
	x	y	z
$\mathbf{L}\mathbf{e}\mathbf{f}\mathbf{t}\mathbf{H}\mathbf{e}\mathbf{m}\mathbf{i}\mathbf{s}\mathbf{p}\mathbf{h}\mathbf{e}\mathbf{r}\mathbf{e}$
Motor execution > rest (T:4.7, p < 0.001)
HbO∩BOLD
Postcentral gyri	−52	−16	38	7
Inferior Parietal BA2	−44	−28	40	164
Postcentral gyri BA3	−54	−12	44	10
Postcentral gyri BA4	−50	−8	46	6
Precentral gyri BA4	−28	−40	50	60
Precentral gyri BA6	−36	−14	52	47
Postcentral gyri	−44	−30	60	15
Precentral gyri BA4	−34	−28	62	26
HbR∩BOLD
Postcentral gyri	−56	−14	38	7
Inferior Parietal	−46	−26	40	171
Precentral gyri BA6	−36	−12	52	41
Postcentral gyri	−40	−42	62	7
Postcentral gyri BA4	−36	−30	64	6
$\mathbf{R}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}\mathbf{H}\mathbf{e}\mathbf{m}\mathbf{i}\mathbf{s}\mathbf{p}\mathbf{h}\mathbf{e}\mathbf{r}\mathbf{e}$
Motor execution > rest (T:1.9, p < 0.05)
HbO∩BOLD
Supplementary motor area	12	−8	56	153
HbR∩BOLD
Postcentral gyri	56	−28	30	132
Precentral gyri	52	0	36	69
Frontal Superior Right	30	−4	60	17

The conjunction analysis shows a greater number of common voxels in the left pre- and post-central gyri than in the right side during the performance of the motor execution. From an anatomical point of view, individual and group results show common regions for signals measured by fMRI and DOT devices.

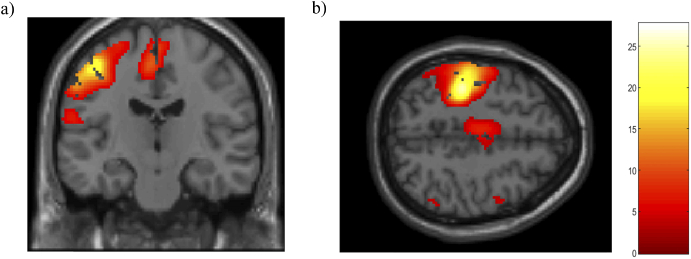
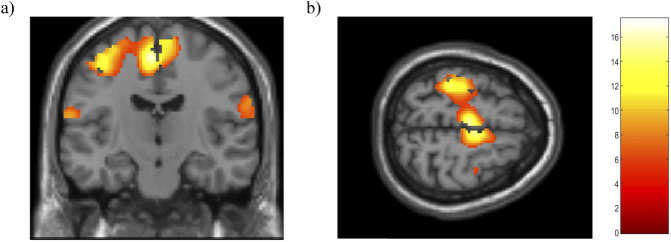
In order to identify cerebral regions implied in motor execution from fMRI data in a more defined manner, the fMRI recordings were processed using an alternative processing method called slice-based. Cerebral activation maps provide spatial networks associated with temporal activation profiles ∼18-20s within the motor execution block, showing the loci in the left pre-postcentral gyri (BA1, BA4 & BA3), left SMA and right precentral gyri (BA4). Figure 10.

Fig. 10.

Cerebral activation maps of the motor execution > rest contrast measured fMRI devices in a subject group (N=8) using slice-based method in a) coronal view and b) axial view mapped onto a standard space (MNI). All results were mapped onto a standard space (MNI). Threshold p<0.001 corrected FDR at the voxel level for BOLD signal. Note the spatially independence networks associated to the maximum temporal activation profile during the motor execution.

3.3. t-contrast maps in the motor imagery paradigm (group analysis)

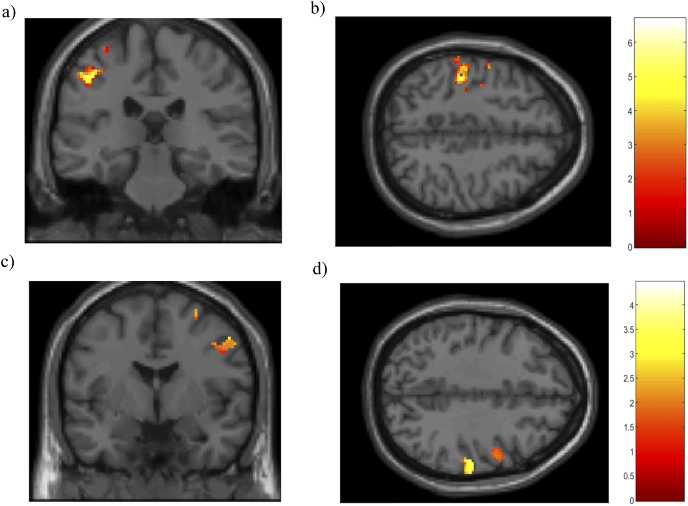
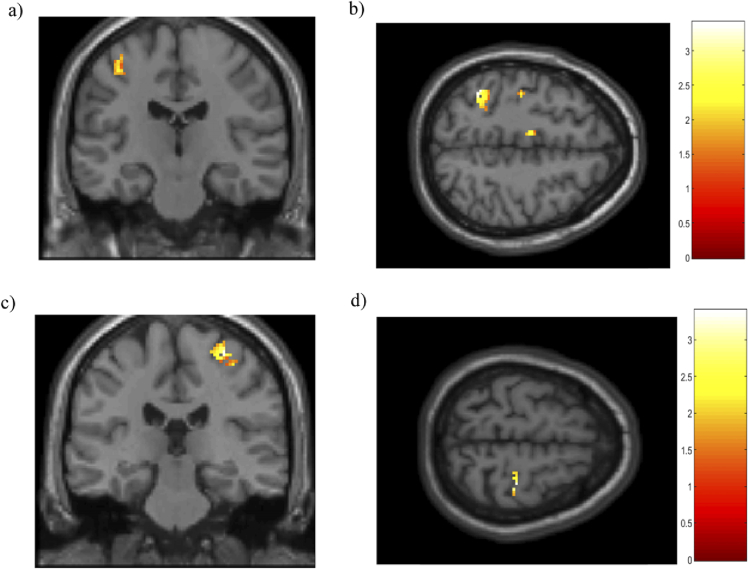
Cerebral activation maps were analyzed during the motor imagery paradigm. t-contrast maps were normalized onto a standard space (MNI). t-contrast maps for the HbO signal in coronal and axial views on the left side (T: 3.09; p<0.001) and on the right side (T: 1.64; p<0.05) are shown in the Fig. 11.

Fig. 11.

t-contrast maps of cerebral activation for the motor imagery > rest contrast measured by DOT device in a subject group (N=8) on the left hemisphere in a) coronal and b) axial views. t-contrast maps on the right hemisphere in c) coronal and d) axial views. All results were mapped onto a standard space (MNI). Threshold p-value corrected FDR at the voxel level for HbO signal. Color bar depicts the HbO signal changes.

t-contrast maps for the HbR signal in coronal and axial views on the left side (T: 3.09; p<0.001) and on the right side (T: 1.64; p<0.05) are shown in the Fig. 12.

Fig. 12.

t-contrast maps of cerebral activation for the motor imagery > rest contrast measured by the DOT device in a subject group (N=8) in the left hemisphere in a) coronal and b) axial views. t-contrast maps of the right hemisphere in c) coronal and d) axial views. All results were mapped onto a standard space (MNI). Threshold p-value corrected FDR at the voxel level for HbR signal. Color bar depicts the HbR signal changes.

Figure 13 depicts the t-contrast maps for the BOLD signal measured by fMRI device during the motor imagery (T:6.3; p <0.001) in coronal and axial views.

Fig. 13.

t-contrast maps of cerebral activation for the motor imagery > rest contrast measured by the fMRI device in a subject group (N=8) in a) coronal and b) axial views. All results were mapped onto a standard space (MNI). Threshold p<0.001 corrected FDR at the voxel level for BOLD signal. Color bar depicts the BOLD signal changes.

From a general point of view, a similar spatial distribution could be distinguished in the loci for DOT and fMRI measurements during the motor imagery. However, a spatial conjunction analysis was performed to corroborate the level of overlapping, as is shown in Table 3. The conjunction analysis shows that DOT and fMRI signals are covering the motor regions and surrounding regions during the motor imagery, as has been described by other authors [39].

Table 3. Representation of the number of common voxels by anatomical area according to HbO-BOLD and HbR-BOLD.

Anatomical region	Peak MNI co-ordinate			No. of common voxels
	x	y	z
$\mathit{L}\mathit{e}\mathit{f}\mathit{t}\mathit{H}\mathit{e}\mathit{m}\mathit{i}\mathit{s}\mathit{p}\mathit{h}\mathit{e}\mathit{r}\mathit{e}$
Motor imagery > rest (T:3.09, p < 0.001)
HbO∩BOLD
Postcentral BA2	−38	−28	44	75
Precentral gyri	−38	−18	56	5
Precentral gyri BA4	−34	−26	64	5
HbR∩BOLD
Postcentral gyri BA2	−54	−6	20	32
Postcentral gyri BA6	−52	−10	40	16
Precentral gyri	−26	−20	56	7
Precentral gyri	−36	−16	60	7
$\mathit{R}\mathit{i}\mathit{g}\mathit{h}\mathit{t}\mathit{H}\mathit{e}\mathit{m}\mathit{i}\mathit{s}\mathit{p}\mathit{h}\mathit{e}\mathit{r}\mathit{e}$
Motor imagery > rest (T:1.64, p < 0.05)
HbO∩BOLD
Supplementary motor area	58	−34	30	6
Supplementary motor area	14	−14	62	49
Precentral gyri	34	−10	50	16
HbR∩BOLD
Precentral gyri	34	−12	50	18

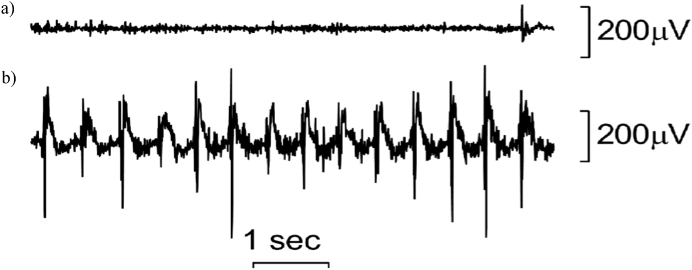
Electromyography recordings were made during the performance of the imagery to ensure that the subjects imagined the movements without moving their hands, Fig. 14. Therefore, the cerebral activity shown in the t-contrast maps corresponds to motor imagery.

Fig. 14.

Electromyographic recordings (EMG) made during a) kinesthetic imagery and b) finger opposition movement (motor execution) by a subject. The positive electrodes were placed over the first dorsal interosseous, the negative electrodes were placed near to the wrist, and the ground electrode was located in the center of the dorsal part of the palm of the hand.

4. Discussion

A wide variety of studies have tried to validate the DOT technique from the physical modelling to DOT data processing using different experimental paradigms because the DOT technique is still being developed [40]. In prior studies, the authors presented a new approach to DOT data processing as if they were fMRI volumes, validated on the prefrontal cortex using a cognitive paradigm [22]. Moreover, the continuous wave system used in the present work can measure through the frontal sinus reaching the frontal cortex, where the scalp-cortex distance is greater than that in other human head regions [41]. These studies indicated that both the DOT data processing and the penetration depth of NIR light are robust enough in a complex region of human head such as the frontal lobule. The authors’ interest now is to study the motor regions for which the scalp-cortex distance is less than frontal regions.

Assuming that the fMRI images are reliable, the individual t-maps provided by DOT measurements showed that it is possible to measure the brain region network implicated in motor execution. Previous studies have identified contralateral activation of the primary sensorimotor cortex (SMC), extending across the pre- and postcentral gyrus during finger to thumb opposition movements [42,43]. Cerebral activations can even extend to the ipsilateral hemisphere when the task is complex e.g., middle finger to thumb opposition movements [44], reaching the supplementary motor area (SMA) which has been widely described during finger to thumb movements [45,46].

Based on the preliminary results, the conjunction analysis between fMRI and DOT t-maps was performed. The results presented here show that the cerebral activations are localized in the contralateral area during the performance of motor execution with the right hand. The loci corresponding to the HbO, HbR and BOLD signals are distributed in the left pre- and postcentral gyri, covering the following Brodmann Areas (BA): BA2, BA3, BA4 which correspond to the SMC, and BA6 which is composed of the premotor cortex [42], and, medially, the SMA, whose function is the planning, preparation and execution of motor actions [47,48]. Other cerebral regions implied in the motor execution such as the thalamus [49], the putamen [50] or the cerebellum [51] are not shown, because the DOT spatial resolution is limited to the cerebral cortex.

Moreover, the loci for the HbO, HbR and BOLD signals during the performance of kinesthetic motor imagery paradigm (KMI) are localized in the BA2, BA4 & BA6. The results presented here agree with other KMI studies such as activations in the BA4 during a transcranial magnetic stimulation [48], or in an individual subject [48]. Besides, an increase in excitability in BA2 & BA6 have been shown during KMI which suppresses the movements that are represented in the motor system [52], as observed in the present work. Somatosensory recruitment is consistent with imagined sensations associated with performing actions. Motor execution models have proposed that sensory information provides the accuracy of movements comparing the actual and predicted sensory consequences [53]. Therefore, the motor imagery could be explained as the generation of sensory efferences without accompanying movement execution [54].

From a neurovascular coupling point of view, the hemoglobin states measured by DOT can potentially provide complementary information regarding fMRI measurements, helping to clarify neurovascular coupling, which is still not well known [55]. HbO and HbR signals have voxels in common with the BOLD signal, when comparing t-contrast maps. Some authors have suggested that there is a stronger relationship between the HbO-BOLD than between the HbR-BOLD [56], as shown in the contralateral hemisphere. However, the results also show that there is a stronger relationship between HbR-BOLD in the ipsilateral hemisphere than in the contralateral hemisphere during motor movement. These discrepancies in hemodynamic behavior are solved by neurovascular coupling. Thus, HbR increases during neuronal activity as a result of initial oxygen consumption. If the neuronal activity is maintained, a vasodilatation phenomenon is generated [57], where the HbR is washed with oxygenated blood arriving from the spatially wider vasodilation from neighboring regions. Unlike fMRI results, even using two approaches in the data processing, the DOT set can show these HbR increases that have not been washed by the vasodilatation.

Continuous-wave DOT system and DOT data processing show hemodynamic differences in a specific anatomical region such as at the cerebral gyri level, which cannot be clearly distinguished in fMRI measurements [21]. Finally, the results from the motor imagery demonstrate the reliability of the DOT set to measure functional changes which are subtler than the changes generated by motor movements. Other authors have reported similar results using time-resolved NIRS system during the motor imagery. [58,59,60]

Nowadays, there is increasing interest in using emerging technologies such as brain computer interfaces and neurofeedback techniques in rehabilitation [61]. One such work indicates that an individual's ability to produce motor imagery can be a determining factor in whether they can interact with such devices [62]. The results presented here suggest that the whole DOT set (including the algorithms used here) can be used to non-invasively monitor hemodynamic changes for all populations, providing functional information at the gyri level, especially for those that cannot tolerate the restrained environment of fMRI such as children and the elderly.

Funding

European Regional Development Fund10.13039/501100008530 (MAC/1.1b/098); Cooperation Program Interreg MAC (Madeira-Azores-Canarias) 2014-2020; Fundación General Universidad de La Laguna10.13039/100015529.

Disclosures

The authors declare no conflicts of interest.