Abstract
This article explores the effectiveness of gamma rays attenuation of various N95 respirator samples by analysing several theoretical parameters such as the Effective Atomic Numbers (Zeff), Half Value Layer (HVL), Mean Free Path (MFP), Mass Attenuation Coefficients (MAC), Tenth Value Layer (TVL), Exposure Build Up Factors (EBF) and Energy Absorption Build Up Factors (EABF). For the selected N95 mask samples, the MAC values corresponding to the energy levels between 0.015 and 20 MeV are measured using the WinXCOM software and the MATLAB code. The parameters including Zeff, TVL, HVL, and MFP are computed using the MAC values derived from the WinXCOM program. EBF and EABF are computed in relation to the penetration depth and incident photon energy by using the (G-P) fitting approximation in estimating the photon build-up factor. The findings showed that having the lowest TVL, HVL, and MFP, the N2 sample has the best output in terms of radiation attenuation purposes. In conclusion, the N2 sample which outperforms other samples is the most promising mask sample when it comes to gamma-ray attenuation features.
Keywords: MAC, HVL Zeff, EBF-EABF, N95 masks
1. Introduction
It is known that COVID-19 disease is transmitted through contaminated respiratory droplets. The size of the respiratory droplets varies, while the size of the novel coronavirus is approximately 100 nm in diameter. The novel coronavirus could also spread via an “airborne route” and it can be transported in microscopic water droplets or due to the air through evaporation form. According to a study published in the New England Journal of Medicine (NEJM), COViD-19 can survive 3 h in the air, 4 h on a copper surface, 48 h on a metal surface, 72 h in plastic, and 24 h in cardboard materials[1]. In addition, it is recommended by Health Institutions to wear face masks in crowded environments to reduce the spread of COVID-19. Because the use of masks will reduce the spread, as it will limit the risk of transmission of people infected with COVID-19 but not showing symptoms. For this reason, personal protection, especially face masks, is important for those who are in close contact with patients infected with COVID-19. Therefore, this form of personal protective equipment (PPE), which offers protection against infectious particles such as coronavirus-laden aerosols, is in extremely short supply worldwide, and medical professionals are already rationing the masks at Covid-19 hotspots.
Standard N95 masks can filter out both large and small particles and that's why they are often acknowledged as safer than other types of masks i.e. surgical, fabric respirators. According to studies investigating the effectiveness of masks for COVID-19; medical masks are sufficient except for aerosol-containing processes and N95/FFP2 masks are required for aerosol-containing processes. It is recommended by health manufacturers and institutions not to reuse N95/FFP2 masks that are visibly contaminated with respiratory, nasal secretions, or other body fluids from patients [2,3].
Medical masks of different types on the market are made of different types of polymeric materials, because they are cheaper, easy to manufacture, and versatile in terms of chemical functionality and formability. Natural polycellulose-based polymers are generally used for cover material in most of the masks and other cheap polymers, such as spun polypropylene fibers/mats, are used as filtering materials (with their submicron scale air gaps) between polymeric cover sheets. The polymeric materials used in a commercial N95 mask are specified in its technical specification sheets [4].
Recent studies have been conducted on the investigation of gamma radiation attenuation of polymeric materials with some dosimetric data as well as effects on the chemical, mechanical, and thermal properties of different polymers[5]. Radiation has been shown to result in crosslinking, chain scission, and some color change due to chemical bond alteration after a certain dose, however, there are still not enough studies on N95/FFP2 masks in the literature.
Although there are different reports in the literature on the maximum dose for use without altering the properties of polymeric materials, the radiation dose should be between 10 and 25 kGy to have enough dose to kill the living organism, such as bacteria and viruses and not to affect the chemical and morphological properties of polymeric material [5].
There are however various in-depth experimental studies about the gamma radiation interaction with different polymers [5], a fast method to obtain the parameters for new candidate polymers to be used in masks is not available [6,7]. Herewith, we have investigated the theoretical extensive data calculated from MATLAB simulation and WinXCOM program on mass attenuation coefficients, effective atomic number, exposure buildup factor and energy absorption build up factors on different polymers used especially for medical masks, and investigate alternative polymers that can be used for filtering part of these types of respirators.
In this study, we explore radiation attenuation properties of polymers that are used in commercial N95 masks. This is an important question since these masks would possibly be used by healthcare workers or by patients during a radiation treatment procedure such as CT (computed tomography) and MRI (magnetic resonance imaging). Therefore, it is important to determine the attenuation properties of these polymer made masks.
2. Materials and methods
N95 masks are made up of multiple layers of material. The most important is the molten fiber layer. The fabric included in the melting process (100–1000 μm thick) consists of microfibres with diameters ranging from 2 to 10 μm. The molten fibers mingle together to form a porous structure [8].
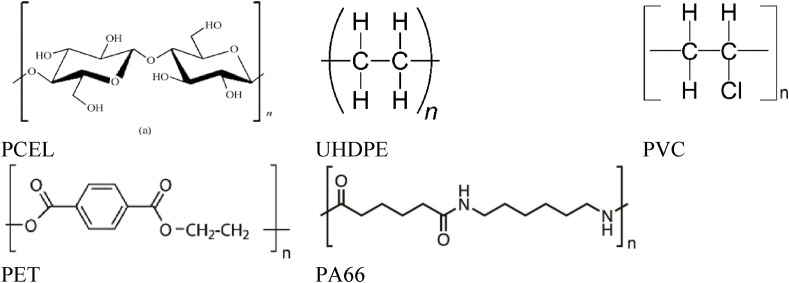
Because of this, such fabrics can retain huge quantities of particulate matter. The fibers themselves are not harmful and are usually charged electrostatically to increase the interaction between the particles, resulting in a much higher filtration efficiency without increasing air resistance. Polymeric contents of N95/FFP2 type masks used by healthcare professionals are shown in Fig. 1 .
Fig. 1.
Chemical structure of studied N95 mask samples.
One of the most used polymers in most of the masks as the outer layer is polycellulose (PCEL). Generally, because of its compatibility, cheapness, and easy to fabricate, ultra-high density polyethylene (UHDPE), polyvinylchloride (PVC), polyethyleneteraphtalate (PET) and polyhexametyleneadipamide (PA66) are studied in order to compare the results. These alternatives are chosen for a range of factors, i.e. different atomic compositions, availability/cheapness, and different physical and chemical properties, such as having different density and chemical resistance.
Atomic weight percentages are calculated theoretically from the chemical structures of the polymers (Fig. 1) under investigation and are given in Table 1 . Since the density values of these polymers can generally vary with respect to their preparation and production methods, the density values of these polymers are retrieved from the Polymer Data Handbook [9].
Table 1.
Chemical compositions (wt %) of studied N95 mask samples.
| Sample code | N95 Mask Samples | C | N | O | Cl | H |
|---|---|---|---|---|---|---|
| N1 | PA66 | 0.6372 | 0.1239 | 0.1416 | – | 0.0973 |
| N2 | PVC | 0.3840 | – | – | 0.5680 | 0.0480 |
| N3 | UHDPE | 0.8571 | – | – | – | 0.1429 |
| N4 | PET | 0.6250 | – | 0.3333 | – | 0.0417 |
| N5 | PCEL | 0.4444 | – | 0.4938 | – | 0.0617 |
The Monte Carlo Simulation codes with MATLAB and XCOM program for the simulation of the transport of photons through three-dimensional components are used in this study[10]. The reason we use the MATLAB program for calculations other than converting the obtained data into graphs is to compare with XCOM data to obtain better visual graphs with more details and fast calculations. The mass attenuation coefficients are also calculated by using the MATLAB codes. The results obtained from the WinXCOM computer program are analysed to verify the results of the data obtained from MATLAB codes. The parameters that are calculated for determining the attenuation properties of N95 masks are the followings: MAC, HVL-TVL, MFP, Zeff, EBF-EABF.
MAC is the ability of the materials involved to absorb radiation per unit of mass. As such, MAC depends on the numbers of energy and atoms, and thus varies as these factors change. This is a constant which defines the fraction of attenuated incident photons in a monoenergetic beam per unit thickness of a material and is calculated using the Lambert-Beer Law:
| (1) |
| (2) |
In equation (1), I 0 and I represent the primary and the attenuated of the photon with the intensities [11,12].
The penetration ratio has represented in the equation which, showed the photon interaction and protection features of the used material. Used the weight section (w i) of ith component forming a matter and μ/ρ is the mass attenuation coefficient, this parameter can be given.
The Half Value Layer (HVL) and the Tenth Value Layer (TVL) equal to the thickness of the used matter necessary to decrease to the beam [13,14].
| (3) |
| (4) |
The mean free path (MFP) shows the average aperture that the wave can move without any interaction along the path inside the masks.
| (5) |
And the following equation is used for calculating the effective atomic number () of mask samples.
| (6) |
where shows the fraction by mole of the individual element providing , is and are the atomic weight and the atomic number, respectively [15].
The EABF and EBF are important parameters for evaluating effectiveness in shielding. These two parameters are a very useful equation for demonstrating the uncollided/unscattered photon movement on matters. Some of the approximate methods for simulating both EABF and EBF are the G-P fitting method, which is an interpolation procedure based on the formula below using the corresponding atomic number (Z eq) [16].
| (7) |
| (8) |
where K(E, x) (the photon dose multiplication factor) and b (the build-up factor corresponding to 1 MFP) are derived from the following equation [[17], [18], [19], [20], [21]]:
| (9) |
3. Results and discussion
Table 1 describes the chemical structures (Fig. 1), the weight fractions, and the densities of the investigated mask samples. By using the MATLAB code and the WinXCOM program, the MAC values are calculated at the energy range between 0.015 and 20 MeV.
Table 2, Table 3 shows the data obtained from the WinXCOM and MATLAB simulation code, and the percentage differences. From Table 2, Table 3, it can be interpreted that the WinXCOM and the MATLAB data are similar to each other, meaning the MATLAB code is reliable for measuring the MAC values of the mask samples. The findings are expressed in Fig. 2 .
Table 2.
The mass attenuation coefficients (cm2/g) values derived from MATLAB and WinXCOM for N95 mask samples.
| N1 |
N2 |
N3 |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Energy (MeV) | Matlab | WinXcom | % Dev. | WinXcom | Matlab | % Dev. | WinXcom | Matlab | % Dev. | ||||||||||
| 0.001 | 2469.728 | 2470.0000 | 0.00011 | 2457.946 | 2457 | 0.00039 | 1896.079 | 1896 | 0.0000 | ||||||||||
| 0.003 | 108.6426 | 106.4000 | 0.020642 | 882.3799 | 871.2000 | 0.01267 | 79.1602 | 77.5000 | 0.0210 | ||||||||||
| 0.005 | 23.03124 | 22.9000 | 0.005698 | 230.0838 | 228.9000 | 0.00515 | 16.54096 | 16.4400 | 0.0061 | ||||||||||
| 0.008 | 5.464623 | 5.5370 | 0.013245 | 62.05584 | 62.8400 | 0.012636 | 3.926125 | 3.9780 | 0.0132 | ||||||||||
| 0.01 | 2.876012 | 2.8730 | 0.001047 | 33.4831 | 33.4500 | 0.00099 | 2.091097 | 2.0890 | 0.0010 | ||||||||||
| 0.03 | 0.285961 | 0.2895 | 0.012377 | 1.522251 | 1.4940 | 0.01856 | 0.268041 | 0.2706 | 0.0095 | ||||||||||
| 0.06 | 0.193324 | 0.1930 | 0.001677 | 0.325745 | 0.3326 | 0.021045 | 0.197173 | 0.1969 | 0.0014 | ||||||||||
| 0.08 | 0.176523 | 0.1767 | 0.001003 | 0.228828 | 0.2298 | 0.004249 | 0.182923 | 0.1822 | 0.0040 | ||||||||||
| 0.1 | 0.166059 | 0.1660 | 0.000353 | 0.188809 | 0.1887 | 0.00058 | 0.171869 | 0.1718 | 0.0004 | ||||||||||
| 0.2 | 0.134706 | 0.1348 | 0.000702 | 0.130721 | 0.1308 | 0.000607 | 0.140014 | 0.1401 | 0.0006 | ||||||||||
| 0.4 | 0.10454 | 0.1046 | 0.000573 | 0.098538 | 0.0986 | 0.000931 | 0.108774 | 0.1089 | 0.0012 | ||||||||||
| 0.6 | 0.088566 | 0.0883 | 0.002775 | 0.083127 | 0.0829 | 0.00273 | 0.09217 | 0.0919 | 0.0027 | ||||||||||
| 0.8 | 0.07772 | 0.0776 | 0.002063 | 0.072561 | 0.0727 | 0.001641 | 0.080587 | 0.0807 | 0.0017 | ||||||||||
| 1 | 0.069767 | 0.0697 | 0.000531 | 0.065331 | 0.0653 | 0.00048 | 0.072608 | 0.0726 | 0.0005 | ||||||||||
| 2 | 0.048654 | 0.0487 | 0.000321 | 0.045841 | 0.0459 | 0.000202 | 0.050593 | 0.0506 | 0.0003 | ||||||||||
| 3 | 0.039134 | 0.0390 | 0.004444 | 0.037512 | 0.0374 | 0.00379 | 0.040604 | 0.0404 | 0.0045 | ||||||||||
| 4 | 0.033228 | 0.0333 | 0.001258 | 0.032568 | 0.0326 | 0.000989 | 0.034377 | 0.0344 | 0.0012 | ||||||||||
| 5 | 0.029544 | 0.0295 | 0.001489 | 0.029615 | 0.0296 | 0.00117 | 0.030475 | 0.0304 | 0.0015 | ||||||||||
| 6 | 0.026924 | 0.0268 | 0.003509 | 0.0276 | 0.0275 | 0.00253 | 0.027686 | 0.0276 | −0.0035 | ||||||||||
| 7 | 0.024873 | 0.0249 | 0.000931 | 0.026094 | 0.0261 | 0.00053 | 0.025492 | 0.0255 | 0.0009 | ||||||||||
| 8 | 0.023492 | 0.0233 | 0.007727 | 0.025119 | 0.0250 | 0.00474 | 0.023776 | 0.0238 | 0.0018 | ||||||||||
| 9 | 0.022242 | 0.0221 | 0.006367 | 0.024275 | 0.0242 | 0.0035 | 0.022662 | 0.0225 | 0.0067 | ||||||||||
| 10 | 0.021128 | 0.0211 | 0.000356 | 0.02357 | 0.0236 | 0.00044 | 0.021455 | 0.0214 | 0.0007 | ||||||||||
| 11 | 0.020458 | 0.0203 | 0.007224 | 0.02318 | 0.0231 | 0.00473 | 0.020725 | 0.0206 | 0.0079 | ||||||||||
| 12 | 0.019675 | 0.0196 | 0.002274 | 0.022727 | 0.0227 | 0.00208 | 0.01987 | 0.0198 | 0.0025 | ||||||||||
| 13 | 0.019097 | 0.0191 | 0.002439 | 0.021792 | 0.0224 | 0.00195 | 0.019237 | 0.0192 | 0.0001 | ||||||||||
| 14 | 0.018565 | 0.0186 | 0.000275 | 0.022 | 0.0221 | 0.005467 | 0.018652 | 0.0187 | 0.0024 | ||||||||||
| 15 | 0.018199 | 0.0181 | 0.003243 | 0.021943 | 0.0219 | 0.00107 | 0.018247 | 0.0182 | 0.0037 | ||||||||||
| 16 | 0.017859 | 0.0178 | 0.004441 | 0.021792 | 0.0218 | 0.00145 | 0.017869 | 0.0178 | 0.0050 | ||||||||||
| 18 | 0.017244 | 0.0172 | 0.00369 | 0.021519 | 0.0215 | 0.000511 | 0.01718 | 0.0171 | 0.0041 | ||||||||||
| 20 | 0.01671 | 0.0167 | 0.00000 | 0.021415 | 0.0214 | 0.0007 | 0.016671 | 0.0166 | 0.0055 |
Table 3.
The mass attenuation coefficients (cm2/g) values derived from MATLAB and WinXCOM for N95 mask samples.
| N4 |
N5 |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Energy (MeV) | Matlab | WinXcom | % Dev. | WinXcom | Matlab | % Dev. | |||||||
| 0.001 | 2326.082 | 2326.0000 | 0.0000 | 3249.881 | 3250 | 0.0000 | |||||||
| 0.003 | 544.6596 | 547.3000 | 0.0048 | 150.4738 | 147.4000 | 0.0204 | |||||||
| 0.005 | 142.7031 | 150.567261 | 0.0551 | 32.35929 | 32.1800 | 0.0055 | |||||||
| 0.008 | 38.2241 | 38.7100 | 0.0127 | 7.779338 | 7.8020 | 0.0029 | |||||||
| 0.01 | 20.60236 | 20.5800 | 0.0011 | 4.022171 | 4.0180 | 0.0010 | |||||||
| 0.03 | 1.001198 | 0.9836 | 0.0176 | 0.325557 | 0.3225 | 0.0094 | |||||||
| 0.06 | 0.259328 | 0.2696 | 0.0396 | 0.192669 | 0.1922 | 0.0024 | |||||||
| 0.08 | 0.202727 | 0.2034 | 0.0033 | 0.173266 | 0.1735 | 0.0014 | |||||||
| 0.1 | 0.1753 | 0.1752 | 0.0006 | 0.162088 | 0.1621 | 0.0001 | |||||||
| 0.2 | 0.1291 | 0.1292 | 0.0008 | 0.130667 | 0.1307 | 0.0003 | |||||||
| 0.4 | 0.0985 | 0.0986 | 0.0009 | 0.101259 | 0.1014 | 0.0014 | |||||||
| 0.6 | 0.083243 | 0.0830 | 0.0028 | 0.085771 | 0.0855 | 0.0028 | |||||||
| 0.8 | 0.072709 | 0.0728 | 0.0017 | 0.074988 | 0.0751 | 0.0016 | |||||||
| 1 | 0.065483 | 0.0655 | 0.0005 | 0.067569 | 0.0675 | 0.0006 | |||||||
| 2 | 0.045835 | 0.0459 | 0.0003 | 0.047165 | 0.0472 | 0.0003 | |||||||
| 3 | 0.037253 | 0.0371 | 0.0041 | 0.038033 | 0.0379 | 0.0043 | |||||||
| 4 | 0.032061 | 0.0321 | 0.0009 | 0.032402 | 0.0324 | 0.0012 | |||||||
| 5 | 0.028902 | 0.0289 | 0.0011 | 0.028909 | 0.0289 | 0.0014 | |||||||
| 6 | 0.026707 | 0.0266 | 0.0029 | 0.026437 | 0.0264 | 0.0033 | |||||||
| 7 | 0.025031 | 0.0250 | 0.0008 | 0.024516 | 0.0245 | 0.0010 | |||||||
| 8 | 0.023925 | 0.0238 | 0.0056 | 0.023027 | 0.0231 | 0.0014 | |||||||
| 9 | 0.022948 | 0.0229 | 0.0043 | 0.022069 | 0.0219 | 0.0058 | |||||||
| 10 | 0.022106 | 0.0221 | 0.0003 | 0.021043 | 0.0210 | 0.0006 | |||||||
| 11 | 0.021502 | 0.0215 | 0.0001 | 0.020383 | 0.0203 | 0.0045 | |||||||
| 12 | 0.021054 | 0.0210 | 0.0021 | 0.019715 | 0.0197 | 0.0023 | |||||||
| 13 | 0.020642 | 0.0206 | 0.0020 | 0.01919 | 0.0192 | 0.0021 | |||||||
| 14 | 0.020274 | 0.0203 | 0.0002 | 0.018709 | 0.0187 | 0.0000 | |||||||
| 15 | 0.020029 | 0.0200 | 0.0019 | 0.018381 | 0.0183 | 0.0028 | |||||||
| 16 | 0.019881 | 0.0198 | 0.0061 | 0.018079 | 0.0180 | 0.0038 | |||||||
| 18 | 0.019435 | 0.0194 | 0.0018 | 0.017534 | 0.0175 | 0.0031 | |||||||
| 20 | 0.019141 | 0.0191 | 0.0000 | 0.017142 | 0.0171 | 0.0042 |
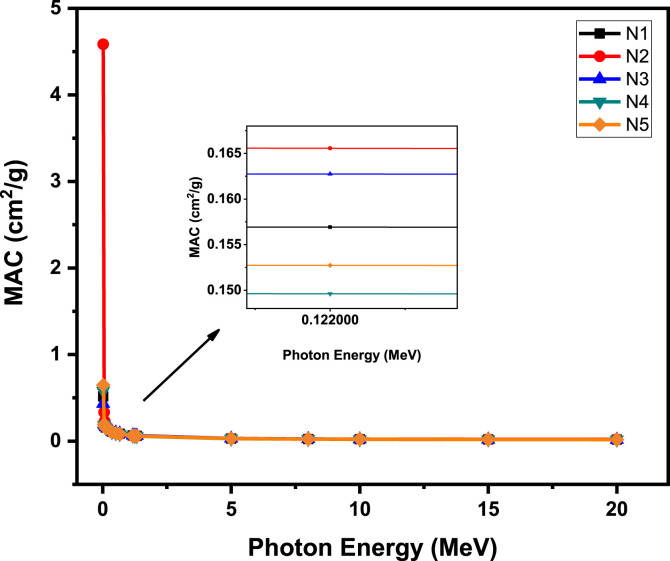
Fig. 2.
Mass attenuation coefficient of the selected N95 mask samples with photon energy 0.02 MeV–20 MeV.
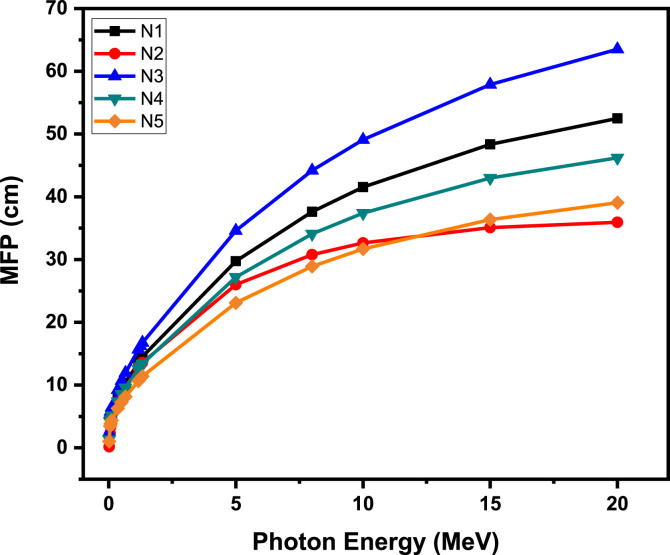
It is noted from the figure that the MAC values are proportional to the energy provided that the MAC values fall while the applied energy level rises to 20 MeV[22]. The energy-material interaction is generally grouped into three energy-material incidents: low-energy and photoelectric incidents; intermediate energy and Compton scattering incidents; high-energy, and pair production incidents. HVL, TVL, and MFP are major factors for the efficiency of the attenuator. The lower these values, the higher quality we have in principle when it comes to attenuation applicability. The MFP (1/μ) values for these mask samples are also reported between the energy range of 0.015 MeV–20 MeV shown in Fig. 3 .
Fig. 3.
Mean free path (MFP) of the N95 mask samples.
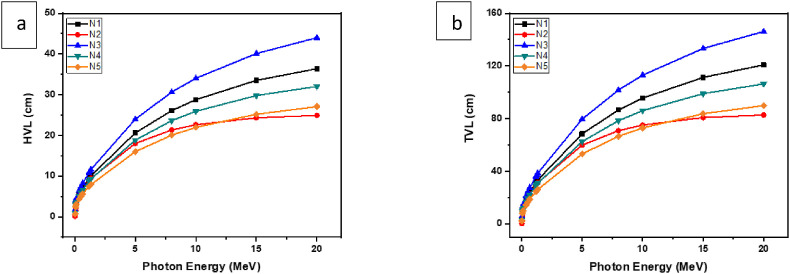
N2 and N5 are the samples with the minimum MFP, which is similar to HVL-TVL. Fig. 4 (a-b) shows the difference between the HVL-TVL values as the energy level varies. It can be seen that the values of HVL – TVL in terms of energy don't change inversely.
Fig. 4.
(a–b): (Half (HVL) and Tenth value layer (TVL) of the N95 mask samples.
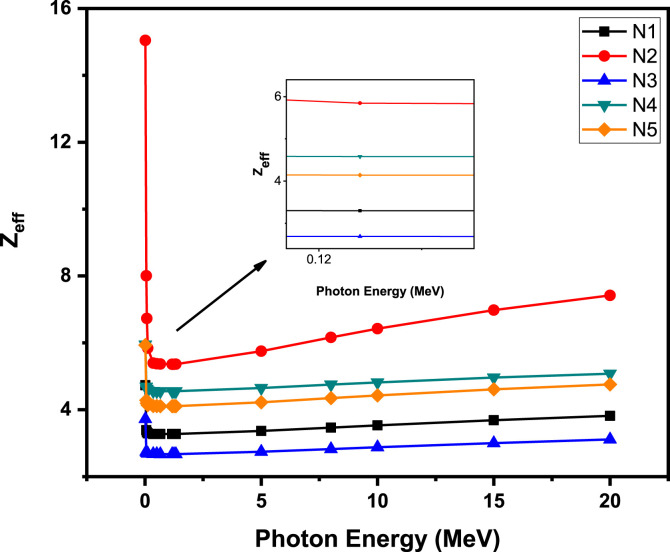
This feature is different from the MAC, which inverted to the changes in the energy levels. The values of HVL, TVL rise while the levels of energy rise. The MFP values, in addition to the HVL – TVL values, are also proportional to the energy levels which yield lower energy values. This has been recorded in Fig. 3 and with Fig. 4(a and b). The chemical structure does not affect the energy-to-matter relationship at low energy levels. As a result, N2 and N5 have lighter HVL, TVL and MFP. Mask density have an opposite influence on the values of MFP and HVL-TVL. For example, N2 and N5 mask higher densities have lower HVL-TVL values than the others. Photon energy is proportional to the value of Zeff. Different effects however occur at different energy levels. For example, the Zeff values in the low-energy region have fallen to 0.356 MeV, as shown in Fig. 5 .
Fig. 5.
Effective atomic numbers of the N95 mask samples with photon energy.
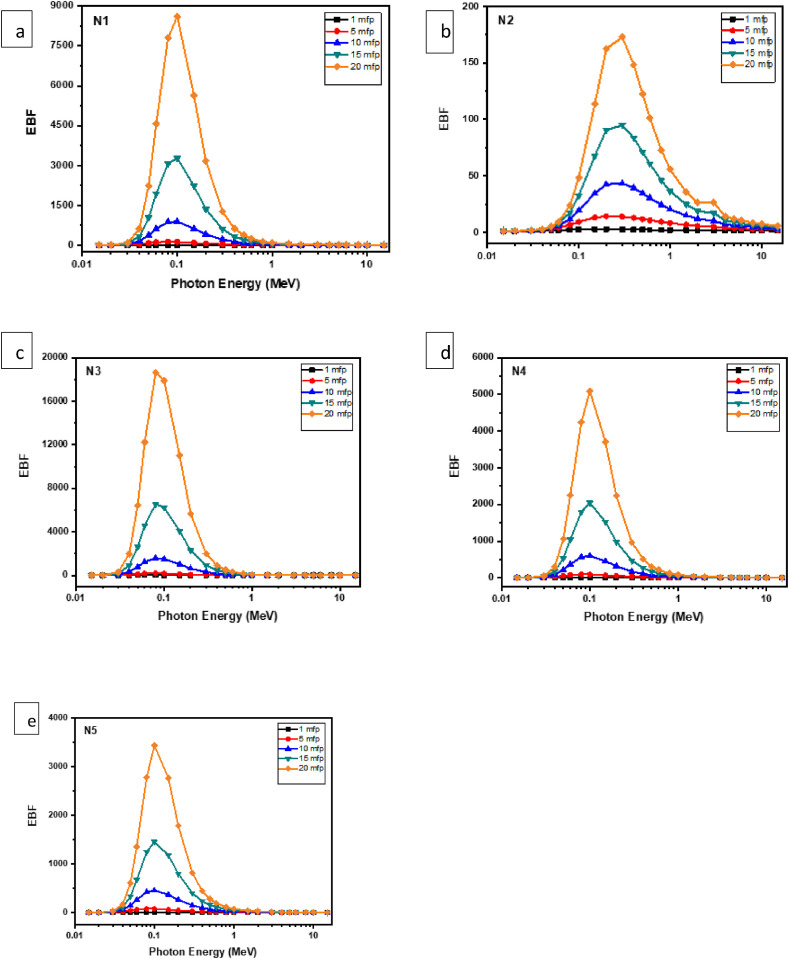
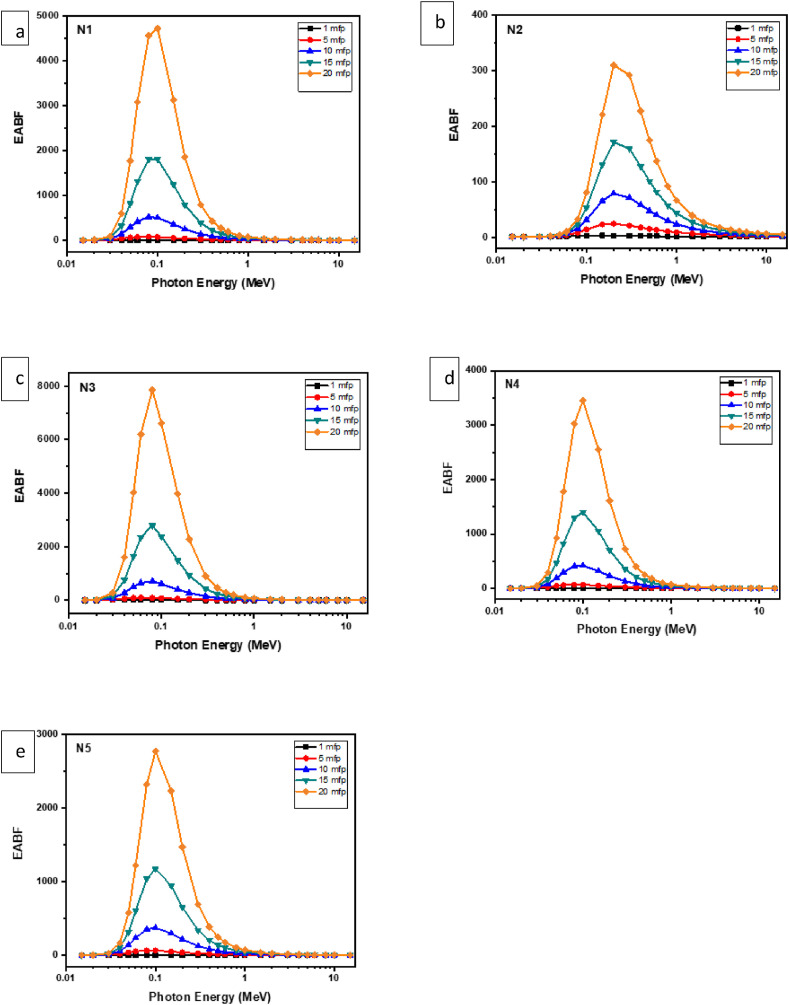
Photoelectric absorption is becoming dominant in that low-energy region. Zeff values are variable over a wide range in the low-energy field. This study investigates a group of mask samples whose structure has no heavy elements. As a consequence, Zeff values are suddenly reduced as the chemical composition of these mask samples affects radiation attenuation quality. In the intermediate energies between 0.511 MeV < E < 1.33 MeV, Compton scattering becomes dominant processes that produce the lowest Zeff. Among the N95 mask samples tested, N2 is one material with the highest Zeff values of 15.05–7.42. In the high energy region between 5 and 20 MeV, pair production grows into the dominant process yielding weaker Z2 dependence. Zeff's variation with respect to changing levels of energy is given in Fig. 5 [[23], [24], [25]]. For all mask samples tested, the values of Zeff decreased in the low energy region (E < 1 MeV). It should be noted that Zeff values are inversely affected by increasing energy in this low-energy region. Yet the larger number of atoms in the Cl element also leads to rising Zeff values. For example, with a larger Cl element in its chemical structure, the N2 mask has the largest Zeff values compared to other materials investigated as shown in Fig. 5. In the medium-energy region, Zeff values remain constant due to cross-section of the Compton process and atomic number changes for almost all the mask samples. For mask samples, the values of exposure build-up factors (EBF) and energy absorption build-up factors (EABF), which are important parameters of gamma shielding, are also determined. The EBF sets out the characteristics of energy absorption in the air. On the other hand, the EABF shows the energy absorbed/accumulated in the attenuation matter and indicates the presence of significant differences in the continuous energy zone between the EABF and EBF. From Fig. 6, Fig. 7 (a-e) it is easy to see that the EBF and EABF values of mask samples vary by the depths of 1, 5, 10, 15, and 20 MFP[[25], [26], [27]].
Fig. 6.
(a–e): The exposure buildup factors in the energy region 0.015–15 MeV at the 1–20 MFP for N95 mask samples.
Fig. 7.
(a–e): The energy absorption buildup factors in the energy region 0.015–15 MeV at the 1–20 MFP for N95 mask samples.
Those values depend on the regions of energy. In the region of low energy, the lowest values are seen. Highest values, on the other hand, occur in the high energy region. This situation is explained by the photoelectric effect predominance in low energies. Whereas for the medium-energy area the EBF and EABF rise with increasing energy. This arises from the effect of multiple scattering processes on Compton scattering. In the higher-energy region the EBF and EABF values rise under the effect of pair production. Pair production is effective in high energies, as photons are fully absorbed. In the mid-energy region, the EBF and EABF values take maximum, and Compton scattering is dominant in this region. Photons are not fully absorbed in this region and their energy is slightly reduced [[28], [29], [30], [31]]. The directions of these photons are also switched, resulting in multiple scattering causing the photons to accumulate in the environment. Also, as can be seen from Fig. 6, Fig. 7, as penetration depth (MFP) values increase, the EBF and EABF values increase as the number of photons dispersed increases accordingly. As the amount of C in the mask samples decreases and increases Cl, the build-up of photons decreases, i.e. the lowest EBF value in the N2 mask sample (Fig. 6(b)). Similarly, with the EBF values, the EABF values show similar effects. Of the mask samples in various MFP values, the minimum value is obtained from the N2 sample (Fig. 7(b)).
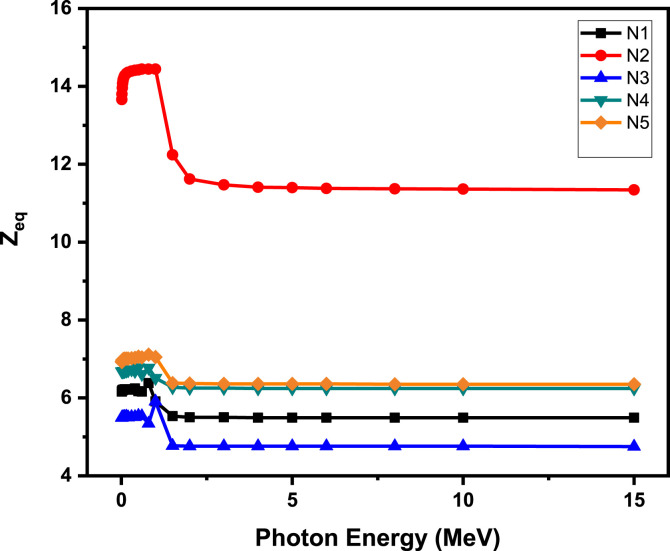
There is an inverse relationship between the values of EABF and EBF and the values of Zeq. So also the EBF-EABF approaches its maximum level as the Zeq approaches its minimum. The EBF-EABF and Zeq reverse relation is shown in Fig. 8 .
Fig. 8.
Equivalent atomic numbers of the N95 mask samples with photon energy.
It may also be noted from the figures that the lowest compound of EBF-EABF is the N2 with the highest of Zeq. The smaller EBF-EABF stands for better radiation attenuation properties. So, in radiation terms, we can say that N2 is safer than samples from the mask.
4. Conclusion
This research analyses the viability of gamma rays attenuation of various N95 face mask samples by assessing numerous theoretical metrics such as the Effective Atomic Numbers (Zeff), Half Value Layer (HVL), Mean Free Path (MFP), Mass Attenuation Coefficients (MAC), Tenth Value Layer (TVL), Exposure Build Up Factors (EBF) and Energy Absorption Build Up Factors (EABF). The MAC values corresponding to the energy levels between 0.015 and 20 MeV for the identified N95 masks are determined using the WinXCOM software and the MATLAB codes. The variables including Zeff, TVL, HVL, and MFP are computed utilizing WinXCOM software derived MAC values. EBF and EABF are determined in respect to the penetration depth and incident photon energy in the estimation of the photon build-up factor by using the G-P fitting approach.
In summary, our study aims at identifying polymers that are best suited to gamma irradiation for manufacturing N95 masks. The findings showed that having the lowest TVL, HVL and MFP, the N2 sample has the best radiation attenuation performance. In conclusion, the N2 sample that outperforms other samples is the most promising mask sample when it comes to gamma-ray attenuation features.
CRediT authorship contribution statement
Ozge Kilicoglu: Conceptualization, Methodology, Calculations, and writing. Umit Kara: Monte Carlo Simulation, Writing - original draft. Ibrahim Inanc: Investigation, of the material and drafting.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Van Doremalen N., Bushmaker T., Morris D.H., Holbrook M.G., Gamble A., Williamson B.N., Lloyd-Smith J.O. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N. Engl. J. Med. 2020;382(16):1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bartoszko J.J., Farooqi M.A.M., Alhazzani W., Loeb M. 2020. Medical Masks vs N95 Respirators for Preventing COVID‐19 in Health Care Workers A Systematic Review and Meta‐Analysis of Randomized Trials. Influenza and other respiratory viruses. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.CDC - Recommended Guidance for Extended Use and Limited Reuse of N95 Filtering Facepiece Respirators in Healthcare Settings - NIOSH Workplace Safety and Health Topic. ” Centers for Disease Control and Prevention, Centers for Disease Control and Prevention; 27 Mar. 2020. www.cdc.gov/niosh/topics/hcwcontrols/recommendedguidanceextuse.html [Google Scholar]
- 4.Technical specification of 3M N95 mask. https://multimedia.3m.com/mws/media/1425070O/3m-particulate-respirator-8210-n95-technical-specifications.pdf
- 5.Harrell C.R., Djonov V., Fellabaum C., Volarevic V. Risks of using sterilization by gamma radiation: the other side of the coin. Int. J. Med. Sci. 2018;15(3):274. doi: 10.7150/ijms.22644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nagaraja N., Manjunatha H.C., Seenappa L., Sridhar K.N., Ramalingam H.B. Selection of shielding materials for gamma/X-ray and neutron radiations among the commonly used polymers. Int. J. Nucl. Energy Sci. Technol. 2019;13(4):325–339. [Google Scholar]
- 7.Bhosale R.R., More C.V., Gaikwad D.K., Pawar P.P., Rode M.N. Radiation shielding and gamma ray attenuation properties of some polymers. Nucl. Technol. Radiat. Protect. 2017;32(3):288–293. [Google Scholar]
- 8.Liao L., Xiao W., Zhao M., Yu X., Wang H., Wang Q., Cui Y. Can N95 respirators Be reused after disinfection? How many times? ACS Nano. 2020 doi: 10.1021/acsnano.0c03597. [DOI] [PubMed] [Google Scholar]
- 9.Mark J.E., editor. Polymer Data Handbook. Oxford university press; 2009. [Google Scholar]
- 10.Sharifi S., Bagheri R., Shirmardi S.P. Comparison of shielding properties for ordinary, barite, serpentine and steel–magnetite concretes using MCNP-4C code and available experimental results. Ann. Nucl. Energy. 2013;53:529–534. [Google Scholar]
- 11.Tekin H.O., Kilicoglu O. The influence of gallium (Ga) additive on nuclear radiation shielding effectiveness of Pd/Mn binary alloys. J. Alloys Compd. 2020;815:152484. [Google Scholar]
- 12.Issa S.A., Saddeek Y.B., Sayyed M.I., Tekin H.O., Kilicoglu O. Radiation shielding features using MCNPX code and mechanical properties of the PbONa2OB2O3CaOAl2O3SiO2 glass systems. Compos. B Eng. 2019;167:231–240. [Google Scholar]
- 13.Kara U., Kilicoglu O., Karaibrahimoglu A., Cavdarli K., Ince F. Radiation attenuation properties of removable partial dentures (RPD) Mater. Chem. Phys. 2020:123301. [Google Scholar]
- 14.Dong M.G., Agar O., Tekin H.O., Kilicoglu O., Kaky K.M., Sayyed M.I. A comparative study on gamma photon shielding features of various germanate glass systems. Compos. B Eng. 2019;165:636–647. [Google Scholar]
- 15.Tekin H.O., Akman F., Issa S.A., Kaçal M.R., Kilicoglu O., Polat H. Two-step investigation on fabrication and characterization of iron-reinforced novel composite materials for nuclear-radiation shielding applications. J. Phys. Chem. Solid. 2020 [Google Scholar]
- 16.Kara U., Kilicoglu O., Ersoy S. Structural and gamma-ray attenuation coefficients of different OAD films for nuclear medicine applications. Radiat. Phys. Chem. 2020;172:108785A. [Google Scholar]
- 17.Kara U., Issa S.A., Yorgun N.Y., Kilicoglu O., Rashad M., Abuzaid M.M.,., Tekin H.O. Optical, structural and gamma ray shielding properties of dolomite doped lithium borate glasses for radiation shielding applications. J. Non-Cryst. Solids. 2020;539:120049. [Google Scholar]
- 18.Issa S.A., Tekin H.O., Elsaman R., Kilicoglu O., Saddeek Y.B., Sayyed M.I. Radiation shielding and mechanical properties of Al2O3-Na2O-B2O3-Bi2O3 glasses using MCNPX Monte Carlo code. Mater. Chem. Phys. 2019;223:209–219. [Google Scholar]
- 19.Kilicoglu O., Tekin H.O. Bioactive glasses and direct effect of increased K2O additive for nuclear shielding performance: a comparative investigation. Ceram. Int. 2020;46(2):1323–1333. [Google Scholar]
- 20.Kilicoglu O. Characterization of copper oxide and cobalt oxide substituted bioactive glasses for gamma and neutron shielding applications. Ceram. Int. 2019;45(17):23619–23631. [Google Scholar]
- 21.Mahmoud I.S., Issa S.A., Saddeek Y.B., Tekin H.O., Kilicoglu O., Alharbi T.,., Elsaman R. Gamma, neutron shielding and mechanical parameters for lead vanadate glasses. Ceram. Int. 2019;45(11):14058–14072. [Google Scholar]
- 22.Kilicoglu O., Tekin H.O. Bioactive glasses with TiO2 additive: behavior characterization against nuclear radiation and determination of buildup factors. Ceram. Int. 2020;46(8):10779–10787. doi: 10.1016/j.ceramint.2020.01.088. In press. [DOI] [Google Scholar]
- 23.Abuzaid M.M., Susoy G., Issa S.A., Elshami W., Kilicoglu O., Tekin H.O. Relationship between melting-conditions and gamma shielding performance of fluoro-sulfo-phosphate (FPS) glass systems: a comparative investigation. Ceram. Int. 2020;46(10):15255–15269. doi: 10.1016/j.ceramint.2020.03.065. In press. [DOI] [Google Scholar]
- 24.Sayyed M.I., Tekin H.O., Kılıcoglu O., Agar O., Zaid M.H.M. Shielding features of concrete types containing sepiolite mineral: comprehensive study on experimental, XCOM and MCNPX results. Results in Physics. 2018;11:40–45. [Google Scholar]
- 25.Saddeek Y.B., Issa S.A., Alharbi T., Tekin H.O., Kilicoglu O., Erguzel T.T.,., Ahmad M. Improvement of radiation shielding properties of some tellurovanadate based glasses. Phys. Scripta. 2020;95(3) [Google Scholar]
- 26.Uosif M.A.M., Mostafa A.M.A., Issa S.A., Tekin H.O., Alrowaili Z.A., Kilicoglu O. Structural, mechanical and radiation shielding properties of newly developed tungsten lithium borate glasses: an experimental study. J. Non-Cryst. Solids. 2020;532:119882. [Google Scholar]
- 27.Tekin H.O., Kassab L.R.P., Kilicoglu O., Magalhães E.S., Issa S.A., da Silva Mattos G.R. Newly developed tellurium oxide glasses for nuclear shielding applications: an extended investigation. J. Non-Cryst. Solids. 2020;528:119763. [Google Scholar]
- 28.Tekin H.O., Kaçal M.R., Issa S.A., Polat H., Susoy G., Akman F.,., Gillette V.H. Sodium dodecatungstophosphate hydrate-filled polymer composites for nuclear radiation shielding. Mater. Chem. Phys. 2020;256:123667. [Google Scholar]
- 29.Tekin H.O.O., Abouhaswa A.S., Kilicoglu O., Issa S.A., Akkurt I., Rammah Y. Fabrication, physical characteristic, and gamma-photon attenuation parameters of newly developed molybdenum reinforced bismuth borate glasses. Phys. Scripta. 2020;95(11) doi: 10.1088/1402-4896/abbf6e. [DOI] [Google Scholar]
- 30.Saddeek Y.B., Tekin H.O., Issa S.A., Kilicoglu O., Elshami W., Alharbi T. An in-depth investigation from mechanical durability to structural and nuclear radiation attenuation properties: B2O3–Na2O–Bi2O3–Nb2O5 glasses experience. Phys. Scripta. 2020;95(10):105701. [Google Scholar]
- 31.Kilic G., Issa S.A., Ilik E., Kilicoglu O., Tekin H.O. A journey for exploration of Eu2O3 reinforcement effect on zinc-borate glasses: synthesis, optical, physical and nuclear radiation shielding properties. Ceram. Int. 2020 doi: 10.1016/j.ceramint.2020.09.103. In press. [DOI] [Google Scholar]