Intrapore energy barriers govern ion transport and selectivity of desalination membranes

A fundamental study elucidates the mechanisms underlying selective ion transport through desalination membranes.

Abstract

State-of-the-art desalination membranes exhibit high water-salt selectivity, but their ability to discriminate between ions is limited. Elucidating the fundamental mechanisms underlying ion transport and selectivity in subnanometer pores is therefore imperative for the development of ion-selective membranes. Here, we compare the overall energy barrier for salt transport and energy barriers for individual ion transport, showing that cations and anions traverse the membrane pore in an independent manner. Supported by density functional theory simulations, we demonstrate that electrostatic interactions between permeating counterion and fixed charges on the membrane substantially hinder intrapore diffusion. Furthermore, using quartz crystal microbalance, we break down the contributions of partitioning at the pore mouth and intrapore diffusion to the overall energy barrier for salt transport. Overall, our results indicate that intrapore diffusion governs salt transport through subnanometer pores due to ion-pore wall interactions, providing the scientific base for the design of membranes with high ion-ion selectivity.

INTRODUCTION

Over 1 billion people lack access to clean water worldwide (1). Rapid population growth, climate change, and water contamination further exacerbate the imbalance between the global water availability and demand (2). With abundant saline water on earth, notably, seawater and brackish groundwater, desalination is now recognized as a promising solution to augment water supply and tackle water scarcity (3, 4). Currently, reverse osmosis (RO) is the most widely used desalination technology because of its remarkable water-salt separation efficiency, low energy consumption, and small footprint (5, 6). The key component in RO is a semipermeable membrane made of a dense polyamide active layer with high water-salt selectivity (7).

The high water-salt selectivity of the polyamide layer originates from the subnanometer free volumes (or pores) between polymer chains that substantially hinder the transport of ions compared to the smaller water molecules (8). While extensive research has sought to further improve water-salt selectivity, more recently, demand has grown for ion-ion selectivity; that is, a selective separation of a single ion from solution (9–12). For example, recent studies discussed the development of selective membranes for recovering valuable ions from seawater [e.g., uranium (13) and lithium (14)] with the purpose of mitigating potential resource scarcity. This research thrust is imperative because ion-ion selectivity of current membranes is inadequate to selectively transport a specific ion (e.g., lithium) and reject other ions (e.g., sodium) (15–17). To synthesize novel membranes with high ion-ion selectivity, there is a crucial need to acquire a better understanding of the mechanisms underlying such selectivity in subnanometer pores (18).

In addition to the established mechanisms of size (steric) and Donnan (charge) exclusion (19), ion dehydration has been recently proposed as a mechanism controlling the selective transport of ions under subnanometer confinement (20, 21). Using molecular simulations, ions that are loosely hydrated (i.e., with low hydration energy) were shown to more easily adjust or remove their surrounding hydration shell to enter the pore, resulting in increased permeation rate (18, 22, 23). Experimentally, ion dehydration has mainly been supported by a qualitative correlation between measured energy barriers for salt transport and the corresponding hydration energies of the ions constituting the salt (9, 24). However, the mechanism by which salt ions traverse the membrane pore remains a hotly debated issue (17).

One major open question is whether and to what extent anions and cations interact with each other during permeation through the membrane pore. Because of the experimental difficulty to measure transport properties of an individual ion (e.g., energy barrier), interpretation of ion transport is currently based on exploring properties of salt transport and relating the results to the inherent properties of the individual salt ions (e.g., hydration energy) (25, 26). However, such interpretation might be erroneous, for example, because of potential ion pairing that affects the behavior of the individual ion under the low dielectric conditions of the small pore (27–29). In addition, since a full and unbiased tracking of ion transport through a long subnanometer channel is challenging to achieve because of computational limitations of simulating ion transport over large time scales (30), the importance of intrapore diffusion in governing ion-ion selectivity might be overlooked (18, 31, 32). More specifically, simulations of transport through smooth and uncharged nanochannels [e.g., carbon nanotubes (CNTs) (18, 33)] highlighted the dominant contribution of ion dehydration at the pore entrance to the overall energy barrier for ion transport, while possible hindering effects arising from ion-pore interactions during intrapore diffusion were neglected. Hence, there is a crucial need to elucidate ion-pore and ion-ion interactions and their role in controlling the energy barriers during the transport of individual ions in each stage: partitioning at the pore entrance and intrapore diffusion.

Here, we use electric field as a driving force to decouple the transport of anions and cations through the subnanometer pores of a negatively charged dense polyamide membrane, allowing us to determine the energy barriers for the permeation of cations (sodium) and anions (fluoride, chloride, bromide, and iodide) independently. Comparing the energy barriers for transport of the individual ions (using electric field) and the energy barrier for salt transport (using concentration gradient) suggests that the cation and anion traverse the membrane pore individually during salt transport in a confined environment, with each ion experiencing a distinct energy barrier. Notably, we reveal that the counterion (i.e., sodium) experiences a higher energy barrier than the co-ion, even when the co-ion has a higher hydration energy (i.e., fluoride). This finding, corroborated by density functional theory (DFT) simulations, challenges the accepted view on the dominant role of ion dehydration at the pore mouth in determining the overall energy barrier for ion transport through subnanometer pores and indicates a notable contribution of intrapore diffusion to this energy barrier. Last, using quartz crystal microbalance (QCM) to determine the difference in the energy state of various salts inside and outside the pore, we show that the energy barrier for intrapore diffusion dominates the overall energy barrier for salt transport in the polyamide membrane due to ion interactions with the pore wall.

RESULTS

Ion pairing versus independent ion transport under confinement

Energy barriers for cotransport of anions and cations (i.e., both charges migrate at the same direction as a salt) through the subnanometer pores of a polyamide membrane were determined in a concentration gradient–driven process (Fig. 1A). Briefly, single salt solution and deionized water were placed on two sides of the membrane, forming a concentration gradient that drove anions and cations to permeate the membrane with a ratio of 1:1. By measuring the temperature-dependent salt flux across the membrane (J_salt; fig. S1), energy barriers for cotransport of anions and cations (E_{P, C}) were determined using an Arrhenius-type equation (Fig. 1B and fig. S2)

$$\text{ln}\left(\frac{J_{\text{salt}}}{C_{\mathrm{s}}-C_{\mathrm{m}}}\right)=\text{ln}(B_{\mathrm{c}})-\frac{E_{\mathrm{P},\mathrm{C}}}{R}\frac{1}{T}$$ (1)

where C_s and C_m are the salt concentrations on the feed and permeate side, respectively, B_c is the preexponential factor, R is the gas constant, and T is the absolute temperature.

Fig. 1. Cotransport of anions and cations through a subnanometer pore membrane.

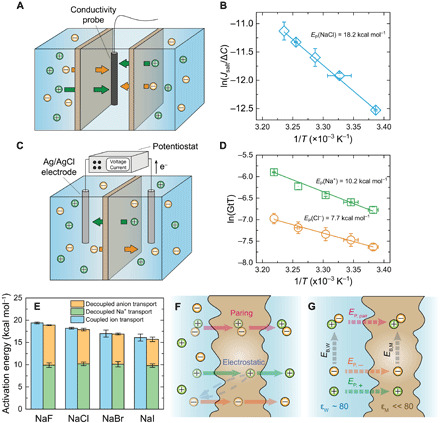
(A) Schematic diagram of the diffusion cell used for salt transport measurements. (B) Example for an Arrhenius plot for salt transport through the membrane (with NaCl). (C) Schematic diagram showing the two-chamber cell for electrochemical characterization of ion transport. (D) Example for Arrhenius plots for decoupled anion (chloride) and cation (sodium) transport through the membrane. (E) Comparison between the energy barriers for salt transport (blue columns) and individual cation (green columns) and anion (orange columns) transport. All the experiments were conducted at pH 5.7. Error bars represent SDs from duplicate measurements. (F) Schematic diagram showing two potential mechanisms for the cotransport of anion (orange spheres) and cation (green spheres) in a concentration gradient–driven process: ion pairing (top) and electrostatic interaction (bottom). (G) Illustration of a thermodynamic cycle for permeation of individual ions and ion pair through the membrane. E_{P, pair}, E_P,−, and E_P,+ are energy barriers for the permeation of ion pair, anion, and cation, respectively. E_B,M and E_B,W are the energies released during ion association in the polyamide membrane and water, respectively.

To study the interactions between anions and cations during salt transport through the membrane pore, an electrochemical method was developed to determine the energy barrier for individual ion transport (Fig. 1C) and compare it to the overall energy barrier for salt transport. Specifically, we applied voltage across the membrane to drive anions and cations in opposite directions and decouple their transport. In charged nanopores, counterions are preferentially transported and the fraction of the total electric current carried by the anion or cation species is defined by its transport number (t₊ for cations and t₋ for anions), which can be estimated by measuring the membrane potential (fig. S3, B and C) (34, 35). Because nanopores in the polyamide membrane are negatively charged at the pH of the experiments (pH 5.7) (36, 37), Na⁺ ions are selectively transported over anions with an observed t₊ over 0.7 (fig. S4A). With t_±, energy barriers for individual anion and cation permeation through the membrane (E_{P, ±}) were calculated using the linearized form of an Arrhenius-type equation (details in the Supplementary Materials; Fig. 1D and fig. S5)

$$\text{ln}(G{t}_{\pm }T)=\text{ln}(B_{\pm })-\frac{E_{\mathrm{P},\pm }}{R}\frac{1}{T}$$ (2)

where G is the overall ion conductance through the membrane and B_± is the preexponential factor for anions or cations. Both G and t_± are temperature-dependent parameters.

Figure 1E shows the energy barriers for salt and individual ion transport for different electrolytes. Energy barriers for salt transport were 19.4, 18.2, 17.0, and 16.1 kcal mol⁻¹ for NaF, NaCl, NaBr, and NaI, respectively (blue columns). These values are significantly higher than the activation energy for ion diffusion in water (38), indicating a major hindrance for salt transport by the membrane compared to diffusion in bulk solution (39). This energy barrier trend is well correlated with the hydration energy of the anions (discussed in the next subsection) and therefore can be related to the energy penalty due to partial ion dehydration at the pore mouth (22, 25). For individual Na⁺ transport, an energy barrier of ~10.0 kcal mol⁻¹ was observed for all four electrolytes (green columns), validating the reliability of our electrochemical method to characterize the energy barrier for individual ion transport. The energy barriers for individual anion transport were measured to be 9.0, 7.7, 6.8, and 5.9 kcal mol⁻¹ for F⁻, Cl⁻, Br⁻, and I⁻, respectively (orange columns). These results validate conclusions from previous studies proposing the mechanism of anion dehydration based on the measurement of energy barriers for salt transport (9, 25). Notably, our results show that the energy barriers for salt transport are equal to the sum of the energy barriers experienced by the individual ions of the specific salt.

Although it is imperative that cations and anions traverse the subnanometer pores at a 1:1 ratio to maintain charge neutrality of the bulk solutions in concentration gradient–driven transport, the interactions between anions and cations during permeation is not well understood. One possible mechanism controlling the cotransport of anions and cations is ion pairing (40, 41), where the association of oppositely charged ions form electroneutral chemical species that transverse the membrane (Fig. 1F) (42). Another possible mechanism is the establishment of a membrane potential due to the initial fast permeation of counterions (i.e., cations) through the negatively charged polyamide membrane, which speeds up the transport of co-ions (i.e., anions) and thus balances the overall transport rate of anions and cations (Fig. 1F) (43, 44). The determination of energy barriers for both salt and individual ion transport enables us to better understand these interactions between anions and cations during their confined transport (27).

Considering the thermodynamic cycle illustrated in Fig. 1G, the difference between the overall energy barrier for the transport of ion pairs (E_{P, Pair}) and the sum of the energy barriers experienced by individual ions is equal to the difference between the energy released during ion association inside the polyamide membrane (E_{B, M}) and ion association in the bulk aqueous solution (E_{B, W})

$$E_{\mathrm{P},\text{Pair}}-(E_{\mathrm{P},-}+E_{\mathrm{P},+})=E_{\mathrm{B},\mathrm{M}}-E_{\mathrm{B},\mathrm{W}}$$ (3)

When ion pairs diffuse from a high-dielectric medium (i.e., bulk water) into a low-dielectric medium (i.e., a polyamide membrane) (45), the electrostatic attraction between anions and cations becomes stronger, rendering E_{B, M} more negative (27) (i.e., E_{B, M} < E_{B, W}). Theoretically, this phenomenon renders the energy barrier for the ion-pair transport (E_{P, Pair}) smaller than the sum of the energy barriers for the transport of individual ions. However, our experimental results show that the energy barrier for salt transport (blue columns) is equal to the sum of the energy barriers of individual ions (green and orange columns). Hence, our results indicate that during transport of monovalent salt in subnanometer pores, anions and cations traverse the pores in a relatively decoupled manner, where each ion experiences a distinct energy barrier.

Dehydration alone is incapable of explaining observed energy barriers

We further examined the mechanisms underlying the energy barriers experienced by individual ions during their transport under subnanometer confinement. Figure 2A compares energy barriers measured for individual ion transport (blue columns, left vertical axis; data from Fig. 1E) and the corresponding ion hydration energies (orange columns, right vertical axis) (46). While the energy barriers for anions correlate well with their hydration energies and can be explained by their partial ion dehydration, the energy barrier for the permeation of Na⁺ is higher than those of the anions, including F⁻ that has a significantly higher hydration energy than Na⁺. This discrepancy implies that dehydration, by itself, cannot fully explain the energy barrier for ion transport through the polyamide membrane.

Fig. 2. Energy barriers to ion transport in subnanometer pores.

(A) Relating the measured energy barrier for transport of individual ions (blue columns, left vertical axis) to ion hydration energy (orange columns, right vertical axis). (B) Schematic diagram showing the partition of ions into the pores. To partition into the pores, hydrated ions have to first undergo partial dehydration at the pore mouth (orange arrows) and then be stabilized inside the pores (pink arrows). (C) Schematic diagram showing the diffusion of cations and anions inside the pores. For cations (green spheres), diffusion inside the pores follows a hopping mechanism, i.e., breaking and reforming electrostatic interactions with the negatively charged carboxyl groups in the pore wall. For anions (orange spheres), intrapore diffusion bypasses the negatively charged functional groups because of electrostatic repulsion. (D) Energy barriers for decoupled (individual) Na⁺ and F⁻ transport at pH 9.5, 5.7, and 4.5. Solution pH was adjusted using aliquots of 0.1 M H₂SO₄ and 0.1 M NaOH. Error bars represent SDs from duplicate measurements. (E) Energy barriers for Na⁺ and F⁻ to enter a subnanometer pore (orange columns) and diffuse inside the pore (green columns) from DFT simulations. Details of the DFT simulations can be found in the Supplementary Materials.

Ion transport through subnanometer pores is composed of two sequential steps: partitioning into the pore and intrapore diffusion (47). Hence, the overall energy barrier for ion transport should be contributed from both steps. The energy barriers for partitioning and intrapore diffusion are dominated by ion dehydration (Fig. 2B) and ion interactions with the pore wall (Fig. 2C), respectively. During intrapore diffusion of the dehydrated ions, ions hop between equilibrium positions (i.e., sites of favorable interactions with the pore wall) (47). Since cations and anions have different interactions with the functional groups in the membrane, the energy barriers experienced by cations and anions during the intrapore diffusion are different. Specifically, deprotonated carboxyl groups are densely distributed in the subnanometer pores of the polyamide layer (37), establishing strong electrostatic attraction to cations that results in energy-favorable binding sites (Fig. 2C). For cations to jump between carboxyl groups, this strong electrostatic attraction needs to be overcome, leading to a large energy barrier for their intrapore diffusion (23). In contrast, the intrapore diffusion of anions inside the pores is less hindered because of their unfavorable interactions with the pore wall. Such fast transport of anions in the pores is analogous to the fast permeation of water molecules through an uncharged, hydrophobic CNT where the intrapore diffusion hardly contributes to the overall energy barrier for their transport (33). Therefore, although Na⁺ experiences a lower energy barrier for dehydration in the partition step compared to F⁻, the overall energy barrier for Na⁺ transport through the subnanometer pores of the polyamide membrane is higher because of its more hindered intrapore diffusion.

To confirm the non-negligible contribution of intrapore diffusion to the overall energy barrier for ion transport, we measured the energy barrier for Na⁺ and F⁻ transport at different solution pH. The charge of the polyamide layer varies with solution pH (48), which is also reflected by the membrane salt rejection behavior (fig. S6A). Results show that the energy barriers for both Na⁺ and F⁻ transport increase when pH was increased from 4.5 to 9.5 (Fig. 2D). For F⁻ transport, the pH-dependent energy barrier is attributed to the change of energy barrier during partition. More specifically, at a higher pH, more carboxyl groups are deprotonated, resulting in an elevated electrostatic repulsion at the pore mouth and increased overall energy barrier for F⁻ transport (49). However, for Na⁺ transport, the dependence of energy barrier on pH cannot be rationalized by the energy barrier during partition. At a higher pH, the energy barrier for Na⁺ partition should decline because the higher electrostatic attraction with more deprotonated carboxyl groups facilitates the partition of Na⁺ into the pores (49). Therefore, if the overall energy barrier for ion transport was only governed by the energy barrier of partition (e.g., dehydration-based barrier), the overall energy barrier for Na⁺ transport would decrease at higher pH, which is contradictory to our experimental observation (Fig. 2D). Instead, our results indicate that the energy barrier for intrapore diffusion is important in determining the overall energy barrier for ion transport. More specifically, at a higher pH, more carboxyl groups in the pores are deprotonated and the electrostatic attraction between Na⁺ and the pore wall is increased, resulting in an elevated energy barrier for the intrapore diffusion step, which, in turn, leads to an increased overall energy barrier for Na⁺ transport.

DFT simulations support our hypothesis on the different transport behaviors of anions and cations during migration through the charged subnanometer pores. Specifically, we used a continuum solvation model to probe the energy change due to ion-pore interactions during ion transport through a subnanometer CNT with a negatively charged oxygen (─O⁻) functional group on the interior wall surface (details in the Supplementary Materials). Figure 2E summarizes the energy barriers for Na⁺ and F⁻ to enter and diffuse inside the subnanometer pore, as calculated from the DFT simulations (fig. S8). While Na⁺ experiences a lower energy barrier to enter the pore (9.8 kcal mol⁻¹) compared to F⁻ (13.7 kcal mol⁻¹) due to the lower dehydration penalty (Fig. 2B), the energy barrier for Na⁺ to diffuse inside the pore (15.3 kcal mol⁻¹) is significantly higher than that for F⁻ (3.9 kcal mol⁻¹), as Na⁺ ions have to overcome the strong electrostatic attraction to the ─O⁻ group (Fig. 2C and fig. S8). The DFT simulations cannot completely reflect our experimental observations because of the limitation of using a simplified CNT to simulate the complex subnanometer channels in the polyamide layer (50, 51). However, the simulations still validate our hypothesis that the strong electrostatic interaction of ions with the charged groups on the pore walls of the polyamide membrane governs their transport behavior.

Intrapore diffusion controls overall energy barrier for salt transport

Considering the independent transport of cations and anions during salt transport (Fig. 1) and the different roles of partitioning at the pore entrance and intrapore diffusion in determining the energy barriers for individual cation and anion transport (Fig. 2), the relative contribution of these two steps to the overall energy barrier for salt transport (i.e., cotransport of anions and cations) remains unclear. According to the solution-diffusion theory (2, 32), salt ions first partition into the polymer matrix and then diffuse through the membrane pore because of a chemical potential gradient. The intrinsic salt permeability can be defined as the product of the partition coefficient (K) and the diffusion coefficient (D) (32). A schematic illustration of the energy barrier landscape for salt transport in subnanometer pores in a polyamide layer is shown in Fig. 3A. During partitioning, salt ions undergo partial dehydration, which results in energetic penalty (E_H); after the dehydrated ions enter the pores, they can be partially stabilized by interactions with the polymer matrix (e.g., cation-π interaction in polyamide), resulting in energy compensation (E_S) for dehydration (21, 52). The difference between E_H and E_S provides the overall energy change during partition (∆E_K ). Hence, the overall energy barrier for salt transport through the membrane pores includes contribution from both the energy change during the partition step (∆E_K) and the energy barrier of intrapore diffusion (E_D) (detailed derivation in the Supplementary Materials)

$$E_{\mathrm{P}}=E_{\mathrm{D}}+{\mathrm{∆}E}_{\mathrm{K}}$$ (4)

Fig. 3. Energy barriers for salt transport in the polyamide membrane.

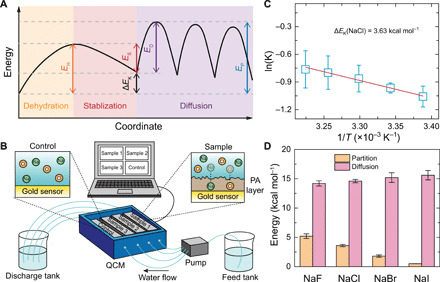
(A) Schematic illustration of the energy barrier landscape for salt transport through the subnanometer pores in the polyamide membrane. During salt partitioning, the energy of salt first increases (E_H) as partial dehydration occurs (orange region) and then declines (E_S) because of stabilization inside the pore (red region). For diffusion inside the pore (purple region), salt ions need to overcome multiple energy barriers of the same size (E_D). The overall energy barrier for salt permeation (E_P) in a subnanometer pore is the sum of the energy change in the partition step (ΔE_K = E_H − E_S) and the energy barrier of intrapore diffusion (E_D). (B) Schematic of QCM setup and experiments. (C) An example of an Arrhenius plot for partition coefficient (with NaCl). (D) Comparison of the measured energy changes in the partitioning step (∆E_K, orange columns) and energy barriers in the diffusion step (E_D, pink columns) for transport of four salts in the subnanometer pore membrane. The energy barrier of intrapore diffusion, E_D, was calculated by subtracting the obtained ∆E_K from the overall energy barrier for the salt transport through the membranes (blue columns in Fig. 1E). All experiments were conducted at pH 5.7. Error bars represent SDs from duplicate measurements.

To quantitatively determine the contribution of intrapore diffusion to the overall energy barrier, we used QCM measurement to directly measure the energy change of the salt partition step (Fig. 3B) (53). Briefly, the partition of salt into the polyamide layer leads to resonance frequency change (∆f) of the QCM sensors, which can be used to calculate the partition coefficient (K) of each salt at various temperatures using the Sauerbrey relationship (54, 55). Energy change for salt partitioning into the polyamide membrane (ΔE_K) was then obtained using a linearized form of an Arrhenius-type equation (Fig. 3C and fig. S10)

$$\text{ln}(K)=\text{ln}(B_{\mathrm{K}})-\frac{\mathrm{\Delta }{E}_{\mathrm{K}}}{R}\frac{1}{T}$$ (5)

where B_K is the preexponential factor.

The energy change for salt partitioning was measured to be 5.2, 3.6, 1.8, and 0.5 kcal mol⁻¹ for NaF, NaCl, NaBr, and NaI, respectively (Fig. 3D). The decrease in the energy change in the partition step from NaF to NaI is consistent with the decrement in their hydration energy, confirming the contribution of dehydration to the energy change in the partition step. According to Eq. 4, the overall energy barrier for salt transport includes contributions from both the energy change in the partition step and the energy barrier during intrapore diffusion. Therefore, the energy barrier that each salt experiences during intrapore diffusion can be calculated by subtracting the energy change in the partition step from the overall energy barrier (Fig. 1E). Specifically, the energy barriers for intrapore diffusion were calculated to be 14.2, 14.6, 15.2, and 15.6 kcal mol⁻¹ for NaF, NaCl, NaBr, and NaI, respectively (Fig. 3D).

In general, the energy barriers for the intrapore diffusion of different salts are similar. This result is consistent with our hypothesis that the energy barrier experienced by Na⁺ during intrapore diffusion dominates the energy barrier for the intrapore diffusion of the salt (Fig. 2E). The small increase in the energy barriers for intrapore diffusion from NaF to NaI can be attributed to the energy barriers for intrapore diffusion for the anions. Here, a strongly hydrated anion that undergoes lower dehydration (e.g., F⁻) interacts less with the pore wall and traverses the membrane pore more easily compared to a weakly hydrated anion (e.g., I⁻) (24). This difference is less pronounced than the difference in energy changes during the partition step as a result of dehydration, leading to a higher permeation rate of NaI over NaF.

Notably, our quantification of the energy change of partition highlights the dominance of intrapore diffusion in the overall energy barrier for salt transport in subnanometer pores. From an energy-barrier perspective, our findings support the prevailing role of intrapore diffusion in determining salt permeability in RO membranes. This result is consistent with a previous study showing that the permeabilities of a wide range of solutes in RO membranes are strongly dependent on their diffusion coefficients instead of partitioning (32).

DISCUSSION

The goal of this study was to elucidate the molecular-level mechanisms underlying salt transport through the subnanometer pores of desalination membranes. Specifically, we used two different experimental strategies to probe the energy barriers for individual ion transport and to determine the energy change during salt partition. Our findings show that monovalent cations and anions transverse the membrane independently and that the overall energy barrier for the salt transport is dominated by the energy barrier for intrapore diffusion of the counterion (i.e., sodium in our case).

Ion pairing can substantially affect salt passage through the subnanometer pores of desalination membranes. For instance, Donnan exclusion should be reduced when cations and anions traverse the membrane in the form of electroneutral ion pairs. However, because of the limited capability to directly monitor ions during their confined transport, previous studies presumed that cations and anions traverse the subnanometer pores independently and related their experimental observations on salt transport to the inherent properties of the individual salt ions (9, 19, 25). With the electrochemical method developed in this work, individual ion transport can be directly probed and explained by the ion inherent properties (e.g., hydration energy). Our comparison between the energy barrier for individual ion and salt transport unequivocally supports the independent transport of cations and anions.

Energy barriers resulting from ion dehydration at the pore mouth have been adopted to explain selectivity between similar ions in subnanometer pores (9). Hence, it was concluded that to facilitate the permeation of specific ions, the ion-pore attraction near the pore entrance should be increased to reduce the energy barrier for the ion to enter the pore (21, 56, 57). However, according to our simulations and experimental results, the overall energy for ion permeation through relatively long subnanometer pores is governed by the intrapore diffusion, rather than partitioning at the pore entrance, due to the strong ion-pore wall interactions. Future investigations should further evaluate this tradeoff between the rate of partitioning into the membrane and diffusion inside the membrane pores using ions of different valence and pore channels with varied diameter, length, tortuosity, and surface chemistry.

The biological K⁺ channel, which is able to transport K⁺ ions nearly 10,000 times faster than Na⁺ ions, has highlighted the significance of both favorable binding sites and pore length in enabling the ultrafast transport of K⁺. Specifically, the binding sites compensate for the energy penalty of K⁺ dehydration at the pore entrance, and the short pore length of ~12 Å (58) reduces the hindrance to the intrapore diffusion of K⁺. By contrast, in state-of-the-art polyamide desalination membranes with an active layer of ~200 nm, the intrapore diffusion plays an important role in determining the ion permeation rate, reducing both the cation-cation and anion-anion selectivity that stem from ion dehydration at the pore entrance (59). Therefore, our study establishes a framework for the design of ion-selective membranes using two potential strategies: (i) fabricating an ultrathin membrane layer with favorable binding sites along the pore (similar to the K⁺ channel) or (ii) designing a longer (asymmetric) membrane with ion-specific binding sites only on the membrane surface and inert (or unfunctionalized) pore interior.

MATERIALS AND METHODS

Materials

A commercial polyamide RO membrane (SW30XLE, Dow FilmTec; 99.5% NaCl rejection according to the manufacturer’s specification) was used for energy barrier measurements of salt and ion transport. The membrane is composed of three polymer layers: a polyamide active layer, a polysulfone support layer, and a polyester nonwoven fabric support. Deionized water (>18.2 megohm·cm) produced from a Milli-Q ultrapure water purification system (Integral 10, Millipore, Billerica, MA) was used for all experiments.

Determination of energy barriers for salt transport

Energy barriers for salt transport through the membrane were measured using a concentration gradient–driven process with single sodium–based salt solutions (i.e., NaF, NaCl, NaBr, and NaI). Two membrane coupons (each with an area of 14.5 cm²) were assembled into a custom-made three-chamber diffusion cell (Fig. 1A). The side chambers were filled with the salt solution (C_s = 10 mM), and the middle chamber was filled with deionized water. Salt flux (J_salt) through the membrane was measured at five temperatures (i.e., 22°, 26°, 30°, 33°, and 37°C) by monitoring the electric conductivity change in the middle chamber over time (fig. S1). The energy barrier for salt transport (E_{P, C}) was then determined using Eq. 1. As the transported salt continuously accumulated in the middle chamber (concentration C_m), solute flux was normalized to the driving force (i.e., C_s − C_m) for each data point to account for the impact of the change in the driving force on salt flux.

Determination of energy barriers for individual ion transport

Energy barriers for individual anion and cation transport through the membrane (E_P,+ and E_P,− for cations and anions, respectively) were measured using an electrochemical method with single sodium–based electrolyte solutions (i.e., NaF, NaCl, NaBr, and NaI) based on Eq. 2. The overall ion conductance (G) was obtained with a linear sweep voltammetry (LSV) technique using a potentiostat (CHI600E, Chenhua, China) at five temperatures (i.e., 22°, 26°, 30°, 33°, and 37°C). For each measurement, a membrane coupon with an area of 0.95 cm² was assembled into a custom-made two-chamber diffusion cell and both chambers were filled with 10 mM sodium electrolytes (Fig. 1C). An Ag/AgCl reference electrode (CHI111, CH Instruments, Austin, TX) was inserted in each chamber. During LSV measurements, the current was recorded while sweeping the voltage difference between the two reference electrodes from −50 to 50 mV at a scan rate of 2 mV s⁻¹ (fig. S3A), and the G was obtained from the current change with voltage difference (details of the experimental procedures are provided in Supplementary Methods).

To obtain E_P,+ and E_P,− based on Eq. 2, besides G, the corresponding transport number of cations or anions (t_±) also needs to be determined at different temperatures (i.e., 22°, 26°, 30°, 33°, and 37°C). For determining the t_±, the electrolyte concentration was maintained constant in one chamber (C_h=10 mM), while the concentration in the other chamber (C_l) was gradually increased from 2 to 5 and 10 mM to obtain concentration ratios of 5:1, 2:1, and 1:1, respectively, between the two chambers. At each concentration ratio, the above-mentioned LSV technique was applied and the membrane potential (∆Φ_mbr) was determined as the intersect between the I-V curve and the voltage (horizontal) axis (fig. S3B). The t_± was then calculated using (fig. S3C) (60, 61)

$$\mathrm{∆}{\mathrm{\Phi }}_{\text{mbr}}=(t_{+}-t_{-})\frac{\mathit{RT}}{F}\text{ln}\left(\frac{C_{\mathrm{h}}}{C_{\mathrm{l}}}\right)=(2t_{+}-1)\frac{\mathit{RT}}{F}\text{ln}\left(\frac{C_{\mathrm{h}}}{C_{\mathrm{l}}}\right)$$ (6)

where F is the Faraday constant (96,485 C mol⁻¹).

DFT to calculate the interaction energy change during ion transport

Our computational method is based on a newly developed hybrid quantum-continuum technique that combines the Kohn-Sham DFT with the effective screening medium (ESM) (62, 63) and reference interaction site model (RISM) (64), known as ESM-RISM. This approach has been successfully applied to solve the complex electrochemical interface under confinement effects (65, 66). The DFT calculation with ESM-RISM was carried out by the Quantum ESPRESSO software (67). For the DFT calculation of explicit CNT and ion, vdW-DF1 functional (68) was used with the ultrasoft pseudopotentials (69) to describe the interaction between valence electrons and core. The plane wave basis sets were used in the expansion of electronic wave function and charge density with the cutoff energy of 40 and 320 rydberg (Ry), respectively. To avoid the interaction with neighbor images under periodic boundary conditions, our CNTs [with the chirality of CNT (5, 6)] were modeled in the center of an orthorhombic cell with a size of 18.52 Å by 18.52 Å by 52.92 Å. Only gamma point was used in the k-point sampling after testing the 2 × 2 × 1 k-mesh on the ion’s binding energy with CNT. The convergence criteria of electronic self-consistent field and structure optimization were set to 10⁻⁶ Ry and 0.002 atomic unit. The structure file of the optimized CNT and CNT-O models were provided as the Supplementary Materials in xyz format. For the solvation part, the implicit electrolyte used in our simulation is 1 M NaF aqueous solution with the simple point charge water model and classical ions (70, 71). The RISM calculation was performed at 300 K with the closure model proposed by Kovalenko and Hirata (72) with the cutoff energy of 144 Ry for the correlation function.

Determination of energy changes of salt partitioning

The energy changes (ΔE_K) of partitioning from bulk solution into the membrane for different salts (i.e., NaF, NaCl, NaBr, and NaI) were calculated on the basis of Eq. 5. A QCM (Biolin Scientific) was used to measure K(T) at temperatures of 22°, 26°, 30°, 33°, and 37°C (Fig. 3B). For sample preparation, a polyamide layer isolated from the RO membrane coupon was attached onto the 5-MHz QCM sensors (details of the experimental procedures are provided in Supplementary Methods). The area of the polyamide layer on the QCM sensor for each measurement was 0.78 cm². The volume of the polyamide layer coated on the sensor was determined by measuring the mass difference of the QCM sensor before and after the polyamide layer was attached (detailed experimental procedures and results are provided in Supplementary Methods and table S2).

For each K(T) measurement, three sensors coated with a polyamide layer (i.e., samples) and one bare sensor (i.e., control) were used at the same time (Fig. 3B). Running QCM tests at varied solution temperatures enabled the determination of the temperature-dependent partition coefficient K(T) (detailed experimental procedures are provided in Supplementary Methods). In all the QCM tests, the salt concentration and pH of the solution were maintained at 0.5 M and 5.7, respectively.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/48/eabd9045/DC1