The arches of chaos in the Solar System

We have discovered an intricate ornamental structure of chaos that leads to very rapid transport for small Solar System bodies.

Abstract

Space manifolds act as the boundaries of dynamical channels enabling fast transportation into the inner- and outermost reaches of the Solar System. Besides being an important element in spacecraft navigation and mission design, these manifolds can also explain the apparent erratic nature of comets and their eventual demise. Here, we reveal a notable and hitherto undetected ornamental structure of manifolds, connected in a series of arches that spread from the asteroid belt to Uranus and beyond. The strongest manifolds are found to be linked to Jupiter and have a profound control on small bodies over a wide and previously unconsidered range of three-body energies. Orbits on these manifolds encounter Jupiter on rapid time scales, where they can be transformed into collisional or escaping trajectories, reaching Neptune’s distance in a mere decade. All planets generate similar manifolds that permeate the Solar System, allowing fast transport throughout, a true celestial autobahn.

INTRODUCTION

Chaos in the Solar System is inextricably linked with the existence of stable and unstable manifolds, intricate structures whose mutual intersection plays a crucial role in chaotic transportation (1–3). The general properties are best described by considering the planar, circular, and restricted three-body problem (PCR3BP) (4), the simplest dynamical model that approximates the motion of both natural and artificial celestial bodies. Two special solutions of this idealized model, the unstable, collinear L₁ and L₂ Lagrange equilibrium points, and their associated invariant manifolds, are of particular interest for close-encounter dynamics (see the Supplementary Materials for details). While the PCR3BP is far from being fully understood, modern geometric insights from Hamiltonian dynamical systems theory have revolutionized the design of spacecraft trajectories (5–7) and have contributed to the development of new space-based astronomical observatories that have transformed our understanding of the cosmos. The space manifold dynamics that enable “Le Petit Prince” grand tour of the Solar System through the “Interplanetary Transport Network” have also been shown to be an important short-term capture and transit mechanism for some Jupiter-family comets (JFCs) (4, 8–11).

Besides the piecemeal treatment of JFCs, however, the influence of such manifolds on natural bodies has been largely underappreciated in astrophysical and celestial dynamics (11). The attention of most dynamical astronomers in the past few decades has been focused upon another important and far-reaching mode of transport, namely, chaotic diffusion from orbital resonances (12). While such resonances can shepherd and sculpt small bodies in metastable zones like the main asteroid and classical Kuiper belts, the instability time scales brought about by their overlap (13) are at least orders of magnitudes longer than those resulting from the manifolds considered herein (4).

The cometary and asteroidal bodies that occupy orbits in the region between Jupiter and Neptune, the Centaurs, are dynamically unstable with reported lifetimes of only a few million years (14). Long-term numerical simulations carried out over the past few decades (15–18) have elucidated the transitory nature of these small bodies, linking their origin to more distant populations, such as the scattered disk objects, and connecting one of their evolutionary end states to the JFCs. To model the detailed dynamical pathways connecting different zones of the outer Solar System, from the trans-Neptunian object (TNO) reservoir, through the Centaur population, to the JFC region and inward, we typically use vastly differing time scales ranging from ∼10⁹ down to ∼10⁴ years (14–17, 19). During the TNO-Centaur-JFC transition, a recent study (19) has identified a short-term orbital gateway, a low-eccentricity region exterior to Jupiter between 5.4 and 7.8 astronomical units (AU), governing the circuitous routes of JFCs and Centaurs. No connection was made, however, about the location of this apparent conduit and that of the unstable Sun-Jupiter L₂ Lagrange point, from which manifolds can emanate (1, 5, 6).

MATERIALS AND METHODS

The fast Lyapunov indicator (FLI) is a dynamical quantity used to detect chaos (20) and has been successfully applied to both idealized (21) and realistic systems (22–24). This tool has traditionally been used to locate the resonances that significantly affect the structure of phase space (20, 23, 24); however, when computed for very short time scales, the FLI captures traces of the stable and unstable manifolds of the considered dynamical model (25). Computing the FLI for refined grids of initial conditions, as done herein, can reveal the topological structure of close encounters for cometary dynamics (26) and localize the manifolds associated to bound orbits (27), whose complex global dynamics leads to intermittent behavior including planetary close approaches (4, 8, 10).

Here, we use the FLI to detect the presence and global structure of space manifolds, and capture instabilities that act on orbital time scales; that is, we use this sensitive and well-established numerical tool to more generally define regions of fast transport within the Solar System (28). We consider the, astronomically speaking, short-term (100-year) evolution of massless test particles (TPs) located on orbits with semimajor axes between that of the main asteroid belt and Uranus, eccentricities varying from zero to unity, and ecliptic inclinations less than 20°. The results are presented in dynamical maps, obtained through the use of two widely used orbit integration software packages, ORBIT9 (29) and REBOUND (30), and adopting a force model that contains the seven major planets (from Venus to Neptune) as perturbers as well as considering the drastically more simple Sun-Jupiter-TP three-body system.

RESULTS

Global structure of space manifolds

The “Greeks” and “Trojans” are co-orbital asteroids that follow essentially the same orbit as Jupiter but, respectively, lead or trail the planet by an angular distance of ∼60° (22, 31, 32). The simulations were set up such that the mean anomaly M of the TPs is initially 60^∘ ahead of Jupiter in its orbit, and where their initial inclination i, argument of perihelion ω, and longitude of ascending node Ω are equal to those of Jupiter at the corresponding epoch. In this way, we map the dynamics of TPs initially in the orbital plane of Jupiter near the location of the stable L₄ Lagrange point (see the Supplementary Materials). The FLI is computed over 100 years for a large grid of initial semimajor axis a and eccentricity e, for fixed initial (i, ω, Ω, M), and represented by a color scale. Lighter regions correspond to orbits located on stable manifolds, and darker colors represent those off of them.

Figure 1 shows short-term FLI maps of the outer edge of the asteroid belt (∼3 AU) up to near the semimajor axis of Uranus (∼20 AU), for all elliptic eccentricities, and considering the seven-planet dynamical model (top) and the Sun-Jupiter-TP–restricted problem (bottom) in ORBIT9. The large stable island at 5.2 AU, nesting the Greeks, is clearly visible in both panels of Fig. 1, as is the niche for the Hildas at 3.97 AU. A shadow of the chaotic borders of the strongest resonance in the outer belt, the 2:1 mean-motion resonance (MMR) with Jupiter at 3.3 AU, begins to appear, indicating the relative weakness of such orbital resonances compared to the manifolds uncovered herein. The notable feature of Fig. 1, however, is the large “V-shaped” chaotic structure that emerges outside of roughly 5.6 AU, which is connected to a series of arches at increasing heliocentric distances that nearly follows the perihelion line (q_j) of Jupiter. Chaos also emanates along the Jovian aphelion line (Q_j) in elongated concentric curves, initiating near 4.8 AU.

Fig. 1. Global arch-like structure of space manifolds in the Solar System.

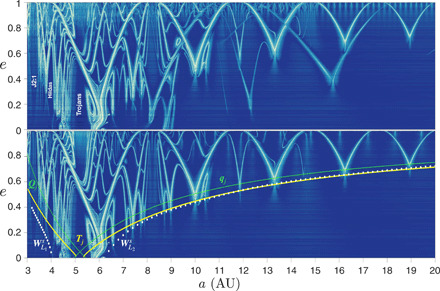
Short-term FLI maps of the region between the outer edge of the main asteroid belt at 3 AU to just beyond the semimajor axis of Uranus at 20 AU, for all elliptic eccentricities, adopting a dynamical model in ORBIT9 that contains the seven major planets (from Venus to Neptune) as perturbers (top) or Jupiter as the only perturber (bottom). Orbits located on stable manifolds appear with a lighter color, while darker regions correspond to trajectories off of them. Three sets of dynamical boundary curves are superimposed on the map in the bottom panel corresponding to the perihelion (q_j) and aphelion (Q_j) lines of Jupiter (thin, green), the contour of Jupiter Tisserand parameter T_j = 3 that dichotomizes asteroids and comets (thick, yellow), and the stable manifolds of L₁ ($W_{L_1}^s$) and L₂ ($W_{L_2}^s$) (dotted, white). The map samples more than 2 million initial values of (a, e), where the initial inclination i, argument of perihelion ω, and longitude of ascending node Ω are set equal to that of Jupiter at the initial epoch 30 September 2012 (table S1). The initial mean anomaly of the TPs is set to 60° ahead of Jupiter in its orbit to reflect the “Greek” L₄ configuration. a, semi-major axis; e, eccentricity.

Some dynamical aspects

Jupiter, being the dominant perturber and having a considerably shorter orbital period (∼12 years), is responsible for the majority of the rich chaotic architecture revealed in Fig. 1. The left branch of the largest V-shaped structure appears after only one orbital revolution of Jupiter, and the subsequent arches, beginning with the right branch of this V, manifest on time spans commensurate with Jupiter’s period (movie S1). That is, the arch spanning 6 to 10 AU occurs after 24 years, that from 10 to 13.5 AU after 36 years, the next after 48 years, and so on, following the q_j line in a damped wave-like fashion asymptotically to e = 1, for which we have tracked to beyond Neptune. Slightly below the vertex of the apsidal line branches is the contour of Jupiter Tisserand parameter, T_j = 3, which is the characteristic demarcation in the dynamical classification of small Solar System bodies in that asteroidal orbits usually fall below it, while comets lie above (17). Notably, the planar L₁ and L₂ stable manifolds in the PCR3BP, known to be strong drivers of short-term chaos (4, 10), when projected onto the (a, e) plane (8), bound the structures more precisely.

We confirmed numerically that the distribution of these manifold structures is similar for all the giant planets, albeit on time scales commensurate with their respective orbital periods. On the top panel of Fig. 1, for instance, we notice the emergence of another sequence of arches, spanning from ∼8 to 18 AU, connected with Saturn. Moreover, the qualitative picture of the bottom panel of Fig. 1 was found to persist even in the lower-fidelity model of Jupiter on a fixed circular orbit, where the small bodies are constrained to move in the same plane as Jupiter’s orbit (i.e., the PCR3BP). We also computed similar FLI maps for initial ecliptic inclinations of 10^∘ and 20^∘ and found that the structures would diminish with increasing inclination, as, loosely speaking, the orbits are no longer in the region controlled by manifolds. When these dynamical maps are constructed over a longer time scale, even 500 years, as was done recently (26) to understand the close-encounter dynamics of comet 67P/Churyumov-Gerasimenko, these short-term structures, hitherto undepicted, become lost in a chaotic sea.

Let us note, furthermore, that the manifolds spread throughout all six dimensions of the phase space, while our maps are limited to a plane of dimension two. In addition, as Fig. 1 represents a forward-time map, it depicts only the stable manifolds; unstable manifolds can be obtained from a backwards-time integration (26). Stable manifolds, despite the epithet, can nevertheless lead to chaotic motion as a result of their complicated interaction with the corresponding unstable manifolds (see the Supplementary Materials). The analytical construction of these manifolds is highly complex, even in a much simpler dynamical models, and is usually described only locally for the very narrow band of three-body energies close to the collinear Lagrange points (2, 3, 9–11, 27). Our maps cover a much wider range of energies than previously considered, which encompass the observational datasets of JFCs and Centaurs. It is very informative, nevertheless, that the PCR3BP is the basic mathematical model giving rise to the arches and foliated substructure, as this puts severe dynamical constraints on their precise origin. Additional studies (not presented here) show that the structures change in time but have a periodicity matching Jupiter’s period; accordingly, Jupiter, in its orbital path around the Sun, carries not only its equilibrium points but also the manifolds emanating from them.

Rapid scattering and collisions

To understand the physical implications of the structures and their dynamical connection with manifold- and close-encounter dynamics, we used the Mercurius package within REBOUND to more accurately track the evolutions through close approaches with Jupiter. Figure 2 portrays a map of the minimum approach distance to Jupiter during the 100-year integrations, obtained with REBOUND, for both the previous “Greek configuration” (top) and a “Trojan scenario” (bottom), in which the initial mean anomaly of each grid point is instead 60^∘ behind that of Jupiter. Only a subset of initial conditions centered around the largest V-shaped structure is considered. Figure 2 shows that all orbits along the chaotic structures in the FLI map (Fig. 1) enter Jupiter’s Hill sphere during the course of their evolutions, where their resulting end states can be appreciated from Fig. 3 (see also movies S2 and S3). The Hill sphere is the planet-dominated region between L₁ and L₂, and we have found, through computing the respective approach distance to these diametrically opposite Lagrange points, that all close-encounter trajectories visit the neighborhood of either L₁ and L₂, further implicating a manifold connection with the uncovered structures (see fig. S3). Also revealed by Fig. 2 is a fundamental asymmetry between the Greek and Trojan maps, which agrees with and could cast additional light on the poorly understood Greek-Trojan dichotomy (31, 32).

Fig. 2. Jovian-minimum-distance maps for the Greek and Trojan orbital configurations.

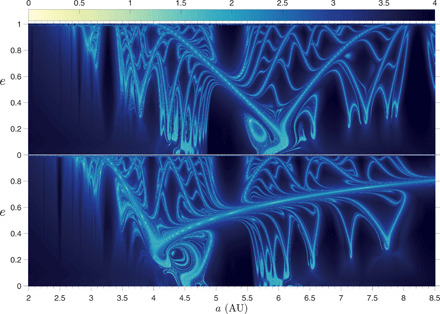
Dynamical map of a zoomed-in portion of Fig. 1 (top), and another made with the same initial orbital configuration, but with the initial mean anomaly trailing Jupiter by 60° (bottom), representing the “Trojan” L₅ scenario. The Mercurius package within REBOUND, with integrator time step of 0.0025 × 2π (equivalent to about 1 day), was used to propagate an equidistant grid of 2.25 million initial (a, e) values for 100 years. The color bar represents the logarithm of the minimum approach distance to Jupiter (in planetary radii) experienced by the TPs in their heliocentric motion under the Sun-Jupiter-TP three-body model. A value of less than 2.87 means that the TP entered the Jovian Hill sphere during its evolution with 0 corresponding to a Jovian impact, and a value above 3.35 implies that it never got within 3 Hill radii. a, semi-major axis; e, eccentricity.

Fig. 3. A finer image of the manifolds with colliding and escaping objects along them.

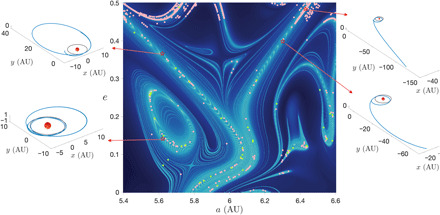
A highly resolved, 1500 × 1500 point, Jovian-minimum-distance map concentrated near the largest V-shaped chaotic structure appearing in Figs. 1 and 2 (top), made using Mercurius with an integrator time step of 0.01 (equivalent to around half a day). Contained in the map is a finer image of the manifolds, where we notice small substructures wrapping around the main ones. Superimposed on the stability map are the orbits that collide with Jupiter (green dots) and all escaping trajectories (pink dots), whose dynamical transitions from elliptic to hyperbolic have been further validated by significantly increasing the tolerance within Mercurius (using a step size of 1 min). Example evolutionary states of four initial conditions (red stars) located on the structures are shown in Cartesian coordinates in the callouts, where the heliocentric orbit of Jupiter is also shown for reference (gray). The specific escaping trajectory in the top right corner was further investigated using the more realistic seven-planet model, finding that it indeed reaches more than 100 AU in less than a century in its unbounded evolution. Animations of collisional and escaping orbits are given in movies S2 and S3, respectively. a, semi-major axis; e, eccentricity.

Among the TPs approaching Jupiter in Fig. 3, a few dozen or so ended up in a direct collision, such that their Jovicentric distances became less than Jupiter’s radius (movie S2). Figure 3 also depicts that nearly 2000 TPs transition in their heliocentric motion from bounded elliptical orbits to unbounded hyperbolic escape orbits, as a result of the manifold-induced close encounters. This subset of transitioning orbits reaches the distances of Uranus and Neptune in 38 and 46 years, on average, respectively, with the fastest TPs arriving to the Neptunian region in under a decade, and 70% of them get kicked to 100 AU over the course of a century (movie S3). Notably, this removal time (scattering or collision with Jupiter) is at least several orders of magnitude shorter than that reported in earlier studies (13, 18, 33), whose long-term integrations otherwise mask the effects of these manifolds.

Centaur-JFC orbital gateway

Seminal work conducted over two decades ago (1, 8) observed that the path of comet 39P/Oterma follows closely the invariant manifold structures associated with L₁ and L₂ and transitions between the exterior 2:3 and interior 3:2 mean-motion resonances with Jupiter. Similar manifold dynamics have been noted about 82P/Gehrels and 111P/Helin-Roman-Crockett (10), as well as the marked capture and demise of comet Shoemaker-Levy 9 (11). Figure 4 shows Jovian-minimum-distance maps, computed for 100 years, tailored to the nominal initial conditions of Oterma at two distinct epochs, 1 January 1910 [date chosen to be consistent with previous studies (1, 8)] and 8 April 1943 (its discovery date), with the contours of constant three-body Hamiltonian energy (≈ − 0.5 T_j) superimposed. In each panel, Oterma lies on the encounter manifolds, further strengthening the connection between the structures of the maps and the Sun-Jupiter invariant manifolds. Note that the abrupt change in Oterma’s energy is the result of a close encounter with Jupiter that occurred in 1937, in between the two chosen epochs (34). Had such a map been made with a constant Tisserand parameter (energy surface) (26) as opposed to a fixed inclination, the rich structures above Oterma’s energy contour line would have all but disappeared.

Fig. 4. JFC, Oterma, located on manifold structures.

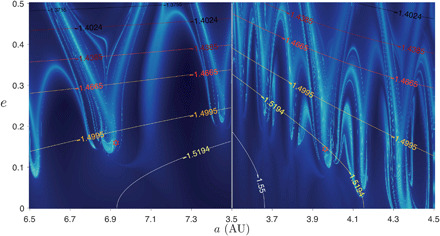
Jovian-minimum-distance maps tailored to Oterma’s orbital conditions (35), obtained using Mercurius with integrator time step of 0.01 (equivalent to around half a day). The maps sample 2.25 million initial (a, e) values over 100-year evolutions, where the initial inclination i, argument of perihelion ω, longitude of ascending node Ω, and mean anomaly M are set equal to that of Oterma at the initial epoch 1 January 1910 (left) or 8 April 1943 (right), adopting a dynamical model with Jupiter as the only perturber (table S2). Several contours of Sun-Jupiter-TP three-body energy are superimposed, with −1.5194 and −1.4995 corresponding to the values of the L₁ and L₄ Lagrange points, respectively. The location of Oterma for each epoch is marked with a red star, showing that it lies on the encounter manifolds, which are illustrated quantitatively in the Sun-Jupiter rotating frame in previous works (1, 8). a, semi-major axis; e, eccentricity.

We have carried out similar analysis for dozens of JFCs and Centaurs, including the four bodies noted to currently occupy the Centaur-JFC gateway region (19), finding similar complex structures associated with their phase-space regions. Of the apparent gateway objects, 494219 (2016 LN8) is far too inclined to be affected by the same dynamical phenomena and should likely not be classed with the Centaurs 29P/Schwassmann-Wachmann 1, P/2010 TO20 (LINEAR-Grauer), and P/2008 CL94 (Lemmon). The true orbital gateway is the invariant manifolds, which appear to influence all low-inclination orbits whose perihelion or aphelion brings them near the Lagrange points (or their dynamical extensions) of the outer planets.

DISCUSSION

The manifolds reported herein act over orbital time scales of several decades, not the tens of thousands to millions of orbital revolutions traditionally considered (13–18, 33) in treating Solar System dynamics. More detailed quantitative studies of the discovered phase-space structures, as revealed by homoclinic-heteroclinic connections and their association with mean-motion resonances (1–3, 11), could provide deeper insight into the transport between the two belts of minor bodies and the terrestrial planet region. Combining observations, theory, and simulation will improve our current understanding of this short-term mechanism acting on the TNO, Centaur, comet, and asteroid populations and merge this knowledge with the traditional picture of the long-term chaotic diffusion through orbital resonances; a formidable task for the large range of energies considered.

It should come at no surprise that Jupiter can induce large-scale transport on decadal time scales, as space missions have been specifically designed for Jupiter-assisted transport, with the flybys of Voyager 1 and Voyager 2 being cardinal examples. That gravity assists can be enabled by manifolds is also well known to astrodynamicists (6, 7); yet, their widespread influence on natural celestial bodies has been largely undervalued and unexplored.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/48/eabd1313/DC1