Abstract
Glioblastoma (GBM) brain tumor is the most aggressive white matter (WM) invasive cerebral primary neoplasm. Due to its inherently heterogeneous appearance and shape, previous studies pursued either the segmentation precision of the tumors or qualitative analysis of the impact of brain tumors on WM integrity with manual delineation of tumors. This paper aims to develop a comprehensive analytical pipeline, called (TS)2WM, to integrate both the superior performance of brain tumor segmentation and the impact of GBM tumors on the WM integrity via tumor segmentation and tract statistics using the diffusion tensor imaging (DTI) technique. The (TS)2WM consists of three components: (i) A dilated densely connected convolutional network (D2C2N) for automatically segment GBM tumors, (ii) A modified structural connectome processing pipeline to characterize the connectivity pattern of WM bundles, (iii) A multivariate analysis to delineate the local and global associations between different DTI-related measurements and clinical variables on both brain tumors and language-related regions of interest. Among those, the proposed D2C2N model achieves competitive tumor segmentation accuracy compared with many state-of-the-art tumor segmentation methods. Significant differences in various DTI-related measurements at the streamline, weighted network, and binary network levels (e.g., diffusion properties along major fiber bundles) were found in tumor-related, language-related, and hand motor-related brain regions in 62 GBM patients as compared to healthy subjects from the Human Connectome Project.
Keywords: Diffusion tensor imaging, Glioblastoma, Tract statistics, Tumor segmentation, White matter integrity
1. Introduction
Diffusion tensor imaging (DTI), a non-invasive diffusion-weighted imaging technique, has been widely used to delineate the white matter (WM) pathway in vivo Basser et al. (1994a,b). DTI processes the diffusion of water about the magnitude, degree, and orientation of diffusion anisotropy in a tensor model Brunberg et al. (1995). Furthermore, DTI can estimate the WM connectivity in a 3D model termed MR tractography Basser et al. (2000). DTI is sensitive to WM changes in many diseases and thus helps resolve neuroscience and clinical problems.
Recently, DTI has been widely used to detect abnormalities in various mild and moderate brain disorders, including Parkinson’s disease Zhang et al. (2011), autism Conturo et al. (2008), brain trauma Rutgers et al. (2008), and dementia Jin et al. (2017). All existing DTI analytical techniques can be roughly categorized into three classes including standard region-based analysis, voxel-based analysis, and tract-specific analysis. The region-based analysis Alexander et al. (2007); Conturo et al. (2008); Masjoodi et al. (2018) depends on summarizing statistical properties in pre-defined regions of interest (ROIs). Although it is convenient to observe abnormal regions, major weaknesses of region-based analysis include manually defined ROIs, and the difficulty in identifying meaningful WM bundles. Voxel-based analysis Rutgers et al. (2008); Smith et al. (2006); Zhang et al. (2011) relies on spatially co-registering brain images across all subjects to a standard coordinate system and then statistically performing voxel-wise analysis. However, a significant limitation of voxel-based analysis is that it cannot explicitly model the underlying fiber architecture of WM bundles. Tract-based spatial statistics (TBSS) Smith et al. (2006) project all the fractional anisotropy (FA) maps of individual subjects onto a standard mean FA skeleton. Tract-specific analysis Jin et al. (2017); Mormina et al. (2015); Ormond et al. (2017); O’Donnell et al. (2017); Zhang et al. (2018) provides three desirable properties including visualization of the detailed WM bundles, statistical analysis on the fiber architecture of WM bundles, and reflection of local alterations in brain disorders. All these existing techniques assume that brain lesions are relatively homogeneous across subjects such that a standard template can be established across patients and normal controls. However, since Glioblastoma (GBM) patients have the inherently heterogeneous appearance and shape of brain tumors, little has been done in the development of DTI analytical techniques for assessing WM integrity in GBM patients.
GBM develops from star-shaped glial cells Holland (2001) and is the most common type of WM invasive cerebral primary neoplasm. GBM brain tumors represent 80% of primary intracranial tumors and 28% of all types of tumors Deighton et al. (2010). GBM that began as a Grade IV tumor with no evidence of a lower grade precursor is classified as a high-grade glioma. It is reported that the survival rate of these malignant tumors is only two years or less and immediate treatment is needed Ohgaki and Kleihues (2005). The low-grade glioma (Grade II or Grade III) may progress to malignant tumors.
GBM distinguishes from many mild and moderate brain disorders in two major aspects. First, GBM leads to potentially significant damages to WM. GBM tumors stem from WM and propagate through WM, and the cerebral neoplasm may influence WM tracts at either the cellular or gross anatomic level. Tumors may replace WM fiber tracts as they invade the surrounding tissues, and thus they may alter the position and orientation of WM fiber tracts. Moreover, neoplasm may infiltrate WM tracts between individual fibers without disrupting their directional organization. Diffusion tensor tractography renders the opportunity to study tumor-related WM integrity. Second, GBM patients have heterogeneous tumor location and shape. The standard region-based analysis is inappropriate for analyzing GBM tumors due to the need of manual delineation of tumors. Moreover, TBSS is also inappropriate since it is problematic to directly project the FA maps of brain tumors and their surrounding tissues, which differ from normal ones at both the cellular and gross anatomic levels, onto a healthy mean FA skeleton.
Previous studies utilized tract-specific analysis to qualitatively and quantitatively analyze GBM tumors Mormina et al. (2015); Ormond et al. (2017); O’Donnell et al. (2017). In Mormina et al. (2015); O’Donnell et al. (2017), they focused on automatically identifying several major WM fiber tracts (e.g., corticospinal tracts and arcuate fasciculus tracts) for neurosurgical planning. However, the impact of GBM tumors on WM integrity is poorly understood. Recently, Ormond et al. Ormond et al. (2017) used a deterministic fiber tracking algorithm in diffusion spectrum imaging (DSI) studio to reconstruct fiber tracts in order to analyze the impact of GBMs on WM integrity globally. This method suffers from three significant drawbacks, including bias in streamline reconstruction (caused by the seeding strategy, the stopping criterion, and the tractography parameters Girard et al. (2014)), ignoring the local information around tumors, and the use of manual delineation of tumors.
A major drawback of current tract-specific analysis of GBM tumors is the manual delineation of GBM tumors by experts. Thus, it is very desirable to develop an automatic method to segment GBM tumors. Developing an automatic GBM tumor segmentation method is very challenging due to the inherently heterogeneous appearance, location, shape, and size of brain tumors. Furthermore, the tumor area is often defined based on the changes of MR image intensity, so significant controversy exists in the precise definition of brain tumors among experts due to the degree of signal changes, partial volume effects, and bias field artifacts. Moreover, the surrounding tissues of tumors can be damaged through necrosis and hypoxia Raza et al. (2002). Generally, various modalities of MRI scans, including T2-weighted (T2), T1, T2-weighted fluid attenuated inversion recovery (Flair), and T1-weighted contrast-enhanced (T1c) MRI, are integrated to delineate tumor-induced tissue changes accurately. All existing segmentation methods Bakas et al. (2018) including both machine learning Menze et al. (2015a) and deep learning Isensee et al. (2017); Islam and Ren (2017); Jesson and Arbel (2017); Shaikh et al. (2017); Soltaninejad et al. (2017); Zhao et al. (2018) focus on pursuing segmentation precision and the prediction of patient’s overall survival time. However, none of these methods can provide a comprehensive profile that delineates the impact of GBM tumors on WM tract integrity and its association with clinical variables of interest.
In this paper, we propose a comprehensive analytical pipeline for integrating both the superior performance of brain tumor segmentation and the impact of GBM tumors on the WM integrity through automatic tumor segmentation and tract statistics ((TS)2WM). Fig. 1 presents the path diagram of (TS)2WM. It consists of three main components. The first one is a dilated densely connected convolutional network (D2C2N) for automatically segmenting GBM tumors. The second one is the modification of a structural connectome processing pipeline, called PSC Zhang et al. (2018), for simultaneously characterizing the structural connectivity patterns of a large amount of WM bundles. The use of PSC allows us to extract diffusion-related, endpoint-related, and geometry-related features. Automatic segmentation of GBM tumors and extraction of WM features through PSC are implemented in parallel. The third one is a functional analysis of tract statistics to investigate the association between DTI measurements (e.g., FA and mean diffusivity (MD)) and a set of covariates (e.g., age, gender, and diagnostic status). Some hypothesis tests are conducted to reveal both local and global significant WM structural differences between GBM patients and normal controls. The integration of all three components in (TS)2WM distinguishes this work from existing GBM tumor studies. The package for (TS)2WM, along with its documentation, is freely accessible from the website https://github.com/BIG-S2.
Fig. 1.
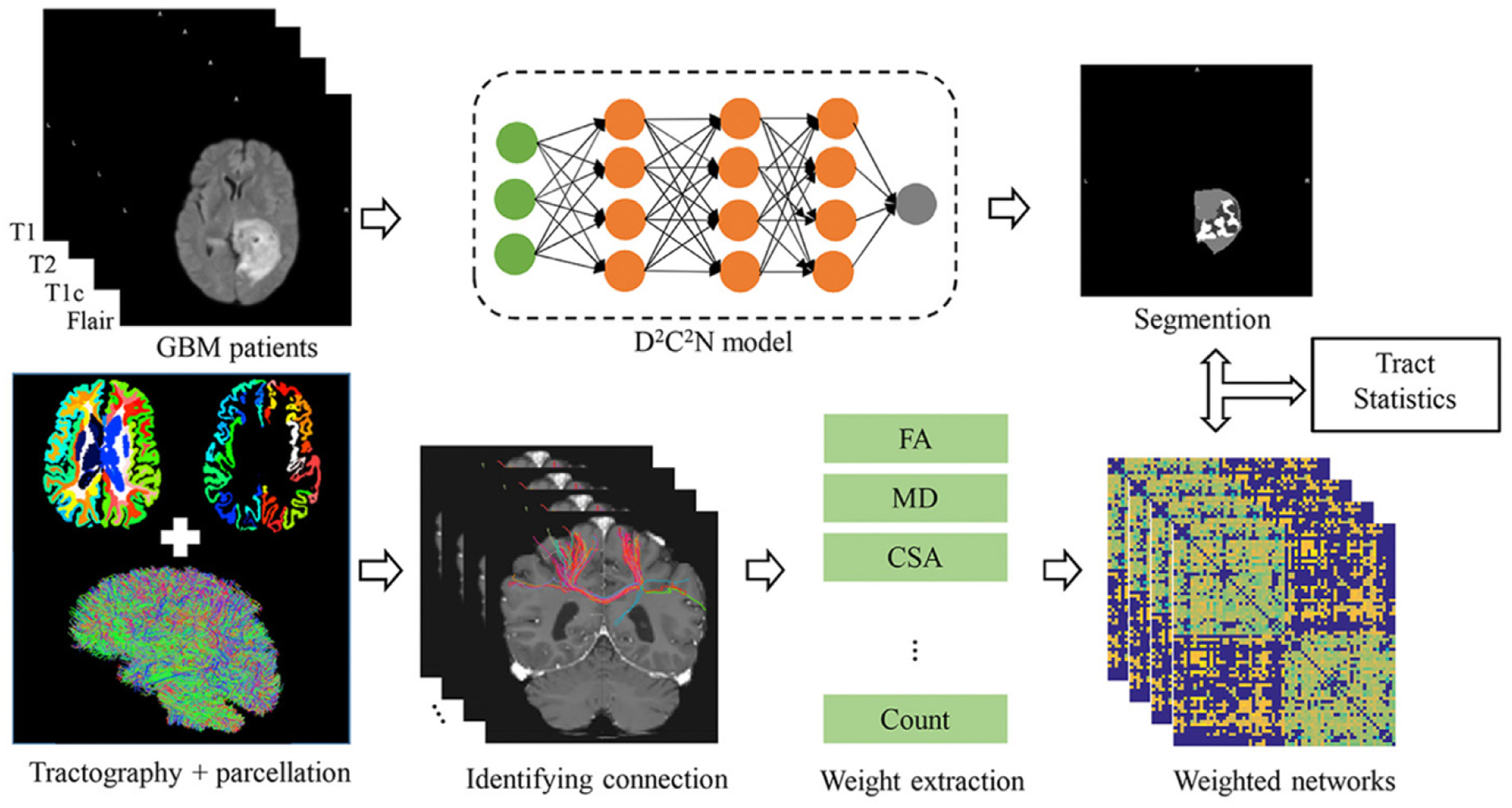
The path diagram of the (TS)2 WM pipeline.
2. Method
2.1. Materials
Three image data sets were used in this study including the Multimodal Brain Tumor Segmentation (BRATS) 2017 Bakas et al. (2017); Menze et al. (2015b), GBM DTI, and Human Connectome Project (HCP).
BRATS 2017 dataset:
In total, 75 patients with lower grade glioma and 210 patients with GBM were provided for training. Moreover, 46 cases with unknown grades and without ground truth labels were provided for validation. The image data were acquired on 3T multi-modal MRI scans with different parameters, including T2, T1, Flair, and T1c. Expert board-certified neuro-radiologists manually revised the ground truth labels. The specific parameters are summarized in Bakas et al. (2017). The main pre-processing steps consisted of co-registering to the same anatomical template, interpolating to 1 mm3 isotropic resolution, and skull stripping.
GBM DTI dataset:
Sixty-two GBM patients (mean age 59.97 ± 11.04 years, range 28 ~ 83 years, 39 males, and 23 females) were retrospectively enrolled. Each patient has at least one MRI protocol image (totally four multi-modal MRI scans as in BRATS 2017 dataset) and one DTI image.
DTI images were acquired on 3T GE Medical systems Signa HDxt or 1.5T Siemens Aera. The diffusion space (q-space) was acquired along 21 ~ 93 directions with a diffusion weighting factor of b = 1000 s/mm2 and a single reference image b0 = 0 s/mm2. Specific MRI scan parameters include 3.5 mm slice thickness with an acquisition matrix of 128 × 128 over a percent phase field of view (FOV) of 100 mm, repetition time (TR) 5700 ~ 10,250 ms, and echo time (TE) 83 ~ 89.8 ms.
Multi-modal MRI scans were acquired on 3T GE Medical systems Signa HDxt or 1.5T Siemens Aera. Each patient has at least one T1 or T1c MRI scan. The specific T1 MRI parameters included the following: slice thickness 5 mm, pixel spacing 0.69 × 0.69 mm2 or 0.43 × 0.43 mm2, TE 11 ~ 13 ms, TR 465 ~ 783 ms, and flip angle 90°. The parameters of T1c MR images are: slice thickness 1 ~ 1.8 mm, pixel spacing 0.94 × 0.94 mm2 or 0.55 × 0.55 mm2, TE 2.1 ~ 4.7 ms, TR 6.7 ~ 8.0 ms, and flip angle 20°. The parameters of T2 MR images are: slice thickness 5 mm, pixel spacing 0.43 × 0.43 mm2 or 0.49 × 0.49 mm2, TE 89 ~ 102.96 ms, TR 5670 ~ 6267 ms, and flip angle 90°. The Flair MRI parameters were listed as: slice thickness 2 or 5 mm, pixel spacing 0.69 × 0.69 mm2 or 0.86 × 0.86 mm2, TE 82 ~ 92 ms, TR 9000 ~ 10,170 ms, and flip angle 150°.
Human Connectome Project (HCP) dataset:
The HCP aims to study and freely share data from 1200 young adult (ages 22 to 35 years) subjects. In this project, only 1064 subjects (mean age 28.74 ± 3.67 years, males 489, and females 575) with both pre-processed DTI and T1 MRI were chosen within the HCP dataset Van Essen et al. (2012). The HCP data were acquired on 3T Siemens Skyra with echo-planar imaging sequence (Acquisition matrix = 168 × 144, TR = 5520 ms, TE = 89.5 ms, FOV = 210 × 180, slice thickness = 1.25 mm, and b value of 1000, 2000, 3000 s/mm2). The DTI protocol includes 6 runs and 3 gradient tables (90 diffusion weighting directions plus 6 b0 acquisitions) with each table acquired once and with right to left and once with left to right phase encoding. More details about HCP data acquisition and pre-processing can be found in Sotiropoulos et al. (2013); Van Essen et al. (2012).
2.2. Pre-processing
Pre-processing is necessary for all three datasets. The BRATS 2017 dataset was distributed after their pre-processing, but it was suffered from both intensity range variation and bias field inhomogeneity. Thus, N4 Bias Field Correction (N4) Tustison et al. (2010) was used to remove bias field inhomogeneity, and a robust intensity normalization method Zhao et al. (2018) was adopted to normalize the intensity of MR images within [0, 255].
Then, the same pre-processing procedure Bakas et al. (2017); Menze et al. (2015b) was applied to our GBM dataset for better transferring the trained D2C2N model. Specifically, N4 was first performed on each patient’s MRI images (except DTI data). FLIRT in FSL1 was first used to rigidly co-register the T1c MRI to b0 image, and a non-linear registration in ANTS2 was used to refine the registration. By following Menze et al. (2015b), the image volumes of each patient were rigidly co-registered to the processed T1c MRI using FLIRT, and all images were re-sampled to 1 × 1 × 1 mm3 using linear interpolation in ANTS and skull stripped using BET in FSL.
2.3. Auto-segmentation of brain tumors
Given a 3D image I, we aim to obtain its segmentation S through training image patches T = {I1, I2,…,In} with the ground true segmentation ς = {S1, S2,…, Sc}, where n is the number of training samples and c is a specific label. Let c = 0,1,2, and 3 denote healthy tissue, necrosis and non-enhancing core, edema, and enhancing core, respectively, and xi is a possible label of c ∈ {0, 1, 2, 3} in the i-th voxel. The marginal probability of xi is given by
| (1) |
These marginal probabilities can be estimated by training a patch-based deep convolutional neural network. The receptive field, model complexity, and memory consumption are three key components of developing a powerful 3D deep learning framework. Ideally, the full size 3D images with 4 channels as the input of the neural network would achieve superior performance. However, since the training of large 3D images is memory-expensive, restricting image resolution and the number of feature maps, and results in low model complexity and representation ability. Thus, we propose a D2C2N model to automatically segment the brain tumors consisting of two major components. The first one is the 3D D2C2N model that generates segmented probability maps. The second one is a 3D conditional random field (CRF) technique Krähenbühl and Koltun (2011) that enforces constrained regularization on the output segmentation probability maps and generates final hard segmentation labels.
2.3.1. D2C2N
Our proposed D2C2N framework illustrated in Fig. 2 integrates two important methods including dilated convolution in Yu and Koltun (2015) and dense block in Huang et al. (2017b).
Fig. 2.
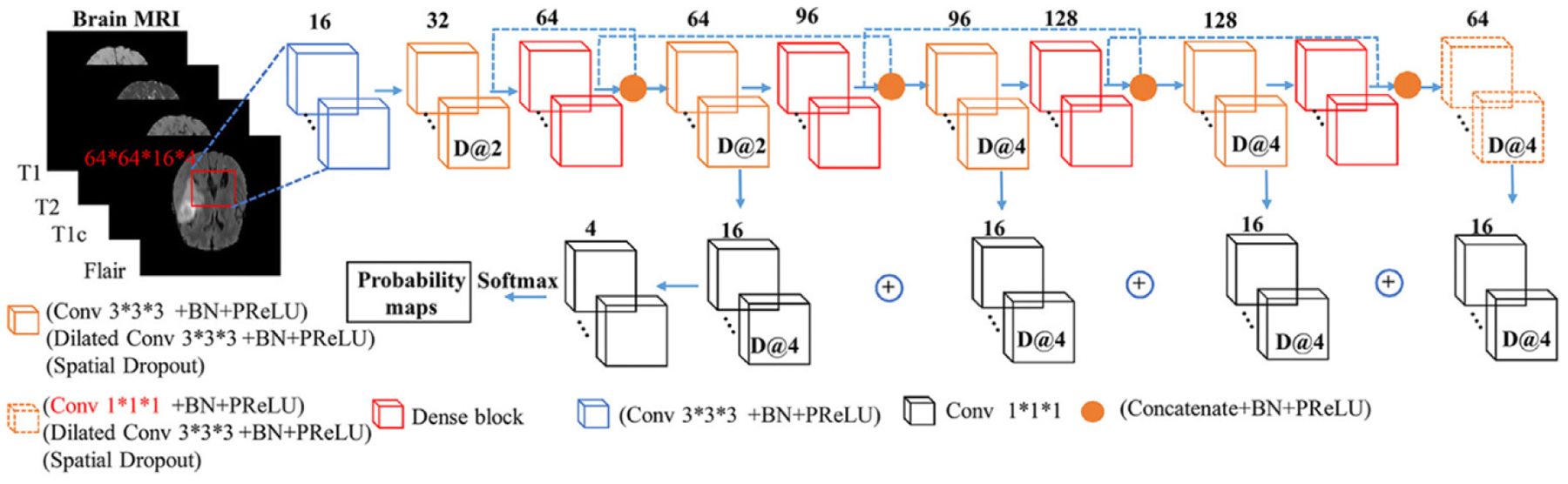
The network structure of our D2C2N.
Dilated convolution.
In Yu and Koltun (2015), the convolutional kernel is dilated by inserting zero holes between the non-zero values of each kernel. The dilated kernels can enlarge the receptive field without introducing additional parameters. This type of network does not need to downsample feature maps to increase the receptive field, and then upsample feature maps to match the input size Badrinarayanan et al. (2015); Ronneberger et al. (2015). Moreover, the dilated convolution is also appropriate for solving the voxel-wise segmentation problem.
Dense block.
The DenseNet architecture Huang et al. (2017b) was developed for general 2D image classification. It addresses not only dense connection in order to avoid the gradient vanishing and exploding problem, but also reduces computational complexity by reusing the previously computed feature maps. The dense block of DenseNet can make the deep model easy to optimize while improving the parameter efficiency. Given an output of the layer in the dense block, the output feature map can be defined as follows:
| (2) |
where and X0 denote the iterative concatenation of all feature maps and the input of the dense block, respectively, and denotes the composite function of operations.
Here the original 2D dense block is extended to a 3D dense block. To overcome the large memory limitation of linear increment of features without downsampling spatial resolution, we remove the concatenation between the input X0 and the output Jégou et al. (2017) in the original dense block (Fig. 3). To improve the rate of convergence, we replace the rectified linear unit Nair and Hinton (2010) by a parametric rectified linear unit (PReLU) He et al. (2015). Moreover, the 3D spatial dropout is used to substitute the normal dropout for improving the independence between feature maps. Similar to Jégou et al. (2017), the first layer H1 is used to create k feature maps and the number of output feature maps becomes 4k by concatenating the output of 4 layers . Also, l × l × l convolutions are used in each branch to compress the associated features, and then concatenate them together.
Fig. 3.
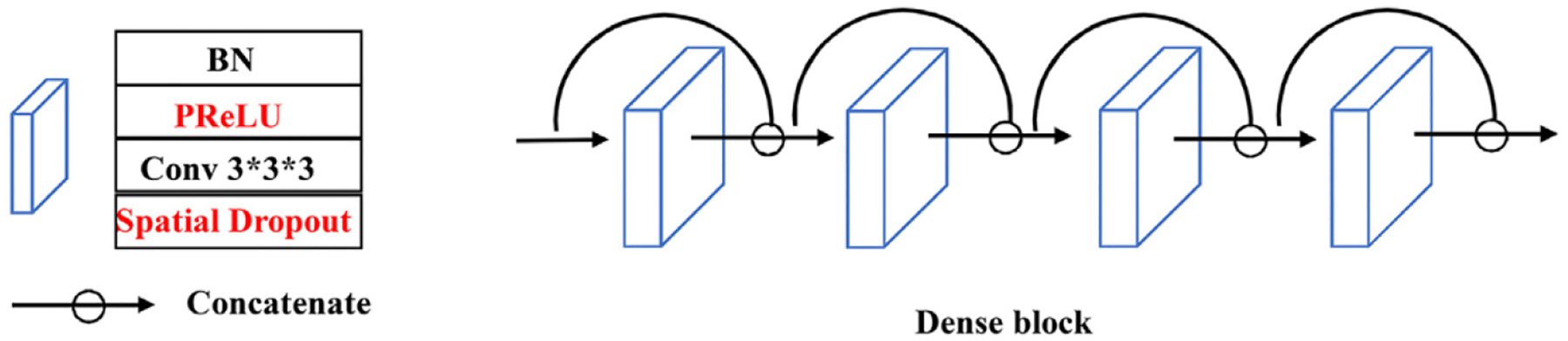
The detailed structure for dense block.
Generalized dice loss.
A crucial step in our D2C2N model is to balance appropriate classes based on their voxel-wise distributions. The generalized dice loss Sudre et al. (2017) was used as a loss function at the training stage to evaluate multi-class segmentation with a single score. The loss function can be written as
| (3) |
where pci and represent the one hot encoding for the ground truth label and the softmax output probability for class c at voxel i, respectively, and wc provides the corresponding invariant properties.
2.3.2. Implementation details
The input size of our network is 64 × 64 × 16 × 4, where the last dimension was supplemented by duplicating images when training with the incomplete MRI modalities. The training dataset was randomly split (80% for training and 20% for validation). The network was trained by minimizing the generalized dice loss Sudre et al. (2017) function using a stochastic gradient descent (SGD) optimizer Bottou (2010) with the momentum of 0.9, batch size of 2, weight decay of 1 × 10−6, an initial learning rate of 0.01, and totally 100 epochs. Data augmentation of the training dataset was added into the network implementation. To further refine the results of segmentation, our D2C2N model and a 3D fully connected conditional random field (CRF) Krähenbühl and Koltun (2011) was applied to refine the segmentation results. The detailed algorithm for 3D CRF method is introduced in the Supplementary Material.
2.4. Mapping population-based fiber tracking
In our proposed (TS)2WM method, automatic segmentation of GBM tumors and extraction of WM features through PSC method are executed sequentially. We use PSC Zhang et al. (2018) to quantify various damages to WM caused by GBM tumors. First, we use the tractography algorithm Girard et al. (2014) to white matter tracts in each individual brain. Second, we warp the Desikan-Killiany parcellation Desikan et al. (2006) to an individual T1-weighted image using FreeSurfer in order to build a coarse parcellation of an individual brain and then define the nodes of the structural connectivity network across subjects. Third, after the segmentation of GBM tumors, we overlay the automatically generated tumors with the parcellation of each individual brain. In this case, for a specific subject, each ROI in the Desikan-Killiany parcellation may contain a portion of tumors. Fourth, even with the presence of tumors in each ROI, we group each tractography dataset into different bundles depending on the regions that each streamline connects. Fifth, we extract various tract-related features, such as the count of streamlines, for each ROI pair. The use of PSC allows us to measure WM integrity within each ROI or each pair of ROIs.
2.5. Statistical methods for quantifying white matter integrity
We quantify white matter integrity at the binary network, weighted network, and streamline levels as follows:
At the binary network level, we threshold the streamline count matrix into a binary matrix, each element of which indicates the presence or absence of a connection for a specific ROI pair.
At the weighted network level, we quantify how different region pairs of interest are connected through white matter tracts by using some features that measure their coupling strength for two ROI pairs. For example, the commonly used metric is the count of streamlines. In addition, we propose to include multiple features of a connection to generate a tensor network for each brain. Specifically, some important diffusion-related features include mean FA, max FA, mean MD, max MD, the mean of generalized FA (GFA), max GFA, the average length, shape, cluster, configuration, the number of end points, and the total connected surface area (CSA) for either each ROI or each ROI pair.
At the streamline level, we calculate the WM integrity measures, such as FA and GFA, along all streamlines for each ROI pair. The diffusion profile along with those tracts combines both the geometric and diffusion properties of a connection.
In either each ROI or each ROI pair, brain regions and their associated streamlines are aligned to a template Zhang et al. (2018). Thus, the WM integrity measures (e.g., FA, MD) can be directly calculated and statistical analyzed according to the following three main scientific questions:
-
(Q1)
At the binary network level, we are interested in detecting any change of a specific binary connection for each specific ROI pair and the whole connection structures across all ROI pairs between GBM patients and healthy subjects.
-
(Q2)
At the weighted network level, we are interested in detecting any change of the diffusion features in terms of the count of streamlines and connected surface area (CSA), among others, in a specific ROI or across all ROIs between GBM patients and healthy subjects.
-
(Q3)
At the streamline level, we are interested in detecting any statistically significant difference in terms of diffusion properties (e.g, factional anisotropy) along major fiber bundles for each ROI pair between GBM patients and healthy subjects.
As for question (Q1), statistical analysis of such binary networks can be done for each ROI pair by using logistic-type regression models and across all ROI pairs by correcting multiple comparisons. Furthermore, statistical analysis of such binary networks can be carried out by treating all ROI pairs as a network-valued data Durante et al. (2017).
As for question (Q2), a statistical approach, called tensor network principal components analysis (TN-PCA) Zhang et al. (2019), was used to quantify the changes of brain structural connectomes between GBM patients and healthy subjects across all ROIs.
To address question (Q3), FADTTS Zhu et al. (2011), a pipeline that describes the variability of DTI measurements along major WM fiber bundles with a set of covariates (age, gender, diagnostic status) Zhu et al. (2011, 2010), was performed on GBM patients and normal controls. Instead of using only scalar mean DTI quantitative values or a skeleton line, FADTTS can localize and reveal the detailed changes in a specific region of a tract. For a specific WM tract of the i-th subject for i = 1,… ,N, let sj denote the j-th grid point along the fiber tract for j = 1,…, M and let yi(sj) be its associated DTI measurement (e.g., FA, MD) at sj. A varying coefficient model can be written as:
| (4) |
where ϵi(sj) is a random noise following , and xi1 and xi2 denote gender and age, respectively. Moreover, a dummy variable xi3 is used to indicate whether an individual belongs to GBM patients or normal controls. The ηi(sj) is a stochastic process following N(0, ση (s, s′)), which measures both subject and location variabilities, where ση(s, s′) is a covariance function.
The comparisons between the two groups can be investigated globally and locally based on the following local and global hypotheses:
| (5) |
| (6) |
As in Zhu et al. (2011), the local test statistic G(s) and the global test statistic G can be defined as:
| (7) |
| (8) |
where e3 = (0,0,1)T, and and are the estimates of and ση(s, s), respectively. A wild bootstrap method is used here as well to compute the p-value Huang et al. (2017a).
3. Experimental results
In this section, we evaluated six aspects of the (TS)2WM framework including (i) segmentation performance on the BRATS dataset with different combinations of MRI modalities, (ii) comparison of D2C2N model with other state-of-the-art segmentation methods, (iii) robustness of (TS)2WM, (iv) analysis of binary network patterns in GBM subjects, (v) analysis of weighted network patterns in GBM subjects, and (vi) analysis of streamline in GBM subjects.
The Keras Chollet et al. (2015) with Tensorflow Abadi et al. (2016) as backend was used to implement our D2C2N model. The training and testing processes were conducted via 24-core E5–2643 Intel Xeon and a 12 GB TITAN Xp NVIDIA GPU. Two metrics including Dice score and Sensitivity Zhao et al. (2018) are used to evaluate the results of tumor segmentation.
3.1. Segmentation performance on BRATS with different combinations of MRI modalities
Due to incomplete MRI modalities in our GBM DTI dataset, different combinations of MRI modalities were needed to be trained based on the BRATS 2017 training set. Subsequently, we evaluated the effectiveness of the segmented results using different modalities of MRI images in the BRATS validation dataset3. The output results were further evaluated by using CBICA’s Image Processing Portal4. Fig. 4 (a)–(c) show the segmentation results for a randomly selected subject from the BRATS 2017 validation dataset for three different modalities. Table 1 summarizes the evaluation metrics including dice ratio and sensitivity based on segmentation results for different combinations of MRI imaging modalities. We consider enhancing tumor (ET), whole tumor (WT), and tumor core (TC). As shown in Table 1, reasonable segmentation results based on the three modalities of MRI images (Flair/T1c/T2) can be obtained by using our proposed method. Moreover, among all four modalities, T1c is the most important one since its corresponding results are slightly worse than those for the best Flair/T1c/T2 combination. The well trained D2C2N model can be transferred from the BRATS 2017 dataset to our GBM DTI dataset for auto-segmenting GBM tumors. Fig. 4 (d)–(f) show the segmentation results for one selected subject in our dataset with three different imaging modalities. The results of Fig. 4 demonstrate that the proposed D2C2N model may be able to segment the GBM tumors precisely.
Fig. 4.
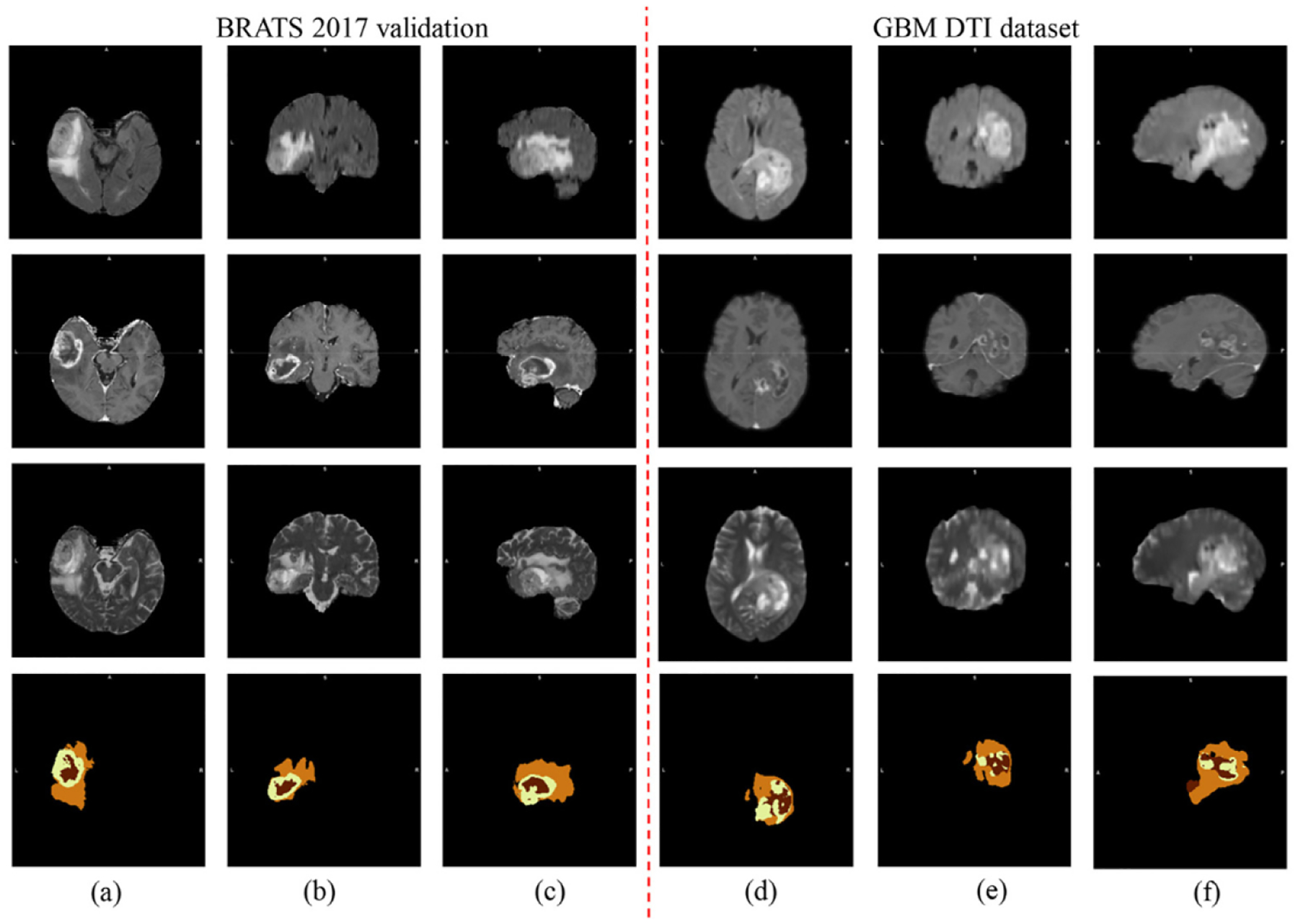
Segmentation results from one randomly selected subject in the BRATS 2017 Challenge dataset (a)-(c) and that in our GBM DTI dataset (d)-(f): four rows from top to bottom are raw Flair, raw T1c, raw T2, and their corresponding segmentation results.
Table 1.
The evaluation metrics (mean ± standard deviation) including dice and sensitivity of D2C2N model for different combinations of MRI imaging modalities based on the BRATS 2017 dataset: The ET, WT, and TC denote enhancing tumor, whole tumor, and tumor core, respectively. Among all combinations, ”Flair/T1c/T2” achieves comparable performance as the complete combination ”Flair/T1c/T2/T1”, while ”T1c” is the most important one among all four modalities.
| Modalities | Dice | Sensitivity | ||||
|---|---|---|---|---|---|---|
| ET | WT | TC | ET | WT | TC | |
| Flair/T1C/T2/T1 | 0.72 ± 0.31 | 0.89 ± 0.07 | 0.68 ± 0.34 | 0.77 ± 0.31 | 0.93 ± 0.08 | 0.65 ± 0.04 |
| Flair/T1c/T2 | 0.76 ± 0.28 | 0.89 ± 0.07 | 0.70 ± 0.33 | 0.78 ± 0.29 | 0.90 ± 0.11 | 0.68 ± 0.34 |
| Flair/T2/T1 | 0.09 ± 0.28 | 0.88 ± 0.07 | 0.51 ± 0.29 | 0.09 ± 0.28 | 0.90 ± 0.10 | 0.48 ± 0.30 |
| Flair/T1c | 0.73 ± 0.31 | 0.89 ± 0.08 | 0.70 ± 0.32 | 0.79 ± 0.30 | 0.89 ± 0.13 | 0.66 ± 0.34 |
| Flair/T1 | 0.09 ± 0.28 | 0.87 ± 0.07 | 0 | 0.09 ± 0.28 | 0.89 ± 0.12 | 0 |
| T1c/T2 | 0.70 ± 0.32 | 0.84 ± 0.12 | 0.66 ± 0.36 | 0.74 ± 0.33 | 0.82 ± 0.18 | 0.64 ± 0.38 |
| T2/T1 | 0.34 ± 0.30 | 0.83 ± 0.10 | 0.55 ± 0.33 | 0.38 ± 0.34 | 0.85 ± 0.16 | 0.54 ± 0.34 |
| T1c | 0.70 ± 0.29 | 0.76 ± 0.16 | 0.68 ± 0.30 | 0.80 ± 0.28 | 0.74 ± 0.23 | 0.68 ± 0.32 |
3.2. Comparison of d2c2n model with other state-of-the-art segmentation methods
To explore the feasibility of the proposed D2C2N model, we compared it with some existing state-of-the-art segmentation methods based on their segmentation results for the BRATS 2017 validation dataset. Considering flexibility and practicability, we do not include the methods that ensembles multiple deep learning models to obtain the final segmentation results here. See Table 2 for the comparisons of different methods. As shown in Table 2, compared with those state-of-the-art methods, our proposed method for the ”Flair/T1c/T2” combination achieves comparable tumor segmentation precision in terms of both dice ratio and sensitivity.
Table 2.
Comparisons between our method for the ”Flair/T1c/T2” combination and some state-of-the-art methods in terms of two evaluation metrics including dice score and sensitivity based on the BRATS 2017 dataset. In each case, we present mean ± standard deviation. N/A indicates that the measure is not provided in the literature.
| Methods | Dice | Sensitivity | ||||
|---|---|---|---|---|---|---|
| ET | WT | TC | ET | WT | TC | |
| Jesson Jesson and Arbel (2017) | 0.71 ± 0.29 | 0.90 ± 0.07 | 0.75 ± 0.24 | 0.73 ± 0.29 | 0.90 ± 0.10 | 0.72 ± 0.26 |
| Islam Islam and Ren (2017) | 0.69 ± 0.30 | 0.88 ± 0.09 | 0.76 ± 0.76 | 0.72 ± 0.29 | 0.86 ± 0.14 | 0.71 ± 0.25 |
| Shaikh Shaikh et al. (2017) | 0.65 ± 0.32 | 0.87 ± 0.11 | 0.68 ± 0.34 | N/A | N/A | N/A |
| Isensee Isensee et al. (2017) | 0.73 ± N/A | 0.90 ± N/A | 0.80 ± N/A | 0.79 ± N/A | 0.90 ± N/A | 0.78 ± N/A |
| Soltaninejad Soltaninejad et al. (2017) | 0.66 ± 0.28 | 0.86 ± 0.09 | 0.78 ± 0.19 | 0.57 ± 0.28 | 0.83 ± 0.13 | 0.72 ± 0.21 |
| our method | 0.76 ± 0.28 | 0.89 ± 0.07 | 0.70 ± 0.33 | 0.78 ± 0.29 | 0.90 ± 0.11 | 0.68 ± 0.34 |
3.3. Robustness of (TS)2WM
We conducted a simulation study to assess how well our (TS)2WM pipeline can detect the changes of brain connectomes in the simulated tumors of 40 randomly selected HCP subjects. As illustrated in Table 3, the regions around the left parahippocampus (L12) have the highest probability of GBM tumorigenesis, so simulated tumors were introduced by randomly distorting the intensities in the left hippocampus region of both the DTI image and the T1-weighted image for each subject. Moreover, the areas of simulated tumors were dilated 6, 12, and 18 pixels to assess the impact of tumor sizes on the performance of our (TS)2WM. Fig. 5 shows the true DTI and T1 images, the corresponding DTI and T1 images with simulated tumors, and the numbers of streamlines in connection (R7, L12) before and after introducing tumors in L12 for one randomly selected subject, in which the area of simulated tumors was dilated for 18 pixels. As shown in Fig. 5, the number of streamlines in connection (R7, L12) decreases greatly from 1273 to 157 due to simulated tumors. To assess the impact of the extent of damage on the robustness of our (TS)2WM, we focus on visualizing the brain connection patterns of L12 across all 40 subjects. Fig. 6 presents the mean CSA connectivity and the mean fiber count connectivity of all healthy HCP subjects and their corresponding images with the simulated tumors in L12. As shown in Fig. 6, the significant reduction of the numbers of CSA and fiber count between L12 and other ROIs can be observed in the images with simulated tumors compared with their original images. Furthermore, we choose ROIs that have the top 10 largest reduction of the mean of fiber counts connecting with L12 and, present their histograms of mean FA, max FA, mean MD, and max MD before and after introducing tumors in Fig. 7. Inspecting Fig. 7 reveals the reduction of mean/max FA and the increase of mean/max MD before and after introducing tumors. Therefore, according to Figs. 5–7, our (TS)2WM pipeline may be able to robustly distinguish the change of brain connectomes, indicating the ability of assessing the differences of brain structural connectomes before and after introducing tumors.
Table 3.
Results from our GBM DTI dataset with 62 subjects. The top nine pairs of regions with highest probability of GBM tumorigenesis, where “lh” and “rh” represent left hemisphere and right hemisphere, respectively. Each row contains a pair of regions of interest (ROIs) and the proportion of subjects with the presence of a connection for the ROI pair. In contrast, all HCP subjects have connections in all nine ROI pairs.
| ROI1 | ROI2 | Proportion |
|---|---|---|
| L12 (lh-parahippocampal) | L14 (lh-medial orbitofrontal) | 67.7% (42/62) |
| L11 (lh-pericalcarine) | L12 (lh-parahippocampal) | 67.7% (42/62) |
| R30 (rh-transverse temporal) | L31 (lh-precentral) | 64.5% (40/62) |
| R11 (rh-pericalcarine) | L14 (lh-medial orbito frontal) | 62.9% (39/62) |
| L12 (lh-parahippocampal) | R14 (rh-medial orbitofrontal) | 59.7% (37/62) |
| R13 (rh-paracentral) | L14 (lh-medial orbitofrontal) | 59.7% (37/62) |
| L19 (rh-rostral anterior cingulate) | L31(lh-precentral) | 59.7% (37/62) |
| L29 (lh-precuneus) | L31 (lh-precentral) | 59.7% (37/62) |
| L29 (lh-precuneus) | R31 (rh-precentral) | 59.7% (37/62) |
Fig. 5.
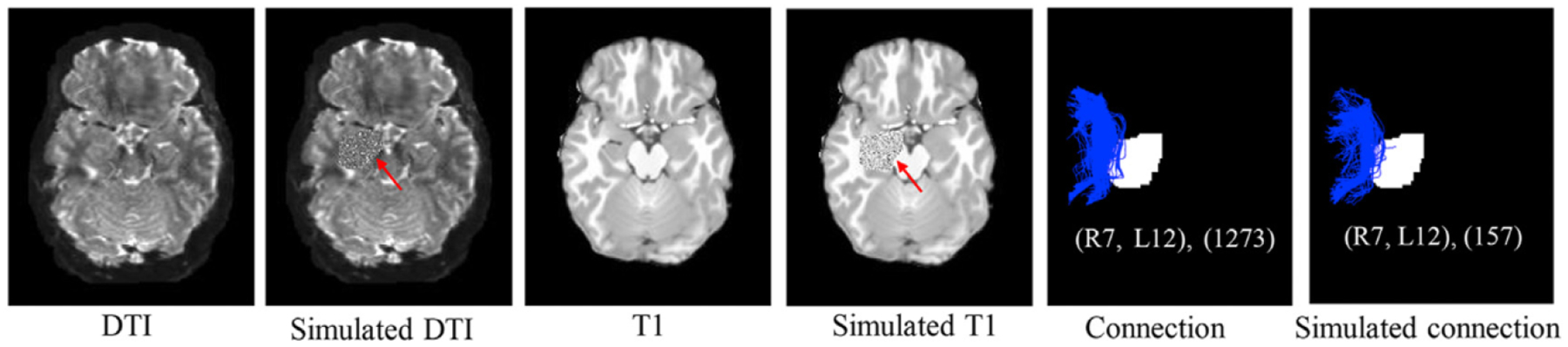
The original DTI image (the first column) and T1 image (the third column) for one randomly selected HCP subject, the corresponding DTI image (the second column) and T1 image (the fourth column) with simulated tumors introduced by randomly distorting the intensities in the left hippocampus region (L12), and streamlines in the (R7, L12) connection before (the fifth column) and after introducing tumors with dilating 18 pixels of left hippocampus region (the sixth column).
Fig. 6.
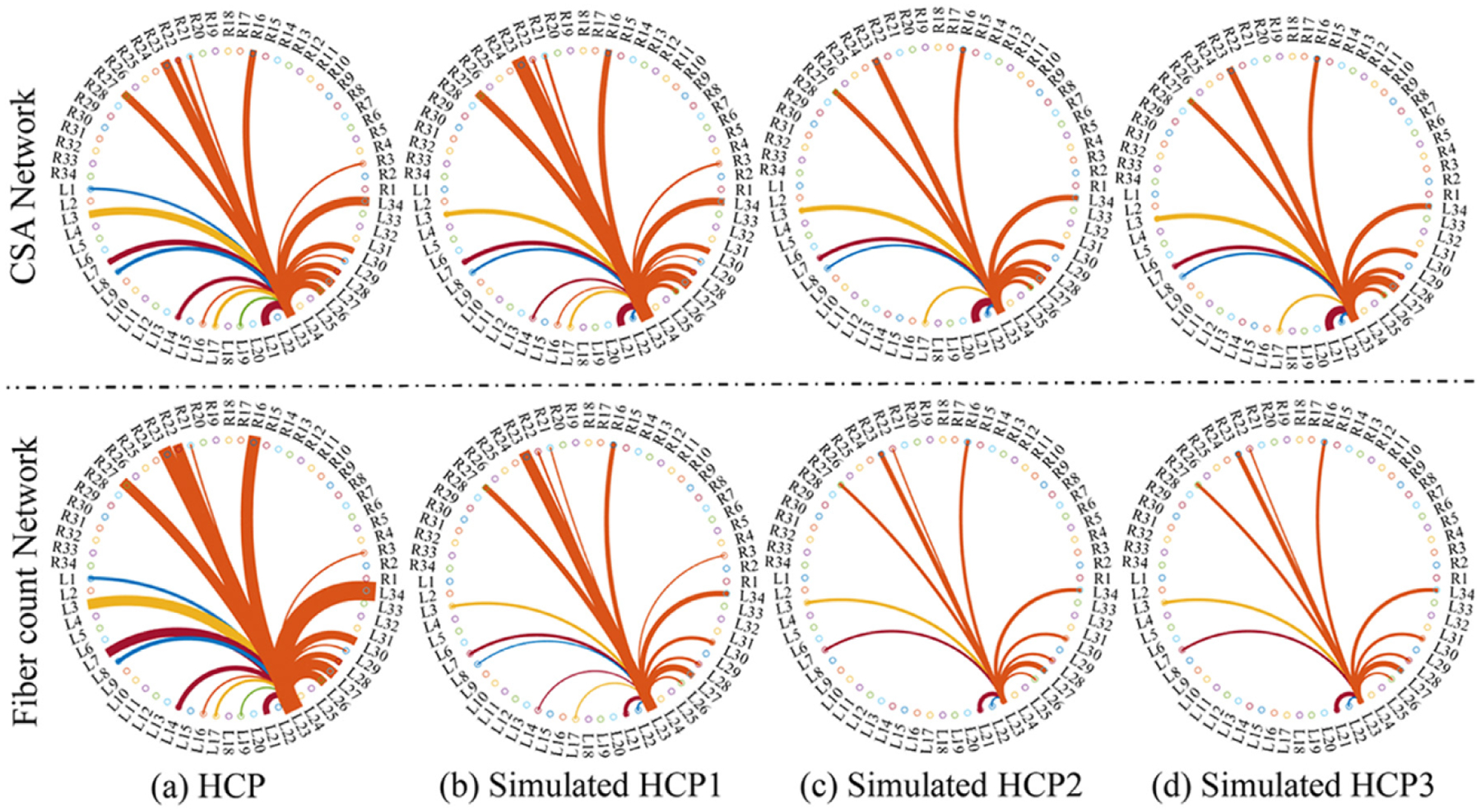
Results from DTI images with simulated tumors in L12: the left parahippocampus related connectome patterns in terms of CSA connectivity and the fiber count before (panel (a)) and after introducing tumors with dilating 6, 12, and 18 pixels of left hippocampus region in panels (b)-(d), respectively. The HCP1, HCP2, and HCP3 correspond to the dilation with 6,12, and 18 pixels, respectively. The thickness of lines represents either the average number of CSA or that of fiber count for each connection between ROI and L12.
Fig. 7.
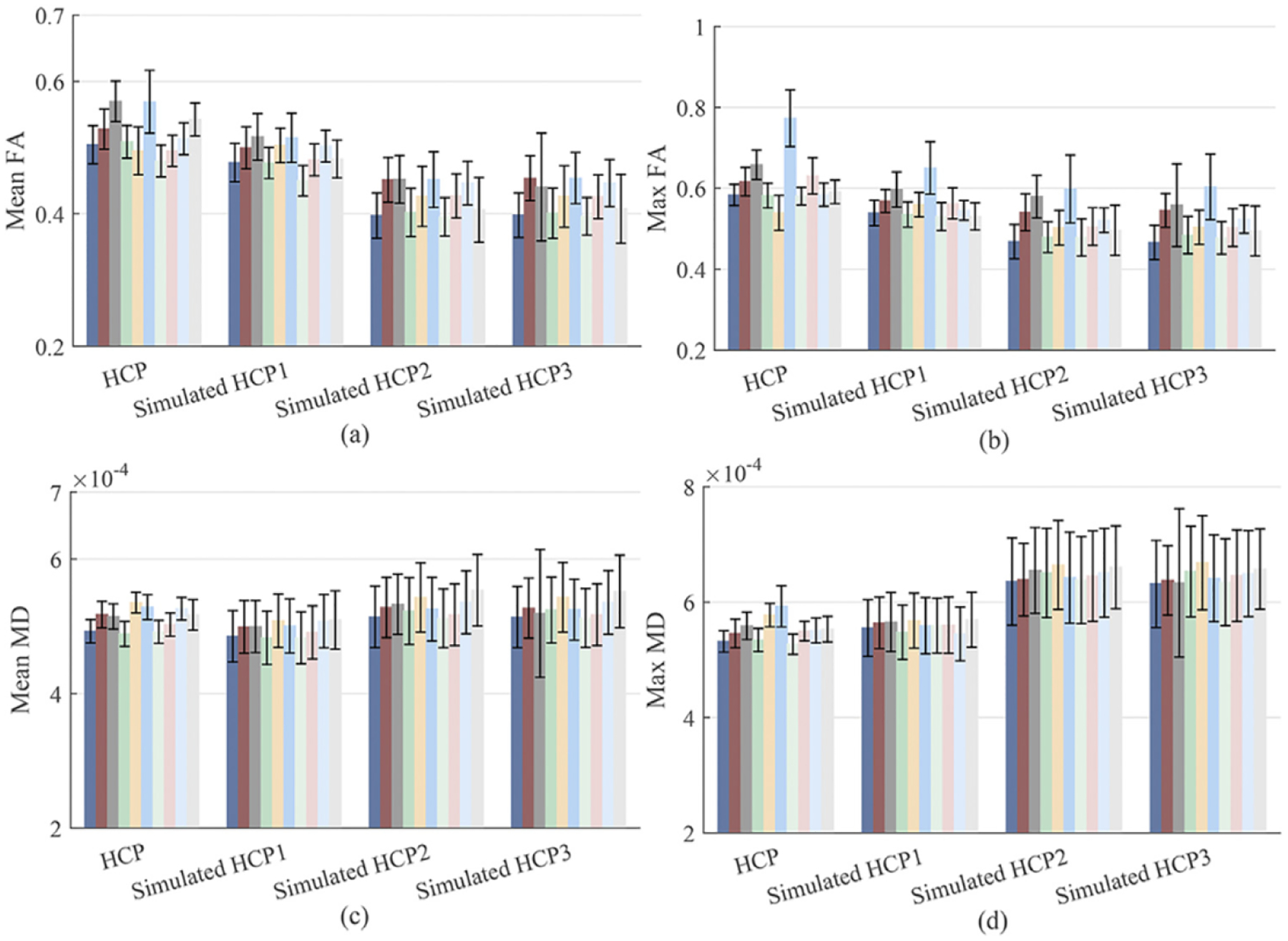
Results from DTI images after introducing tumors with dilating 6, 12, and 18 pixels of left hippocampus region in L12: The histograms of mean FA in panel (a), max FA in panel (b), mean MD in panel (c), and max MD in panel (d) before and after introducing tumors across the 10 ROIs that have the top 10 largest reduction of the mean of fiber counts connecting with L12. The HCP1, HCP2, and HCP3 correspond to the dilation with 6, 12, and 18 pixels, respectively.
3.4. Analysis of binary network patterns in GBM subjects
Besides the GBM tumor segmentation in our dataset, statistical analysis of WM integrity at the binary network level is another focus in this study. In our (TS)2WM pipeline, the Desikan-Killiany atlas Desikan et al. (2006) is used to combine the tracts with labels and partition the connectivities. Details of Desikan-Killiany ROIs are provided in the supplemental materials. Table 3 shows the top nine ROI pairs with the highest probability of GBM tumorigenesis. As illustrated in Table 3, most patients have GBM tumors in the frontal lobe that controls motor function, problem solving, spontaneity, memory, language, initiation, judgment, impulse control, and social and sexual behavior Stuss et al. (1992). Fig. 8 shows whole brain fiber tracts, the fiber connections among ROIs with tumors, and fiber tracts connecting six selected ROI pairs for one randomly selected GBM patient. Inspecting Fig. 8 reveals that some fiber connections remain among the tumor ROIs.
Fig. 8.
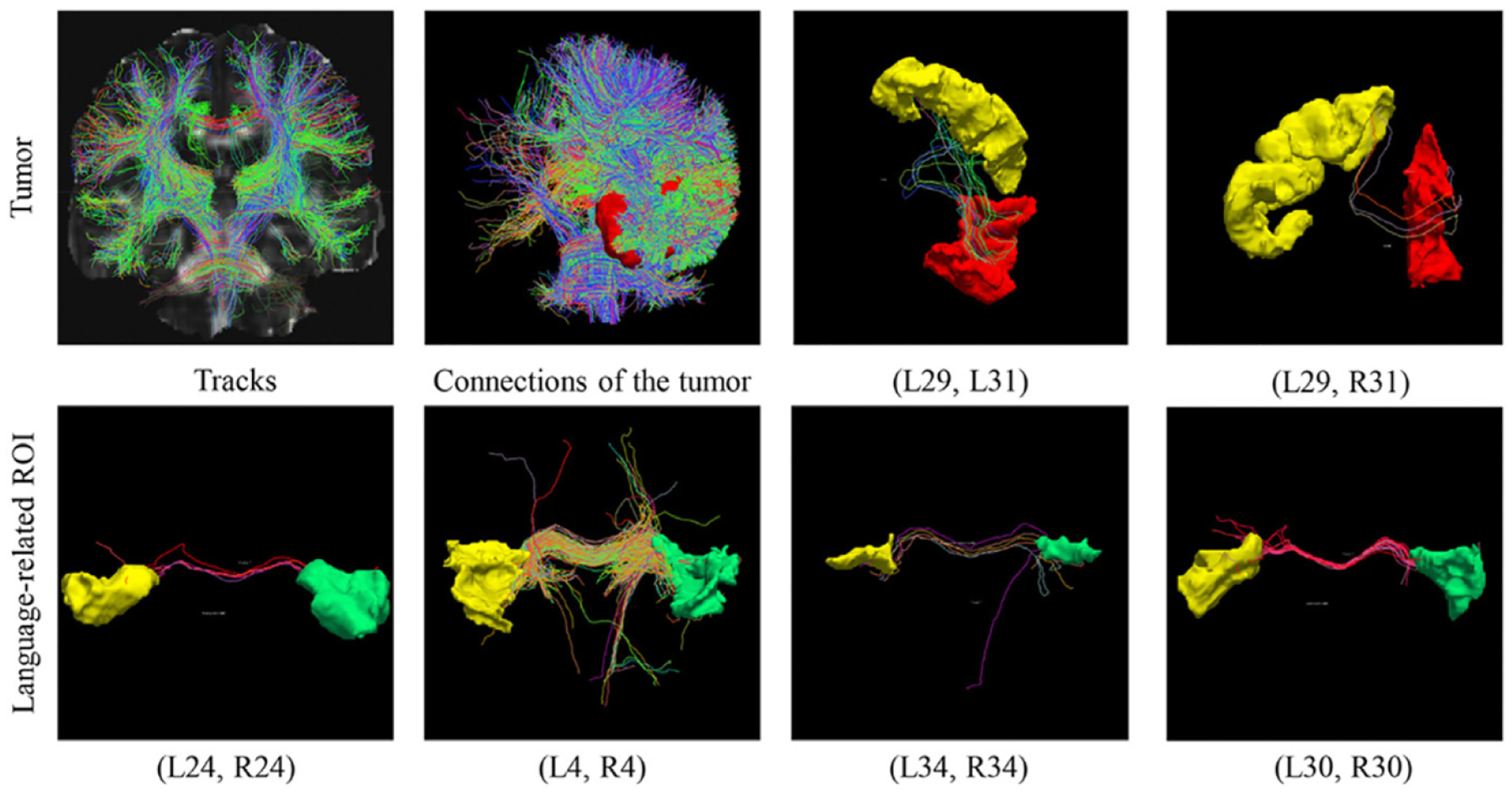
Results from one randomly selected GBM subject: the whole brain fiber tracts, fiber tracts among ROIs with tumors, fiber tracts connecting two tumor-related pairs (L29, L31) and (L29, R31), and fiber tracts connecting language-related ROI pairs including (L24, R24), (L4, R4), (L34, R34), and (L30, R30).
3.5. Analysis of weighted network patterns in GBM subjects
In our (TS)2WM pipeline, each type of diffusion features for each individual can be represented as a weighted adjacency matrix of the brain connectome. We quantified the changes in different weighted network matrices between the GBM group of all 62 patients and the healthy group of all HCP subjects as follows. Specifically, we applied TN-PCA Zhang et al. (2019) to visualizing variation among individuals in their brain connectomes and the statistical analysis of studying differences between the GBM group and the healthy group. Fig. 9 presents the principal component (PC) scores of the GBM patient group and those of the HCP healthy group based on the count of streamlines, CSA, mean and max values of FA, and the mean and max values of MD. Clear separation can be observed between the GBM patient group and the HCP healthy group in these plots, indicating different brain connection patterns between the two groups. The principal brain network, which exhibits major patterns of structural connectivity, was used to further explain the changes of network structure across all ROIs between the two groups. Fig. 10 shows the connection structures derived from the CSA network and the count of streamlines network. Only the top 100 most connected ROI pairs were selected to improve presentation. Inspecting Fig. 10 reveals that there is a remarkable variation of the connection structures between the GBM group and the HCP group.
Fig. 9.
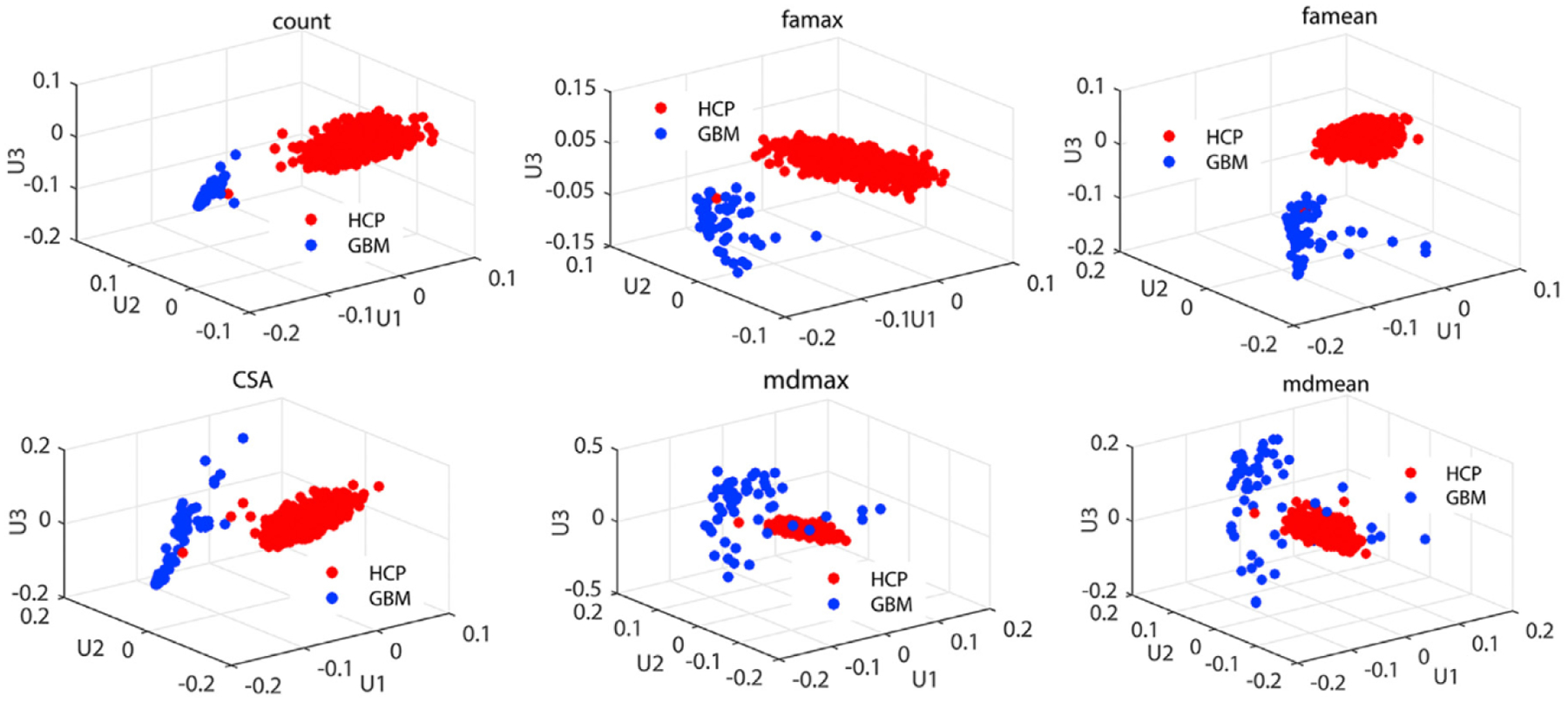
Results from the TN-PCA analysis of comparing between the GBM group and the HCP group: the top three PC scores of six diffusion properties including the count of streamlines, CSA, mean and max values of FA, and mean and max values of MD for the GBM group and the healthy group.
Fig. 10.
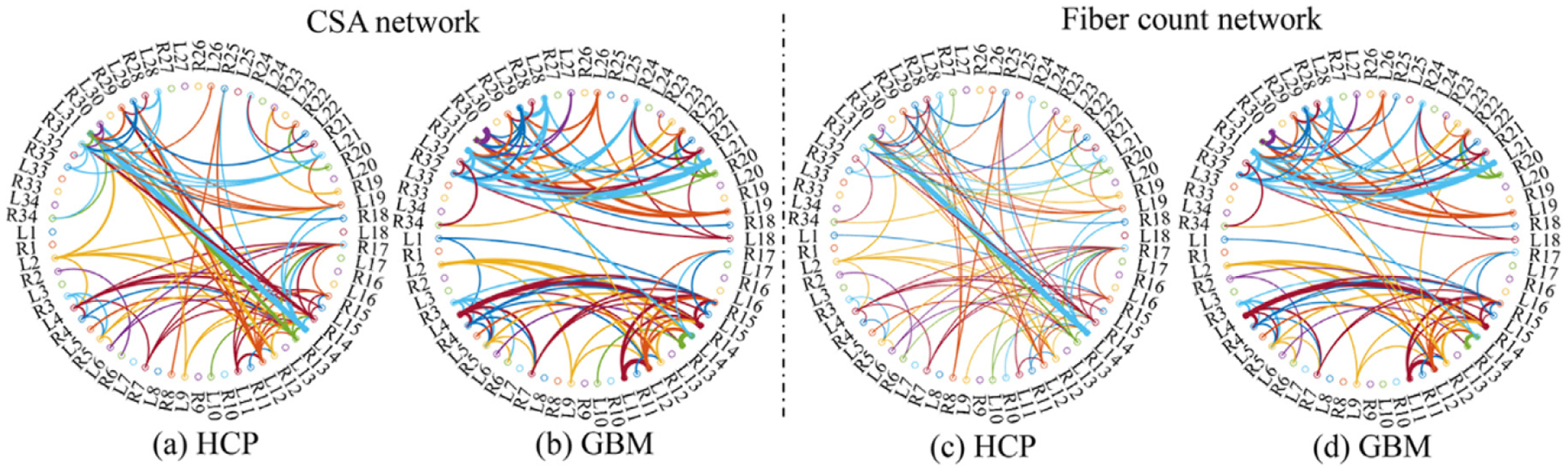
Results from comparing between the GBM and HCP groups: the CSA network and the fiber count network of the GBM group and the HCP group, in which only the top 100 most connected ROI pairs are presented.
3.6. Analysis of streamline in GBM subjects
As reported in Roberts et al. (2005), GBM tumors result in reduced FA. Fig. 11 presents the boxplots of four DTI measurements over the nine tumor-related ROI pairs in Table 3 across the GBM and normal groups. In each ROI pair, the values of mean/max FA for the GBM group are smaller than those for the healthy group, whereas those of mean/max MD reverse. It may be due to the fact that some portion of fiber tracts may be entirely damaged by GBM tumors Jellison et al. (2004). Moreover, both local and global hypothesis tests were used to detect significant differences along WM bundles between the GBM and normal groups for three types of ROI pairs. Specifically, both ROIs in each ROI pair are either tumor-related, language-related, or hand motor-related. In each ROI pair, FADTTS was applied to the fiber bundles of FA and MD values Zhang et al. (2018). At the global and local levels, we conducted the hypothesis testing in both (5) and (6). At the local level, we set the number of grid points to be M = 100. Fig. 12 (a) shows the local percentage of significant grid points, each of which has the FDR corrected p < .05, over the total 100 grid points within each ROI pair. Most ROI pairs have more than 90% of significant grid points except that (R11, L14) and (R34, L34) have 45% and 18% significant grid points, respectively. Fig. 12 (b) shows the global p-values of all 15 ROI pairs. Inspecting Fig. 12 reveals that most ROI pairs are significantly different between the GBM and normal groups.
Fig. 11.
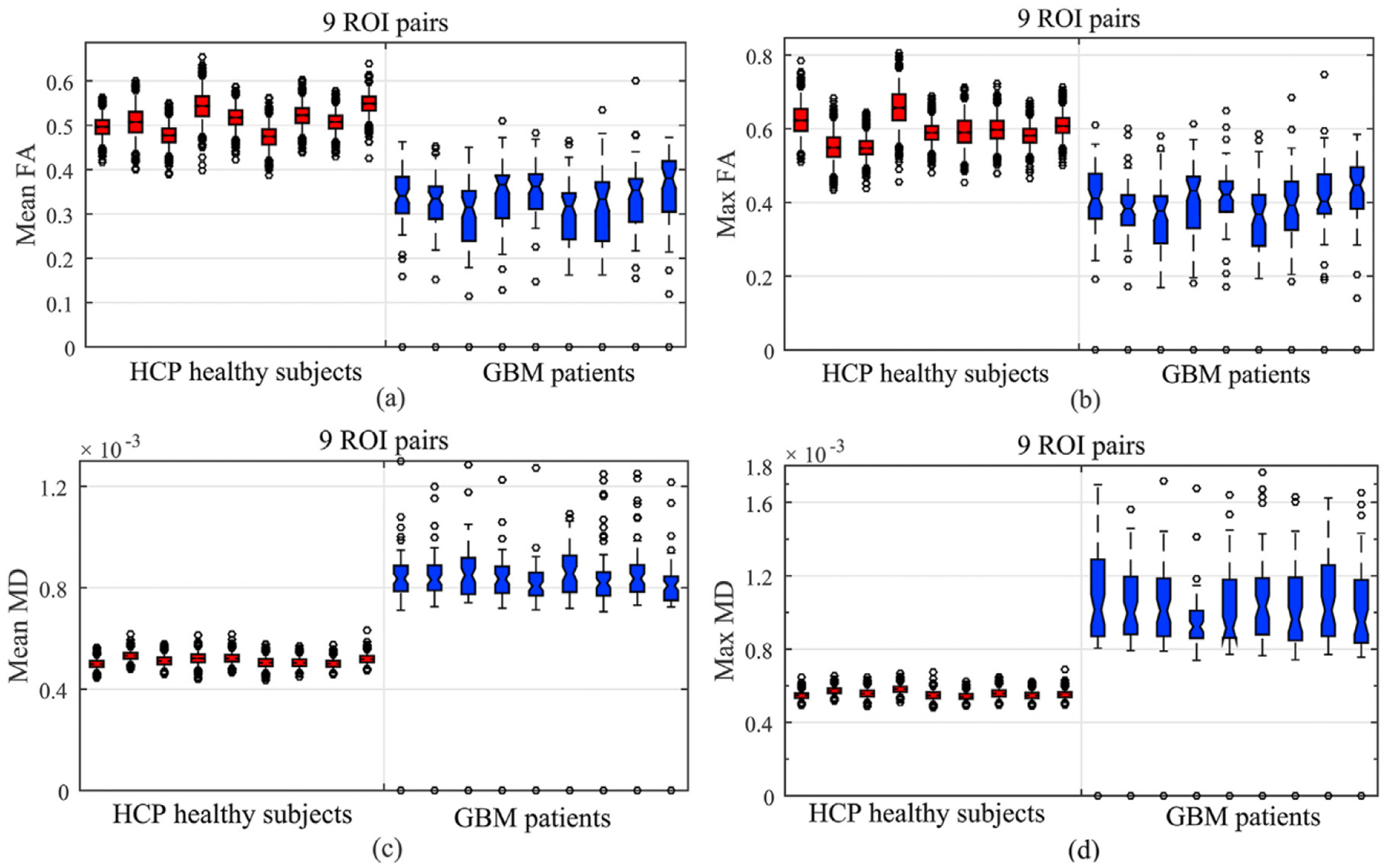
Results from comparing between the GBM and HCP groups: the boxplots of the mean FA, max FA, mean MD, and max MD values of the 9 ROI pairs in Table 3.
Fig. 12.
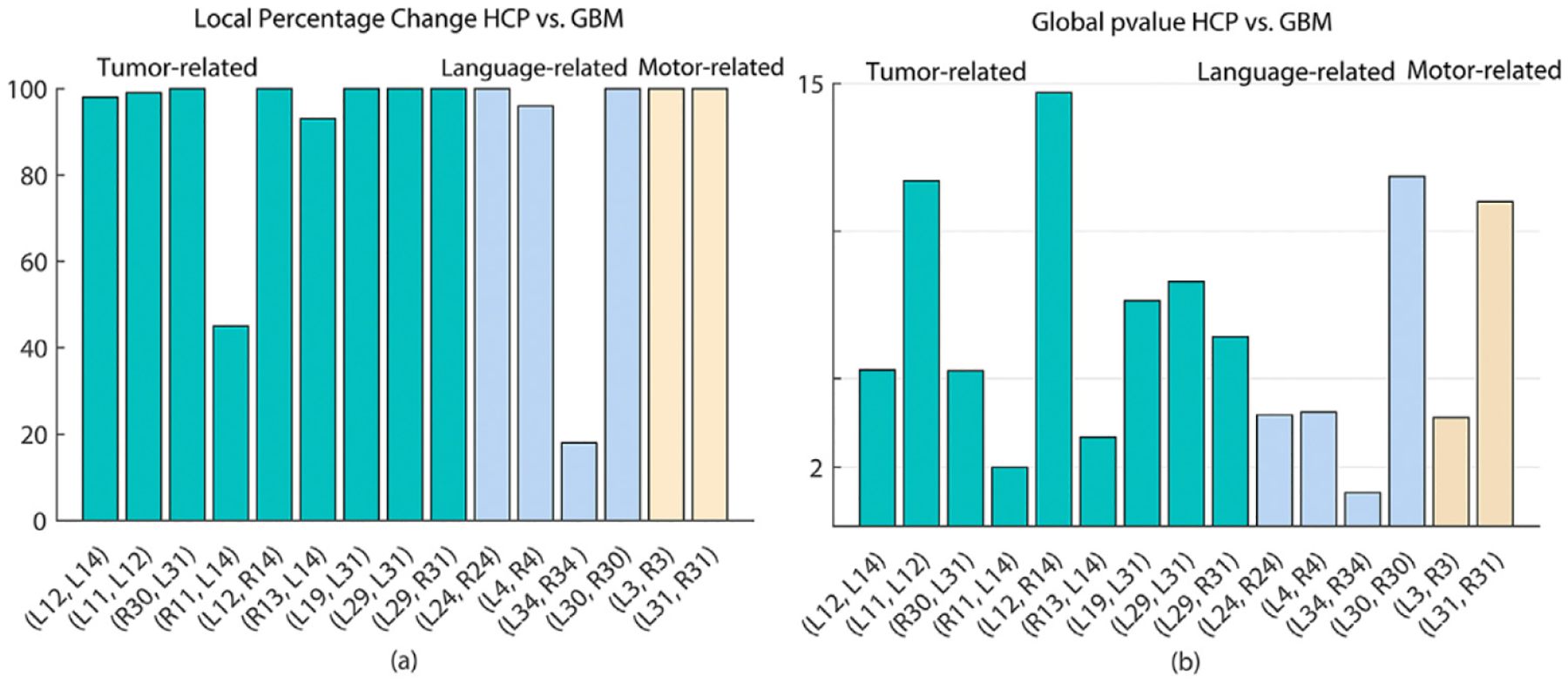
Results from comparing between the GBM and HCP groups: the global and local test analyses of GBM tumor tracts within the three type of ROI pairs including tumor-related, language-related, and hand motor-related ROI pairs. Panel (a) shows the percentage of significant grid points over the total 100 grid points across all ROI pairs; panel (b) shows the global p-values (− log 10 scale) across all ROI pairs.
4. Discussion
Due to its ability of tracking water diffusion, DTI has been widely used to investigate the integrity of WM structure. However, the use of DTI for analyzing the impact of GBM tumors on WM fiber bundles has not been fully explored yet. Recently developed GBM-related methods have either pursued the precision of tumor segmentation or detected abnormalities in various brain disorders with manual delineation of GBM tumors by experts. Instead, we propose the (TS)2WM pipeline to perform the statistical analysis of the effects of GBM on WM integrity.
The auto-segmentation of GBM tumors is a critical step in our (TS)2WM pipeline. Pre-processing the GBM DTI dataset appropriately is critical for transferring the trained D2C2N model based on the BRATS 2017 data set to our GBM DTI dataset. As discussed in Menze et al. (2015b), the BRATS 2017 data set was collected from different centers, different MR scanners vendors, different field strengths (1.5T and 3T), and different MRI parameters. The key parameters of our GBM DTI data set are similar to those of the BRATS 2017 data set, so we follow the same pre-processing steps Menze et al. (2015b) to homogenize our GBM DTI dataset. In Zhang et al. (2018), the T1 or T1c images were needed for segmenting different types of tissues to provide the soft criterion for guiding the growth and termination of streamlines. Since our GBM DTI dataset does not have all MRI modalities, we trained different combinations of MRI modalities to address this issue based on the BRATS 2017 data set. As illustrated in Table 1, our method can achieve competitive performance even for only three imaging modalities (Flair, T1c, and T2). The Dice scores of ET and TC using Flair + T1 and T2 + T1 are low because the enhancing core and the necrotic and non-enhancing core are segmented by T1c Menze et al. (2015b). Recently, the ensembles of multiple deep learning models Kamnitsas et al. (2017); Wang et al. (2017) and the k-fold cross-validation ensembles in training dataset have become popular for boosting the precision of segmentation. In terms of pursuing the precision of GBM segmentation, our D2C2N model can be further improved. However, we aim to develop a pipeline including both the brain tumor segmentation and WM tract statistics. Although ensemble strategies may lead to about 1% improvement Kamnitsas et al. (2017), it is computationally extensive. Given the computational complexity and implementation effectiveness of ensemble strategies, we do not include them in our (TS)2WM pipeline. As shown in Table 2, our proposed method can achieve competitive precision of tumor segmentation, while facilitating the tumor-based statistical analysis of WM bundles.
The geometry related features, including the average length of streamlines, the number of streamline clusters, and deviations of streamline shapes, can be extracted in our (TS)2WM pipeline for characterizing the geometric information of streamlines. As demonstrated in TN-PCA Zhang et al. (2019), the geometry related features are poorly related to the brain structural connectomes. Thus, at the weighted network level, the geometry related features are excluded for detecting any change in a specific ROI or across all ROIs between GBM patients and healthy subjects. Moreover, at the streamline level, the diffusion profile along with those tracts combines both the geometric and diffusion properties of a connection.
Table 3 shows the top nine pairs of tumor-related ROIs Zhang et al. (2018) with high probability of GBM tumorigenesis. The regions around the left hippocampus have the highest probability. Since few patients have the DTI data before being diagnosed as GBM, we randomly selected 40 HCP subjects to conduct a simulation to assess how well our (TS)2WM pipeline can detect the changes of brain connectomes. Due to inherently heterogeneous appearance, location, shape, and size of GBM, it is difficult to strictly simulate all appearances and shapes of GBM. To maintain the robust analysis, the area of simulated tumor was dilated 18 pixels to assess the impact of the extent of damages. As shown in Figs. 5,6, 7, our (TS)2WM pipeline may be able to robustly distinguish the change of brain connectomes.
We investigate the sensitivity of our coarse brain parcellation based on Freesurfer in our pipeline. We conducted a simulation study that simulates tumors with different sizes and locations on 40 randomly selected HCP subjects. The simulated tumors were introduced by randomly distorting the intensities in a randomly selected region with different sizes in the T1-weighted image for each subject. Several example brains are shown in Figure S1 of the supplementary material. The mean dice score between the parcellation of brain using the original HCP brains and their corresponding tumoral brains is 0.89 ± 0.01, which indicates a high similarity between their corresponding brain parcellations. In this study, we focus on segmenting GBM tumors and quantifying the impact of tumors on the connectivity pattern of WM bundles, so only a coarse brain parcellation for each individual is needed in our pipeline Zhang et al. (2018). Our nodes are those relatively large cortex surface regions so that they should be robustly to GBM tumors with relatively small and moderate sizes. In addition, we agree that it is notoriously difficult to accurately register brains with large GBM tumors, which would have large impact on WM bundles, leading to big signal-to-noise ratio. Therefore, our pipeline is sensitive enough to capture such large impacts.
DTI has major limitations in characterizing complex tissue microarchitecture. Advanced diffusion imaging sequences, including diffusion kurtosis imaging (DKI) and diffusion spectrum imaging (DSI), have been developed to overcome the limitation of DTI Duc et al. (2018). DKI, which is an extension of DTI, can be used to assess microstructure properties of tissue Van Cauter et al. (2012). DKI has been widely used in distinguishing the pathologic grading of glioma for selecting an appropriate treatment and improving patient prognosis Falk Delgado et al. (2018); Raja et al. (2016); Van Cauter et al. (2012). As compared with DTI, DKI can more accurately quantify diffusion limits. Besides, DSI has the capacity to resolve crossing fibers and to accurately reconstruct confluence of pathways. However, due to high demands in scanner performance and in-scanner subject time, the clinical applicability of DKI and DSI remains very limited. Moreover, it has been demonstrated that combining high angular resolution diffusion imaging (HARDI) and Q-ball imaging (used in our pipeline) can improve the resolution of tractography in regions with crossing fiber populations. We will extend our work to DKI in a future study and combine the DKI into assessing the WM integrity of glioma.
There are some limitations to be addressed in our future work. It is time-consuming for PSC method to construct whole brain structural connectomes. The reconstruction of tracts by using our PSC method is affected by edema and infiltration. Once tumors wholly disrupt the tracts, the diffusion parameters change. This will inevitably lead to missing the regions. Moreover, disrupted tracts make it challenging in presurgical planning. A possible solution is to develop a robust method that can track through edema and reconstruct partial tracts. Moreover, validating the impact of different MRI parameters on the performance of tumor segmentation is also an important topic for our future research.
5. Conclusion
In this paper, we proposed a comprehensive pipeline to analyze the effects of tumors on WM integrity and its association with clinical variables of interest via tumor segmentation and tract statistics. Our proposed deep learning model can effectively segment the GBM tumors with competitive accuracy. Our (TS)2WM pipeline is more stable in tumor based tractographic reconstructions as compared to two widely used DTI post-processing techniques. Our statistical analysis method depicts the local and global variability in diffusion properties along the tracts, as well as the changes of diffusion features and connection structures between the GBM patients and the healthy subjects. Our framework will be further extended to develop a robust method to track trough edema and reconstruct partial tracts.
Supplementary Material
Acknowledgments
This work was finished when Drs. Zhong, Shu, Li, and Zhu worked at MD Anderson Cancer Center. This work was partially supported by the startup funds from University of North Carolina at Chapel Hill. The research of Dr. Zhu was supported by NIH grants MH116527 and MH086633.
Footnotes
Ethics approval and consent to participate
The institutional review board approved this work, the need for informed patient consent for inclusion was waived.
Supplementary material
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.neuroimage.2020.117368
References
- Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, Devin M, Ghemawat S, Irving G, Isard M, et al. , 2016. Tensorflow: a system for large-scale machine learning In: OSDI, Vol. 16, pp. 265–283. [Google Scholar]
- Alexander AL, Lee JE, Lazar M, Boudos R, DuBray MB, Oakes TR, Miller JN, Lu J, Jeong E-K, McMahon WM, et al. , 2007. Diffusion tensor imaging of the corpus callosum in autism. Neuroimage 34 (1), 61–73. [DOI] [PubMed] [Google Scholar]
- Badrinarayanan V, Kendall A, Cipolla R, 2015. Segnet: a deep convolutional encoder-decoder architecture for image segmentation. arXiv preprint arXiv:1511.00561. [DOI] [PubMed] [Google Scholar]
- Bakas S, Akbari H, Sotiras A, Bilello M, Rozycki M, Kirby JS, Freymann JB, Farahani K, Davatzikos C, 2017. Advancing the cancer genome atlas glioma MRI collections with expert segmentation labels and radiomic features. Sci Data 4,170117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakas S, Reyes M, Jakab A, Bauer S, Rempfler M, Crimi A, Shinohara RT, Berger C, Ha SM, Rozycki M, et al. , 2018. Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge. arXiv preprint arXiv:1811.02629. [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D, 1994. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance, Series B 103 (3), 247–254. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D, 1994. Mr diffusion tensor spectroscopy and imaging. Biophys. J 66 (1), 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A, 2000. In vivo fiber tractography using DT-MRI data. Magn Reson Med 44 (4), 625–632. [DOI] [PubMed] [Google Scholar]
- Bottou L, 2010. Large-scale Machine Learning with Stochastic Gradient Descent In: Proceedings of COMPSTAT’2010. Springer, pp. 177–186. [Google Scholar]
- Brunberg JA, Chenevert TL, McKeever PE, Ross DA, Junck LR, Muraszko KM, Dauser R, Pipe JG, Betley AT, 1995. In vivo MR determination of water diffusion coefficients and diffusion anisotropy: correlation with structural alteration in gliomas of the cerebral hemispheres. American Journal of Neuroradiology 16 (2), 361–371. [PMC free article] [PubMed] [Google Scholar]
- Chollet F, et al. , 2015. Keras, https://github.comAeras-team/keras.
- Conturo TE, Williams DL, Smith CD, Gultepe E, Akbudak E, Minshew NJ, 2008. Neuronal fiber pathway abnormalities in autism: an initial MRI diffusion tensor tracking study of hippocampo-fusiform and amygdalo-fusiform pathways. Journal of the International Neuropsychological Society 14 (6), 933–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deighton RF, McGregor R, Kemp J, McCulloch J, Whittle IR, 2010. Glioma pathophysiology: insights emerging from proteomics. Brain Pathology 20 (4), 691–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, et al. , 2006. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31 (3), 968–980. [DOI] [PubMed] [Google Scholar]
- Duc NM, Huy HQ, Bang MTL, Truong LM, Tri VH, Canh BN, Hoa PN, Thong PM, 2018. Clinical applications of diffusion-weighted magnetic resonance imaging. Imaging Med 10 (3), 79–84. [Google Scholar]
- Durante D, Paganin S, Scarpa B, Dunson DB, 2017. Bayesian modelling of networks in complex business intelligence problems. Journal of the Royal Statistical Society 66 (3), 555–580. [Google Scholar]
- Falk Delgado A, Nilsson M, Van Westen D, Falk Delgado A, 2018. Glioma grade discrimination with MR diffusion kurtosis imaging: a meta-analysis of diagnostic accuracy. Radiology 287 (1), 119–127. [DOI] [PubMed] [Google Scholar]
- Girard G, Whittingstall K, Deriche R, Descoteaux M, 2014. Towards quantitative connectivity analysis: reducing tractography biases. Neuroimage 98, 266–278. [DOI] [PubMed] [Google Scholar]
- He K, Zhang X, Ren S, Sun J, 2015. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification In: Proceedings of the IEEE international conference on computer vision, pp. 1026–1034. [Google Scholar]
- Holland EC, 2001. Progenitor cells and glioma formation. Curr. Opin. Neurol 14 (6), 683–688. [DOI] [PubMed] [Google Scholar]
- Huang C, Thompson P, Wang Y, Yu Y, Zhang J, Kong D, Colen RR, Knick-meyer RC, Zhu H, Initiative ADN, et al. , 2017. Fgwas: functional genome wide association analysis. Neuroimage 159,107–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang G, Liu Z, Van Der Maaten L, Weinberger KQ, 2017. Densely connected convolutional networks In: CVPR, Vol. 1, p. 3. [Google Scholar]
- Isensee F, Kickingereder P, Wick W, Bendszus M, Maier-Hein KH, 2017. Brain tumor segmentation and radiomics survival prediction: Contribution to the BRATS 2017 challenge In: International MICCAI Brainlesion Workshop. Springer, pp. 287–297. [Google Scholar]
- Islam M, Ren H, 2017. Multi-modal pixelnet for brain tumor segmentation In: International MICCAI Brainlesion Workshop. Springer, pp. 298–308. [Google Scholar]
- Jégou S, Drozdzal M, Vazquez D, Romero A, Bengio Y, 2017. The one hundred layers tiramisu: Fully convolutional s for semantic segmentation. In: Computer Vision and Pattern Recognition Workshops (CVPRW), 2017 IEEE Conference on IEEE, pp. 1175–1183. [Google Scholar]
- Jellison BJ, Field AS, Medow J, Lazar M, Salamat MS, Alexander AL, 2004. Diffusion tensor imaging of cerebral white matter: a pictorial review of physics, fiber tract anatomy, and tumor imaging patterns. American Journal of Neuroradiology 25 (3), 356–369. [PMC free article] [PubMed] [Google Scholar]
- Jesson A, Arbel T, 2017. Brain tumor segmentation using a 3d FCN with multi-scale loss In: International MICCAI Brainlesion Workshop. Springer, pp. 392–402. [Google Scholar]
- Jin Y, Huang C, Daianu M, Zhan L, Dennis EL, Reid RI, Jack CR, Zhu H, Thompson PM, Initiative ADN, 2017. 3 D tract-specific local and global analysis of white matter integrity in a lzheimer’s disease. Hum. Brain Mapp 38 (3), 1191–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamnitsas K, Bai W, Ferrante E, McDonagh S, Sinclair M, Pawlowski N, Rajchl M, Lee M, Kainz B, Rueckert D, et al. , 2017. Ensembles of multiple models and architectures for robust brain tumour segmentation In: International MICCAI Brainlesion Workshop. Springer, pp. 450–462. [Google Scholar]
- Krähenbühl P, Koltun V, 2011. Efficient inference in fully connected crfs with gaussian edge potentials In: Advances in neural information processing systems, pp. 109–117. [Google Scholar]
- Masjoodi S, Hashemi H, Oghabian MA, Sharifi G, 2018. Differentiation of edematous, tumoral and normal areas of brain using diffusion tensor and neurite orientation dispersion and density imaging. Journal of biomedical physics & engineering 8 (3), 251. [PMC free article] [PubMed] [Google Scholar]
- Menze BH, Jakab A, Bauer S, Kalpathy-Cramer J, Farahani K, Kirby J, Burren Y, Porz N, Slotboom J, Wiest R, et al. , 2015. The multimodal brain tumor image Segmentation benchmark (BRATS). IEEE Trans. Med. Imaging 34 (10), 1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menze BH, Jakab A, Bauer S, Kalpathy-Cramer J, Farahani K, Kirby J, Burren Y, Porz N, Slotboom J, Wiest R, et al. , 2015. The multimodal brain tumor image Segmentation benchmark (BRATS). IEEE Trans. Med. Imaging 34 (10), 1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mormina E, Longo M, Arrigo A, Alafaci C, Tomasello F, Calamuneri A, Marino S, Gaeta M, Vinci SL, Granata F, 2015. Mri tractography of corticospinal tract and arcuate fasciculus in high-grade gliomas performed by constrained spherical deconvolution: qualitative and quantitative analysis. American Journal of Neuroradiology 36 (10), 1853–1858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair V, Hinton GE, 2010. Rectified linear units improve restricted boltzmann machines. In: Proceedings of the 27th international conference on machine learning (ICML-10), pp. 807–814. [Google Scholar]
- Ohgaki H, Kleihues P, 2005. Population-based studies on incidence, survival rates, and genetic alterations in astrocytic and oligodendroglial gliomas. Journal of Neuropathology & Experimental Neurology 64 (6), 479–489. [DOI] [PubMed] [Google Scholar]
- Ormond DR, D’Souza S, Thompson JA, 2017. Global and targeted pathway impact of gliomas on white matter integrity based on lobar localization. Cureus 9 (9). [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell LJ, Suter Y, Rigolo L, Kahali P, Zhang F, Norton I, Albi A, Olubiyi O, Meola A, Essayed WI, et al. , 2017. Automated white matter fiber tract identification in patients with brain tumors. Neuroimage: Clinical 13, 138–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raja R, Sinha N, Saini J, Mahadevan A, Rao KN, Swaminathan A, 2016. Assessment of tissue heterogeneity using diffusion tensor and diffusion kurtosis imaging for grading gliomas. Neuroradiology 58 (12), 1217–1231. [DOI] [PubMed] [Google Scholar]
- Raza SM, Lang FF, Aggarwal BB, Fuller GN, Wildrick DM, Sawaya R, 2002. Necrosis and glioblastoma: a friend or a foe? a review and a hypothesis. Neurosurgery 51 (1), 2–13. [DOI] [PubMed] [Google Scholar]
- Roberts TPL, Liu F, Kassner A, Mori S, Guha A, 2005. Fiber density index correlates with reduced fractional anisotropy in white matter of patients with glioblastoma. American Journal of Neuroradiology 26 (9), 2183–2186. [PMC free article] [PubMed] [Google Scholar]
- Ronneberger O, Fischer P, Brox T, 2015. U-net: Convolutional networks for biomedical image segmentation In: International Conference on Medical image computing and computer-assisted intervention. Springer, pp. 234–241. [Google Scholar]
- Rutgers DR, Toulgoat F, Cazejust J, Fillard P, Lasjaunias P, Ducreux D, 2008. White matter abnormalities in mild traumatic brain injury: a diffusion tensor imaging study. American Journal of Neuroradiology 29 (3), 514–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaikh M, Anand G, Acharya G, Amrutkar A, Alex V, Krishnamurthi G, 2017. Brain tumor segmentation using dense fully convolutional neural network In: International MICCAI Brainlesion Workshop. Springer, pp. 309–319. [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, Watkins KE, Ciccarelli O, Cader MZ, Matthews PM, et al. , 2006. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. Neuroimage 31 (4), 1487–1505. [DOI] [PubMed] [Google Scholar]
- Soltaninejad M, Zhang L, Lambrou T, Yang G, Allinson N, Ye X, 2017. Mri brain tumor segmentation and patient survival prediction using random forests and fully convolutional networks In: International MICCAI Brainlesion Workshop. Springer, pp. 204–215. [Google Scholar]
- Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, et al. , 2013. Advances in diffusion MRI acquisition and processing in the human connectome project. Neuroimage 80,125–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuss DT, Gow CA, Hetherington CR, 1992. ”No longer gage”: frontal lobe dysfunction and emotional changes. J. Consult. Clin. Psychol 60 (3), 349. [DOI] [PubMed] [Google Scholar]
- Sudre CH, Li W, Vercauteren T, Ourselin S, Cardoso MJ, 2017. Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations In: Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Springer, pp. 240–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC, 2010. N4ITK: Improved n3 bias correction. IEEE Trans. Med. Imaging 29 (6), 1310–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Cauter S, Veraart J, Sijbers J, Peeters RR, Himmelreich U, De Keyzer F, Van Gool SW, Van Calenbergh F, De Vleeschouwer S, Van Hecke W, et al. , 2012. Gliomas: diffusion kurtosis MR imaging in grading. Radiology 263 (2), 492–501. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens T, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, et al. , 2012. The human connectome project: a data acquisition perspective. Neuroimage 62 (4), 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G, Li W, Ourselin S, Vercauteren T, 2017. Automatic brain tumor segmentation using cascaded anisotropic convolutional neural networks In: International MICCAI Brainlesion Workshop. Springer, pp. 178–190. [Google Scholar]
- Yu F, Koltun V, 2015. Multi-scale context aggregation by dilated convolutions. arXiv preprint arXiv:1511.07122. [Google Scholar]
- Zhang K, Yu C, Zhang Y, Wu X, Zhu C, Chan P, Li K, 2011. Voxel-based analysis of diffusion tensor indices in the brain in patients with parkinson’s disease. Eur. J. Radiol 77 (2), 269–273. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Allen GI, Zhu H, Dunson D, 2019. Tensor network factorizations: relationships between brain structural connectomes and traits. Neuroimage 197, 330–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Descoteaux M, Zhang J, Girard G, Chamberland M, Dunson D, Srivastava A, Zhu H, 2018. Mapping population-based structural connectomes. Neuroimage 172, 130–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X, Wu Y, Song G, Li Z, Zhang Y, Fan Y, 2018. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation. Med. Image Anal 43, 98–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu H, Kong L, Li R, Styner M, Gerig G, Lin W, Gilmore JH, 2011. Fadtts: functional analysis of diffusion tensor tract statistics. Neuroimage 56 (3), 1412–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu H, Styner M, Li Y, Kong L, Shi Y, Lin W, Coe C, Gilmore JH, 2010. Multivariate varying coefficient models for DTI tract statistics. In: International Conference on Medical Image Computing and Computer-Assisted Intervention Springer, pp. 690–697. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


