De novo post-SELEX optimization of a G-quadruplex DNA aptamer binding to marine toxin gonyautoxin 1/4

Graphical abstract

Abstract

Ligand-binding aptamers obtained by SELEX (Systematic Evolution of Ligands by EXponential enrichment) often have low affinity or/and specificity, and post-SELEX optimization is usually needed. Due to experimental difficulty in determining three-dimensional (3D) structures of aptamer-ligand complexes, there are few structure-guided methods for rational post-SELEX optimization. Here, we employed a de novo optimization approach to engineer high-affinity variants for a G-quadruplex (GQ) aptamer (GO18-T-d) that specifically binds to marine toxin gonyautoxin 1/4 (GTX1/4). First, temperature-dependent modeling was carried out to predict the atomic structure of GO18-T-d. Then, to identify key bases for the optimization, spontaneous binding simulations were performed to reveal the complex structure of GO18-T-d with GTX1/4. Finally, binding energy analysis was conducted to evaluate the designed variants for high affinity. We predicted that GO18-T-d has the typical parallel GQ topology, consistent with circular dichroism (CD) measurements. Our simulations showed that the 5′-end of GO18-T-d hinders the GTX1/4 movement toward the binding pocket, leading to a designed variant that removes the first 5 nucleotides at the 5′-end. Microscale thermophoresis (MST) experiments verified that the binding affinity of the engineered aptamer increases by ~20 folds. Thus, this study not only provides a high-affinity variant of GO18-T-d, but also suggests that our computational approach is useful for the structure-guided optimization of GQ aptamers.

1. Introduction

Aptamers are single-stranded DNA or RNA obtained by in vitro Systematic Evolution of Ligands by EXponential enrichment (SELEX) that can bind to target molecules [1], [2]. Of them, G-quadruplexes (GQs) are particular aptamers with four-stranded helical structures formed by consecutively stacked guanine tetrad (G-tetrad). In recent years, GQs have aroused tremendous curiosity because they play vital roles in regulating various biological processes [3], [4], [5], [6]. Besides, GQs have excellent thermostabilities and abilities to specifically recognize different molecules, organelles and even whole cells, and thus are promising candidates as biosensors [7], [8], [9], [10], [11].

Gonyautoxin 1/4 (GTX1/4) is a notorious marine neurotoxin that associates with paralytic shellfish poisoning (PSP) events around the world [12]. At present, preventive detecting is the first way to deal with this top-level biological hazard, because there is no effective treatment. Although several detection methods have been developed, the low sensitivity and high cost make them difficult to be applied [13], [14]. GO18-T-d, obtained using SELEX by Gao et al., is the only molecule that specifically recognizes GTX1/4 with binding affinity (K_d) in the range of nanomoles [15]. The sequence of GO18-T-d (5′-AACCTTTGGTCGGGCAAGGTAGGTT-3′) possesses the basic features of GQs, indicating that it is a GQ aptamer. As known, to develop an aptamer as a detection kit, high binding affinity for its target ligand is crucial. However, binding affinities of GQ aptamers obtained by the conventional SELEX are not always strong enough for detecting ultra-trace ligands. This is also the main obstacle to apply GO18-T-d to on-site detection. Hence, rational post-SELEX optimizations are necessary for improving the binding affinity of such a suboptimal GQ aptamer.

In general, structure-guided rational optimization is a very promising approach to improve the GQs’ binding affinity [16]. However, due to the structural flexibility of the DNA aptamers, it remains challenging to determine the three-dimensional (3D) structures of aptamer-ligand complexes by X-ray crystallography or nuclear magnetic resonance (NMR) [17]. With the rapid development of computational technology, it is possible to predict the structures of GQs in silico [18]. Unfortunately, most of the reported prediction methods focused on the two-dimensional (2D) structures, seldom on the 3D atomic structures [19]. The difficulty in the 3D structure prediction may lie in the fact that each GQ aptamer contains ten possible folded topological types (i.e., Q1 to Q5 and Q14 to Q18, as shown in Supplementary Fig. S1). So, it is very difficult to determine the native structure of the aptamer from all these possible topological types. Also, the 3D structure of the aptamer monomer usually gives little information about the binding site of the ligand; meanwhile, the monomer structure may also change when the ligand associates with the aptamer. Thus, to obtain structural information for the post-SELEX optimization, both the monomer structure of GO18-T-d and the complex structure of GO18-T-d:GTX1/4 are required to be predicted reliably.

In the past, several studies have optimized and designed non-GQ aptamers via simulating the interactions with their ligands [20], [21], [22], [23]. A critical step for these studies was to predict the 3D atomic structures of the aptamers accurately. The secondary structures of these aptamers are stem-loops, which can be predicted by software such as Mfold [24]. Usually, the binding sites of these aptamers binding to their ligands were obtained by molecular docking. However, the prediction methods in these studies could not be directly applied to the prediction and optimization of the GQ aptamers, such as GO18-T-d, due to the entirely different folding topologies of GQs.

Here, we employed a de novo computational approach to engineer aptamer variants of GO18-T-d with higher affinity for GTX1/4. This approach consists of three steps: first, temperature-dependent molecular dynamics (TdMD) simulations were used to predict the 3D structure of GO18-T-d directly from its sequence; second, spontaneous binding simulations were performed to reveal the stable complex structure of GO18-T-d:GTX1/4; third, binding energy landscapes [25] were constructed to identify the aptamer variants optimal for the GTX1/4 binding. By this approach, a truncated variant of GO18-T-d was engineered; and microscale thermophoresis (MST) [26] experiments verified that the binding affinity of this new aptamer increases by ~ 20 folds.

2. Materials and methods

2.1. 3D structure prediction of GQ aptamer

As illustrated in Supplementary Fig. S2, we predict the 3D structure of the GQ aptamer directly from its nucleotide sequence by a general pipeline. This prediction pipeline consists of three steps:

Step 1: Building all possible 3D models of GQ-cores. We first predicted the composition and distribution of QGRS (Quadruplex forming G-Rich Sequences) in the aptamer nucleotide sequence by submitting the sequence to the QGRS Mapper web server (http://bioinformatics.ramapo.edu/QGRS/analyze.php) [27]. The QGRS results were then sorted by the likelihood to form a stable GQ. As shown in Supplementary Fig. S1, for a monomeric GQ, there are 9 types of GQ-core topology except for the theoretical one Q18, according to the relative orientations of the guanine tracts. Then, all possible GQ-core structures with the highest QGRS G-score were predicted by the G-Quadruplex module of the 3D-Nus web server (https://www.iith.ac.in/3dnus/Quadruplex.html) [28]. Based on the output GQ-core models, the full-length 3D structures of the GQ aptamer were constructed by extending its non-GQ-core segments (i.e., 5′-end and 3′-end), according to its nucleotide sequence using the AutoPSF VMD plugin [29]. Since the G-tetrad center of a GQ aptamer contains cations, to be general, commonly used K⁺ ion was placed in the center of each GQ-core at this stage [30]. Finally, energy minimization of 5,000 iterations was carried out to remove possible geometric deficiencies using the program NAMD (Ver. 2.10) [31] and the CHARMM force fields [32].

Step 2: Performing temperature-dependent MD simulations for the full-length models. Because GQs possess excellent thermostability, in all possible models, it is reasonable to consider that the full-length model with the highest thermostability is the native one. So, we identified the most stable model that endures higher temperatures than the others by two-phase TdMD simulations: constant-temperature and heating simulations. In the constant-temperature phase, the GQ system was simulated at 293 K for 10 ns; subsequently, in the heating phase the system was simulated for another 10 ns by increasing temperature at the speed of 40 K·ns⁻¹. All the simulations were performed using GROMACS (Ver. 5.1.4) [33] with explicit solvent (see more details in Subsect. 2.2).

Step 3: Identifying the native structure of the aptamer. To assess the thermostability of the full-length candidate models of the aptamer, we analyzed their MD trajectories by calculating RMSDs (root mean square deviations) with the simulation time. Because the stacking of G-tetrads is essential for the GQ formation and its stability [30], the RMSD calculations merely considered the guanine atoms of the G-tetrads. Then, the model with the smallest RMSDs was considered as the native structure of the monomeric aptamer.

Please see more details in Supplementary User Manual for the 3D structure prediction.

2.2. Temperature-dependent MD (TdMD) simulation

We employed GROMACS (Ver. 5.1.4) [33] to perform the TdMD simulations with the AMBER99bsc1 force fields [34] and the SPC water model. In each simulation system, the candidate model of the aptamer was placed in the center of a water box, with distances from its surface to the boundaries >15 Å. K⁺ and Cl^- ions were randomly placed by replacing the water molecules for neutralizing the system and mimicking an ionic concentration of 150 mM. Periodical boundary conditions were used. The electrostatic interactions were calculated with the Particle-Mesh-Ewald (PME) method [35]. A cut-off distance of 14 Å was used for electrostatic and van der Waals forces. The LINCS algorithm was employed to constrain all bonds in the system, and a time step of 2.0 fs was used [36]. The pressure was maintained at 1 atm by the Berendsen method, and the temperature at 293 K by the velocity rescaling method [37], [38]. The heating simulations were carried out by the simulated annealing protocols in GROMACS.

2.3. Spontaneous binding simulation of ligand to aptamer

The protocols used in the spontaneous binding simulations were almost the same as those of the above TdMD simulations. And the toxin molecules were prepared by Antechamber with the General Amber Force Field (GAFF) [39], [40]. The topology and coordinate files of these molecules were generated by the LEaP program in AmberTools 17 and converted to GROMACS-compatible files by ACPYPE [41]. For each system, the aptamer was located in the center of the water box, and a toxin molecule was randomly placed 15 Å away from the aptamer. To mimic the experimental conditions in this study, the cation in the center of the GQ-core was changed to Mg²⁺, and the salt concentration of the system was set to 150 mM MgCl₂. Each independent spontaneous binding simulation was performed at 300 K for at least 500 ns.

2.4. Binding free energy calculation

Similar to our previous study [25], we employed the AutoDock semiempirical free energy force field [42] to calculate the binding free energy of the toxin ligand to the aptamer. Many studies in the past decade have confirmed its ability to correctly predict the binding affinities of small molecules to receptors, including our study. The binding free energy includes six pairwise terms (V) and a change of the conformational entropy ($\mathrm{\Delta }{S}_{\mathit{conf}}$) of the ligand:

$$\mathrm{\Delta }G=\left(V_{\mathit{bound}}^{L-L}-V_{\mathit{unbound}}^{L-L}\right)+\left(V_{\mathit{bound}}^{R-R}-V_{\mathit{unbound}}^{R-R}\right)+\left(V_{\mathit{bound}}^{R-L}-V_{\mathit{unbound}}^{R-L}+\mathrm{\Delta }{S}_{\mathit{conf}}\right)$$ (1)

In our case, the GQ aptamer is the receptor ($R$), and the marine toxin is the ligand ($L$). In the equation, the terms in the first and second brackets are the change in intramolecular energies for the bound and unbound states of the ligand and the aptamer, respectively; and the terms in the third bracket is the change in the intermolecular energy between the ligand and the aptamer. Each term was calculated as in our previous study [25]; and Python programs in AutoDockTools [42] were used to calculate the parameters of the aptamers, toxins and ions according to standard procedures.

2.5. Construction of binding energy landscape of ligand to the aptamer

As in our previous study [25], to display the binding free energies for an aptamer-ligand complex system, we considered the aptamer as a sphere, and defined the MD positions of the ligand by using the geographical coordinate system. The cation in the GQ-core center was set as the origin; the X- and Y-axes were the lines connecting the origin to P atoms of G19 and G14 (GO18-T-d) or G14 and G9 (tGO18-T-d), respectively; the Z-axis was determined by forming a right-hand system, as shown in Supplementary Fig. S11. The positions of the ligand were defined by longitude and latitude, respectively. Following that, the 3D sphere of the aptamer was transformed into a 2D flat map by equal angle projection. Longitude and latitude were converted to the X- and Y-axis of the 2D flat map, respectively. Then, this map was divided into 7,200 grids; for each grid, the size is 3 × 3 square degrees; and the energy in a grid is the exponential average of the binding energies found in this grid in the simulations. The discrete binding free energies of the aptamer with the ligand were smoothed by thin-plate splines, as contours projected onto the 2D flat map [43]. All the smooth energy landscapes were constructed using the FIELDS and PLOT3D packages in R (Ver. 3.5.1) [44], [45], [46].

2.6. Circular dichroism (CD)

Aptamer samples with concentrations of 20 μM were prepared in Tris-HCl buffer (20 mM, pH 7.4), supplemented with 150 mM MgCl₂ if not stated otherwise. The aptamers were dissolved directly in the buffer with ions, heated at 95 °C for 10 min, then quenched in an ice bath for 5 min, and finally allowed to stand at room temperature for 5 min before circular dichroism (CD) experiments. CD spectra were recorded using a Chirascan spectrometer (Applied Photophysics, Ltd.) with 0.1 cm path length quartz cuvettes at 25℃. Scanning from 200 to 360 nm was performed with a scan speed of 120 nm/min. Each spectrum is an average of 3 scans. Data were buffer subtracted and normalized to provide molar ellipticity values.

2.7. Microscale thermophoresis (MST)

MST experiments to detect the binding affinity between GTX1/4 and aptamers were performed on a Monolith NT.115 system (NanoTemper Technologies, Germany) using 10% LED- and 40% IR-laser power. The times of the laser on and off were set at 30 s and 5 s, respectively. A twofold dilution series for unlabelled ligand GTX1/4 were prepared. Equal volumes of 6-FAM labeled aptamers at the 3′-end (400 nM) were added, resulting in GTX1/4 concentrations ranging from 0.12 to 4000 nM with a constant aptamer concentration of 200 nM in the binding buffer (20 mM Tris-HCl, pH 7.4, 150 mM MgCl₂ supplemented with 0.05% Tween-20). Aptamers were treated in the same way as described in CD experiments to form the GQ topology and detected at 25 °C. Experiments were performed at least three times, and the data were imported into the MO.Affinity Analysis Software to calculate the K_d value of the ligand binding to the aptamer.

2.8. Materials and reagents

All DNA aptamers were purchased from Sangon Biotech Co., Ltd. (Shanghai, China). The sequences of the aptamers are listed in Supplementary Table S2. GTX1/4 was purchased from National Research Council Canada. Tris, NaCl, MgCl₂, KCl, LiCl and Tween-20 were purchased from Sangon Biotech Co., Ltd. (Shanghai, China). NaOH and HCl were purchased from Sinopharm Chemical Reagent Co., Ltd (Shanghai, China). All chemical reagents were of analytical grade and used without further purification.

3. Results

3.1. Structure prediction of GO18-T-d

To validate the prediction pipeline in Supplementary Fig. S2, we tested the pipeline by predicting the 3D structures of five GQ aptamers with known 3D structures in the Protein Data Bank (PDB). As shown in Supplementary Fig. S3, the predicted GQ-core topology types of these aptamers are consistent with their native types, and the RMSDs of the predicted structures with respect to corresponding experimental structures are in the range of 1.3 to 4.0 Å (Supplementary Table S1). These RMSD values indicate that the pipeline could predict the structure of a GQ aptamer with accuracy enough for the MD investigations in this study, and thus provides a solid basis for the following GO18-T-d structure prediction.

To build the GQ-core models of GO18-T-d, we first identified the composition bases of the G-tetrads by the QGRS prediction. The result showed that GO18-T-d has two possible QGRS sequences with G-scores of 19 and 20, respectively. Since the QGRS with a higher score is more likely to form a stable GQ, we used the QGRS with the score of 20 to build possible GQ-core models for GO18-T-d. Then, by extending the non-GQ-core segments (i.e., 5′-end: AACCTTT; and 3′-end: TT) in the sequence, we obtained 9 candidate full-length models named Q1 to Q5 and Q14 to Q17.

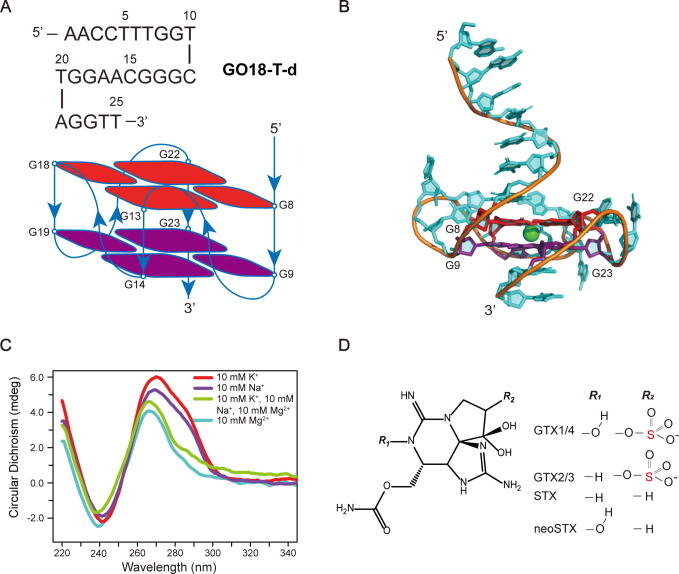
To identify the native model from the 9 possible models of GO18-T-d, we performed TdMD simulations for each model. In the constant-temperature simulation phase, the RMSDs of Q5, Q14, Q15 and Q16 were found to fluctuate dramatically (Supplementary Fig. S4A). These drastic fluctuations indicate that these four models are not stable structures of GO18-T-d; indeed, their GQ-cores were found to be broken at about 10 ns (Supplementary Fig. S5). So, these four models were excluded in this phase. In the heating simulation phase, we found that the RMSD fluctuations of Q3 with a parallel topology are the smallest with increasing temperatures (Supplementary Fig. S4B). Moreover, among the remaining models, Q3 is the only one to stably maintain the conformation in the simulation timescale (Supplementary Fig. S6). Thus, we employed the Q3 conformation at the end of the constant-temperature phase as the model of the native structure of GO18-T-d (Fig. 1A, B).

Fig. 1.

Structure prediction and CD experiments for DNA aptamer GO18-T-d. (A) The sequence and GQ-core pattern of GO18-T-d. (B) Full-length 3D model of GO18-T-d. (C) CD spectra of GO18-T-d in the presence of different cations. Aptamers were annealed directly in the buffers (20 mM Tris-HCl, pH 7.4) with ions. (D) Chemical structures of GTX1/4, GTX2/3, STX and neoSTX.

To experimentally verify the built model of GO18-T-d, we performed CD experiments to examine its GQ-core topology. As shown in Fig. 1C, GO18-T-d has a negative band at 240 nm and a positive band around 265 nm, in agreement with the reported CD spectrum of typical parallel GQ structure [47]. Besides, in order to investigate the folding topology of GO18-T-d in different ionic conditions, we also carried out CD experiments using buffers with different cations. We found that the absorption bands in these buffer conditions are quite similar, suggesting that the ionic types have no significant effect on the GO18-T-d conformation, including Li⁺, which was ever reported to destabilize the RNA GQ (Supplementary Fig. S7) [48]. Taken together, we successfully predicted the 3D atomic structure of GO18-T-d directly with its nucleotide sequence.

3.2. Spontaneous association of GTX1/4 with GO18-T-d

To obtain the stable complex structure of GTX1/4 binding to GO18-T-d, we performed spontaneous binding simulations to investigate the association of GTX1/4 with GO18-T-d. At the same time, to further validate the spontaneous binding simulations, we also simulated the association processes of three GTX1/4 analogues with GO18-T-d. They are gonyautoxin 2/3 (GTX2/3), saxitoxin (STX) and neosaxitoxin (neoSTX). These three analogues have similar chemical structures to GTX1/4 (Fig. 1D), but different toxicity (35). As described in Materials and methods, we performed multiple independent simulations for each GO18-T-d:toxin system for at least 500 ns. The simulation results show that GTX1/4 and GTX2/3 could spontaneously associate with GO18-T-d to form stable conformations. However, STX and neoSTX were found to contact GO18-T-d transiently, but could not form stable complexes with GO18-T-d. These indicate that only GTX1/4 and GTX2/3 could stably associate with GO18-T-d in the simulations.

To further understand the binding ability of GO18-T-d to GTX1/4 and its analogues, we calculated the average binding free energies of each GO18-T-d:toxin complex in its typical simulated trajectories. The binding energies with the simulation time show that 700–900 ns is the period for the toxins in the stably bound state (Supplementary Fig. S8), so we choose this period to calculate the average binding energies. Results show that the average binding energies of GO18-T-d with GTX1/4, GTX2/3, STX and neoSTX are −10.07, −4.43, −2.86 and −3.43 kcal·mol⁻¹, respectively. As seen, the average binding energy of GO18-T-d with GTX1/4 is much lower than that of GO18-T-d with other toxins. And the free energy landscape analyses also show that except for GTX1/4, there is no deep energy well (binding energy ≤ -8.0 kcal·mol⁻¹) for the other 3 toxins (Supplementary Fig. S12). This indicates that GO18-T-d could stably bind to GTX1/4, and thus is a specific aptamer of GTX1/4.

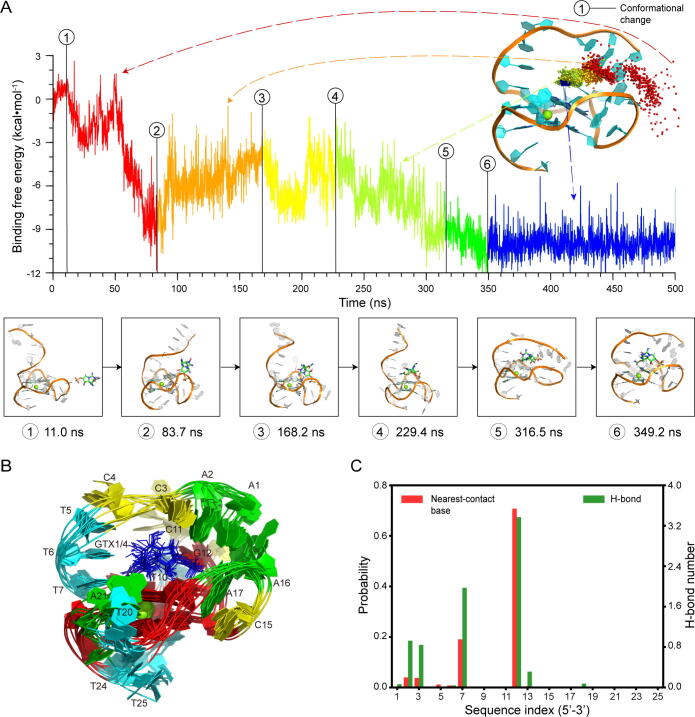
To reveal the key molecular interactions for the specific binding of GTX1/4, we examined the typical spontaneous binding process of GTX1/4 with GO18-T-d (Fig. 2A and Supplementary Movie S1). The distance between the center of mass of GTX1/4 and the Mg²⁺ in the center of GQ-core and the gyration radius (Rg) of the GO18-T-d:GTX1/4 system can visually represent the association process, as shown in Supplementary Fig. S9, S10A. The association process could be summarized as follows: GTX1/4 first starts from a random position far away from GO18-T-d, then diffuses to the right of A16 of the aptamer, and moves to the 5′-end of GO18-T-d. Next, GTX1/4 adjusts its conformations along the 5′-end, then stretches across the G-tetrad consisting of G8, G13, G18 and G22, and is bound to the G-tetrad. When GTX1/4 is stably located on the G-tetrad, the 5′-end continues to adjust its conformations by the interplay with GTX1/4, and finally stabilizes itself via the π-π stacking by bases A1 and A16. We found that in the binding process, there is not any π-π stacking between GTX1/4 and GO18-T-d. Thus, the main driving forces of the GTX1/4 binding to GO18-T-d are the van der Waals (vdW) forces and the hydrogen bonds (H-bonds).

Fig. 2.

Spontaneous association of GTX1/4 with GO18-T-d and the complex structure of GO18-T-d:GTX1/4. (A) Time-dependent binding free energies of the GO18-T-d:GTX1/4 complex, and corresponding positions of the center of mass of GTX1/4 (spheres in rainbow colors) on the GO18-T-d. Six representative conformational changes are given in the panels below. Corresponding movie showing the spontaneous association process is presented in Supplementary Movie S1. (B) Ten superimposed structures (A: green, T: cyan, C: yellow, G: red and GTX1/4: blue). (C) Residue-based interactions: (red) the probabilities of aptamer bases as the nearest-contact base of GTX1/4; (green) the average H-bond numbers between GTX1/4 and the bases. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

To obtain the dominant conformation of the GO18-T-d:GTX1/4 complex, we extracted the ten complex conformations with the lowest energies in the simulations and then superimposed them, as illustrated in Fig. 2B. The MD complex structure with the lowest binding energy appears at the simulation time of 349.2 ns, and the average RMSD value of other nine complexes with respect to this structure is 2.67 Å. The high similarity of these ten lowest-energy structures indicates that the lowest-energy conformation is the dominant conformation of the GO18-T-d:GTX1/4 complex. The distance relationship between the nucleotides of GO18-T-d in the complex is shown in the contact map (Supplementary Fig. S10B). Therefore, this complex structure was considered as the native structure of the GO18-T-d:GTX1/4 complex.

To determine the binding regions and sites of GTX1/4 to GO18-T-d, we examined the binding pocket of the GO18-T-d:GTX1/4 complex. We found that the binding pocket resembles a combination of a platform and an arch-like structure. The platform is the G-tetrad consisting of G8, G13, G18 and G22, and the arch-like structure is the 5′-end of GO18-T-d. So the 5′-end is stabilized by the π-π stacking by A1 with A61, and T7 with G22, respectively. Meanwhile, we determined the key binding sites by calculating the average vdW forces and H-bonds for each base to GTX1/4. To characterize the vdW forces, we first calculated all the pairwise distances between the GTX1/4 atoms and those of the GO18-T-d bases for each MD frame in the period of stable binding, then found out the base with the smallest distance, and designated that base as the nearest-contact base. Then, we calculated the probabilities of the GO18-T-d bases as the nearest-contact base of GTX1/4 in the MD simulations. As shown in Fig. 2C, the probabilities of T7 and G12 as the nearest-contact base are 0.19 and 0.71, respectively, and those of A2 and C3 are 0.04; the others are less than 0.02. To characterize the H-bonds, we calculated the average numbers of H-bonds between GTX1/4 and the GO18-T-d bases in the MD simulations (Fig. 2C). As seen, the H-bond numbers formed by GTX1/4 with A2, C3, T7 and G12 are 0.93, 0.84, 1.97 and 3.37, respectively; and the others are less than 0.5. Taken together, our simulations showed that GTX1/4 mainly contacts the GO18-T-d bases A2, C3, T7 and G12, with an importance order: G12 > T7 > A2 ≥ C3. Thus, we used this structural information to guide the following post-SELEX optimization of GO18-T-d.

3.3. Structure-guided optimization of GO18-T-d

As mentioned, in the stable GO18-T-d:GTX1/4 complex, the 5′-end of GO18-T-d was found to form an arch-like structure with A16 and G22 via the π-π stacking interaction. However, the spontaneous binding simulations also show that the 7 nucleotides at the 5′-end are very flexible and able to adopt various transient conformations before forming the stable arch-like structure. And these conformations frequently cover the binding pocket of GO18-T-d and then hamper the entry of GTX1/4 into the binding pocket (Supplementary Movie S1 and Fig. S13). Hence, it is natural to consider that a shorter 5′-end may expose the binding pocket of GO18-T-d for GTX1/4, and thereby enhances the association of GTX1/4 with GO18-T-d.

To optimize GO18-T-d by shortening its 5′-end, we subsequently determined how many bases at the 5′-end could be removed. In the spontaneous binding simulations, among the 7 bases at the 5′-end, the base T7 processes the strongest interactions with GTX1/4. Thus, we decided to retain this base. Meanwhile, to avoid these strong interactions being disrupted or disturbed by the solvent, T6 was also kept for protecting T7. Since C4 and T5 increase the flexibility of the 5′-end, these bases could be removed. Therefore, we engineered a new aptamer by removing the first 5 nucleotides at the 5′-end, and named this truncated variant of GO18-Td as tGO18-T-d.

Next, we also performed spontaneous binding simulations for the GTX1/4 association with tGO18-T-d, with the same methods for GO18-T-d. The 3D structure of tGO18-T-d is also predicted by our prediction pipeline directly from its sequence (5′-TTGGTCGGGCAAGGTAGGTT-3′). To examine whether the shortening of the 5′-end improves the binding affinity for GTX1/4, we employed binding energy landscapes to analyze the association trajectories of GTX1/4 to GO18-T-d and tGO18-T-d, respectively, as in our previous study [25]. Based on the simulation trajectories, the binding energy landscapes of GO18-T-d and tGO18-T-d were constructed, as shown in Fig. 3.

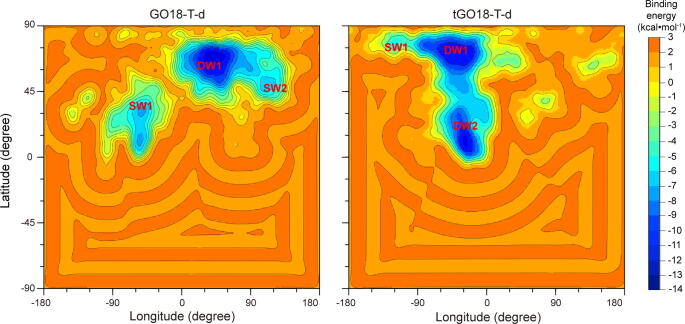
Fig. 3.

The binding energy landscapes of GO18-T-d:GTX1/4 and tGO18-T-d:GTX1/4 complexes.

As seen, the energy landscapes show that the energy basins and valleys (i.e., △G less than 0.0 kcal·mol⁻¹) favorable for the binding are distributed in the upper half. As in our previous study [25], to clarify the binding ability, three energy grades were used according to the local energy minima: deep energy well (DW: binding energy ≤ -8.0 kcal·mol⁻¹), shallow energy well (SW: −8.0 < binding energy ≤ -4.0 kcal·mol⁻¹) and energy barriers (-4.0 < binding energy ≤ 0.0 kcal·mol⁻¹). In this way, only when GTX1/4 enters into the DWs, GTX1/4 was considered to successfully associate with the aptamer.

In the energy landscape of GO18-T-d, there is one DW and two SWs. By contrast, there are two DWs and one SW in that of tGO18-T-d, and the SW occupies few grids (Fig. 3). Importantly, the DWs in the energy landscape of tGO18-T-d occupy about 304 grids, while the DW in that of GO18-T-d occupies166 grids. This indicates that GTX1/4 is more likely to enter into the DWs of tGO18-T-d. So, the binding energy landscape analyses illustrate that the removal of the first 5 nucleotides at the 5′-end could enhance the association of GTX1/4 with the truncated aptamer tGO18-T-d.

To reveal how the truncated variant exposes the binding pocket, we examined the typical binding process of GTX1/4 to tGO18-T-d (Supplementary Fig. S14 and Movie S2). The association process could be summarized as follows: GTX1/4 first starts from a random position far away from tGO18-T-d, then diffuses to the right side of its A11, and then moves on the G-tetrad consisting of G3, G8, G13 and G17. Next, GTX1/4 adjusts its conformations on the G-tetrad, then rotates about 180°in the horizontal direction, and finally reaches a stable state at ~90 ns. Compared with that of GTX1/4 to GO18-T-d, tGO18-T-d:GTX1/4 complex could reach a stable state more quickly. Indeed, the rapid binding of GTX1/4 to tGO18-T-d indicates that the exposure of the binding pocket of GO18-T-d could enhance the spontaneous association of GTX1/4 with tGO18-T-d.

3.4. Experiment verifications

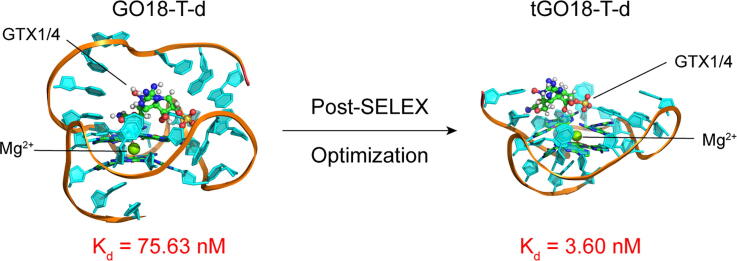
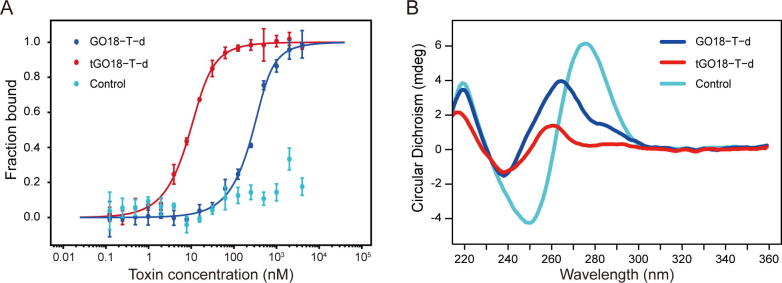
Our computational simulations have predicted that the removal of the first 5 nucleotides (AACCT) from the 5′-end of GO18-T-d might enhance the binding probability of GTX1/4. To verify this computational prediction, we used MST experiments to measure the binding affinities of GTX1/4 to GO18-T-d and tGO18-T-d. Corresponding K_d values of GO18-T-d and tGO18-T-d, determined by the average of 8 independent measurements, were 75.63 nM and 3.60 nM, respectively. Our K_d value of GO18-T-d is greater than that (17.7 nM) by Bio-Layer Interferometry (BLI) [15]; this may be attributed to the difference in the buffers and detection methods. Meanwhile, we also used a 25-nt random, non-GQ sequence as the control aptamer to verify the binding specificity of GO18-T-d and tGO18-T-d for GTX1/4. As expected, the control aptamer shows no binding affinity for GTX1/4 (Fig. 4A). Thus, compared with GO18-T-d, the binding affinity of tGO18-T-d to GTX1/4 is increased by ~20 folds. This strongly supports our prediction that to expose the binding site by removing certain flexible segments in the vicinity of the pocket is an effective strategy for optimization.

Fig. 4.

MST and CD experiments for aptamers. (A) MST experiments for GO18-T-d (blue), tGO18-T-d (red), and Control (random sequence, cyan). The K_d values of GO18-T-d and tGO18-T-d are 75.63 ± 25.33 and 3.60 ± 0.67 nM, respectively. The control aptamer shows no binding affinity for GTX1/4. (B) CD spectra of three aptamers. And the concentration for each aptamer is 20 μM. The buffer is 20 mM Tris-HCl (pH 7.4) with 150 mM MgCl₂. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Since the GQ conformation is essential for the GTX1/4 binding, the prerequisite for optimizing GO18-T-d is to ensure the integrity of its GQ-core. The GQ-core sequence of GO18-T-d starts at G8 and ends at G23 (5′-AACCTTTGGTCGGGCAAGGTAGGTT-3′). In principle, tGO18-T-d has the same GQ-core structure. So, we used CD experiments to analyze their conformations, with a random, 25-nt sequence as the control. The results showed that GO18-T-d and tGO18-T-d have similar CD spectrum with the same characteristic bands, while the control aptamer displays a very different CD spectrum (Fig. 4B). The binding of GTX1/4 does not change the CD spectra of the two GQ aptamers (Supplementary Fig. S15). In the presence of Li⁺, tGO18-T-d still presents a similar CD spectrum, though tGO18-T-d has a slightly lower melting temperature (Supplementary Fig. S16 and S17). Hence, both GO18-T-d and its variant tGO18-T-d possess the same GQ-core structure.

4. Discussion and conclusion

In this study, we have used a de novo computational approach to optimize the SELEX aptamer GO18-T-d that specifically targets the marine toxin GTX1/4. By this approach, we not only predicted the 3D model of GO18-T-d directly with its nucleotide sequence, but also revealed the complex structure of GO18-T-d:GTX1/4. These provided very useful structural information that enabled the rational design of the high-affinity variants of GO18-T-d. By removing its 5 nucleotides at the 5′-end, we successfully engineered a GO18-T-d variant (tGO18-T-d) with an about 20-fold increase in the binding affinity for GTX1/4. Indeed, our binding energy analyses clearly illustrated that the removal of the 5′-end nucleotides could enhance the association of GTX1/4 with the binding pocket of the aptamer.

As mentioned, although several post-SELEX optimization methods have been reported, including truncation, chemical modification, mutagenesis, and multivalent aptamer construction, rational post-SELEX optimization remains challenging [49], [50]. A major reason for this is the difficulty in accurately identifying aptamer bases or/and segments for the optimization. To overcome this problem, structural information about the key bases and segments for the ligand binding to the aptamer is necessary. Due to the experimental limitations, this information is usually unavailable, especially for a large number of aptamers obtained by the conventional SELEX approach. Indeed, it is usually unfeasible to determine the complex structure for every aptamer and its ligand by the X-ray crystallographic and NMR methods. To compensate for this issue, computational approaches are very helpful.

As we have shown, computational approaches such as the spontaneous binding simulations could reveal the key bases and segments important for affinity optimization. The importance of individual nucleotides of the aptamers can be evaluated according to their H-bond, vdW, π-π stacking, and hydrophobic interactions with the ligand in the simulations. Besides, spontaneous binding simulations also provide atomic-level, dynamic information inaccessible by experimental methods, such as the binding pathways of a ligand to the aptamer (e.g., Supplementary Movies S1 and S2). In fact, the binding pathway of GTX1/4 to GO18-T-d revealed by the simulations led to the engineering hypothesis that the removal of the first 5 nucleotides could expose the binding pocket and enhance the binding of GTX1/4. Also, based on the information about the importance of individual bases, we were able to predict that the binding affinity of tGO18-T-d for GTX1/4 is greater than those of other truncated two variants (i.e., t4_GO18-T-d and t6_GO18-T-d in Supplementary Fig. S18).

In summary, this study has successfully engineered an aptamer variant of GO18-T-d with higher affinity for GTX1/4, and thereby offers a new molecule for the detection-kit development of ultra-trace GTX1/4. Also, our rational design of the high-affinity variant demonstrates that the employed approach is very promising for the structure-guided post-SELEX optimization of GQ DNA aptamers.

CRediT authorship contribution statement

Menghua Song: Investigation, Formal analysis, Visualization, Writing - original draft, Writing - review & editing. Gan Li: Methodology, Formal analysis, Visualization, Writing - original draft, Writing - review & editing. Qi Zhang: Investigation, Visualization, Writing - original draft. Jianping Liu: Supervision, Conceptualization, Writing - original draft. Qiang Huang: Supervision, Conceptualization, Writing - original draft, Writing - review & editing, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: