Biomarker discovery for predicting spontaneous preterm birth from gene expression data by regularized logistic regression

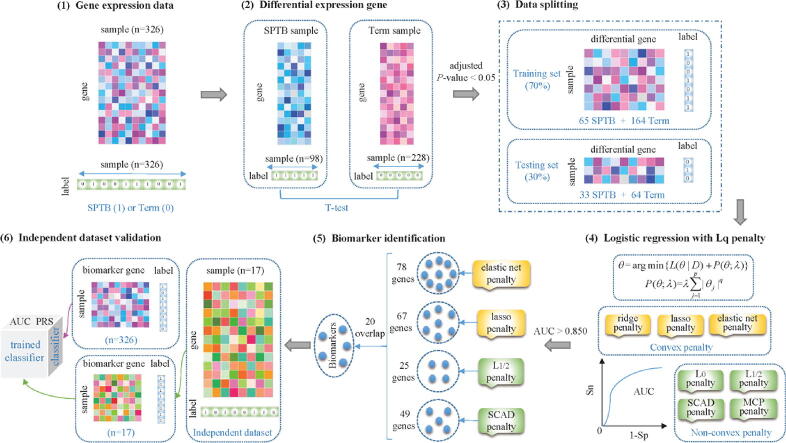
Graphical abstract

Abstract

In this work, we provide a computational method of regularized logistic regression for discovering biomarkers of spontaneous preterm birth (SPTB) from gene expression data. The successful identification of SPTB biomarkers will greatly benefit the interference of infant gestational age for reducing the risks of pregnant women and preemies. In recent years, various approaches have been proposed for the feature selection of identifying the subset of meaningful genes that can achieve accurate classification for disease samples from controls. Here, we comprehensively summarize the regularized logistic regression with seven effective penalties developed for the selection of strongly indicative genes of SPTB from microarray data. We compare their properties and assess their classification performances in multiple datasets. It shows that elastic net, lasso, $L_{1/2}$ and SCAD penalties get the better performance than others and can be successfully used to identify biomarkers of SPTB. Particularly, we make a functional enrichment analysis on these biomarkers and construct a logistic regression classifier based on them. The classifier generates an indicator of preterm risk score (PRS) for predicting SPTB. Based on the trained predictor, we verify the identified biomarkers on an independent dataset. The biomarkers achieve the AUC value of 0.933 in the SPTB classification. The results demonstrate the effectiveness and efficiency of the built-up strategy of biomarker discovery with regularized logistic regression. Obviously, the proposed method of discovering biomarkers for SPTB can be easily extended for other complex diseases.

1. Introduction

Preterm birth (PTB) refers to the birth of a fetus before the completion of 37 weeks of gestation. In accordance with the World Health Organization (WHO) report, about 20 million premature babies are born every year worldwide [1]. PTB is the leading cause of mortality in children under the age of five [2], as well as the main reason of disability, illness and death in newborns. It has become a major challenge in the field of obstetrics and gynecology worldwide [3]. The consequences of PTB persist from early childhood into adolescence and adulthood [4]. The mortality rate accounts for about $0.1\%$ of the number of newborn premature babies [5]. At present, the mechanism of PTB is far from clear although it consumes a lot of medical resources and brings a big burden to family and society [6]. In medicine, approximately one-third of PTB is due to maternal or fetal accident reasons, and the other two-thirds are classified as spontaneous preterm birth (SPTB), which includes spontaneous preterm labor (SPTL) and preterm premature rupture of the membranes (PPROM) [7]. Specifically, SPTL is defined as spontaneous onset of labor $⩽$37 weeks of gestation resulting in preterm delivery. PPROM is defined as spontaneous rupture of membranes at $<$37 weeks without labor [8]. However, there is no effective diagnosis method to detect the SPTB or use intervention approach ahead to prolong the labor process and extend the pregnancy to term. Thus, the discovery of diagnostic biomarkers is of great significance for the early detection of SPTB [9]. A major effect on the associated mortality and morbidity in preemies will be achieved only by accurate identification of women at high-risk of SPTB firstly and then by effective development of interventions to prevent this complication [10], [11].

Discovering biomarkers for SPTB in asymptomatic women remains a great challenge. Accurate and reproducible screening tools are still not available in clinical practice [12]. Fortunately, the high-throughput omics technologies such as microarray and RNA-seq have provided amount of data which are beneficial to discover diagnostic biomarkers [13]. Recently, increasing attention has been paid to the application of microarray for premature diagnosis [14], [15], [16], [17]. The selection of certain indicative genes serving as biomarkers based on gene expression microarray profiling data has been popular in bioinformatics and machine learning [18]. Nevertheless, microarray usually measures a large number of genes with a small number of samples [19]. That is to say, there are a massive amount of predictor genes (i.e., large p) and a small number of clinical samples (i.e., small n). The difficulty of ‘large p small n’ problem brings great challenge in the selection of characteristic genes as biomarkers [20]. From a computational perspective, the main difficulty is underlying the massive number of combinatorial gene sets in the thousands of human genes. We need identify an optimal subset of genes that are associated with SPTB and can be identified as biomarkers. Effective gene selection methods are desirable to classify different phenotypic states of SPTB. The classification accuracy is our objective function of optimization in biomarker discovery [21], [22]. From a statistical perspective, too many variables may lead to multicollinearity [23]. The more variables, the more likely the multicollinearity occurs. It almost definitely occur when the number of genes is much greater than the number of samples [20]. The failure of independence between variables makes the traditional statistical methods numerically unstable and often unrecognizable [24]. How to use the high-throughput data to identify feature genes as biomarkers of classifying phenotypes has become a new investigation topic [25].

Obviously, the core in biomarker discovery from gene expression data is classification and feature selection. Numerous classification algorithms have been proposed, such as AdaBoost (AB), K-nearest neighbor (KNN), neural network (NN), random forest (RF) and support vector machine (SVM). These methods may lead to satisfactory classification performance. However, the learning process is with poor explainability [26]. In these methods, all variables are used for classification and they often result in the nonsense of biomedical implications. Differently, logistic regression method has a specific expression formula. It is intuitive and easy to be understood as an explainable machine learning method [27]. Moreover, according to the integration with classification methods, feature selection methods can be divided into three categories: Filter method separates feature selection from classifier construction [28]. Wrapper method evaluates the classification performance of selected features and keeps searching until certain defined accuracy criteria is satisfied [29]. Embedded method integrates feature selection within the classifier construction simultaneously [30]. As such a kind of embedded method, regularized logistic regression is a combination of feature selection and classifier construction, both of which are completed in the same optimization process. The feature selection is automatically performed during training the classifier. It can improve the classification accuracy by shrinking the regression coefficients and can select a small number of genes simultaneously. It is with far less computational complexity than wrapper method [31]. The logistic regression not only directly gives a class of probabilities that explain the combination of variables (genes), but also generates a classification label for samples [20]. The regularization can solve the problem of multicollinearity and avoid the over-fitting caused by high-dimensional data [32]. Therefore, regularized logistic regression has become a typical method for classifying diseases based on microarray data [33], [34].

The fundamental idea of regularization in regression is to constrain the regression coefficients by a penalty function. According the property of penalties, the existing regularization methods can be briefly categorized as convex penalty and non-convex penalty. The convex category contains the penalties of ridge [35], lasso [36] and elastic net [37]. The ridge penalty is the $L_2$ norm of the coefficient vector. It has successfully solved the collinearity problem [38]. Since $L_2$ norm is differentiable, it can be solved by the coordinate descent method [39]. Instead, lasso penalty is based on $L_1$ norm, it can be solved by the efficient LARS approach [40], [41]. Although lasso can bring the sparsity of coefficients, the solution is not unique in some cases and it does not own the oracle property, which brings trouble to practical applications [36]. To overcome this limitation, Zou and Hastie proposed a logistic regression model with elastic net penalty that linearly combines $L_1$ norm and $L_2$ norm. The elastic net penalty has the grouping property beyond the oracle property, which is critical for analyzing high-dimensional biomedical data [42].

So far, many non-convex penalty functions have been developed for regularized logistic regression for classification and feature selection. A natural choice is the $L_0$ penalty, which directly counts the number of non-zeros in the coefficients. However, the non-differentiable of $L_0$ function makes it impossible to employ any efficient optimization technique to solve [38]. To obtain a more sparse solution than $L_1$ regularization, Xu et al. proposed the $L_{1/2}$ penalty [43]. As a representative of $L_q(0<p<1)$ penalty, $L_{1/2}$ takes into account both sparsity and computational efficiency. It is unbiased and has oracle properties [44]. Frank and Friedman described a broader framework with the penalty term of $L_q(0<p⩽2)$ norm [45]. Interestingly, they named it as a bridge regression for bridging the $L_0$ regression and the $L_2$ regression (ridge) [24]. Easily, the former $L_0,L_{1/2},L_1$ and $L_2$ norms are all special cases of bridge regression. Knight and Fu derived the theoretical properties of bridge regression [46]. They defined an ideal penalty estimation operator that should have three characteristics: sparsity, unbiasedness and continuity. Thereafter, various variants of $L_1$ norm have been proposed [24]. For instances, Fan and Li proposed a smoothly clipped absolute deviation (SCAD) penalty [47]. Zhang proposed a maximum concave penalty (MCP) which has the maximum convexity in the penalty function that satisfies all unbiased conditions and has good theoretical properties [48]. It is worth mentioning that Breheny and Huang demonstrate the utility of convexity diagnostics to determine regions of the parameter space in which the objective function of logistic regression with SCAD or MCP penalty is locally convex, even though the penalty is not [49].

In this paper, we summarize the regularized logistic regression methods with $L_q$ penalties and provide a comparative study on seven popular penalties, i.e., ridge, lasso, elastic net, $L_0,L_{1/2}$, SCAD and MCP, in the discovery of SPTB biomarkers. Based on some datasets for training, we evaluate their individual classification performances in terms of accuracy (Acc), precision (Pre), sensitivity (Sn), specificity (Sp), F-measure and AUC value. We optimize the parameters that balance the log-likelihood function and penalty for achieving the better classification performance respectively. The logistic regression with elastic net, lasso, $L_{1/2}$ and SCAD penalties achieve the higher AUC values that generate a feature subset with 20 genes that can be served as SPTB biomarkers. By training on the gene expression profiles underlying these biomarkers, we construct a logistic regression classifier and define an indicator called preterm risk score (PRS) to predict the high-risk subjects of SPTB based on the maternal whole blood gene expression data. In the independent validation of identified biomarkers, the SPTB samples achieve significantly different PRS scores compared to Term-birth samples. The validation classification achieves the AUC value of 0.933. The results demonstrate the effectiveness and efficiency of the proposed biomarker discovery method and the identified biomarkers. All data and source code used in this paper can be available at https://github.com/zpliulab/LogReg.

2. Materials and methods

2.1. Data

The gene expression profiling data of pregnant women are downloaded from NCBI GEO database (Accession IDs: GSE59491 and GSE73685). Table 1 lists the details of the two datasets. Briefly, GSE59491 collects maternal whole blood samples at two different time periods (17–23 weeks and 27–33 weeks of gestation). The 326 samples are from 165 asymptomatic pregnant women. It consists of 98 SPTB samples and 228 Term-birth samples. In each microarray, 24,478 genes are measured after data preprocessing [8]. GSE73685 totally contains 183 samples from eight tissues (maternal blood, chorion, amnion, placenta, decidua, fetal blood, myometrium from the uterine fundus and lower segment) [50]. In their paper, Bukowski et al. generated the original data is to compare women who delivers preterm and term with or without labor. Based on the timing and presence of labor, they studied four complementary phenotypes: delivery in women at term with labor (TL), delivery at term without labor (TNL), delivery after preterm labor (PL) and preterm delivery without labor (PNL), due to fetal or maternal indications [50]. According to the definition of SPTL (one subtype of SPTB), the PL samples can be selected as SPTB samples, while PNL can not. In more details, the dataset contains two phenotypes, PPROM no labor and PPROM with labor, of which the former type belongs to the SPTB samples we studied here according to the definition of PPROM (another subtype of SPTB). After data preprocessing, each sample contains 20,909 gene expressions.

Table 1.

The detailed information of the two datasets used in this work. The numbers in parentheses are the sample size.

Dataset	# of samples	# of genes	Samples type	Phenotype of samples
GSE59491	326	24478	$•$Maternal whole blood (326)	$•$SPTB (98)/ Term-birth (228)
GSE73685	183	20909	$•$ Amnion (24)	$•$ TL (5)/ TNL (7)/ PL (3)/ PNL (5)/ PPROM no labor (2)/ PPROM with labor (2)
			$•$ Chorion (24)	$•$ TL (5)/ TNL (7)/ PL (3)/ PNL (4)/ PPROM no labor (3)/ PPROM with labor (2)
			$•$ Cord blood (23)	$•$ TL (5)/ TNL (7)/ PL (4)/ PNL (5)/ PPROM no labor (1)/ PPROM with labor (1)
			$•$ Decidua (23)	$•$ TL (5)/ TNL (7)/ PL (2)/ PNL (5)/ PPROM no labor (2)/ PPROM with labor (2)
			$•$ Fundus (20)	$•$ TL (3)/ TNL (7)/ PL (1)/ PNL (4)/ PPROM no labor (3)/ PPROM with labor (2)
			$•$ Lower segment (24)	$•$ TL (5)/ TNL (7)/ PL (3)/ PNL (5)/ PPROM no labor (2)/ PPROM with labor (2)
			$•$Maternal whole blood (24)	$•$TL (5)/ TNL (7)/ PL (3)/ PNL (5)/ PPROM no labor (2)/ PPROM with labor (2)
			$•$ Placenta (21)	$•$ TL (5)/ TNL (7)/ PL (2)/ PNL (4)/ PPROM no labor (3)

We perform the biomarker discovery experiments in the dataset of GSE59491. Specifically, we firstly identify the differentially expressed genes (DEGs) by Welch’s t-test. After adjusting P-values by Benjamini and Hochberg (BH) method [51], we obtain 359 genes with significant difference (adjusted P-value $<0.05$) between SPTB and Term-birth samples. The gene lists are shown in Table S1 in the Additional file. We will implement the methods of logistic regression with $L_q$ penalties in these genes for identifying gene biomarkers. For training and testing purpose, we randomly divide all samples into two subsets, 229 samples ($70\%$, 164 positive, 65 negative) for learning and training and 97 samples ($30\%$, 64 positive, 33 negative) for evaluating in the biomarker discovery section. We use the independent data of GSE73685 for validating the discovered biomarkers. In order to be consistent with the sample source in the previous dataset, we select 17 samples from maternal blood (excluding PNL and PPROM with labor) as the independent test dataset. We have also bolded these selected samples in Table 1, in which 5 samples are SPTB (PL  + PPROM no labor) samples and the rest 12 ones are Term-birth (TL  + TNL) samples.

2.2. Framework

Fig. 1 illustrates the framework of identifying biomarkers from gene expression data by logistic regression with $L_q$ penalties. At first, we identify DEGs in GSE59491 dataset and find out 359 candidates with adjusted P-value $<0.05$. Second, we randomly select $70\%$ of the samples as the training dataset, the rest as the test dataset in the biomarker identification. The optimal tuning parameter lambda is determined through 10-fold cross-validation with the minimum misclassification error in the training dataset. In order to ensure the reliability of the results, we repeat the process 30 times by setting 30 different random seeds. Third, we evaluate the classification performance by logistic regression with seven types of penalties. The comparison proves that the elastic net, lasso, $L_{1/2}$ and SCAD penalties own the better classification and feature selection. Fourth, the overlap genes of four feature subsets obtained by logistic regression with the above four penalties are treated as the identified biomarkers for SPTB. Fifth, we validate their classification ability in the independent validation dataset. After training a logistic regression classifier with the gene expression profiles of the biomarker genes, we obtain the AUC and PRS of these biomarkers in the validation dataset. Then we prove the effectiveness of these identified biomarkers in distinguishing preterm from Term-birth samples.

Fig. 1.

The framework of identifying predictive biomarkers of SPTB from gene expression data.

2.3. Logistic regression

As mentioned, we essentially focus on a binary classification problem with feature selection by logistic regression with regularization term. For logistic regression, suppose we have observations $({\mathit{X}}_{\mathit{i}},y_i),i=1,2,\cdots ,n$ independently and identically distributed, from n samples. Taking these observations as a dataset $\mathcal{D}$,

$$\mathcal{D}=\left\{({\mathit{X}}_{\mathbf{1}},y_1),({\mathit{X}}_{\mathbf{2}},y_2),\cdots ,({\mathit{X}}_{\mathit{n}},y_n)\right\},$$

where ${\mathit{X}}_{\mathit{i}}={(x_{i1},x_{i2},\cdots ,x_{\mathit{ip}})}^{\mathrm{T}}\in {\mathbb{R}}^p$ denotes the p-dimensional gene expression vector associated with the $i^{\mathit{th}}$ sample, $x_{\mathit{ij}}$ represents the gene expression value of the $j^{\mathit{th}}$ gene in the $i^{\mathit{th}}$ sample. $y_i$ is a corresponding variable that takes a value of 0 or 1. It represents the true disease state of the $i^{\mathit{th}}$ sample ($y_i=1$ if the $i^{\mathit{th}}$ sample is SPTB and $y_i=0$ if Term-birth). Define a classifier $f(x)=\exp (x)/(1+\exp (x))$ such that for any input of class label $y,f(x)$ predicts y correctly. The logistic regression is considered as follows

$${\pi }_i=\mathrm{Pr}\left(y_i|{\mathit{X}}_{\mathit{i}}\text{;}\mathit{\theta }\right)=f\left({\mathit{X}}_{\mathit{i}}^{\mathrm{T}}\mathit{\theta }\right)=\frac{\exp \left({\mathit{X}}_{\mathit{i}}^{\mathrm{T}}\mathit{\theta }\right)}{1+\exp \left({\mathit{X}}_{\mathit{i}}^{\mathrm{T}}\mathit{\theta }\right)},i=1,2,\cdots ,n,$$ (1)

where $\mathit{\theta }=\left({\theta }_0,{\theta }_1,\dots ,{\theta }_p\right)$are the unknown coefficients to be estimated, and ${\theta }_0$ is the intercept.

After running a logit transformation on Eq. (1), we have

$$\mathrm{l}\mathit{ogit}({\pi }_i)=\log \frac{{\pi }_i}{1-{\pi }_i}={\theta }_0+{\theta }_1{x}_{i1}+{\theta }_2{x}_{i2}+\cdots +{\theta }_p{x}_{\mathit{ip}}\text{.}$$ (2)

Note Eq. (2) is not only the logistic regression classifier for training and validation, but also the indicator of PRS for identifying the SPTB risk of pregnant women.

What’s more, because $y_i~B(0,1),(1⩽i⩽n)$, let its co-probability (occurrence) be ${\pi }_i$, we can write the probability function of $y_i$ as

$$\mathrm{Pr}(y_i)={\pi }_i^{y_i}{(1-{\pi }_i)}^{1-y_i},1⩽i⩽n\text{.}$$ (3)

The likelihood function is given by

$$\mathcal{L}({\pi }_i)=\underset{i=1}{\overset{n}{\mathrm{\Pi }}}\mathrm{Pr}(y_i)=\underset{i=1}{\overset{n}{\mathrm{\Pi }}}{\pi }_i^{y_i}{(1-{\pi }_i)}^{1-y_i}\text{.}$$ (4)

Then take the logarithm of Eq. (4) and the log-likelihood function can be expressed as

$$\mathcal{L}(\mathit{\theta }|\mathcal{D})={\displaystyle \sum _{i=1}^n}\left\{y_i\log \left[f\left({{\mathit{X}}_{\mathit{i}}}^{\mathrm{T}}\mathit{\theta }\right)\right]+\left(1-y_i\right)\log \left[1-f\left({{\mathit{X}}_{\mathit{i}}}^{\mathrm{T}}\mathit{\theta }\right)\right]\right\},$$ (5)

where ${\mathit{X}}_{\mathit{i}}^{\mathrm{T}}\mathit{\theta }={\theta }_0+{\theta }_1{x}_{i1}+{\theta }_2{x}_{i2}+\cdots +{\theta }_p{x}_{\mathit{ip}},(1⩽i⩽n)$. Obviously, Eq. (5) is a function of the regression coefficient vector $\theta$. The estimation of the parameter vector $\mathit{\theta }$ can be obtained by minimizing the inverse of Eq. (5).

However, Eq. (5) is ill-posed in the case of high-dimensional variables and small samples $(p\gg n)$. If we solve it directly, that may result in over-fitting. Fortunately, regularization can be employed to solve the problem. So we test and choose an appropriate penalty to Eq. (5) by defining the $L_q$ regularized logistic regression model as

$$\mathit{\theta }=\arg \min \left\{\mathcal{L}(\mathit{\theta }|\mathcal{D})+\mathcal{P}\left(\mathit{\theta }\text{;}\lambda \right)\right\},$$ (6)

where $\mathcal{L}(\mathit{\theta }|\mathcal{D})$ is the loss function, $\mathcal{P}(\mathit{\theta }\text{;}\lambda )$ is the penalty function, $\lambda$ is a positive tuning parameter used to balance the loss term and penalty term.

2.4. $L_q$ penalties

Different $L_q$ penalties have been developed in the regularized logistic regression models. They take into account different relationship between input variables. Generally, we formulate the penalty function $\mathcal{P}(\mathit{\theta }\text{;}\lambda )$ with the $L_q$ norm of coefficient vector $\mathit{\theta }$ as the corresponding penalty term

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda {\displaystyle \sum _{j=1}^p}|{\theta }_j{|}^q,$$ (7)

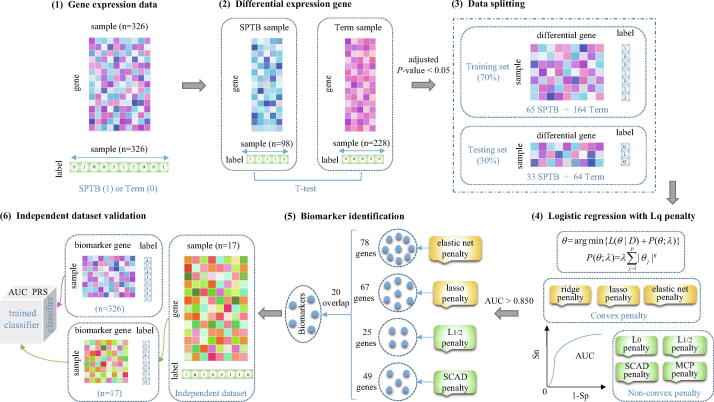
where q is a positive shrinkage parameter of norm. Table 2 lists some properties of the former seven penalty functions. The unbiased, sparse, continuous, convex and oracle properties are often regarded as standards of the selection of penalty [24]. Fig. 2 shows the function images in one-dimension when $\lambda =1$ for these penalties.

Table 2.

The properties of $L_q$ penalties.

Penalty	Unbiased	Sparse	Continuous	Convex	Oracle property
Ridge	No	No	Yes	Yes	No
Lasso	No	Yes	Yes	Yes	Asymptotic
Elastic net	No	Yes	Yes	Yes	No
$L_0$	No	Yes	No	No	No
$L_{1/2}$	Yes	Yes	Yes	No	Yes
SCAD	Yes	Yes	Yes	No	Yes
MCP	Yes	Yes	Yes	No	Yes

Fig. 2.

One-dimensional images for $L_q$ penalty functions.

Clearly, $q=2$ refers to the ridge ($L_2$ penalty) logistic regression, $q=1$ refers to the lasso ($L_1$ penalty) logistic regression, the mixture of $q=2$ and $q=1$ corresponds to the elastic net logistic regression, $q=0$ refers to the $L_0$ penalty logistic regression, $q=1/2$ refers to the $L_{1/2}$ penalty logistic regression. Differently, SCAD and MCP are the other two widely-used penalty terms for achieving some expected properties in regularization, e.g., oracle property.

As shown in Fig. 2(b), when the value of coefficient $\theta$ is small $(|\theta |<1)$, the smaller the value of q, the harsher penalty the $L_q$ regularization imposed on the coefficient $\theta$. Fig. 2(c) further points out that the larger the absolute value of coefficient $\theta$, the greater the $L_q(q⩾1)$ penalty and elastic net imposed on it. Thus these penalties also have the problem of biased estimation of larger coefficients. In addition, from Fig. 2(a), we can also find that when the absolute value of coefficient $\theta$ is sufficiently large ($|\theta |>a\lambda$), the SCAD and MCP penalty become a constant (the constant can be given by their expressions blow, respectively). Although the SCAD penalty value is greater than the MCP penalty value, their images are both parallel to the $\theta$-axis, just like $L_0$ penalty.

If and only if $q⩾1$ and the mixture of $q=2$ and $q=1,L_q$ penalty is a convex function, then Eq. (6) is easier to solve. Theoretically, when $q\to 0$, the sparsest solution can be obtained. But the $L_0$ norm is non-convex and non-continuous, which makes Eq. (6) difficult to solve. When $q⩽1,L_q$ penalty, as well as SCAD and MCP, is non-differentiable at the origin point (0,0). Fan and Li proved that the singularity of the penalty at the origin point is a necessary condition for generating a sparse solution [47]. More importantly, existing research shows that some non-convex penalties have many good properties, such as sparsity [43], unbiased [52], and oracle property [46]. Therefore, the $L_q(q<1)$, SCAD and MCP regularization methods have received widespread attention in recent years.

2.4.1. Ridge

Ridge regression, also known as Tikhonov regularization [53], is one of the most frequently used regularization methods of ill-posed regression analysis [54]. The regularization term is defined as $\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda {‖\theta ‖}_2^2$, where ${‖\theta ‖}_2^2={\sum }_{j=1}^p{\theta }_j^2$, i.e., the sum of the square of coefficients, aka the square of Euclidian distance. Namely

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda {\displaystyle \sum _{j=1}^p}{\theta }_j^2\text{.}$$ (8)

2.4.2. Lasso

With the advent of the age of big data, sparsity has become an important means underlying the data [24]. Using the $L_1$ norm as the penalty, Tibshirani proposed the seminal lasso model [36]. In lasso, the regularization is defined as $\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda {‖\theta ‖}_1$, where ${‖\theta ‖}_1={\sum }_{j=1}^p|{\theta }_j|$, i.e. the sum of the absolute values of coefficients, also known as the Manhattan distance. Namely

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda {\displaystyle \sum _{j=1}^p}|{\theta }_j|\text{.}$$ (9)

2.4.3. Elastic net

From a biological perspective, some groups of correlated features, i.e., genes, are embedded in the same in functional pathway. In microarray gene expression data analysis, experiments have shown that lasso regression sometimes performs poorly in inter-correlated features. To overcome this limitation, Zou and Hastie proposed the elastic net regularization method for feature selection. Elastic net regularization attempts to combine $L_2$ penalty with $L_1$ penalty together to better select all relevant features simultaneously. The elastic net penalty is defined as

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda \left[\alpha {\displaystyle \sum _{j=1}^p}|{\theta }_j|+(1-\alpha ){\displaystyle \sum _{j=1}^p}{\theta }_j^2\right],$$ (10)

where $\alpha \in [0,1]$ is a parameter to balance the effects of $L_2$ penalty and $L_1$ penalty. Obviously, when $\alpha =0$, the penalty refers to ridge penalty, and when $\alpha =1$, the penalty refers to lasso penalty, respectively. $\alpha$ can be set literally to be $0<\alpha <1$, the penalty is an elastic net penalty [22].

2.4.4. $L_0$ penalty

Since it directly counts the number of non-zero elements in a vector, the $L_0$ norm of the coefficient vector $|\beta {|}_0={\sum }_{j=1}^{p}1\left[{\theta }_j\ne 0\right]$ is a natural definition for the penalty term $\mathcal{P}(\mathit{\theta }\text{;}\lambda )$. $L_0$ regularization limits the number of non-zero elements to a certain range, which is obviously sparse, and hence implies the variable selection. In Eq. (7), let $q=0$, we get the $L_0$ penalty function

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda {\displaystyle \sum _{j=1}^p}1\left[{\theta }_j\ne 0\right]\text{.}$$ (11)

Solving logistic regression with $L_0$ penalty has been demonstrated to be NP-hard [55].

However, if we define the formulation $\frac{0}{0}=1$, it is easy to get

$$|\beta {|}_0={\displaystyle \sum _{j=1}^p}1\left[{\theta }_j\ne 0\right]={\displaystyle \sum _{j=1}^p}\frac{{\theta }_j^2}{{\theta }_j^2},$$ (12)

Substituting Eq. (12) into Eq. (6), it derives

$${\widehat{\theta }}_{L_0}=\arg {\displaystyle \underset{\theta }{\min }}\left\{-\mathcal{L}(\mathit{\theta }|\mathcal{D})+\lambda {\displaystyle \sum _{j=1}^p}\frac{{\theta }_j^2}{{\theta }_j^2}\right\}\text{.}$$ (13)

Here, we employ the former sparse-generalized linear regression model with $L_0$ approximation to solve the regression with $L_0$ penalty [56].

2.4.5. $L_{1/2}$ penalty

In theory, the $L_q$ penalty with a smaller value of q would lead to solutions with more sparsity. To this end, Xu et al. explored the properties of $L_q(0<q<1)$ regularization, especially its special effects. The $L_{1/2}$ penalty function is defined as

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )=\lambda {\displaystyle \sum _{j=1}^p}|{\theta }_j{|}^{\frac{1}{2}}\text{.}$$ (14)

Note that the penalty function (14) is not differentiable when $\mathit{\theta }$ has zero components. The singularity causes the standard gradient-based methods to fail in solutions. Motivated by the method of [47], Huang approximates the bridge penalty with $q=\frac{1}{2}$ by

$${\displaystyle \sum _{j=1}^p}{\int }_{-\infty }^{{\theta }_j}\left[\mathrm{sgn}(u)/\left(|u{|}^{1/2}+\eta \right)\right]\mathrm{d}u\text{.}$$ (15)

For a small $\eta >0$, it has a finite gradient at zero. Note that this function and its gradient converge to the bridge penalty with $q=\frac{1}{2}$ and its gradient when $\eta \to 0$, respectively. The approximation of $L_{1/2}$ penalty is called modified bridge (mbridge) [57] in the sense of approximation.

2.4.6. SCAD penalty

The SCAD penalty is defined as

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )={\displaystyle \sum _{j=1}^p}{\mathcal{P}}_a\left(|{\theta }_j|\text{;}\lambda \right),$$ (16)

where

$${\mathcal{P}}_a(|\theta |\text{;}\lambda )=\left\{\begin{array}{cc}\lambda |\theta |,\hfill & |\theta |⩽\lambda ,\hfill \\ \frac{-\left({\theta }^2-2a\lambda |\theta |+{\lambda }^2\right)}{2(a-1)},\hfill & \lambda <|\theta |⩽a\lambda ,\hfill \\ \frac{(a+1){\lambda }^2}{2},\hfill & |\theta |>a\lambda ,\hfill \end{array}\right)$$

for $a>2$ and $\lambda >0$. Eq. (16) is a function of the coefficients $\mathit{\theta }$ indexed by a parameter $\lambda$ that controls the tradeoff between the loss function and penalty function in Eq. (5), and that also may be shaped by one or more tuning parameters a [47]. The rationale behind SCAD penalty can be obtained by its first derivative

$${\mathcal{P}}_a^{\prime }(|\theta |\text{;}\lambda )=\left\{\begin{array}{cc}\lambda ·\mathrm{s}\mathit{gn}(\theta ),\hfill & |\theta |⩽\lambda ,\hfill \\ \frac{(a\lambda -|\theta |)}{a-1}\mathrm{s}\mathit{gn}(\theta ),\hfill & \lambda <|\theta |⩽a\lambda ,\hfill \\ 0,\hfill & |\theta |>a\lambda ,\hfill \end{array}\right)$$

where

$$\mathrm{s}\mathit{gn}(\theta )=\left\{\begin{array}{cc}-1,\hfill & \theta <0,\hfill \\ 0,\hfill & \theta =0,\hfill \\ 1,\hfill & \theta >0\text{.}\hfill \end{array}\right)$$

SCAD begins by applying the same rate of penalization as lasso, but continuously reduce the rate until, when $|\theta |>a\lambda$, the rate of penalization drops to 0 [49]. We also note that the penalty is continuously differentiable in the interval $(-\infty ,0)\cup (0,\infty )$, but not differentiable when ${\theta }_k=0(k=1,2,\cdots ,p)$, and its derivative is 0 outside the interval $[-a\lambda ,a\lambda ]$. Therefore, SCAD regularized regression can produce sparse solutions and unbiased estimates for large coefficients.

2.4.7. MCP penalty

The MCP penalty refers to

$$\mathcal{P}(\mathit{\theta }\text{;}\lambda )={\displaystyle \sum _{j=1}^p}{\mathcal{P}}_a\left({\theta }_j\text{;}\lambda \right),$$ (17)

where

$${\mathcal{P}}_a(\theta \text{;}\lambda )=\lambda {\int }_0^{|\theta |}{\left(1-\frac{x}{\lambda a}\right)}_{+}\mathrm{d}x=\left\{\begin{array}{cc}\lambda |\theta |-\frac{{\theta }^2}{2a},\hfill & |\theta |⩽\lambda a,\hfill \\ \frac{{\lambda }^{2}a}{2},\hfill & |\theta |>\lambda a,\hfill \end{array}\right)$$

for $a>1$ and $\lambda >0$. In particular, a is the shape (or concavity) tuning parameter making MCP a bridge between $L_0(a\to 1_{+})$ and $L_1(a\to \infty )$ [48]. More information can be obtained by its first derivative

$${\mathcal{P}}_a^{\prime }(\theta \text{;}\lambda )=\lambda {\left(1-\frac{|\theta |}{\lambda a}\right)}_{+}·\mathrm{s}\mathit{gn}(\theta )=\left\{\begin{array}{cc}\lambda ·\mathrm{s}\mathit{gn}(\theta )-\frac{\theta }{a},\hfill & |\theta |⩽\lambda a,\hfill \\ 0,\hfill & |\theta |>\lambda a\text{.}\hfill \end{array}\right)$$

The rationale behind MCP penalty is similar to that of SCAD. Both penalties begin by applying the same rate of penalization as lasso, and reduce that rate to 0 as $|\theta |$ gets further away from zero, the difference is in the way that they make the transition. Note that the MCP penalty is not differentiable at ${\theta }_k=0(k=1,2,\cdots ,p)$ too.

2.5. Classification evaluation criteria

To evaluate the performance of logistic regression with these seven $L_q$ penalties in classifying SPTB samples by selecting certain genes, we employ some metrics, e.g., Acc, Pre, Sn, Sp, F-measure and AUC to measure the performance. They are defined as formulas (18)–(22) respectively:

$$\mathrm{A}\mathit{cc}=\frac{\mathit{TP}+\mathit{TN}}{\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN}},$$ (18)

$$\mathrm{P}\mathit{re}=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}},$$ (19)

$$\mathrm{S}n=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FN}},$$ (20)

$$\mathrm{S}p=\frac{\mathit{TN}}{\mathit{FP}+\mathit{TN}},$$ (21)

$$\mathrm{F}-\mathit{measure}=2\frac{\mathrm{S}n\times \mathrm{P}\mathit{re}}{\mathrm{S}n+\mathrm{P}\mathit{re}},$$ (22)

where $\mathit{TP},\mathit{TN},\mathit{FP}$ and FN refer to true positive, true negative, false positive and false negative in the classification respectively. We also plot the receiver operating characteristic (ROC) curve for demonstrating the correspondence between true positive rate (TPR) and false positive rate (FPR). AUC (area under the ROC curve) value is also calculate to display the authenticity of the logistic regression classification with $L_q$ penalty [58].

3. Results and discussion

3.1. Identified biomarkers

We randomly select 70% of the samples from whole training data (GSE59491) for training, and the remaining 30% for testing, which ensures the seven regularized logistic regression methods are learned and tested on the same dataset for fair comparison [59]. We perform the classification and feature selection simultaneously on the SPTB gene expression dataset using logistic regression with the seven penalties, i.e., ridge, lasso, elastic net, $L_0,L_{1/2}$, SCAD and MCP, respectively. The selected feature genes in these embedded classifiers can serve as biomarkers of classifying samples with different phenotypes of SPTB and Term-birth.

In order to select the tuning parameter $\lambda$ of $L_q$ penalties, we employ a 10-fold cross-validation on the training dataset to obtain the optimal $\lambda$ that makes the minimum misclassification error (see the next section for details). After setting 30 random seeds to repeat the cross-validation procedure 30 times, the averaged misclassification errors of these classifiers in the test data set based on the regularized logistic regression models are shown in Table 3. We find these classifiers achieve both low training and testing errors. For instance, logistic regression with $L_{1/2}$ penalty obtains the lowest training error of $0/229$ and that with elastic net penalty obtains the lowest test error. The number of identified biomarker genes are also diverse. Ridge regression selects the largest number of biomarkers and $L_{1/2}$ obtains the fewest number of genes as biomarkers.

Table 3.

The average misclassification errors by the logistic regression with seven penalties on the SPTB data in 30 random experiments.

Penalty	Training error	Testing error	# of selected biomarker genes
Ridge	47/229	21/97	359
Lasso	10/229	19/97	67
Elastic net	13/229	18/97	78
$L_0$	48/229	24/97	31
$L_{1/2}$	0/229	19/97	25
SCAD	18/229	22/97	49
MCP	24/229	24/97	27

In these identified biomarkers, we find that there is a lot of overlaps between the gene sets selected by different logistic regression with $L_q$ penalties. For instance, 67 feature genes selected by $L_1$ penalty also appear in the 78 features selected by elastic net penalty. 28 out of 31 features selected by $L_0$ penalty also appear in the 67 feature genes selected by $L_1$ penalty. As expected, $L_2$ penalty owns the full features of 359 genes. The feature sets selected by $L_2$ penalty and elastic net penalty have a large intersection of 78 genes. More precisely, we calculate the number of overlapping genes selected by these embedded logistic regression classifiers. The results are shown in the lower triangle of Table 4. The overlap significance of P-values between different penalties is also shown in the corresponding upper triangle of Table 4. As shown, the overlaps are evaluated by hypergeometric test and also highlighted by different colors.

Table 4.

The number of overlapping biomarker genes and its significance between any two penalties.

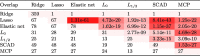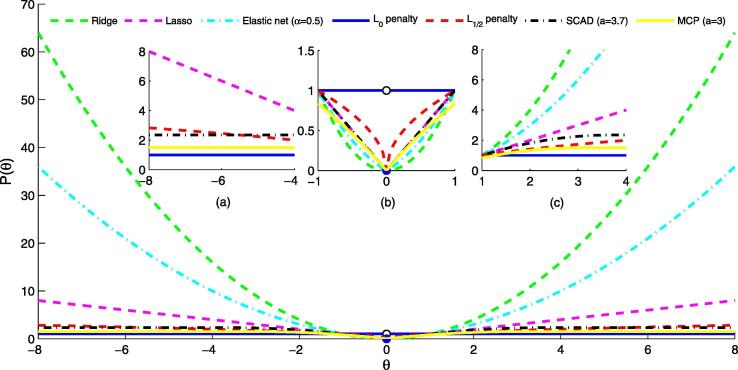
We identify the biomarker genes by classification and feature selection in an integrative embedded way. The corresponding ROC curves of different classifiers are shown in Fig. 3. The details of classification performance are shown in Table 5. For classifying the SPTB samples, we find that logistic regression with elastic net penalty achieves the highest AUC value of 0.912. Lasso achieves a close AUC value with elastic net. The ridge penalty obtain the lowest AUC value of 0.781. From the comparison study, we also find the convex penalties with mean of 0.867 obtain higher classification performance than the non-convex penalties with mean of 0.852. In the prediction of SPTB, the logistic regression classifiers with the convex penalties tend to achieve higher accuracy in distinguishing disease samples from controls.

Fig. 3.

The ROC curves of seven methods after 10-fold cross-validation repeated 30 times.

Table 5.

The classification performance details of seven penalties for SPTB.

Penalty	Acc	Pre	Sn	Sp	F-measure	AUC
Ridge	0.936	0.929	0.394	0.997	0.553	0.781
Lasso	0.942	0.818	0.545	0.986	0.655	0.907
Elastic net	0.945	0.857	0.545	0.990	0.667	0.912
$L_0$	0.920	0.574	0.818	0.932	0.675	0.839
$L_{1/2}$	0.942	0.733	0.667	0.973	0.698	0.872
SCAD	0.933	0.762	0.485	0.983	0.593	0.875
MCP	0.926	0.737	0.424	0.983	0.538	0.822

As shown in Table 5, logistic regression classifier with elastic net, lasso, $L_{1/2}$ and SCAD penalties in the feature selection obtain the AUC of over 0.850. Thus, we select the overlapping features as our identified biomarker genes for classifying phenotypic samples. Using the overlap genes, 20 genes are identified as the screened biomarkers of SPTB, namely FADS2, TRAV4, PCDHGB5, ZNF284, ASRGL1, MFSD4A, TARS, MCM2, CDKN2A-DT, FBXO31, ZNF649-AS1, PLEC, SPRTN, VAMP2, PRKAG1, CLASRP, PAICS, GOLGA7, MIR3117, GLYR1.

3.2. Selection of parameters

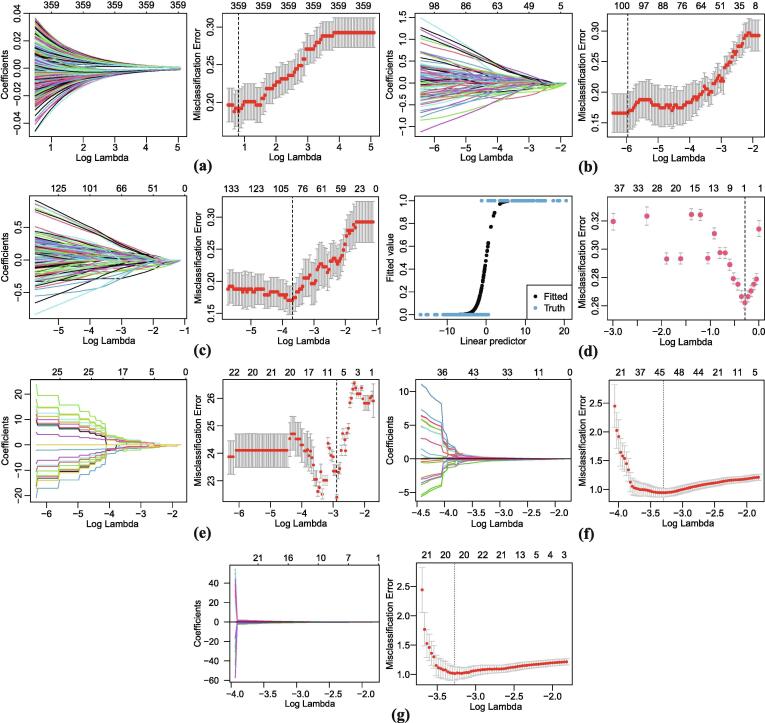
We compare the classification performances by logistic regression with seven penalties. We recognize the parameters in these penalties have great impacts on the solution of regression coefficients. Here we consider an attempt to perform logistic regression using $\alpha =0.5$ for elastic net, $a=3.7$ for SCAD penalty and $a=3$ for MCP penalty [49], the values are suggested for linear regression in Fan and Li [47]. For a fair comparison, we optimize the selection of tuning parameter $\lambda$ for each classifier individually. The best turned models are implemented in the former comparisons. Figs. 4 demonstrates the solution paths and the gene selection results of the seven penalties in the same training data set. By setting up different $\lambda$ values, Figs. 4 records the regression coefficients and cross-validation errors in these classifiers of regularized logistic regression.

Fig. 4.

The solution paths and the gene selection results of the logistic regression with $L_q$ penalty.

As shown in Fig. 4, the x-axis displays the $\log (\lambda )$ as $\lambda$ varies. The left subfigures (Ridge (a), Lasso (b), Elastic net (c), $L_{1/2}$ (e), SCAD (f), MCP (g)) of regression coefficients show the paths of regression coefficients as $\lambda$ varies, each curve in a subfigure corresponds to a gene variable respectively, the y-axis refers to the coefficient of this gene. The axis above indicates the number of nonzero coefficients at the current $\lambda$, which correspond to the effective degrees of freedom for the above seven penalties. Moreover, in the left subfigure $L_0$ (d), according to the approximated $L_0$ method [56], it is a plot of the fitted value against linear predictor.

What’s more, the right subfigures (Ridge (a), Lasso (b), Elastic net (c), $L_0$ (d), $L_{1/2}$ (e), SCAD (f), MCP (g)) display the cross-validation error curves (red dotted lines), include the upper and lower standard deviation of the errors along the $\lambda$ sequence (black error bars). Especially, the optimal $\lambda$ value of seven penalties is shown as the vertical dotted line correspondingly, which indicates the logarithm of the optimal $\lambda$ , called ${\lambda }_{\mathrm{m}\mathit{in}}$. It minimizes the prediction error and gives the most accurate model with each penalty. In our experiments, we use ${\lambda }_{\mathrm{m}\mathit{in}}$ with the minimum misclassification error on training dataset as the selected optimal tuning parameter for each regularized logistic regression method.

3.3. Function analysis of biomarkers

To investigate the pathological implications of these identified biomarker genes of SPTB, we perform a functional enrichment analysis. This will verify the biomarkers and in turn prove the effectiveness of logistic regression with $L_p$ penalties in biomarker discovery. First, we perform gene ontology (GO) enrichment analysis on these 20 genes. Table 6 lists the top 10 enriched biological process (BP) terms with P-value$<0.01$. The detailed results are shown in Table S2 in the Additional file.

Table 6.

The enriched GO terms in the biomarkers.

ID	Description	BgRatio	P-value	P.adjust	Qvalue	Gene symbol	Count
GO:0043001	Golgi to plasma membrane protein transport	32/17913	$<$0.001	0.092	0.075	VAMP2/GOLGA7	2
GO:0006893	Golgi to plasma membrane transport	43/17913	$<$0.001	0.092	0.075	VAMP2/GOLGA7	2
GO:0061951	Establishment of protein localization to plasma membrane	48/17913	$<$0.001	0.092	0.075	VAMP2/GOLGA7	2
GO:0098876	Vesicle-mediated transport to the plasma membrane	70/17913	0.002	0.141	0.115	VAMP2/GOLGA7	2
GO:0006892	Post-Golgi vesicle-mediated transport	77/17913	0.002	0.141	0.115	VAMP2/GOLGA7	2
GO:0006633	Fatty acid biosynthetic process	144/17913	0.008	0.196	0.159	FADS2/PRKAG1	2
GO:0006188	IMP biosynthetic process	10/17913	0.009	0.196	0.159	PAICS	1
GO:0046040	IMP metabolic process	10/17913	0.009	0.196	0.159	PAICS	1

Second, we summarize the biological functions of these 20 biomarker genes, which have been verified to be closely associated with the occurrence and development of SPTB. The detailed functional interpretation are shown in Table S3 in the Additional file. Some representative biomarker genes with their functions are listed in Table 7. In Table 7, we find that some of biomarker genes have been proved to be closely related to SPTB in many literatures. The enriched functions also indicates the method of identifying biomarkers of SPTB by logistic regression with $L_q$ penalties is effective.

Table 7.

Some representative SPTB biomarker genes with the summaries of their functions.

Gene symbol	Gene name	Gene functions
ASRGL1	Asparaginase And Isoaspartyl Peptidase 1	$•$ Diseases associated with ASRGL1 include Telogen Effluvium and Masa Syndrome. Among its related pathways are Histidine, lysine, phenylalanine, tyrosine, proline and tryptophan catabolism and Metabolism [60].
FADS2	Fatty Acid Desaturase 2	$•$ Diseases associated with FADS2 include Fanconi Anemia, Complementation Group D2 and Best Vitelliform Macular Dystrophy. Among its related pathways are alpha-linolenic acid (ALA) metabolism and fatty acid beta-oxidation (peroxisome) [61], [62], [63], [64].
GOLGA7	Golgin A7	$•$ GOLGA7 (Golgin A7) is a Protein Coding gene. Among its related pathways are Innate Immune System [65].
MCM2	Minichromosome Maintenance Complex Component 2	$•$ Diseases associated with MCM2 include Deafness, Autosomal Dominant 70 and Autosomal Dominant Non-Syndromic Sensorineural Deafness Type Dfna. Among its related pathways are E2F mediated regulation of DNA replication and Mitotic G1-G1/S phases [66], [67], [68], [69].
PLEC	Plectin	$•$ Diseases associated with PLEC include Epidermolysis Bullosa Simplex, Ogna Type and Muscular Dystrophy, Limb-Girdle, Autosomal Recessive 17. Among its related pathways are Cell junction organization and Apoptotic cleavage of cellular proteins [70], [71], [72], [73].
VAMP2	Vesicle Associated Membrane Protein 2	$•$ Diseases associated with VAMP2 include Tetanus and Infant Botulism. Among its related pathways are Vesicle-mediated transport and Neurotransmitter Release Cycle [74], [75], [76].

3.4. Independent dataset validation

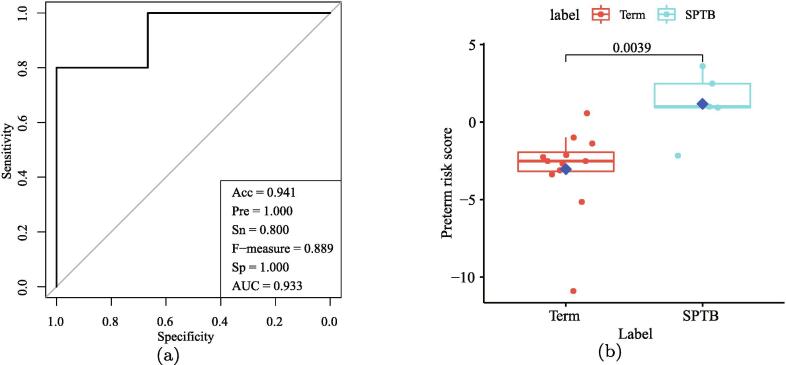
For further justifying the identified biomarker genes of SPTB, we validate our findings in an independent dataset (GEO ID:GSE73685). We firstly test the classification ability of these biomarkers in distinguishing SPTB from Term-birth samples. We find 17 overlap genes (FADS2, PCDHGB5, ZNF284, ASRGL1, MFSD4A, TARS, MCM2, FBXO31, ZNF649-AS1, PLEC, SPRTN, VAMP2, PRKAG1, CLASRP, PAICS, GOLGA7, GLYR1) in the identified 20 biomarkers are contained in the 20,909 measured genes in the validation data. We firstly train a logistic regression classifier (2) using the 17 biomarker genes (set to $x_{i1},x_{i2},\cdots ,x_{i17}$) from the training data to obtain the logistic regression parameters (e.g., intercept and coefficients). Then, using the trained logistic regression classifier to predict the value of a response variable by the corresponding expression values of the 17 biomarkers in the independent validation data. Finally, the value of response variable is subjected to logit transformation to obtain the PRS of each sample. Fig. 5 (a) illustrates the ROC curve with the performance details of classification on the validation dataset. The AUC value achieves as high as 0.933. Table 8 shows the confusion matrix about the sample classification. The classification performance might be improved further when more validation datasets become available in the future [3]. The independent validation proves the efficiency of our identified biomarkers in classifying SPTB samples from the Term-birth ones.

Fig. 5.

(a) The ROC curve of classifying samples on the independent dataset. (b) The boxplot PRS of SPTB and Term-birth samples on the independent data.

Table 8.

The confusion matrix.

		Forecast category
		Term-birth	SPTB
Actual category	Term-birth	12	0
	SPTB	1	4

Here, we define the PRS for indicting the risk of SPTB based on the former logistic regression model. In the validation dataset, Fig. 5 (b) shows the boxplot of PRS in the independent dataset. It is clear that there is a significant difference in the PRS for the samples of SPTB when compared to the Term-birth samples (P-value  = 0.0039, Wilcoxon test).

A great challenge in preventing SPTB is to identify pregnant women at greatest risk [77]. When a risk measure of SPTB for individuals is scored, appropriate intervention of preventing SPTB could be directed. The proposed PRS is intended as a screening score to identify high-risk subjects. It may encourage a person with higher risk value to perform a whole blood gene expression test during pregnancy. Because many individuals with a high PRS may have unrecognized asymptomatic SPTB heterogeneity, a full blood test may be required for diagnosis, treatment, and other clinical assessments. We regard PRS could provide a practical way to identify pregnant women at high-risk SPTB in general population. In the PRS model (2), the multivariate logistic regression coefficients are often used to assign weights to each biomarker gene. In our case study of SPTB, our aim is to generate a simple and easy-to-use risk calculator that could conveniently predict SPTB in asymptomatic pregnant women. Totally, 17 biomarker genes are selected to enter the model (2) without considering the interaction between these variables. More comprehensive cohorts are still required to generate a more reliable PRS scoring system from a clinical practice perspective.

3.5. Compared with alternative machine learning methods

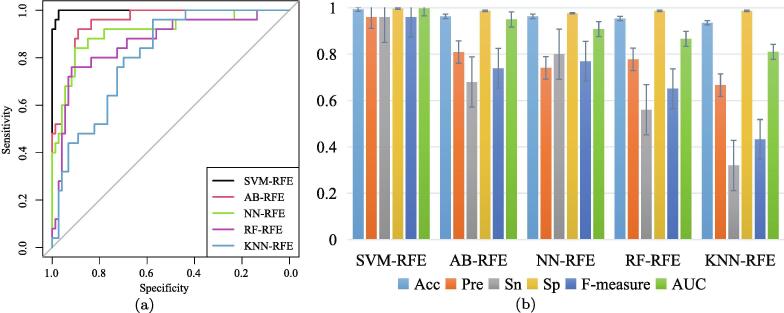
From a comparison with other machine learning methods in biomarker discovery, we employ the recursive feature elimination (RFE) technique to eliminate redundant and irrelevant feature genes. We use an empirical Bayes (EB) method to select 694 DEGs as the candidates for selection [51]. Then the ranking files of gene importance, obtained by five machine learning with feature selection methods, i.e., SVM-RFE, AB-RFE, NN-RFE, RF-RFE and KNN-RFE, are implemented to identify feature genes as biomarkers. We also randomly select $70\%$ samples to form the training dataset, then the remaining $30\%$ as the testing dataset, and construct the five classifiers to learn and evaluate the classification performance. In each classifier, the optimal parameters, e.g., gamma and cost in SVM, are determined through 10-fold cross-validation with the minimum misclassification error in the training dataset individually. The ROC curves are shown in Fig. 6(a), and the other performance results are shown in Fig. 6(b). The details are listed in Table S4 in the Additional file.

Fig. 6.

Classification performance. (a) ROC curves of five methods. (b) Classification results of five methods.

The legend annotation of Fig. 6 and the horizontal axis of Fig. 6 (b) are arranged in descending order of the five methods according to their AUC values. Compared with AB-RFE, NN-RFE, RF-RFE and KNN-RFE, the AUC of SVM-RFE is relatively higher. SVM-RFE achieves the highest AUC value of 0.998, and KNN-RFE obtains the lowest AUC value of 0.810. Although all the AUC values of the five methods are higher than 0.800, the performance metrics of Acc, Pre, Sn, Sp and F-measure by these methods are also lower than our former proposed method of regularized logistic regression in the training dataset.

We select top-ranked 50 genes by the five machine learning and feature selection methods to construct five feature subsets respectively. We intersect the genes in these feature subsets and select out 54 genes in the overlapping as the discovered biomarkers by the five popular machine learning methods. The biomarker genes are listed in Table S5 in the Additional file. We find that there are 14 overlaps between the 20 genes selected by our method and these 54 genes selected by alternative machine learning methods. The GO function enrichment analysis on these 54 genes, we also find the enriched functions are related to plasma membrane transport, which is consistent with our findings.

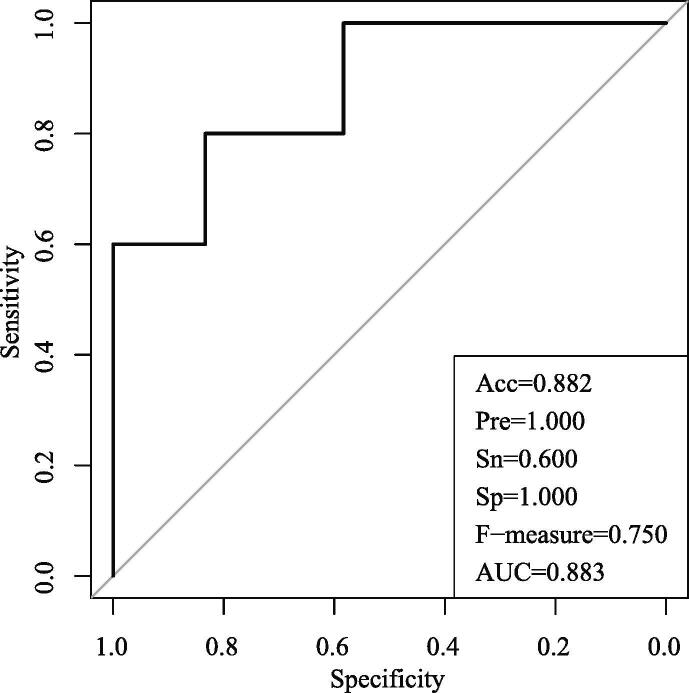
In the independent validation dataset of GSE73685, there are 46 genes included in the above 54 gene set. Using the 46 genes to train an SVM classifier in the training dataset of GSE59491, the classification result in the validation data is shown in Fig. 7. The AUC value is 0.883, which is also lower than the regularization methods we proposed. The comparison study further proves the effectiveness and advantage of our proposed method.

Fig. 7.

Independent dataset verification results.

4. Conclusions

In this paper, we developed a method for predicting SPTB biomarkers with regularized logistic regression. Specifically, the definitions of seven penalties were introduced in details. Their properties and characteristics with applications in biomarker discovery from gene expression data have been presented. For achieving fair comparisons, we used 10-fold (tenfold) cross-validation on the same training dataset to get the optimal tuning parameter for each penalty. We compared these regularized logistic regression classifiers in their various performance metrics and resulted in the best performance of that with elastic net penalty. By combining the selected genes in the classifiers with top performances, we identified 20 biomarker genes of SPTB. These selected biomarkers have been verified by functional enrichment analyses and literature checks. We also validated these biomarkers on an independent dataset. We further proved the advantage of our proposed method by comparing the discovered biomarkers with those identified by the other alternative machine learning methods. The distinct ability of distinguishing SPTB samples from Term-birth samples indicate the efficacy of identified biomarkers. Furthermore, the established PRS indicator provides a potential index for identifying high-risk SPTB subjects in clinical application. The results also illustrate the power of sparse statistical learning model in discovering diagnostic biomarkers.

Funding

This work was partially supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 61973190, 61572287 and 61533011; Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) under Grant No. 2019JZZY010423; Key Research and Development Project of Shandong Province, China under Grant No. 2018GSF118043; the Innovation Method Fund of China (Ministry of Science and Technology of China) under Grant No. 2018IM020200; the Program of Qilu Young Scholars of Shandong University.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.