Toward Developing Intuitive Rules for Protein Variant Effect Prediction Using Deep Mutational Scanning Data

Abstract

Protein structure and function can be severely altered by even a single amino acid mutation. Predictions of mutational effects using extensive artificial intelligence (AI)-based models, although accurate, remain as enigmatic as the experimental observations in terms of improving intuitions about the contributions of various factors. Inspired by Lipinski’s rules for drug-likeness, we devise simple thresholding criteria on five different descriptors such as conservation, which have so far been limited to qualitative interpretations such as high conservation implies high mutational effect. We analyze systematic deep mutational scanning data of all possible single amino acid substitutions on seven proteins (25153 mutations) to first define these thresholds and then to evaluate the scope and limits of the predictions. At this stage, the approach allows us to comment easily and with a low error rate on the subset of mutations classified as neutral or deleterious by all of the descriptors. We hope that complementary to the accurate AI predictions, these thresholding rules or their subsequent modifications will serve the purpose of codifying the knowledge about the effects of mutations.

1. Introduction

Randomly occurring mutations can cause a loss of structure or/and function of proteins or provide improved functionality in diverse cellular contexts. The degree of tolerance to a mutation at a given site has been used to interpret the role of the amino acid in forming or stabilizing the protein structure^1,2 or in its function.³ Predicting the functional effects of mutations is important to understand disease biology and antibiotic resistance as well as how proteins function. Mutational scanning has been a standard biochemical tool to understand these intricate effects of amino acid substitutions. Sequence–structure–function relationships in proteins can be explored systematically, from the perspectives of evolution as well as protein design. Alanine being nonbulky and chemically inert was chosen to replace the natively occurring amino acids in 62 positions of human growth hormone to understand its interactions with its receptor.³ This alanine scanning study shed light on the direct involvement of the amino acids in complexes and also suggested how different amino acids modulated the formation and stability of proteins. Most mutational scans remained limited to a systematic alanine scanning of the important amino acids⁴ or even otherwise to a maximum of about a hundred mutations.

A combination of several factors including a desire to circumvent inherent problems associated with protein purification, development of sequencing technologies, and interest in phenotypic screening led to newer methods or rather newer philosophies of mutational scanning. Deep mutational scanning^5,6 and site saturation mutagenesis⁷ are among the emerging methodologies performing a comprehensive mutation of all of the amino acids in a protein to all 19 possible alternatives and measuring their phenotypic outcomes.⁵ For example, some studies have explored the fitness (dis)advantage in Escherichia coli under drug-pressure by performing a few thousand single-point mutations on β-lactamase.⁸ Recent double and triple mutant studies have further pushed the boundaries to the order of hundred thousand independent mutations in a protein.^9,10 Identifying pairwise amino acid interactions¹¹ and also structure prediction have become possible through these advances in mutational scans.^12,13 The efforts in interpreting protein variants have important implications in disease biology as well.¹⁴

Concurrent with the data explosion in molecular biology such as next-generation sequencing, deep mutational scanning⁵ studies have also been generating unprecedented amounts of data.¹⁵⁻²⁰ There have been parallel developments in the efforts to computationally predict the outcomes of these deep mutational scanning experiments. Some analyses such as the ones based on coevolutionary coupling energies^21,22 use sequence data from thousands of homologs of a protein to predict the effect of a substitution at a site. Some other predictors²³ were trained on the mutational effect data collated from the Protein Mutant Database.²⁴ A few other studies focused on an accurate prediction of the fitness outcomes of mutations using artificial intelligence (AI)-based models²⁵⁻²⁷ that are trained on data from deep mutational scanning experiments. These models use tens to hundreds of variables that represent the site-specific factors or the interactions with the immediate neighborhood. Though all of these predictors may not work well for all proteins, as the detailed analysis of the predictive power of different predictors shows,²⁸ the performance of these AI-based computational models may be considered satisfactory depending on the specific requirements, and many of these are easy to use with a web interface.^23,25 Thus, the experimental data or its computational predictions are at a stage where they can reliably generate libraries of the effects of mutations. Both these approaches are used referentially for determining the effects of specific mutations rather than to contribute toward an understanding of the mutational landscape. However, in general, there has been a growing criticism against the lack of transparency in the AI-based models, which is leading to the emergence of interpretable or explainable AI.²⁹ The approach can be used to understand the contributions of each variable to individual predictions.³⁰ However, even with the accurate predictions of AI, and interpretable contributions to these predictions, there is no codification of the knowledge or a reconciliation with the classical intuitions about the effects of mutations.

In the field of rational drug discovery, two very different approaches are used to screen through the leads to identify the activity or the drug-likeness. One is using highly accurate prediction models for quantitative structure–activity relationships,³¹ and the other is using intuitive rules of thumb, known as Lipinski’s rules,³² to classify the drug candidates. The latter, while not meant to be an accurate prediction of activity, is an intuitive and practically useful tool, and our approach in this work is inspired by it. We revisit the qualitative intuitions on how different physicochemical factors are independently likely to affect the function of proteins, most of which are based on site-specific descriptors such as conservation and neighborhood descriptors such as number of contacts. We ask if quantitative rules of thumb can be derived. The limitations in accuracies arising from such rules are also quantified along with these thresholds. We demonstrate the results of combining different intuitive rules for improving the reliability of predictions, albeit for a small set of mutations.

2. Methods

Inclusion of Deep Mutational Scanning Studies

The present analyses are based on the deep mutational scanning data obtained for seven proteins—β-lactamase,⁸ aminoglycoside 3′-phosphotransferase (APH(3′)-II),³³ heat shock protein 90 (Hsp90),³⁴ mitogen-activated protein kinase 1 (MAPK1),³⁵ ubiquitin-conjugating enzyme E2 I (UBE2I),²⁶ thiamin pyrophosphokinase (TPK1),²⁶ and β-glucosidase (Bgl3).³⁶

For β-lactamase, the mutational effect scores quantified as the relative fitness,⁸R = log₁₀(f^mutant/f^wild-type), where f is the ratio of allele counts in the selected and unselected population, were used. Zero, negative, and positive R reflect neutral, loss of function, and gain of function mutations, respectively. Interestingly, two independent deep mutational scanning studies^8,37 of β-lactamase in E. coli reported highly correlated (but nonlinear) outcomes (Figure S1). We chose to work with the data of Stiffler et al.⁸ as it was 100% complete with all 19 substitutions studied for all wild-type amino acids in the mutagenized region. For the proteins APH(3′)-II, Hsp90, and MAPK1, the data was obtained from the study of Gray et al.,³⁸ where the mutational scores are available as relative fitness (R). Fitness scores as growth rates for TPK1 and UBE2I were obtained from Weile et al.²⁶ The log₂ enrichment ratio for variants of Bgl3 was taken from the study of Romero et al.³⁶

Mutational Effects Classification

Since the deep mutational scanning data we used was quantitative, to perform a classification analysis, a choice of fitness threshold was required. The fitness distribution from each protein was fit to a bi-Gaussian using the “curve_fit” function in the scipy³⁹ module of Python. The two modes of the distribution were supposed to represent the neutral and deleterious mutation groups. All mutations with a fitness score more than (μ – 2σ), where μ and σ are, respectively, the mean and standard deviation of the Gaussian mode corresponding to the neutral mutations, are considered neutral and others as deleterious. Unlike the case of other proteins, for MAPK1, the positive and negative scores represented deleterious and neutral mutations, respectively, and the choice of threshold was adapted accordingly for this data set. Although we performed our analyses and estimation of the thresholds of the physicochemical descriptors of the mutations using this bi-Gaussian classification approach, we also used a clustering based on the Gaussian Mixture Model (“GMM” function in scikit-learn⁴⁰ with all default parameters and n_components = 2) implemented in Python to classify the mutational effects. Many mutational effects in the boundary region of the two Gaussians got reclassified, but the overall prediction quality did not change (data not reported).

Calculation of the Physicochemical Descriptors

The structures of all proteins were obtained from the protein data bank repository using PDB identities 1M40 (β-lactamase), 1ND4 (APH(3′)-II), 2CG9 (Hsp90), 4NIF (MAPK1), 2UYZ (UBE2I), 3S4Y (TPK1), and 1GNX (Bgl3). Hydrogen atoms were added to the structure using GROMACS.⁴¹ Solvent-accessible surface area (SASA) for each wild-type residue was calculated using these structures with the gmx_sasa tool of GROMACS⁴¹ and a probe radius of 1.4 Å. For β-lactamase and β-glucosidase, homologous sequences were obtained from the Pfam database⁴² (Pfam ID: PF13354 and PF00232, respectively) using PDB ID as the query. For other proteins, sequences obtained through five iterations of the PSI-BLAST search with default parameters were aligned using Clustal Omega. The alignment was then truncated to the reference sequence, and sequences with more than 20% gaps were discarded. Conservation is quantified as the frequency of the most common amino acid at each position in the alignment. While studying the effect of a categorical charge-type change, amino acids were grouped into four categories—positively charged (R, H, K), negatively charged (D, E), polar (S, T, N, Q, C), and hydrophobic (A, V, I, L, M, F, Y, W). P and G were not included in any group.

Statistical Analyses

Analysis Scripts

All statistical analyses presented were performed using different python libraries. The functions used were “pearsonr” and “spearmanr“ from scipy³⁹ for the correlation analysis and “accuracy_score”, “f1_score”, “KFold”, and “auc” of scikit-learn⁴⁰ for the accuracy score, F1 score, k-fold cross-validation, and area under ROC curve (AUC ROC) analysis, respectively. The logistic regression model for mutational effect prediction was developed using the “LogisticRegression” function of scikit-learn.⁴⁰

10-Fold Cross-Validation

The data set comprising the variants of all six proteins was divided into 10 groups of nearly equal size using the “KFold” function in scikit-learn.⁴⁰ The classification threshold for a variable was determined by training on 9 of these 10 groups and validating on the remaining 10th group. This was repeated until all 10 groups were used as a validation set.

Box Plots

The variants were binned according to the values of the variable under consideration, and the fitness distributions of variants in each bin are represented using a box plot. The bins are of equal width, and boxes are plotted centered at the midpoint of each bin. The bin widths used are 0.1, 6, 0.3, and 1, respectively, for conservation, number of contacts, SASA, and BLOSUM.

3. Results

3.1. Developing Thresholds for Classification

We analyzed the 25153 mutations obtained from the deep mutational scanning data of seven proteins, β-lactamase, APH(3′)-II, Hsp90, MAPK1, UBE2I, TPK1, and Bgl3, for which structural information as well as mutational effect data of at least 2500 substitutions are available (Section 2). Six of these data sets (22 421 variants) were used for obtaining the thresholds, and the data on Bgl3 (2732 variants) was used for an independent validation. Six variables, capturing the physicochemical and evolutionary nature of the wild-type amino acid and the substitution–conservation, charge-type change, solvent-accessible surface area (SASA), number of structural contacts, BLOSUM substitution matrix score, and distance from the catalytic site, were studied for identifying correlations with fitness. Each of these descriptive variables depends on the protein structure, sequence, or the nature of substitutions. All variables are intuitive and are widely used for inferring mutational effects. In the following sections, the fitness data of each protein was individually studied relative to each of these variables. Specifically, for the mutational data of β-lactamase, we studied in detail to see if correlations of the variables and the deviations from them were intuitive.

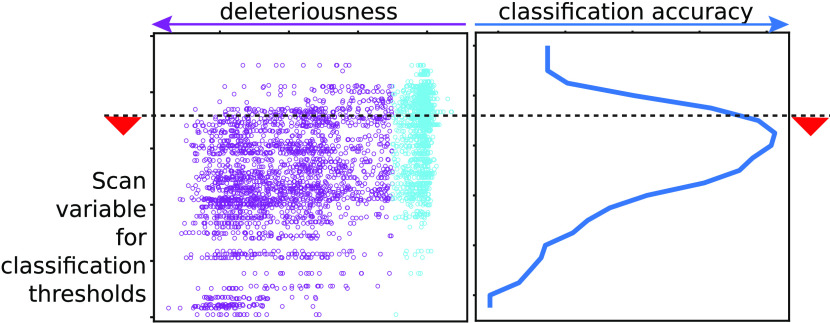
When it appeared that all of the mutational effects could be inferred from one variable or the other, we quantified this correlation between phenotypic effects and every descriptive variable using Spearman’s correlation coefficient (Supporting File 1). This analysis prompted us to explore the possibility of developing thresholding criteria relative to each of these variables for classifying variants as neutral and deleterious. To identify the threshold for a given variable, we scan across the complete range of the variable and use the F1 score⁴³ to quantify the quality of classification at each value of the variable for both the neutral and deleterious classes. The F1 score was used since it reduces biases due to over-representation of one class over the other in the data. F1_neutral can be calculated as F1_neutral = 2 × (precision × recall)/(precision + recall). Here, precision is the ratio of the number of true neutral predictions to the total number of neutral predictions and recall is the ratio of the number of true neutral predictions to the number of observed neutral mutations. Similarly, F1_deleterious is also calculated, and the threshold at which the average of F1 scores of both neutral and deleterious classes (F1_avg = (F1_neutral + F1_deleterious)/2) is the maximum was chosen as optimal. The procedure was repeated with each variable for all proteins except Bgl3, which was used as an independent validation set (discussed later).

3.2. Conservation Threshold

Typically, evolutionary conservation reflects the functional importance of an amino acid. Figure 1 shows the relation between conservation and the fitness effects from deep mutational scanning data of TEM-1 β-lactamase. As suggested by the mean fitness value for a given range of conservation highlighted in Figure 1, there is a reduction in fitness when conserved amino acids are mutated. However, conservation alone does not clearly resolve the effect on fitness as one can see several exceptions with high fitness consequences for substitutions at poorly conserved sites and low fitness consequences at highly conserved positions. We highlight the exceptions to the expected intuitions. (1) The amino acids that have less than 20% conservation and yet severely affect function upon mutation (relative fitness, R < −1). The mutations N52C, K55(C, P), E58(C, F, H, I, L, M, P, V, W, Y), S82(C, P), S98P, N100C, T140P, T141(F, K, P, W, Y), E197(F, L), P219(F, I, W, Y), F230(C, D, E, G, I, K, L, N, P, Q, R, S, T), and S258P are deleterious even though the wild-type residue is poorly conserved. All of these substitutions are away from the catalytic sites, and other than N52C, S82C, N100C, F230I, and F230L, involved a charge-type change. Interestingly, most of these substitutions also lead to a loss of solubility,⁴⁴ which could be the reason for the reduced functional fitness. (2) The amino acids were conserved (>80%), but their substitution did not affect the function significantly. G156D, G156E, G156N, and G236A are the substitutions that are neutral despite high conservation. Also, in these cases, the wild-type amino acid is substituted with amino acid of a different charge type. As conservation quantifies only variability at a specific position and does not distinguish different substitutions, we calculated the Position-Specific Scoring Matrix (PSSM) using PSI-BLAST (version 2.2.28) with the default parameters and explored its relation with fitness. We observed only a weak correlation (Figure S2).

Figure 1.

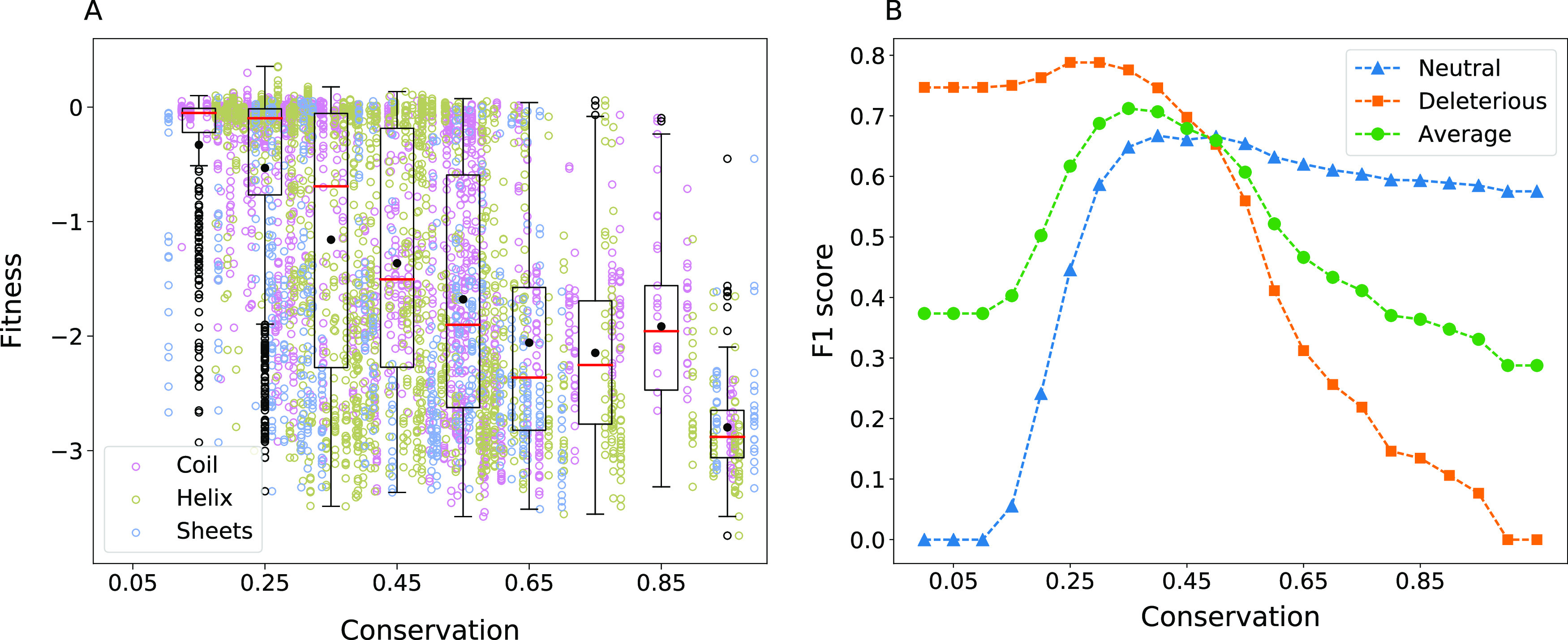
Effect of conservation. (A) Relationship between conservation and fitness was studied using the homologous sequences for TEM-1 β-lactamase (Pfam ID PF13354). It can be seen that the number of neutral substitutions decreases considerably for amino acids with conservation >60%. In the box-plot representation, the black filled circle and the red line represent the mean and median of the fitness, respectively. The whiskers are plotted at the lowest data point greater than Q1 − 1.5 × (Q3 − Q1) and the greatest data point less than Q3 + 1.5 × (Q3 − Q1) where Q1 and Q3 represent the first and the third quartile respectively. Black open circles represent the outliers. (B) Changes in the F1 score for the neutral and deleterious classes and the average of both plotted, as the threshold for conservation to classify the mutations is varied.

We further attempted to quantify a threshold for the general intuition that the higher the conservation, the greater are the fitness consequences of substituting it. We scanned across for different values of the threshold and quantified the F1 score for both neutral and deleterious classes (Figure 1). The same analysis performed for the other five proteins is shown in Figure S3. It can be seen that the intuition holds for all proteins, as indicated by the change in the mean fitness with conservation, though the correlation is weak for TPK1. We checked if an alternative descriptor of conservation based on entropy captures the correlations with fitness better. Entropy was calculated as ∑_i–p_i log₂(p_i), where p_i is the probability of finding amino i at the given site in the aligned sequences. There was no considerable improvement in the correlation for TPK1 (Pearson’s correlation 0.14 versus 0.12 with and without using entropy). We thus performed the estimations of the optimal threshold using the simpler definition of conservation, rather than entropy. F1_avg was maximum for the β-lactamase data when the conservation threshold was 0.35. For the other five proteins we studied, the threshold varied in the range 0.45–0.9 (Table 1).

Table 1. Threshold for Variables^a.

	protein
variable	β-lactamase	APH(3′)-II	Hsp90	MAPK1	UBE2I	TPK1	average threshold	standard deviation
fitness cutoff	–0.5	–2.5	–0.3	0.5	0.2	0.4
conservation	0.35	0.5	0.85	0.9	0.45	0.55	0.6	0.2
SASA (nm2)	0.3	0.2	0.2	0.1	0.2	0.4	0.2	0.1
contacts	14	19	25	20	18	14	18	4
BLOSUM	–1	–3	–3	–3	–2	–1	–2	1

^aThresholds for different variables were obtained by maximizing F1_avg, which is the average of F1 scores of neutral and deleterious class predictions. The thresholds were obtained for each variable and data from every single protein. For a variable, the average of thresholds obtained for the six proteins was calculated to obtain the average threshold.

3.3. Solvent-Accessible Surface Area (SASA) Threshold

The relation between fitness and SASA of wild-type amino acid, which reflects how buried the amino acids are, is shown in Figure 2 (alanine scanning results in Figure S4). The intuitive learning from this figure is that substitutions at amino acids, which are completely buried, can potentially range from neutral to deleterious, while the effect tapers off for amino acids with high SASA values, which have minimal effect on fitness. The mutations defining the frontier and showing the highest fitness compromise at any given SASA were recorded by taking note of the alanine scanning mutations near the triangular border in the plot. Of the amino acids P27, L57, R61, R65, F66, S70, K73, R93, Y105, S130, N132, N136, D157, R161, E166, R222, W229, and W290, which are on the frontier of the highest fitness loss, most are near the binding pocket. W229 is known to have an allosteric effect on the function.⁴⁵ R222 could be playing a role in structural stability as it forms a salt bridge with D233. However, the reasons for the functional compromise of mutations at P27 are not clear. The data on average supports the intuition that amino acids, which are completely buried and have a zero or reduced solvent-accessible area, do not tolerate mutations. At intermediate solvent-accessibility conditions, interestingly, a reduction in the volume of the amino acid seems to be more deleterious in general. This could be because of the cavities being created, which affects the packing of the residues. It is known that cavity creating mutations reduce the stability of proteins.⁴⁶ Applying a thresholding condition on SASA that classifies the fitness consequences of mutations as neutral or deleterious, we obtain 0.3 nm² as the optimal threshold (Figure 2 and Table 1). For other proteins, the optimal threshold for SASA was observed to be in the range 0.1–0.4 nm² (Table 1). The fitness distributions at different ranges of SASA for these proteins are given in Figure S5. The distributions for APH(3′)-II, Hsp90, and MAPK1 follow a similar trend as seen in the case of β-lactamase, and for TPK1 and UBE2I, there is a comparatively higher variability in fitness even at lower solvent accessibility.

Figure 2.

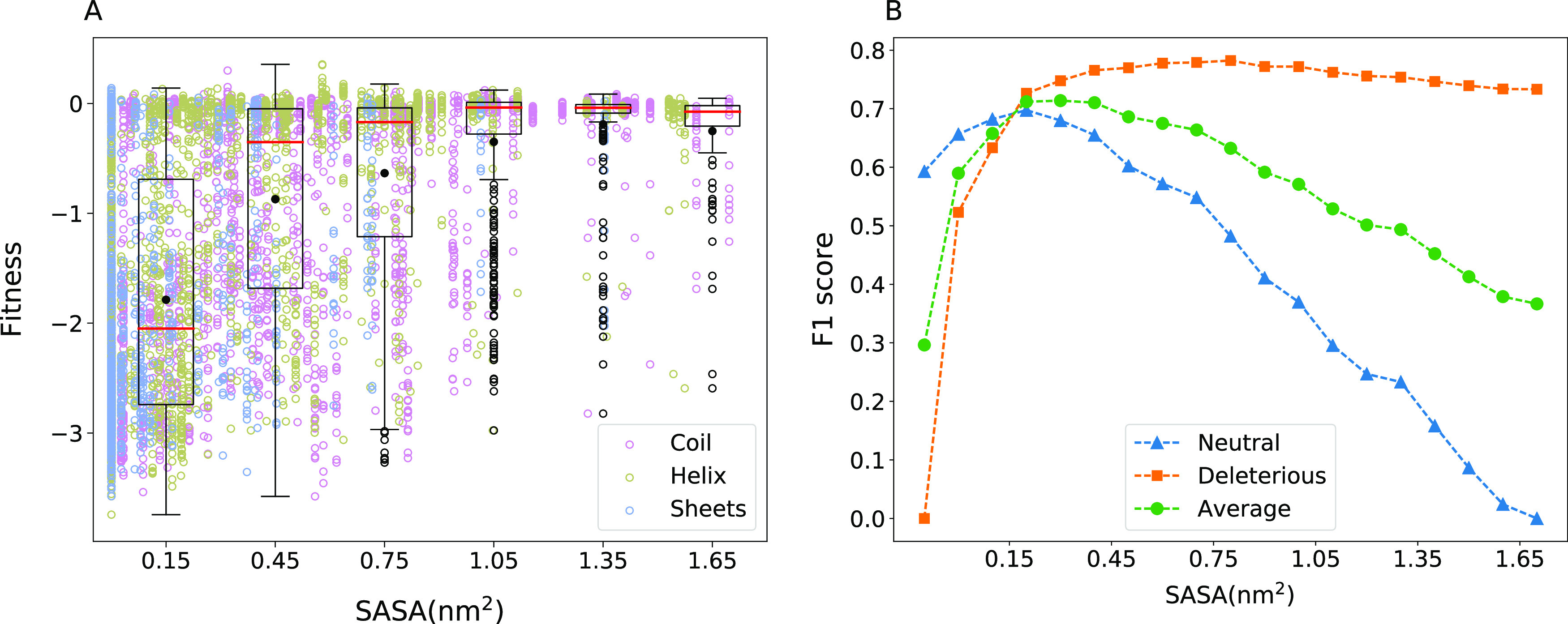
Effect of solvent accessibility. (A) Solvent accessibility for all amino acids of β-lactamase was calculated using the three-dimensional (3D) protein structure (PDB ID: 1M40). SASA versus fitness shows a half-triangular pattern. The deviations from this half-triangular pattern are noted in the main text. For details about the box-plot representation, see Figure 1. (B) Substitutions are classified as neutral and deleterious based on a chosen SASA threshold, and the quality of the resulting classification is quantified using the F1 score. F1 scores when different SASA thresholds are used are shown.

3.4. Threshold for Number of Inter-Residue Contacts

Inter-amino acid interactions mediated by hydrogen bonds, salt bridges, stackings, etc. determine how much a substitution disturbs the overall structural stability and function. While the biochemical details of the different interactions may be explored, and whether or not the nature of the substitutions conforms with the existing interactions may also be investigated, a simpler metric is the total number of inter-residue interactions any given residue is involved in. We studied this by counting the number of atom-level interactions that an amino acid is involved in and the sensitivity to its substitution. We used the native structure of the protein obtained from the protein data bank and an interaction cutoff of 4 Å to count interactions. Figure S6 shows that the relation between fitness and number of contacts is weak. While the average trends are intuitive, like substitutions of residues with a higher number of contacts result in a larger fitness effect, the variation in fitness for a given number of contacts is high. An optimal threshold for the number of inter-residue contacts was found to be 14 for β-lactamase. The F1 score variation with respect to the number of contacts for other proteins and the optimum thresholds obtained are given in Figure S7 and Table 1, respectively. There is an intuitive monotonous variation in mean fitness with the number of contacts for the cases of APH(3′)-II and UBE2I, whereas for Hsp90, TPK1, and MAPK1, the fitness changes do not seem to depend on the number of contacts.

3.5. BLOSUM Threshold

All other physicochemical metrics mentioned so far depend on the wild-type amino acid alone and do not reflect the nature of the substitution. We used the BLOSUM65 matrix, which statistically summarizes the naturally occurring substitution probabilities across all proteins to see if the fitness effects of an amino acid substitution can be captured by it. A plot of the BLOSUM score of substitutions and their fitness effects in β-lactamase are shown in Figure 3. One can also infer an optimal threshold for the BLOSUM score for β-lactamase from this. The dependence of fitness on the BLOSUM matrix score can be seen for all proteins in Figure S8.

Figure 3.

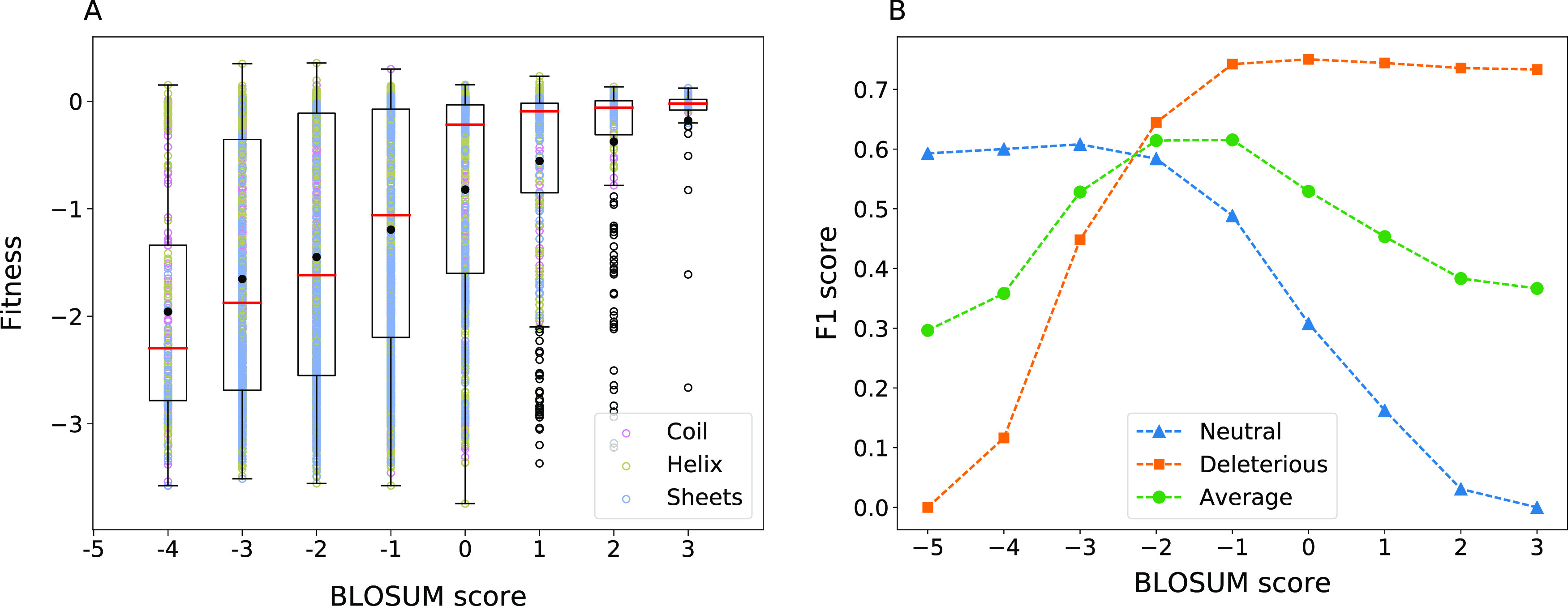
Effect of the BLOSUM substitution score. (A) Fitness scores for substitutions in β-lactamase as a function of the BLOSUM62 score for the substitution. See Figure 1 for details of the box-plot representation. (B) F1 score when each of the substitution matrix scores is used as a threshold to classify mutations as neutral and deleterious. Average of F1 scores of both classes is also shown.

3.6. Charge-Invariant Fitness Map

Another physical intuition about the nature of the substitutions is that charge-type changes can disrupt local interactions or solvent accessibility and lead to a loss of structure and function. Four amino acid categories were considered—positively charged, negatively charged, polar, and hydrophobic (Section 2). In an attempt to highlight the functional effects that are not intuitively expected, we present the analysis only for the mutations where the charge-type of the mutant is the same as that of the wild-type, yet the mutation causes a severe loss in fitness (Figure 4). Since charge-type change is categorical in nature, the consequences of this prediction can be summarized in a contingency table rather than a parameterized dependence as 2401 true deleterious, 569 true neutral, 1536 false deleterious, and 491 false neutral predictions.

Figure 4.

Effect of charge variation. The mutational effect scores are shown in a two-dimensional matrix representation, with each column representing the position along the amino acid sequence of β-lactamase and each row representing the amino acid substituted with. The red dots and their sizes illustrate the exceptions to the intuitions, where there is no charge-type change and yet a fitness effect denoted by the size of the dot. There are many substitutions for which the fitness is heavily compromised even with no change in the charge type. The amino acid substitutions that involved a charge-type change (shown in blue) are not the focus of this graphic, and hence their fitness effects are not indicated.

3.7. Threshold for Distance from the Catalytic Site

Substitution of Catalytic and Binding Pocket Residues

Substitution of catalytic residues is expected to be mostly deleterious, which is also the reason for the correlation between conservation and the distance from the catalytic site.⁴⁷ Any substitution in the five reported catalytic residues in β-lactamase—S70, K73, S130, E166, and A237, other than A237S and A237G—leads to high fitness compromise. In catalysis, the backbones of S70 and A237 in conjunction form an oxyanion hole stabilizing a reaction intermediate,⁴⁸ thus tolerating some side-chain substitutions at A237. The intolerance of all substitutions except of S and G could probably be because of size constraints. In addition to the catalytic sites noted above, residues M69, Y105, N132, N170, K234, S235, G236, G238, E240, and M272 form the binding pocket. Among these, N132 and K234 are the most sensitive ones as all 19 mutations at these positions result in reduced fitness (R < −0.5).

Substitution of Distal Amino Acids

From all mutations that lead to a loss of function,⁸ the mutations that also were independently seen to lead to a loss of solubility⁴⁴ were eliminated. Fifty-seven substitutions of 16 wild-type amino acids were more than 15 Å away from the catalytic residues and yet lead to R < −1.5. All these substitutions are either buried (SASA < 0.3 nm²) or have higher inter-residue contacts (>15) except for two, which are evolutionarily not favored (BLOSUM > 0). It is also possible that the substitutions had long-range effects as has been observed in the case of some other proteins.^49,50 The fitness effects of all the amino acid mutations studied in β-lactamase are summarized as a function of the distance from the catalytic site in Figure 5. A threshold distance of 15 Å from the catalytic residues to classify the effects of mutations optimized the true and false positive predictions.

Figure 5.

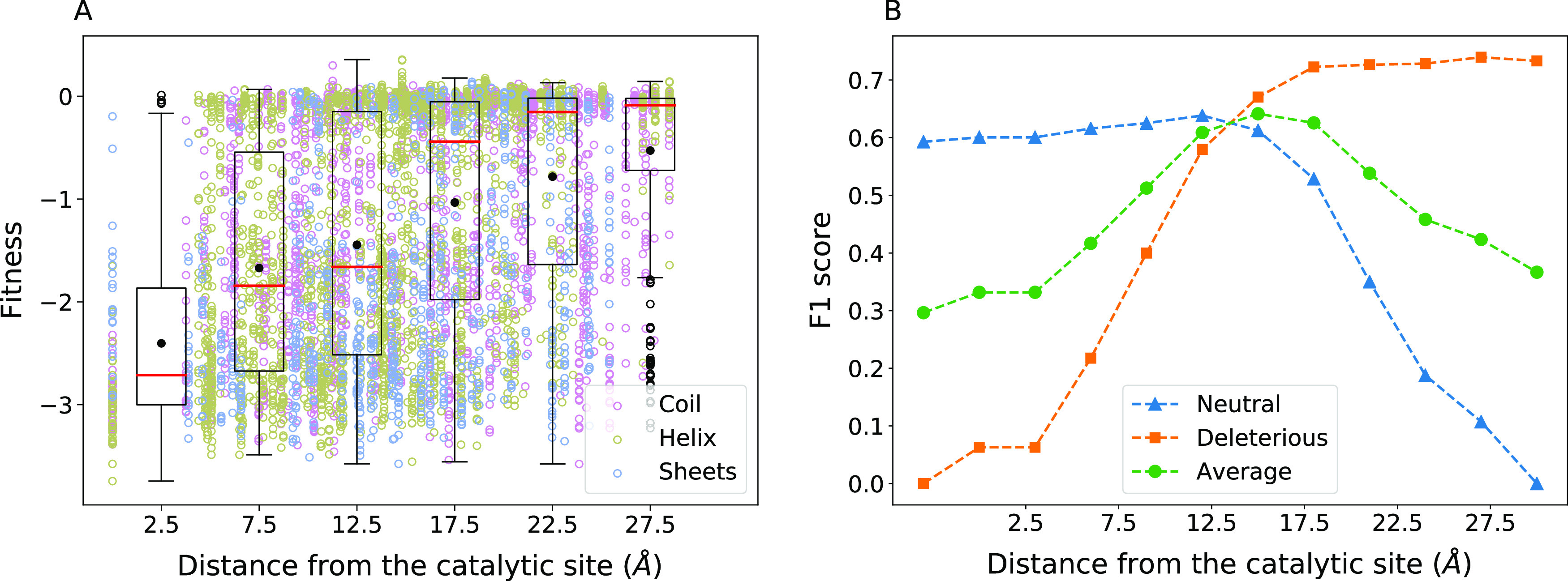
Effect of distance from the catalytic site. (A) Fitness changes are shown with respect to the distance between the wild-type residue and the closest catalytic residue. See Figure 1 for details about the box-plot representation. (B) F1 score for the neutral, deleterious classes, and the average of both are plotted as the classification threshold for distance from the catalytic site is varied.

3.8. Multifactorial Classification

Before attempting a multifactorial classification based on thresholding, we developed a logistic regression model by training on 70% of the data from the six proteins. The probability of a substitution being deleterious (P_del) we obtained was

P_del = 1/[1 + exp(1.99 – 1.97 × conservation – 0.014 × contacts + 0.72 × SASA + 0.33 × BLOSUM + 0.12 × Q_c)]

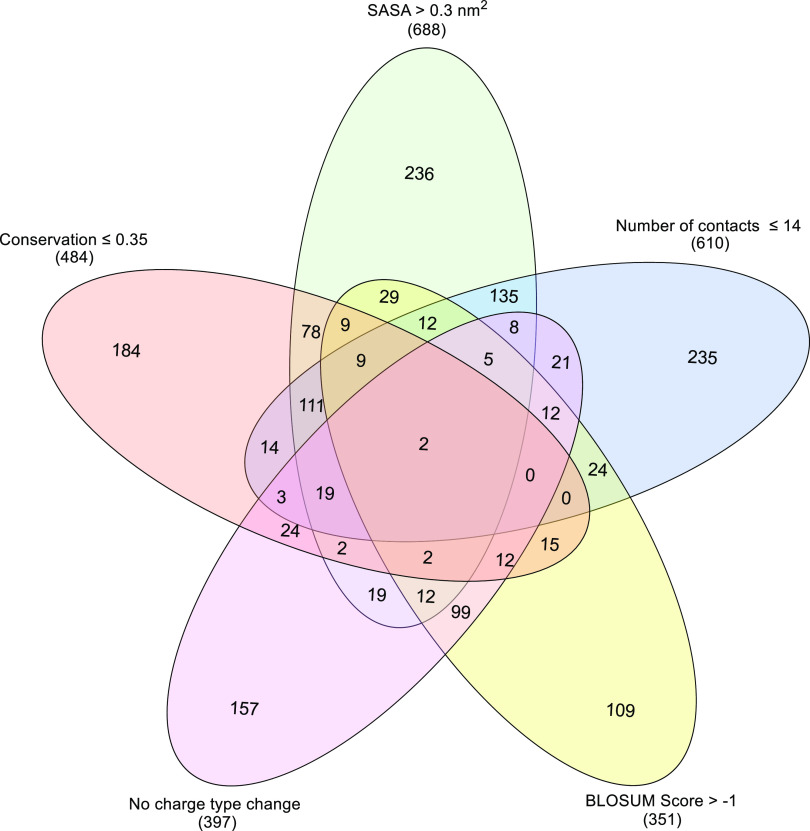
where Q_c represents a charge-type change, 1 if there is no change, and 0 otherwise. The model was tested on the remaining 30% and had an accuracy of 0.70, better than the accuracy of prediction using individual variables. A 10-fold cross-validation of the model yielded an average accuracy of 0.70 with standard deviation 0.01 for the test set. Taking cue from this, a threshold-based classification with several biochemical intuitions was systematically explored in Figure 6. In the analysis, a subset of mutations (2892 of them) from β-lactamase, which result in a fitness compromise (R ≤ −0.5), was analyzed. Each mutation was independently classified as neutral or deleterious using different descriptors and their corresponding threshold values. The numbers appearing in the different overlap regions in Figure 6 indicate the number of mutations for which the variables defining the overlap all result in a false neutral prediction. The interesting region in the center shows that when all five variables classify a mutation as neutral, there are only two false predictions. In addition to this combined representation, one can also see how the number of false neutral predictions reduces as the number of descriptors is increased one after another (Figures S9 and S10). Of course, in this approach, now a new kind of uncertainty will remain for a fraction of the substitutions when about half of the descriptors suggest a deleterious effect and the others point to neutrality.

Figure 6.

Reducing false predictions by combining variables. Venn diagram showing the number of substitutions that do not follow the intuitions related to different structural and sequence-related properties of the wild-type and the substituting amino acids. Thresholds indicated in the figure were used on each of the individual variables to classify the mutations as deleterious or neutral. The central region indicates that there are only two false neutral predictions when all five variables classify the mutation as neutral. The number of total false neutral predictions when only one variable is used is given in brackets below the variable labels.

3.9. Common Thresholds for Many Proteins

It is clear that the thresholds of the variables we obtained for different proteins varied significantly. For each protein, when multiple threshold criteria were satisfied, the error rate was smaller. We asked if it is possible to define universal thresholds or at least common thresholds for the data sets we have studied. For each of the variables, we used an average derived from the different proteins, i.e., the row averages in Table 1. Using these averages as thresholds, we recalculated how the error rate drops for all six proteins, as shown in Figures S11 and S12. The results are encouraging at this stage and suggest that by qualifying for at least three conditions with the threshold criterion, the chance of false predictions drops significantly. The details of true and false predictions when these average thresholds are applied individually on each protein are given in Supporting File 1. The classification based on average thresholds performs better for variants, which are suggested as either neutral or deleterious by all variables compared to the classification based on the BLOSUM substitution score as variants with score <0 are considered as deleterious and all others as neutral (accuracy 0.76 versus 0.66, McNemar’s p-value = 0).

We examined whether these thresholds vary on using another criterion for threshold determination such as maximizing the difference between the true positive rate (TPR) and the false positive rate (FPR) as obtained from an ROC analysis (Supporting File 1). While there were small changes in the threshold for individual proteins, the average of the thresholds for the number of contacts and the BLOSUM score remained the same. For conservation and SASA, the thresholds changed from 0.6 to 0.5 and from 0.2 to 0.3, respectively.

We also explored another approach to define common thresholds in which the F1 score analysis to find the threshold for each variable was performed on the data set containing variants of all six proteins. The thresholds obtained from this analysis were the same as the average threshold for the variables SASA, BLOSUM, and number of contacts, and for conservation, a threshold of 0.5 was obtained. The prediction quality when these thresholds are used individually for classification was evaluated using a 10-fold cross-validation approach. It was found that the thresholds determined had similar performances for both the training and validation sets in all of the cases. Also, the performance was stable across different folds as shown by the standard deviation of the performance (Supporting File 1).

3.10. Validation of the Common Thresholds

Since the common thresholds determined using different approaches did not differ significantly, we chose to perform all further analyses with one set of thresholds, the average of thresholds given in Table 1. We tested the predictive ability of the average thresholds on an independent data set of β-glucosidase (Bgl3)³⁶ that was not used for obtaining the common thresholds. Interestingly, for the set of variants suggested as either neutral or deleterious by all five variables, the fractions of false neutral and false deleterious predictions obtained were low, 0.07 and 0.16, respectively. The leave-one-protein-out³⁸ analysis, in which the thresholds obtained for five proteins are averaged and the quality of predictions is tested on the data set of the sixth protein, was performed as another validation. In all cases, the quality of predictions was similar to that with the average of thresholds of all six proteins (Supporting File 1).

4. Discussion

4.1. From Intuitions to Thresholds

Conservation of an amino acid has been a traditional benchmark to understand the functional relevance of amino acids as well as to infer the potential effects of their mutations. The intuitions such as when the conservation of an amino acid is sufficiently high, the chance of its mutation affecting the function is also high, were developed either from mutational studies or by comparing homologous proteins with sequence alignments. In this intuitive classification, two aspects remain qualitative: how high the conservation should be for it to be important and the quality of the resulting classification. Technically, this information may be derived by compiling the data on all the mutations available, but has not been done to our knowledge. However, the variations across proteins and experiments make comparisons difficult. The present work uses the publicly available systematic large data sets on mutational effects to shed light on both these aspects for six proteins. The thresholds obtained for the six proteins are all summarized in Table 1. It appears that the conservation threshold optimizing the false positives and false negatives varies widely from 0.35 to 0.9 for different proteins. The question then arises whether the thresholds vary with larger data sets or if one can identify universal thresholds. To address this question, one has to work with relatively large data sets, with reliable quantitative measurements of the mutational effects. At this stage, the deep mutational scanning measurements with different assay conditions and varying levels of stressor concentrations are indicative of the overall trends rather than precise measurements. Since to the best of our knowledge the thresholds have not been defined to date, we suggest the use of averages of the thresholds obtained from the different proteins and defer the universality aspect until a later occasion.

4.2. Optimization Has to Balance Several Factors

Any classification method has to balance between true and false positives and is likely to be biased by the over-representation of the neutral or deleterious class in the training set. The same is true for the rules of thumb we developed. We chose the F1_avg score as a measure to quantify this balance. However, as the F1 score focuses only on one class, we decided the optimal threshold as the one that maximizes the average of F1_neutral and F1_deleterious. It is clear from the data that there is no clear parameter that can be used as a threshold or a rule of thumb for improving the true positives, without also increasing the false positives. The false positives and false negatives were both minimized simultaneously using the sum of F1_neutral and F1_deleterious scores. Because of this optimization, any threshold- or rule-based classification will be partly incorrect. Further, the data we used from the deep mutational scanning has a larger fraction of neutral mutations (64%). Thus, there may be unavoidable biases in making predictions, which may be addressed with larger data in the future. Notwithstanding this limitation, we probed in detail the exceptions to the thresholding rules for β-lactamase. What appears to be an exception to the monotonous relation between conservation and fitness was explained by a charge-type change. The ambiguity in the sensitivity of amino acids that are in the intermediate ranges of SASA could be clarified by the change in volume upon mutation. Thus, while each of the variables studied is not complete, they may complement each other. This is expected, since proteins are complicated, and predicting structural or functional consequences of mutations with a single biophysical or biochemical variable is nontrivial.

4.3. Effect of Experimental Error on the Thresholds

We wanted to check whether the thresholds identified are robust against the uncertainty in the experimentally determined fitness scores, using the measurement errors available for β-lactamase, TPK1, and UBE2I. In the present work, any variant is first classified as neutral or deleterious by checking its fitness relative to a bi-Gaussian distribution, and then the predictive capacity of the variable was evaluated. However, for some of the variants, the two extremes for their fitness accounting for the error (variant fitness – standard deviation and variant fitness + standard deviation) can suggest different classifications, creating an uncertainty in what was meant to be a reference. We eliminated these uncertain variants from our analysis and recalculated the thresholds for the variables. For TPK1, eliminating these variants did not change any threshold; for β-lactamase, the BLOSUM threshold changed from −1 to −2; and for UBE2I, the threshold on the number of contacts changed from 18 to 22. However, while averaging to obtain the common thresholds, only the average threshold for the number of contacts changed from 18 to 19. This variation was within the scope of the sensitivity analysis we performed in Section 4.4 below, and practically the threshold may be considered robust relative to the experimental errors.

4.4. Sensitivity Analysis

Since the thresholds from different proteins varied, and the data was not sufficient to comment on universal thresholds, we performed a sensitivity analysis for the qualitative changes in conclusions with small changes in the thresholds. We varied the average thresholds (th_av) by an amount δth, which is approximately equal to 10% of the maximum value for that variable. We quantified the fraction of wrong predictions for both the neutral and deleterious classes when the threshold for a variable was varied, one at a time, as (th_av ± δth). We find that for the mutations that are predicted as neutral or deleterious by all five variables, this fraction remains the same in most of the cases although there are differences in the number of mutations identified on changing the threshold (Supporting File 1).

4.5. Scope of the Present Work in the Context of Existing AI Predictors

Advances in artificial intelligence are leading discoveries in several areas of science and engineering. The same is true for protein variant effect predictions, where models such as SNAP,²³ Envision,²⁵ or others²⁶ continue to improve the accuracy of classifications or fitness predictions. Many of the models have even created an easy-to-use web-based interface. The SNAP predictions are analyzed from this perspective by choosing only those mutations that were classified with an expected accuracy greater than 80%. The numbers of neutral or deleterious predictions we obtain with the average thresholds listed in Table 1 are shown in Table 2. It can be seen that though for a smaller set, the fraction of false predictions when thresholding criteria are used is comparable to that of SNAP. Clearly, when considering the complete set of mutations, the present work is no match to the AI models.

Table 2. Comparison with SNAP^a.

	SNAP predictions with expected accuracy ≥80%				using averaged thresholds
protein	number of mutations predicted as neutral	fraction of false neutral predictions	number of mutations predicted as deleterious	fraction of false deleterious predictions	number of mutations predicted as neutral	fraction of false neutral predictions	number of mutations predicted as deleterious	fraction of false deleterious predictions
β-lactamase	802	0.13	1317	0.04	200	0.18	183	0
APH(3′)-II	1156	0.03	673	0.47	289	0.04	186	0.45
Hsp90	578	0.01	1151	0.59	231	0.02	260	0.58
MAPK1	594	0.02	1507	0.44	185	0.03	447	0.40
UBE2I	32	0.06	751	0.26	146	0.14	161	0.11
TPK1	655	0.41	668	0.31	183	0.37	207	0.31
Bgl3b	665	0.14	695	0.17	140	0.07	190	0.16

^aSNAP predictions with expected accuracy ≥80% were selected and the fractions of false neutral/deleterious predictions for this set of mutations were calculated. Using the average of thresholds tabulated in Table 1, mutations predicted as neutral or deleterious by all five variables were identified, and the fractions of false predictions for these sets are given in the table. It can be seen that the quality of classification achieved using just simple thresholding criteria compare with that of SNAP though for a smaller set of mutations.

^bBgl3 data, which was not used for training, was added as an independent validation.

However, in several areas of AI, there has been a concern about the lack of transparency in the way AI treats the predictions, with a twofold motivation: (1) assuming that the predictions are correct, is it possible to find the contributions to each individual prediction so that one has a better understanding of the final output. For example, such factor contributions can help find mutations where the solubility and fitness changes from the mutation are both acceptable. (2) Although on average the prediction quality is high, how can one be sure that a specific prediction is reliable? Is it possible to, for example, correlate the factor contributions with known intuitions so that one gains confidence in the final prediction of the effects? Thus, there is always a need for intuitions or at least rules of thumb that empirically codify the observations. Further, despite the ability to have accurate calculations, in other parts of the literature, qualitative statements about critical variables being high or low continue to exist. The present work, while acknowledging its shortcomings relative to the AI-based models, aims to improve the qualitative intuitions by quantifying them with thresholds. Of course, the limitations are that it is not easy to comment on mutations where the suggestions from the five variables are not correlated, and it is possible to comment only on mutations where all the variables suggest the mutation to be neutral or deleterious. Given this limitation, when a mutation is implicated for a disease, for example, the present method is not useful for classifying such critical mutations. Instead, it can be used as an inverse approach where the mutations suggested by the thresholds to be deleterious or neutral can be believed to be so with a high degree of accuracy. The limitation of the thresholding could be related to the small training set or the site-specific nature of the descriptors we chose, which may fail to capture the distal effects of mutations. The present approach is an important step toward codifying the learnings from a pedagogical perspective and is helpful for quick analysis when all variables suggest a similar outcome. The question of whether these thresholds can be universal is beyond the scope of the present work and should be revisited with data much larger than what has been used and descriptors that capture long-range effects of mutations.

5. Conclusions

Different physicochemical and evolutionary factors describing native amino acids or their substitutions were evaluated in this work for their potential to capture the loss of protein function upon mutation. Visual representations of the large-scale mutational data on six proteins were used to establish correlations, albeit weak ones, between the individual descriptors and the functional effects. We attempted to obtain a double quantification of the common intuitions, such as when the descriptor is sufficiently large, it is likely to have a significant effect. Threshold values for the descriptors that can be used for classification and the consequent false predictions were discussed. Combination of these simple rules of thumb improves the confidence in the predictions, although of a smaller set of mutations. The approach thus attempts to quantify the physicochemical intuitions, which we believe is complementary to the more accurate but complex machine-learning-based approaches.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c02402.

• Comparison of the fitness effects of mutations in β-lactamase reported in two different deep mutational scanning experiments; comparison of fitness with ΔPSSM (= PSSM_wildtype − PSSM_mutant); conservation-fitness correlation and F1 score analysis; SASA versus fitness for the alanine substitutions; relation between fitness and SASA and the F1 score variation as the SASA threshold is changed; fitness dependence on the number of contacts and the F1 score analysis for β-lactamase; number of contacts-fitness correlation and changes in F1 score with changes in the number of contacts threshold for the proteins APH(3′)-II, Hsp90, MAPK1, UBE2I and TPK1; BLOSUM score versus fitness and the F1 score analysis; reduction in the chance of false neutralpredictions on increasing the number of threshold criteria used for classification; variation in the number of false neutral predictions with respect to the number of threshold criteria, chance of false neutral predictions versus number of variables used for classification for all proteins (PDF)

• Descriptive variables: data used for calculation (Sheet 1); variable-fitness correlations: correlation of variables with the fitness score (Sheet 2); classification using thresholds: the number of true and false predictions when average thresholds are used (Sheet 3); ROC analysis: the thresholds obtained based on ROC analysis and the area under the ROC curve (Sheet 4); cross-validation analysis: the mean and standard deviation of performances for the training and validation sets (Sheet 5); classification leave-one-out: the number of true and false predictions for the leave-one-protein-out analysis (Sheet 6); sensitivity analysis: the consequences of having a 10% variation in the thresholds (Sheet 7) (Supporting File 1) (XLS)

The authors declare no competing financial interest.