Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Nov 10;5(46):29780–29794. doi: 10.1021/acsomega.0c03679

The Impact of Spatially Correlated Heterogeneity and Adsorption on Modified Salinity Water in Carbonates

Mirhossein Taheriotaghsara 1,*, Seyedbehzad Hosseinzadehsadati 1,*, Hamidreza M Nick 1
PMCID: PMC7689675  PMID: 33251413

Abstract

graphic file with name ao0c03679_0020.jpg

Modified salinity water (MSW) core flooding tests conducted in carbonates often exhibit a delay in the additional oil recovery. It has been suggested that the ionic adsorption process controls this delay. In this study, we examine the adverse effect of the adsorption process on the performance of MSW flooding in various models categorized as layered and heterogeneous reservoirs and a North Sea field sector model. To evaluate the impact of porous media’s heterogeneity on the delay caused by the adsorption, we introduce the net present volumetric value based on which the cost of delay is calculated. This evaluation is achieved by comparing the calculated cost of delay for heterogeneous systems and that of their equivalent homogeneous porous media. It is found that, as the level of reservoir heterogeneity increases, the adverse effect of ionic adsorption on the improved oil production decreases. Further, computational results suggest that the connectivity index, which is defined as the effective permeability between injection and production wells divided by the average permeability, is a better alternative to the vorticity index to describe the impact of the delay of additional oil recovery in heterogeneous reservoirs subjected to MSW flooding.

1. Introduction

Modified salinity water (MSW) flooding is a developing enhanced oil recovery (EOR) technique that aims at decreasing the residual oil saturation and speeding up the rate of oil production.1−3 MSW is fabricated through modification of ionic composition or/and salinity reduction of injecting brine.4−6 Extensive studies have been conducted on the framework of MSW flooding in sandstone and carbonate rocks to explain the principal mechanisms for the enhancement of oil recovery.2,7−14 The forced core flooding test is one of the most commonly used techniques that is served as the primary evidence for the efficiency of MSW on the improvement of oil recovery at the core scale. MSW core flooding tests are usually studied in two different ways, namely, secondary and tertiary modes. Secondary mode refers to the injection of MSW into a core saturated with formation brine and crude oil. Tertiary mode refers to the mobilization of the residual oil after secondary mode oil production by switching the injecting brine composition from high-salinity formation brine to MSW (e.g., low-salinity brine). The variation of ionic composition in injecting brine disturbs the physicochemical equilibrium condition in the porous medium that may lead to the detachment of residual oil from the rock surface and possibly improvement of oil recovery.15

1.1. Modified Salinity Water Flooding in Homogeneous Systems

Generally, homogeneous core plug samples are selected for core flooding tests to eliminate the influences of heterogeneity. During core flooding tests, several parameters such as the produced volume of oil and water, the pressure difference across the core sample, and the ionic concentrations of injecting and producing brine are monitored as a function of time or pore volume (PV) of the injected brine. Figure 1 schematically illustrates the behavior of the mentioned parameters during the secondary and tertiary modes of MSW flooding in a homogeneous porous medium. For a responsive oil-rock-brine system to the implementation of MSW flooding, the oil recovery in both secondary and tertiary modes increases compared to that obtained from the formation water (FW) flooding.13,14,16−18 During MSW flooding, the pressure difference along the core sample may reduce compared to FW flooding mainly due to lower water relative permeability for MSW injection than that of FW and possible viscosity reduction of injecting brine (Figure 1b,g).17,19,20Figure 1c,h shows the profile of water saturation as a function of dimensionless distance, xD = x/L, over dimensionless time, tD = Qt/(AφL) where Q (m3/s), t (s), A (m2), φ (−), and L (m) are the rate of injection, time, cross-sectional area, porosity, and the length of the core, respectively. Injection of MSW reduces the residual oil saturation that results in the formation of a second oil bank ahead of the MSW shock front. The water-cut shows a dual-step behavior (Figure 1d,i). In secondary mode, the water-cut jumps and then levels off until the extra oil due to MSW flooding is produced. When MSW saturation shock front reaches to the end of the core, the water-cut exhibits another jump. However, in tertiary mode, the water-cut reduces (Figure 1i) and becomes constant due to the formation of a new oil bank ahead of the saturation shock front and jumps again as the saturation shock front reaches to the end of the core.21−23 The ionic concentration profiles may exhibit considerable delay compared with a nonreactive tracer concentration because of the reactivity of the rock surface with the displacing brine (see Figure 1e,j).20,24,25 Taheriotaghsara et al.17 linked the transport of adsorptive ionic species in the porous medium to the process of the wettability change on the rock surface from oil-wet to more water-wet conditions. They analyzed several core flooding tests and observed that the oil breakthrough in the tertiary mode takes place with a delay, i.e., later than the time at which the injected MSW breaks through. For instance, Figure 1a,f suggests that the adsorption effect results in a delay for the extra oil production. This means that for a homogeneous system, the practical (economic) benefit from the implementation of MSW comes with a delay when the adsorption process is considered for the calculation of ionic species, oil, and brine transportation. The impact of the delay on the water saturation profile is the shift on the shock-front that translates into the delay for the arrival of a new oil bank. Also, this delay postpones the appearance of the secondary jump in water-cut.

Figure 1.

Figure 1

Open in a new tab

Schematics of modified salinity water flooding effect during secondary (upper figures) and tertiary (lower figures) modes on oil recovery (a, f), pressure difference (b, g), water saturation (c, h), water-cut (d, i), and outlet potential determining ions (PDI) concentration profiles (e, j). Solid black, blue, and red lines illustrate the response to formation water (FW) flooding, MSW flooding with and without adsorption processes, respectively. The circle markers (BT) show the water breakthrough time during secondary mode water flooding. The black vertical dotted lines indicate the beginning of the tertiary mode water flooding.

1.2. Modified Salinity Water Flooding in Heterogeneous Systems

It is well documented that the presence of heterogeneities in physical, chemical, and mechanical properties of the reservoir’s rock and fluid can affect the macroscopic sweep efficiency and oil recovery.26−30 For instance, the effects of porosity and permeability heterogeneity on the final oil recovery can be influenced by the flow direction, well patterns, depositional environment, and driven mechanisms.31−34 In addition, in a viscous dominated flow regime, the presence of a high permeable zone in layered reservoirs results in the channelling of displacing fluid, hence causing the reduction of final oil recovery.35 The effect of channelling on the ultimate oil recovery can be even more detrimental when there is an adverse viscosity ratio between the displaced and displacing fluids. The adverse viscosity ratio results in the formation of viscous fingering problems leading to an early breakthrough in displacing fluid.36−38 Moreover, the density gradient between the displaced and displacing fluids accompanied by the presence of heterogeneity in a layered reservoir may result in the deviation of the flow direction.39 Commonly, the presence of heterogeneity in the reservoirs develops poor areal sweep efficiency that leads to large packets of bypassed oil.40 Similar to the conventional water flooding, the performance of MSW flooding in the improvement of oil recovery is dependent on both geological and physicochemical heterogeneities.41−44 For instance, the initial spatial heterogeneity in salinity and ionic composition of formation brine,14,45−51 rock wetting preference,52−55 mineralogy and chemical activity of the rock surface,14,55−58 and thermodynamic properties of oil-rock-brine (ORB) system46,47,49,51,59−64 in the reservoir may have an adverse effect on the success of MSW flooding. Due to the presence of various forms of heterogeneity at the reservoir scale, the scalability of the obtained responses from MSW core flooding experiments to the larger scale requires considerable precautions. The application of MSW at the oil field scale is still limited due to the unknown effects of geological uncertainty and heterogeneity on the performance of MSW flooding.65 Reservoir simulations are commonly used to study the impact of heterogeneity on the performance of MSW flooding. Al-Ibadi et al.66 provided a predictive analytics tool for estimating waterfront in a noncommunicating stratified porous medium using the analytical solution of one-dimensional fluid flow and solute transport in the porous medium. Attar et al.67,68 investigated the influence of geological heterogeneity on the oil recovery and water breakthrough time as a function of slug size of MSW injection during secondary and tertiary modes. It was shown that as the level of heterogeneity increases, less oil could be recovered and the water breakthrough time occurs earlier compared with those of the equivalent homogeneous system. As the initial wetting condition is vital in the performance of MSW flooding, Aladasani et al.69 studied the modelling of MSW in a five-spot reservoir under the various wetting states. They concluded that the increment of oil recovery in oil-wet carbonate rock is more rapid compared with other wetting conditions.69

1.3. Problem Statement

The analyses of several MSW flooding tests in various types of homogeneous carbonate core plug samples (e.g., chalk, dolomite, limestone) revealed that tertiary oil breakthrough typically occurs after a 0.6 pore volume of MSW injection.17 The observed delay has been associated with the adsorptive transport of some key ions and the diffusion-controlled wettability alteration.70 Upscaling such a delay to the reservoir scale without considering the presence of heterogeneity is equivalent to decades of waiting time. However, the analysis of oil production from a few field trials of MSW flooding shows that the timing of oil bank production coincides with MSW flooding injection.21,22,71 The objective of this study is to investigate the role of geological heterogeneity on the delay in oil production caused by the ionic adsorption process through the application of MSW flooding in carbonate rocks. With this aim, first, we present the governing equations of the two-phase flow and transport of the PDIs. Then, we illustrate various types of heterogeneous systems, such as a simple layered system, heterogeneous reservoirs, and a sector-scale model with contrasting petrophysical properties. Finally, we compare the cost of delay calculated for homogeneous reservoirs with that of heterogeneous reservoirs.

2. Methodology

Through the following section, the method for simulating MSW flooding in various reservoir models is described. Also, several techniques for ranking of the complexity of the studied heterogeneous models are presented.

2.1. MSW Flooding Simulator

Eclipse 100 (Schlumberger’s simulator) is used to investigate the effect of heterogeneity on the performance of MSW flooding in two- and three-dimensional models. Eclipse 100 uses the salinity thresholds for MSW flooding72 by interpolating between the oil and water relative permeability curves as a function of salt concentration.73 Four sets of heterogeneous models are generated, and the details of their configurations are discussed in section 2.2. The level of complexity for the heterogeneous models is evaluated through the calculation of probability density function (PDF) of single-phase velocity, vorticity index, and connectivity index (see section 2.3). Table 1 shows the employed Broke–Corry parameters and fluid properties that are used for the simulation of MSW flooding in models 1–3. To exclude the problem of viscous fingering and deviation of the flow direction due to the adverse viscosity ratio and gravity gradient, the viscosity and density for both phases of oil and water are kept equal to 0.001 Pa·s and 1000 kg/m3, respectively. The Broke–Corry parameters of the relative permeability and ionic composition of intrinsic and injecting brine (Tables 1 and 2) are extracted from the analysis of a limestone core flooding experiment, conducted by Gupta et al.18 that is reported in a reference (core ID: L1).17 The ionic composition of intrinsic and injecting brine for all designed models are considered the same. Figure 2 shows the shape of oil and water relative permeability curves for FW and MSW. This figure illustrates that the wettability of the rock surface shifts toward the more water-wet condition by the application of MSW flooding. The injection rate and initial pressure are equal to 50 m3/day and 2.73×107 Pa, respectively.

Table 1. Fluid Properties and Employed Brock–Corry Parameters for Oil and Water Phase Relative Permeability17.

  fluid properties
 Corey’s relative permeability parameters
brine μw (Pa·s) μo (Pa·s) ρw (kg/m3) ρo (kg/m3) krw0 kro0 nw no Swc Sor
FW 0.001 0.001 1000 1000 0.066 0.417 2.586 1.917 0.108 0.394
MSW 0.001 0.001 1000 1000 0.063 0.592 3.264 1.648 0.102 0.358
Open in a new tab

Table 2. Ionic Concentrations of FW and MSW (ppm)17.

ions Na+ Ca2+ Mg2+ k+ SO4–2 Cl– HCO3–
FW 51,820 15,992 1280 0.0 272 111,516 391
MSW 10,345 521 1094 391 9222 11,911 0.0
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

Oil and water relative permeabilities for oil-wet (FW) and water-wet (MSW) systems.

We implemented ionic adsorption, the amount of adsorbed species on the rock surface as a function of ionic concentration, by using the tracer option in Eclipse 100. For this aim, the procedure described in ref (17) is followed. The interested reader is referred to ref (17) for a detailed description of the methods. The linearized form of the Langmuir isotherm, eq 1, is used to estimate the amount of single-ion species adsorption on the rock surface as a function of the ionic concentration in the injecting brine.

2.1. 1

where Γi (mol/m2) is the amount of adsorbed component, Ci (mol/m3) is the concentration of component i in the injecting water, and kc (m) and β (m3/mol) are the Langmuir’s constants. The Langmuir constants for the relevant ions for the MSW flooding are determined through defining a background electrolyte concentration for the solution in PHREEQC and changing the other ion concentration successively. In doing so, an initial concentration of NaCl of 0.5 M is considered as a background electrolyte. In this study, the adsorption of SO42– ion is taken into account as the wettability modifier. Therefore, the SO42– ion concentration is increased from 0.01 to 0.1 M by adding the necessary concentrations of Na2SO4 to the background electrolyte, i.e., NaCl. Other parameters required in the implementation of the surface complexation model in PHREEQC are related to the surface. We set a specific surface area (SSA) of 2.5 m2/g, and the amount of active surface site density is equal to 4.95 #/nm2.74−77 The initial solutions are charged balanced, and we perform the calculations at the equilibrium pH predicted by PHREEQC. We then represent 1/Γi against 1/Ci and from the equation of the linear trend line passing through different data points, Langmuir constants are obtained (Figure 3). In this study, it is assumed that the rock types for all models is calcite.

Figure 3.

Figure 3

Open in a new tab

Amount of component adsorbed Γi vs concentration in the aqueous phase (Ci) for SO42–.

2.2. Model Configuration for the Numerical Examples

Four different models are prepared to evaluate how the observed delay in the MSW core flooding experiments manifests itself at the reservoir scale in the presence of porosity and permeability heterogeneity. These models are introduced in the following.

2.2.1. Model-1: Layered Reservoirs

Figure 4 shows various reservoir models comprising 1, 2, 4, and 20 layers with the same original oil in place (OOIP) equal to 54,400 m3. The models are discretized with 500 × 1 × 200 blocks. The lengths of models in x, y, and z-directions are 200, 200, and 80 m, respectively. It is assumed that the producing and injecting wells are completed in the first and last columns of the grids, respectively. The performance of MSW in layered reservoir models is studied for two sets of permeability distribution. Model-1-I and Model-1-II have the permeability range between 0.1 and 10 mD and 1 and 10 mD, respectively.

Figure 4.

Figure 4

Open in a new tab

Schematics of layered models (a) 1-layer, (b) 2-layer, (c) 4-layer, and (d) 20-layer. The permeabilities for the top layer in Model-1-I and Model-1-II are 0.1 and 1 mD, respectively, and the bottom layer permeabilities in both models are 10 mD. The permeability in the middle layers is the log spaced between the top and bottom layers. The average absolute permeabilities for the layered reservoirs from a to d in the Model-1-I are 10, 5.05, 3.18, and 2.3 mD, respectively. Also, the average permeabilities for Model-1-II are 10, 5.5, 4.45, and 3.99 mD.

2.2.2. Model-2: Heterogeneous Media

Figure 5 depicts various heterogeneous realizations for a single-layer reservoir model (Model-2). The lengths of the models and discretization are similar to the Model-1. Similar to Nick et al.,78 correlated fields are generated with a mean of 0.5 mD and variance, σ2 = 0.5. Three sets of permeability fields with the correlation length in the y-direction equal to 1, 5, and 10 m are considered. For each of these sets, four permeability fields are generated with different correlation lengths in the x-direction equal to 1, 5, 50 and 200 m. In total, 3 × 4 = 12 permeability fields are made. The porosity is calculated using eq 2.79

2.2.2. 2

Due to the presence of heterogeneity, the local fluctuation of the velocity occurs in the reservoir. The histogram of single-phase flow velocity provides quantitative insights into the complexity in heterogeneous systems. For instance, the probability density function (PDF) of velocity for Ly = 1 m shows that as the correlation length in the x-direction increases, Lx = 1, 5, 20, 200 m; the distribution of velocity range becomes wider; however, the maximum value for PDF reduces. For models with Ly = 1 m, the fluid flow encounters less disturbance for the displacement inside the reservoir compared to models with higher Ly. On the other hand, for models with Lx = 1 m, as the correlation length in the y-direction increases, the distribution of the velocity range becomes more narrow; however, the maximum value of PDF increases. For this example, the direction of single-phase flow displacement is perpendicular to the direction of the maximum principal equivalent permeability, which renders the single-phase movement harder in the reservoir.

Figure 5.

Figure 5

Open in a new tab

Twelve permeability fields generated for Model-2. The flow is from left to right.

2.2.3. Model-3: Quarter Five-Spot

Figure 6 displays the permeability fields for Model-3. The correlated fields are generated with a mean of 0.5 mD and variance, σ2 = 0.5. The lengths of models in x, y, and z-directions are 200, 200, and 80 m, and the models are discretized with 200 × 200 × 1 blocks, respectively. The locations of producing and injecting wells are shown with red and blue circles, respectively. Figure 7 shows the PDF of velocity for the heterogeneous systems in Model-3. Both models have the same distribution of velocity, approximately.

Figure 6.

Figure 6

Open in a new tab

Schematics of Model-3 with three permeability fields for quarter 5-spot well pattern.

Figure 7.

Figure 7

Open in a new tab

Probability density function (PDF) of velocity with the intervals of 50 for two heterogeneous realizations of Model-3.

2.2.4. Model-4: Sector Field Scale

A North Sea sector model is selected to study the effect of the adsorption process on MSW flooding performance (Figure 8). The 3D-sector model has a size of 440 × 5264 × 860 m3 and discretized into 78 × 45 × 88 grid-blocks for the simulations. A horizontal producing well is located between two horizontal water injection wells. In the original model, parallel hydraulical fracture exists along the injection wells to increase the sweep efficiency and injectivity. For the sake of simplicity, the fractures are not included in the model in this study. Note that the initial spatial heterogeneity of initial water saturation, porosity, and permeability in all directions are defined in the current model.

Figure 8.

Figure 8

Open in a new tab

3D North Sea reservoir sector model with three horizontal wells. The color illustrates the distribution of permeability in the x-direction

2.3. Analysis Strategy

Three different characteristic parameters are calculated as follows: (1) vorticity index, Hs, (2) connectivity index, α, and (3) normalized cost of delay, NCD.

2.3.1. Vorticity Index

It works based on the variation of the share-strain rate of the single-phase-velocity field to characterize heterogeneity and rank the geological realization based on their effects on secondary-recovery performance.40 The shear deformation rate describes how the shape of a rectangular packet of single-phase fluid may change as it moves from one location to another one. Rashid et al.40 used eq 3 as the definition of rate-of-share-deformation.

2.3.1. 3

where Δu(m/s) and Δv(m/s) are the gradients of velocity in x- and y-directions, respectively. The level of heterogeneity is calculated by40

2.3.1. 4

The value of Hs tends to zero as the reservoir becomes more heterogeneous, and Hs tends to infinity as the reservoir becomes more homogeneous.40

2.3.2. Connectivity Index

The interconnectivity of different sections of a reservoir with respect to the injection and production wells can reflect another aspect of complexity in a heterogeneous system. The connectivity index is defined as effective permeability between injection and production wells divided by the average permeability α = Keff/K̅. The arithmetic average permeability K̅ is equal to 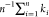Inline graphic where ki is the permeability value in a block, i, and n is the total number of blocks in a model. The effective permeability (m2) values for Model-1 and Model-2 are calculated from Darcy flow equation, as (eq 5)

2.3.2. 5

where Q (m3/s) is the injection rate, μ (Pa·s) is the fluid viscosity, A (m2) is the cross-section area, L (m) is the distance between injection and production wells in Model-1 and Model-2, and ΔP (Pa) is the pressure difference between injection and production wells. In Model-3, the effective permeability of the system is calculated using the radial flow equation, as (eq 6)

2.3.2. 6

where re (m) is the distance between injection and production wells, which is equal to 200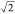Inline graphic m, and rw (m) is a wellbore radius (we assumed that rw = 0.13 m in the simulations).

2.3.3. Cost of Delay

Figure 1a,f shows the profiles of oil recovery with/without consideration of the adsorption process during secondary and tertiary modes of MSW flooding, respectively. The difference between the blue and red lines is equivalent to the amount of induced delay due to consideration of the adsorption process. In practice, the earlier oil production worth more than later oil production from an economic standpoint. Therefore, to incorporate delay in our evaluations, the cumulative net present volumetric value (NPVV) of produced oil as a function of time subjected to the discount rate of 8% is calculated. Eq 7 shows the employed NPVV where Vp (m3), R (−), and t (year) denote the yearly volume of produced oil, interest rate, and production time, respectively. The cost of delay induced by the adsorption process on oil NPVV and the normalized cost of delay (NCD) are calculated using eqs 8 and 9, respectively.

2.3.3. 7
2.3.3. 8
2.3.3. 9

3. Results and Discussion

Through this section, we discuss the performance of MSW flooding with and without consideration of the adsorption process in several heterogeneous systems.

3.1. Mesh Sensitivity

In this section, the sensitivity of the observation of the water breakthrough time with the adsorption effect and delay as a function of the block size are studied. We generated a heterogeneous system with a mesh of 25 × 1 × 10 grid-blocks and a similar size to the Model-1 and Model-2. Then, we started reducing the block size to obtain the response of water breakthrough and delay to mesh refinement, as shown in Figure 9. As the number of blocks increases (i.e., the size of each grid block reduces), the estimation of water breakthrough time increases and approaches a constant value. The calculation of error for water breakthrough time considering the finest grid as the reference solution shows that selecting 500 × 200 blocks results in an acceptable error (<0.5%). As it is shown in Figure 9b, the calculated delay is less sensitive to the mesh size. Based on these analyses, the size of the employed blocks for the Model-1 and Model-2 simulations is set to 0.4 m, and for Model-3, the element size is 1 m. Current simulation refers to the mesh size used for Model-1 and Model-2.

Figure 9.

Figure 9

Open in a new tab

Sensitivity of (a) water breakthrough time with the consideration of adsorption effect and (b) calculated delay during secondary mode MSW flooding to the block size. h = L/n where L = 200 m and n are the length and number of blocks, respectively. The time step is set equal to 6 (h).

3.2. Model-1: MSW Flooding in Layered Reservoirs

Figure 10 shows the performance of secondary and tertiary modes of MSW flooding in various layered reservoir systems for Model-1-I. The plots with dashed and solid lines display the result of simulations with and without consideration of the adsorption process, respectively. The induced delay due to the adsorption process in a single-layer homogeneous reservoir results in the separation of the solid and dashed line in oil recovery, water-cut, and salt concentration curves. This behavior is observed both in secondary and tertiary modes. As the number of layers increases, for instance, the 20-layer reservoir case, the difference between the dashed and solid lines in oil recovery curve can hardly be distinguished. Also, the presence of several layers affects the level of final oil recovery for a constant volume of MSW injection (e.g., after injection of 1 PV). For both secondary and tertiary modes of MSW flooding, the rate of oil production increases as the number of layers increases. The 2-layer shows the lowest value of vorticity index, Hs, and connectivity, α, which translates into the most heterogeneous case. However, as the number of layers increases, the homogeneity level and connectivity of the defined cases improve, which is in line with the trend of final oil recovery. The profile of water-cut during secondary mode shows that, as the number of layers increases, the water breakthrough occurs faster compared to the homogeneous system. High permeable layers cause an early water breakthrough since most of the injection water preferentially flows into. Also, during the tertiary mode, the water-cut drops sooner in a multilayer reservoir compared to the homogeneous system. Similar behaviour is observed for the profile of producing salt concentration during the secondary and tertiary modes.

Figure 10.

Figure 10

Open in a new tab

Performance of MSW flooding in secondary (first column) and tertiary (second column) modes in the layered reservoirs, Model1-I. The tertiary mode starts after the injection of a 0.5 pore volume of FW. The level of homogeneity improves as the number of layers increases. The ionic adsorption process is included for the model results shown with dashed lines, while for the solid lines, the ionic adsorption is ignored.

The saturation fields for Model-1-I and Model-1-II with/without consideration of the adsorption process are shown in Figure 11 to illustrate the sensitivity of the delay in layered reservoir cases to the permeability contrast. The yellow and black dashed lines show the location of the water saturation shock front for the studied cases with/without consideration of the adsorption process, respectively. The obtained results show that as the number of layers increases, the difference between the black and yellow dashed lines reduces implying that the delay in oil production is less significant. Figure 11 shows that more layers contribute to oil production in Model-1-II, and water breakthrough occurs slower than the scenarios with Model-1-I.

Figure 11.

Figure 11

Open in a new tab

Water saturation fields for heterogeneous systems in Model-1. The water saturation fronts (due to MSW injection) for the simulation with and without consideration of the adsorption process are shown with yellow and black dashed lines, respectively.

3.3. Model-2: MSW Flooding in Heterogeneous Media

The profile of oil recovery, water-cut, and salt concentration during secondary and tertiary modes of MSW flooding for Model-2 with/without consideration of the adsorption process are shown in the Supporting Information (Figure S3). Figure 12 shows the profile of the normalized cost of delay (NCD) for the discount rate of 8% that is calculated using eq 9. The obtained results for a constant correlation length in the y-direction show that as the connectivity index, α, increases; the maximum of NCD reduces; however, NCD becomes more dispersed as a function of time. This trend is observed for both secondary and tertiary modes of MSW injection and all other correlation lengths in the y-direction. Moreover, there are two differences between the profile of NCD in secondary and tertiary modes. First, the maximum delay in the secondary mode is slightly higher than the maximum delay in the tertiary mode for all heterogeneous cases. For instance, the maximum NCD for the case “Lx = 200 Ly = 200 m” in secondary and tertiary mode is approximately 0.73 and 0.67 (−), respectively. The second difference is the shift on the profile of NCD during tertiary mode compared with that of the secondary mode. This shift is due to the production of extra oil at a later time in tertiary mode compared with the secondary mode. In Figure 13, the maximum NCD for all heterogeneous systems for Model-2 is shown as a function of connectivity and vorticity index, Hs, during secondary and tertiary modes of MSW flooding. The obtained results show that the maximum NCD has a reducing trend as the connectivity, α, increases; however, no correlation for the maximum value of NCD as a function Hs is obtained.

Figure 12.

Figure 12

Open in a new tab

Calculated normalized cost of delay during secondary (upper row) and tertiary (lower row) modes for Model-2.

Figure 13.

Figure 13

Open in a new tab

Maximum normalized cost of delay as a function of (a) connectivity and (b) vorticity index.

Figure 14 shows the profile of water saturation after 0.3 PV of MSW injection in heterogeneous cases with a constant correlation length of 5 m in the x-direction. The dashed lines indicate the water saturation front at the tip. The difference between the black and yellow dashed lines is due to the retardation caused by the adsorption process. For the model with the smaller correlation length in the y-direction, e.g., Ly = 1 m, the heterogeneous systems results in more pronounced fingering; however, as correlation length in the y-direction increases, e.g., Ly = 10 m, a more piston-like displacement of the phase can be observed. The water saturation fields for all considered cases in Model-2 are presented in the Supporting Information (Figure S2).

Figure 14.

Figure 14

Open in a new tab

Profile of saturation distribution for isotropic single-layer reservoir with a constant correlation length of Lx = 5 m across various correlation lengths in the y-direction. The yellow and black dashed lines show the water saturation fronts (due to MSW injection) for the model with and without consideration of the adsorption process, respectively, after 0.3 PV MSW injection.

3.4. Model-3: MSW Flooding in the Quarter Five-Spot

Similar to the effect of heterogeneity on NCD observed in Model-2, the delay induced by the adsorption process is reduced considerably for heterogeneous systems in Model-3 (Figure 15). It is evident that this reduction is more pronounced in tertiary scenarios. The maximum NCD observed for the heterogeneous cases under tertiary mode is limited to 30% of that of the homogeneous reservoir. The reduced adverse impact of adsorption on recovery is due to velocity variation controlled by heterogeneous permeability. Figure 16 compares the saturation distribution of homogeneous and heterogeneous models with/without consideration of the adsorption process. The difference between the yellow and black dashed lines representing the saturation fronts for MSW illustrates the effect of the induced delay. Note that the pore volumes of the considered examples in Model-3 are different, leading to the observation of various oil breakthrough times.

Figure 15.

Figure 15

Open in a new tab

Calculated normalized cost of delay during (a) secondary and (b) tertiary modes, Model-3.

Figure 16.

Figure 16

Open in a new tab

Profile of saturation distribution for the isotropic single-layer reservoir with well arrangement of quarter 5-spot. The upper and lower figures show the result of the simulation without and with consideration of the adsorption process, respectively. The yellow and black dashed lines show the water saturation fronts (for MSW flooding) for the model with and without consideration of the adsorption process, respectively, after 0.3 PV MSW injection.

3.5. Model-4: MSW Flooding in Field-Scale

The performance of MSW flooding in a North Sea field sector model is displayed in Figure 17. The obtained result for the oil recovery during secondary and tertiary modes of MSW flooding with/without consideration of the adsorption process showed a marginal difference. The results suggest that the manifestation of the delay observed in the core flooding experiments may not be significant at the field scale. Figure 18 compares the profile of the normalized cost of delay during secondary and tertiary modes for the North Sea sector model. The obtained profiles show that the cost of delay is considerably low for both secondary and tertiary modes. Also, due to the effect of the discount rate plus the time of oil production at a later time, the cost of delay for secondary mode is higher than the tertiary mode. It should be noted that MSW is injected after 20 years of seawater injection in tertiary mode.

Figure 17.

Figure 17

Open in a new tab

Profile of oil recovery for (a) the secondary mode and (b) the tertiary mode for North Sea sector model with and without consideration of the adsorption process.

Figure 18.

Figure 18

Open in a new tab

Profile of normalized cost of delay during secondary and tertiary mode for North Sea sector model.

It should be noted that the adsorption coefficient obtained from the core flooding test is employed directly for the field sector model with a somewhat large element size. Raoof et al.80 suggested that the equilibrium adsorption coefficients are scale-dependent. Therefore, further investigations are required for scaling up of the adsorption parameters from the core to field scale to provide better predictive models. Note that the costs of delay values for this example are normalized through dividing the volumetric cost of delay by cumulative oil production within the 60 years.

4. Conclusions

The objective of this study is to investigate the influence of heterogeneity in various forms on the performance of modified salinity water flooding. To study the effect of geological heterogeneity systematically, several models are built, and the performance of the different models with and without considerations of the adsorption process is studied. The main findings of this study are as follows:

  • The anticipation of field response to the injection of MSW just by scaling the results from core flooding tests to the field scale induces a considerable error on the estimation of final oil recovery improvement and the oil breakthrough time.

  • The results for the layered reservoir models during secondary and tertiary modes of MSW flooding suggest that, as the number of layers in the model increases, the induced delay for oil breakthrough time due to the adsorption process is reduced.

  • In the heterogeneous reservoirs (Model-2), as the connectivity between the injection and production well increases, the maximum normalized cost of delay (NCD) is reduced.

  • The calculated delay in various heterogeneous models shows a nonmonotonic response to the variation of the vorticity index.

Acknowledgments

We would like to thank Danish Hydrocarbon Research and Technology Centre for supporting and funding this research.

Glossary

Abbreviations

MSW

modified salinity water

PDI

potential determining ions

FW

formation water

CWF

conventional water flooding

NCD

normalized cost of delay

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c03679.

  • Performance of MSW in stratified Model-1-II (Figure S1), profile of water saturation distribution in Model-2 (Figure S2), performance of MSW in Model-2 (secondary mode) (Figure S3), performance of MSW in Model-2 (tertiary mode) (Figure S4), and performance of MSW flooding in Model-3 (Figure S5) (PDF)

Author Contributions

M.T. Methodology, Formal analysis, Investigation, Validation, Data curation, Writing - original draft, Writing - review & editing, Visualization. S.H. Software, Methodology, Formal analysis, Investigation, Validation, Writing -review & editing. Visualization. M.H.N. Conceptualization, Methodology, Writing - review & editing, Supervision, Project administration, Funding acquisition.

The research leading to these results has received funding from the Danish Hydrocarbon Research and Technology Centre under the Advanced Water Flooding program.

The authors declare no competing financial interest.

Supplementary Material

ao0c03679_si_001.pdf (3.2MB, pdf)

References

  1. Bartels W.-B.; Mahani H.; Berg S.; Hassanizadeh S. M. Literature Review of Low Salinity Waterflooding from a Length and Time Scale Perspective. Fuel 2018, 236, 338–353. 10.1016/j.fuel.2018.09.018. [DOI] [Google Scholar]
  2. Nasralla R. A.; Van Der Linde H. A.; Marcelis F. H. M.; Mahani H.; Masalmeh S. K.; Sergienko E.; Brussee N. J.; Pieterse S. G. J.; Basu S.. Low Salinity Waterflooding for a Carbonate Reservoir Experimental Evaluation and Numerical Interpretation. In Abu Dhabi International Petroleum Exhibition & Conference; Society of Petroleum Engineers: 2016; 1–20, 10.2118/183086-MS. [DOI]
  3. Mahani H.; Menezes R.; Berg S.; Fadili A.; Nasralla R.; Voskov D.; Joekar-Niasar V. Insights into the Impact of Temperature on the Wettability Alteration by Low Salinity in Carbonate Rocks. Energy Fuels 2017, 31, 7839–7853. 10.1021/acs.energyfuels.7b00776. [DOI] [Google Scholar]
  4. Austad T.; Rezaeidoust A.; Puntervold T.. Chemical Mechanism of Low Salinity Water Flooding in Sandstone Reservoirs. In SPE Improved Oil Recovery Symposium; Society of Petroleum Engineers: 2010; 1–17, 10.2118/129767-MS. [DOI]
  5. Ashraf A.; Hadia N.; Torsaeter O.; Tweheyo M. T.. Laboratory Investigation of Low Salinity Waterflooding as Secondary Recovery Process: Effect of Wettability. SPE Oil and Gas India Conference and Exhibition; Society of Petroleum Engineers: 2010; No. 1998, 10.2118/129012-MS. [DOI]
  6. Mahani H.; Keya A. L.; Berg S.; Bartels W. B.; Nasralla R.; Rossen W. R. Insights into the Mechanism of Wettability Alteration by Low-Salinity Flooding (LSF) in Carbonates. Energy Fuels 2015, 29, 1352–1367. 10.1021/ef5023847. [DOI] [Google Scholar]
  7. Yousef A. A.; Al-Saleh S.; Al-Jawfi M.. New Recovery Method for Carbonate Reservoirs through Tuning the Injection Water Salinity: Smart WaterFlooding. SPE EUROPEC/EAGE Annual Conference and Exhibition; Society of Petroleum Engineers: 2011; 4, 2814–2830, 10.2118/143550-MS. [DOI]
  8. Zhang P.; Austad T.. Waterflooding in Chalk: Relationship between Oil Recovery, New Wettability Index, Brine Composition and Cationic Wettability Modifier. In SPE Europec/EAGE Annual Conference; Society of Petroleum Engineers: 2005; 10.2118/94209-MS. [DOI]
  9. Ding H.; Rahman S. Experimental and Theoretical Study of Wettability Alteration during Low Salinity Water Flooding-an State of the Art Review. Colloids Surf., A 2017, 520, 622–639. 10.1016/j.colsurfa.2017.02.006. [DOI] [Google Scholar]
  10. Mahani H.; Keya A. L.; Berg S.; Nasralla R.. The Effect of Salinity, Rock Type and PH on the Electrokinetics of Carbonate-Brine Interface and Surface Complexation Modeling. In SPE Reservoir Characterisation and Simulation Conference and Exhibition; Society of Petroleum Engineers: 2015; 25, 10.2118/175568-MS. [DOI]
  11. Andersen P. Ø.; Evje S.; Madland M. V.; Hiorth A. A Geochemical Model for Interpretation of Chalk Core Flooding Experiments. Chem. Eng. Sci. 2012, 84, 218–241. 10.1016/j.ces.2012.08.038. [DOI] [Google Scholar]
  12. Taheriotaghsara M.; Bonto M.; Eftekhari A.; Torrijos I. D. P.; Puntervold T.; Strand S.. Analyzing the Smart Water Core-Flooding Data in Carbonates by Modelling the Oil Breakthrough Time Using a Novel Reactive Transport Model. IOR 2019 – 20th Eur. Symp. Improv. Oil Recovey; 2019; 2019, 10.3997/2214-4609.201900071. [DOI] [Google Scholar]
  13. Yousef A. A.; Al-Saleh S. H.; Al-Kaabi A.; Al-Jawfi M. S. Laboratory Investigation of the Impact of Injection-Water Salinity and Ionic Content on Oil Recovery From Carbonate Reservoirs. SPE Reserv. Eval. Eng. 2011, 14, 578–593. 10.2118/137634-PA. [DOI] [Google Scholar]
  14. Fathi S. J.; Austad T.; Strand S. “smart Water” as a Wettability Modifier in Chalk: The Effect of Salinity and Ionic Composition. Energy Fuels 2010, 24, 2514–2519. 10.1021/ef901304m. [DOI] [Google Scholar]
  15. Lager A.; Webb K. J.; Black C. J. J.; Singleton M.; Sorbie K. S. Low Salinity Oil Recovery - An Experimental Investigation1. Petrophysics 2008, 49, 28–35. [Google Scholar]
  16. Gandomkar A.; Rahimpour M. R. Investigation of Low-Salinity Waterflooding in Secondary and Tertiary Enhanced Oil Recovery in Limestone Reservoirs. Energy Fuels 2015, 29, 7781–7792. 10.1021/acs.energyfuels.5b01236. [DOI] [Google Scholar]
  17. Taheriotaghsara M.; Bonto M.; Eftekhari A. A.; Nick H. M. Prediction of Oil Breakthrough Time in Modified Salinity Water Flooding in Carbonate Cores. Fuel 2020, 274, 117806. 10.1016/j.fuel.2020.117806. [DOI] [Google Scholar]
  18. Gupta R.; Smith P. G. Jr.; Hu L.; Willingham T. W.; Lo Cascio M.; Shyeh J. J.; Harris C. R.. Enhanced Waterflood for Middle East Carbonate Cores - Impact of Injection Water Composition. In SPE Middle East Oil and Gas Show and Conference; Society of Petroleum Engineers: 2011; 3 ( (2010), ), 2052–2072, 10.2118/142668-MS. [DOI]
  19. Hamouda A. A.; Gupta S. Enhancing Oil Recovery from Chalk Reservoirs by a Low-Salinity Water Flooding Mechanism and Fluid/Rock Interactions. Energies 2017, 10, 576. 10.3390/en10040576. [DOI] [Google Scholar]
  20. Nasralla R. A.; Sergienko E.; Masalmeh S. K.; van der Linde H. A.; Brussee N. J.; Mahani H.; Suijkerbuijk B.; Alqarshubi I.. Demonstrating the Potential of Low-Salinity Waterflood to Improve Oil Recovery in Carbonate Reservoirs by Qualitative Coreflood. In Abu Dhabi International Petroleum Exhibition and Conference; Society of Petroleum Engineers: 2014; 10.2118/172010-MS. [DOI]
  21. Seccombe J.; Lager A.; Jerauld G.; Jhaveri B.; Buikema T.; Bassler S.; Denis J.; Webb K.; Cockin A.; Fueg E.. Demonstration of Low-Salinity EOR at Interwell Scale, Endicott Field. In SPE Improved Oil Recovery Symposium; Society of Petroleum Engineers: 2010; 10.2118/129692-MS. [DOI]
  22. Vledder P.; Gonzalez I.; Carrera Fonseca J.; Wells T.; Ligthelm D.. Low Salinity Water Flooding: Proof Of Wettability Alteration On A Field Wide Scale. In SPE Improved Oil Recovery Symposium; Society of Petroleum Engineers: 2010; 1–10, 10.2118/129564-MS. [DOI]
  23. Lager A.; Webb K. J.; Collins I. R.; Richmond D. M.. LoSal Enhanced Oil Recovery: Evidence of Enhanced Oil Recovery at the Reservoir Scale. In SPE Symposium on Improved Oil Recovery; Society of Petroleum Engineers: 2008; 10.2118/113976-MS. [DOI]
  24. Awolayo A.; Sarma H.; AlSumaiti A. M.. A Laboratory Study of Ionic Effect of Smart Water for Enhancing Oil Recovery in Carbonate Reservoirs. In SPE EOR Conference at Oil and Gas West Asia; Society of Petroleum Engineers: 2014; 46–69, 10.2118/169662-MS. [DOI]
  25. Awolayo A. N.; Sarma H. K.; Nghiem L. X. Modeling the Characteristic Thermodynamic Interplay between Potential Determining Ions during Brine-Dependent Recovery Process in Carbonate Rocks. Fuel 2018, 224, 701–717. 10.1016/j.fuel.2018.03.070. [DOI] [Google Scholar]
  26. Alkhatib A.; Babaei M. Applying the Multilevel Monte Carlo Method for Heterogeneity-Induced Uncertainty Quantification of Surfactant/Polymer Flooding. SPE J. 2016, 21, 1192–1203. 10.2118/172635-PA. [DOI] [Google Scholar]
  27. Tamayo-Mas E.; Mustapha H.; Dimitrakopoulos R. Testing Geological Heterogeneity Representations for Enhanced Oil Recovery Techniques. J. Pet. Sci. Eng. 2016, 146, 222–240. 10.1016/j.petrol.2016.04.027. [DOI] [Google Scholar]
  28. Babaei M.; Nick H. M. Performance of Low-Enthalpy Geothermal Systems: Interplay of Spatially Correlated Heterogeneity and Well-Doublet Spacings. Appl. Energy 2019, 253, 113569. 10.1016/j.apenergy.2019.113569. [DOI] [Google Scholar]
  29. Mahdizadeh M.; Eftekhari A. A.; Nick H. M. Numerical Modeling of Water-Soluble Solvents for Enhancing Oil Recovery in Heterogeneous Chalk Reservoirs. J. Pet. Sci. Eng. 2018, 175, 681–692. 10.1016/j.petrol.2018.12.083. [DOI] [Google Scholar]
  30. Ziabakhsh-Ganji Z.; Nick H. M.; Bruhn D. F. Investigation of the Synergy Potential of Oil and Geothermal Energy from a Fluvial Oil Reservoir. J. Pet. Sci. Eng. 2019, 181, 106195. 10.1016/j.petrol.2019.106195. [DOI] [Google Scholar]
  31. Weber K. J. Influence of Common Sedimentary Structures on Fluid Flow in Reservoir Models. J. Pet. Technol. 1982, 34, 665–672. 10.2118/9247-PA. [DOI] [Google Scholar]
  32. Giordano R. M.; Salter S. J.; Mohanty K. K.. The Effects of Permeability Variations on Flow in Porous Media. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: 10.2523/14365-ms. [DOI]
  33. Tidwell V. C.; Wilson J. L. Heterogeneity, Permeability Patterns, and Permeability Upscaling: Physical Characterization of a Block of Massillon Sandstone Exhibiting Nested Scales of Heterogeneity. SPE Reserv. Eval. Eng. 2000, 3, 283–291. 10.2118/65282-PA. [DOI] [Google Scholar]
  34. Kjonsvik D.; Doyle J.; Jacobsen T.; Jones A.. Effects of Sedimentary Heterogeneities on Production from a Shallow Marine Reservoir - What Really Matters? In SPE Annual Technical Conference and Exhibitiony; Society of Petroleum Engineers: 1994; 1, 27–40.
  35. Greenkorn R. A.; Haselow J. S.. Unstable Flow in Heterogenreous Porous Media; Society of Petroleum Engineers: 1988.
  36. Romano C.; Rosen M. Viscous Fingering in Heterogeneous Media. Int. J. Heat Technol. 2003, 21, 135–141. [Google Scholar]
  37. Houseworth J. E.Sensitivity of Large-Scale Water/Oil Displacement Behavior to Fine-Scale Permeability Heterogeneity and Relative Permeabilities. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: 1991; 25–40, 10.2523/22590-ms. [DOI]
  38. Waggoner J. R.; Castillo J. L.; Lake L. W. Simulation of EOR Processes in Stochastically Generated Permeable Media. SPE Form. Eval. 1992, 7, 173–180. 10.2118/21237-PA. [DOI] [Google Scholar]
  39. Pande K. K.Effects of Gravity and Viscous Crossflow on Hydrocarbon Miscible Flood Performance in Heterogeneous Reservoirs. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: 1992; 839–850, 10.2523/24935-ms. [DOI]
  40. Rashid B.; Muggeridge A.; Bal A.-L.; Williams G. J. J. Quantifying the Impact of Permeability Heterogeneity on Secondary-Recovery Performance. SPE J. 2012, 17, 455–468. 10.2118/135125-PA. [DOI] [Google Scholar]
  41. Mahani H.; Berg S.; Ilic D.; Bartels W.-B.; Joekar-Niasar V. Kinetics of Low-Salinity-Flooding Effect. SPE J. 2015, 20, 008–020. 10.2118/165255-PA. [DOI] [Google Scholar]
  42. Chen S. Y.; Kristiansen K.; Seo D.; Cadirov N. A.; Dobbs H. A.; Kaufman Y.; Schrader A. M.; Andresen Eguiluz R. C.; Alotaibi M. B.; Ayirala S. C.; et al. Time-Dependent Physicochemical Changes of Carbonate Surfaces from SmartWater (Diluted Seawater) Flooding Processes for Improved Oil Recovery. Langmuir 2019, 35, 41–50. 10.1021/acs.langmuir.8b02711. [DOI] [PubMed] [Google Scholar]
  43. Fredriksen S. B.; Rognmo A. U.; Fernø M. A.. Pore-Swcale Mechanisms during Low Salinity Waterflooding: Water Diffusion and Osmosis for Oil Mobilization. In SPE Bergen One Day Seminar; Society of Petroleum Engineers: 2016; No. 1997, 10.2118/180060-ms. [DOI]
  44. Fang C.; Yang Y.; Sun S.; Qiao R. Low Salinity Effect on the Recovery of Oil Trapped by Nanopores: A Molecular Dynamics Study. Fuel 2019, 261, 261. 10.1016/j.fuel.2019.116443. [DOI] [Google Scholar]
  45. Austad T.; Strand S.; Høgnesen E. J.; Zhang P.. Seawater as IOR Fluid in Fractured Chalk. In SPE international symposium on oilfield chemistry; Society of Petroleum Engineers: 2005; No. 3, 1–10, 10.2118/93000-MS.. [DOI]
  46. Høgnesen E. J.; Strand S.; Austad T.; Stavanger U.. Waterflooding of Preferential Oil-Wet Carbonates: Oil Recovery Related to Reservoir Temperature and Brine Composition. In SPE Europec/EAGE Annual Conference; Society of Petroleum Engineers: 2005; 3, 1–9, 10.2118/94166-MS. [DOI]
  47. Strand S.; Høgnesen E. J.; Austad T. Wettability Alteration of Carbonates - Effects of Potential Determining Ions (Ca2+ and SO42-) and Temperature. Colloids Surf., A 2006, 275, 1–10. 10.1016/j.colsurfa.2005.10.061. [DOI] [Google Scholar]
  48. Zhang P.; Tweheyo M. T.; Austad T. Wettability Alteration and Improved Oil Recovery by Spontaneous Imbibition of Seawater into Chalk: Impact of the Potential Determining Ions Ca2+, Mg2+, and SO42. Colloids Surf., A 2007, 301, 199–208. 10.1016/j.colsurfa.2006.12.058. [DOI] [Google Scholar]
  49. Zhang P.; Tweheyo M. T.; Austad T. Wettability Alteration and Improved Oil Recovery in Chalk: The Effect of Calcium in the Presence of Sulfate. Energy Fuels 2006, 20, 2056–2062. 10.1021/ef0600816. [DOI] [Google Scholar]
  50. Pierre A.; Lamarche J. M.; Mercier R.; Foissy A.; Persello J. Calcium as Potential Determining Ion in Aqueous Calcite Suspensions. J. Dispersion Sci. Technol. 1990, 11, 611–635. 10.1080/01932699008943286. [DOI] [Google Scholar]
  51. Zhang P.; Austad T. Wettability and Oil Recovery from Carbonates: Effects of Temperature and Potential Determining Ions. Colloids Surf., A 2006, 279, 179–187. 10.1016/j.colsurfa.2006.01.009. [DOI] [Google Scholar]
  52. Xie X.; Morrow N. R. N. Oil Recovery by Spontaneous Imbibition from Weakly Water-Wet Rocks. Petrophysics 2001, 42, 313–322. [Google Scholar]
  53. Puntervold T.; Strand S.; Austad T. Water Flooding of Carbonate Reservoirs: Effects of a Model Base and Natural Crude Oil Bases on Chalk Wettability. Energy Fuels 2007, 21, 1606–1616. 10.1021/ef060624b. [DOI] [Google Scholar]
  54. Shariatpanahi S. F.; Strand S.; Austad T. Initial Wetting Properties of Carbonate Oil Reservoirs: Effect of the Temperature and Presence of Sulfate in Formation Water. Energy Fuels 2011, 25, 3021–3028. 10.1021/ef200033h. [DOI] [Google Scholar]
  55. Fernø M. A.; Grønsdal R.; Åsheim J.; Nyheim A.; Berge M.; Graue A. Use of Sulfate for Water Based Enhanced Oil Recovery during Spontaneous Imbibition in Chalk. Energy Fuels 2011, 25, 1697–1706. 10.1021/ef200136w. [DOI] [Google Scholar]
  56. Strand S.; Austad T.; Puntervold T.; Høgnesen E. J.; Olsen M.; Barstad S. M. F. “Smart Water” for Oil Recovery from Fractured Limestone: A Preliminary Study. Energy Fuels 2008, 22, 3126–3133. 10.1021/ef800062n. [DOI] [Google Scholar]
  57. Megawati M.; Hiorth A.; Madland M. V. The Impact of Surface Charge on the Mechanical Behavior of High-Porosity Chalk. Rock Mech. Rock Eng. 2013, 46, 1073–1090. 10.1007/s00603-012-0317-z. [DOI] [Google Scholar]
  58. Ligthelm D. J.; Gronsveld J.; Hofman J. P.; Brussee N. J.; Marcelis F.; van der Linde H.. Novel Waterflooding Strategy by Manipulation of Injection Brine Composition. In EUROPEC/EAGE Conference and Exhibition; Society of Petroleum Engineers: 2009; 1, 1–22, 10.2118/119835-MS. [DOI]
  59. Vdović N.; Bišćan J. Electrokinetics of Natural and Synthetic Calcite Suspensions. Colloids Surf., A 1998, 137, 7–14. 10.1016/S0927-7757(97)00179-9. [DOI] [Google Scholar]
  60. Karimi M.; Al-Maamari R. S.; Ayatollahi S.; Mehranbod N. Mechanistic Study of Wettability Alteration of Oil-Wet Calcite: The Effect of Magnesium Ions in the Presence and Absence of Cationic Surfactant. Colloids Surf., A 2015, 482, 403–415. 10.1016/j.colsurfa.2015.07.001. [DOI] [Google Scholar]
  61. Alroudhan A.; Vinogradov J.; Jackson M. D. Zeta Potential of Intact Natural Limestone: Impact of Potential-Determining Ions Ca, Mg and SO4. Colloids Surf., A 2016, 493, 83–98. 10.1016/j.colsurfa.2015.11.068. [DOI] [Google Scholar]
  62. Mahani H.; Keya A. L.; Berg S.; Nasralla R. Electrokinetics of Carbonate/Brine Interface in Low-Salinity Waterflooding: Effect of Brine Salinity, Composition, Rock Type, and PH on ζ-Potential and a Surface-Complexation Model. SPE J. 2017, 22, 053–068. 10.2118/181745-PA. [DOI] [Google Scholar]
  63. Romanuka J.; Hofman J.; Ligthelm D. J.; Suijkerbuijk B.; Marcelis F.; Oedai S.; Brussee N.; van der Linde B.; Aksulu H.; Austad T.. Low Salinity EOR in Carbonates. In SPE Improved Oil Recovery Symposium; SPE Improved Oil Recovery Symposium: 2012; 1–16, 10.2118/153869-MS. [DOI]
  64. Bonto M.; Eftekhari A. A.; Nick H. M. An Overview of the Oil-Brine Interfacial Behavior and a New Surface Complexation Model. Sci. Rep. 2019, 9, 1–16. 10.1038/s41598-019-42505-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Al-Ibadi H.; Stephen K.; MacKay E. H. Heterogeneity Effects on Low Salinity Water Flooding. Soc . In SPE Europec featured at 82nd EAGE Conference and Exhibition; Society of Petroleum Engineers: 2020; 10.2118/200547-ms. [DOI]
  66. Al-Ibadi H.; Stephen K.; Mackay E.. Analytical and Numerical Solutions of Chemical Flooding in a Layered Reservoir with a Focus on Low Salinity Water Flooding. In IOR 2019–20th European Symposium on Improved Oil Recovery; European Association of Geoscientists & Engineers: 2019; 10.3997/2214-4609.201900131. [DOI]
  67. Attar A.; Muggeridge A.. Impact of Geological Heterogeneity on Performance of Secondary and Tertiary Low Salinity Water Injection. In SPE Middle East Oil & Gas Show and Conference; Society of Petroleum Engineers: 2015; 2015, 2452–2463, 10.2118/172775-ms. [DOI]
  68. Attar A.; Muggeridge A. Low Salinity Water Injection: Impact of Physical Diffusion, an Aquifer and Geological Heterogeneity on Slug Size. J. Pet. Sci. Eng. 2018, 166, 1055–1070. 10.1016/j.petrol.2018.03.023. [DOI] [Google Scholar]
  69. Aladasani A.; Bai B.; Wu Y. S.; Okasha Q.. 3D Simulation of Low Salinity, Polymer, Conventional, Water-Flooding & Combination IOR Methods - Heterogeneous & Varying Wetting Conditions. In SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition; Society of Petroleum Engineers: 2015.
  70. Taheriotaghsara M.; Eftekhari A. A.; Nick H. M.. Adsorption- and Diffusion-Controlled Wettability Change in Modified-Salinity Water Flooding. Energy Fuels: 2020.
  71. Mahani H.; Sorop T.; Ligthelm D. J.; Brooks D.; Vledder P.; Mozahem F.; Ali Y.. Analysis of Field Responses to Low-Salinity Waterflooding in Secondary and Tertiary Mode in Syria. In SPE Europec/EAGE Annual Conference and Exhibition; Society of Petroleum Engineer: 2011; 10.2118/142960-MS. [DOI]
  72. Jerauld G. R.; Webb K. J.; Lin C.-Y.; Seccombe J.. Modeling Low-Salinity Waterflooding. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: 2006; 24–27, 10.2118/102239-MS. [DOI]
  73. Hordy P.Technical Description. In Drawn after Nature; KNNV Publishing: 2008; 22–27, 10.1163/9789004278004_005. [DOI] [Google Scholar]
  74. Heberling F.; Bosbach D.; Eckhardt J.-D.; Fischer U.; Glowacky J.; Haist M.; Kramar U.; Loos S.; Müller H. S.; Neumann T.; et al. Reactivity of the Calcite–Water-Interface, from Molecular Scale Processes to Geochemical Engineering. Appl. Geochem. 2014, 45, 158–190. 10.1016/j.apgeochem.2014.03.006. [DOI] [Google Scholar]
  75. Heberling F.; Trainor T. P.; Lützenkirchen J.; Eng P.; Denecke M. A.; Bosbach D. Structure and Reactivity of the Calcite–Water Interface. J. Colloid Interface Sci. 2011, 354, 843–857. 10.1016/j.jcis.2010.10.047. [DOI] [PubMed] [Google Scholar]
  76. Song J.; Zeng Y.; Wang L.; Duan X.; Puerto M.; Chapman W. G.; Biswal S. L.; Hirasaki G. J. Surface Complexation Modeling of Calcite Zeta Potential Measurements in Brines with Mixed Potential Determining Ions (Ca2+, CO32–, Mg2+, SO42–) for Characterizing Carbonate Wettability. J. Colloid Interface Sci. 2017, 506, 169–179. 10.1016/j.jcis.2017.06.096. [DOI] [PubMed] [Google Scholar]
  77. Wolthers M.; Charlet L.; Van Cappellen P. The Surface Chemistry of Divalent Metal Carbonate Minerals; a Critical Assessment of Surface Charge and Potential Data Using the Charge Distribution Multi-Site Ion Complexation Model. Am. J. Sci. 2008, 308, 905–941. 10.2475/08.2008.02. [DOI] [Google Scholar]
  78. Nick H. M.; Schotting R.; Gutierrez-Neri M.; Johannsen K. Modeling Transverse Dispersion and Variable Density Flow in Porous Media. Transp. Porous Media 2009, 78, 11–35. 10.1007/s11242-008-9277-x. [DOI] [Google Scholar]
  79. Amour F.; Nick H. M.. Porosity and Permeability Variability across a Chalk Reservoir in the Danish North Sea: Quantitative Impacts of Depositional and Diagenetic Processes. Engineering Geology; 2020. Submitted for publication
  80. Raoof A.; Hassanizadeh S. M. UPSCALING TRANSPORTOF ADSORBING SOLUTES IN POROUS MEDIA. J. Porous Media 2010, 13 (5), 395–408. 10.1615/JPorMedia.v13.i5.10. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c03679_si_001.pdf (3.2MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES