Abstract
Sewall Wright developed F ST for describing population differentiation and it has since been extended to many novel applications, including the detection of homomorphic sex chromosomes. However, there has been confusion regarding the expected estimate of F ST for a fixed difference between the X‐ and Y‐chromosome when comparing males and females. Here, we attempt to resolve this confusion by contrasting two common F ST estimators and explain why they yield different estimates when applied to the case of sex chromosomes. We show that this difference is true for many allele frequencies, but the situation characterized by fixed differences between the X‐ and Y‐chromosome is among the most extreme. To avoid additional confusion, we recommend that all authors using F ST clearly state which estimator of F ST their work uses.
Keywords: FST, sex chromosomes
1. BACKGROUND
Genetic sex determination is common in both plants and animals (Bachtrog et al., 2014) and the pair of chromosomes where the sex‐determination gene resides are referred to as the sex chromosomes. Sex chromosomes are hypothesized to often emerge from autosomes once they have acquired a novel mutation for sex determination (Abbott, Nordén, & Hansson, 2017; Bachtrog et al., 2014). Linked, sexually antagonistic alleles can help to drive a novel sex‐determination allele to a higher frequency in the population (van Doorn & Kirkpatrick, 2010) and mechanisms that reduce recombination between sexually antagonistic loci and the novel sex‐determination locus are selectively favoured (Charlesworth, Charlesworth, & Marais, 2005; Rice, 1987). Due to the reduction in recombination, deleterious mutations accumulate and gradually decay the gene content within this region (Bachtrog, 2013; Blaser, Grossen, Neuenschwander, & Perrin, 2012). In some systems, large‐scale deletions or expansions of repetitive elements occur and lead to heteromorphic sex chromosomes (Bachtrog, 2013; Charlesworth et al., 2005). As a result of this process, sex chromosomes exist on a spectrum between harbouring a single nucleotide polymorphism (SNP) responsible for sex determination with no reduction in recombination from the surrounding region, as seen in fugu (Kamiya et al., 2012), to the highly decayed and heteromorphic sex chromosomes observed in many eutherian mammals (Bellott et al., 2014; Cortez et al., 2014).
Two common methods have been developed to identify sex chromosomes at different points on this spectrum using next‐generation sequencing data sets. In the more advanced stages of sex chromosome evolution the X‐ and Y‐chromosome share little genomic content. As a result, short reads from the Y‐chromosome align poorly to an X‐chromosome reference, resulting in a higher coverage in females than in males. These differences in coverage between males and females can be used to detect putatively nonrecombining regions of sex chromosomes (Fraïsse, Picard, & Vicoso, 2017; Huylmans, Toups, Macon, Gammerdinger, & Vicoso, 2019; Pal & Vicoso, 2015; Roesti, Moser, & Berner, 2013; Vicoso & Bachtrog, 2011, 2013, 2015; Vicoso, Kaiser, & Bachtrog, 2013). In the less advanced stages of sex chromosome evolution, the X‐ and Y‐chromosome differ only by a few base substitutions. Therefore, short reads from the X‐ and Y‐chromosome align in nearly equal proportions to an X‐chromosome reference and the identification of sex chromosomes instead relies on differences in allele frequencies in males and females (Böhne et al., 2019; Conte, Gammerdinger, Bartie, Penman, & Kocher, 2017; Dixon, Kitano, & Kirkpatrick, 2018; Fontaine et al., 2017; Gammerdinger, Conte, Acquah, Roberts, & Kocher, 2014; Gammerdinger, Conte, Baroiller, D’Cotta, & Kocher, 2016; Gammerdinger, Conte, Sandkam, Penman, & Kocher, 2019; Gammerdinger, Conte, Sandkam, & Ziegelbecker, 2018; Toups, Rodrigues, Perrin, & Kirkpatrick, 2018; Veltsos et al., 2019). Typically, SNPs are first identified among subpopulations of males and females, and regions with high levels of genetic differentiation between males and females are presumed to be sex‐linked. This genetic differentiation between males and females is often described in terms of F ST.
F ST is a relative measure of population differentiation (Cruickshank & Hahn, 2014) and was outlined along with other F‐statistics by Sewall Wright (Wright, 1949). Estimates of F ST have been used for many novel applications, such as examining parallel adaptation in sticklebacks (Hohenlohe, Bassham, Etter, & Cresko, 2010), introgression in canaries (Lopes et al., 2016) and local adaptation in high‐altitude populations of Tibetans (Peng et al., 2011; Xu et al., 2011). Recent work has used estimates of F ST to identify and describe the divergence between relatively homomorphic sex chromosomes (Bergero, Gardner, Bader, Yong, & Charlesworth, 2019; Böhne et al., 2019; Conte et al., 2017; Dixon et al., 2018; Fontaine et al., 2017; Gammerdinger et al., 2014, 2016, 2018, 2019; Kirkpatrick & Guerrero, 2014; Natri, Shikano, & Merilä, 2013; Rodrigues & Dufresnes, 2017; Toups et al., 2018; Veltsos et al., 2019). However, there is a discrepancy within the literature regarding the expected estimate of F ST for a fixed difference between the X‐ and Y‐chromosome. When comparing males and females for an allele that is either fixed on the X‐ or Y‐chromosome of an XY pair, some studies expect an F ST estimate of (Gammerdinger et al., 2014, 2016, 2018, 2019; Kirkpatrick & Guerrero, 2014; Toups et al., 2018), while other studies expect an F ST estimate of 0.5 (Böhne et al., 2019; Fontaine et al., 2017; Rodrigues & Dufresnes, 2017). The difference in these expectations is not typically justified, nor is the specific estimator of F ST employed stated, leading to some confusion in the field.
A recent study highlighted inconsistencies between different estimators of F ST (Berner, 2019) and in particular pointed out that, for an SNP fixed on the Y‐chromosome, one common estimator of F ST yields a value of (Nei, 1973) while another yields 0.5 (Weir & Cockerham, 1984). How other popular estimators behave for an SNP that is alternatively fixed between the X‐ and Y‐chromosome, and, importantly, why these discrepancies arise, have yet to be systematically reviewed.
Here, we aim to clarify why such discrepancies in the expected estimates of F ST can arise when comparing males and females for alternatively fixed alleles between the X‐ and Y‐chromosome. Note that this difference in expectations of F ST is symmetric for ZW systems, so this analysis will only describe an XY system. Importantly, while this analysis focuses on the specific case of sex chromosomes, we also illustrate that the difference between F ST estimators can be substantial for a wide range of allele frequencies, making direct comparisons of F ST estimates between studies problematic in many contexts. Last, we apply a variety of population genetics software packages, which often generically refer to F ST, to estimate F ST for alternatively fixed alleles between the X‐ and Y‐chromosome under various sampling schemes. Because these programs use different estimators and corrections for sample size and composition, a diverse range of expected F ST values can be recovered (0.16–0.67) and, as a result, further complicates the interpretation of experimental studies that use F ST to assess sex chromosome differentiation.
2. METHODS
We evaluated estimators of F ST across different commonly used software packages, including vcftools version 0.1.15 (Danecek et al., 2011), arlequin 3.5 (Excoffier & Lischer, 2010), genepop 1.0.5 (Rousset, 2008), popgenome 2.61 (Pfeifer, Wittelsbürger, Ramos‐Onsins, & Lercher, 2014), hierfstat 0.04‐29 (Goudet, 2005), diversity 1.9.90 (Keenan, McGinnity, Cross, Crozier, & Prodöhl, 2013) and dnasp 6.12.03 (Rozas et al., 2017). Programs that used R were run on R 3.5.1 (R Core Team, 2016). Scripts for software packages that did not have a GUI are provided in File S1. During our use of these software packages, we analysed the effect of sample sizes on F ST estimators. To perform this analysis, we created mock VCF files containing 20 fixed differences between the X‐ and Y‐chromosome for males and females (File S1) following the defined VCF format (Danecek et al., 2011). When necessary, we used pgdspider (Lischer & Excoffier, 2012) to convert our mock VCF files into fasta, arlequin, fstat and genepop formats.
3. WRIGHT’S F ST
Since Wright introduced F ST (Wright, 1949), it has been unclear if this definition represents a parameter or an estimate of the parameter (Hahn, 2018; Holsinger & Weir, 2009). Nonetheless, F ST for a biallelic system is most traditionally described as:
| (1) |
where is the variance in the allele frequency for p and and are the average allele frequencies across the subpopulations for p and q, respectively (Hedrick, 2005; Weir & Cockerham, 1984). When comparing the sex chromosomes of males and females, we will define subpopulation 1 to be males and subpopulation 2 to be females, while p is the frequency of the allele on the X‐chromosome and q is the frequency of the allele on the Y‐chromosome (Table 1). When using Equation 1 and the values in Table 1, the resulting F ST is .
TABLE 1.
Description of values for p and q in males and females
| Subpopulation 1 (males) | Subpopulation 2 (females) | Average of the subpopulations | F ST | ||
|---|---|---|---|---|---|
| p (frequency of the allele fixed on the X‐chromosome) | p 1 = 0.5 | p2 = 1 | = 0.75 |
|
|
| q (frequency of the allele fixed on the Y‐chromosome) | q 1 = 0.5 | q2 = 0 | = 0.25 |
4. ESTIMATORS OF F ST
In practice, the parameter values for allele frequencies are unknown and thus many methods have been proposed to estimate F ST. Here, we contrast two common estimators of F ST, which we will denote as and . The difference between these estimators has been previously discussed by others (Bhatia, Patterson, Sankararaman, & Price, 2013; Charlesworth, 1998), but not specifically in the context of sex chromosomes. While some estimators handle multiple alleles and multiple subpopulations, we will be considering only the biallelic state for two subpopulations. We make these simplifications because they provide a direct comparison between estimators and they reflect a situation with alternatively fixed alleles on the X‐ and Y‐chromosome when comparing males and females. Also, we will focus on the example of a fixed difference between the X‐ and Y‐chromosome because it is the fundamental component of these elevated estimates of F ST. However, F ST estimates for various degrees of difference in the allele frequencies between males and females, going from equal frequencies in both sexes to alternatively fixed differences between the X‐ and Y‐chromosome, can be found in Figure S1. In an empirical study, the identification of an XY system would typically show a region overrepresented with these fixed differences between the X‐ and Y‐chromosome.
4.1. Nei's estimator of F ST
One estimator of F ST comes from Nei (1973) and is often referred to as G ST. G ST uses heterozygosity data to estimate F ST. G ST quantifies the difference between the total heterozygosity of the population and the average heterozygosity of the subpopulations and normalizes this difference by the total heterozygosity of the population. It was defined by Nei (1973) as:
| (2) |
When considering two alleles in two subpopulations, this estimator can be simplified to:
| (3) |
Thus, by comparing males and females for an allele that is alternatively fixed on the X‐ and Y‐chromosome using Nei’s (1973) estimator, the expected estimate of F ST is .
A similar estimator of F ST, called γ ST, is generally used in the context of haplotypes and estimates F ST using nucleotide diversity. Nucleotide diversity, π, is the mean number of nucleotide differences between two randomly selected sequences from a population. γ ST is described as the difference between the total nucleotide diversity of the population and the average nucleotide diversity of the subpopulations normalized to the total nucleotide diversity of the population (Nei, 1982). Nei (1982) defined γ ST as:
| (4) |
where π T the total nucleotide diversity of the population and π S is the mean of the subpopulations’ nucleotide diversities. Notably, when considering a single, biallelic SNP, G ST and γ ST are equivalent (Nei, 1982). As a result, we will describe nucleotide diversities in terms of p and q, since nucleotide diversities and heterozygosities are equivalent for a SNP. We introduce γ ST because it will lead to the most direct comparison between Nei’s (1973) estimator and Hudson, Slatkin, et al. (1992) estimator in the next section.
π T estimates nucleotide diversity from and , the mean of p and q across the subpopulations, respectively. Importantly, π T makes comparisons between all alleles in the whole population. When considering a biallelic SNP in two subpopulations, π T in Nei’s (1982) estimator can be simplified to:
| (5) |
Using the values from Table 1, we can estimate π T as 0.375. The nucleotide diversity, π, of each subpopulation can be computed using Nei and Li’s (1979) definition for this statistic and averaged together to become π S. For a biallelic SNP in two subpopulations, π S can be simplified to:
| (6) |
When utilizing the values in Table 1, π S is 0.25 and therefore Equation 4 recovers an expected estimate of F ST to be .
4.2. Hudson, Slatkin and Maddison's estimator of F ST
A second, alternative estimator of F ST comes from Hudson, Slatkin, et al. (1992). This estimator considers the difference in the average nucleotide diversity between subpopulations and the average subpopulation nucleotide diversity and then normalizes this difference to the average nucleotide diversity between subpopulations. This estimator of F ST is defined as:
| (7) |
where π W is similar to Nei’s (1982) π S, except π W excludes pairwise comparisons of haplotypes against themselves and is thus dependent on the subpopulation sample sizes. π W can be expressed as:
| (8) |
where n 1 and n 2 are the number of diploid individuals sampled from subpopulation 1 and 2, respectively. (A full derivation that can be found in the supplementary information of Bhatia et al. (2013). Note that in the Bhatia et al. (2013) derivation, n 1 and n 2 represent allele counts not diploid individual counts as are used here). As the subpopulation sample sizes go to infinity, π W will approach π S and thus the difference between π S and π W is often negligible with large subpopulation sample sizes. π B is an alternative estimator of nucleotide diversity, defined by Nei and Li (1979) as πXY, and it can be quite numerically different from π T. πXY is the mean number of nucleotide differences between two randomly selected DNA sequences, each of which is drawn from separate subpopulations. In the case of a biallelic SNP in two subpopulations, Hudson, Slatkin, et al. (1992) estimator for π B can be rewritten as:
| (9) |
The values in Table 1 yield an estimate of π B to be 0.5. As subpopulation sample sizes approach infinity, estimating F ST for a biallelic locus in two subpopulations with this estimator can be written as:
| (10) |
As subpopulation sizes go to infinity and using either Equation 7 or 10 with the values in Table 1, we arrive at an estimate of F ST approaching 0.5. F ST estimates for finite sample sizes using this estimator are demonstrated in Figure 1. Importantly, regardless of the subpopulation sample sizes employed, Nei’s (1973) estimator and Hudson, Slatkin, et al. (1992) estimator are always quite different for the case of sex chromosomes (Figure 1).
FIGURE 1.
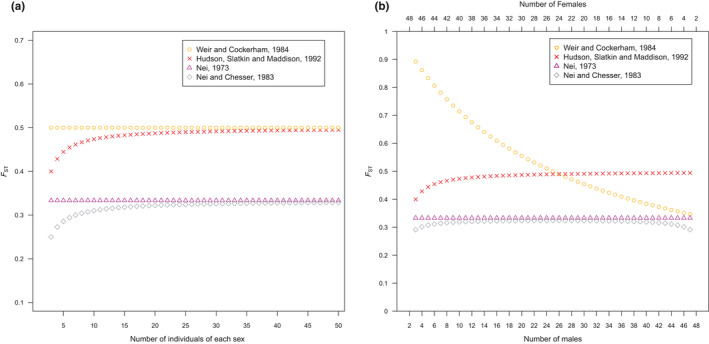
Various estimates of F ST for a fixed difference between the X‐ and Y‐chromosome when (a) using equal subpopulation sample sizes for two subpopulations, males and females, and (b) using unequal subpopulation sample sizes for the two subpopulations, males and females, while keeping the total sample size constant
4.3. Why is there a difference in the expected estimate of FST?
By comparing Equations 4 and 7 with large subpopulation sample sizes, it is clear that the important difference in Nei’s (1973, 1982) estimator and Hudson, Slatkin, et al. (1992) estimator arises in how they handle π T and π B. Nei’s (1982) π T uses two randomly drawn sequences from the population as a whole, while Hudson, Slatkin, et al. (1992) π B requires that the two randomly drawn sequences be from the separate subpopulations. Figure 2 illustrates the difference between these two estimators for (a) a biallelic SNP present on an autosome in two subpopulations and for (b) sex chromosomes when comparing males and females. Figure 3 shows the F ST estimates produced from Nei’s (1973) estimator and Hudson, Slatkin, et al. (1992) estimator when considering infinitely large subpopulation sample sizes, as well as the difference between these two estimators. Interestingly, the regions corresponding to an SNP that is alternatively fixed between the X‐ and Y‐chromosome are among the regions where the difference in these estimators is highest. However, these estimators can differ substantially across the range of plausible allele frequencies observed in two subpopulations. For example, SNPs that are not yet fixed differences between the X‐ and Y‐chromosome also show this discordance between F ST estimators (Figure 3; Figure S1). Additionally, the difference in these two F ST estimates when p 1 is 0.20, p 2 is 0.80 and both subpopulation samples sizes are 20 is slightly larger than the difference produced by sex chromosomes. This importantly illustrates that the disagreement in F ST estimators is not the byproduct of the unique scenario of sex chromosomes, but is a disagreement that many researchers using F ST estimators should consider.
FIGURE 2.
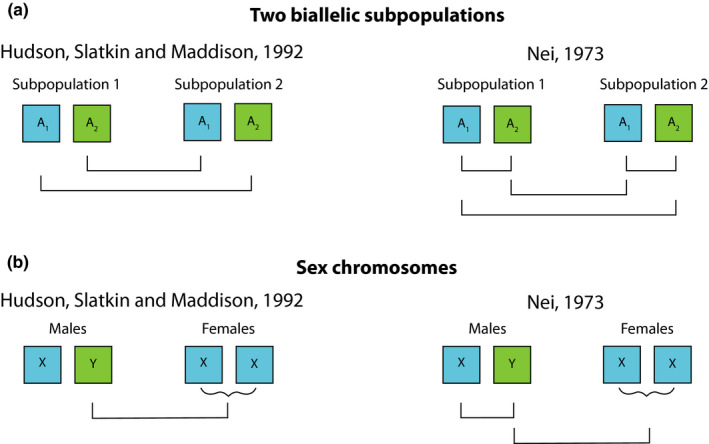
Comparison of the nonzero components of π B in Hudson, Slatkin, et al. (1992) estimator and π T in Nei’s (1973) estimator for biallelic SNPs in (a) two subpopulations and (b) an XY system. Each bar under the alleles represents a nonzero comparison that occurs in the formulation of π B or π T. The curly bracket beneath females in the sex chromosome comparison illustrates that females are homomorphic for this allele despite being diploid and thus only one nonzero comparison is made
FIGURE 3.
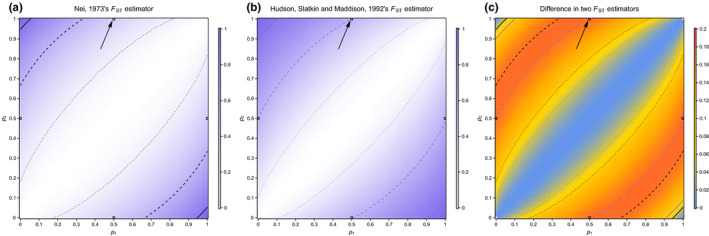
Visualizations of Nei (1973), Hudson, Slatkin, et al. (1992) and the difference between the two estimators. (a) Estimates of F ST using the Nei (1973) estimator with white being no differentiation and dark blue being complete differentiation. (b) Estimates of F ST using the Hudson, Slatkin, et al. (1992) estimator given infinitely large subpopulation sizes with white being no differentiation and dark blue being complete differentiation. (c) A heatmap of the difference between Hudson, Slatkin, et al. (1992) estimator and Nei’s (1973) estimator for F ST (Hudson, Slatkin, et al. (1992) minus Nei (1973)) given infinitely large subpopulation sample sizes and the allele frequencies of p in subpopulations 1 and 2. Warmer colours show more difference between the estimators, while cooler colours show less difference between the estimators. Because the assignment of p and q along with subpopulation 1 and 2 is arbitrary, we have placed black boxes at all of the locations that could fit the description of a fixed difference between the X‐ and Y‐chromosome and provided an arrow to the scenario we outlined in Table 1. Dotted lines show an F ST estimate equal to 0.1, dashed lines show an F ST estimate equal to 0.5 and solid lines show an F ST estimate equal to 0.9. Black dotted, dashed and solid lines are used to signify Nei’s (1973) estimator in panels (a) and (c), while purple dotted, dashed and solid lines are used to signify Hudson, Slatkin, et al. (1992) estimator in panels (b) and (c)
4.4. Additional corrections to F ST
There are several estimators of F ST that attempt to provide corrections for sampling biases and can cause further deviations from the expected estimate of F ST. Some estimators, such as that proposed by Hudson, Slatkin, et al. (1992), change with the total number of individuals sampled (Hudson, Boos, & Kaplan, 1992; Hudson, Slatkin, et al., 1992; Nei & Chesser, 1983) (Figure 1a; Table 2). Additionally, some estimators change as the proportion of individuals sampled from each subpopulation changes even when the total number of individuals sampled is held constant (Hudson, Boos, et al., 1992; Hudson, Slatkin, et al., 1992; Nei & Chesser, 1983; Weir & Cockerham, 1984) (Figure 1b; Table 2).
TABLE 2.
Software packages for estimating F ST and their estimates using mock input. These input files contained fixed differences between the X‐ and Y‐chromosome for various sample sizes of males and females
| Package (version) | Option | 5 Males and 5 females | 10 Males and 10 females | 20 Males and 20 females | 5 Males and 15 females | 15 Males and 5 females | Referenced estimator |
|---|---|---|---|---|---|---|---|
| vcftools (0.1.15) | weir‐fst‐pop | 0.5 | 0.5 | 0.5 | 0.667 | 0.4 | Weir and Cockerham, (1984) |
| popgenome (2.61) | F_ST.stats: nucleotide.F_ST | 0.444 | 0.474 | 0.487 | 0.444 | 0.483 | Hudson, Slatkin, et al. (1992) |
| F_ST.stats: nuc.F_ST.pairwise | 0.444 | 0.474 | 0.487 | 0.444 | 0.483 | Hudson, Slatkin, et al. (1992) | |
| F_ST.stats: Nei.G_ST | 0.333 | 0.333 | 0.333 | 0.333 | 0.333 | Nei (1973) | |
| F_ST.stats: Nei.G_ST.pairwise | 0.333 | 0.333 | 0.333 | 0.333 | 0.333 | Nei (1973) | |
| F_ST.stats: Hudson.H_ST | 0.296 | 0.316 | 0.325 | 0.45 | 0.163 | Hudson, Boos, et al. (1992) a | |
| F_ST.stats: Hudson.G_ST | 0.286 | 0.310 | 0.322 | 0.378 | 0.195 | Hudson, Boos, et al. (1992) b , c | |
| diversity (1.9.90) | diffCalc(fst = TRUE) | 0.5 | 0.5 | 0.5 | 0.667 | 0.4 | Weir and Cockerham (1984) |
| diffCalc() | 0.286 | 0.310 | 0.322 | 0.3023 | 0.3023 | Nei and Chesser (1983) | |
| hierfstat (0.04–29) | pairwise.fst | 0.333 | 0.333 | 0.333 | 0.429 | 0.2 | Nei (1973) c |
| genet.dist(method = Nei87) | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | Nei (1987) d | |
| pairwise.neifst | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | Nei (1987) d | |
| basic.stats(fst) | 0.333 | 0.333 | 0.333 | 0.333 | 0.333 | Nei (1987) | |
| genet.dist(method = WC84) | 0.5 | 0.5 | 0.5 | 0.667 | 0.4 | Weir and Cockerham, (1984) | |
| pairwise.WCfst | 0.5 | 0.5 | 0.5 | 0.667 | 0.4 | Weir and Cockerham, (1984) | |
| genepop (1.0.5) | Fst | 0.5 | 0.5 | 0.5 | 0.667 | 0.4 | Weir and Cockerham, (1984) |
| arlequin (3.5) | Compute pairwise FST | 0.444 | 0.474 | 0.487 | 0.647 | 0.362 | Excoffier, Smouse, and Quattro (1992) |
| dnasp (6.12.03) | Gene Flow and Genetic Differentiation: GST | 0.286 | 0.310 | 0.322 | 0.378 | 0.194 | Nei (1973) b , c |
| Gene Flow and Genetic Differentiation: GammaSt | 0.333 | 0.333 | 0.333 | 0.429 | 0.2 | Nei (1982) c | |
| Gene Flow and Genetic Differentiation: Fst | 0.444 | 0.474 | 0.487 | 0.444 | 0.483 | Hudson, Slatkin, et al. (1992) |
This implementation appears to use a weighting factor.
These estimates are most consistent with Nei and Chesser (1983), which is also discussed in Hudson, Boos, et al. (1992).
These metrics appear to use a weighting factor, while Nei (1982) and Nei and Chesser (1983) state that in most practices the subpopulations can be assumed to be weighted equally.
The referenced estimator is consistent with F′ST in Nei (1987).
As similarly pointed out by Berner (2019), Weir and Cockerham’s (1984) estimator appears to respond dramatically to unequal numbers of males and females. As the proportion of the males in a constant sample size increases, the total variance of the sample increases and thus decreases the estimate of F ST (Figure 1b). Regardless, in the case of a fixed difference between the X‐ and Y‐chromosome, is defined as 0.75. Thus, there is little need to correct for subpopulation sample sizes because this differentiation is similar whether a single male and female are analysed or a very large number of each sex are considered. However, this type of sample size correction may be applicable when considering SNPs that are more frequent on the Y‐chromosome but not yet fixed or if it is unknown whether an SNP is alternatively fixed between the X‐ and Y‐chromosome.
An additional correction considers the number of subpopulations sampled (Hedrick, 2005; Weir & Cockerham, 1984). This correction is related to an infinite island model that assumes that the researcher is sampling a few subpopulations from a larger metapopulation. Because there are only two subpopulations, males and females, these corrections are probably unsuitable in this context.
Additionally, it has also been pointed out that F ST underestimates differentiation at highly polymorphic loci, such as microsatellites (Charlesworth, 1998; Hedrick, 2005; Meirmans & Hedrick, 2011). Some estimators are particularly concerned with correcting for this bias (Hedrick, 2005; Meirmans & Hedrick, 2011); however, this correction for highly polymorphic loci is unlikely to be necessary for the biallelic locus in question.
While some of these corrections are probably inappropriate, authors may be using them as some software packages refer to their implementation generically as F ST (Table 2). Table 2 and Figure 1 highlight the wide range of results that researchers could get for estimating F ST depending on the subpopulation sample sizes and estimator employed. One may argue that any large deviation away from zero in F ST estimates is sufficient enough evidence for sex chromosomes. However, estimates of F ST that include the various aforementioned corrections may never reach or 0.5 (Table 2) and thus the expected maximum estimate of F ST for a particular data set should ideally be considered and stated. Otherwise, deviations from the theoretical maximum due to these corrections could lead to an erroneous interpretation that there are no fixed differences between the X‐ and Y‐chromosome.
While the particular case of variants on sex chromosomes leads to some of the largest differences between these estimators, substantial differences can occur under alternative scenarios as well, and it would often be helpful to know how much of the variance between studies is driven by how F ST is estimated. For instance, whether sexually antagonistic selection can explain the range of F ST values that are found between males and females of different species (Cheng & Kirkpatrick, 2016; Flanagan & Jones, 2017; Lucotte, Laurent, Heyer, Ségurel, & Toupance, 2016; Wright et al., 2018; Wright, Rogers, Fumagalli, Cooney, & Mank, 2019) has recently been the subject of debate (Kasimatis, Nelson, & Phillips, 2017; Kasimatis, Ralph, & Phillips, 2019). While Kasimatis et al. (2019) compare Wright's F ST to Weir and Cockerham's estimator of F ST, the variability introduced by the various estimators used in the previously cited experimental work (Hudson, Slatkin, et al., 1992; Nei, 1986; Weir, 1996; Wright, 1949) was not considered. In the future, we strongly urge researchers to justify their estimator, so that appropriate F ST estimators are employed and estimates from various studies can be comparable.
5. CONCLUSIONS
When considering fixed differences between the X‐ and Y‐chromosome, we conclude that it is appropriate to use Nei’s (1973) estimator since it is most consistent with the work of Wright and others. However, both Nei’s (1973) and Hudson, Slatkin, et al. (1992) estimators are useful estimators of differentiation and there could be questions, such as those regarding polymorphisms that are not fully linked to the X‐ or Y‐chromosome, which are better answered with different estimators that implement some of the previously mentioned corrections. Moving forward, we encourage researchers to state which estimator they choose, their rationale for that choice and what the expected estimate of F ST is for the data set they are investigating.
AUTHOR CONTRIBUTIONS
W.J.G. conceived the commentary, drafted the manuscript and created the figures. M.A.T. and B.V. aided in drafting the manuscript and contributed intellectually to the commentary. M.A.T. also ran the software packages for the estimates of F ST in Table 2.
CONFLICTS OF INTEREST
The authors declare no conflicts of interest.
Supporting information
Fig S1
ACKNOWLEDGEMENTS
We would like to thank Matthew Hahn, Mark Kirkpatrick and Thomas Kocher for their thoughtful and timely insights as we have tried to differentiate between these estimators of F ST. This work was funded by an ISTPlus Fellowship to W.J.G. and by an ERC grant (Project P 28842) to B.V.
Gammerdinger WJ, Toups MA, Vicoso B. Disagreement in F ST estimators: A case study from sex chromosomes. Mol Ecol Resour. 2020;20:1517–1525. 10.1111/1755-0998.13210
DATA AVAILABILITY STATEMENT
All data needed for reproducing these conclusions are within this work and Supporting Information.
REFERENCES
- Abbott, J. K. , Nordén, A. K. , & Hansson, B. (2017). Sex chromosome evolution: Historical insights and future perspectives. Proceedings of the Royal Society B: Biological Sciences, 284, 20162806 10.1098/rspb.2016.2806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachtrog, D. (2013). Y‐chromosome evolution: Emerging insights into processes of Y‐chromosome degeneration. Nature Reviews Genetics, 14, 113–124. 10.1038/nrg3366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachtrog, D. , Mank, J. E. , Peichel, C. L. , Kirkpatrick, M. , Otto, S. P. , Ashman, T.‐L. … Vamosi, J. C. (2014). Sex determination: Why so many ways of doing it? PLoS Biology, 12, e1001899 10.1371/journal.pbio.1001899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellott, D. W. , Hughes, J. F. , Skaletsky, H. , Brown, L. G. , Pyntikova, T. , Cho, T.‐J. … Page, D. C. (2014). Mammalian Y chromosomes retain widely expressed dosage‐sensitive regulators. Nature, 508, 494–499. 10.1038/nature13206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergero, R. , Gardner, J. , Bader, B. , Yong, L. , & Charlesworth, D. (2019). Exaggerated heterochiasmy in a fish with sex‐linked male coloration polymorphisms. Proceedings of the National Academy of Sciences of the United States of America, 116, 6924–6931. 10.1073/pnas.1818486116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berner, D. (2019). Allele Frequency Difference AFD – An intuitive alternative to F ST for quantifying population differentiation. Genes, 10, 308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhatia, G. , Patterson, N. , Sankararaman, S. , & Price, A. L. (2013). Estimating and interpreting F ST: The impact of rare variants. Genome Research, 23(9), 1514–1521. 10.1101/gr.154831.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaser, O. , Grossen, C. , Neuenschwander, S. , & Perrin, N. (2012). Sex‐chromsome turnovers induced by deleterious mutation load. Evolution, 67, 635–645. [DOI] [PubMed] [Google Scholar]
- Böhne, A. , Weber, A. A.‐T. , Rajkov, J. , Rechsteiner, M. , Riss, A. , Egger, B. , & Salzburger, W. (2019). Repeated evolution versus common ancestry: Sex chromosome evolution in the Haplochromine Cichlid Pseudocrenilabrus philander. Genome Biology and Evolution, 11(2), 439–458. 10.1093/gbe/evz003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, B. (1998). Measures of divergence between populations and the effect of forces that reduce variability. Molecular Biology and Evolution, 15, 538–543. 10.1093/oxfordjournals.molbev.a025953 [DOI] [PubMed] [Google Scholar]
- Charlesworth, D. , Charlesworth, B. , & Marais, G. (2005). Steps in the evolution of heteromorphic sex chromosomes. Heredity, 95, 118–128. 10.1038/sj.hdy.6800697 [DOI] [PubMed] [Google Scholar]
- Cheng, C. , & Kirkpatrick, M. (2016). Sex‐specific selection and sex‐biased gene expression in humans and flies. PLoS Genetics, 12, 1–18. 10.1371/journal.pgen.1006170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conte, M. A. , Gammerdinger, W. J. , Bartie, K. L. , Penman, D. J. , & Kocher, T. D. (2017). A high quality assembly of the Nile tilapia (Oreochromis niloticus) genome reveals the structure of two sex determination regions. BMC Genomics, 18, 341 10.1186/s12864-017-3723-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortez, D. , Marin, R. , Toledo‐Flores, D. , Froidevaux, L. , Liechti, A. , Waters, P. D. , … Kaessmann, H. (2014). Origins and functional evolution of Y chromosomes across mammals. Nature, 508, 488–493. 10.1038/nature13151 [DOI] [PubMed] [Google Scholar]
- Cruickshank, T. E. , & Hahn, M. W. (2014). Reanalysis suggests that genomic islands of speciation are due to reduced diversity, not reduced gene flow. Molecular Ecology, 23, 3133–3157. 10.1111/mec.12796 [DOI] [PubMed] [Google Scholar]
- Danecek, P. , Auton, A. , Abecasis, G. , Albers, C. A. , Banks, E. , DePristo, M. A. , … Durbin, R. (2011). The variant call format and VCFtools. Bioinformatics, 27, 2156–2158. 10.1093/bioinformatics/btr330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixon, G. , Kitano, J. , & Kirkpatrick, M. (2018). The origin of a new sex chromosome by introgression between two stickleback fishes. Molecular Biology and Evolution, 36, 28–38. 10.1093/molbev/msy181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier, L. , & Lischer, H. E. L. (2010). Arlequin suite ver 3.5: A new series of programs to perform population genetics analyses under Linux and Windows. Molecular Ecology Resources, 10, 564–567. 10.1111/j.1755-0998.2010.02847.x [DOI] [PubMed] [Google Scholar]
- Excoffier, L. , Smouse, P. E. , & Quattro, J. M. (1992). Analysis of molecular variance inferred from metric distances among DNA haplotypes: Application to Human mitochondrial DNA restriction data. Genetics, 131, 479–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flanagan, S. P. , & Jones, A. G. (2017). Genome‐wide selection components analysis in a fish with male pregnancy. Evolution, 71, 1096–1105. 10.1111/evo.13173 [DOI] [PubMed] [Google Scholar]
- Fontaine, A. , Filipovi, I. , Fansiri, T. , Hoffmann, A. A. , Cheng, C. , Kirkpatrick, M. … Lambrechts, L. (2017). Extensive genetic differentiation between homomorphic sex chromosomes in the mosquito vector, Aedes aegypti . Genome Biology and Evolution, 9, 2322–2335. 10.1093/gbe/evx171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraïsse, C. , Picard, M. A. L. , & Vicoso, B. (2017). The deep conservation of the Lepidoptera Z chromosome suggests a non‐canonical origin of the W. Nature Communications, 8, 1486 10.1038/s41467-017-01663-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gammerdinger, W. J. , Conte, M. A. , Acquah, E. A. , Roberts, R. B. , & Kocher, T. D. (2014). Structure and decay of a proto‐Y region in tilapia, Oreochromis niloticus . BMC Genomics, 15, 975 10.1186/1471-2164-15-975 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gammerdinger, W. J. , Conte, M. A. , Baroiller, J.‐F. , D’Cotta, H. , & Kocher, T. D. (2016). Comparative analysis of a sex chromosome from the blackchin tilapia, Sarotherodon melanotheron . BMC Genomics, 17, 808 10.1186/s12864-016-3163-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gammerdinger, W. J. , Conte, M. A. , Sandkam, B. A. , Penman, D. J. , & Kocher, T. D. (2019). Characterization of sex chromosomes in three deeply diverged species of Pseudocrenilabrinae (Teleostei: Cichlidae). Hydrobiologia, 832, 397–408. 10.1007/s10750-018-3778-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gammerdinger, W. J. , Conte, M. A. , Sandkam, B. A. , & Ziegelbecker, A. (2018). Novel sex chromosomes in three cichlid fishes from Lake Tanganyika. Journal of Heredity, 1, 12. [DOI] [PubMed] [Google Scholar]
- Goudet, J. (2005). HIERFSTAT, a package for R to compute and test hierarchical F‐statistics. Molecular Ecology Notes, 5, 184–186. 10.1111/j.1471-8286.2004.00828.x [DOI] [Google Scholar]
- Hahn, M. W. (2018). Molecular population genetics. New York: Oxford University Press. [Google Scholar]
- Hedrick, P. W. (2005). A standardized genetic differentiation measure. Evolution, 59, 1633–1638. 10.1111/j.0014-3820.2005.tb01814.x [DOI] [PubMed] [Google Scholar]
- Hohenlohe, P. A. , Bassham, S. , Etter, P. D. , & Cresko, W. A. (2010). Population genomics of parallel adaptation in threespine stickleback using sequenced RAD tags. PLoS Genetics, 6, e1000862 10.1371/journal.pgen.1000862 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holsinger, K. E. , & Weir, B. S. (2009). Genetics in geographically structured populations: Defining, estimating and interpreting FST . Nature Reviews Genetics, 10, 639–650. 10.1038/nrg2611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R. , Boos, D. D. , & Kaplan, N. L. (1992). A statistical test for detecting geographic subdivision. Molecular Biology and Evolution, 9, 138–151. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R. , Slatkin, M. , & Maddison, W. P. (1992). Estimation of levels of gene flow from DNA sequence data. Genetics, 589, 583–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huylmans, A. K. , Toups, M. A. , Macon, A. , Gammerdinger, W. J. , & Vicoso, B. (2019). Sex–biased gene expression and dosage compensation on the Artemia franciscana Z‐chromosome. Genome Biology and Evolution, 11:1033–1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamiya, T. , Kai, W. , Tasumi, S. , Oka, A. , Matsunaga, T. , Mizuno, N. … Kikuchi, K. (2012). A trans‐species missense SNP in Amhr2 is associated with sex determination in the tiger pufferfish, Takifugu rubripes (fugu). PLoS Genetics, 8, e1002798 10.1371/journal.pgen.1002798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasimatis, K. R. , Nelson, T. C. , & Phillips, P. C. (2017). Genomic signatures of sexual conflict. Journal of Heredity, 108, 780–790. 10.1093/jhered/esx080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasimatis, K. R. , Ralph, P. L. , & Phillips, P. C. (2019). Limits to genomic divergence under sexually antagonistic selection. G3 Genes, Genomes, Genetics, 9(11), 3813–3824. 10.1534/g3.119.400711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keenan, K. , McGinnity, P. , Cross, T. F. , Crozier, W. W. , & Prodöhl, P. A. (2013). diveRsity: An R package for the estimation and exploration of population genetics parameters and their associated errors. Methods in Ecology and Evolution, 4, 782–788. [Google Scholar]
- Kirkpatrick, M. , & Guerrero, R. (2014). Signatures of sex‐antagonistic selection on recombining sex chromosomes. Genetics, 197, 531–541. 10.1534/genetics.113.156026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lischer, H. E. L. , & Excoffier, L. (2012). PGDSpider: An automated data conversion tool for connecting population genetics and genomics programs. Bioinformatics, 28, 298–299. 10.1093/bioinformatics/btr642 [DOI] [PubMed] [Google Scholar]
- Lopes, R. J. , Johnson, J. D. , Toomey, M. B. , Ferreira, M. S. , Araujo, P. M. , Melo‐Ferreira, J. … Carneiro, M. (2016). Genetic basis for red coloration in birds. Current Biology, 26, 1427–1434. 10.1016/j.cub.2016.03.076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucotte, E. A. , Laurent, R. , Heyer, E. , Ségurel, L. , & Toupance, B. (2016). Detection of allelic frequency differences between the sexes in humans: A signature of sexually antagonistic selection. Genome Biology and Evolution, 8, 1489–1500. 10.1093/gbe/evw090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meirmans, P. G. , & Hedrick, P. W. (2011). Assessing population structure: FST and related measures. Molecular Ecology Resources, 11, 5–18. 10.1111/j.1755-0998.2010.02927.x [DOI] [PubMed] [Google Scholar]
- Natri, H. M. , Shikano, T. , & Merilä, J. (2013). Progressive recombination suppression and differentiation in recently evolved neo‐sex chromosomes. Molecular Biology and Evolution, 30, 1131–1144. 10.1093/molbev/mst035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M. (1973). Analysis of gene diversity in subdivided populations. Proceedings of the National Academy of Sciences of the United States of America, 70, 3321–3323. 10.1073/pnas.70.12.3321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M. (1982). Evolution of Human races at the gene level In Alan L. R. (Ed.), Human genetics, part A: The unfolding genome (pp. 167–181). New York: Liss. [PubMed] [Google Scholar]
- Nei, M. (1986). Definition and estimation of fixation indices. Evolution, 40, 643–645. 10.1111/j.1558-5646.1986.tb00516.x [DOI] [PubMed] [Google Scholar]
- Nei, M. (1987). Molecular evolutionary genetics. New York: Columbia University Press. [Google Scholar]
- Nei, M. , & Chesser, R. K. (1983). Estimation of fixation indices and gene diversities. Annals of Human Genetics, 47, 253–259. 10.1111/j.1469-1809.1983.tb00993.x [DOI] [PubMed] [Google Scholar]
- Nei, M. , & Li, W.‐H. (1979). Mathematical model for studying genetic variation in terms of restriction endonucleases. Proceedings of the National Academy of Sciences of the United States of America, 76, 5269–5273. 10.1073/pnas.76.10.5269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pal, A. , & Vicoso, B. (2015). The X chromosome of Hemipteran insects: Conservation, dosage compensation and sex‐biased expression. Genome Biology and Evolution, 7, 3259–3268. 10.1093/gbe/evv215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng, Y. , Yang, Z. , Zhang, H. , Cui, C. , Qi, X. , Luo, X. … Su, B. (2011). Genetic variations in Tibetan populations and high‐altitude adaptation at the Himalayas. Molecular Biology and Evolution, 28, 1075–1081. 10.1093/molbev/msq290 [DOI] [PubMed] [Google Scholar]
- Pfeifer, B. , Wittelsbürger, U. , Ramos‐Onsins, S. E. , & Lercher, M. J. (2014). PopGenome: An efficient swiss army knife for population genomic analyses in R. Molecular Biology and Evolution, 31, 1929–1936. 10.1093/molbev/msu136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . (2016). A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Rice, W. R. (1987). The accumulation of sexually antagonistic genes as a selective agent promoting the evolution of reduced recombination between primitive sex chromosomes. Evolution, 41, 911–914. 10.1111/j.1558-5646.1987.tb05864.x [DOI] [PubMed] [Google Scholar]
- Rodrigues, N. , & Dufresnes, C. (2017). Using conventional F ‐statistics to study unconventional sex‐chromosome differentiation. PeerJ, 5, e3207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesti, M. , Moser, D. , & Berner, D. (2013). Recombination in the threespine stickleback genome — patterns and consequences. Molecular Ecology, 22, 3014–3027. 10.1111/mec.12322 [DOI] [PubMed] [Google Scholar]
- Rousset, F. (2008). GENEPOP’007: A complete re‐implementation of the GENEPOP software for Windows and Linux. Molecular Ecology Resources, 8, 103–106. 10.1111/j.1471-8286.2007.01931.x [DOI] [PubMed] [Google Scholar]
- Rozas, J. , Ferrer‐Mata, A. , Sánchez‐DelBarrio, J. C. , Guirao‐Rico, S. , Librado, P. , Ramos‐Onsins, S. E. , & Sánchez‐Gracia, A. (2017). DnaSP 6: DNA sequence polymorphism analysis of large data sets. Molecular Biology and Evolution, 34, 3299–3302. 10.1093/molbev/msx248 [DOI] [PubMed] [Google Scholar]
- Toups, M. A. , Rodrigues, N. , Perrin, N. , & Kirkpatrick, M. (2018). A reciprocal translocation radically reshapes sex‐linked inheritance in the common frog. Molecular Ecology, 10.1111/mec.14990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Doorn, G. S. , & Kirkpatrick, M. (2010). Transitions between male and female heterogamety caused by sex‐antagonistic selection. Genetics, 186, 629–645. 10.1534/genetics.110.118596 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veltsos, P. , Ridout, K. E. , Toups, M. A. , González‐Martínez, S. C. , Muyle, A. , Emery, O. , … Pannell, J. R. (2019). Early sex‐chromosome evolution in the diploid dioecious plant Mercurialis annua . Genetics, 212, 815–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicoso, B. , & Bachtrog, D. (2011). Lack of global dosage compensation in Schistosoma mansoni; a female‐heterogametic parasite. Genome Biology and Evolution, 3, 230–235. 10.1093/gbe/evr010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicoso, B. , & Bachtrog, D. (2013). Reversal of an ancient sex chromosome to an autosome in Drosophila . Nature, 499, 332–335. 10.1038/nature12235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicoso, B. , & Bachtrog, D. (2015). Numerous transitions of sex chromosomes in Diptera. PLoS Biology, 13, e1002078 10.1371/journal.pbio.1002078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicoso, B. , Kaiser, V. B. , & Bachtrog, D. (2013). Sex‐biased gene expression at homomorphic sex chromosomes in emus and its implication for sex chromosome evolution. Proceedings of the National Academy of Sciences of the United States of America, 110, 6453–6458. 10.1073/pnas.1217027110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir, B. S. (1996). Genetic data analysis II. Sunderland, MA: Sinauer Associates Inc. [Google Scholar]
- Weir, B. , & Cockerham, C. C. (1984). Estimating F‐statistics for the analysis of population structure. Evolution, 38, 1358–1370. [DOI] [PubMed] [Google Scholar]
- Wright, A. E. , Fumagalli, M. , Cooney, C. R. , Bloch, N. I. , Vieira, F. G. , Buechel, S. D. … Mank, J. E. (2018). Male‐biased gene expression resolves sexual conflict through the evolution of sex‐specific genetic architecture. Evolution Letters, 2, 52–61. 10.1002/evl3.39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, A. E. , Rogers, T. F. , Fumagalli, M. , Cooney, C. R. , & Mank, J. E. (2019). Phenotypic sexual dimorphism is associated with genomic signatures of resolved sexual conflict. Molecular Ecology, 28, 2860–2871. 10.1111/mec.15115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S. (1949). The genetical structure of populations. Annals of Eugenics, 15, 323–354. 10.1111/j.1469-1809.1949.tb02451.x [DOI] [PubMed] [Google Scholar]
- Xu, S. , Li, S. , Yang, Y. , Tan, J. , Lou, H. , Jin, W. … Jin, L. (2011). A genome‐wide search for signals of high‐altitude adaptation in Tibetans. Molecular Biology and Evolution, 28, 1003–1011. 10.1093/molbev/msq277 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1
Data Availability Statement
All data needed for reproducing these conclusions are within this work and Supporting Information.


