Efficient and selective alkene hydrosilation promoted by weak, double Si–H activation at an iron center

Cationic iron complexes [Cp*(ⁱPr₂MeP)FeH₂SiHR]⁺, generated and characterized in solution, are very efficient catalysts for the hydrosilation of terminal alkenes and internal alkynes by primary silanes at low catalyst loading (0.1 mol%) and ambient temperature.

Abstract

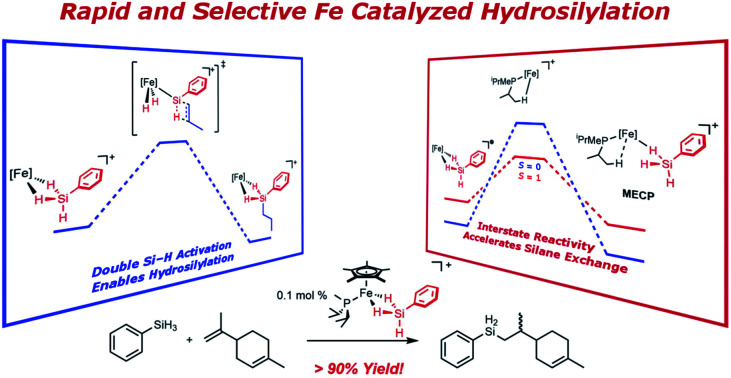
Cationic iron complexes [Cp*(ⁱPr₂MeP)FeH₂SiHR]⁺, generated and characterized in solution, are very efficient catalysts for the hydrosilation of terminal alkenes and internal alkynes by primary silanes at low catalyst loading (0.1 mol%) and ambient temperature. These reactions yield only the corresponding secondary silane product, even with SiH₄ as the substrate. Mechanistic experiments and DFT calculations indicate that the high rate of hydrosilation is associated with an inherently low barrier for dissociative silane exchange (product release).

Introduction

Olefin hydrosilation is one of the most commercially important reactions, used to produce various silicon-containing materials and fine chemicals.1,2 As practiced, this reaction mainly employs Pt-based catalysts3,4 which, given the limited supply and high demand for platinum, creates a strong motivation for development of alternative catalysts based on more earth-abundant metals such as Fe, Co, and Ni.5–22 There are profound differences between the chemical properties of Pt and those of the base metals; most notably the lighter 3d metals have a higher propensity for one-electron reaction steps, which may preclude the oxidative addition/reductive elimination cycles associated with noble metal catalysis. For this reason, the search for base metal hydrosilation catalysts must include discovery of alternative mechanistic pathways suitable for the 3d metals.23

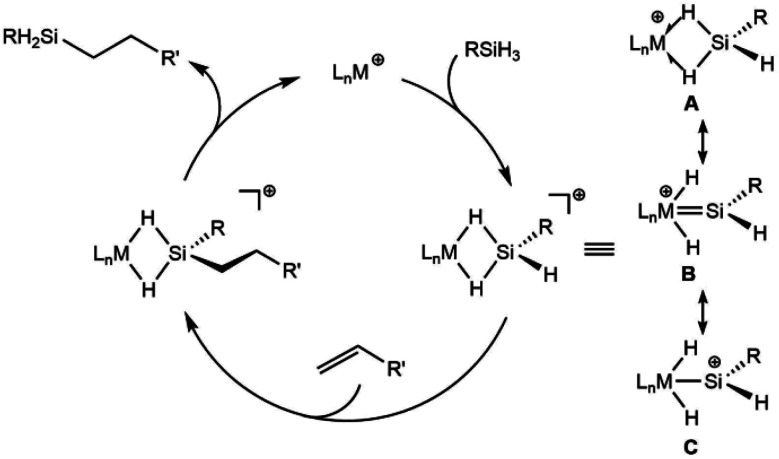
Previous work in this laboratory identified a new mechanism for hydrosilation24,25 associated with cationic silylene complexes of Ru24,26 and Ir.27 Unique to this mechanism is the Si–C bond forming step, in which a Si–H bond in a silylene ligand directly adds across the olefin.2,28 This process is attractive for the design of new hydrosilation catalysts based on 3d metals such as iron, as this critical bond formation does not rely on a metal-centered redox process. Hydrosilation reactions catalyzed by cationic silylene complexes form secondary silane products with linear regioselectivity for the Si–H addition. This selectivity represents an advantage over the more conventional Chalk–Harrod mechanism, which can result in a mixture of linear and branched products due to its reliance on reversible olefin insertion into a metal hydride.

Another aspect of a silylene-based mechanism is the double Si–H bond activation that occurs at the metal center.25,30 Double Si–H activations of this type occur to varying degrees, from moderate activation to give η³-silane complexes (A, Scheme 1),30–32 to more strongly activated cases that have undergone a double oxidative addition to form a silylene dihydride (B, C).26,33–35 Structures along this continuum exhibit high electrophilicity at silicon and greater reactivity for the terminal Si–H bond.

Scheme 1. Representation of the cationic silylene mechanism for hydrosilation with three selected resonance structures for the cationic complexes.

Since the silylene-based mechanism is well established for ruthenium complexes of the type [Cp*(ⁱPr₃P)Ru(H)₂SiHR]⁺, catalytic transformations with analogous iron complexes could provide increased activity due to the enhanced lability of metal–ligand bonds in 3d complexes. This report describes the utility of Cp*(ⁱPr₂MeP)FeH(N₂)36 (1) as a precatalyst for alkene hydrosilation via generation of a cationic iron intermediate. This Fe system is associated with higher rates of conversion for many substrates, and a marked selectivity toward terminal olefins that underscores fundamental mechanistic differences with the related Ru catalyst.

Results and discussion

Precursors to the catalytic species of interest are neutral iron complexes of the type Cp*(ⁱPr₂MeP)Fe(H)₂SiH₂R. Compound 1 reacts with primary silanes (RSiH₃, R = Trip,37 Ph, p-Tol, Mes; Trip = 2,4,6-triisopropylphenyl) by oxidative addition of an Si–H bond to form the corresponding dihydrides Cp*(ⁱPr₂MeP)Fe(H)₂SiH₂R (2_R, eqn (1)). Note that related half-sandwich complexes have been reported previously.36,38,39 These silyl dihydride complexes do not promote hydrosilations up to 80 °C, but they are converted to active cationic catalysts by hydride abstraction.

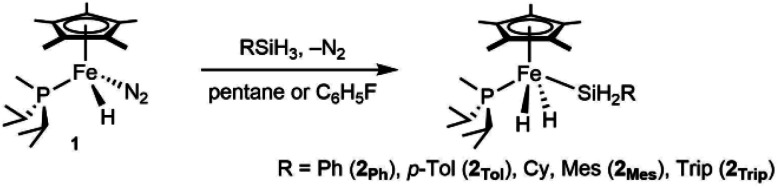1

The cationic complex [Cp*(ⁱPr₂MeP)FeH₂SiHPh][BAr^F₄] (3_Ph; BAr^F₄ = tetrakis(pentafluorophenyl)borate) was generated by treatment of 1 with 1000 equiv. of PhSiH₃ followed by 1 equiv. [Ph₃C][BAr^F₄] in fluorobenzene at –35 °C. After warming to ambient temperature, treatment with 1100 equiv. of 1-octene resulted in quantitative conversion of the silane substrate over 6 h to the linear product Ph(ⁿOct)SiH₂ (eqn (2)), corresponding to a turnover frequency (TOF) of at least 170 h^–1. This selectivity toward primary silanes is reminiscent of the cationic Ru silylene hydrosilation catalyst, but other selectivities (vide infra) suggest that there are fundamental differences in the mechanistic pathways.24,26,28,29 For this reaction the iron catalyst is more active, as the ruthenium catalyst required a higher loading (1 mol%) and elevated temperature (80 °C) to achieve a comparable conversion.26 This activity is in the range of the most active iron catalysts for the hydrosilation of olefins by primary silanes (Table S1†).22,40–43

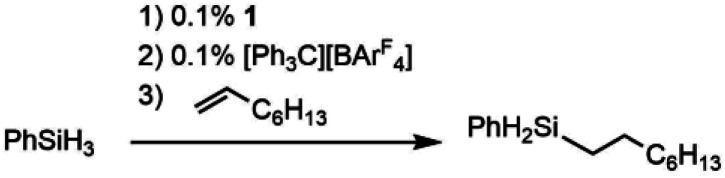2

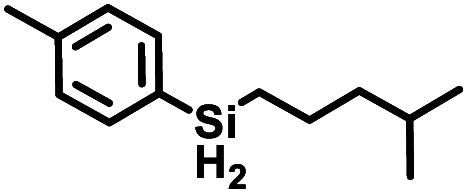
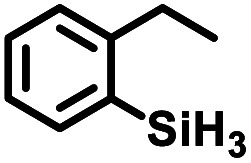
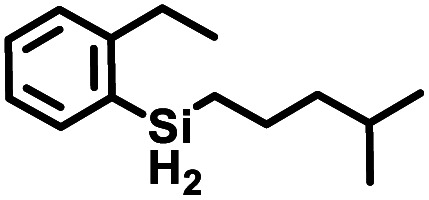
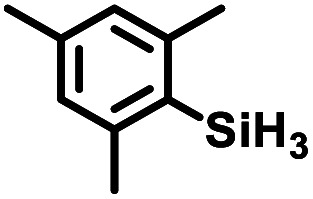
Aryl- and alkyl-substituted primary silanes are suitable substrates for this catalysis (Table 1), but steric factors play an important role. While (o-ethylphenyl)silane is a competent substrate, hydrosilation of 4-methylpentene with mesitylsilane did not proceed even at 80 °C. No hydrosilation products were observed with secondary or tertiary silanes (e.g. PhMeSiH₂ and Et₃SiH) up to 1 mol% catalyst loading over 20 h at ambient temperature. Unlike the Ru silylenes, the Fe catalysts are highly selective toward hydrosilation of terminal olefins (Table 2). This difference in substrate tolerance may arise from the size difference between ruthenium and iron, resulting in greater steric demands from the Fe ancillary ligands in the hydrosilation transition state, and is most dramatically illustrated by the hydrosilation of limonene (entry k) which resulted in complete selectivity for the terminal double bond.

Table 1. Silane scope for hydrosilation of 4-methylpentene. Conditions: fluorobenzene, 0.1 mol% 1, 0.1 mol% [Ph₃C][BAr^F₄], ambient temperature.

	Silane	Product	Time (h)	Yield a
a			6	>98
b			20	>98
c			20	>98
d		N. R.	20	0 b
e			20	>98

^aIsolated yield.

^bSilane redistribution observed at 80 °C.

Table 2. Olefin and alkyne scope for hydrosilation by PhSiH₃. Conditions: fluorobenzene, 0.1 mol% 1, 0.1 mol% [Ph₃C][BAr^F₄], ambient temperature.

	Alkene/alkyne	Product	Time (h)	Yield a
f			6	>98
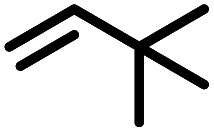
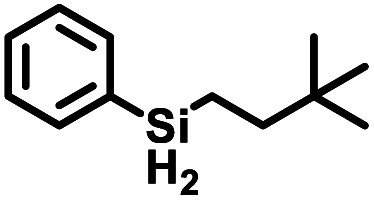
g			0.5	95 (97)
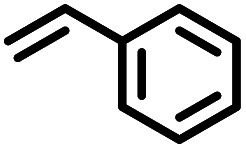
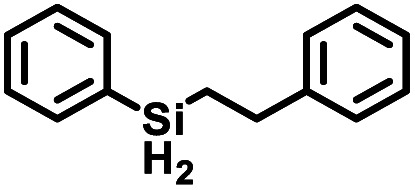
h			20	97 (98)
i		N. R.	20	0
j		N. R.	20	0
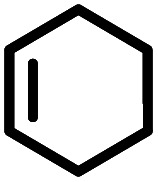
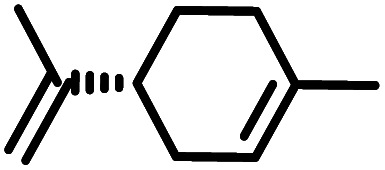
k			20	92 (97) b
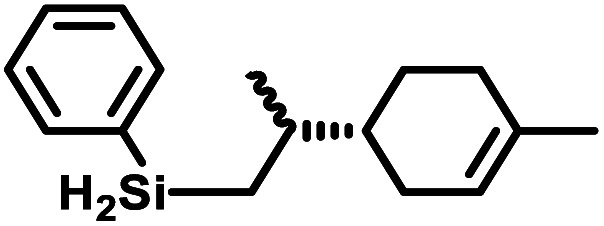
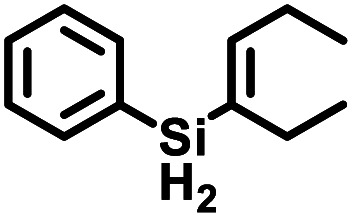
l			5	87 (95)
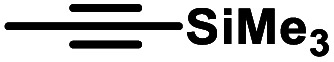
m			20	89 (97) c
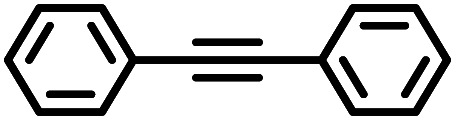
n		N. R.	20	0
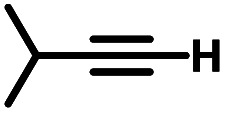
o		N. R.	20	0

^aIsolated yield (NMR yield).

^bDiastereomeric excess = 15%.

^cR = Me, R′ = SiMe₃, 87.5%; R = SiMe₃, R′ = Me, 12.5%.

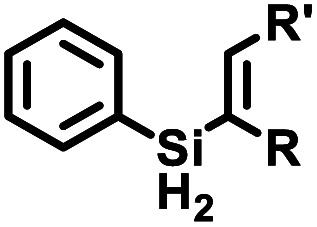
The iron catalysts selectively give cis-hydrosilation of internal alkyne substrates (entries l and m; Table 2, by ¹H NMR spectroscopy), which is consistent with direct Si–H addition. No conversion was observed for diphenylacetylene (entry n), presumably due to steric factors, and further evidence that catalyst selectivity is driven by steric factors is seen with propynyltrimethylsilane as substrate, to predominantly form 2-phenylsilyl-1-trimethylsilylpropene (∼90% selectivity). The intolerance for the terminal acetylenic substrate (entry o) is most likely due to side reactions with the acetylenic C–H bond.

The selectivity of this catalyst system suggested the use of SiH₄ to form secondary silanes (eqn (3)). For this reaction, the catalyst was generated by reaction of 2_Mes with [Ph₃C][BAr^F₄] in fluorobenzene, which was then treated with 400 equiv. of 4-methylpentene and exposed to 1 atm of 15% silane in nitrogen. While the yield of (4-Me-pentyl)₂SiH₂ was only 2.6% after 18 h (based on olefin; TON = 52), the reaction is highly selective in that only the secondary silane was observed as product (by ¹H NMR spectroscopy and TLC). The low yield is attributed to the low concentration of SiH₄; higher pressures of silane and longer reaction times would likely give greater turnover.

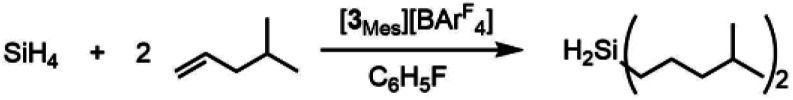3

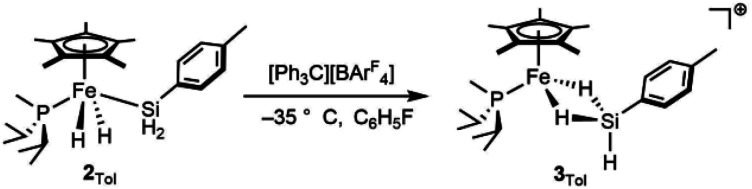
Attempts to isolate the activated catalysts as crystalline solids were not successful; in all cases, crystallization attempts produced impure oils, prompting characterization in situ by NMR spectroscopy. Complex 2_Tol was treated with 1 equiv. of [Ph₃C][BAr^F₄] at –35 °C in fluorobenzene in an attempt to generate [Cp*(ⁱPr₂MeP)FeH₂SiH(p-Tol)]⁺ (3_Tol, eqn (4)), which resulted in a color change to blue. Integration against a C₆Me₆ internal standard indicated that 3_Tol was formed in >99% yield. The ¹H NMR spectrum at room temperature did not contain obvious Fe–H–Si or Si–H resonances, suggesting the possibility of exchange between such positions. Upon cooling a solution of 3_Tol in fluorobenzene-d₅ to –30 °C, Fe–H (–15.12 ppm, J_HP = 20.9 Hz, J_Si(μ-H) = 90 Hz) and Si–H (6.74 ppm, J_SiH = 180 Hz) resonances were observed. These resonances display cross peaks to a downfield ²⁹Si resonance at 188 ppm in the HMBC spectrum (J_Si(μ-H) 90 Hz).

4

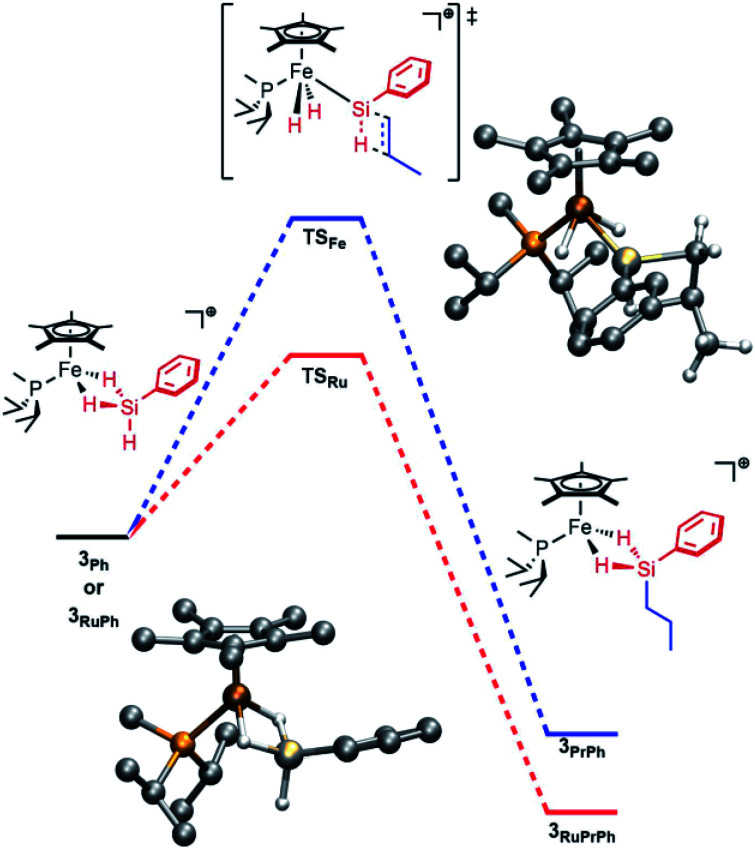
Computations on the structure of 3_Ph were found to be highly dependent upon the choice of functional, particularly with respect to the extent of Si–H activation at the Fe center. The experimentally determined structure of the related Ru complex, [Cp*(ⁱPr₃P)Ru(H)₂ Si(H)Mes]⁺, was used to calibrate the choice of functional, and the range-separated-hybrid functional ωB97X-D3 was found to be in best agreement with this structure. For the Fe complex, calculations at the ωB97X-D3/def2-TZVP/SVP level of theory are consistent with the interpretation that Si–H activation at Fe is modest. The geometry of the molecule resembles an η³-silane structure (Fig. 1), with the hydrides symmetrically bridging the Fe and Si atoms and minimal Si–H activation relative to free silane (d_FeSi = 2.20 Å; FSR = 0.95). The Si–H_(bridge) distances are slightly longer than the terminal Si–H distance (1.59 vs. 1.47 Å) and the Fe–H distances average to 1.68 Å (FSR = 1.14). The FeH₂Si unit is planar (Σ_∠ = 358°). In contrast, [Cp*(ⁱPr₂MeP)RuH₂SiHPh]⁺ (3_RuPh) is computed to have proceeded significantly further along the double Si–H activation continuum, and toward a structure that may be regarded as a silylene dihydride. To wit, 3_RuPh is computed to possess an extremely short Ru–Si distance (2.25 Å; FSR = 0.93), Si–H_(bridge) distances which are elongated relative to those in 3_Ph (1.67 Å), and short Ru–H interactions (1.75 Å; FSR = 1.11).

Fig. 1. Computed energy profile for addition of propylene to 3_Ph (blue) or 3_RuPh (red). Bottom left: computed structure of 3_Ph. Top right: computed structure of TS_Fe.

The selectivity of the Fe catalysts with respect to the olefin substrates prompted an investigation into the hydrosilation mechanism. For [Cp*(ⁱPr₃P)RuH₂SiHR]⁺, the rate-limiting step in catalysis is the dissociative exchange of the product silane with silane substrate.26 For the corresponding osmium complexes, catalytic activity was not observed, even though stoichiometric Si–H addition to olefins proceeds rapidly.24,44 This suggests that dissociative silane exchange is even less favorable for Os. In light of this trend toward lower barriers to silane exchange from Os to Ru, a reasonable hypothesis is that the barrier to silane exchange for Fe is even lower, to the extent that the rate of direct Si–H addition to the olefin may become competitive. This would explain both the increased activity of the Fe catalysts for unhindered substrates and the sterically-based selectivity for terminal olefins.

This hypothesis is supported by computational investigations of the catalytic cycle using geometries calculated at the ωB97X-D3/def2-TZVP/SVP level of theory, with single point energies corrected at the DLPNO-CCSD(T)/def2-TZVP level of theory. The computed energy profile for the olefin addition (Fig. 1) indicates that the transition state for Si–H addition to the olefin (TS) is at a higher energy than that for the Ru system (ΔG^‡ = 19.1 kcal mol^–1 for Fe vs. 11.7 kcal mol^–1 for Ru; previous computations indicated a 8–15 kcal mol^–1 barrier for Ru).28,29 Importantly, this barrier height is comparable to that of silane exchange (vide infra), and a consequence is that the rate-determining step for catalysis is substrate dependent. Thus, in at least some cases the Si–H addition is slow enough (e.g., due to steric factors) to render this step rate-determining. This substrate-dependent reactivity could explain the novel selectivity of this Fe system.

Notably, while the 3_Ph ground state involves bridging Fe–H–Si interactions, the Si–H interactions are considerably weaker in transition state TS_Fe, manifested in elongation of the Si–H_Fe interactions from 1.59 to 1.89 Å, and shortening of the Fe–H (from 1.68 to 1.52 Å; ΔFSR = –0.11) and Fe–Si (from 2.20 to 2.15 Å; ΔFSR = –0.02) distances, consistent with generation of an electrophilic silylene in this transition state by a “double α-migration”.45

A dissociative mechanism for silane exchange is supported by VT NMR spectroscopy. The complex [Cp*(ⁱPr₂MeP)FeH₂SiH(p-Tol)][BAr^F₄] (3_Tol) was generated in fluorobenzene solution in the presence of 1 equiv. of p-tolylsilane, and the tolyl CH₃ and silane SiH₃¹H NMR resonances were monitored from 246 to 330 K. Above 290 K, the resonances attributed to free and bound p-TolSiH₃ broaden and coalesce, consistent with chemical exchange between the two species. Rate constants for the exchange between p-tolylsilane and 3_Tol were determined based on lineshape analyses of the p-CH₃ resonances; an Eyring plot gave the activation parameters ΔH^‡ = 27.0(4) kcal mol^–1 and ΔS^‡ = 34(1) cal mol^–1 K^–1 (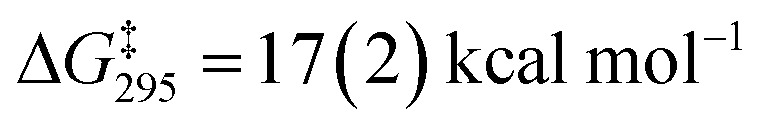 at 298 K; see ESI†). These activation parameters are consistent with a dissociative exchange mechanism similar to that proposed for the Ru silylene system (ΔH^‡ = 32(2) kcal mol^–1 and ΔS^‡ = 19(1) cal mol^–1 K^–1, 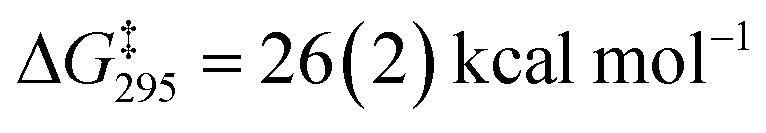). The somewhat lower enthalpy of activation for Fe likely reflects the weaker bonding of the η³-H₃SiR ligand to the metal, and the lower activation of the Si–H bonds in the Fe system relative to Ru.

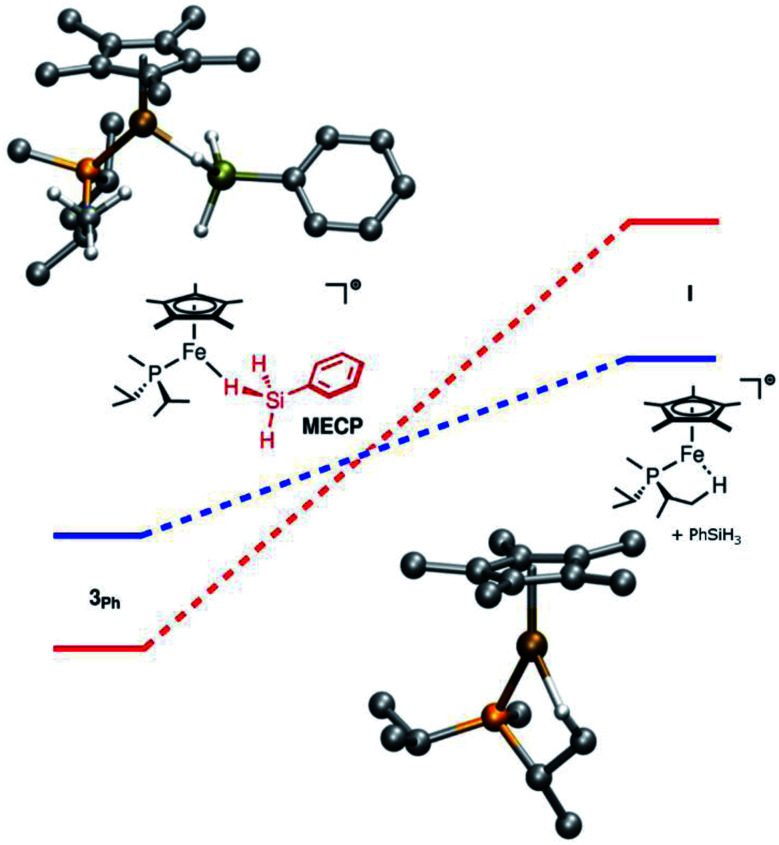
Computationally, the dissociative mechanism for silane exchange involving the coordinatively unsaturated intermediate Cp*(ⁱPr₂MeP)Fe⁺ (I, Fig. 2) is reasonable. This structure includes an agostic interaction with one of the phosphine ⁱPr substituents, as evidenced by a close contact with a C-bound H atom (d_FeH = 1.943 Å). Additionally, the triplet state for I is lower in energy than the singlet state by 12.5 kcal mol^–1 suggesting a two-state mechanism for dissociative silane exchange at Fe in this system. In the triplet structure, the Fe–H distance in the agostic interaction is shorter (d_FeH = 1.893 Å). Notably, this situation is not observed computationally for [Cp*(ⁱPr₂MeP)Ru]⁺, for which the triplet state is higher in energy than the singlet state by 18.1 kcal mol^–1. A minimum energy crossing point (MECP) was found along the reaction coordinate for silane dissociation from 3_Ph. Note that the MECP computed using the ωB97X-D3 functional most likely does not reproduce either the energy or geometry of the MECP well, as this functional overstabilizes triplet states in both the present and related systems.37 Thus, using the B3LYP functional (for which the singlet-triplet gap of I agrees much better with DLPNO-CCSD(T)) the MECP is found to be 4.6 kcal mol^–1 above 3_Ph, and still lower in energy than the fully dissociated triplet species. In this structure, the Fe–Si bond has lengthened by ca. 0.2 Å, and one of the ⁱPr-Me groups from the phosphine has approached the Fe center.

Fig. 2. Computed energy profile for the dissociation of silane from 3_Ph. The singlet pathway is shown in red, and the triplet pathway is shown in blue. Top left: structure of the MECP (minimum-energy crossing point). Bottom right: structure of the triplet state of I. Both structures were computed at the ωB97X-D3/def2-TZVP/SVP level of theory.

While we were unable to fully optimize a transition state structure for silane dissociation, nudged elastic band (NEB) calculations of the silane dissociation coordinate indicate a very late transition state for the triplet state of I (Table S4†). Thus, the energetics of this intermediate can be used as a proxy for activation energies for silane dissociation; these energies are summarized in Table S3.† For dissociation to the triplet state of I, ΔH = 22.7 kcal mol^–1 and ΔS is extremely positive (52.7 cal mol K^–1). However, since the true transition state for dissociation likely involves a closely-associated silane···I pair, all the translational and rotational entropy from dissociation will not have manifested in the Eyring analysis. Additionally, MECPs prior to the transition state can result in inefficient spin crossover, which should lead to a decrease in the rate relative to that of an analogous one-state process. These factors would result in a less positive experimental ΔS^‡ in an Eyring analysis.

Conclusions

The cationic Fe catalysts described here are highly active in the hydrosilation of unhindered olefins with primary silanes. This discovery provides the foundation for new catalyst design strategies involving the first-row transition metals. Importantly, the mechanistic pathway for these catalysts is non-oxidative in character, in that distinct oxidative additions are not required. The observed rate accelerations and enhanced selectivities relative to a related Ru system highlight the distinctly different catalysis that is possible for the 3d metals. In this case, mechanistic studies suggest that the promising characteristics of the iron catalysts relate to a modest degree of Si–H bond activation in the silane substrate, and therefore weaker metal–silane binding and a faster dissociative exchange of the product silane for the silane substrate. The lower cost and greater sustainability of Fe makes the present system highly attractive for the synthesis of unsymmetrical secondary silanes, and multiply-substituted silicon centers derived therefrom.

Conflicts of interest

There are no conflicts to declare.