Systematic comparison of epidemic growth patterns using two different estimation approaches

Abstract

Background

Different estimation approaches are frequently used to calibrate mathematical models to epidemiological data, particularly for analyzing infectious disease outbreaks. Here, we use two common methods to estimate parameters that characterize growth patterns using the generalized growth model (GGM) calibrated to real outbreak datasets.

Materials and methods

Data from 31 outbreaks are used to fit the GGM to the ascending phase of each outbreak and estimate the parameters using both least squares (LSQ) and maximum likelihood estimation (MLE) methods. We utilize parametric bootstrapping to construct confidence intervals for parameter estimates. We compare the results including RMSE, Anscombe residual, and 95% prediction interval coverage. We also evaluate the correlation between the estimates from both methods.

Results

Comparing LSQ and MLE estimates, most outbreaks have similar parameter estimates, RMSE, Anscombe, and 95% prediction interval coverage. Parameter estimates do not differ across methods when the model yields a good fit to the early growth phase. However, for two outbreaks, there are systematic deviations in model fit to the data that explain differences in parameter estimates (e.g., residuals represent random error rather than systematic deviation).

Conclusion

Our findings indicate that utilizing LSQ and MLE methods produce similar results in the context of characterizing epidemic growth patterns with the GGM, provided that the model yields a good fit to the data.

1. Introduction

Mathematical models are frequently used to assess, investigate, and forecast epidemic outbreaks. For instance, models can be useful to gain a better understanding of the underlying mechanisms of disease transmission and control. Complexity varies from simple growth models consisting of one or two equations and 2–3 parameters, such as the generalized-growth model (GGM) and generalized logistic model (GLM), to complex mechanistic SIR-type models at variable spatial scales (Roosa et al., 2020a; Viboud et al., 2018). The latter range from population-level models that assume homogeneous mixing to individual-level models that incorporate heterogeneous mixing and levels of susceptibility and infectivity (Sattenspiel & Lloyd, 2009). Using mathematical models helps understand several different outbreak characteristics, including epidemiological parameters and control or intervention effects (Chowell, 2017).

A defining characteristic of an outbreak is the functional form of early epidemic growth patterns, which are shaped by a combination of multiple factors, including the mode of disease transmission and the early onset of behavioral changes or control interventions (Chowell, Viboud, Hyman, & Simonsen, 2015). While simple compartmental SEIR-type transmission models assume exponential epidemic growth patterns in large susceptible populations (Anderson & May 1991), outbreaks often display sub-exponential (polynomial) growth, as reported in prior studies (Chowell et al., 2016; Roosa et al., 2020b; Viboud, Simonsen, & Chowell, 2016).

For some infectious diseases, exponential growth may be facilitated by an airborne transmission route, a short incubation period, and a relatively low case fatality rate. In contrast, infectious diseases with longer incubation periods that spread by direct contact with bodily fluids of an infected patient, such as HIV (Poorolajal, Hooshmand, Mahjub, Esmailnasab, & Jenabi, 2016), tend to spread following slower growth patterns. Another example is the Ebola virus disease, which has a generation interval of about 2 weeks, but it spreads via close or intimate contact with an infected patient and is frequently associated with a high case fatality rate in settings with sub-optimal health infrastructure. Such infections are expected to spread at a slower rate compared to the influenza virus, which is also capable of airborne spread and characterized by a short incubation period (~1–2 days); therefore, sub-exponential growth patterns in disease transmission occur frequently (Chowell et al., 2015).

Several methods have been proposed to estimate model parameters that characterize disease spread, including least squares estimation (LSQ) and maximum likelihood estimation (MLE). The choice of parameter estimation method often depends on model complexity and data availability. With count data, like outbreak data, it is assumed that Poisson-MLE will perform better than LSQ, as the error structure of count data more closely resembles a Poisson distribution than a normal distribution, as assumed by LSQ. However, a Poisson error structure can be incorporated with LSQ using bootstrapping techniques to model uncertainty (Roosa & Chowell, 2019). In this paper, we compare the performance of the LSQ and MLE methods with a Poisson error structure for characterizing the early ascending phase of a variety of epidemic outbreaks.

Previous work shows that LSQ with parametric bootstrapping and MLE assuming Poisson distribution yielded very similar results using simulated data from simple epidemic growth models (Roosa & Chowell, 2019). Here we employ real outbreak datasets and the generalized-growth model to compare the performance of LSQ and MLE methods using several performance metrics, including RMSE, Anscombe residual, and the coverage of the 95% prediction interval (95% PI). We also assess the suitability of the Poisson distribution to model the uncertainty of the early ascending phase of the outbreaks.

2. Data and methods

Using datasets from 31 historical outbreaks, we employ two methods to estimate the best-fit parameters of the generalized-growth model to characterize epidemic growth patterns. Our data encompasses several infectious diseases including Zika, foot-and-mouth disease (FMD), Ebola, cholera, measles, pandemic influenza, plague, and smallpox (Table 1, Table 2). The temporal scale of the datasets varies from daily to weekly case counts.

Table 1.

Results of r and p parameters with 95% CI, RMSE, Anscombe residual, prediction coverage, and the length of ascending phase by LSQ for each outbreak.

Outbreaks	r (95% CI)	p (95% CI)	RMSE	Anscombe	Prediction interval coverage (%)	length of ascending phase	Data source
Zika(Antioquia, 2015)	1.70 (0.79, 2.90)	0.42 (0.23, 0.65)	3.04	16.38	100.00	15/104 days	Chowell et al. (2016)
Zika(Antioquia, 2015)	1.40 (0.79, 2.50)	0.47 (0.30, 0.64)	2.50	16.40	100.00	16/104days	Chowell et al. (2016)
Zika(Antioquia, 2015)	1.40 (0.74, 2.40)	0.48 (0.31, 0.66)	3.15	16.31	100.00	17/104days	Chowell et al. (2016)
FMD (UK, 2001-120days)	0.55 (0.35, 0.78)	0.70 (0.59, 0.83)	4.01	37.98	92.00	25/229days	Shanafelt et al. (2018)
Ebola (Tonkolili, 2014)	0.12 (0.08, 0.29)	0.92 (0.61, 1.00)	3.63	5.94	100.00	5/69 weeks	Ebola Response Roadmap, 2015
Ebola (Tonkolili, 2014)	0.19 (0.08, 0.38)	0.77 (0.52, 1.00)	7.54	8.21	100.00	6/69 weeks	Ebola Response Roadmap, 2015
Ebola (Tonkolili, 2014)	0.09 (0.08, 0.15)	0.97 (0.83, 1.00)	8.67	10.63	100.00	7/69 weeks	Ebola Response Roadmap, 2015
Cholera (Aalborg, 1853)	0.55 (0.35, 0.79)	0.78 (0.70, 0.88)	6.70	36.80	90.00	20/108 days	“Det Kongelige Sundhedskollegiums Aarsberetning for, 1853,"
Ebola (Bo, 2014)	0.13 (0.08, 0.21)	0.80 (0.67, 0.96)	8.85	27.47	80.00	10/67 weeks	Ebola Response Roadmap, 2015
Ebola (Bombali, 2014)	0.08 (0.06, 0.14)	0.94 (0.78, 1.00)	5.92	17.20	87.50	8/64 weeks	Ebola Response Roadmap, 2015
Ebola (Bomi, 2014)	1.20 (0.51, 2.00)	0.12 (0.00, 0.36)	6.31	19.68	75.00	8/66 weeks	Ebola Response Roadmap, 2015
Ebola (Congo, 1976)	1.30 (0.69, 2.20)	0.44 (0.27, 0.62)	2.77	19.59	100.00	20/52 days	Breman, 1978; Camacho et al., 2014
Ebola (Grand Bassa, 2014)	0.42 (0.13, 0.90)	0.34 (0.06, 0.70)	4.23	7.72	100.00	9/64 weeks	Ebola Response Roadmap, 2015
Ebola (Gueckedou, 2014)	0.14 (0.05, 0.35)	0.64 (0.35, 0.93)	5.05	18.04	81.82	11/90 weeks	Ebola Response Roadmap, 2015
Ebola (Kenema, 2014)	0.58 (0.33, 0.92)	0.47 (0.33, 0.61)	5.21	17.61	87.50	8/70weeks	Ebola Response Roadmap, 2015
Ebola (Margibi, 2014)	0.10 (0.09, 0.12)	0.98 (0.91, 1.00)	11.80	22.77	77.78	9/68 weeks	Ebola Response Roadmap, 2015
Ebola (Margibi, 2014)	0.20 (0.14, 0.27)	0.75 (0.66, 0.85)	16.26	68.20	40.00	10/68 weeks	Ebola Response Roadmap, 2015
Ebola (Margibi, 2014)	0.22 (0.16, 0.29)	0.72 (0.64, 0.80)	12.82	73.79	54.55	11/68 weeks	Ebola Response Roadmap, 2015
Ebola (Montserrado, 2014)	0.09 (0.08, 0.11)	0.98 (0.90, 1.00)	6.99	46.94	50.00	10/71 weeks	Ebola Response Roadmap, 2015
Ebola (Port Loko, 2014)	0.55 (0.34, 0.81)	0.51 (0.40, 0.64)	4.00	2.85	100.00	8/64 weeks	Ebola Response Roadmap, 2015
Ebola (Uganda, 2000)	0.34 (0.19, 0.52)	0.67 (0.53, 0.85)	1.47	2.01	100.00	6/18 weeks	Chowell, Hengartner, Castillo-Chavez, Fenimore, & Hyman, 2004; World Health Organization, 2001
Ebola (Western Area Rural, 2014)	0.32 (0.23, 0.45)	0.62 (0.52, 0.70)	8.68	12.49	90.00	10/63 weeks	Ebola Response Roadmap, 2015
Ebola (Western Area Urban, 2014)	0.50 (0.32, 0.77)	0.53 (0.43, 0.63)	8.54	12.14	90.00	10/62 weeks	Ebola Response Roadmap, 2015
FMD (Uruguay, 2001)	2.90 (2.40, 3.00)	0.69 (0.68, 0.72)	96.47	321.44	45.45	11/27 days	Chowell, Rivas, Hengartner, Hyman, & Castillo-Chavez, 2006; Chowell, Rivas, Smith, & Hyman, 2006
Measles (London, 1948)	1.70 (1.40, 2.30)	0.51 (0.47, 0.55)	82.18	135.84	44.44	9/40 weeks	Measles Time-Series Data,
Pandemic influenza (San Fran, 1918)	0.29 (0.28, 0.35)	0.99 (0.94, 1.00)	9.71	57.93	57.89	19/63days	Chowell, Nishiura, and Bettencourt (2007)
Pandemic influenza (San Fran, 1918)	0.29 (0.28, 0.34)	0.99 (0.95, 1.00)	9.10	58.60	60.00	20/63days	Chowell et al. (2007)
Pandemic influenza (San Fran, 1918)	0.29 (0.28, 0.33)	0.99 (0.96, 1.00)	15.66	69.34	71.43	21/63days	Chowell et al. (2007)
Plague (Bombay, 1905–06)	0.11 (0.07, 0.17)	0.88 (0.79, 1.00)	5.82	5.11	100.00	9/41weeks	“XXII. Epidemiological observations in Bombay City," 1907
Plague (Madagascar-wave2, 2017)	0.12 (0.07, 0.19)	0.81 (0.70, 0.93)	5.74	8.33	100.00	11/50weeks	World Health Organization, 2017
Smallpox (Khulna, Bangladesh, 1972)	0.16 (0.11, 0.21)	0.85 (0.78, 0.92)	13.73	17.41	88.89	9/13 weeks	Sommer, (1974)

Table 2.

Results of r and p parameters with 95% CI, RMSE, Anscombe residual, prediction coverage, and the length of ascending phase by MLE for each outbreak.

Outbreaks	r (95% CI)	p (95% CI)	RMSE	Anscombe	Prediction interval coverage (%)	length of ascending phase	Data Sources
Zika(Antioquia, 2015)	1.30 (0.75, 2.30)	0.49 (0.31, 0.66)	3.46	15.63	100.00	15/104 days	Chowell et al. (2016)
Zika(Antioquia, 2015)	1.20 (0.72, 2.00)	0.51 (0.36, 0.66)	3.82	16.02	100.00	16/104days	Chowell et al. (2016)
Zika(Antioquia, 2015)	1.2 (0.74, 2.00)	0.51 (0.37, 0.66)	3.90	16.02	100.00	17/104days	Chowell et al. (2016)
FMD (UK, 2001-120days)	0.50 (0.37, 0.68)	0.73 (0.64, 0.82)	4.71	37.28	92.00	25/229days	Shanafelt et al. (2018)
Ebola (Tonkolili, 2014)	0.11 (0.08, 0.25)	0.93 (0.65, 1.00)	9.38	5.66	100.00	5/69 weeks	Ebola Response Roadmap, 2015
Ebola (Tonkolili, 2014)	0.16 (0.08, 0.32)	0.82 (0.58, 1.00)	5.20	8.02	100.00	6/69 weeks	Ebola Response Roadmap, 2015
Ebola (Tonkolili, 2014)	0.09 (0.08, 0.14)	0.96 (0.85, 1.00)	9.33	10.66	100.00	7/69 weeks	Ebola Response Roadmap, 2015
Cholera (Aalborg, 1853)	0.49 (0.35, 0.65)	0.81 (0.74, 0.88)	8.07	36.45	90.00	20/108 days	“Det Kongelige Sundhedskollegiums Aarsberetning for, 1853,"
Ebola (Bo, 2014)	0.13 (0.09, 0.19)	0.81 (0.70, 0.92)	7.32	27.44	70.00	10/67 weeks	Ebola Response Roadmap, 2015
Ebola (Bombali, 2014)	0.08 (0.06, 0.11)	0.97 (0.84, 1.00)	3.08	16.04	87.50	8/64 weeks	Ebola Response Roadmap, 2015
Ebola (Bomi, 2014)	1.10 (0.45, 1.90)	0.15 (1.00, 0.39)	5.16	19.68	75.00	8/66 weeks	Ebola Response Roadmap, 2015
Ebola (Congo, 1976)	1.10 (0.68, 2.00)	0.46 (0.29, 0.62)	3.55	19.36	100.00	20/52 days	Breman et al., 1978; Camacho et al., 2014
Ebola (Grand Bassa, 2014)	0.35 (0.14, 0.82)	0.39 (0.07, 0.68)	2.62	7.50	100.00	9/64 weeks	Ebola Response Roadmap, 2015
Ebola (Gueckedou, 2014)	0.12 (0.04, 0.28)	0.69 (0.40, 0.98)	4.64	28.90	90.91	11/90 weeks	Ebola Response Roadmap, 2015
Ebola (Kenema, 2014)	0.52 (0.36, 0.84)	0.49 (0.36,0.61)	6.26	17.35	87.50	8/70weeks	Ebola Response Roadmap, 2015
Ebola (Margibi, 2014)	0.10 (0.09, 0.12)	0.98 (0.92, 1.00)	11.64	22.65	77.78	9/68 weeks	Ebola Response Roadmap, 2015
Ebola (Margibi, 2014)	0.14 (0.11, 0.17)	0.86 (0.78, 0.93)	15.55	57.18	50.00	10/68 weeks	Ebola Response Roadmap, 2015
Ebola (Margibi, 2014)	0.15 (0.13, 0.19)	0.81 (0.75, 0.87)	16.32	63.31	63.64	11/68 weeks	Ebola Response Roadmap, 2015
Ebola (Montserrado, 2014)	0.15 (0.12, 0.20)	0.80 (0.72, 0.88)	12.09	29.42	80.00	10/71 weeks	Ebola Response Roadmap, 2015
Ebola (Port Loko, 2014)	0.56 (0.38, 0.78)	0.51 (0.41, 0.60)	7.31	2.83	100.00	8/64 weeks	Ebola Response Roadmap, 2015
Ebola (Uganda, 2000)	0.40 (0.25, 0.62)	0.62 (0.48, 0.76)	1.91	1.55	100.00	6/18 weeks	Chowell et al., 2004; World Health Organization, 2001
Ebola (Western Area Rural, 2014)	0.32 (0.24, 0.42)	0.62 (0.55, 0.69)	6.87	12.50	100.00	10/63 weeks	Ebola Response Roadmap, 2015
Ebola (Western Area Urban, 2014)	0.52 (0.35, 0.72)	0.52 (0.45, 0.60)	8.75	12.08	90.00	10/62 weeks	Ebola Response Roadmap, 2015
FMD (Uruguay, 2001)	2.90 (2.50, 3.00)	0.69 (0.68, 0.72)	94.25	305.75	36.36	11/27 days	Chowell, Rivas, Hengartner, et al., 2006; Chowell, Rivas, Smith, & Hyman, 2006
Measles (London, 1948)	2.80 (2.40, 3.00)	0.44 (0.43, 0.47)	81.64	118.57	44.44	9/40 weeks	Measles Time-Series Data,
Pandemic influenza (San Fran, 1918)	0.40 (0.33, 0.49)	0.91 (0.86, 0.96)	9.53	47.22	78.95	19/63days	Chowell et al. (2007)
Pandemic influenza (San Fran, 1918)	0.35 (0.30, 0.41)	0.95 (0.91, 0.98)	14.80	52.59	70.00	20/63days	Chowell et al. (2007)
Pandemic influenza (San Fran, 1918)	0.30 (0.28, 0.33)	0.99 (0.96, 1.00)	13.92	68.31	61.90	21/63days	Chowell et al. (2007)
Plague (Bombay, 1905–06)	0.12 (0.08, 0.17)	0.86 (0.78, 0.95)	7.33	4.99	100.00	9/41weeks	“XXII. Epidemiological observations in Bombay City," 1907
Plague (Madagascar-wave2, 2017)	0.10 (0.07, 0.15)	0.84 (0.75, 0.93)	9.06	7.57	100.00	11/50weeks	World Health Organization, 2017
Smallpox (Khulna, Bangladesh, 1972)	0.14 (0.11, 0.18)	0.87 (0.82, 0.93)	13.71	16.36	77.78	9/13 weeks	Sommer, (1974)

The length of the ascending phase used for calibration varied across the outbreaks based on the generation interval of the disease outbreak (Table 1, Table 2) (Viboud et al., 2016). For three of the outbreaks, we also explore multiple lengths of the ascending phase: 15, 16, and 17 data points for Zika (Antioquia, 2015), 19, 20 and 21 data points for pandemic influenza (San Francisco, US, 1918), and 10, 11, and 12 data points for Ebola (Margibi, 2014) for comparison with previous studies (Ganyani, Faes, & Hens, 2019).

2.1. Generalized growth model (GGM)

The generalized growth model allows for slower than exponential growth patterns. The GGM includes a “deceleration of growth parameter” p and a growth rate parameter, r > 0. C(t) represents the cumulative number of cases at time t and C′(t) represents the incidence curve. When the “deceleration of growth” parameter (p) lies within the range of 0 and 1, it depicts sub-exponential growth patterns; p = 0 shows constant/linear growth, and p = 1 shows an exponential pattern (Viboud et al., 2016).

The GGM equation is the following:

$$\raisebox{1ex}{$dC\left(t\right)$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.=C΄\left(t\right)=rC{\left(t\right)}^p$$

The GGM has been used to model various outbreaks, including Zika (Gordon et al., 2019; Pell, Kuang, Viboud, & Chowell, 2018), Foot and Mouth disease (Shanafelt, Jones, Lima, Perrings, & Chowell, 2018), Ebola (Chowell et al., 2015), and HIV/AIDS (Dinh, Chowell, & Rothenberg, 2018).

2.2. Parameter estimation

To estimate the parameters, we conduct parametric bootstrap analyses using LSQ and MLE methods. A previous study shows that one can evaluate parameter uncertainty with a simple computational bootstrap-based method, by replicating several data sets through repeated sampling from the best-fit model (Roosa & Chowell, 2019). When estimating parameters, the initial parameter values can impact the results due to local maxima or minima. Therefore, we utilize Latin hypercube sampling with different initial parameter guesses to estimate the best set of initial parameters, or those with the lowest SSE, for the ‘best-fit’ model to the incidence curve. We then use these parameter values and employ the bootstrapping method to simulate 500 curves (M = 500) from the best-fit model, and further, re-estimate the parameters for each of these new datasets. We then utilize the distributions of parameter estimates to calculate 95% confidence intervals (CIs; 2.5th, 97.5th percentiles), and the distribution of simulated datasets is used to define the 95% prediction intervals. We also assess the root mean squared error and Anscombe residuals of the best-fit curve. We perform these analyses for both LSQ and MLE to compare results.

2.2.1. Least squares estimation (LSQ)

Least squares estimation yields the best fit solution by exploring the parameters to find the parameter set $\hat{\theta }$that minimizes the sum of the squared deviations between the data and the model solution. The equation as follows:

$$\hat{\theta }=argmin\sum _{t=1}^n{\left(f\left(t;\theta \right)-y_t\right)}^2$$

where, y_t is the data and f (t$;\hat{\theta }$) = C′(t|$\hat{\theta })$ is the best-fit solution of the model to the data. We use the fmincon function in Matlab 2017 to get the nonlinear least squares estimation results for our model parameters.

2.2.2. Maximum likelihood estimation (MLE)

Maximum likelihood estimation aims to find the values of the parameter set that are most likely to have generated the observed data. For a parameter set θ, the value of θ that maximizes the likelihood function is the MLE estimate $\hat{\theta }$, where

$$\hat{\theta }=argmax\sum _{t=1}^n\left[y_{t}log\left(f\left(t;\theta \right)\right)-f\left(t;\theta \right)\right]$$

We again employ the fmincon function in Matlab. We compare parameter estimation results of fitting the GGM to real outbreak data across LSQ and MLE methods.

2.3. Performance

The residual shows the deviation of the model fit from the data and assesses the performance of model fit (Kuhn & Johnson, 2013). One widely used metric is root mean squared error (RMSE), which is calculated as follows (where T is the number of data points):

$$RMSE=\sqrt{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T$}\right.\sum _{t=1}^T{\left[y_t-f\left(t;\theta \right)\right]}^2}$$

To account for individual weights of the data points, we use the Anscombe residual, which is as follows (McCullagh & Nelder, 2013):

$$ANSCOMBERESIDUAL=\raisebox{1ex}{$\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left[{y_t}^{2/3}-f{\left(t;\theta \right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right]$}\!\left/ \!\raisebox{-1ex}{$f{\left(t;\theta \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}$}\right.$$

$$ANSCOMBE=\sum _{t=1}^T{\left(\raisebox{1ex}{$\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left[{y_t}^{2/3}-f{\left(t;\theta \right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right]$}\!\left/ \!\raisebox{-1ex}{$f{\left(t;\theta \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}$}\right.\right)}^2$$

For each outbreak, the root mean squared error (RMSE) and Anscombe residual are calculated for both LSQ and MLE to compare the performance of the best-fit model for each method. Further, prediction interval coverage is calculated as the percentage of data points contained within the 95% prediction interval, where the prediction intervals provide information on the uncertainty of the estimates for a future value.

3. Results

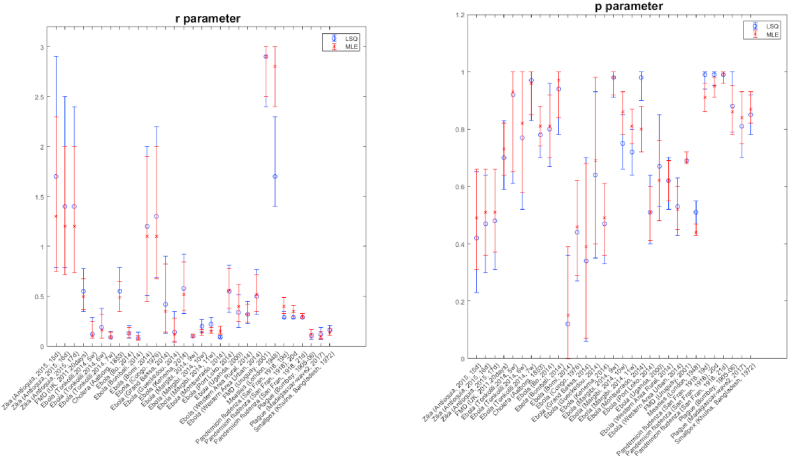
Parameter estimates and their uncertainty (95% CIs) for each of the 31 outbreaks using two different estimation methods, LSQ and MLE, are displayed in Fig. 1. In terms of performance metrics, we find very similar results between the two estimation methods for most outbreaks; however, below we report a few differences and their possible causes (Table 1, Table 2). Figures with model fits and prediction intervals, Anscombe residuals, and empirical distributions of parameters for both estimation methods are included in the appendices for each outbreak (Appendices. Figures. S1-1 & S1-2).

Fig. 1.

Parameter error bars. For each outbreak, the graphs show the mean and 95% confidential interval of r and p estimates from LSQ and MLE methods. Left graph is for r parameter and right one is for p parameter. The blue color represents LSQ and the red color represents MLE.

Estimates of the scaling of growth parameter, p, are very similar across outbreaks (Table 1, Table 2; Fig. 1). Results show high correlation between the mean estimates of the parameters derived from each estimation method (Table 3). Specifically, 29 outbreaks show similar mean estimates with overlapping confidence intervals for estimates derived using LSQ and MLE (Fig. 1). However, for two outbreaks, Ebola in Montserrado (2014) and Measles in London (1948), the 95% CIs for the p parameter do not overlap (Fig. 1). For Ebola in Montserrado (2014), the estimation is likely restricted by the upper estimation bound of 1, especially for LSQ, as the 95% CI interval is (0.9, 1.0) with a skewed distribution favoring the upper bound of 1 (Appendices. Figure S 1-1, s-1); thus, a wider range for p may improve model fit for this outbreak.

Table 3.

Log correlation coefficient. This table shows that log correlation coefficient for the r and p parameters, Anscombe residual, and prediction interval coverage between LSQ and MLE methods.

Variable	Log correlation coefficient (p-value)
r parameter	0.98 (<0.05)
p parameter	0.98 (<0.05)
Anscombe residual	0.99 (<0.05)
95% PI coverage	0.92 (<0.05)

In terms of the RMSE, both estimation methods yield similar model-fit performance. About half of the outbreaks have better fit with LSQ, while the remainder have better fit with MLE (e.g. lower RMSE values; Table 1, Table 2); however, the differences are relatively small. The highest RMSE difference of 5.75 is obtained for Ebola in Tonkolili (2014), with a short ascending phase consisting of 5 data points (RMSE_LSQ = 3.63, RMSE_MLE = 9.38). For the three outbreaks with the greatest difference in RMSE, RMSE results are higher for MLE compared to LSQ, including Ebola in Tonkolili (2014) with 5 data points, Ebola in Montserrado (2014) and pandemic influenza in San Francisco (1918) (Table 1, Table 2). This indicates that when the methods differ in goodness of fit, LSQ performs better in terms of RMSE.

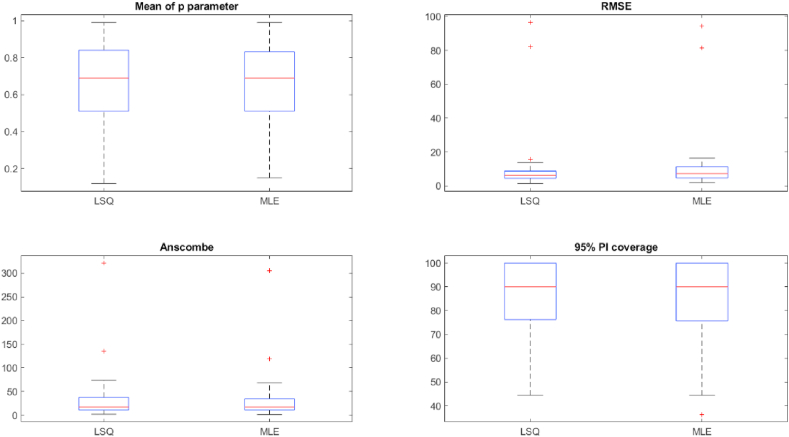
Anscombe residuals also yield similar results between LSQ and MLE (Table 1, Table 2). The outbreak with the highest difference in Anscombe residuals is Ebola in Montserrado (2014), with Anscombe_LSQ = 46.93 and Anscombe_MLE = 29.42 (Table 1, Table 2). The second highest difference in Anscombe residuals is measles in London (1948), with Anscombe_LSQ = 135.84 and Anscombe_MLE = 118.57 (Table 1, Table 2). These differences show that MLE performs better in terms of Anscombe when the methods deviate in performance, which is not surprising as the Anscombe is defined assuming a Poisson error structure, which underlines the MLE method that we employ here. A total of 20 outbreaks have Anscombe values that differ by less than 1.0 between the estimation methods, indicating comparable performance (Table 1, Table 2; Fig. 2). Across outbreaks, the log correlation of the Anscombe residuals show very high correlation between LSQ and MLE (0.99, p < 0.05; Fig. 2; Table 3). The log correlation shows how close the results are between LSQ and MLE.

Fig. 2.

Boxplot between LSQ and MLE for p parameter, RMSE, Anscombe, and 95% prediction interval (PI) coverage.

We also assess the uncertainty of the model fit using the coverage of the 95% prediction interval associated with each estimation method. The 95% PI coverage is greater than 80% for 21 out of 31 outbreaks with LSQ and 20 outbreaks with MLE (Table 1, Table 2). 9 of the 10 outbreaks with PI coverage lower than 80% have consistent coverage comparing LSQ and MLE (Table 1, Table 2), aside from smallpox in Bangladesh (1972), which has PI coverage of 77.78% using MLE and 88.89% using LSQ (Table 1, Table 2).

A total of 21 outbreaks have the same coverage results for LSQ and MLE. For the 10 outbreaks with different coverage across methods, 7 have higher coverage with MLE than LSQ. The highest difference in coverage is obtained for pandemic influenza in San Francisco (1918) with 19 data points: 57.89% with LSQ and 78.95% with MLE (Table 1, Table 2). Between the two methods, we observe MLE tends to yield higher coverage than LSQ overall, but it is not a large difference. Further, there is high log correlation between results of the two methods (0.91, p < 0.05; Table 3).

4. Discussion

Results for LSQ with parametric Poisson-bootstrap and Poisson-MLE indicate that both parameter estimation methods perform comparably for fitting the GGM to various outbreaks in terms of parameter estimates, RMSE, Anscombe residual and 95% PI coverage. For outbreaks that deviate in performance metrics, LSQ performs better with respect to RMSE, and MLE performs better with respect to Anscombe, which is expected given the optimization of the respective estimation methods.

We use three different calibration phase lengths for four of the outbreaks, including Zika in Antioquia, Colombia (2015), Ebola in Tonkolili, Sierra Leone (2014), Ebola in Margibi, Liberia (2014), and pandemic influenza in San Francisco, US (1918). The results indicate that the number of data points in the calibration phase do not significantly affect the parameter estimation results for the GGM when the length of the ascending phase is increased by a few data points (Table 1, Table 2). However, different results can be expected when the models are unable to provide a good fit to the data, as indicated by the temporal variation in the residuals. This was the case for the outbreaks of Ebola in Montserrado (2014) and Measles in London (1948).

Both estimation methods based on a Poisson error structure yield a high coverage of the 95% prediction intervals. Some outbreaks, such as Ebola in Margibi (2014) and measles in London (1948), have low coverage, but the coverage is comparably low for both methods (40% and 50%, respectively). In a previous study (Ganyani et al., 2019), authors analyzed the growth pattern of 4 outbreaks analyzed here (Zika in Antioquia (2015), Ebola in Tonkolili (2014), Ebola in Margibi (2014) and influenza in San Francisco (1918)) using MLE to estimate GGM parameters using both a Poisson error structure and a negative binomial (NB) error structure; parameter estimates were similar to those reported here. Regarding the presence of overdispersion, their results show that the outbreaks of Ebola (Margibi) and influenza (San Francisco) display substantial variability in incidence that is better captured using extra-Poisson variation. We argue that this apparent overdispersion could also arise from systematic deviations of the model ("mean") to the data due to model misspecification (Roosa & Chowell, 2019), which could influence the predictive power of the model.

Our analysis is not exempt of limitations. Time series case data are prone to errors and sensitive to reporting rates that are affected by several factors including testing rates. Indeed, some of the outbreaks studied here took place at a time when diagnostic capacity was limited. Further, because we are utilizing real data, we do not know the ground truth of the parameter estimates and cannot assess bias of estimation results. Another limitation is the validity of the GGM for some outbreaks, like FMD (Uruguay, 2001) and Measles (London, 1948), as the RMSE and Anscombe results are high and PI coverage percentage is low. It would useful to further study which virus outbreaks the GGM is suitable for, and what mechanisms may lead to poorer model fit.

In conclusion, our results demonstrate that LSQ and MLE produce similar parameter estimation results in the context of characterizing epidemic growth patterns with the GGM, provided that the model yields a good fit to the data (e.g., residuals indicate random error rather than systematic deviations of the model to the data).

Author contributions

YL analyzed the data. YL, KR, and GC wrote and revised the paper.

Declaration of competing interest

None.

Handling editor: Dr. J Wu

Appendix A. Supplementary data

The following is the Supplementary data to this article: