Virtual Monoenergetic CT Imaging via Deep Learning

Summary

Conventional single-spectrum computed tomography (CT) reconstructs a spectrally integrated attenuation image and reveals tissues morphology without any information about the elemental composition of the tissues. Dual-energy CT (DECT) acquires two spectrally distinct datasets and reconstructs energy-selective (virtual monoenergetic [VM]) and material-selective (material decomposition) images. However, DECT increases system complexity and radiation dose compared with single-spectrum CT. In this paper, a deep learning approach is presented to produce VM images from single-spectrum CT images. Specifically, a modified residual neural network (ResNet) model is developed to map single-spectrum CT images to VM images at pre-specified energy levels. This network is trained on clinical DECT data and shows excellent convergence behavior and image accuracy compared with VM images produced by DECT. The trained model produces high-quality approximations of VM images with a relative error of less than 2%. This method enables multi-material decomposition into three tissue classes, with accuracy comparable with DECT.

Highlights

• •A ResNet model is modified to map polyenergetic to virtual monoenergetic CT images
• •The modified ResNet is trained on DECT-derived virtual monoenergetic (VM) images
• •The trained model produces high-quality approximations of DECT-derived VM images
• •Learned VM images are used to generate multi-material decomposition images

The Bigger Picture

The physical process of X-ray CT imaging is described by an energy-dependent non-linear integral equation. However, this equation is noninvertible using an efficient solution and is practically approximated as a linear integral model in the form of the Radon transform. Because the approximation suppressed energy-dependent information, the resultant image reconstruction requires beam-hardening correction to suppress image artifacts. To overcome the limitation, dual-energy CT (DECT) uses two energy spectra and produces virtual monoenergetic (VM) and material-specific images at the cost of increased system complexity and additional radiation dose. In this work, we present a physics-based deep learning approach to map polyenergetic CT images to monoenergetic images at pre-specified energy levels, accurately and robustly approximating VM images from DECT using only single-spectrum images. This method enables multi-material decomposition with a performance comparable with that of DECT.

We present a deep learning approach for extraction of a non-linear transform from a training dataset to map a polyenergetic (single-spectrum) CT image to virtual monoenergetic (VM) images at pre-specified energy levels, thus reconstructing VM images using only a single-spectrum dataset. Multi-material decomposition (MMD) is then applied to decompose the monoenergetic images into three tissue classes.

Introduction

Computed tomography (CT) is widely used for cross-sectional and volumetric imaging, allowing visualization and quantification of internal structures for screening, diagnosis, therapeutic planning, and monitoring. The number of CT examinations per year has increased almost 30-fold in 4 decades with over 80 million CT scans annually in the US alone. In a clinical CT scanner, the X-ray tube emits a polyenergetic X-ray spectrum, and the X-ray detector operates in the energy-integrating mode to acquire energy intensity.¹ This physical process is accurately described by an energy-dependent non-linear integral equation, the Beer-Lambert law. The non-linear equation is not invertible using a computationally efficient solution and is often approximated as a linear integral model, which is also referred to as the Radon transform or X-ray transform. X-ray energy-dependent information is unconveyed in such a linear approximation model.^1,2 Thus, conventional CT reveals tissue morphology, but does not provide any information about the elemental composition of the tissues.

Biological tissues (except bone) are mainly composed of hydrogen, oxygen, nitrogen, and carbon. Their attenuation characteristics are substantially different from those of elements with higher atomic number (Z), such as calcium (found in bone and calcified plaques) and iodine. Hence, iodinated contrast media are often used in medical CT examinations to enhance subtle differences between soft tissues and to visualize vasculature, which improves detectability and diagnosis of cardiac disease, cancer, and other pathologies.³ However, contrast-enhanced structures may have similar density to bone or calcified plaques, making them difficult to be distinguished using single-spectrum CT. Dual-energy CT (DECT) is a well-established technology to obtain virtual monoenergetic (VM) images and material-specific images.

Physically, photon attenuation is both material and energy dependent, and is a combinational effect of photoelectric absorption and Compton scattering. Photoelectric absorption occurs when an incident X-ray photon collides with an inner-shell electron in an atom. The probability of photoelectric interaction is proportional to the third power of the atomic number (Z) of the absorber. Compton scattering is the result of the interaction between an X-ray photon and an outer orbital electron. The probability of Compton scattering is proportional to the electron density. DECT acquires two projection datasets using different polyenergetic spectra, which allows for determination of the electron density and effective atomic number of materials.4, 5, 6 These essential physical data are instrumental to characterize material mixtures and distinguish tissue types.

There are several mainstream DECT technologies. For example, DECT can be implemented with fast kVp switching (GE Healthcare), dual-layer detection (Philips), and dual-source scanning (Siemens Medical Solutions).^7,8 DECT methods can use either projections or reconstructed images.^9,10 Relative to conventional single-spectrum CT, DECT suffers from increased system complexity and cost, as well as additional processing steps and sometimes increased radiation dose. Material decomposition provides quantitative information about tissue composition to distinguish soft tissues, calcium, and iodine for important clinical applications.10, 11, 12 Currently, material decomposition is widely applied for tissue characterization, kidney stone analysis, vascular mapping, nodule classification, and proton therapy planning.13, 14, 15, 16

A method to approximate the energy-dependent information using only a single-spectrum scan would enable improved clinical diagnosis of patients for whom DECT scans are not available. Although an approximate solution in the absence of true DECT data cannot provide precise energy-dependent information as from DECT, even a reasonable approximation could be transformative, offering improved care for tens of millions of patients globally each year.

Emerging machine learning (ML), especially deep learning (DL), techniques can extract non-linear relationships in a data-driven manner, discovering complicated features and representations.^17,18 Impressively, deep neural networks can perform various types of intelligence-demanding tasks through learning from training data and inferencing on new data.¹⁷ These techniques have been widely and successfully applied for image classification, super-resolution imaging,¹⁹ and image denoising.20, 21, 22 For example, the “learned experts” assessment-based reconstruction network (LEARN) incorporates DL and iterative reconstruction into a unified network framework for accurate and robust image reconstruction.²³ In 2017, the first DL-based VM imaging method was proposed for image reconstruction from a single-spectrum CT dataset using a fully connected network.²⁴ Then, a cascade deep convolutional neural network was developed to simulate pseudo high-energy images from low-energy CT images.²⁵ In 2018, a DL method was proposed to reconstruct virtual VM images from multi-energy CT images using a fully connected neural network to reduce image noise and suppress artifacts.²⁶ Also, a Wasserstein generative adversarial network with a hybrid loss transforms several polyenergetic images in different energy bins to VM images.²⁷ Furthermore, using a convolutional neural network, DECT imaging was achieved from standard single-spectrum CT data.28, 29, 30 Recently, a deep generative model was developed to generate energy-resolved CT images in multiple energy bins from given energy-integrating CT images using a generative adversarial network framework.³¹ These studies all suggest the feasibility of synthesized X-ray VM imaging using DL/ML methods. However, an effective and efficient solution has been missing for directly mapping clinical single-spectrum CT images to VM CT images. In this study, a residual neural network (ResNet) is modified to transform clinical single-spectrum CT images to VM counterparts at a pre-specified energy level. This network can be efficiently trained on clinical DECT images to generate a stable network model, effectively overcoming beam hardening and accurately synthesizing VM images. This DL-based VM estimation method is applied to estimate multi-material decomposition (MMD) images that are close approximations to those produced by DECT using projections from two spectra.

Results

VM Imaging

From single-spectrum images and using our modified ResNet DL network, we produced VM images that very closely approximate those produced by DECT reconstruction from two spectrally distinct projection datasets. Figure 1 compares the VM images reconstructed by DECT with their counterparts produced using our modified ResNet models. The trained neural network delivered high-quality VM images with a relative error less than 2% for the testing dataset. We calculated peak signal-to-noise ratio (PSNR) for 165 virtual VM images produced by our DL method, achieving an average PSNR of 55.88 ± 0.125 (p < 0.05). Structural similarity (SSIM) was 0.9991 ± 0.0018 (p < 0.05), showing that structural information, especially texture features, are well preserved by the ML method.

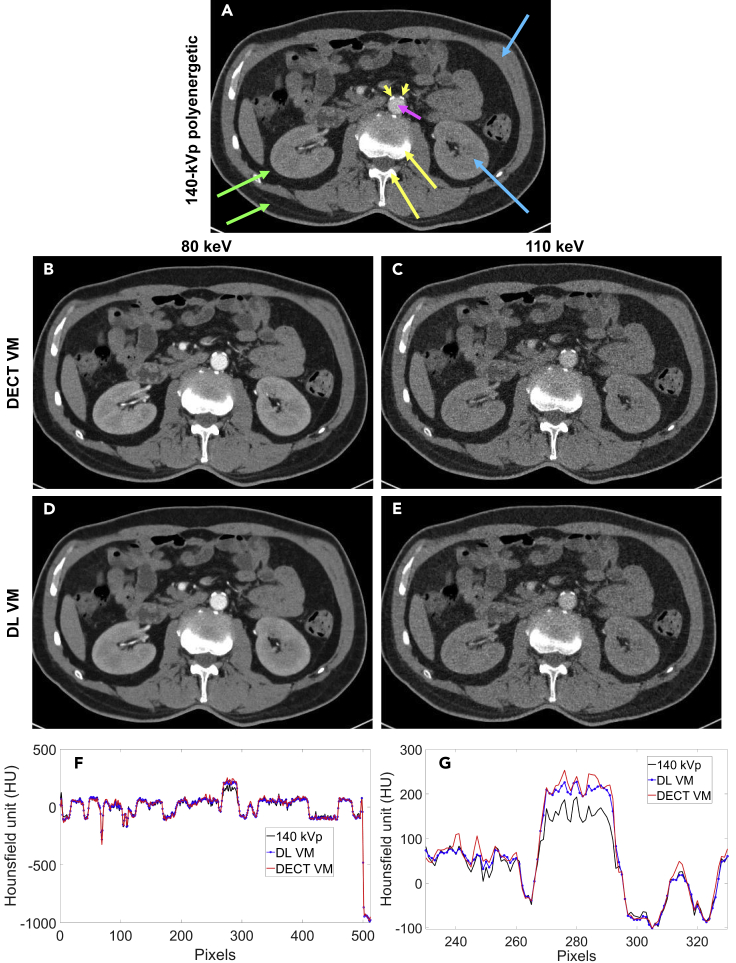
Figure 1.

VM Image Construction

(A) Polyenergetic 140-kVp image; (B) and (C) benchmark VM images from DECT using 80- and 140-kVp projection data, reconstructed at 80 and 110 keV, respectively; (D) and (E) the corresponding VM images produced at the same energies using our DL approach from only 140-kVp images; (F) the horizontal profiles through the abdominal aorta in the 140-kVp, 80-keV DECT VM, and 80-keV DL VM images; (G) the data of (F) zoomed to the central region, including the aorta. All images are displayed with a window width of 200 HU centered at 50 HU. In these images, some representative structures are compared, including the adipose tissue (green arrows), contrast-enhanced muscle and kidneys (blue arrows), contrast-enhanced blood in the abdominal aorta (pink arrow), calcified plaques (yellow arrowheads), and bone (yellow arrows).

MMD

DECT VM and MMD images of a patient were reconstructed on a DECT scanner and used to evaluate the MMD images based on the VM images produced using the proposed approach. The results show that this MMD led to high-quality material-specific images. In particular, the bone image was clearly separated from the reconstructed VM images, as shown in Figure 2H and, notably, a calcification in the abdominal aorta that is inconspicuous in the original polychromatic image is visible in our synthesized 110-keV image and in our bone image (as in the DECT bone image), thus demonstrating the potential clinical utility of the DL method.

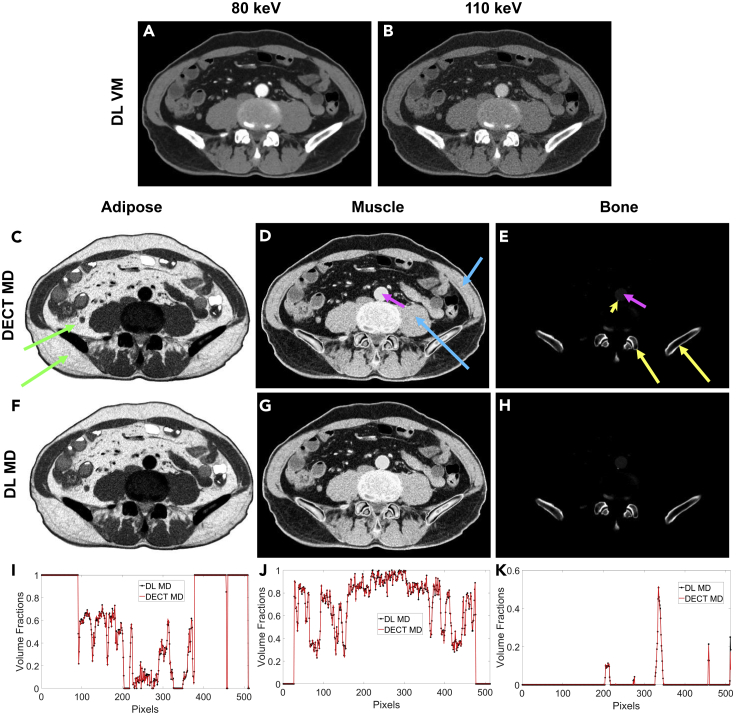
Figure 2.

MMD into Three Basis Materials (Adipose, Muscle, and Bone)

(A) and (B) DL VM reconstructions at 80 and 110 keV, respectively, as the input for MMD; (C), (D), and (E) MMD images from DECT for adipose, muscle, and bone, respectively; (F), (G), and (H) MMD images from our DL approach for adipose, muscle, and bone, respectively; (I), (J), and (K) the profiles along the vertical midlines through the adipose, muscle and bone images, respectively, showing excellent agreement between the DECT and DL results. The adipose tissue is bright only in the adipose image (green arrows), the muscle and kidneys are bright only in the muscle image (blue arrows), and the bone is bright only in the bone image (yellow arrows). However, iodine in the contrast-enhanced abdominal aorta (pink arrows) causes this structure to appear in both the muscle image and (faintly) the bone image. Notably, the calcified plaque in the abdominal aorta (yellow arrowhead) appears in the bone image and is substantially brighter than the blood.

Discussion

All commercial CT scanners use standard beam-hardening correction techniques to convert polyenergetic projections to approximate monochromatic projections. The popular water beam-hardening correction method assumes a single material and does not completely correct for the beam-hardening effect. Multi-material beam-hardening correction includes a first-pass reconstruction and a threshold-based segmentation to correct for beam hardening in the presence of more than one material. DECT has the advantage that it differentiates different materials even if their X-ray attenuation coefficients are in the same range, while threshold-based techniques cannot discriminate between those materials. DECT does so by performing measurements with two energy spectra and evaluating the energy dependence of the X-ray attenuation properties. In this paper, we utilized a dedicated DL network to convert single-spectrum images to approximate VM counterparts. The basic idea is to learn a non-linear mapping from a single-spectrum image to a VM image at a pre-specified energy level. This process is repeated for two different VM energies so that the pair of resultant VM images approximately represent the material composition in each voxel. This methodology essentially performs an implicit segmentation step, which is learned from the image context information contained in big data. This approach is not expected to perfectly discriminate materials when their X-ray attenuation properties match closely, and their structures are similar. However, our goal is to obtain a relatively accurate implicit material characterization of each voxel, represented by two VM attenuation values. It is expected to perform better than an explicit segmentation in practical tasks.

Specifically, our modified ResNet was trained on clinical dual-energy data, showing an excellent convergence behavior. The trained network produced high-quality VM images on testing data. The VM images generated with our ResNet model were evaluated in terms of PSNR and SSIM. The results showed excellent agreement between our VM images and the two-spectrum DECT counterparts. It has been clearly demonstrated in our study that a conventional CT energy-integrating dataset coupled with DL can deliver a close approximation of DECT images. Thus, it is potentially feasible to just use conventional CT to perform some important tasks of DECT.

An example application of our method is in computing proton stopping power for proton therapy planning. For this application, it is not critical to differentiate iodine from calcium, for instance, but it is important to accurately represent material concentrations and distributions of most common tissues (muscle, adipose, bone, iodine) along the therapeutic radiation beam. In other words, after the reconstruction of energy-dependent linear attenuation coefficients, the electron density image and effective atomic number image of a patient can be computed for proton therapy treatment planning. Since the deep network does not require any hardware modification on a conventional CT scanner, this ML method is highly cost-effective, avoiding geometrical mismatches of projection datasets collected at two energy spectra and inaccurate energy spectral correspondence in the image-based material decomposition, and the hardware cost associated with a DECT scanner.

Another important application of DL VM imaging is photon-counting micro-CT for in vivo preclinical applications. Currently, spectral micro-CT (MARS Bioimaging, Christchurch, New Zealand) is available for preclinical imaging.³² With our learning-based virtual VM imaging method, the neural network model can be trained from datasets collected in multiple energy bins with photon-counting micro-CT. After that, instead of acquiring photon-counting data, the trained model can be applied to single-spectrum images reconstructed from energy-integrating micro-CT projection data and then produce VM image reconstructions. This VM imaging method would significantly reduce scanning time and radiation dose associated with a photon-counting micro-CT scan. In particular, iodinated contrast agents are rapidly cleared from the blood stream in a living mouse, and there is only a very short time window available for in vivo imaging after injection of contrast agents. Hence, this learning-based VM imaging method allows for fast acquisition of raw data and is suitable for contrast-enhanced living mouse imaging.

In addition, our method produces monochromatic images and performs MMD from single-spectrum CT images that rely on the energy spectrum of an X-ray tube. As a result, the trained ResNet network model is also associated with the characteristics of the X-ray tube. Hence, the trained network model should be applied for a CT scanner with the same type of the X-ray tube and setting. With a DECT scan, images are reconstructed from two projection datasets with two different energy spectra, for example, a high-energy dataset of 140 kVp and a low-energy dataset of 80 kVp. If a network is trained in a specific DECT imaging setting to generate paired polyenergetic and VM images for supervised learning, the trained network should be applied to process polyenergetic CT images from the same (or similar) energy spectral setting for optimal VM imaging performance.

Nowadays, a clinical CT scanner uses a polyenergetic X-ray tube and energy-integrating detectors to reconstruct spectrally integrated CT images. The modified ResNet network can be trained on a VM dataset for supervised learning. Ideal monochromatic images are not available in clinical practice, since VM images are only an estimation from DECT data. However, the emerging photon-counting detectors can count X-ray photons in an energy-discriminating fashion, and are ideal for VM X-ray imaging.^33,34 The photon-counting detector technology promises to improve contrast resolution and facilitate material/tissue differentiation. However, there are several challenges that still prevent photon-counting CT from immediately translating to routine clinical applications, including its high cost, insufficient material homogeneity and stability, and physical degrading factors, such as pulse pileup and charge-sharing effects.³³ Once these challenges are overcome, X-ray spectral CT can produce nearly “true” monochromatic images directly, albeit at a potentially higher system cost.

Experimental Procedures

Resource Availability

Lead Contact

Ge Wang, PhD (email:wangg6@rpi.edu).

Materials Availability

The DL model in this study are made publicly available via GitHub (https://github.com/wenxiangcong-sys/Deep-Learning/tree/master/Machine-learning-model).

Data and Code Availability

The working code and testing data can be obtained at GitHub (https://github.com/wenxiangcong-sys/Deep-Learning/tree/master/code).

Methodology

The universal approximation theorem states that neural networks are capable of representing a wide variety of continuous functions after being trained on big data.¹⁷ Our learning-based VM CT method establishes a non-linear mapping $M$ from a spectrally averaged polyenergetic CT image $\tilde{I}$ to a corresponding VM image $I\left(E\right)$ at a pre-specified energy level $E$; that is, $I\left(E\right)=M\left(\tilde{I},\theta \right)$ with a model parameter vector $\theta$. The mapping can be established as a neural network in the supervised learning mode with a representative dataset. Because VM images are structurally very similar to a corresponding polyenergetic CT image, it is relatively easy for a network to learn the non-linear function $M$ in the supervised mode. Our DL approach sufficiently utilizes energy-resolved information of training data in linking polyenergetic to corresponding VM CT images, with the convolution and activation functions in ResNet being continuous. These ensure the regularity and consistency of output images with the ground truth VM images.

ResNet Network Modification

The convolution neural network (CNN) is a popular network architecture for image processing and analysis.³⁵ Typically, the CNN network consists of several convolution layers and the associated activation functions. The convolutional layer has filter kernels to process its input data and output results that serve as input signals to the next layer. After convolution, activation is applied to introduce non-linearity. Through training by minimizing a loss function, the CNN network can extract features for a specific task. However, a deep CNN often suffers from vanishing and/or diverging gradients, which hampers the information flow during backpropagation from the output layer through hidden layers toward the input layer.³⁶ The ResNet has a great ability to extract complex and detailed features from data more efficiently and more effectively than a generic CNN network.³⁶ Specifically, with the introduction of shortcuts, ResNet alleviates overfitting, suppresses vanishing/diverging gradients, and allows for the neural network to converge rapidly. We modified a ResNet for our virtual VM imaging as follows.

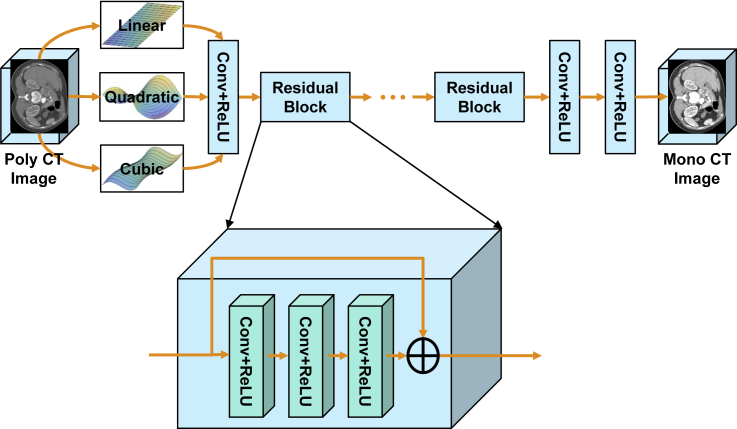
Because the relationship between VM and polyenergetic CT images is non-linear and complicated, we use a cubic (or higher order) polynomial transform in the first convolutional layer to approximate this relationship and then learn the residual with ResNet. In the first layer, a convolution is performed upon a 3D image (1, I, I², I³) formed from an input image $I$ with a filter of a 4 × 1 × 1 kernel to accelerate the convergence of network training. The next layers in the ResNet network are 2 residual blocks of 3 convolution layers with 64 filters of 7 × 7 kernels, followed by 2 residual blocks of 3 convolutional layers with 64 filters of 5 × 5 kernels, and 5 residual blocks of 3 convolution layers with 64 filters of 3 × 3 kernels. Each residual block works in a feedforward fashion with the shortcut connection skipping three layers to implement an identity mapping. Then, 1 convolution layer with 64 filters of 3 × 3 kernels is followed by 1 convolution layer with 32 filters of 3 × 3 kernels, and the last layer generates only 1 feature map with a single 3 × 3 filter as the output. Every layer is followed by a ReLu unit. The loss function is formulated as a weighted linear combination of the l₁ norm and the SSIM that is $Loss=\alpha \cdot SSIM+\left(1-\alpha \right)\cdot l_1$ with an empirical weighting factor α = 0.70. The l₁ norm is used to evaluate the difference between predicted and label VM images, while the SSIM measures structural and textural similarity between the predicted and label VM images. Figure 3 presents the network architecture. It was implemented using Python 3.6 with the TensorFlow library.

Figure 3.

Architecture of Our Modified ResNet

Network Training

The network was trained with image patches. The standard training cycle was followed through the training, validation, and testing stages. Dual-energy CT datasets of 8 patients (3,182 slices in total) were collected on a SOMATOM Definition Flash DECT scanner (Siemens Healthineers, Forchheim, Germany) at Ruijin Hospital in Shanghai, China. The DECT scanner works in the dual-source scanning mode, operated at 100 kVp/210 mA and 140 kVp/162 mA with a wedge filter and a flat filter, respectively. The scanning speed was set to two rotations per second. Polyenergetic CT images at 140 kVp were reconstructed using the filtered back-projection (FBP) algorithm provided on the CT scanner. The entire dataset consists of 3,182 polyenergetic 140-kVp CT images, and corresponding 3,182 VM images at 80 keV and 3,182 VM images at 110 keV. The dataset was split into training, validation, and testing sets, which were obtained from 5, 2, and 1 patients, respectively. In other words, 2,195 polyenergetic CT images at 140 kVp and the 2,195 corresponding VM images at 80 keV formed training dataset I, while 2,195 polyenergetic CT images at 140 kVp and the 2,195 VM images at 110 keV formed training dataset II. Polyenergetic CT images at 140 kVp were input to the ResNet networks I and II to estimate VM images at 80 and 110 keV, respectively.

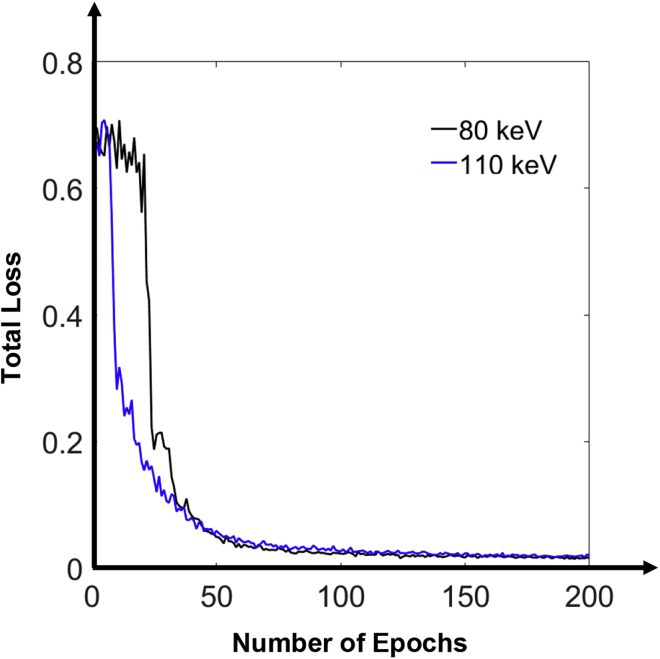
The training procedure was programmed in Python and TensorFlow on a PC computer with an NVIDIA Titan XP GPU of 12 GB memory. At the beginning of training, the network parameters in the convolution kernels were randomly initialized according to the Gaussian distribution with mean of zero and variance of 0.001. During training, the loss function was minimized using the adaptive moment estimation (ADAM) optimizer to update the parameters via backpropagation. The network was trained using 200 epochs at the learning rate of 10⁻⁴ for the first 50 epochs and 10⁻⁵ for the remaining 150 epochs. In early iterations, setting a relatively high learning rate is beneficial for accelerating the training process. The decay rates for the two learning rates in the ADAM optimizer were set to 0.9 and 0.999, respectively. The training process took about 12 h. The training process of the ResNet network showed excellent convergence and stability. Figure 4 shows the curves of the loss versus the number of epochs. The trained ResNet models I and II output VM images at 80 and 110 keV, respectively.

Figure 4.

Convergence Curves of the ResNet Models I and II during the Training Process

MMD

The mass attenuation coefficient of a material depends on the energy of incident X-rays. Based on the physical mechanisms of the X-ray and matter interactions, the linear attenuation coefficient can be decomposed into the contributions from photoelectric absorption, incoherent (Compton) and coherent (Rayleigh) scattering. Equivalently, the linear attenuation coefficient can be expressed as a linear combination of three basis materials. Hence, the mass attenuation coefficient of mixtures can be computed as a weighted average of the mass attenuation coefficients of basis materials according to the additivity principle:³⁷

$$\frac{\mu \left(E\right)}{\rho }=m_a\frac{{\mu }_a\left(E\right)}{{\rho }_a}+m_b\frac{{\mu }_b\left(E\right)}{{\rho }_b}+m_c\frac{{\mu }_c\left(E\right)}{{\rho }_c}\text{,}$$ (Equation 1)

where $\left(\frac{{\mu }_a}{{\rho }_a}\right)$, $\left(\frac{{\mu }_b}{{\rho }_b}\right)$, and $\left(\frac{{\mu }_c}{{\rho }_c}\right)$ are mass attenuation coefficients of three basis materials, $m_a$, $m_b$, and $m_c$ are the mass fractions of the three constituents respectively, ${\rho }_a$, ${\rho }_b$, and ${\rho }_c$ are densities of these basis materials, and $\rho$ is the density of the mixture. According to the relationship between mass, volume, and density, we have

$$m_a=\frac{{\rho }_a{v}_a}{\rho },m_b=\frac{{\rho }_b{v}_b}{\rho },m_c=\frac{{\rho }_c{v}_c}{\rho }.\text{,}$$ (Equation 2)

where $v_a$, $v_b$, and $v_c$ are the volume fractions of the material constituents and have a relationship: $v_a+v_b+v_c=1$. From Equations 1 and 2, we have

$$\mu \left(E\right)=v_a{\mu }_a\left(E\right)+v_b{\mu }_b\left(E\right)+v_c{\mu }_c\left(E\right)\text{.}$$ (Equation 3)

Using the learning-based reconstruction approach, we can reconstruct two virtual VM images $\mu \left(E_L\right)$ and $\mu \left(E_H\right)$ at low- and high-energy levels $E_L$ and $E_H$ from the trained ResNet models I and II, respectively. These data define the following equations for decomposition into three material types:³⁸

$$\{\begin{array}{l}\mu \left(E_L\right)=\left[v_a{\mu }_a\left(E_L\right)+v_b{\mu }_b\left(E_L\right)+v_c{\mu }_c\left(E_L\right)\right]\\ \mu \left(E_H\right)=\left[v_a{\mu }_a\left(E_H\right)+v_b{\mu }_b\left(E_H\right)+v_c{\mu }_c\left(E_H\right)\right]\\ v_a+v_b+v_c=1\end{array}\text{.}$$ (Equation 4)

The direct matrix inversion can be used to solve Equation 4, which may be subject to noise amplification. Hence, an optimization method is preferred for a stable solution. With the reconstructed volume fractions $v_a$, $v_b$, and $v_c$, the VM images can be converted into material-specific images. The left and right sides of Equation 4 have consistent energy spectral information, accurately describing the relationship between the linear attenuation coefficients of the mixture and those of the basis materials. On the other hand, the conventional image-based material decomposition method first reconstructs the polyenergetic linear attenuation coefficients at low and high energies and uses those to reflect a combination of basis material images, which is an inaccurate energy spectral correspondence.

One hundred and sixty-five 140-kVp single-spectrum CT images were input to the trained ResNet models to produce VM images at 80 and 110 keV, as shown in Figure 2. The reconstructed VM images were used for MMD described above. We selected adipose tissue, muscle with iodine contrast agent, and bone as the basis materials. Their linear attenuation coefficients (Table 1) were calculated from their mass attenuation coefficients and masses,^39,40 as obtained from the database of the National Institute of Standards and Technology, as shown in Table 1. For muscle with contrast agent, attenuation values were obtained from Boke,³⁹ Çakır,⁴⁰ and Behrendt and colleagues.⁴¹

Table 1.

Linear Attenuation Coefficients of Basis Materials

	Attenuation (cm−1)
Energy (keV)	Adipose Tissue	Muscle Tissues	Bone
80	0.1660	0.2343	0.4280
110	0.1516	0.2065	0.3418

From these data, we established the following linear equations:

$$\left[\begin{array}{c}\mu \left(E_L\right)\\ \mu \left(E_H\right)\\ 1\end{array}\right]=\left[\begin{array}{ccc}0.1660& 0.2343& 0.4280\\ 0.1516& 0.2065& 0.3418\\ 1.0000& 1.0000& 1.0000\end{array}\right]\left[\begin{array}{c}{v}_w\\ v_t\\ v_b\end{array}\right]$$

The condition number of the coefficient matrix with the l₂ norm is 543.06. To suppress image noise for a stable solution, we used the nonnegative linear least-squares method to solve the above system of linear equations to separate three base components from the VM images at 80 and 110 keV reconstructed by the trained network models I and II, respectively.

Published: October 19, 2020