Hilbert-Space Fragmentation from Strict Confinement

Abstract

We study one-dimensional spin-1/2 models in which strict confinement of Ising domain walls leads to the fragmentation of Hilbert space into exponentially many disconnected subspaces. Whereas most previous works emphasize dipole moment conservation as an essential ingredient for such fragmentation, we instead require two commuting U(1) conserved quantities associated with the total domain-wall number and the total magnetization. The latter arises naturally from the confinement of domain walls. Remarkably, while some connected components of the Hilbert space thermalize, others are integrable by Bethe ansatz. We further demonstrate how this Hilbert-space fragmentation pattern arises perturbatively in the confining limit of ${\mathbb{Z}}_2$ gauge theory coupled to fermionic matter, leading to a hierarchy of timescales for motion of the fermions. This model can be realized experimentally in two complementary settings.

Introduction.—

Generic nonintegrable quantum many-body systems eventually reach thermal equilibrium under unitary time evolution from initial states having a finite energy density with respect to the Hamiltonian [1]. Such behavior arises in models satisfying the eigenstate thermalization hypothesis (ETH) [2,3], which posits that highly excited eigenstates of generic Hamiltonians at the same energy density are indistinguishable in the thermodynamic limit as far as local observables are concerned.

Recent experimental and theoretical investigations indicate that ETH in its strongest form can be violated even in nonintegrable systems with translation symmetry. Experiments on Rydberg-atom chains, where persistent revivals in quench dynamics starting from certain initial states are observed [4], led to the identification of certain atypical eigenstates that are embedded in an otherwise thermalizing spectrum [5,6]. Another mechanism leading to ETH violations is dynamical constraints. Fractonic systems, where such constraints manifest themselves in the restricted mobility of excitations, turn out to be natural candidates along this direction [7–10]. Mobility restrictions in fractonic systems can be implemented by imposing both charge (Q) and dipole moment (P) conservation [11,12], providing a simple guiding principle for systematic studies of constrained models. It is shown in Refs. [13–16] that these two conservation laws cause the Hilbert space to fracture into disconnected subspaces that are invariant (i.e., closed) under the action of the Hamiltonian; moreover, these invariant subspaces cannot be distinguished by their (Q, P) quantum numbers alone [17]. This “fragmentation” of Hilbert space [14,15,18–23] leads to a broad distribution of the eigenstate entanglement entropies within an energy window, violating the strong ETH.

Fractonic systems bear a phenomenological resemblance to lattice models exhibiting quasiparticle confinement [24]. One simple example is the one-dimensional (1D) Ising model in transverse and longitudinal magnetic fields, where the latter induces a confining potential for pairs of Ising domain-wall excitations that grows linearly with their separation [25,26]. Recent studies of confining systems have mainly focused on physics near the ground state, where domain walls and their bound states are well-defined quasiparticles [24,27–36]. This leaves open the question of the effects of confinement at finite energy density, where there are generically no well-defined quasiparticles.

In this Letter, we show that Hilbert-space fragmentation (HSF) can arise in models conserving both domain-wall number (n_DW) and total magnetization (S^z). These two commuting U(1) conserved quantities naturally arise from strict confinement, where isolated domain walls cannot move without changing the S^z quantum number, naturally leading to HSF. We exemplify this phenomenon with a 1D spin-1/2 model that features exponentially many invariant subspaces. These include exponentially many frozen configurations (i.e., subspaces of dimension one), as well as exponentially large subspaces generated by certain “root configurations” that we enumerate. The pattern of HSF that we find is extremely rich, featuring large subspaces within which the dynamics is thermalizing, as well as others spanning entire (n_DW, S^z) sectors that are integrable by Bethe ansatz. We further demonstrate how the same HSF pattern arises perturbatively in the extreme confining limit of a 1D n_DW-conserving spin model that maps exactly onto ${\mathbb{Z}}_2$ gauge theory coupled to fermionic matter [31,37], which can be realized experimentally using state-of-the-art techniques in cold atoms [38,39]. We show that HSF gives rise to a complex hierarchy of timescales for quench dynamics that depends crucially on the initial state. Our results thus establish HSF as a mechanism for slow dynamics in gauge theories at finite energy density.

Model.—

To see how the simultaneous conservation of S^z and n_DW gives rise to HSF, we study a simple model

$$H=\sum _{i=2}^{L-1}\left[J{P}_{i-1,i+2}\left({\sigma }_i^{+}{\sigma }_{i+1}^{-}+{\sigma }_i^{-}{\sigma }_{i+1}^{+}\right)+{\mathrm{\Delta }}_2{\sigma }_i^z{\sigma }_{i+2}^z\right],$$ (1)

where $P_{i-1,i+2}=1+{\sigma }_{i-1}^z{\sigma }_{i+2}^z$ projects out configurations with opposite spins on sites i − 1 and i + 2 (see also Ref. [27]). Note that $[H,{\sigma }_{1,L}^z]=0$, so that we can fix the two edge spins to point down. Adopting the notation 1 ≡ ↑, 0 ≡ ↓ for the local spin states, we see that the kinetic term in Eq. (1) hops a magnon while preserving n_DW: 0100 ↔ 0010, and 1011 ↔ 1101. Since the nearest-neighbor Ising interaction couples to the conserved quantity n_DW, we add a next-nearest-neighbor Ising interaction Δ₂ to make the model more generic (see below). Equation (1) has two U(1) conserved quantities (n_DW, S^z); for our choice of boundary conditions, we have n_DW = 0, 2, …, L − 2, and S^z = −L + n_DW, −L + n_DW + 2, …, L − n_DW − 2 for n_DW ≠ 0. This gives rise to ${\sum }_{n_{\text{DW}}=2}^{L-2}\left(L-n_{\text{DW}}\right)+1=(L/2)(L/2-1)+1$ sectors labeled by these two quantum numbers. As we show later [see Eq. (3)], one can think of Hamiltonian (1) as describing an n_DW-conserving spin-1/2 system in a uniform confining longitudinal field $h{\sum }_i{\sigma }_i^z$ in the strict-confinement limit h → ∞. In this limit, S^z becomes a conserved quantity. Isolated domain walls (“quarks”) cannot move without changing S^z, costing infinite energy. However, tightly bound pairs of domain walls (magnons, or “mesons”) can move without violating S^z conservation.

Strong HSF.—

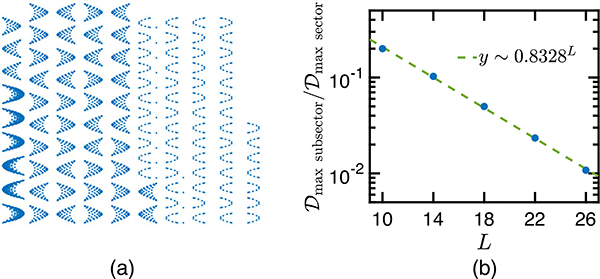
Naively, one would expect that the Hilbert space of Hamiltonian (1) organizes into $\mathcal{O}\left(L^2\right)$ symmetry sectors. In Fig. 1(a), we visualize the symmetry sector (n_DW = 8, S^z = −2) as a graph whose nodes are z-basis configurations and whose edges correspond to nonzero matrix elements of H. We find that the Hilbert space within this symmetry sector further fractures into many disconnected emergent subsectors (invariant subspaces) of various sizes. In particular, there are isolated nodes in Fig. 1(a), indicating the existence of frozen configurations constituting subsectors of dimension one. In Fig. 1(b) we show that Hamiltonian (1) exhibits strong HSF as defined in Ref. [15]: the ratio of the dimension of the largest emergent subsector within the largest (n_DW, S^z) sector to that of the whole sector decreases exponentially with L. This implies that, in the thermodynamic limit, even the largest emergent subsector constitutes a vanishing fraction of the full (n_DW, S^z) sector. Intriguingly, the same HSF pattern arises in a different context in Ref. [22], which studies a disordered fermionic system with strong nearest-neighbor interactions.

FIG. 1.

(a) Connectivity within the sector (n_DW = 8, S_z = −2) for L = 18. This sector has a total Hilbert-space dimension of 4410. (b) Ratio of the size of the largest emergent subsector within the largest (n_DW, S_z) sector to that of the entire sector, for different system sizes.

We now develop an understanding of the pattern of HSF evident in Fig. 1, starting with the origin of the frozen states in Fig. 1(a). As discussed below Eq. (1), the only nonzero off-diagonal matrix elements of H are between configurations differing by the nearest-neighbor exchange of a single magnon. This immediately implies that the kinetic term in Eq. (1) annihilates any configuration containing no isolated magnons and that such configurations are disconnected from all others. Since an isolated magnon is equivalent to a pair of domain walls occupying neighboring bonds, it follows that any configuration in which no two neighboring bonds host a domain wall is frozen (see Supplemental Material [40]). This nearest-neighbor exclusion is sometimes called the “Fibonacci constraint,” which also arises in systems of Rydberg atoms with strong interactions [4]. The number of states satisfying this constraint grows as φ^L, where φ is the golden ratio. Configurations in which every bond is occupied by a domain wall (e.g., 0101…) are also frozen because domain walls are hardcore objects; however, the number of such configurations is independent of system size [40].

Next, we identify a class of root configurations from which each connected subsector can be built. Consider configurations of the following form:

$$0\underset{L-2-2k}{\underbrace{\boxed{\mathrm{frozen}\mathrm{state}}}}\underset{2k}{\underbrace{\boxed{0101\cdots 01}}}0,$$ (2)

which are constructed by appending a Néel state of length 2k to the right of any magnon-free frozen state. The two outermost zeros denote the edge spins that remain fixed. Since the Néel region contains k magnons, we shall call (2) a “k-magnon state.” One can explicitly check that, although the two constituent subsystems are both frozen, the boundary between them becomes active once they are joined together [40]. To show that any connected subsector can be built from a k-magnon state, we first point out an important property in our system that is in stark contrast to spin-1 systems with (Q, P) conservation [14,15,44]. Whereas these models allow mobile excitations to be contained within a finite domain by constructing appropriate “shielding regions,” there are no such regions in the model (1): an isolated mobile magnon can propagate all the way to the boundary of the system. Therefore, the model (1) does not support spatially separated thermal and nonthermal domains, while fractonic systems do [14,15,44]. Using this fact, one can then prove [40] that any configuration that is not frozen can be brought into the form (2) by propagating all mobile magnons to the right boundary using Eq. (1). Therefore, any connected subsector can be built from an appropriate k-magnon state.

Subsector thermalization and integrability.—

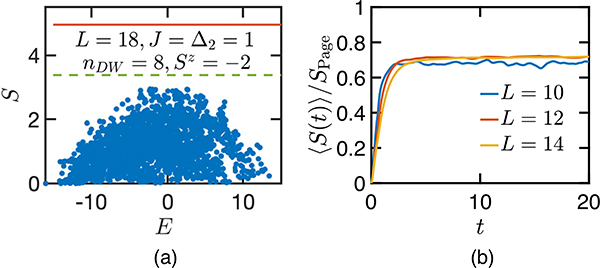
The fracturing of the Hilbert space into exponentially many disconnected subsectors indicates that the eigenstates of Hamiltonian (1) strongly violate ETH, as can be diagnosed from the entanglement entropy. In Fig. 2(a), we plot the entanglement entropy of the eigenstates within an (n_DW, S^z) symmetry sector. There is clearly a broad distribution in the entanglement entropy, even for eigenstates that are close in energy. In particular, the frozen states have exactly zero entanglement entropy although they reside in the middle of the energy spectrum. Moreover, the maximal value of the entanglement entropy stays far below the “Page value,” i.e., that of a random state in the corresponding (n_DW, S^z) sector [45]. The nonthermalizing behavior of the full Hamiltonian also manifests itself in quantum quenches starting from random initial product states that do not belong to any particular symmetry sector. In Fig. 2(b), we find that the final entanglement entropy under time evolution only saturates to 70% of the Page value, confirming that the system does not thermalize under time evolution.

FIG. 2.

(a) Entanglement entropy of the eigenstates within the sector (n_DW = 8, S^z = −2) under an equibipartitioning of the system. Red line, Page value of the (n_DW, S^z) sector; green line, Page value of the largest connected subsector. (b) Entanglement entropy growth (normalized by the Page value) after a quantum quench starting from random product states, averaged over 200 initial states.

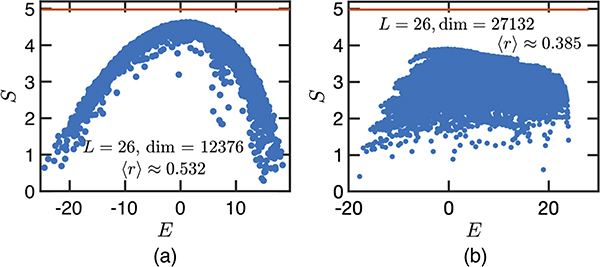
The fragmentation of Hilbert space seems to suggest that a more appropriate comparison of the entanglement entropy might be the Page value restricted to a connected subsector. To this end, we extract the effective Hilbert-space dimensions of the left and right halves of the chain ${\mathcal{D}}_L$ and ${\mathcal{D}}_R$ within the largest emergent subsector, and then compute the corresponding Page value using the exact formula: ${\sum }_{k=n+1}^{mn}(1/k)-(m-1)/(2n)$, where $m=\min \left[{\mathcal{D}}_L,{\mathcal{D}}_R\right]$, and $n=\max \left[{\mathcal{D}}_L,{\mathcal{D}}_R\right]$ [45]. As shown in Fig. 2(a) (green dashed line), the maximal eigenstate entanglement entropy is close to the Page value restricted to the largest subsector. This strongly indicates that the system thermalizes within each invariant subspace [16]. Testing this scenario numerically requires larger system sizes with bigger subsector dimensions. Fortunately, armed with the knowledge of the root configurations (2), one can directly construct the projection of Hamiltonian (1) into an arbitrary emergent subsector. In Fig. 3(a), we show the entanglement entropy for eigenstates within a connected subsector built from the root configuration $0\boxed{111111000000}\boxed{010101010101}0$. It is clear that the eigenstate entanglement entropy within this subsector forms a narrow ETH-like band, with maximal value close to the subspace-restricted Page value. Moreover, we compute the average energy level spacing ratio for the eigenenergies of the projected Hamiltonian: r_i = min{δ_i,δ_i+1}/max{δ_i,δ_i+1}, where δ_i = E_i − E_i+1 is the gap between adjacent energy levels [46]. We find $\langle r\rangle \approx 0.532$, consistent with the Gaussian orthogonal ensemble in random matrix theory [46]. Taken together, these facts suggest that there is indeed a notion of “subsector thermalization” in the present model. In the absence of Δ₂ in Eq. (1), we numerically find that the spectral properties strongly deviate from nonintegrability, which confirms the necessity of including a nonzero Δ₂.

FIG. 3.

(a) Entanglement entropy of eigenstates within an emergent subsector built from the root configuration $0\boxed{111111000000}\boxed{010101010101}0$ for system size L = 26. This subsector has dimension 12 376 and is nonintegrable. (b) Entanglement entropy of eigenstates within an emergent subsector built from the root configuration $0\boxed{000000000000}\boxed{010101010101}0$ for system size L = 26. This subsector has dimension 27 132 and is integrable. Red lines mark the Page value of the corresponding subsector.

At this point, it may seem that all sufficiently large connected subsectors at finite energy density thermalize when considered separately. However, as we now show, this is not the case. Consider the sequence of symmetry sectors (n_DW = 2k, S^z = −L + 2k), which have the smallest possible S^z for a given n_DW. These sectors can be generated from root configurations $0\boxed{00\cdots 0}\boxed{0101\cdots 01}0$ and are, in fact, fully connected; i.e., they do not fracture into subsectors. The projection of Hamiltonian (1) into these symmetry sectors yields a constrained XXZ model in which neighboring up spins are separated by at least two sites [31,47]. For Hamiltonian (1) this constraint is automatically satisfied within these symmetry sectors, since bringing two up spins next to one another annihilates a pair of domain walls, which is forbidden by n_DW conservation. Remarkably, the constrained XXZ model, although interacting, is exactly solvable via Bethe ansatz, and hence integrable [47]. This is also seen numerically in Fig. 3(b), where the entanglement entropy does not form an ETH-like band, and where $\langle r\rangle \approx 0.385$ indicates Poissonian energy level statistics characteristic of integrability [46]. Notice from Fig. 3(b) that, although these sectors are integrable, they reside within the same energy window as the nonintegrable subsectors.

HSF in gauge theory.—

We now show how the pattern of HSF described above arises in the strict-confinement limit of ${\mathbb{Z}}_2$ gauge theory coupled to fermionic matter and study its breakdown as the strict-confinement limit is relaxed. We first demonstrate that the pattern of HSF observed in Hamiltonian (1) naturally arises in the n_DW-conserving model [31,37]

$$H_{{\mathbb{Z}}_2}=\sum _i\left[\lambda \left({\sigma }_i^x-{\sigma }_{i-1}^z{\sigma }_i^x{\sigma }_{i+1}^z\right)+h{\sigma }_i^z\right].$$ (3)

As shown in Ref. [31], this model maps exactly onto ${\mathbb{Z}}_2$ gauge theory coupled to spinless fermions in 1D, where the Ising domain-wall number operator in the spin model is reinterpreted as the fermion number operator in the gauge theory. With this in mind, we will henceforth use the terms “domain wall” and “fermion” interchangeably. The kinetic term in Eq. (3) induces nearest-neighbor hopping of domain walls, while the longitudinal field introduces a linearly confining potential. This model can be realized experimentally in two complementary settings. The spin model (3) can be realized by Floquet engineering in periodically driven transverse-field Ising chains [48,49], while the gauge theory itself can be realized in ultracold atomic gases [50]. Experimental steps toward the latter have already been reported in Refs. [38,39].

To understand the effect of confinement in Eq. (3), we work in the limit h ≫ λ. At h = ∞, the energy spectrum of Hamiltonian (3) becomes highly degenerate, with each S^z sector forming a degenerate manifold. The dynamics at h = ∞ is trivial; the leading nontrivial behavior is determined by performing degenerate perturbation theory in λ/h. Formally, this is carried out by a Schrieffer-Wolff transformation [40], which yields an effective Hamiltonian $H_{\text{eff}}={\sum }_n{H}_{\text{eff}}^{(n)}$, where $H_{\text{eff}}^{(n)}$ is of order (λ/h)ⁿ and conserves n_DW and S^z by construction. Strictly speaking this analysis is valid up to an order $n_{*}\sim h/\lambda$ (up to logarithmic corrections), which sets an exponentially long prethermal timescale ~e^cn* for some constant c [51].

The leading contribution in perturbation theory appears at second order [40],

$$H_{\text{eff}}^{(2)}=\frac{{\lambda }^2}{h}\sum _i\left[{\sigma }_{i-1}^z{P}_{i-1,i+2}\left({\sigma }_i^{+}{\sigma }_{i+1}^{-}+\text{H}.\text{c}.\right)-{\sigma }_{i-1}^z{\sigma }_i^z{\sigma }_{i+1}^z\right].$$ (4)

The kinetic term in Eq. (4) coincides with that of Eq. (1) up to a configuration-dependent local sign due to the extra factor of ${\sigma }_{i-1}^z$; this only affects the signs of certain matrix elements, so that Eqs. (4) and (1) exhibit the same pattern of HSF. Moreover, although Eq. (4) sports a three-body rather than a two-body interaction, this has no effect on the (non) integrability of the various (sub)sectors. In the integrable sectors, the spin between any two up spins must point down by (n_DW, S^z) conservation. The three-body interaction in $H_{\text{eff}}^{(2)}$ thus reduces (up to a constant shift) to Δ₂ upon setting ${\sigma }_i^z=-1$ in ${\sigma }_{i-1}^z{\sigma }_i^z{\sigma }_{i+1}^z$. Moreover, the nonintegrable subsectors remain nonintegrable regardless of whether Δ₂ or the three-body term is used. In the Supplemental Material [40], we numerically verify the above claims by reproducing Figs. 2 and 3 using $H_{\text{eff}}^{(2)}$.

Corrections to the pattern of HSF discussed so far arise for n > 2, where further-neighbor domain-wall hopping processes appear [40]. Such processes reduce the strong HSF of Eq. (4) to weak HSF, defined in Ref. [15]; in particular, each (n_DW, S^z) sector collapses into an exponentially large connected cluster that remains disconnected from a set of exponentially many frozen configurations. The base of the exponential number of such frozen configurations depends on the order in perturbation theory being considered; for example, at n = 4 the number of frozen states grows as 1.466^L [40]. One can show that a pair of domain walls separated by a distance d_DW becomes mobile at order ${(\lambda /h)}^{2d_{\text{DW}}}$ in perturbation theory [24,40]. Thus, a configuration containing two domain walls with d_DW > 1, which is frozen at second order, remains frozen for any n < 2d_DW. Frozen configurations with n_DW > 2 unfreeze at order n = min(d_DW), where the minimum is taken over all pairs of domain walls.

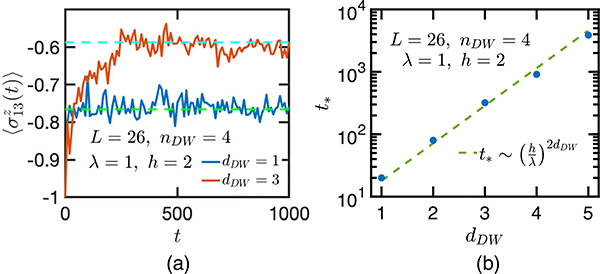
The preceding considerations indicate that the thermalization time when evolving with Eq. (3) from a configuration with minimum domain-wall separation d_DW will be lower bounded by a timescale $t_{*}\sim {(h/\lambda )}^{2d_{\text{DW}}}$. In Fig. 4(a), we show the evolution under Eq. (3) of $\langle {\sigma }_{L/2}^z(t)\rangle$, starting from initial configurations with two well-separated pairs of domain walls: $00\cdots 0\underset{d_{\text{DW}}}{\underbrace{11\cdots 1}}00\cdots 0\underset{d_{\text{DW}}}{\underbrace{11\cdots 1}}00\cdots 0$. Indeed, we find that, even for reasonably small h/λ = 2, the timescale for the local observable to saturate to the diagonal ensemble value [52] expected at late times is longer for initial states with a larger d_DW. Scaling analysis of this timescale is also in agreement with the prediction $t_{*}\sim {(h/\lambda )}^{2d_{\text{DW}}}$, as shown in Fig. 4(b). We thus find that the above reasoning provides a basis to estimate relaxation timescales in the confining limit of the gauge-theory model (3) and the correlations between these timescales and the initial state. Deeper investigations of these timescales could be carried out in experimental realizations of the model (3).

FIG. 4.

(a) Expectation value of the spin in the middle of the chain under time evolution with Hamiltonian (3), starting from initial configurations with two pairs of domain walls: 00 · · · 011…100 · · · 011…100 · · · 0. The dashed lines mark the diagonal ensemble average values: ${\langle {\sigma }_{13}^z\rangle }_{\text{diag}}={\sum }_n\langle n\left|{\sigma }_{13}^z\right|n\rangle {\left|c_n\right|}^2$, where |n⟩ denotes the eigenstate of the Hamiltonian and c_n = $\langle n\mid {\psi }_0\rangle$ is the overlap between the initial state and each eigenstate. (b) Scaling of the saturation timescale t_* as a function of d_DW.

Conclusion.—

In this Letter, we demonstrate that HSF naturally arises in lattice models exhibiting strict confinement. We uncover a highly unusual feature in the models we study, namely, the coexistence of nonintegrable emergent subsectors with Bethe-ansatz integrable fully connected symmetry sectors. This Letter also elucidates the role of HSF in determining the hierarchy of relaxation timescales in the confining phases of lattice gauge theories and related spin models in 1D, paving the way for experimental tests of these ideas in emerging quantum simulation platforms. These ideas can be generalized to higher dimensions, e.g., by allowing magnons to hop only if they remain isolated. We leave this for future work.