pH Tuning of Water‐Soluble Arylazopyrazole Photoswitches

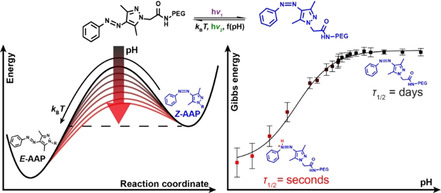
Abstract

Arylazopyrazoles are an emerging class of photoswitches with redshifted switching wavelength, high photostationary states, long thermal half‐lives and facile synthetic access. Understanding pathways for a simple modulation of the thermal half‐lives, while keeping other parameters of interest constant, is an important aspect for out‐of‐equilibrium systems design and applications. Here, it is demonstrated that the thermal half‐life of a water‐soluble PEG‐tethered arylazo‐bis(o‐methylated)pyrazole (AAP) can be tuned by more than five orders of magnitude using simple pH adjustment, which is beyond the tunability of azobenzenes. The mechanism of thermal relaxation is investigated by thorough spectroscopic analyses and density functional theory (DFT) calculations. Finally, the concepts of a tunable half‐life are transferred from the molecular scale to the material scale. Based on the photochromic characteristics of E‐ and Z‐AAP, transient information storage is showcased in form of light‐written patterns inside films cast from different pH, which in turn leads to different times of storage. With respect to prospective precisely tunable materials and time‐programmed out‐of‐equilibrium systems, an externally tunable half‐life is likely advantageous over changing the entire system by the replacement of the photoswitch.

Arylazopyrazoles are an emerging class of photoswitches with redshifted switching wavelength, high photostationary states, long thermal half‐lives and facile synthetic access. Understanding pathways for a simple modulation of the thermal half‐lives, while keeping other parameters of interest constant, is an important aspect for out‐of‐equilibrium systems design and applications. Here, it is demonstrated that the thermal half‐life of a water‐soluble PEG‐tethered arylazo‐bis(o‐methylated)pyrazole (AAP) can be tuned by more than five orders of magnitude using simple pH adjustment, which is beyond the tunability of azobenzenes.

Introduction

Photochromism is the light‐induced transformation of a compound between two (or more) forms having different absorption spectra and therefore different colors.1 Reversible molecular photoswitches feature photochromic characteristics and exploit light of different wavelengths to reversibly interconvert between two (or more2) states, which are linked to conformational or electronical changes of the molecule. Among the different classes of photoswitches, azobenzenes and their derivatives are the most prominent compounds whose thermodynamically stable E‐isomer is switched to the metastable Z‐isomer upon irradiation with (mostly) UV light.3 The back switching is either induced by light of longer wavelength or occurs spontaneously by thermal relaxation in the dark, depending on the energy barrier between the metastable and thermodynamically stable state. The conformational switching goes along with a change in the dipole moment and has been exploited for switchable host–guest inclusion complexes, for switchable self‐assemblies4 and responsive materials design, ranging from ionic liquids with controlled sol‐gel transitions to polymers with photoswitchable glass transition temperatures.5

In particular, in the context of dissipative, light‐fueled non‐equilibrium self‐assemblies and materials, it is of profound importance to be able to adjust the thermal half‐life, because the autonomous temporal fate, for instance in the disassembly of nanoparticle assemblies, is directly linked to the thermal relaxation.6 Undeniably, depending on the type of application one would be in the position to relatively freely adjust the thermal half‐life, while keeping the spectral characteristics identical. This would also minimize synthetic efforts to change the half‐life by tuning of the conformational restraints. For instance, fast relaxation is necessary in applications, such as real‐time optical information‐transmitting materials7 or in in vivo applications due to their temporally limited action,8 whereas long thermal relaxations are needed for logic devices9 or optical data storage.10 Common ways to tune the thermal half‐lives of photoswitches are based on the introduction of different functional groups.11 For instance, the redshifted ortho‐tetrafluoro azobenzene12 possesses a half‐life of approximately 700 days compared to azobenzene with a half‐life of 2 days. Conversely, push‐pull azobenzenes feature extremely short relaxation times, ranging from ms to μs.7 This already demonstrates that purely synthetic design per se is a promising approach to reach the half‐life of interest, but it may not allow to concurrently tune the half‐life and spectral characteristics on‐demand and independently.

As early as 1938, Hartley discovered that the thermal relaxation of Z‐azobenzene and some derivatives of it can be accelerated by acids.13 Among other groups,14 Woolley et al. systematically extended this work and reported the pH dependence of the thermal half‐life of redshifted azobenzene derivatives in aqueous solutions with four bulky methoxy moieties in ortho‐position.15 They elaborated that the pK _a value of the protonated Z‐isomer is a decisive factor for the thermal relaxation. Although this approach allowed to tune the thermal relaxation behavior and the spectral characteristics concurrently, the thermal half‐life could only be varied between μs and s depending on the substitution patterns and the pH. This is only a relatively narrow temporal range, which may not be ideally suited for all application scenarios. For instance, considering applications at the physiological pH, the short relaxation times (<ms) lead to a vanishingly small content of the Z‐isomer unless very intense light sources are used, which impedes applicability in photopharmacology.16

More recently, the library of azo photoswitches has been extended by azoheteroarenes.17 Among them, azopyrimidine is an ultra‐fast relaxing system with a half‐life of 40 ns in phosphate buffer at pH 7.8.18 Conversely, arylazopyrazoles feature the longest reported half‐life of up to 1000 days in DMSO.19 Such arylazopyrazoles typically show very high photostationary states, that exceed the typical ones found for azobenzenes. For instance, arylazo‐bis(o‐methylated)pyrazole (AAP) switches nearly quantitatively from the E‐ to the Z‐state and backwards upon irradiation with UV and green light.20 Calculations using time dependent density functional theory (TDDFT) indicated that the two methyl groups of the pyrazole ring force the Z‐isomer into a twisted confirmation, which leads to a large n–π* absorbance.19a Additionally, the π–π* and the n–π* transitions of the Z‐isomer are well separated, which is why AAP features high photostationary distributions (PSDs>98 %) in both directions at the respective photostationary states (PSSs). Interestingly, when arylazopyrazoles are mixed with strong acids in acetonitrile, it could be qualitatively shown that stronger acids lead to faster thermal relaxation.21 This, in conjunction with applications in aqueous systems, motivates to understand pH effects in a quantitative manner as an additional control parameter for the thermal half‐life extending beyond synthetic (re)design.

Considering applications in aqueous medium, such as for hydrogels in regenerative medicine, the thermal relaxation of azobenzenes have been characterized in‐depth, both computationally and experimentally.3 In case of azoheteroarenes, Ravoo and co‐workers determined the half‐lives of various AAPs in aqueous solution featuring PEG‐chains to solubilize them.22 Depending on the substitution pattern of the phenyl ring, the half‐lives vary from seconds to years in MilliQ water at 25 °C.23 However, the authors did not investigate the effect of the pH on the half‐life. Indeed, as we will show below, our findings suggest that the pH is a decisive factor to tune the thermal half‐lives of water‐soluble AAPs by several orders of magnitude.

In this study, we quantify spectroscopically the Gibbs free energy of activation and thermal half‐life as a function of the pH, and further underpin our results by DFT calculations of the transition state trajectories in order to identify changes in the mechanistic pathways of relaxation. Additionally, we demonstrate the use as a photobase and develop bulk materials for tunable transient information storage. We anticipate that these findings are of importance in the field of nanotechnology and photopharmacology as they enable to program the time domain in systems with temporally limited action exploiting the Z‐isomer as the active species.

Results and Discussion

This article focuses on finding pathways to tune the thermal half‐life of self‐reverting photoswitches in water. We selected an AAP derivative as an attractive photoswitch class due its high PSD and slightly red‐shifted switching wavelengths, and because those AAPs are known to feature long half‐lives to provide sufficient flexibility in elucidating the concept. Our photoswitch of interest is a PEG‐tethered (polyethylene glycol with three ethylene glycol units) arylazo‐bis(o‐methylated)pyrazole derivative (PEG‐AAP), that readily dissolves in water, and which is accessible by simple synthetic transformations as outlined in the experimental section. We selected this particular AAP, because the non‐PEGylated AAP is known to feature nearly quantitative photoisomerization in both directions (PSD>98 %) in organic solvents.19a In water, the PSD of the PEG‐AAP (structure in Scheme 1 a) is however slightly reduced. NMR analyses upon irradiation with 370 nm and 540 nm reveal a PSD of $\mathrm{PSD}\genfrac{}{}{0pt}{}{370}{E\to Z}$ =91% and $\mathrm{PSD}\genfrac{}{}{0pt}{}{540}{E\to Z}$ =95%, respectively (Figure S1), which is still a very satisfactory PSD for potential applications.

Scheme 1.

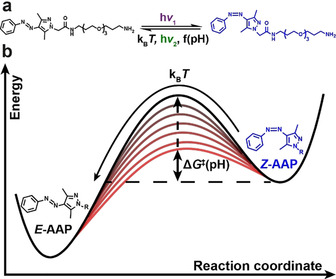
Photoisomerization and the energy barrier for thermal relaxation of PEG‐AAP in water.

Beside the photoisomerization of the PEG‐AAP, the switching from the Z‐ to the E‐form can be induced by thermal relaxation in the dark. In the course of this article, we will elaborate that the Gibbs free energy of activation ΔG ^≠ of the thermal relaxation and at the same time the thermal half‐life τ _1/2 is a function of the pH, as indicated by the increasing energy barriers in Scheme 1 b.

We start by quantifying the thermal relaxation behavior of the PEG‐AAP in aqueous solution. To this end, we adjusted the pH of aqueous solutions of E‐PEG‐AAP (100 μm) with suitable buffers (citric acid and phosphate, 10 mm) in the range of pH 4 to 8 and with aqueous hydrochloric acid and sodium hydroxide in the strongly acidic and basic pH regime. Subsequently, we irradiated those solutions with UV light (370 nm, 10 min, 80 mW, see Supporting Information for spectroscopic characteristics) to form the PSS of the Z‐PEG‐AAP and monitored how the Z‐PEG‐AAP relaxes back to its thermodynamic E‐isomer in the dark (Scheme 1) using time‐dependent UV/Vis spectroscopy (Figure 1 a, b). Profound differences can be observed between the acidic and the neutral regime. The UV/Vis spectra change distinctly at pH 2.0 and 20 °C over the course of two hours, which is indicative of the thermal relaxation from the Z‐PEG‐AAP to the E‐PEG‐AAP (Figure 1 a). In contrast, there is hardly any change at pH 7.4 because the thermal relaxation of Z‐PEG‐AAP is significantly less pronounced in the neutral pH regime within two hours (Figure 1 b). This clearly confirms a strong pH‐dependence of the thermal half‐life in aqueous media. According to the Beer–Lambert law, the absorbance at a certain wavelength is linearly correlated to the concentration of an attenuating species in a highly diluted sample. Thus, when plotting the absorbance A _335 nm at 335 nm against the time t, the relaxation rate constant k of the Z‐PEG‐AAP can be determined by a mono‐exponential decay fit function [Eq. (1)]:

$${\displaystyle A_{335nm}\left(t\right)=\Delta A_{0,335nm}\times \mathrm{e}\mathrm{x}\mathrm{p}(-kt)+A_{0,335nm}(E-PEG-AAP)}$$ (1)

Figure 1.

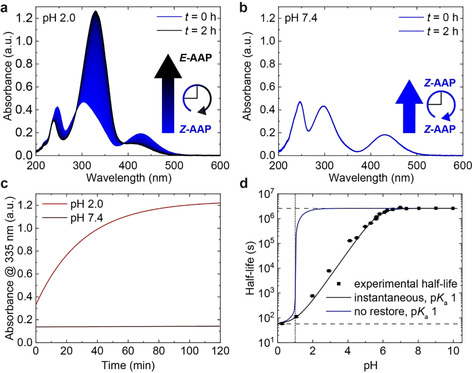
Half‐life of Z‐AAP as a function of pH. UV/Vis spectra of AAP were recorded at 20 °C over the course of two hours (a) at pH 2.0 and (b) at pH 7.4 after irradiation with 370 nm to the PSS. Time‐dependent data is based on 200 UV/Vis spectra. (c) Comparison of the thermal relaxation at pH 2.0 (red) and 7.4 (brown). The absorbance at 335 nm (A _335 nm) illustrates how fast the relaxation proceeds within two hours at the respective pH. While there is hardly any change at pH 7.4, Z‐AAP almost entirely relaxes back to E‐AAP at pH 2.0 in that time. (d) Thermal half‐life at 25 °C as a function of pH. The thermal half‐life is tunable over more than five orders of magnitude by adjusting the pH and features a sigmoidal dependence on the pH (black squares). The simulated half‐lives as a function of the pH are based on two assumptions [Eq. (8)]: no restore of P _p(t) (blue curve) vs. constant ratio of P _p(t)/P ₀(t) (black curve). The model uses the experimental half‐lives τ _1/2 (pH>6.5)=2.60×10⁶ s (upper dashed line) and τ _1/2 (pH 0.3)=59.1 s (lower dashed line) as well as a numerically optimized pK _a(Z) of 1 (dotted line).

assuming first order kinetics. The offset A _{0, 335 nm} of the fit function was set constant to the absorbance of the E‐isomer at 335 nm, whereas ΔA _{0, 335 nm} represents the difference in absorbance between both isomers at the respective PSS. The Equation (2) relates the relaxation rate constant k to the thermal half‐life τ _1/2, which is defined as the time needed so that 50 % of Z‐PEG‐AAP relaxes back to the E‐isomer.

$${\displaystyle {\tau }_{1/2}=\frac{ln2}{k}}$$ (2)

Interestingly, at the start, the pH 2.0 solution already features a higher absorbance at 335 nm than the pH 7.4 solution (Figure 1 c). This phenomenon is due to the fact that the π–π* and the n–π* transitions of Z‐PEG‐AAP tend to overlap more strongly in a highly acidic environment (pH<3.0), leading to a decreased $\mathrm{PSD}\genfrac{}{}{0pt}{}{370}{E\to Z}$ and therefore to a higher absorbance at 335 nm (Figure S2,3). When calculating the thermal half‐life of the Z‐PEG‐AAP according to Equation (1) and (2), it becomes evident that 50 % of Z‐PEG‐AAP relaxes back to the E‐isomer within 22 minutes at pH 2.0 as opposed to 62 days at pH 7.4 and 20 °C. In order to access such long relaxation time scales, we measured the relaxation kinetics at higher temperatures T and used the linearized Eyring equation24 [Eq. (3)]:

$${\displaystyle ln\frac{k}{T}=-\frac{{\Delta H}^{\ne }}{RT}+\frac{{\Delta S}^{\ne }}{R}+ln\frac{k_B}{h}}$$ (3)

to extrapolate the thermal half‐life at 25 °C using the gas constant R, the Boltzmann constant k _B and the Planck constant h (Figure S4). ΔH ^≠ and ΔS ^≠ represents the enthalpy and entropy of activation, respectively, which determine the Gibbs free energy of activation ΔG ^≠. [Eq. (4)]:

$${\displaystyle \Delta G^{\ne }=\Delta H^{\ne }-T\Delta S^{\ne }}$$ (4)

This procedure has been applied previously by others as it shortens the measuring time considerably.12, 19a, 25

To further justify the extrapolation of the thermal half‐lives, we performed two control experiments. First, we determined the relaxation rate k over a wide temperature range (5–85 °C) for a system at pH 4.0 (Figure S5). The data shows a linear correlation between the logarithmic k constant divided by T (lnk/T) and the inverse temperature (T ⁻¹) over the entire temperature range. Thus, the enthalpy and entropy of activation (ΔH ^≠ and ΔS ^≠) do not show a temperature dependence and are therefore considered as constant, which in the end justifies the extrapolation of the thermal half‐life. Secondly, we also compared the extrapolated half‐lives at given pH values to long‐term measurements at various pH (3.4–9.9), while keeping the samples in the dark for up to three months (Figure S6). Indeed, the long‐term measurements show the same trend as for the extrapolated ones, that is, that the half‐life is faster with decreasing pH.

Figure 1 d summarizes the pH‐dependent relaxation behavior and strikingly illustrates how the thermal half‐life can be tuned over more than five orders of magnitude in time by adjusting the pH. The half‐lives show a sigmoidal dependence on the pH with a minimum half‐life of 59 s at 25 °C in the acidic regime (e.g. at pH 0.3), while it reaches to 31 days in the neutral region. It is important to note that these half‐lives are substantially above previous pH‐dependent half‐lives of azobenzene derivatives (full comparison in Table S2) and that the tunable range is comparably larger, considering the minimally and maximally accessible half‐lives.14b, 14c, 14d, 15 This opens up opportunities for their application where azobenzenes may not be suitable due to their fast relaxation. To analyze the pH dependence in detail, we assume that the apparent relaxation rate k _app equals to the sum of two different rates of thermal relaxation, [Eq. (5)]:

$${\displaystyle k_{app}=k_0+k_p}$$ (5)

one for the unprotonated form (k ₀) and one for the protonated form (k _p). These rates are characterized by the time constants τ ₀ and τ _p which correspond to the inverse relaxation rate constants k ₀ ⁻¹ and k _p ⁻¹. Thus, the probability P(t) of AAP being in the Z‐state can also be split into the sum of two parts; namely the part of the neutral state P ₀(t) and the part of the protonated state P _p(t), where both depend on the time t. Hereby, P(t) satisfies the differential equation [Eq. (6)]:

$${\displaystyle \frac{dP\left(t\right)}{dt}=-\frac{1}{{\tau }_0}{P}_0\left(t\right)-\frac{1}{{\tau }_p}{P}_p\left(t\right)}$$ (6)

To be able to integrate the differential Equation (6), we set P(0)=1 as a boundary condition after reaching the PSS of Z‐AAP. Additionally, P ₀(0) and P _p(0) are in equilibrium initially, whose ratio is determined by the acid dissociation constant K _a [Eq. (7)]:

$${\displaystyle K_a=\frac{c\left(AAP\right)}{c(AAP-H^{+})}\times c\left(H_3{O}^{+}\right)=\frac{P_0\left(0\right)}{P_p\left(0\right)}\times c\left(H_3{O}^{+}\right)}$$ (7)

Rearranging Equation (6) reveals [Eq. (8)]:

$${\displaystyle \frac{P_p\left(0\right)}{P_0\left(0\right)}={10}^{-pH+{pK}_a\left(Z\right)}}$$ (8)

which expresses the ratio of P ₀(0) and P _p(0) in dependence on the pH and the pK _a(Z) of the Z‐form.

If τ ₀ and τ _p are very different, as it is the case considering Z‐AAP, the faster decay of the protonated form will drive the ratio of P ₀(0) and P _p(0) out of its equilibrium. The system tends to restore this equilibrium in time, which is why, we may consider two extreme situations for the protonation of Z‐APP: 1) slow protonation compared to the time frame of thermal relaxation, so that P _p(t) decreases fast and is not restored at all; 2) instantaneous protonation, where the equilibrium is restored immediately according to Le Chatelier's principle so that the quotient of P _p(t) and P ₀(t) is constant at any time t.

To solve the differential Equation (6) numerically with these two assumptions, we used the experimentally determined time constants τ ₀=3.75×10⁶ s and τ _p=85.2 s [τ _x=τ _1/2×(ln2)⁻¹] as well as a computationally optimized, best fitting of pK _a(Z)=1 (in agreement with experiments, see below), which leads to the simulated pH‐dependence depicted in Figure 1 d. Analogously to the experimentally determined half‐lives, both simulated curves show a sigmoidal dependence on the pH. In case of the first assumption of a slow protonation (blue curve), however, the sigmoidal curve illustrates a steep rise of the half‐life at pH 1 [pK _a(Z)=1], which is not in agreement with the experimental results. In contrast, the simulated half‐lives (black curve) using the second assumption of an instantaneous protonation fit well to the pH‐dependence of the experimental half‐lives. The fact that the instantaneous protonation describes the experimental values more precisely agrees with previous studies because protonation reactions belong to the fastest reactions in aqueous media.26 This makes it unambiguously clear that there is a H₃O⁺‐based effect on the relaxation mechanisms in dependence on the pK _a value of the Z‐isomer. In addition, the simulated curve is a highly relevant feature when thinking about applications as it enables a precise and deterministic tuning of the half‐life of a single water‐soluble AAP by the adjustment of the pH.

When we solved the differential Equation (6), we used different pK _a values for Z‐PEG‐AAP‐H⁺. The simulated curve with a pK _a(Z) of 1 features the smallest deviation from the experimental half‐lives according to the mean squared error. As the pK _a(Z) gives access to the ratio of Z‐PEG‐AAP and Z‐PEG‐AAP‐H⁺, which evidently show a different relaxation behavior, we determined the pK _a value of Z‐PEG‐AAP‐H⁺ experimentally as well. As discussed above (Figure S2), however, the PSD decreases with decreasing pH and the thermal half‐life shortens rapidly, which impedes an accurate determination of the pK _a value by common pH titrations and via UV/Vis spectroscopy. Both, the absorption spectra and at the same time the concentration of Z‐PEG‐AAP and Z‐PEG‐AAP‐H⁺, change as a function of the pH in the strongly acidic range. In contrast, there is hardly any change of E‐PEG‐AAP in terms of absorbance and hence concentration (no protonation) (Figure S2). During the thermal relaxation of the AAP, the isosbestic points remain unchanged at a specific pH and are independent of the PSD, but they change with decreasing pH (highlighted by red circles, Figure 2 a). Hence, if there is hardly any change of the absorbance of E‐PEG‐AAP in the acidic regime, the change of the isosbestic point in dependence on the pH is an indication for the ratio of Z‐PEG‐AAP and Z‐PEG‐AAP‐H⁺. Thus, the development of the isosbestic point with pH, which exhibits a sigmoidal function (black squares, Figure 2 b), was used as means to determine the pK _a(Z) value. After calculating the first derivative of the sigmoidal curve (blue circles), the data were analyzed using a Gaussian fit function (blue curve). The center of the Gaussian curve is located at a pH of 1.55±0.10, which thus corresponds to the pK _a value of the Z‐PEG‐AAP‐H⁺ (dashed line). This pK _a value can be used to plot the fraction of the protonated Z‐PEG‐AAP species and is in very good agreement with the numerical simulation (pK _a=1) discussed above (Figure 2 c). The small deviation between the simulated and the experimental pK _a‐value stems from the assumptions which need to be made in both cases. While the simulated approach approximates the time constant of the fully protonated Z‐isomer (τ _p), the experimental pK _a(Z) relies on invariant UV/Vis spectra of the E‐isomer. Both assumptions are valid to a great extent, which leads to a very good agreement of these values, despite the experimentally challenging pH regime at low pH.

Figure 2.

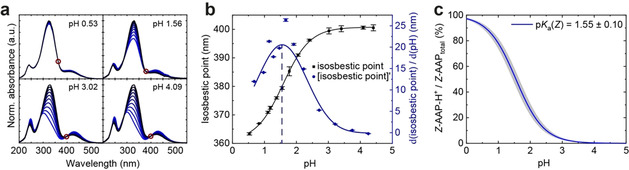
Determination of the pK _a‐value of Z‐PEG‐AAP‐H⁺. (a) UV/Vis spectra of PEG‐AAP at different stochiometric ratios of E‐ and Z‐PEG‐AAP to identify the isosbestic point as a function of the pH. (b) Plot of the isosbestic point vs. pH. The pK _a value of the Z‐PEG‐AAP‐H⁺ was determined by the derivative and a subsequent Gaussian fit function to be located at 1.55±0.10. (c) Degree of protonation of Z‐PEG‐AAP in dependence on the pH.

Of equal importance next to the determination of the pK _a of Z‐PEG‐AAP‐H⁺ is to identify the position at which the Z‐PEG‐AAP‐H⁺ is protonated, since it enables the further mechanistic understanding of the thermal relaxation. AAP features four different nitrogen atoms that might be protonated (two azo nitrogens and two pyrazole nitrogens). Since Z‐PEG‐AAP‐H⁺ is strongly acidic in water, the protonation site cannot be determined by NMR at such high proton concentrations (low pH). Instead, we computationally examined the structure to identify which nitrogen is most likely protonated using DFT calculations as implemented in the GPAW‐package.27 The Kohn–Sham orbitals and the electronic density were described in the projector augmented wave method,28 where the smooth wave‐functions were represented on real space grids. The exchange‐correlation functional was approximated in the generalized gradient correction (GGA) as devised by Perdew, Burke and Ernzerhof (PBE).29 Non‐self‐consistent energy evaluations with the meta‐GGAs TPSS30 and M06‐L31 and the hybrids PBE032 and B3LYP33 using PBE density and Kohn–Sham states were performed to obtain the influence of the functional. The grid spacing for the wave‐functions was chosen to 0.2 Å. The structures were relaxed until all atomic forces were found to be below 0.05 eV Å⁻¹. Solvent effects were considered using the polarizable continuum model (PCM).34 The calculations were performed spin paired and the local structural minima as well as transition states were checked to lead to the same energy if spin relaxation is allowed. The DFT computations reveal that the preferred protonation site for both isomers is the azo nitrogen N1, which is adjacent to the phenyl ring and the resulting structures are at least 20 kJ mol⁻¹ more stable than other positions (Figure 3). This finding agrees with Fuchter and co‐workers who similarly identified N1 as the preferred protonation site in acetonitrile.21 Setting E‐ and Z‐AAP‐H⁺ protonated at N1 as reference, Figure 3 illustrates the energy differences between all four nitrogen atoms. While protonating N1−3 are within the reach of k _BT, the fourth nitrogen is distinctly higher in energy due to its saturation. For the further mechanistic investigation of the thermal relaxation, only the preferred protonation site N1 was taken into account. In addition, the previously determined pK _a(Z) is considered as the pK _a value of protonating and deprotonating N1.

Figure 3.

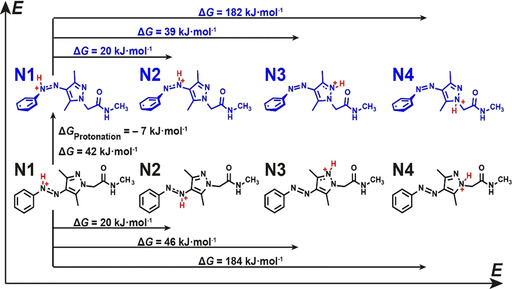
Comparison of the protonation site of E‐ and Z‐AAP based on DFT calculations. The nitrogen N1 adjacent to the phenyl ring is the most probable protonation site for both isomers. The energy difference between E‐ and Z‐AAP‐H⁺ is ΔG=42 kJ mol⁻¹. The protonation energy difference (ΔG _Protonation= −7 kJ mol⁻¹) indicates that Z‐AAP is more basic than E‐AAP.

The DFT calculations also reveal that the protonated Z‐AAP‐H⁺ has a higher energy than E‐AAP‐H⁺ (ΔG=42 kJ mol⁻¹) and therefore is less stable (Figure 3). This is in line with the expectations as otherwise the thermal relaxation will not proceed from Z‐AAP‐H⁺ to E‐AAP‐H⁺. When comparing the protonation energy of Z‐ and E‐AAP, the energy difference is ΔG _Protonation=−7 kJ mol⁻¹, which indicates that Z‐AAP is more basic than E‐AAP. A related photoswitchable basicity was previously shown for a different azoheteroarene, namely azobis(2‐imidazole).35 To confirm the DFT prediction, we alternatingly irradiated a PEG‐AAP solution (10 mm, without buffer) with 370 nm (1 mW, 30 min, purple background) and with 540 nm (100 mW, 30 min, green background) and measured the pH during irradiation (Figure 4 a). The pH measurements illustrate that the pH increases during the irradiation with UV light until a saturation is reached. This phenomenon confirms that the formed Z‐PEG‐AAP acts indeed as a photobase and is partially protonated once formed. Subsequent irradiation with green light leads to the photoisomerization back to E‐PEG‐AAP, which again decreases the pH. The reason for this behavior is the fact that E‐PEG‐AAP is less basic than Z‐PEG‐AAP, and E‐PEG‐AAP‐H⁺ is more acidic than Z‐PEG‐AAP‐H⁺, respectively. The irradiation cycle was repeated five times and confirms the predictive results of the DFT computations. Figure 4 b schematically illustrates the underlying mechanism how the pH changes as a function of the stochiometric ratio of E‐ and Z‐PEG‐AAP. Starting from the thermodynamic E‐PEG‐AAP (bottom left), Z‐PEG‐AAP is formed by the irradiation with 370 nm. Depending on the present pH and the pK _a(Z), Z‐PEG‐AAP is partially pronated generating Z‐PEG‐AAP‐H⁺, which in turn increases the pH. The transition back to E‐PEG‐AAP is either induced by irradiation with 540 nm or by thermal relaxation. In case of the latter, the thermal isomerization of Z‐PEG‐AAP and Z‐PEG‐AAP‐H⁺ are described by the relaxation rate constants k ₀ and k _p, respectively. In agreement with the previously illustrated half‐life in the acidic regime (Figure 1 d) and based on Equation (2), k _p is distinctly greater than k ₀. This means that the thermal relaxation is fastened upon protonation and therefore a function of the pH. As soon as Z‐PEG‐AAP‐H⁺ relaxes back to E‐PEG‐AAP‐H⁺ a proton is released because E‐PEG‐AAP‐H⁺ is more acidic than Z‐PEG‐AAP‐H⁺, which decreases the pH again. In addition, upon thermal relaxation of Z‐PEG‐AAP‐H⁺ to E‐PEG‐AAP‐H⁺, the equilibrium between Z‐PEG‐AAP and Z‐PEG‐AAP‐H⁺ is adjusted according to Le Chatelier's principle, which leads to an overall isomerization network as shown in Figure 4 b.

Figure 4.

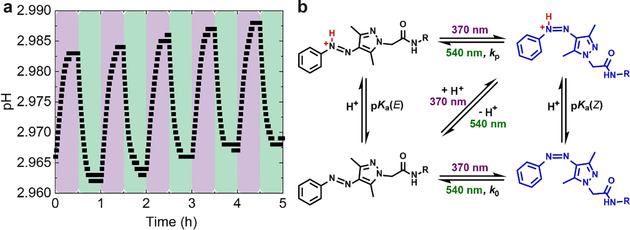
Photobase activity of PEG‐AAP. (a) pH as a function of the stochiometric ratio of E‐ and Z‐PEG‐AAP. Since Z‐AAP is more basic than E‐AAP, the pH of an E‐AAP solution (10 mm) increases upon irradiation with 370 nm (highlighted in purple) and vice versa upon irradiation with 540 nm (highlighted in green). The irradiation cycle was repeated five times to illustrate the reversibility. (b) Scheme of the isomerization network of AAP in dependence on the irradiation wavelengths and the protonation of Z‐ and E‐AAP.

In the next step, we are going to analyze the transition state trajectories of the thermal relaxation of AAP in water. Four different photoisomerization pathways are known for azobenzene that are (I) rotation, (II) inversion, (III) concerted inversion and (IV) inversion‐assisted rotation (Scheme S2).3 These paths are also valid for the thermal relaxation and strongly depend on the substitution patterns and the environmental conditions.36 To understand the thermal relaxation pathways of AAP in water, we analyzed these pathways computationally by DFT aiming to identify the most probable transition states. The actual process leading to thermal conversion without protonation is still under debate in that either rotation or inversion barriers are discussed.17, 37 Calculations based on hybrid DFT functionals find inversion transition states in AAPs,19b, 38 while a CASSCF/CASSPT approach is in favor of a rotation barrier of diradicalic nature in azobenzene.39 Zhang and co‐workers characterized the inversion mechanism in terms of potential energy profiles, dihedral angles and bond lengths in depth, but could not simulate the rotational reaction coordinate in acetonitrile although trying several different initial structures.38a Conversely, we simulated the transition state trajectories of the thermal relaxation of Z‐AAP and Z‐AAP‐H⁺ according to the mechanisms of rotation and inversion in water and identified the respective transition states using the nudged elastic band (NEB) method (Figure 5 a, b; see Figures S7–S9 for more details).40 In case of Z‐AAP, the rotational isomerization features the lowest Gibbs energy (ΔG ^≠ _calc=98 kJ mol⁻¹, highlighted by blue arrows) and is therefore the preferred pathway for the thermal relaxation of Z‐AAP. The preference of the rotation path can be clearly attributed to the PBE functional used here, which may better describe admixtures of diradical states than hybrid functionals used earlier (see further comparison in Tables S3, S4).41

Figure 5.

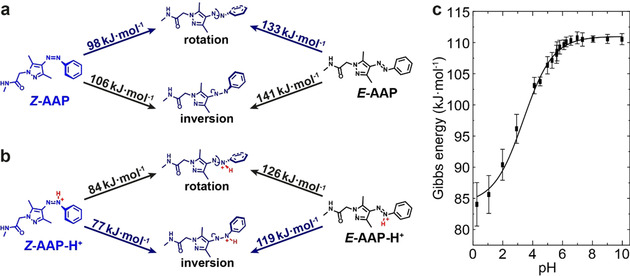
Gibbs free energy of activation ΔG ^≠ in dependence on the transition state trajectories. DFT‐computed energy barriers according to the two pathways of thermal relaxation of (a) Z‐AAP and (b) Z‐AAP‐H⁺. The energy profiles of the transition states reveal the preferred relaxation paths highlighted in blue. Z‐AAP rotates around the N1=N2 double‐bond, whereas Z‐AAP‐H⁺ relaxes according to the inversion mechanism. (c) Experimentally determined Gibbs free energy of activation ΔG ^≠ based on linearized Eyring plots. The experimental Gibbs energies show a sigmoidal dependence on the pH (black curve, guide for the eye) and are in good agreement with the calculated ones; both for Z‐AAP‐H⁺ in the acidic and for Z‐AAP in the neutral pH range.

To compare with experiments, we determined the experimental Gibbs free energy of activation ΔG ^≠ from the slope m and the y intercept c of the calculated linear regression based on Equation (3) and (4) and the linearized Eyring plots (Figure S4). Analogously to the thermal half‐life, the experimentally determined Gibbs energy displays a sigmoidal dependence on the pH, ranging from 84.0 kJ mol⁻¹ in the acidic to 110.6 kJ mol⁻¹ in the neutral regime (Figure 5 c). Above pH 6.5, the averaged experimental Gibbs energy is ΔG ^≠ _exp=110.5±1.6 kJ mol⁻¹, which coincides well with the computed value (ΔG ^≠ _calc=98 kJ mol⁻¹), thus supporting the accuracy of the DFT calculations.

A comparison of the thermal relaxation of Z‐AAP and Z‐AAP‐H⁺ shows that the overall computed energy barriers are lower once the Z‐isomer is protonated (Figure 5 b). This phenomenon is in line with the determined half‐lives in the acidic region (Figure 1 d), because a faster thermal relaxation indicates a lower energy barrier that needs to be overcome. This is due to the formed azonium ion which reduces the Gibbs free energy of activation ΔG ^≠ and thus, accelerates the thermal relaxation. While Z‐APP relaxes rotationally around the azo bridge, the preferred transition state trajectory of Z‐AAP‐H⁺ proceeds according to inversion (also calculated by the PBE method). Once the azo bridge is protonated at N1, the character of the N1=N2 double bond is decreased which accelerates the inversion more strongly than the rotation. Consequently, inversion (ΔG ^≠ _calc=77 kJ mol⁻¹) is energetically favored compared to rotation (ΔG ^≠ _calc=84 kJ mol⁻¹). Again, the computed Gibbs energy is in good agreement with the experimental one. At pH 0.3 for instance, at which N1 of Z‐AAP is almost entirely protonated (Figure 2 c), the experimental Gibbs energy [ΔG ^≠ _exp (pH 0.3)=84.0±3.5 kJ mol⁻¹] has a deviation of less than 10 % from the calculations, again underpinning the accuracy of the DFT calculations.

To illustrate an application of the tunable half‐life on the material scale, we prepared an AAP‐Polymer (Figure 6 a) consisting of PEG‐AAP‐acrylamide (5 mol‐%), 4‐vinylbenzenesulfonate (4VBS, 20 mol‐%) and OEGMA ((oligo ethylene glycol)methacrylate; 75 mol‐%). In this case, the sulfonic acid moieties of 4VBS serve as strong, non‐volatile acids, which allow to adjust the solid‐state acidity via pH adjustment prior to film formation. In addition, we incorporated POEGMA to increase the solubility in water, and cast films in presence of cellulose nanocrystals (CNC) to prevent coffee ring effects and lower the polymer content.42 A comparison of the half‐lives of PEG‐AAP and the polymer‐appended AAP in solution shows a small difference at pH 7.4 and 25 °C [τ _1/2(PEG‐AAP) ≈29 days vs. τ _1/2(AAP‐Polymer) ≈22 days, Figure 6 b]. The linearized Eyring plots illustrate that the logarithmic relaxation rate constants divided by T (ln k/T) are generally greater and that the slope m is a bit lower for AAP attached to the polymer as opposed to free PEG‐AAP in solution. Thus, also the Gibbs energy of the AAP‐Polymer is slightly reduced [ΔG ^≠(PEG‐AAP)=110.5±1.1 kJ mol⁻¹ vs. ΔG ^≠(AAP‐Polymer)=109.8±1.4 kJ mol⁻¹]. Inside the polymer, the AAPs are in close proximity to the strongly acidic sulfonate groups, which may promote their relaxation already in solution. This phenomenon is even more pronounced in bulk where the acidity is stronger than in solution as shown in the following.

Figure 6.

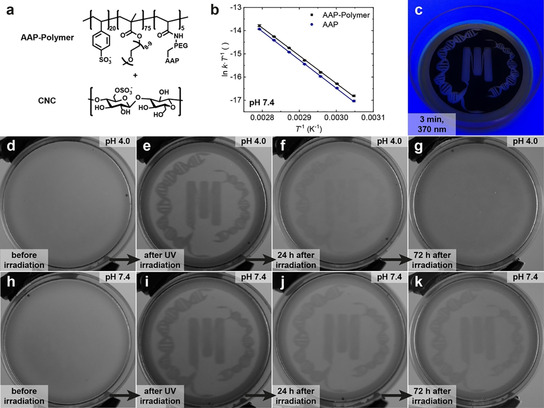
Application of the AAP‐photoswitch with tunable half‐lives to write transient information patterns in solid state polymer films. (a) Scheme of the AAP‐Polymer and CNC which are both equipped with sulfonic acid moieties. (b) Linearized Eyring plots determining the Gibbs energy (ΔG ^≠=109.8±1.4 kJ mol⁻¹) and the half‐life [τ _1/2 (25 °C)=21.9±0.5 d] of AAP attached to the polymer (black squares) compared to free PEG‐AAP in solution (blue circles). (c) Photopatterning of CNC/AAP‐Polymer films via irradiation through an inkjet‐printed photomask with a UV lamp (370 nm) for 3 min. (d,h) Homogenous films before UV irradiation. (e,i) After UV irradiation, both films clearly illustrate the pattern of the exposed areas. (f,j) While the pattern is clearly visible after 24 h in case of films cast from pH 7.4 (j), it is strongly faded already in the same time for films cast from pH 4.0 (f). (g,k) After 72 h, the pattern is not visible anymore at pH 4.0 (g), because most Z‐AAP is converted back into E‐AAP. In contrast, the film cast from pH 7.4 clearly illustrates the pattern after 72 h in the dark (k).

To show relevant differences in time‐programmed transient information storage, we cast two films from aqueous dispersions of the AAP‐Polymer (6 mL, 1.0 wt %) and CNC (6 mL, 0.2 wt %) at an initial pH of 4.0 and 7.4, respectively (Figure 6 a). Subsequently, we irradiated the films with a UV lamp (370 nm, 3 min) through an inkjet‐printed photomask to spatially control the photoisomerization from E‐ to Z‐AAP within the transparent area (Figure 6 c). Since there is only a weak color contrast between the E‐ and the Z‐AAP in full color images (mostly yellow films), we filtered the RGB channels using ImageJ and only report the blue channel as a grey scale color image. These grey scale images correspond to acquisitions using blue emission filters. Consequently, the presence of Z‐AAP is clearly discernible by higher grey values as shown in Figure 6 d–k.

Before UV irradiation, both films are homogenous without any patterns (Figure 6 d,h). After UV irradiation and with the aid of a photomask, the films are imprinted by the pattern as visible by darker grey color within the exposed areas (Figure 6 e,i). These images clearly confirm the spatial control of the photoisomerization from E‐ to Z‐AAP. When keeping the films in the dark after UV irradiation, the film cast at pH 4.0 displays a quick disappearance of the pattern within 24 hours as opposed to the film cast at pH 7.4, which is only slightly faded in the same time period (Figure 6 f,j). This behavior is caused by the fastened thermal relaxation of Z‐AAP back to E‐AAP inside the first film as a result of the initial pH 4.0. In contrast, Z‐AAP relaxes more slowly inside the film cast at pH 7.4 illustrated by higher persistent grey values (Figure 6 j). Consequently, temporal control is gained by the initial pH before film casting. After 72 hours, the pattern in case of the first film (pH 4.0) is not visible anymore since Z‐AAP almost entirely relaxed back to E‐AAP within that period (Figure 6 g). Conversely, Figure 6 k still displays the pattern after 72 hours in the dark because of the slower thermal relaxation inside the film cast from pH 7.4. In summary, Figure 6 illustrates that the thermal half‐life of a single AAP can be tuned in polymers as well as in bulk. Here, the transient information storage shown in form of the patterns depends on the acidity of the sulfonic acid moieties whose relative abundance can be adjusted by the pH.

Conclusions

We demonstrated how the thermal half‐life of a single water‐soluble AAP can be tuned by more than five orders of magnitude in time, ranging from seconds to weeks, via the adjustment of the pH. These half‐lives extend substantially into longer timescales compared to previously reported azobenzene derivatives and the tunability range is also comparably large. Under acidic conditions, there is a sigmoidal correlation between the half‐life and the pH, which can be precisely described by the differential Equation (6) in dependence on the pK _a(Z), and the thermal half‐life in the neutral and in the acidic regime. This correlation enables the precise tunability of the thermal half‐life as needed for an application of interest. We suggest that tuning of the substitution patterns of AAPs will lead to similar pH‐dependent behavior, but with a further tunability of the metastable time frames in other ranges. Thus, when speaking of systems with temporally limited action, the combination of a certain substitution pattern plus the tunability through the pH enables the precise design according to prerequisites, which can be adjusted on‐demand by the pH.

Furthermore, we revealed that the nitrogen N1 adjacent to the phenyl ring is the most alkaline nitrogen of Z‐AAP and its corresponding acid has a pK _a value of 1.55±0.10 according to our experiments and of 1 based on numerical simulations. Considering a Z‐AAP derivative as a prodrug in photopharmacology, the gastric acid possesses a pH regime low enough to form E‐AAP as the reactive species in a time frame which is suitable for the resorption into the circulatory system. Thus, it might be a promising approach to exploit Z‐AAP as unreactive prodrug which forms the reactive species after oral uptake. In addition, the first pass effect of drug metabolism is generally related to a higher hydrophobicity. As a consequence of the stronger dipole moment of Z‐AAP as compared to E‐AAP, the hydrophilicity of Z‐AAP is increased, which could lead to a greater bioavailability of the respective drug. Moreover, we demonstrated that Z‐AAP is more basic than E‐AAP and illustrated its effect as a photobase. Referring to molecular design, AAPs with more moderate pK _a values can be obtained by increasing the electron density of the azo bridge. Thus, the incorporation of electron donating moieties will shift the pK _a(Z) and therefore the tuning window of the thermal half‐life to less acidic pH ranges. This will be of interest in photoresponsive hydrogels, for instance, exploiting AAPs inside the polymer backbone or as side chains. Interestingly, not only the thermal half‐life of AAPs can be tuned by the pH, also the pH can be locally tuned inside hydrogels by the photoisomerization of AAP depending on the pK _a values of the respective E‐ and Z‐isomer.

Moreover, we elaborated on the transition state trajectories of the thermal relaxation via DFT according to the mechanisms of rotation and inversion and identified different most probable transition states as well as energy barriers depending on the protonation. The use of the gradient corrected functional lead to the preference of the rotation mechanism, while an inversion mechanism is proposed in case of protonation. The excellent agreement between experiments and calculations underlines the accuracy of the DFT computations. More importantly, the precise calculations enable to predict the properties of newly designed molecular photoswitches, which represents a timesaving alternative to laborious synthetic efforts.

Finally, we demonstrated that the half‐life of AAP can also be tuned when attached to polymers and even further in bulk by the incorporation of acidic groups in proximity to the AAP. Hereby, the relative abundance of acidic groups can be adjusted by the pH and the resulting acidity determines the half‐life. We foresee that the quantitative understanding of pH effects in AAP derivatives in aqueous solutions and in bulk may provide additional important design criteria beyond the possibilities of synthetic (re)design, as needed for example, for advanced materials and nanoscience applications and for time‐programmed characteristics of transient materials systems.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

S. Ludwanowski, M. Ari, K. Parison, S. Kalthoum, P. Straub, N. Pompe, S. Weber, M. Walter, A. Walther, Chem. Eur. J. 2020, 26, 13203.