Abstract
Purpose
We developed a target‐based cone beam computed tomography (CBCT) imaging framework for optimizing an unconstrained three dimensional (3D) source‐detector trajectory by incorporating prior image information. Our main aim is to enable a CBCT system to provide topical information about the target using a limited angle noncircular scan orbit with a minimal number of projections. Such a customized trajectory should include enough information to sufficiently reconstruct a particular volume of interest (VOI) under kinematic constraints, which may result from the patient size or additional surgical or radiation therapy‐related equipment.
Methods
A patient‐specific model from a prior diagnostic computed tomography (CT) volume is used as a digital phantom for CBCT trajectory simulations. Selection of the best projection views is accomplished through maximizing an objective function fed by the imaging quality provided by different x‐ray positions on the digital phantom data. The final optimized trajectory includes a limited angular range and a minimal number of projections which can be applied to a C‐arm device capable of general source‐detector positioning. The performance of the proposed framework is investigated in experiments involving an in‐house‐built box phantom including spherical targets as well as an Alderson‐Rando head phantom. In order to quantify the image quality of the reconstructed image, we use the average full‐width‐half‐maximum (FWHMavg) for the spherical target and feature similarity index (FSIM), universal quality index (UQI), and contrast‐to‐noise ratio (CNR) for an anatomical target.
Results
Our experiments based on both the box and head phantom showed that optimized trajectories could achieve a comparable image quality in the VOI with respect to the standard C‐arm circular CBCT while using approximately one quarter of projections. We achieved a relative deviation <7% for FWHMavg between the reconstructed images from the optimized trajectories and the standard C‐arm CBCT for all spherical targets. Furthermore, for the anatomical target, the relative deviation of FSIM, UQI, and CNR between the reconstructed image related to the proposed trajectory and the standard C‐arm circular CBCT was found to be 5.06%, 6.89%, and 8.64%, respectively. We also compared our proposed trajectories to circular trajectories with equivalent angular sampling as the optimized trajectories. Our results show that optimized trajectories can outperform simple partial circular trajectories in the VOI in term of image quality. Typically, an angular range between 116° and 152° was used for the optimized trajectories.
Conclusion
We demonstrated that applying limited angle noncircular trajectories with optimized orientations in 3D space can provide a suitable image quality for particular image targets and has a potential for limited angle and low‐dose CBCT‐based interventions under strong spatial constraints.
Keywords: cone beam computed tomography (CBCT), image‐guided therapy (IGT), limited angle noncircular scan orbits, source‐detector trajectory optimization, tomographic reconstruction
1. INTRODUCTION
The introduction of digital x‐ray detectors has paved the way for compact isocentric C‐arm systems in the past two decades. 1 , 2 , 3 , 4 , 5 Their comparatively small form factor and the possibility to integrate three dimensional (3D) imaging systems into larger devices, like linear accelerators, for radiation therapy have opened a plethora of clinical applications. Nowadays, cone beam computed tomography (CBCT) has become a vital tool for interventional radiology. Still, the image quality cannot be compared to standard computed tomography (CT), mainly due to truncation artifacts, readout noise, and increased scatter radiation. From the imaging geometry used in isocentric C‐arms, it is evident that the volume to be reconstructed without loss of image quality is limited by the size of the detector, and as a result, conventional isocentric C‐arms are still quite massive and kinematic problems especially in situations where space is limited, for example in surgery, interventional radiology or special applications of radiotherapy such as hadron therapy with added instrumentation close to the patient is inevitable. 6 , 7
It is possible to modify C‐arm source‐detector trajectories in order to overcome these limitations. Davis et al. 6 tried to find imaging trajectories that avoid collisions using a virtual isocenter and variable magnification during acquisition. Meng et al. 7 proposed a CBCT verification strategy using unconventional and limited imaging angles for patients undertaking noncoplanar radiation therapy. Stayman et al. 8 investigated the integration of prior imaging data for designing customized trajectories using a greedy approach based on sequential forward selection (SFS) as the trajectory optimization method. Gang et al. 9 proposed a task‐based imaging framework using a gradient‐based optimization for joint optimization of the orbital tilt (range: ±30°), tube current, and reconstruction kernel. Fischer et al. 10 proposed a greedy optimization algorithm to investigate optimal scan trajectories for industrial x‐ray CT using CAD model of the object. Noncircular source‐detector trajectories are suggested in using periodic and B‐spline base functions in simulation studies as well as in the neuroradiology application. 11 , 12 An increased performance in a volume of interest (VOI) over standard orbits was the result of these studies. 8 , 9 , 10 , 11 , 12
Our work aims at facilitating the design of patient‐specific limited angle trajectories for a dedicated VOI, which takes kinematic constraints into account. As a result, highly compact imaging units allowing for a variety of intra‐interventional image update tasks for image‐guided radiotherapy, computer‐aided surgery, and interventional radiology are facilitated. It is our aim to enable CBCT systems under kinematic constraints where standard circular trajectories are not feasible. CBCT scans with lower x‐ray dose may be another potential advantage of our proposed trajectories. Usually hard constraints on the rotation angle were used to avoid collision limits. 8 , 9 , 11 , 12 Our approach enhances those earlier efforts by optimizing a sequence of arbitrary short scan trajectories, including rotations in cranio/caudal direction, with a technique similar to dose planning in volume‐modulated arc therapy or other advanced radiotherapy method. Instead of optimizing dose in the target volume and organ sparing like in radiotherapy, we use a numerical simulation of potential trajectories, which optimizes image quality based on prior tomographic data by means of finding optimal 3D orientation for reconstructing a given VOI. Kinematic constraints serve as boundary conditions in this approach. While it is obvious that image quality is sacrificed compared to a standard circular trajectory, it is our aim to achieve a reasonable image quality in the VOI. It is also assumed that a high‐quality dataset is available.
As complex and unconventional source‐detector trajectories are the result of this approach, we developed a new feature for the open source Tomographic Iterative GPU‐based Reconstruction (TIGRE) toolkit to facilitate reconstruction of such trajectories. 13 Adaptive steepest descent projection onto convex sets (ASD‐POCS) algorithm was selected as the reconstruction algorithm for this study. The performance of the proposed methodology is investigated in experiments involving an in‐house‐developed box phantom featuring spherical targets at different locations as well as an Alderson‐Rando head phantom.
2. MATERIALS AND METHODS
2.A. Workflow for the customized CBCT
The proposed customized CBCT imaging workflow is illustrated in Fig. 1. In this study, we propose acquiring a case‐specific model from prior CT and use that as the digital phantom for x‐ray simulations of the imaging device (Section 2.B). In the simulation phase, we define a set of possible x‐ray source‐detector trajectories (Section 2.C), which take into account the kinematic constraints of the imaging device and the operating room setup. Using the entire set of trajectories, synthetic digitally rendered radiographs (DRRs) of projections are generated. Using a trajectory optimization method (Section 2.D), possible arcs are selected, reconstructed with iterative algorithms, and quantitatively evaluated in order to find the combination of sub‐trajectories that best fit the selected objective function. This process is repeated for optimization.
Fig. 1.
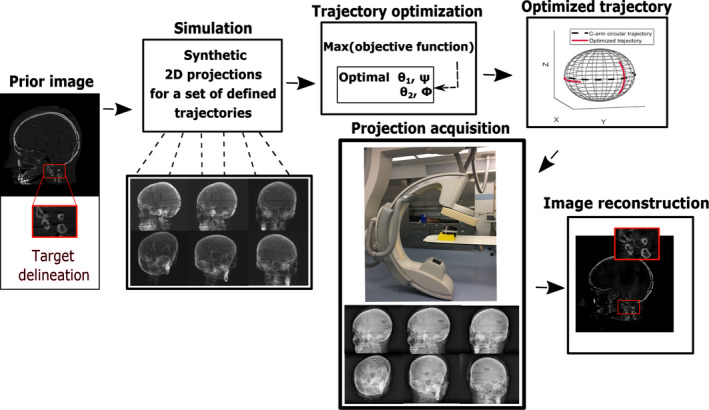
Diagram of the workflow for our proposed customized cone beam computed tomography. [Color figure can be viewed at wileyonlinelibrary.com]
Finally, the selected trajectory will be applied to the device in the real situation to acquire projections for reconstruction.
2.B. Imaging device
For our study, a Philips Allura FD20 Xper C‐arm was used. The FD20 C‐arm has 810 mm source‐axis distance, 1195 mm source‐detector distance, and a 30 × 40 cm2 detector with 0.776 mm pixel pitch. This device can rotate by angle θ1 toward right anterior oblique (RAO)/left anterior oblique (LAO) direction while having an oblique degree‐of‐freedom (DOF) ψ at various fixed cranial (CRA)/caudal (CAU) angles [Fig. 2(a)]. It also can rotate by angle θ2 toward CRA/CAU direction while having an oblique DOF φ at various fixed RAO/LAO angles [Fig. 2(b)]. The rotation axes for the RAO/LAO and CRA/CAU rotations are the Z and X axes, respectively [shown with blue axes in the Figs. 2(a), and 2(b)].
Fig. 2.
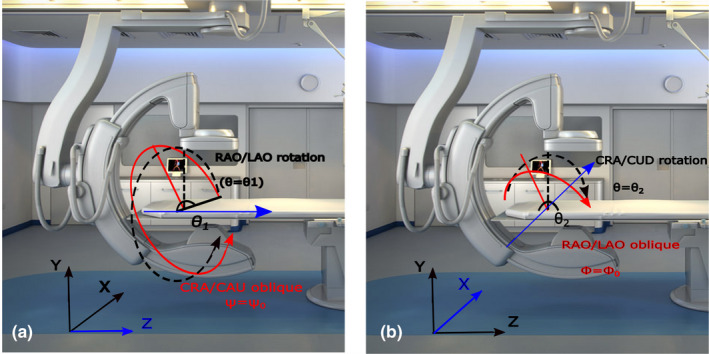
Possible rotation of Philips Allura FD20 Xper C‐arm. (a) right anterior oblique (RAO)/left anterior oblique (LAO) rotation with cranial (CRA)/caudal (CAU) oblique, (b) CRA/CAU rotation with RAO/LAO oblique. Rotation axes for RAO/LAO and CRA/CAU rotations are Z and X, respectively, and are shown in blue color. [Color figure can be viewed at wileyonlinelibrary.com]
2.C. Arc definition
As the search space for possible trajectories in 3D is continuous but the problem is non‐convex, our proposed optimization method requires a user‐defined initial set of possible arcs. These can be arbitrary as long as they are feasible with the imaging device. The particular subset of arcs to be used as an input to the optimization process is constrained by mechanical limitations, patient and table position, and other medical devices in the treatment room. In this work, the geometry of the Philips Allura C‐arm is used to define the set of possible arcs (see also Section 2.B), but the methodology is not device‐specific.
In this work, the maximum angular range is limited to 160° in the final trajectory. Limited angle noncircular scan trajectories allow for increased flexibility under inevitable kinematic constraints and can be efficient for a wide variety of applications. This has been widely investigated in the image reconstruction literature. 14 , 15 , 16 , 17 The selected reconstruction algorithm (ASD‐POCS) has proven to efficiently reconstruct at such limited range which was confirmed by our results. 18 Two subset of arcs have been defined (Fig. 3), each corresponding to a rotation on the Philips Allura, and rotation on RAO/LAO and CRA/CAU directions. In each of those directions, the machine can have an oblique angle Ψ and Φ that define the rotation on that direction of the arc. The C‐arm start position is shown in Fig. 2, where the source and detector have zero rotation in both directions.
Fig. 3.
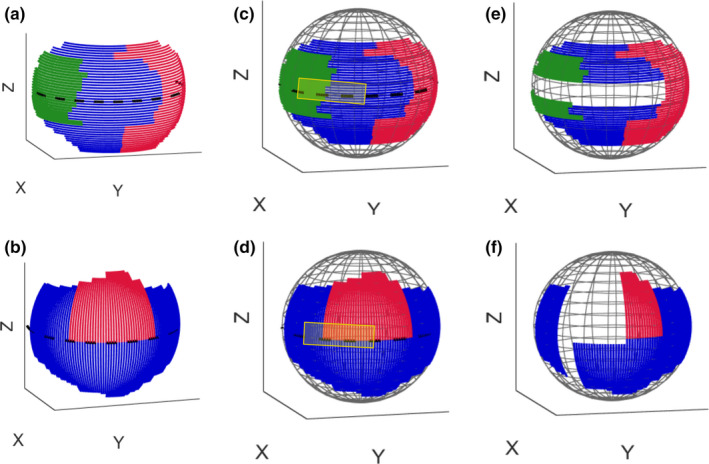
The possible rotations are divided into arcs with 80° maximum. Colors were added to differentiate between the individual arc partitions in continuous paths. (a) right anterior oblique (RAO)/left anterior oblique (LAO) arcs with cranial (CRA)/caudal (CAU) oblique shown in green, blue, and red color, (b) CRA/CAU arcs with RAO/LAO oblique shown in red and blue color, (c) and (d) spherical plot of arcs with representation of forbidden area as the area inside the yellow rectangle, (e) and (f) spherical plot of the remaining arcs after removing those which are inside the forbidden area. Only these remaining arcs consist the search space for our trajectory optimization. [Color figure can be viewed at wileyonlinelibrary.com]
Taking into account the patient table, each of those rotations is sampled with an angle step of 2° covering as much angular range as geometrically possible (180° for RAO/LAO and 87° for CRA/CAU). Then each of the resulting arcs is subdivided into arcs of maximum 80°, uniformly sampled at a rate of a projection every 2° [arcs with different colors in Figs. 3(a), 3(b)]. This lower than standard sampling rate is chosen in order to reduce x‐ray dose. The final trajectory will consist of two arcs in order to not exceed the imposed 160° degrees maximum view. By dividing the arcs into RAO/LAO and CRA/CAU rotation axes, we allow for additional DOF compared to a limited view single arc. This approach facilitated CBCT under severe kinematic constraints, for instance when arcs larger than 80° are not possible. In addition, it allows flexibility that could enhance reconstruction compared to just a continuous limited view single arc, but the optimization procedure will select the best combination, which can be a continuous arc (combination of two connected arcs). The resulting search space consists of 237 small arc paths in total (112 RAO/LAO arcs with CRA/CAU oblique angle and 125 CRA/CAU arcs with RAO/LAO oblique angle).
2.C.1. Kinematic constraints
In the setup as shown in Fig. 2, the major kinematic constraint is the potential collision of the C‐arm and patient table limiting when we apply tilts on normal CRA/CAU and RAO/LAO rotation [shown as edges in Figs. 3(a) and 3(b)]. Additional constraints due to patient size and other medical devices may also occur. In this study, we simulate such a constraint as a forbidden area on the geometry of the system [shown as a yellow rectangle in Figs. 3(c) and 3(d)]. Arcs that have more than 10% of their angular range in the forbidden area are removed and those that have <10% in it are cropped. This excludes 44 arcs from the search space and thus leaves 193 arcs to search through [Figs. 3(e) and 3(f)].
2.D. Trajectory optimization method
We use a greedy approach for arc selection similar to Refs. [8, 10]. The optimization is presented in Algorithm 1. First, a VOI — the area where the image quality is to be optimized — is selected. Then, DRRs are simulated on the CT‐based digital phantom for all defined arcs. An image reconstruction step is then run for the entire set of possible arcs (193 in our example, as explained in Section 2.C.1), and the objective function (Section 2.E.1) is evaluated in the VOI, choosing the arc with best value. The selected arc is removed from the search list, appended to all other paths in the search space, and the algorithm is rerun as many time as desired. As mentioned before, we have constrained ourselves to have two arcs in this study. The number of angles of the final trajectory (maximum 160°) is considered as the termination criteria here. Other criteria, such as a measure of absolute image quality or imaging dose, are feasible as well.
| Algorithm 1. Trajectory optimization framework |
|---|
|
Step 1: Acquire image data to be used as a digital phantom for DRR simulation Step 2: Define a set of arcs for the search space Step 3: Simulate DRRs for all defined arcs with the digital phantom Step 4: FOR 1: number of arcs Reconstruct the image using the set of DRRs related to the corresponding arc Crop the reconstructed image at the VOI Calculate the objective function at the cropped area ENDFOR Step 5: Find the best candidate as and remove it from the search space Step 6: Append best candidate to all other arcs in the search space Step 7: IF NOT stopping criteria are met Go to Step 4 ENDIF Step 8 Return selected trajectory (combined arcs) |
2.D.1. Projection simulations
In order to simulate CBCT data, DRRs were simulated for all predefined arcs from the prior CT. For DRR rendering, a monoenergetic forward model with added Poisson noise was used. Bare‐beam fluence was modeled with 104 photons per detector element approximating device exposure with 350 mAs and beam energy of 80 kV. Source‐detector distance is considered 1195 mm, whereas source‐isocenter distance is 810 mm corresponding to the geometry of the Philips Allura FD20 Xper C‐arm. All DRRs feature 512 × 512 pixels and a 30 × 40 cm2 detector size. 0.776 mm pixel pitch was simulated according to the detector specifications. In our study, the forward projections are computed using the ray‐driven method, particularly a GPU implementation exploiting the hardware‐accelerated trilinear interpolation. 13 , 19 Future research should also include a refinement of this procedure, for instance, by taking into account a more precise energy model and the increased amount of scatter radiation.
Modification of the TIGRE toolbox for arbitrary 3D source‐detector trajectories
We developed an appropriate environment for algebraic reconstruction by the modification of the TIGRE toolbox to perform forward and backward projections and reconstruction based on arbitrary 3D orientations. 13 We added a new feature to the TIGRE toolkit to perform reconstruction based on variety of arbitrary/non‐isocentric trajectories. 20 , 21 We also released the resulting code at https://github.com/CERN/TIGRE/releases/tag/v1.3 for other research groups to use.
2.D.2. Image reconstruction
Cone beam computed tomography reconstruction aims to estimate the unknown patient attenuation from the projection value for the given rotation angle of an x‐ray source. For the ray from the focal spot to the point on a detector, the measured projection can be expressed as:
| (1) |
Source location is defined as and , where and are the source‐axis and source‐detector distances, respectively. is the unit vector from the source to the point on the detector. Image reconstruction from the projection model in Eq. (1) can be formulated by solving a linear equation expressed as:
| (2) |
where is a vector containing image voxel values to be reconstructed, represents vector containing measured projection data, represents the errors, for example noise in the measurements, and is the system matrix which relates to Tomographic inversion is ill posed, thus often the optimization of in Eq. (2) is proposed as a regularized minimization problem as:
| (3) |
where is a regularization term. There is a wide range of regularization functions proposed in the literature to aid reconstruction. In our study, we use the total variation (TV) of the image, which encodes changes in the gradient. Minimizing this function ensures sparsity of the gradient, that is generates piecewise flat images. It is widely used in the literature due to its noise canceling effect. The TV of an image is defined as:
| (4) |
where are the image voxel indices for the three dimensions.
Adaptive steepest descent projection onto convex sets (ASD‐POCS)
In our study, we use ASD‐POCS algorithm for the reconstruction. 22 , 23 ASD‐POCS has been proposed to solve a TV regularized reconstruction that optimizes the following equation:
| (5) |
which is subject to (a) a data fidelity constraint , where defines an acceptable error between the observed and predicted projection data and (b) the non‐negativity constraint which means the attenuation coefficient needs be positive. The ASD‐POCS algorithm includes two phases for each iteration. The first phase includes running a purely data fidelity optimizer, such as the simultaneous algebraic reconstruction technique (SART), to impose data consistency based on the two described constraints. The second phase includes TV optimization achieved by the steepest descent algorithm for the TV objective function given in Eq. (5). These two phases are run consecutively until the stopping criterion is fulfilled. The optimal parameters for the reconstruction based on the ASD‐POCS algorithm investigated in a previous study were used in our study. 24 ASD‐POCS has two effective stopping criteria: The first is a balance of the two convex optimizations (TV and data constraint) given that the image is within acceptable L2 error in the data constraint (selected as the L2 norm of an OS‐SART reconstruction with 60 iterations). This balance is measured by computing the angle between gradient updates, and when bigger than 160° (both updating in opposite directions), the algorithm is stopped. The second one is a maximum number of iterations, controlled both by the iteration number and the absolute value of β, which is a continuously reduced data constraint hyperparameter. 24 In our work, the algorithm stopped due to the second criteria, but the angle between the optimizer was not far from the first stopping criteria. Iteration number was selected as 10 in this study.
We reconstruct a 2563 voxel volume (with 1 mm3 voxels) for all experiments based on ASD‐POCS method implemented in TIGRE toolkit. This algorithm was selected due to its demonstrated increased image quality under sparse view and limited angle scanning. 16 , 18 , 25
We validated the high performance of ASD‐POCS under our proposed scanning strategy by reconstructing a series of simulated projections and cross‐checking with the other available algorithms in TIGRE. This was later validated with real data.
2.D.3. Computational time
Computational time for iterative reconstruction is considerable and in this work, we propose a procedure that requires hundreds of reconstructions [for instance, 386 (=193 × 2) in our setup for two iterations of arc selection]. In order to address this issue, we have modified the TIGRE toolbox implementation of ASD‐POCS to reconstruct completely on the GPU, mainly by removing CPU‐GPU memory transfer operations. This implementation takes approximately 7.5 and 15 s for each ASD‐POCS reconstruction including 40 and 80 projection angles on a consumer grade GPU. The 2563 voxel volumes with 5122 projections were used for the reconstruction. Optimizing the first optimal arc (including 40 projections) required 193 times reconstruction runs which took approximately 24 min (=193 × 7.5 s) and optimizing the second optimal arc (including 80 projections) required 193 times reconstruction runs which took approximately 48 min (=193 × 15 s). The overall time needed for the whole procedure including also the calculation of the objective functions and projection simulations was approximately 80 min.
2.E. Image quality evaluation parameters
2.E.1. Image quality metrics used as the objective function
In this study, we use the value of full‐width‐half‐maximum (FWHM) as the objective function for the trajectory optimization for the spherical targets. In addition, we use the value of feature similarity index (FSIM) as the objective function to select the optimal combination of arcs for the anatomical target.
3D Point spread function (PSF)
We used the 3D PSF as a measure to evaluate the performance of the reconstructed image for spherical targets. The spatial variance was assessed as FWHM of the local PSFs for each particular target. In order to calculate the 3D PSF, we consider the separability assumption and decomposition scheme proposed in Ref. [26]. According to this scheme, a 3D PSF is decomposed into 2D PSFs for three orthogonal planes, and then in turn a 2D PSF is decomposed into 1D PSFs for two orthogonal directions. In our study, we consider three cross‐section D planes passing through the sphere center for each of X, Y, and Z directions. A group of 180 radial lines passing across the sphere center for each 2D plane is assumed. Finally, an average over all the lines for each 2D plane related to X, Y, and Z directions is considered as FWHMX, FWHMY, and FWHMZ, respectively. We then calculate the FWHMavg which is the average of FWHM values over all lines over the all three planes. The lower value of FWHMavg shows better spatial resolution of reconstruction results. The value of 1/FWHMavg was defined as the objective function and the arc with maximum value of 1/FWHMavg was selected as the best arc () in the trajectory optimization algorithm (Algorithm 1, Step 5).
| (6) |
| (7) |
Feature similarity index (FSIM)
Feature similarity index was used as the objective function for the anatomical target in this study. Zhang et al. 27 introduced the FSIM in order to quantify the distortion of important low‐level features. The metric between two images, and , is calculated based on phase congruency (PC) and gradient magnitude (GM) maps. PC is a dimensionless metric for the significance of a local structure. GM is a measure for high‐frequency changes in the image. The computation of PC and GM is explained in Ref. [27]. The subsequent calculation of their similarity (),
| (8) |
| (9) |
is followed by their combination reusing the PC as a weighting function:
| (10) |
where and are constants depending on the dynamic range of PC and GM values. corresponds to the whole image spatial domain and . FSIM has a value between 0 and 1, in dependence of the level of similarity. The value of FSIM was used as the objective function and arc with maximum value of FSIM was selected as the best arc () in the trajectory optimization algorithm (Algorithm 1, Step 5).
| (11) |
| (12) |
In addition to FWHMavg and FSIM, the two other image quality metrics, including universal quality index (UQI) and contrast‐to‐noise ratio (CNR), were used in order to evaluate the final real‐data reconstructed image:
2.E.2. Universal quality index (UQI)
Universal quality index 28 is a common image quality index which is defined as follows:
| (13) |
where , , and correspond to the respective mean, variance, and covariance values of the images and . Universal quality index has a value between 0 and 1, which increases with similarity.
2.E.3. Contrast‐to‐noise ratio (CNR)
Contrast‐to‐noise ratio is an image quality metric which is used to quantify the contrast and noise characteristics of an image within a selected region of interest (ROI). 29 The CNR is defined as follows:
| (14) |
where and denote the mean over the signal‐ROI and background‐ROI, respectively. and are the corresponding variances.
2.F. Phantoms
The proposed customized CBCT workflow was assessed using two phantoms (Fig. 4). We developed a box phantom [Fig. 4(b)] which consists of several small polytetrafluoroethylene spheres located at regular distances through the entire phantom. Solid spheres are arranged in six layers with 6 cm distance from each other in both horizontal and vertical direction. They have a diameter of 6 mm and are supported by different layers of light foam. Each of these spheres serves as a target inside a particular VOI. In this study, we used five spheres in three different layers and locations [Fig. 4(b)] as targets inside the box phantom. The relative position of the five spherical targets in different layers of the box phantom to the C‐arm source‐detector trajectory is shown in Figs. 4(a) and 4(b). We also used an anthropomorphic head phantom [Fig. 4(c)] and used the neck as an anatomical target for our experiments.
Fig. 4.
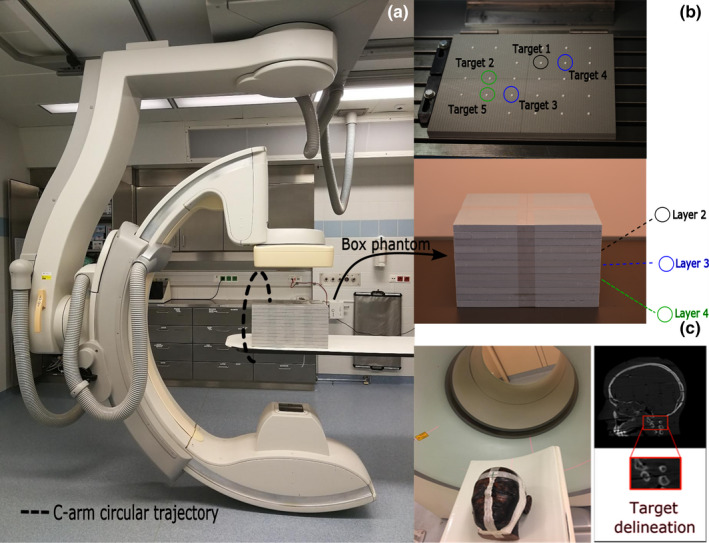
(a) and (b) Philips Allura FD20 Xper C‐arm located at Institute of Diagnostic, Interventional Radiology and Nuclear Medicine, Landesklinikum, Wiener Neustadt, Austria with the box phantom positioned on the patient table showing the relative position of the five spherical targets in different layers of the box phantom to the C‐arm source‐detector trajectory, (c) an Alderson‐Rando head phantom in which the neck area is selected as the VOI. [Color figure can be viewed at wileyonlinelibrary.com]
2.G. Experimental methods
2.G.1. Box phantom experiments
Trajectory optimization simulations
Investigation of the optimized trajectories for spherical targets is accomplished in the simulations using a CT scan (120 kV, 350 mAs, 1 mm3 voxel size, SOMATOM Definition AS, Siemens Healthineers, Erlangen, Germany) of the box phantom. In this study, we used the 3D PSF analysis and considered FWHMavg as the objective function (Section 3D Point spread function (PSF)) in order to investigate the optimized trajectories (Section 2.D) for spherical targets in our simulations.
Physical experiments
The selected optimized trajectories based on simulations (Section Trajectory optimization simulations) were realized with step‐and‐shoot protocol by positioning the C‐arm to each projection angle. We compared the reconstruction results from optimized trajectories with the standard C‐arm circular trajectory. Standard C‐arm circular CBCT scans with the FD20 device include 313 projections and are acquired over a 210° rotation. In order to make an appropriate comparison with optimized trajectories, we reconstructed an image using ASD‐POCS algorithm from the C‐arm circular trajectory (313 projections and 210°) as a ground truth image for our experiments. For each target, we also made a comparison with CBCT image reconstructed from a circular trajectory with equivalent angular sampling as selected for the optimized trajectory. This is called partial circular trajectory in this study. In order to quantify the reconstruction results based on real data, we calculated the values of FWHMX, FWHMY, FWHMZ, and FWHMavg for all sphere targets reconstructed from both optimized and short circular trajectories. We also report the relative deviation of FWHMavg value between reconstructed CBCT from the optimized/short circular trajectories and the C‐arm circular trajectory.
2.G.2. Alderson‐Rando head phantom experiments
Trajectory optimization simulations
In this study, the value of FSIM was used as the objective function [Section Feature SIMilarity Index (FSIM)] in order to investigate the optimized trajectory (Section 2.D) for the neck target (C1/C2 region of the cervical spine) based on our simulations. FSIM is used for comparing the reconstructed CBCT image obtained from the simulated projections and the prior CT (same parameters as described in Section Trajectory optimization simulations). The metric is computed between the two images after cropping both images to include the cervical neck region contained in a 44 × 48 × 52 subset of voxels in the cranial‐caudal, lateral and anterior‐posterior directions.
Physical experiments
Similar to the spherical targets, the selected optimized trajectory based on simulation for the neck target (Section Trajectory optimization simulations) was realized on the C‐arm device. We compared the reconstruction results from optimized trajectory for the neck target based on real data with the standard C‐arm circular trajectory and a short circular trajectory (Section Physical experiments). As with the box phantom, the reconstruction algorithm was kept the same (ASD‐POCS) for reconstructing projections from optimized, C‐arm circular, and short circular trajectories. For the quantitative assessment of the image at the neck target based on the real data, the resultant image was cropped around the same area as the simulations and the three image quality metrics, FSIM, UQI, and CNR (Section 2.E), were used. For FSIM and UQI indexes, the image quality metric was calculated between the C‐arm circular CBCT and the prior CT images from the phantom and was called Reference. Furthermore, the metric value was also computed between reconstructed images from optimized/partial circular trajectory with respect to prior CT image and was called Measured. Image quality was also analyzed using CNR similar to a previous study by considering two small regions in the reconstructed bony and soft parts inside the ROI as signal and background areas, respectively. 30 For this metric, the CNR calculated from reconstructed images related to C‐arm circular CBCT and the optimized/partial circular trajectories was considered as Reference and Measured, respectively. Finally, the relative deviation between the Reference and Measured was computed.
3. RESULTS
3.A. Box phantom results
3.A.1. Trajectory optimization results
The CBCT reconstructed images based on simulations related to the optimized trajectories for all five sphere targets are represented in Fig. 5(a). The selected angulation and the total number of projection views for the optimized trajectories are summarized in Table I. The sign (+) represents rotation to the left/cranial and the sign (−) represents rotation to the right/caudal directions both with respect to the patient reference position. From Table I, we can see some similarity between the selected optimized angles for some targets (arc2 is the same for target 1 and target 5 and arc1 is the same for target 4 and target 5). In spite of these similarities, we observed that a particular trajectory was chosen for each specific target. 3D visualization of the optimized trajectories with respect to the C‐arm circular trajectory as well as a short circular trajectory for all five sphere targets is given in Fig. 6.
Fig. 5.

Reconstruction results for all five sphere targets related to (a) optimized trajectory based on simulation data, (b) optimized trajectory based on real data, (c) standard C‐arm circular trajectory based on real data, and (d) partial circular trajectory based on real data. The display window shows linear attenuation coefficient and is set to the range [200–800] for (a) and gray value range [0–3.5] for (b–d), respectively.
Table I.
The angulations and projection number of the two selected arcs for the optimized trajectories related to all five sphere targets, total of projections number for the final trajectories related to all five sphere targets.
| Trajectory | Arc | Angle | Projection number per arc | Total of projections number |
|---|---|---|---|---|
|
Target 1 Opt. |
Arc 1 | θ1 = −3:2:+67, ψ = +40 | 36 | 67 |
| Arc 2 | θ2 = −28:2:+32, φ = −52 | 31 | ||
|
Target 2 Opt. |
Arc 1 | θ1 = +10:2:+80, ψ = +32 | 36 | 76 |
| Arc 2 | θ2 = −40:2:+38, φ = −32 | 40 | ||
|
Target 3 Opt. |
Arc 1 | θ1 = −90:2:−30, ψ = +14 | 31 | 60 |
| Arc 2 | θ2 = −56:2:0, φ = +6 | 29 | ||
|
Target 4 Opt. |
Arc 1 | θ1 = +10:2:+80, ψ = +34 | 36 | 67 |
| Arc 2 | θ2 = −28:2:+32, φ = −54 | 31 | ||
|
Target 5 Opt. |
Arc 1 | θ1 = +10:2:+80, ψ = +34 | 36 | 67 |
| Arc 2 | θ2 = −28:2:+32, φ = −52 | 31 |
Opt. = optimized.
Fig. 6.
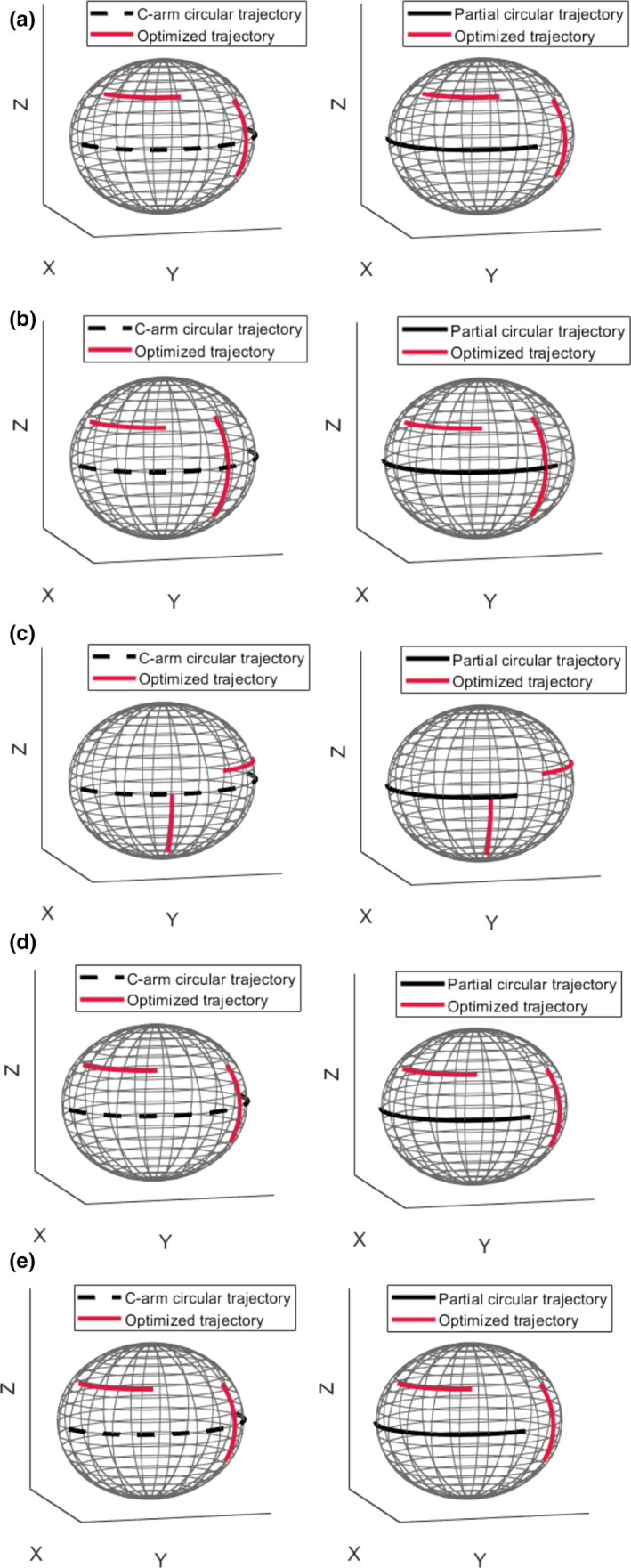
Three‐dimensional visualization of the optimized trajectories with respect to the C‐arm circular and partial circular trajectories for all five sphere targets. Plots a, b, c, d, and e correspond to target 1, 2, 3, 4, and 5, respectively. Black dashed and solid plots represent the C‐arm circular and short circular trajectories, respectively. Red solid plots represent optimized trajectories. [Color figure can be viewed at wileyonlinelibrary.com]
3.A.2. Physical experiment results
Reconstruction results for the optimized, standard C‐arm circular, and short circular trajectories related to all five sphere targets based on real data are shown in Figs. 5(b)–5(d), respectively. As seen from Figs. 5(b) and 5(d), the reconstructed spheres using optimized trajectories show better spatial resolution compared to the partial circular trajectories in almost all targets. The calculated values for FWHMX, FWHMY, FWHMZ, and FWHMavg for all sphere targets and the relative deviation of FWHMavg value (see Section Physical experiments) are presented in Table II. Based on the results, the relative deviation <6.988% was achieved for all sphere targets for the optimized trajectories while a relative deviation up to 7.499% was found for the partial circular trajectories.
Table II.
Values of FWHMX, FWHMY, FWHMZ, and FWHMavg for all five sphere targets for both optimized and short circular trajectories compared to the C‐arm circular trajectory, the relative deviation of FWHMavg value between reconstructed CBCT from the optimized/partial circular trajectories and the C‐arm circular trajectory.
| Trajectory | FWHMx (voxel) | FWHMy (voxel) | FWHMz (voxel) | FWHMavg (voxel) | Relative deviation (%) | |
|---|---|---|---|---|---|---|
| Target 1 | Opt. | 5.404 | 5.513 | 5.330 | 5.415 | 2.907 |
| Partial‐circ. | 5.754 | 5.720 | 5.327 | 5.600 | 6.423 | |
| C‐arm‐circ. | 5.420 | 4.937 | 5.428 | 5.262 | – | |
| Target 2 | Opt. | 5.337 | 5.558 | 5.541 | 5.478 | 4.224 |
| Partial‐circ. | 5.324 | 5.667 | 5.662 | 5.551 | 5.613 | |
| C‐arm‐circ. | 5.096 | 5.409 | 5.262 | 5.256 | – | |
| Target 3 | Opt. | 5.159 | 5.286 | 5.467 | 5.304 | 6.059 |
| Partial‐circ. | 5.496 | 5.404 | 5.205 | 5.368 | 7.339 | |
| C‐arm‐circ. | 5.245 | 4.995 | 4.764 | 5.001 | – | |
| Target 4 | Opt. | 5.647 | 5.494 | 5.616 | 5.586 | 5.595 |
| Partial‐circ. | 5.410 | 5.610 | 5.832 | 5.617 | 6.181 | |
| C‐arm‐circ. | 5.370 | 5.155 | 5.346 | 5.290 | – | |
| Target 5 | Opt. | 5.314 | 5.360 | 5.379 | 5.351 | 6.988 |
| Partial‐circ. | 5.512 | 5.428 | 5.189 | 5.376 | 7.499 | |
| C‐arm‐circ. | 4.890 | 5.082 | 5.031 | 5.001 | – |
Opt. = Optimized, Partial‐circ. = partial‐circular, C‐arm‐circ. = C‐arm‐circular
3.B. Alderson‐Rando head phantom results
3.B.1. Trajectory optimization results
The CBCT reconstructed image based on simulations related to the optimized trajectory for the cervical neck target is represented in Fig. 7(a). The selected angulation and the total number of projection views for the optimized trajectory are reported in Table III. Three‐dimensional visualizations of the optimized trajectory with respect to the C‐arm circular trajectory as well as partial circular trajectory are also given in Fig. 8.
Fig. 7.
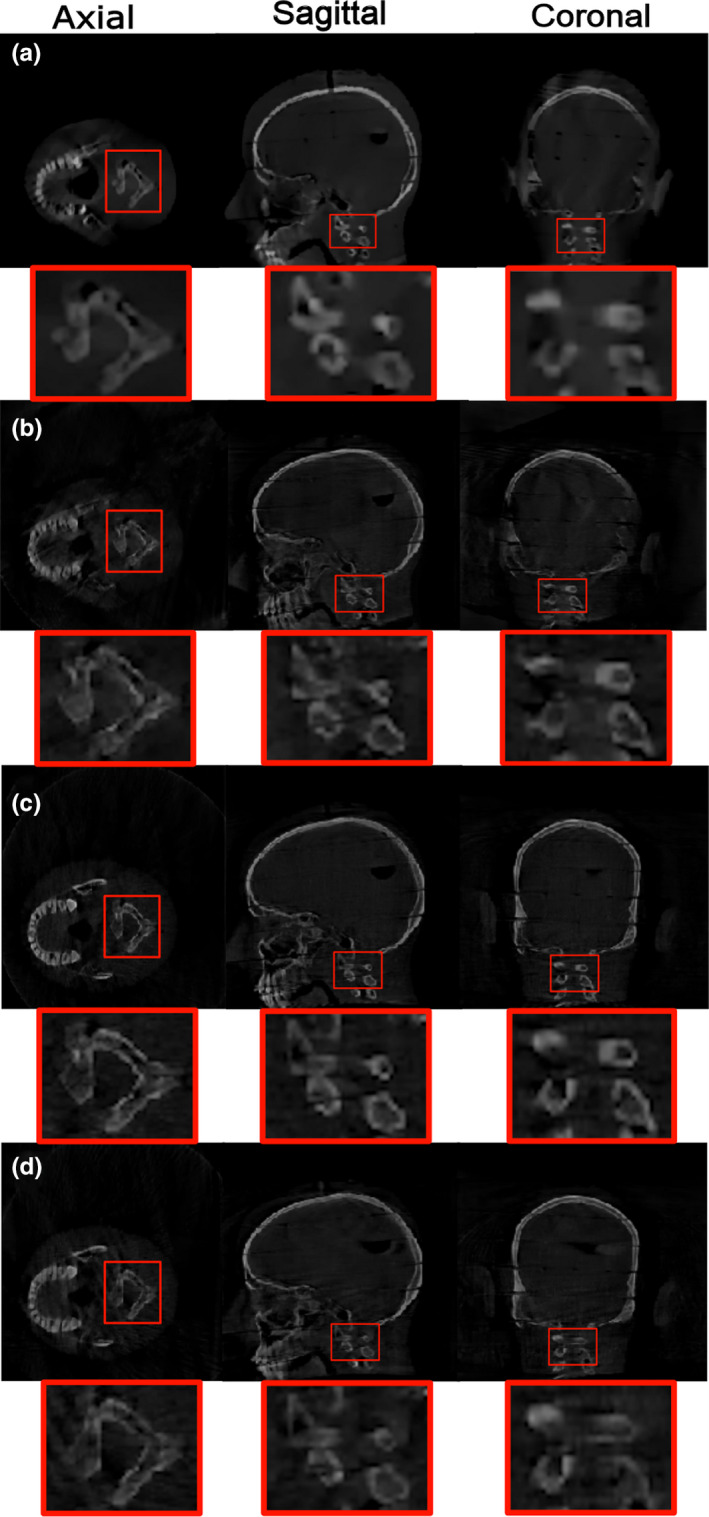
Reconstruction results for the neck target related to (a) optimized trajectory based on simulation data, (b) optimized trajectory based on real data, (c) C‐arm circular trajectory based on real data, and (d) partial circular trajectory based on real data. The display window shows linear attenuation coefficient and is set to the range [600–3000] for (a) and gray value range [0–10] for (b–d), respectively. [Color figure can be viewed at wileyonlinelibrary.com]
Table III.
The angulations and projection number of the two selected arcs for the optimized trajectory related to neck target, total of projections number for the final trajectory related to neck target.
| Trajectory | Arc | Angle | Projection number per arc | Total of projections number |
|---|---|---|---|---|
| Opt. | Arc 1 | θ1 = +44:2:+118, ψ = −6 | 38 | 78 |
| Arc 2 | θ2 = −40:2:+38, φ = −32 | 40 |
Opt. = Optimized.
Fig. 8.
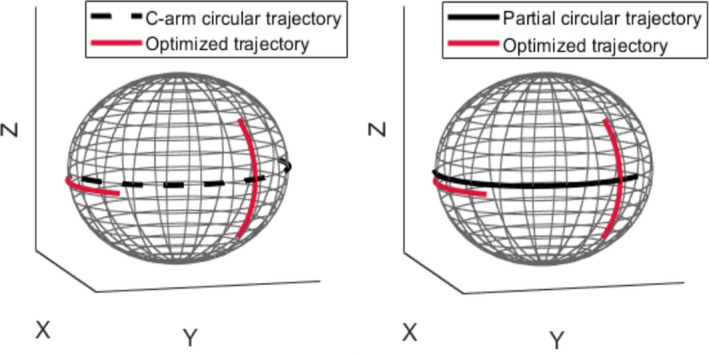
Three visualization of the optimized trajectories with respect to the C‐arm circular and short circular trajectory for the neck target. Black dashed and solid plots represent the C‐arm circular and partial circular trajectories, respectively. Red solid plots represent optimized trajectories. [Color figure can be viewed at wileyonlinelibrary.com]
3.B.2. Physical experiment results
Reconstruction results for the optimized, standard C‐arm circular, and partial circular trajectories related to the neck target based on real data are shown in Figs. 7(b)–7(d), respectively. For the neck target, the optimized trajectory exhibits a good visualization of the neck target as illustrated in Fig. 7(b), while image reconstructed from the short circular trajectory reveals missing structure in the reconstructed VOI specially in the coronal view as shown in Fig. 7(d). The calculated values for Reference and Measured (as explained in Section Physical experiments ) and the relative deviation between the Reference and Measured were computed and presented in Table IV. According to the results, for the reconstructed image related to the optimized trajectory, relative deviation of 5.061, 6.887, and 8.644 was achieved for FSIM, UQI, and CNR, respectively. In addition, for the reconstructed image related to partial circular trajectory, the relative deviation of 7.524, 10.331, and 13.562 was achieved, respectively, for the same three metrics. According to the results, an increased reconstruction performance in the VOI was achieved using the three image quality metrics for optimized trajectory compared to the partial circular trajectory.
Table IV.
Values of image quality measures feature similarity index (FSIM), universal quality image (UQI), and contrast‐to‐noise ratio (CNR) for Reference, Measured, and their relative deviation calculated for the neck target for both optimized and partial circular trajectories.
| Image quality metric | Trajectory | Measured | Reference | Relative deviation (%) |
|---|---|---|---|---|
| FSIM | Opt. | 0.694 | 0.731 |
5.061 7.524 |
| Partial‐circ. | 0.676 | 0.731 | ||
| UQI | Opt. | 0.703 | 0.755 |
6.887 10.331 |
| Partial‐circ. | 0.677 | 0.755 | ||
| CNR | Opt. | 1.839 | 2.013 |
8.644 13.562 |
| Partial‐circ. | 1.740 | 2.013 |
Opt. = Optimized, Partial‐circ. = partial‐circular.
4. DISCUSSION
In this study, we presented a framework for target‐based trajectory design with CBCT imaging systems. The proposed protocol uses information about the imaging target based on a prior CT and incorporates this information into the image acquisition process by optimizing a customized CBCT trajectory. We enable CBCT under kinematic constraints when standard circular trajectories are not feasible. In order to achieve this aim, we optimize out‐of‐plane rotations in 3D space and minimize projection views while providing the highest information content for a specific VOI.
Our results based on both the box and head phantoms demonstrate that optimized trajectories achieve a reasonable image quality with respect to the reference C‐arm circular CBCT for a given VOI while reducing projections. This lower number of projections makes our limited angle noncircular scan orbits suitable for low‐dose CBCT interventions. Still, performing an exact dose measurement for our optimized trajectories compared with the standard C‐arm trajectories is a future perspective of our study. Our results also showed that optimized trajectories could improve the reconstruction performance compared to circular trajectories with equivalent angular sampling in the VOI for all targets.
Typically, an angular range between 116° and 152° was used for optimized trajectories. Compared to the C‐arm CBCT with 210° angular range, our trajectories employ limited angle view data with at least 58° less compared to standard C‐arm CBCT. This makes our proposed trajectories suitable for a limited angle CBCT reconstruction. 31 Moreover, the additional flexibility of incorporating CRA/CAU partial rotations provides the flexibility to perform CBCT under severe kinematic constraints (eg, when large RAO/LAO rotations are not feasible). The possible arbitrary arcs in 3D space, which are accessible, can be determined and incorporated into our optimization protocol and therefore be selected in order to compensate the missing information. In this study, we simulated one forbidden area to investigate the performance of the optimization process. Investigation of the performance of our methods under more complex cases will be subject to further research. The trajectory optimization framework has no special requirements for the trajectories or a fixed isocenter in order to reconstruct the VOI. Therefore, it is evident that inclusion of different source‐detector distances, rotations and translations, and general non‐isocentric trajectories is feasible.
In the current study, optimized trajectories were realized using a step‐and‐shoot protocol by positioning the C‐arm to each projection separately as the proposed methodology assumed a precise positioning of the source and detector. For a clinical implementation, the motion of the C‐arm gantry can lead to gantry wobble; an accurate geometric calibration might prove beneficial in future applications. 32
One other important prerequisite for our work is that our proposed methodology assumes a registered preoperative CT for trajectory optimization design. Hence, a registration step is required to have a practical workflow. This can be done based on some initial projections and 2D/3D registration. 33 , 34 , 35
The proposed trajectory optimization is a time‐consuming process, but as prior image information is assumed to be available, the optimization process can be done offline and therefore does not impact interventional workflow. In this study, trajectory optimization is done in around 80 min. We already have a fast optimization framework, but further improvement is to be expected by using multiple GPUs or other parallelization methods. It is therefore realistic to expect an adaptive and intraoperative trajectory optimization in a couple of minutes. This higher speed also opens perspectives for adding a higher number of arcs and other trajectory shapes to the search space and using more advanced heuristic optimization approaches for the trajectory optimization process.
5. CONCLUSIONS
While traditional approaches ignore the benefit of prior knowledge in the image acquisition process, we propose to integrate the prior information available in interventional images and combine that with target‐based trajectory optimization protocol. Within a realistic clinical scenario, we demonstrated that CBCT under kinematic constraints becomes feasible by applying some limited angle noncircular scan trajectories with a minimal dedicated set of projection angles and optimized orientations in the 3D space.
CONFLICT OF INTEREST
The authors have no conflict to disclose.
ACKNOWLEDGMENTS
This work has been supported by ACMIT — Austrian Center for Medical Innovation and Technology — which is funded within the scope of the COMET program and funded by Austrian BMVIT and BMWFW and the governments of Lower Austria and Tyrol. We also gratefully acknowledge the support of NVIDIA Corporation for the donation of Titan Xp GPU used for this research. The support from the personnel of the Institute of Diagnostic, Interventional Radiology and Nuclear Medicine, Landesklinikum, Wiener Neustadt, Austria to perform measurements is also gratefully appreciated.
REFERENCES
- 1. Akpek S. Three‐dimensional imaging and cone beam volume CT in C‐arm angiography with flat panel detector. Diagn Interv Radiol. 2005;11:10–3. [PubMed] [Google Scholar]
- 2. Orth R. C‐arm cone‐beam CT: general principles and technical considerations for use in interventional radiology. J Vasc Interv Radiol. 2008;19:814–820. [DOI] [PubMed] [Google Scholar]
- 3. Czerny CH, Eichler K, Croissant Y, et al. Combining C‐arm CT with a new remote operated positioning and guidance system for guidance of minimally invasive spine interventions. J NeuroIntervent Surg. 2015;7:303–308. [DOI] [PubMed] [Google Scholar]
- 4. Kettenbach J, Kronreif G. Robotic systems for percutaneous needle‐guided intervention. Minim Invasiv Ther. 2015;24:45–53. [DOI] [PubMed] [Google Scholar]
- 5. Floridi C, Radaelli A, Abi‐Jaoudeh N, et al. C‐arm cone‐beam computed tomography in interventional oncology: technical aspects and clinical applications. Radiol Med. 2014;119:521–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Davis AM, Pearson EA, Pan X, Pelizzari CA, Al‐Hallaq H. Collision‐avoiding imaging trajectories for linac mounted cone‐beam CT. J Xray Sci Technol. 2019;27:1–16. [DOI] [PubMed] [Google Scholar]
- 7. Meng B, Xing L, Han B, Koong A, Chang D, Cheng J, Li R. Cone beam CT imaging with limited angle of projections and prior knowledge for volumetric verification of non‐coplanar beam radiation therapy: a proof of concept study. Phys Med Biol. 2013;58:7777–7789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Stayman JW, Siewerdsen JH. Task‐based trajectories in iteratively reconstructed interventional cone‐beam CT. The 12th Int'l Mtg. Fully 3D Image Recon. in Radiology and Nuc. Med., Lake Tahoe, June 16–21; 2013.
- 9. Gang GJ, Stayman JW, Ehtiati T, Siewerdsen JH. Task‐driven image acquisition and reconstruction in cone‐beam CT. Phys Med Biol. 2015;60:3129–3150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Fischer A, Lasser T, Schrapp M, Stephan J, Noël PB. Object specific trajectory optimization for industrial x‐ray computed tomography. Sci Rep. 2016;6:19135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Stayman JW, Capostagno S, Gang GJ, Siewerdsen JH. Task‐driven source–detector trajectories in cone‐beam computed tomography: I. Theory and methods. J Med Imaging. 2019;6:025002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Capostagno S, Stayman JW, Jacobson M, Ehtiati T, Weiss CR, Siewerdsen JH. Task‐driven source–detector trajectories in cone‐beam computed tomography: II. Application to neuroradiology. J Med Imaging. 2019;6:025004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Biguri A, Dosanjh M, Hancock S, Soleimani M. TIGRE: a MATLAB‐GPU toolbox for CBCT image reconstruction. Biomed Phys Eng Express. 2016;2:055010. [Google Scholar]
- 14. Je Uikyu, Cho Hyosung, Lee Minsik. Dental cone‐beam CT reconstruction from limited‐angle view data based on compressed‐sensing (CS) theory for fast, low‐dose X‐ray imaging. J Korean Phys Soc. 2014;64:1907–1911. [Google Scholar]
- 15. Sidky EY, Pan X, Reiser IS, Nishikawa RM, Moore RH, Kopans DB. Enhanced imaging of microcalcifications in digital breast tomosynthesis through improved image‐reconstruction algorithms. Med Phys. 2009;36:4920–4932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Xu F, Helfen L, Baumbach T, Suhonen H. Comparison of image quality in computed laminography and tomography. Opt Express. 2012;20:794–806. [DOI] [PubMed] [Google Scholar]
- 17. Hatamikia S, Biguri A, Kronreif G, Furtado H, Kettenbach J, Figl M, Birkfellner W. Source‐detector trajectory optimization for C‐arm CBCT. Supplement of the International Journal of CARS (IJCARS), June 18 – 21; 2019, Rennes, France.
- 18. Zhang Z, Han X, Bian J, Manak J, Sidky EY, Pan X. Initial Experience in Image Reconstruction from Limited‐angle C‐arm CBCT Data. IEEE Nuclear Science Symposium Conference. Record; 2011:3977–3979.
- 19. Chou CY, Chuo YY, Hung Y, Wang W. A fast forward projection using multithreads for multirays on GPUs in medical image reconstruction. Med Phys. 2011;38:4052–4065. [DOI] [PubMed] [Google Scholar]
- 20. Hatamikia S, Biguri A, Kronreif G, Kettenbach J, Birkfellner W. CBCT reconstruction based on arbitrary trajectories using TIGRE software tool. Proceeding of the 19th joint conference on new technologies for Computer/Robot Assisted Surgery (CRAS); 2019, 21‐22 March, Genoa, Italy.
- 21. Pio R. Euler angle transformations. IEEE Trans Autom. 1966;11:707–715. [Google Scholar]
- 22. Sidky EY, Pan X. Image reconstruction in circular cone‐beam computed tomography by constrained, total‐variation minimization. Phys Med Biol. 2008;53:4777–4807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Sidky EY, Kao KM, Pan X. Accurate image reconstruction from few‐views and limited‐angle data in divergent‐beam CT. J X‐Ray Sci Technol. 2009;14:119–139. [Google Scholar]
- 24. Lohvithee M, Biguri A, Soleimani M. Parameter selection in limited data cone‐beam CT reconstruction using edge‐preserving total variation algorithms. Phys Med Biol. 2017;62:9295–9321. [DOI] [PubMed] [Google Scholar]
- 25. Bian J, Siewerdsen JH, Han X, Sidky EY, Prince JL, Pelizzari CA, Pan X. Evaluation of sparse‐view reconstruction from flat‐panel‐detector cone beam CT. Phys Med Biol. 2010;55:6575–6599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Chen Z, Ning R. Three‐dimensional point spread function measurement of cone‐beam computed tomography system by iterative edge‐blurring algorithm. Phys Med Biol. 2004;49:1865–1880. [DOI] [PubMed] [Google Scholar]
- 27. Zhang L, Zhang L, Mou X, Zhang D. FSIM: a feature similarity index for image quality assessment. IEEE Trans Image Process. 2011;20:2378–2386. [DOI] [PubMed] [Google Scholar]
- 28. Wang Z, Bovik A. A universal image quality index. IEEE Signal Proc Lett. 2002;9:81–84. [Google Scholar]
- 29. Bechara B, McMahan CA, Moore WS, Noujeim M, Geha H, Teixeira FB. Contrast‐to‐noise ratio difference in small field of view cone beam computed tomography machines. J Oral Sci. 2012;54:227–232. [DOI] [PubMed] [Google Scholar]
- 30. Vaegler S, Stsepankou D, Hesser J, Sauer O. Incorporation of local dependent reliability information into the prior image constrained compressed sensing (PICCS) reconstruction algorithm. Zeitschrift für Medizinische Physik. 2015;25:375–390. [DOI] [PubMed] [Google Scholar]
- 31. Hatamikia S, Biguri A, Kronreif G, Russ T, Kettenbach J, Birkfellner W. Short scan source‐detector trajectories for target‐based CBCT. IEEE Engineering in Medicine and Biology Conference (IEEE EMBC), Montreal, Canada, July 20–24, 2020. [DOI] [PubMed]
- 32. Ouadah S, Stayman JW, Gang GJ, Ehtiati T, Siewerdsen JH. Self‐calibration of cone‐beam CT geometry using 3D–2D image registration. Phys Med Biol. 2016;61:2613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Birkfellner W, Stock M, Figl M, et al. Stochastic rank correlation: a robust merit function for 2D/3D registration of image data obtained at different energies. Med Phys. 2009;36:3420–3428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Birkfellner W, Figl M, Furtado H, Rennes A, Hatamikia S, Hummel J. Multi‐modality imaging: a software fusion and image‐guided therapy perspective. Front Phys. 2018;6: 1–12. 10.3389/fphy.2018.00066 [DOI] [Google Scholar]
- 35. Furtado H, Gendrin C, Spoerk J, et al. FIRE: an open‐software suite for real‐time 2D/3D image registration for image guided radiotherapy research. In Proceedings Volume 9784, Medical Imaging 2016: Image Processing, 978449; 2016. 10.1117/12.2216082 [DOI]


