Abstract
Purpose:
To develop a simultaneous T1, T2, and apparent diffusion coefficient mapping method that provides co-registered, distortion-free images and enables multi-parametric quantification of 3D brain coverage in a clinically feasible scan time with the MR Multitasking framework.
Methods:
T1-T2-diffusion weighting was generated by a series of T2-preparations and diffusion-preparations. The underlying multidimensional image containing 3 spatial dimensions, 1 T1 weighting dimension, 1 T2-preparation duration dimension, 1 b-value dimension, and 1 diffusion direction dimension was modeled as a 5-way low-rank tensor. A separate real-time low-rank model incorporating time-resolved phase correction was also used to compensate for both inter- and intra-shot phase inconsistency induced by physiological motion. The proposed method was validated on both phantom and 16 healthy subjects. The quantification of T1/T2/ADC was evaluated for each case. Three post-surgery brain tumor patients were scanned for demonstration of clinical feasibility.
Results:
Multitasking T1/T2/ADC maps were perfectly co-registered and free from image distortion. Phantom studies showed substantial quantitative agreement (R2 = 0.999) with reference protocols for T1/T2/ADC. In vivo studies showed nonsignificant T1 (P=0.248), T2 (P=0.097), ADC (P=0.328) differences between frontal, parietal, and occipital regions. Despite Multitasking showed significant differences of T1 (P=0.03), T2 (P<0.001), and ADC (P=0.001) biases against the references, the mean bias estimates were small (ΔT1% < 5%, ΔT2% < 7%, ΔADC% < 5%), with all intraclass correlation coefficients >0.82 indicating “excellent” agreement. Patient studies showed that Multitasking T1/T2/ADC maps were consistent with the clinical qualitative images.
Conclusion:
The Multitasking approach simultaneously quantifies T1/T2/ADC with substantial agreement with the references and is promising for clinical applications.
Keywords: simultaneous T1/T2/ADC quantification, MR Multitasking, low-rank tensor imaging, time-resolved phase correction, co-registered and distortion-free mapping
Introduction
Quantitative multi-parametric mapping of relaxation and diffusion has the potential for comprehensive tissue characterization, which is clinically promising for the identification, diagnosis, and follow-up assessment of brain, breast, cardiac, prostate diseases, and more. For example, mapping the relaxation parameters T1 and T2 is promising for monitoring tumors in glioblastoma patients and brain tumor characterization1-4. T1/T2 mapping has also been used to diagnose cardiac diseases, including myocardial fibrosis, myocarditis, and chronic myocardial infarction5-9. The quantification of diffusion parameters, e.g., ADC, not only differentiates normal brain tissue and brain tumors10, but also contributes to brain tumor characterization11 and may also be useful in grading astrocytic tumors12,13. Furthermore, ADC is promising for monitoring treatment response of breast cancer14-16 and has been well established as a key role in the detection and assessment of prostate cancer17.
Although there are significant clinical benefits of quantifying multiple relaxation and diffusion parameters, T1/T2/ADC mapping are typically performed in separate scans which are not only time-consuming, but also subject to intra-scan mis-registrations due to subject motion. Additionally, the clinical DWI scans used to map ADC mostly adopt single-shot multi-slice EPI acquisition, leading to image distortion and additional challenges in image registration. Simultaneous T1/T2/ADC mapping approaches that produce distortion-free, co-registered maps would be vastly desirable in the clinic.
Joint T1/T2 mapping has recently been achieved using MR Fingerprinting18, which has been validated in many clinical applications including brain tumor and prostate cancer1,19. Our group has recently developed a quantitative imaging framework, MR Multitasking, which allows motion-resolved or motion-robust quantitative imaging, including joint T1/T2 mapping, but has yet to be used to quantify ADC20,21. Joint T1/T2/ADC mapping methods have also been proposed, such as the dual-echo-steady-state (DESS) protocol22. However, DESS can be significantly sensitive to physiological motion because it relies on the gradients that are placed within each TR to generate diffusion contrast. MR-Fingerprinting-based23 and stimulated-echo-based (STEM)24 approaches are also proposed. However, these methods do not provide a comprehensive quantification of ADC because they only measure diffusion along a single direction. Hutter et al. proposed an integrated approach (ZEBRA)25 to quantify T1/T2*/ADC simultaneously which demonstrated the efficiency and sampling flexibility but employed single-shot EPI readout that may suffer from B0-inhomogeneity which compromises high resolution image quality and leads to image distortion.
In this work we extend the MR Multitasking framework to achieve a 3D simultaneous brain T1/T2/ADC mapping in <10min which is a feasible duration for clinical practice. This augmentation of the MR Multitasking framework conceptualizes the overlapping image dynamics to be quantified as different temporal dimensions20 and uses a low-rank tensor (LRT) model26 to accelerate imaging by exploiting the high spatiotemporal correlation of images corresponding to different T1 weightings, T2-preparation (T2prep) durations, b-values and diffusion directions. A time-resolved phase correction technique, which is allowed by the high temporal resolution of the Multitasking framework, is applied along with a separate “real-time” low-rank matrix imaging model to compensate for both inter- and intra-shot phase inconsistencies resulting from physiological motion and/or eddy currents, by modeling the phase inconsistencies in a time-resolved phase map27-29. We demonstrate that the proposed method enables fully quantitative T1/T2/ADC mapping of the brain with clinically acceptable image resolution (1.5x1.5x5mm3) and scan time (<10min).
Methods
Sequence Design
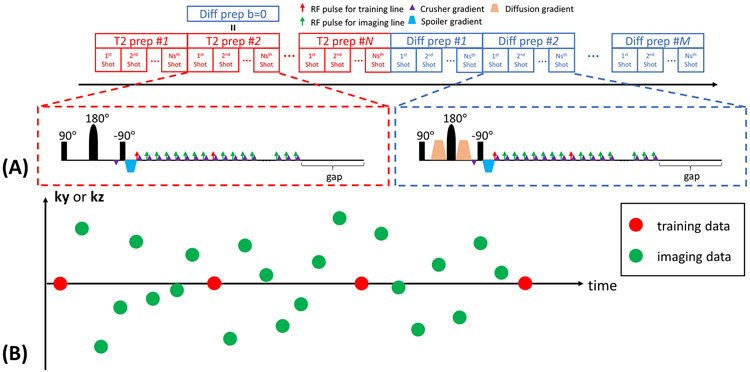
In this work, we generate multiple T1-T2-diffusion weighting by concatenating a series of T2preps with different durations τ and a series of diffusion-preparations with a fixed duration but different b-values b and diffusion directions d (Figure 1A). The duration of one of the T2preps matches the duration of the diffusion-preparations, so that this T2prep also serves as a b=0 diffusion-preparation. For all the diffusion-preparations, two unipolar diffusion-weighted gradients are placed on each side of the 180° adiabatic refocusing pulse. A 3D segmented FLASH readout is used to sample the k-space data.
Figure 1.
(A) The sequence diagram of the Multitasking framework. A series of T2preps with different durations are concatenated with a series of diffusion-preparations with different b-values and directions. The duration of one of the T2prep matches the duration of the diffusion prep, so that this T2prep also serves as a b=0 diffusion prep. The crusher gradient scheme is used to avoid tipping inconsistent phase errors onto the longitudinal magnetization and maintain the magnitude consistency by complete dephasing before the tip-up pulse and subsequent rephasing immediately before each readout. A 3D segmented FLASH readout is used for data acquisition. A gap is placed immediately prior to each preparation to allow sufficient signal recovery. (B) The k-space sampling illustration. Imaging data are collected using 3D random Cartesian trajectory with Gaussian variable density along phase encoding (ky) and partition encoding (kz) direction. Subspace training data are collected every 8 readouts for temporal subspace estimation.
The magnetization preparation module uses a 90° tip-up pulse to store the prepared signal in the longitudinal magnetization. The accumulated phase generated by the preparation will also be tipped onto z-axis, adding a cosine term to the magnitude. In practice, even two identical preparations may generate different phase patterns because of physiological motion and bulk motion, which is especially common for diffusion-preparations30. Consequently, such inconsistent phase patterns would convert to magnitude inconsistency that can never be recovered30,31. We employ a crusher gradient scheme that has been proposed to address this issue30-34. An 8π crusher gradient is placed immediately before the 90° tip-up pulse to completely dephase the transverse magnetization, creating a uniform phase dispersion. The same crusher gradient with opposite polarity is placed immediately after each FLASH pulse to rephase the transverse magnetization that was stored in the z-axis and encoded with the phase of the preparation, and to remove the longitudinal magnetization that arises from free relaxation, thus forming the echo that retains the phase of the preparation and maintains the magnitude consistency31. However, the penalty of using the crusher gradient scheme is a loss of SNR because the spoiler gradient removes half of the overall signal (those remaining in the transverse plane), and the longitudinal magnetization that contributes to the echo formulation (those encoded with the phase of the preparation) follows a monotonic T1 decay34. To counteract this loss in SNR, we add a gap in acquisition immediately prior to each preparation, to allow sufficient signal recovery of long-T1 tissues towards thermal equilibrium. The resulting signal equations after T2preps and diffusion-preparations are:
| (1) |
and
| (2) |
respectively, where A absorbs overall coil sensitivity, proton density and T2* weighting, n is the readout index (resetting with each preparation pulse) indicating different T1 weightings, α is the FLASH flip angle, D represents the diffusion coefficient associated with d. Derivation of the signal equation is in the Supporting Information Section A. By employing the crusher gradient scheme, the magnitude consistency is guaranteed. Some shot-to-shot phase inconsistency still remains, which we address in our proposed imaging model.
Imaging Model
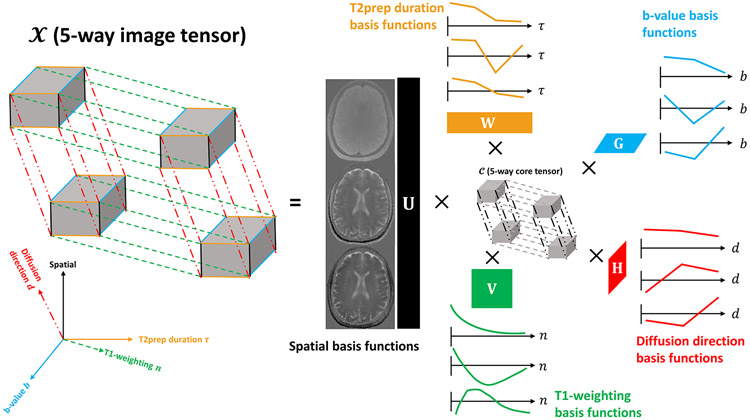
We propose to use the Multitasking framework to represent the underlying image as a 7D function x(r, n, τ, b, d), with three spatial dimensions (i.e., voxel location r = [x, y, z]) and four dimensions indexing the four timing/parameter variables n, τ, b, and d respectively. We can further represent x as a 5-way tensor with the first dimension concatenating all voxel locations r, and the other four dimensions indexing the four timing/parameter variables (Figure 2). This tensor is low-rank due to high spatiotemporal correlation throughout x, resulting in the partially-separable26,35,36 image function:
| (3) |
| (4) |
where , , , , and represent spatial, T1, T2, b-value and diffusion direction basis functions; J, K, L, M, N represents the number of basis functions for each dimension; cjklmn are the elements of the core tensor governing the interaction between different basis functions; and the functions span the multi-dynamic subspace (as they describe the multiple dynamic processes of T1 relaxation, T2 relaxation, and diffusion). This LRT structure can be explicitly expressed through matrix factorization as:
| (5) |
| (6) |
where X(1) and C(1) are the mode-1 matricizations of and , respectively; where the columns of U, V, W, G, H are basis functions spanning the spatial, T1, T2, b-value and diffusion direction subspaces, respectively; and where the J rows of Φ span the multi-dynamic subspace. Modeling the image as an LRT significantly reduces the degrees of freedom, offering considerable potential for accelerated acquisition.
Figure 2.
Illustration of multiple temporal dimensions of the 5-way low-rank tensor for simultaneous T1, T2, and ADC mapping. The 5-way image tensor contains spatial, T1-weighting, T2prep duration, b-value and diffusion direction dimensions. The low-rank tensor structure can be explicitly expressed through tensor factorization between 5 sets of basis functions assigned to each dimension and the 5-way core tensor governing the interaction between different basis functions. Here only the three most significant basis functions describing each dimension of the tensor are provided.
In practice, (k, t)-space data are collected with a single “real-time” dimension t from an underlying image xrt(r, t) = p(r, t)x(r, n(t), τ(t), b(t), d(t)), which experiences phase inconsistencies over time, as modeled by a unit-magnitude phase map p(r, t). Note that the functions n(t), τ(t), b(t), and d(t) describe the timing/parameter schedule throughout the experiment. Low-rank structure of xrt in the so-called “real-time” domain can also be expressed, as:
| (7) |
where Xrt is the image matrix corresponding to xrt(r, t); where the J′ rows of Φrt span the real-time subspace (as they describe the continuous dynamic processes of the measured signals); and where the J′ columns of Urt span the spatial subspace containing the real-time image. We note that because Xrt includes the contribution of phase inconsistencies over time, whereas and X(1) do not, Eqs. (5) and (7) represent two different image models, both of which will be useful during different stages of image reconstruction.
Phase inconsistencies reduce image correlation and increase image rank27, so the real-time subspace is generally higher-dimensional than the multi-dynamic subspace, i.e., J′ > J. Here, the time-resolved, unit-magnitude phase map p(r, t) is represented in matrix form as , where Nv and Nt denote the number of voxels and number of time stamps respectively, similarly to what we previously proposed for cardiac diffusion tensor imaging27. The approximation connecting the real-time subspace model and the multi-dynamic subspace model is therefore:
| (8) |
where ∘ denotes Hadamard (elementwise) multiplication. The multi-dynamic to real-time reordering matrix is where Nn, Nτ, Nb, Nd denotes the total number of T1-weightings, T2prep durations, b-values and diffusion directions, respectively. Rjk is equal to 1 if the (n, τ, b, d) sequence parameter combination corresponding to the j-th column of X(1) was collected by the k-th readout and equal to 0 otherwise.
K-Space Sampling
We acquire two sets of data for LRT image reconstruction, namely, subspace training data (dtr) used to estimate Φ, and imaging data (dimg) used to determine U (Figure 1B). The imaging data are collected using a 3D Cartesian trajectory with Gaussian random variable density along the phase encoding direction (ky) and partition encoding direction (kz) to increase sampling incoherence. The subspace training data are frequently collected at the k-space center line (i.e., ky = kz = 0) every 8 readouts to capture the overlapping image dynamics containing T1 weightings, T2prep durations, b-values and diffusion directions.
Image Reconstruction
In this work we augment the reconstruction strategy described in the original MR Multitasking framework20 with an additional time-resolved phase correction component. We propose to serially estimate P, Φ and U following four steps:
1) Estimate a heuristic P: The time-resolved phase map P is estimated from I0, a preliminary least-squares reconstruction enforcing the real-time subspace model (i.e., Eq. (7)):
| (9) |
where the real-time temporal basis functions Φrt,0 are estimated from the singular value decomposition (SVD) of the subspace training data drt, Ω denotes the undersampling operator, F performs Fourier encoding, and S represents the coil sensitivity matrix.
2) Pre-determine heuristic T1 decay basis functions : Because the T1 relaxation is physically governed by the Bloch equations, a set of feasible signal curves following a T1 decay pattern can be pre-determined ahead of time to generate a T1 relaxation training dictionary37-39 using a range of T1 values and flip angles. Specifically, we use 101 T1 values logarithmically spaced from 100ms to 3000ms, and 15 FLASH flip angles equally spaced from 0.5° to 7.5° representing 90% underestimation to 50% overestimation of the prescribed flip angle covering a possible range of B1 inhomogeneities. A total of 1515 T1 decay signal curves are generated to construct a training dictionary, the SVD of which produces the T1 decay basis functions in V.
3) Estimate a heuristic multi-dynamic Φ: In the original MR Multitasking framework, the subspace training data dtr are binned (i.e., mapped from the real-time domain to the multi-dynamic domain) to form a training tensor 20. However, in this work, naively mapping dtr from the real-time (k, t)-space to the multi-dynamic (k, n, τ, b, d)-space without accounting for the inconsistent phase patterns would result in signal cancellation in . As an alternative, we use features extracted from the real-time magnitude images ∣I0∣ as the new subspace training data, i.e., we define a matrix of training data from the J′ > J most significant right singular vectors of ∣I0∣. The training tensor can be solved via a Bloch-constrained small-scale LRT completion problem:
| (10) |
where ∥·∥F denotes the Frobenius norm, ∥·∥* denotes the nuclear norm, λ is the regularization parameter weighting the nuclear norm penalties, Dtr,(n) denotes the mode-n matricization of , and R(·) is a regularization function which in this work, penalizes total variation (TV) along the diffusion direction dimension. Once is completed, Φ = C(1)(H ⊗ G ⊗ W ⊗ V)T can be quickly extracted from via the high-order SVD (HOSVD)40.
4) Obtain the spatial coefficient maps U. With the heuristic P and Φ, the remaining unknown U could in principle be directly recovered by incorporating the phase correction into the multi-dynamic imaging model (i.e., Eq. (5)):
| (11) |
where Rs(·) is an optional additional spatial constraint, e.g., which also leverages compressed sensing. However, solving this iterative optimization problem directly as posed above would involve storing and manipulating many real-time Nv × Nt matrices—not just P but also auxiliary variables used during optimization—and can therefore require large amounts of memory.
In practice, rather than solving Eq. (11), we instead solve an alternative optimization problem that additionally relies on the memory-efficient image model in Eq. (7). We first enforce the real-time subspace model to obtain a phase-varying Φrt (which incorporates some phase variation from P) and Urt, then we obtain U by mapping the result back to the multi-dynamic subspace model according to Eq. (8). This is achieved via three sub-steps:
4.1) Map Φ back to the phase-varying real-time subspace by incorporating phase information from P into a heuristic Φrt. Note that as is, Φ lies in the phase-corrected multi-dynamic domain, which is free from phase inconsistencies. We first map Φ onto the phase-corrected real-time subspace as ΦR, then we project the phase-free ∣I0∣ onto this subspace. This provides the best approximation of the initial magnitude image in the phase-corrected real-time subspace:
| (12) |
where + denotes the pseudoinverse. We then apply the time-resolved phase map P to include the phase-varying information, and finally calculate the SVD of the resulting phase-varying real-time image, i.e.,
| (13) |
This new basis Φrt reflects the phase inconsistencies in the real-time subspace as well as the multi-dynamic modeling performed in step (3).
4.2) Recover Urt using the real-time subspace model (i.e., Eq. (7)). With heuristic Φrt, the coordinates in the phase-varying real-time subspace, Urt, can be recovered as:
| (14) |
which without the explicit phase map can be entirely solved in the J′-dimensional real-time subspace rather than the much more memory-intensive (r, t)-space, due to the block diagonal structure of 41,42. Here Rs(·) is chosen as a spatial TV penalty.
4.3) Obtain U. We map the spatial coefficients from the J′-dimensional phase-varying real-time subspace to the J-dimensional phase-corrected multi-dynamic subspace, i.e., Urt → U. This mapping is based on Eq. (8), and is performed as:
| (15) |
Note that Eq. (15) relies on both image models described in Eq. (5) and Eq. (8), whereas Eq. (11) only uses the multi-dynamic image model described in Eq. (5). Eq. (15) therefore does not directly approximate Eq. (11), but rather finds alternative coordinates in the phase-corrected multi-dynamic subspace by a mapping from coordinates in the phase-varying real-time subspace.
The operations in Eqs. (12) and (15) map between two distinct image models: the multi-dynamic subspace model and the phase-varying real-time subspace model. A solution satisfying both models typically only exists when J′ is selected high enough to fully represent the phase variation in p(r, t); however, for lower values of J′ as used in practice, a solution exactly satisfying both models may not exist, and the mappings in Eqs. (12) and (15) modify the solution. A detailed mapping analysis can be seen in the Supporting Information Section B.
Phantom Study
To evaluate the T1/T2/ADC mapping accuracy of the proposed method, an ISMRM/NIST T1/T2 phantom (Model 130, High Precision Devices) and a diffusion phantom (Model 128, High Precision Devices) were scanned on a 3T scanner (MAGNETOM Vida, Siemens Healthineers) using a 64-channel head coil. Because the T1/T2 phantom lacked ADC variety, we performed ADC mapping on the diffusion phantom as well. Reference T1/T2/ADC maps were obtained via an inversion recovery turbo spin echo (IR-TSE) sequence, a multi-echo spin echo (ME-SE) sequence and a single-shot EPI (SS-EPI) sequence, respectively. The Multitasking sequence was implemented with 7 T2preps and 6 diffusion-preparations. Each preparation is repeated 10 times before the next preparation is implemented. The detailed imaging protocol is in Supporting Information Table S1.
In vivo Study
The in vivo study was approved by the institutional review board (IRB) of our institute. All volunteers/patients gave written informed consent before the study. Sixteen healthy volunteers were recruited and were scanned also on Vida scanner. Localizers were implemented to locate the volume of interest which covered from the top of the brain to the pons. Reference T1/T2/ADC maps were obtained via IR-TSE, ME-SE, and SS-EPI respectively. The total scan time of references was 19min. The Multitasking sequence was implemented with 4 T2preps and 6 diffusion-preparations. Each preparation is repeated 20 times before the next preparation is implemented, resulting in a total scan time of 9.3min. The approximately maximum diffusion encoding gradient amplitude (55mT/m) was turned on to shorten the diffusion-preparation duration (31.4ms) for SNR purposes. The slice positions of all scans matched exactly. The detailed imaging protocol is in Supporting Information Table S1.
In addition, 3 post-surgery patients who were previously diagnosed with a brain tumor and were likely to possess residual/recurrent tumor were scanned on a 3T scanner (MAGNETOM Skyra, Siemens Healthineers) using a 20-channel head coil. The Multitasking scan was incorporated in a clinical brain MRI scan aimed for follow-up assessment before the administration of contrast agents. The clinical protocols included pre-contrast T1-MPRAGE, pre-contrast T2-FLAIR, DWI (RESOLVE), post-contrast T2-TSE, and post-contrast T1-MPRAGE. A relaxed diffusion gradient amplitude (35mT/m) was used to protect the gradient system, resulting in a 39.6ms diffusion-preparation duration.
Exploration of Motion Effects
Head movement is commonly seen during clinical scans because of patient discomfort, which will lead to mis-registration or image artifacts if not properly addressed. Furthermore, the bulk motion will not only affect the magnetization preparation, but also damage the refocusing crusher gradients, resulting in uncorrelated signal or significant signal loss.
We explored the motion effects on our method in four healthy volunteers. For each volunteer, a motion-free scan was performed followed by a motion-corrupted scan. A sticker was placed on the inside of the coil right on top of the subject’s nose to fix the initial position. The motion-free scan contained one Multitasking protocol (9.3min), during which the subject was clearly instructed not to move their head. The motion-corrupted scan contained two consecutive Multitasking protocols (18.6min) to span the scan duration so that the subject was likely to move multiple times. The subject was instructed beforehand that he/she could move at will during the motion-corrupted scan, meaning that he/she could perform any type of motion (e.g., itching face, adjusting head position, deep breath, etc.) at any time, instead of being instructed to perform only certain types of motion at certain times explored in Fingerprinting studies43,44. This aimed to mimic realistic motion scenario in an actual clinical scan. There are many options for motion handling in the Multitasking framework, including motion-removed imaging, motion-resolved imaging, and motion-compensated imaging. In this study, we performed motion removal to simplify data processing, so the subjects were asked to return to the initial position after each movement.
The motion-free data were reconstructed as a reference. For each of the two motion-corrupted datasets, we identified the amount of corrupted data based on the real-time image series I0 via manual inspection. Specifically, within each motion-corrupted dataset, all the shots that were observed with the occurrence of motion artifacts were considered motion-corrupted. The percentage of the corrupted data was thus:
| (16) |
where Nm,i is the number of motion-corrupted shots in the i-th motion-corrupted dataset. We only reconstruct the -th dataset, where (i.e., the worse of the two motion-corrupted datasets). Motion removal was performed by removing all shots in the -th dataset from dtr and dimg along with the corresponding sampling locations from Ω and R.
Image Analysis
All the reconstructions were performed on a Linux workstation with a 2.70GHz dual 12-core Intel Xeon processor equipped with 256GB RAM and running MATLAB 2017a. Reconstruction parameters (rank of respective dimensions, λ, etc.) are in Supporting Information Table S2. In this work, the λ used to weight the nuclear norm penalties was chosen based on the discrepancy principle45 for one dataset and then used for all datasets. The ranks of the spatial and T1-weighting dimensions were determined from the −40dB threshold on the normalized singular value curves of the training dictionary and the full training data respectively. The ranks of the T2prep duration, b-value, and diffusion direction dimensions were not truncated, as the nuclear norm low-rank constraint implemented for the training tensor completion already performed a soft constraint on the tensor ranks for those dimensions.
For each healthy subject, 3 slices located in the upper, mid, and lower regions of the acquired 3D volume were chosen for voxel-by-voxel multi-parametric fitting of A, α, T1, T2, and the diffusion coefficients of 3 directions D1, D2 and D3 based on Eq. (1)-(2). ADC is then derived by:
| (17) |
For qualitative analysis, the following comparisons were made:
The proposed method versus no phase correction (i.e., assuming P = I and using dtr directly for tensor subspace estimation) to evaluate the effectiveness of the proposed phase correction strategy.
The proposed method versus reference protocols to evaluate quantification.
Motion-free maps, motion-corrupted maps and motion-removed maps to evaluate the motion effect and the behavior of motion removal.
For quantitative analysis, 12 ROIs were drawn on the frontal, parietal, and occipital regions of the gray matter (GM) and white matter (WM) of both left and right hemispheres of the mid slice46. ROIs of the reference protocols and the Multitasking protocol were drawn at the same locations.
For each patient, the surgery/tumor region was manually identified on the standard clinical protocols. Three slices surrounding the surgery/tumor region were chosen for the multi-parametric fitting and were compared with the standard clinical protocols on approximately matched slice positions.
Statistical Analysis
T1/T2/ADC values of the GM and WM of frontal, parietal, and occipital regions were calculated as the mean values of the corresponding ROIs of the left and right lobes. A three-way repeated measures ANOVA was performed using IBM SPSS Statistics. Specifically, the two tissue types, the three regions and the two methods are all set as within subject variables. The significance level was set as P<0.05. Intra-class correlation coefficient (ICC) was calculated using IBM SPSS Statistics with a two-way mixed model and a confidence level of 95% to demonstrate the consistency between Multitasking and the references. Bland-Altman analysis was performed between Multitasking and the references to demonstrate the bias.
Results
Phantom Study
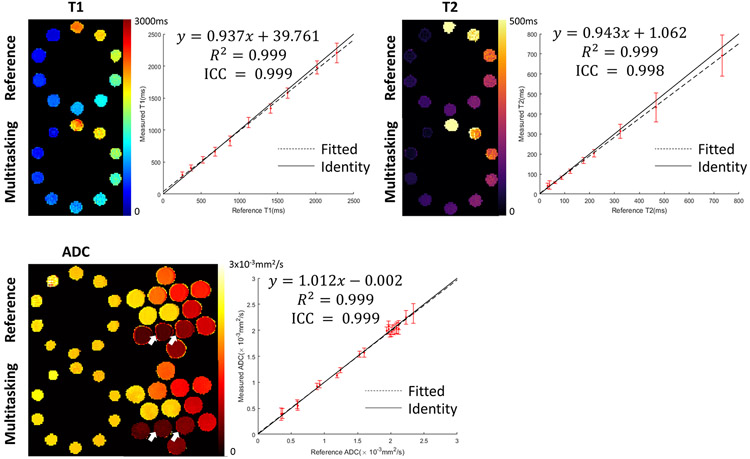
The proposed Multitasking approach provides good phantom image quality (Figure 3). Multitasking quantitative maps are free from the image distortion present in the SS-EPI ADC reference. The measured T1/T2/ADC are in substantial quantitative agreement with references, with R2 = 0.999 and ICC>0.998 for T1/T2/ADC. Detailed phantom measurements are shown in Supporting Information Tables S3-S5, where Multitasking results in higher standard deviation for some (but not all) vials. On average, simultaneous acquisition of T1/T2/ADC using Multitasking provides 2.41x, 1.59x, and 0.72x the multi-parametric SNR efficiency compared to separate acquisition using the respective reference methods (Supporting Information Figure S2). We note that the reference methods were chosen for their accepted accuracy, but may not have the optimal SNR efficiency47.
Figure 3.
Comparison of T1/T2/ADC mapping between Multitasking and the references. Multitasking provides good image quality with substantial correlation with references and is free from image distortion present in SS-EPI ADC references (white arrows). The solid line represents identity while the dotted line represents the linear fitting. ICC between Multitasking and the references indicates substantial consistency.
In vivo Study
The phase measured at the first time point after each preparation (i.e., n = 1) can be extracted from the full time-resolved phase map as a good representation for the phase resulting from the preparation. The phase resulting from the 1st, 10th, and 20th preparation of each type of T2 and diffusion-preparation demonstrates very little shot-to-shot phase inconsistency between T2preps and substantial shot-to-shot phase inconsistency between diffusion-preparations (Supporting Information Figure S3). The reconstructed T1 and T2 maps using Multitasking with and without phase correction agree with the references. Multitasking ADC maps only agree with the reference when phase correction is used; the ADC maps without phase correction show elevated ADC values across all slices (Supporting Information Figure S4).
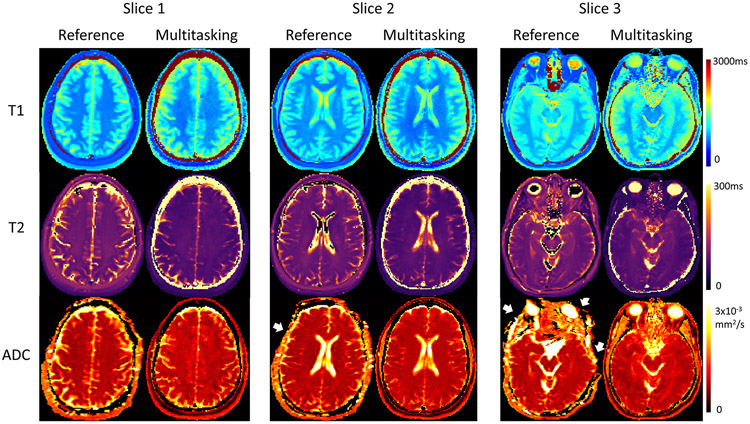
Multitasking produces perfectly co-registered and distortion-free T1/T2/ADC maps that qualitatively agree with the references (Figure 4) and produces similar distributions of T1/T2/ADC measurements of GM and WM (Table 1). Some T1 values appear higher compared to IR-TSE, particularly very long T1 species around the brain sulci and fissures. For T2 maps, GM, WM, and cerebrospinal fluid (CSF) are distinguishable but appear slightly lower than ME-SE. ADC values of CSF and around the brain sulci and fissures are also slightly lower than SS-EPI. Despite these differences, all the measurements are within the literature range (GM T1: 968-1820ms; WM T1: 750-1110ms; GM T2: 71-132ms; WM T2: 56-84ms; GM ADC: 0.78-1.09x10−3mm2/s; WM ADC: 0.60-1.05x10−3mm2/s)46,48-50.
Figure 4.
Representative in vivo T1/T2/ADC mapping of 3 slices using Multitasking and the respective reference protocols for a healthy volunteer. Multitasking provides T1/T2/ADC maps with good qualitative agreement with the references, and without image distortion (white arrows) which can be observed on SS-EPI ADC maps.
Table 1.
Frontal, parietal, and occipital gray matter and white matter T1/T2/ADC measurements of 16 healthy volunteers using Multitasking and the references.
| Gray Matter Measurements (n=16) | ||||||
|---|---|---|---|---|---|---|
| Frontal | Parietal | Occipital | ||||
| Multitasking | Reference | Multitasking | Reference | Multitasking | Reference | |
| T1(ms) | 1250.6±52.5 | 1225.9±40.9 | 1231.8±40.5 | 1223.9±39.8 | 1205.8±43.1 | 1205.4±40.4 |
| T2(ms) | 97.8±5.7 | 105.8±5.7 | 96.9±5.5 | 104.8±5.2 | 98.7±6.1 | 104.1±5.0 |
| ADC(x10−3mm2/s) | 0.95±0.05 | 0.92±0.04 | 0.92±0.08 | 0.91±0.06 | 0.95±0.08 | 0.93±0.07 |
| White Matter Measurements (n=16) | ||||||
| Frontal | Parietal | Occipital | ||||
| Multitasking | Reference | Multitasking | Reference | Multitasking | Reference | |
| T1(ms) | 807.4±39.1 | 792.9±45.1 | 811.9±40.6 | 811.3±40.4 | 820.2±41.0 | 814.5±38.7 |
| T2(ms) | 71.3±4.8 | 78.5±4.6 | 78.2±4.2 | 82.1±4.9 | 74.4±4.5 | 80.3±3.4 |
| ADC(x10−3mm2/s) | 0.80±0.03 | 0.77±0.03 | 0.80±0.04 | 0.77±0.04 | 0.78±0.04 | 0.75±0.04 |
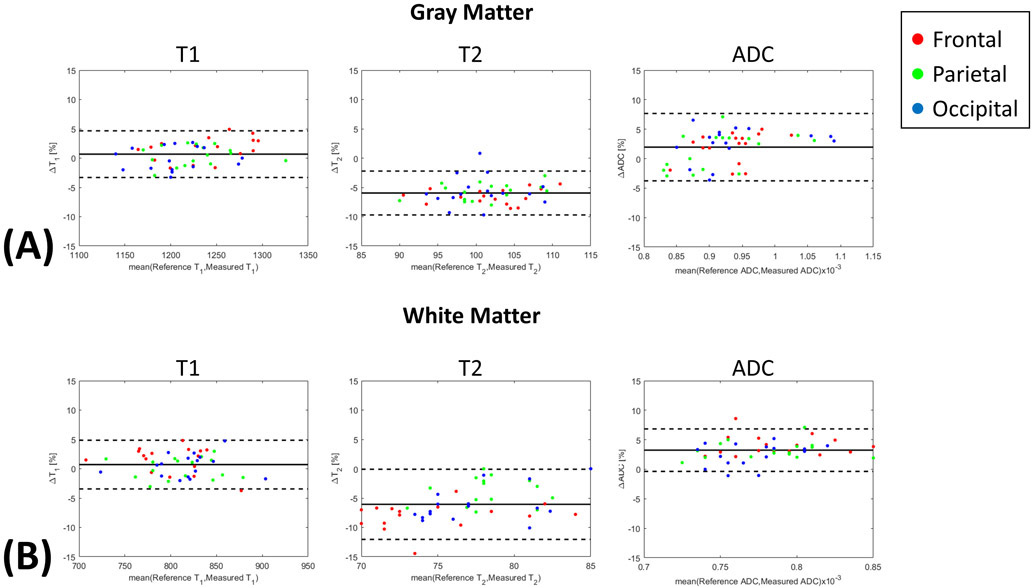
Supporting Information Table S6 shows the complete three-way ANOVA table, indicating nonsignificant differences between regions for T1 (p=0.248), T2 (P=0.097), and ADC (P=0.328), significant differences between tissues for all parameters (P<0.001), and significant differences of T1 (P=0.03), T2 (P<0.001), and ADC (P=0.001) biases between Multitasking and the respective references. Despite the statistical significance of these biases, the Bland-Altman plots show that the mean bias estimates are small (ΔT1% < 5%, ΔT2% < 7%, ΔADC% < 5%) (Figure 5), and all ICC measurements are >0.82, well within the established “excellent” range (ICC>0.75)51 (Table 2).
Figure 5.
(A) Gray matter and (B) white matter Bland-Altman plots of frontal, parietal, and occipital T1/T2/ADC.
Table 2.
Intra-class correlation coefficients of frontal, parietal, occipital gray matter and white matter T1/T2/ADC between Multitasking and the references.
| Gray Matter Intra-Class Correlation Coefficients | |||
|---|---|---|---|
| Frontal | Parietal | Occipital | |
| T1 | 0.88 | 0.93 | 0.86 |
| T2 | 0.98 | 0.97 | 0.88 |
| ADC | 0.89 | 0.93 | 0.95 |
| White Matter Intra-Class Correlation Coefficients | |||
| Frontal | Parietal | Occipital | |
| T1 | 0.92 | 0.95 | 0.93 |
| T2 | 0.88 | 0.82 | 0.87 |
| ADC | 0.94 | 0.91 | 0.87 |
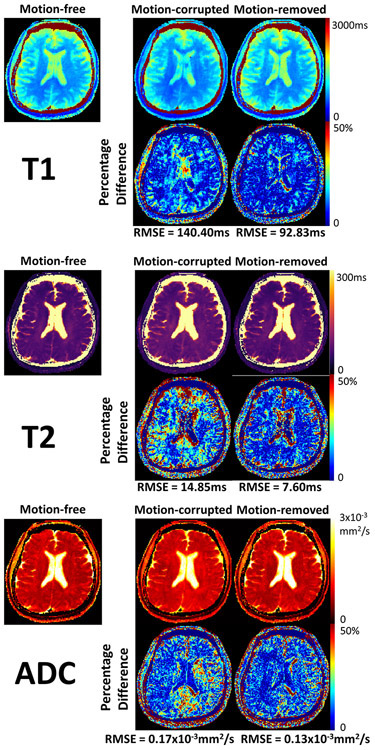
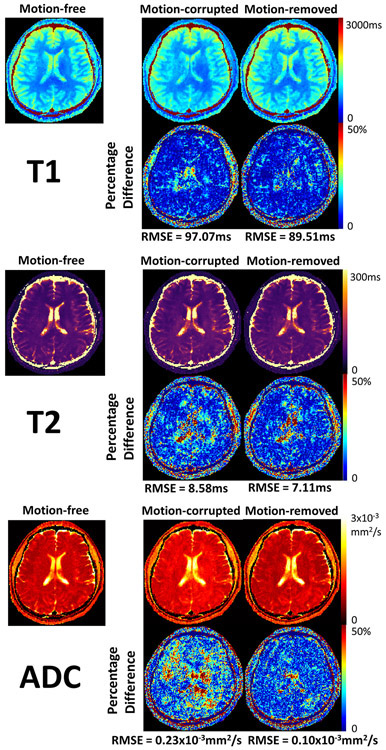
Identifying motion from I0 is straightforward, as motion-corrupted images are subject to significant signal loss and image artifacts. After motion removal, artifacts and signal voids are removed (Supporting Information Figure S5). T1/T2/ADC mapping from two subjects are shown. For the first subject, 20% of the measured data are corrupted by motion. Specifically, 39% T2preps are corrupted, and 8% diffusion-preparations are corrupted. With motion-corrupted data left in for reconstruction, the T1 map exhibits blurring artifacts, the T2 map and the ADC map show elevated T2 and ADC values, resulting in RMSEs of 140.40ms, 14.85ms, and 0.17x10−3mm2/s respectively. After motion removal, T1 features are restored and motion artifacts are removed. Abnormal T2 and ADC values on most regions are restored. RMSEs drop to 92.83ms, 7.60ms, and 0.13x10−3mm2/s respectively (Figure 6). For the second subject, 33% of data are corrupted by motion. Specifically, 21% T2preps are corrupted, and 40% diffusion-preparations are corrupted. T1 and T2 maps with motion do not exhibit substantial differences compared against the motion-free case. However, significantly elevated ADC values result from motion. RMSEs are 97.07ms, 8.58ms, and 0.23x10−3mm2/s respectively under motion. After motion removal, ADC values in most regions are again restored and RMSEs drop to 89.51ms, 7.11ms, 0.10x10−3mm2/s respectively (Figure 7).
Figure 6.
Motion effect exploration for subject 1, where 39% T2preps and 8% diffusion-preparations (20% data in total) are corrupted and removed. Comparison between motion-free, motion-corrupted, and motion-removed quantitative T1/T2/ADC maps, as well as the respective percentage difference maps against the motion-free reference are shown. The percentage difference map is generated by normalizing the absolute difference with the motion-free map. The motion results in substantial blurring artifacts in the T1 map, as well as elevated T2 and ADC values. After motion removal, the artifacts are removed and the biased T2 and ADC measurements are restored, resulting in lower root-mean-squared errors (RMSE) for all measurements.
Figure 7.
Motion effect exploration for subject 2, where 21% T2preps and 40% diffusion-preparations (33% data in total) are corrupted and removed. Comparison between motion-free, motion-corrupted, and motion-removed quantitative T1/T2/ADC maps, as well as the respective percentage difference maps against the motion-free reference are shown. The percentage difference map is generated by normalizing the absolute difference with the motion-free map. Motion-corrupted and motion-removed T1/T2 maps do not show much differences with the motion-free maps. ADC values are substantially elevated due to motion. After motion removal, most biased ADC measurements are restored, resulting in slightly reduced root-mean-squared errors (RMSE) for T1 and T2, as well as substantially reduced RMSE for ADC.
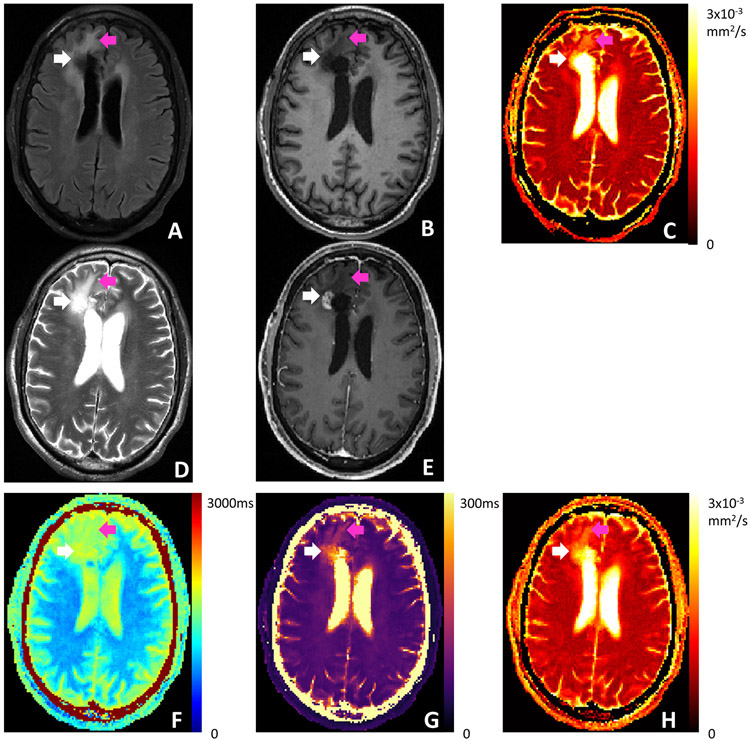
One patient example is shown in Figure 8. The patient was diagnosed with glioblastoma and underwent chemoradiation and surgery for tumor resection prior to this imaging session. A surgical cavity is present in the right anterior frontal lobe. A nodular enhancement area is present at the inferior lateral margin of the cavity, which was confirmed to represent recurrent tumor by MR spectroscopy. The recurrent tumor, the surgical cavity and the surrounding edema appear dark on pre-contrast T1-MPRAGE, indicating long T1, in agreement with the Multitasking T1 map. The tumor and surgical cavity appear dark on FLAIR, indicating that such regions are occupied by fluid with less tissue structures and more unrestricted diffusion, confirmed by the clinical ADC map using RESOLVE. The surrounding edema shows higher ADC. The Multitasking ADC map is consistent with the clinical ADC map. The tumor, the surgical cavity and the edema appear bright on T2-TSE, indicating long T2. Specifically, the fluid in the tumor and cavity shows even longer T2 compared to the edema. All these T2 features are reflected on the Multitasking T2 map.
Figure 8.
Clinical images and Multitasking T1/T2/ADC maps of a patient who was previously diagnosed with glioblastoma and underwent chemoradiation and surgery for tumor resection. (A) T2 FLAIR. (B) Pre-contrast T1 MPRAGE. (C) Clinical ADC map using RESOLVE. (D) T2 TSE. (E) Post-contrast T1 MPRAGE. (F-H) T1/T2/ADC maps obtained from Multitasking. White arrows point to the nodular enhancement area identified on post-contrast T1 MPRAGE. Purple arrows point to the surrounding edema. Multitasking T1/T2 maps reflect the tissue characteristics indicated by the clinical qualitative images. Multitasking ADC map is consistent with the clinical ADC map.
Discussion
We propose a novel approach to achieve 3D simultaneous brain T1/T2/ADC mapping by incorporating diffusion-preparation and phase correction into the MR Multitasking framework. This method enables full quantification of T1/T2/ADC in a single 9.3min scan for 100mm brain coverage. Phantom experiments and healthy volunteer experiments were performed for validation, showing substantial consistency and “excellent” agreement of T1/T2/ADC measurements between the proposed method and reference protocols by ICC. Multitasking produced co-registered T1/T2/ADC maps free from image distortion. Motion robustness was demonstrated via simple motion removal. Three post-surgery patients who were previously diagnosed with brain tumor and were likely to possess residual/recurrent tumor were scanned to demonstrate clinical feasibility. The Multitasking T1/T2/ADC maps were consistent with the clinical protocols and were able to reflect the tissue characteristics and contrasts indicated by the qualitative clinical images.
Since the emergence of MR Fingerprinting, simultaneous multi-parametric quantification has drawn substantial interest due to its great promise for clinical applications1,19,52. The Multitasking framework has several advantages over previous methods in simultaneous T1/T2/ADC mapping. We generate T1-T2-diffusion contrast using a concatenation of separate T2preps and diffusion-preparations, which because only the preparation modules are sensitive to physiological motion (as opposed to each readout), mitigating physiological motion sensitivity in comparison to DESS22. In addition, compared to Fingerprinting23 and STEM24, we achieve a comprehensive T1/T2/ADC quantification in three noncolinear diffusion directions, which matches the clinical DWI protocol. The proposed method achieves 100mm coverage (20 slices) in 9.3min, which outperforms DESS (32slices, 32mm coverage in 23min), Fingerprinting (1 slice in 60s) and STEM (2slices with 5mm thickness in 13min20s) in terms of acquisition efficiency. ZEBRA has higher acquisition efficiency (28slices with 2.6mm thickness in 2min42s) but it quantifies T2* rather than T2 and is limited to 2D acquisition25. Furthermore, we use a 3D segmented FLASH readout which produces co-registered quantitative maps free from image distortion, as compared to the SS-EPI readout employed in STEM and ZEBRA.
The proposed method yields consistent GM and WM T1/T2/ADC measurements with substantial agreement compared to the references, with all ICC in the range of 0.82 to 0.98, considered “excellent”. T1 and ADC were accurately measured with <5% bias. T2 is underestimated with <7% bias which is far less than the difference of T2 values between normal tissue and brain tumors (>50%)53 and therefore should not affect differentiation in clinical studies. Possible sources of differences in measurements between Multitasking and the references are the difference in T1 signal evolution (i.e., the T1-decay model in Multitasking vs the inversion-recovery model in IR-TSE), insufficient removal of phase inconsistencies resulting in a reduced diffusion-weighted signal (and therefore ADC overestimation), and the effect of B1 inhomogeneities on T2preps (incomplete refocusing or reduced tip-down/tip-up efficiency) that results in a reduced signal (and therefore T2 underestimation)54.
The existence of shot-to-shot (inter-shot) phase variation55,56 in diffusion-prepared MRI is well-known and has previously been addressed by approaches such as navigator-based phase estimation55,57-59 and navigator-free phase correction28,29,60-62. The highly time-resolved nature of Multitasking imaging allowed by the high temporal resolution (5.78ms) also revealed slight intra-shot phase variation (i.e., variation in successive readouts after a single preparation) (Supporting Information Video S1). Here, our time-resolved phase correction compensates for both the inter- and intra-shot phase inconsistencies by performing model-based phase correction27-29 at each timepoint. We observed that the diffusion-preparations may produce completely different phase patterns; T2preps, however, consistently produce approximately the same phase pattern. As a result, the phase inconsistencies will lead to severe cancellation of signals mostly in diffusion-weighted signals, resulting in significantly increased ADC measurements if uncorrected. T1 and T2 are less affected because i) the T1 fitting is primarily dominated by the signal evolution following the shortest T2prep, and ii) the signals encoded with different T2 weightings do not experience these phase inconsistencies.
Motion effects were explored by identifying corrupted shots on the preliminary real-time images and performing data removal. Advanced motion compensation approaches will be included in future work to make sure no re-acquisition is necessary in clinical settings. Compared to MR Fingerprinting studies where the quantitative mapping accuracy is affected by exactly when the motion occurs during the scan43,44, our Multitasking framework appears less sensitive to the timing of motion. The sensitivity to the timing of motion can potentially be further reduced by interleaving the T2preps and diffusion-preparations (i.e., one acquisition block contains 4 T2preps and 6 diffusion-preparations, and the whole acquisition block repeats). For this evaluation, manual inspection identified motion-corrupted images, as the image artifacts and signal loss are significant. An automatic data removal algorithm may be included in future work, similar to a method which successfully identified the abnormal segments of data using the real-time temporal basis functions63. Here, Multitasking T1/T2/ADC mapping was robust to motion when up to 39% T2preps are corrupted or up to 40% diffusion-preparations are corrupted. The effectiveness of simple data removal indicates that even shorter scan times may be achievable by cutting down the number of repetitions for each preparation.
Separate ADC acquisition using SS-EPI showed higher SNR efficiency than the ADC from Multitasking; however, Multitasking has the additional benefit of producing distortion-free ADC maps which are co-registered with T1 and T2 maps, which could potentially benefit machine-learning-based radiomic algorithms to provide predictive biomarkers for diagnosis and prognosis64,65. In scenarios where ADC SNR efficiency is preferred, an alternative approach to achieve efficient T1/T2/ADC mapping could be simultaneous T1/T2 mapping with Multitasking20,66 followed by a separate fast, distorted DWI acquisition67. The best acquisition strategy remains an open question, and it can be for the clinicians to determine which strategy to adopt in a specific clinical practice.
One limitation of the proposed method is the long reconstruction time, which currently takes 3-4 hours for image reconstruction. The reconstruction speed may improve in the future with successive generations of workstations, computational hardware improvements, or the use of GPUs. Another limitation is that the SNR of the proposed method is relatively low. The spoiler gradient removes half of the signal, and the FLASH readout with 5° flip angle (chosen to minimize B1+ corruption of T1 maps) also leads to low SNR. A potential alternative is to switch to bSSFP readouts but may be subject to off-resonance and eddy current artifacts and have more complicated signal evolution.
Conclusion
We have proposed a novel MR Multitasking framework to achieve 3D simultaneous brain T1/T2/ADC mapping in <10min. The proposed method provides co-registered images without distortion, quantifies T1/T2/ADC measurements with substantial agreement with reference protocols, and demonstrates clinical feasibility. Extending this work to leverage the established ability of the Multitasking framework to obtain motion-resolved quantitative mapping is a potential avenue to achieve simultaneous T1/T2/ADC mapping of the abdomen and heart.
Supplementary Material
Supporting Information Figure S1. The sequence diagram and the corresponding signal evolution of the transverse magnetization (Mxy) and the longitudinal magnetization (Mz). Mxy experiences a T2/T2+diffusion decay during the preparation, and is sufficiently dephased by the crusher gradient. The spoiler gradient removes all the transverse magnetization after the tip-up pulse, resulting in a half signal loss. Mxy reappears due to the rephasing of the subsequent crusher gradients immediately after each FLASH RF pulse, and follows a T1 decay pattern. The decay component of Mz originates from Mxy that is encoded with the phase of the preparation and tipped onto the z-axis, which is refocused subsequently by the crusher gradients and forms the imaging echo. The recover component of Mz arises from zero towards the FLASH steady state, which does not experience the preparation and is fully dephased by the crusher gradients in each FLASH TR. The gap allows sufficient signal recovery towards the thermal equilibrium for SNR purposes.
Supporting Information Table S1. Phantom and in vivo imaging protocols.
Supporting Information Table S2. Reconstruction parameters.
Supporting Information Table S3. Phantom T1 measurements.
Supporting Information Table S4. Phantom T2 measurements.
Supporting Information Table S5. Phantom ADC measurements.
Supporting Information Figure S2. The comparison of the multi-parametric SNR efficiency of T1, T2, and ADC measurements between the reference and Multitasking for each vial. T1 and T2 show the results of the NIST phantom, and ADC shows the combined results of the NIST phantom and the diffusion phantom. The SNR of each measurement of each vial is assessed as the respective mean value over standard deviation in the vial. The multi-parametric SNR efficiency for Multitasking is assessed as SNR per (Tmultitasking/3)1/2, where Tmultitasking represents the Multitasking scan time. The multi-parametric SNR efficiency for one reference method is assessed as SNR per (Treference)1/2, where Treference represents the specific reference scan time. The factor for the Multitasking SNR efficiency accounts for all three parameters being of interest but acquired in one single scan. On average, simultaneous acquisition of T1/T2/ADC using Multitasking provides 2.41x, 1.59x, and 0.72x multi-parametric SNR efficiency compared to separate acquisition using the respective reference methods.
Supporting Information Figure S3. Phase maps at n=1 of the 1st, 10th, and 20th shot of the 4 T2preps and 6 diffusion preps extracted from the full time-resolved phase map. For T2preps, little phase inconsistency can be observed between shots or between different T2preps. For diffusion-preparations, substantial phase inconsistency can be observed between shots or between different diffusion preparations.
Supporting Information Figure S4. Representative T1/T2/ADC mapping using reference protocols, Multitasking with the proposed time-resolved phase correction (PC), and Multitasking without phase correction (No PC). White arrows point to regions where substantial elevation of ADC can be observed without phase correction.
Supporting Information Table S6. Three-way repeated measures ANOVA table for T1, T2, and ADC indicating nonsignificant differences between regions and significant differences between tissues and acquisition methods.
Supporting Information Figure S5. Example clean motion-free image with clear brain tissue, motion-corrupted image with blurring artifacts and significant signal loss, and clean motion-removed image with restored tissue structures corresponding to the sequence parameter combination (n, τ, b, d) = (50,1,1,1).
Supporting Information Video S1. The intra-shot phase variation observed from the time-resolved phase map. Top row: time-resolved phase maps of 4 T2 preps. Bottom row: time-resolved phase maps of 6 diffusion-preparations. The 320 frames in the video correspond to the 320 time points within the shot. Although the crusher gradient scheme aims to maintain magnitude consistency and provide the same phase pattern within the shot, some practical factors such as eddy currents and physiological motion may contribute to the intra-shot phase variation.
Acknowledgements
This work was supported by NIH 1R01EB028146. Anthony G. Christodoulou and Debiao Li contributed equally to this work.
References
- 1.Badve C, Yu A, Dastmalchian S, Rogers M, Ma D, Jiang Y, et al. MR Fingerprinting of Adult Brain Tumors: Initial Experience. AJNR Am J Neuroradiol. 2017;38(3):492–499. DOI: 10.3174/ajnr.A5035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lescher S, Jurcoane A, Veit A, Bahr O, Deichmann R, Hattingen E. Quantitative T1 and T2 mapping in recurrent glioblastomas under bevacizumab: earlier detection of tumor progression compared to conventional MRI. Neuroradiology. 2015;57(1):11–20. DOI: 10.1007/s00234-014-1445-9. [DOI] [PubMed] [Google Scholar]
- 3.Ellingson BM, Lai A, Nguyen HN, Nghiemphu PL, Pope WB, Cloughesy TF. Quantification of Nonenhancing Tumor Burden in Gliomas Using Effective T2 Maps Derived from Dual-Echo Turbo Spin-Echo MRI. Clin Cancer Res. 2015;21(19):4373–4383. DOI: 10.1158/1078-0432.CCR-14-2862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Muller A, Jurcoane A, Kebir S, Ditter P, Schrader F, Herrlinger U, et al. Quantitative T1-mapping detects cloudy-enhancing tumor compartments predicting outcome of patients with glioblastoma. Cancer Med. 2017;6(1):89–99. DOI: 10.1002/cam4.966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hinojar R, Foote L, Arroyo Ucar E, Jackson T, Jabbour A, Yu CY, et al. Native T1 in discrimination of acute and convalescent stages in patients with clinical diagnosis of myocarditis: a proposed diagnostic algorithm using CMR. JACC Cardiovasc Imaging. 2015;8(1):37–46. DOI: 10.1016/j.jcmg.2014.07.016. [DOI] [PubMed] [Google Scholar]
- 6.Kim PK, Hong YJ, Im DJ, Suh YJ, Park CH, Kim JY, et al. Myocardial T1 and T2 Mapping: Techniques and Clinical Applications. Korean J Radiol. 2017;18(1):113–131. DOI: 10.3348/kjr.2017.18.1.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Messroghli DR, Walters K, Plein S, Sparrow P, Friedrich MG, Ridgway JP, et al. Myocardial T1 mapping: application to patients with acute and chronic myocardial infarction. Magn Reson Med. 2007;58(1):34–40. DOI: 10.1002/mrm.21272. [DOI] [PubMed] [Google Scholar]
- 8.Moon JC, Treibel TA, Schelbert EB. T1 mapping for diffuse myocardial fibrosis: a key biomarker in cardiac disease? J Am Coll Cardiol. 2013;62(14):1288–1289. DOI: 10.1016/j.jacc.2013.05.077. [DOI] [PubMed] [Google Scholar]
- 9.Thavendiranathan P, Walls M, Giri S, Verhaert D, Rajagopalan S, Moore S, et al. Improved detection of myocardial involvement in acute inflammatory cardiomyopathies using T2 mapping. Circ Cardiovasc Imaging. 2012;5(1):102–110. DOI: 10.1161/CIRCIMAGING.111.967836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Maier SE, Bogner P, Bajzik G, Mamata H, Mamata Y, Repa I, et al. Normal brain and brain tumor: multicomponent apparent diffusion coefficient line scan imaging. Radiology. 2001;219(3):842–849. DOI: 10.1148/radiology.219.3.r01jn02842. [DOI] [PubMed] [Google Scholar]
- 11.Server A, Kulle B, Maehlen J, Josefsen R, Schellhorn T, Kumar T, et al. Quantitative apparent diffusion coefficients in the characterization of brain tumors and associated peritumoral edema. Acta Radiol. 2009;50(6):682–689. DOI: 10.1080/02841850902933123. [DOI] [PubMed] [Google Scholar]
- 12.Higano S, Yun X, Kumabe T, Watanabe M, Mugikura S, Umetsu A, et al. Malignant astrocytic tumors: clinical importance of apparent diffusion coefficient in prediction of grade and prognosis. Radiology. 2006;241(3):839–846. DOI: 10.1148/radiol.2413051276. [DOI] [PubMed] [Google Scholar]
- 13.Murakami R, Hirai T, Sugahara T, Fukuoka H, Toya R, Nishimura S, et al. Grading astrocytic tumors by using apparent diffusion coefficient parameters: superiority of a one- versus two-parameter pilot method. Radiology. 2009;251(3):838–845. DOI: 10.1148/radiol.2513080899. [DOI] [PubMed] [Google Scholar]
- 14.Fangberget A, Nilsen LB, Hole KH, Holmen MM, Engebraaten O, Naume B, et al. Neoadjuvant chemotherapy in breast cancer-response evaluation and prediction of response to treatment using dynamic contrast-enhanced and diffusion-weighted MR imaging. Eur Radiol. 2011;21(6):1188–1199. DOI: 10.1007/s00330-010-2020-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sharma U, Danishad KK, Seenu V, Jagannathan NR. Longitudinal study of the assessment by MRI and diffusion-weighted imaging of tumor response in patients with locally advanced breast cancer undergoing neoadjuvant chemotherapy. NMR Biomed. 2009;22(1):104–113. DOI: 10.1002/nbm.1245. [DOI] [PubMed] [Google Scholar]
- 16.Woodhams R, Ramadan S, Stanwell P, Sakamoto S, Hata H, Ozaki M, et al. Diffusion-weighted imaging of the breast: principles and clinical applications. Radiographics. 2011;31(4):1059–1084. DOI: 10.1148/rg.314105160. [DOI] [PubMed] [Google Scholar]
- 17.Barentsz JO, Weinreb JC, Verma S, Thoeny HC, Tempany CM, Shtern F, et al. Synopsis of the PI-RADS v2 Guidelines for Multiparametric Prostate Magnetic Resonance Imaging and Recommendations for Use. Eur Urol. 2016;69(1):41–49. DOI: 10.1016/j.eururo.2015.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, et al. Magnetic resonance fingerprinting. Nature. 2013;495(7440):187–192. DOI: 10.1038/nature11971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yu AC, Badve C, Ponsky LE, Pahwa S, Dastmalchian S, Rogers M, et al. Development of a Combined MR Fingerprinting and Diffusion Examination for Prostate Cancer. Radiology. 2017;283(3):729–738. DOI: 10.1148/radiol.2017161599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie YB, Wang N, et al. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng. 2018;2(4):215–226. DOI: 10.1038/s41551-018-0217-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shaw JL, Yang Q, Zhou Z, Deng Z, Nguyen C, Li D, et al. Free-breathing, non-ECG, continuous myocardial T1 mapping with cardiovascular magnetic resonance multitasking. Magn Reson Med. 2019;81(4):2450–2463. DOI: 10.1002/mrm.27574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gras V, Farrher E, Grinberg F, Shah NJ. Diffusion-weighted DESS protocol optimization for simultaneous mapping of the mean diffusivity, proton density and relaxation times at 3 Tesla. Magn Reson Med. 2017;78(1):130–141. DOI: 10.1002/mrm.26353. [DOI] [PubMed] [Google Scholar]
- 23.Jiang Y, Hamilton J, Lo W. Simultaneous T1, T2 and diffusion quantification using multiple contrast prepared magnetic resonance fingerprinting. In Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, HI, 2017. p. 1171. [Google Scholar]
- 24.Zhang Y, Wells SA, Hernando D. Stimulated echo based mapping (STEM) of T1 , T2 , and apparent diffusion coefficient: validation and protocol optimization. Magn Reson Med. 2018. DOI: 10.1002/mrm.27358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hutter J, Slator PJ, Christiaens D, Teixeira R, Roberts T, Jackson L, et al. Integrated and efficient diffusion-relaxometry using ZEBRA. Sci Rep. 2018;8(1):15138 DOI: 10.1038/s41598-018-33463-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.He J, Liu Q, Christodoulou AG, Ma C, Lam F, Liang Z-P. Accelerated high-dimensional MR imaging with sparse sampling using low-rank tensors. IEEE Trans Med Imaging 2016;35(9):2119–2129. DOI: 10.1109/TMI.2016.2550204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ma S, Nguyen CT, Christodoulou AG, Luthringer D, Kobashigawa J, Lee SE, et al. Accelerated Cardiac Diffusion Tensor Imaging Using Joint Low-Rank and Sparsity Constraints. IEEE Trans BioMed Eng 2018;65(10):2219–2230. DOI: 10.1109/TBME.2017.2787111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Haldar JP, Wedeen VJ, Nezamzadeh M, Dai G, Weiner MW, Schuff N et al. Improved diffusion imaging through SNR-enhancing joint reconstruction. Magn Reson Med. 2012;69(1):277–289. DOI: 10.1002/mrm.24229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gao H, Li L, Zhang K, Zhou W, Hu X. PCLR: Phase-constrained low-rank model for compressive diffusion-weighted MRI. Magn Reson Med. 2013;72(5):1330–1341. DOI: 10.1002/mrm/25052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gao Y, Han F, Zhou Z, Zhong X, Bi X, Neylon J, et al. Multishot diffusion-prepared magnitude-stabilized balanced steady-state free precession sequence for distortion-free diffusion imaging. Magn Reson Med. 2019;81(4):2374–2384. DOI: 10.1002/mrm.27565. [DOI] [PubMed] [Google Scholar]
- 31.Van AT, Cervantes B, Kooijman H, Karampinos DC. Analysis of phase error effects in multishot diffusion-prepared turbo spin echo imaging. Quant Imaging Med Surg. 2017;7(2):238–250. DOI: 10.21037/qims.2017.04.01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nguyen C, Fan Z, Sharif B, He Y, Dharmakumar R, Berman DS, et al. In vivo three-dimensional high resolution cardiac diffusion-weighted MRI: a motion compensated diffusion-prepared balanced steady-state free precession approach. Magn Reson Med. 2014;72(5):1257–1267. DOI: 10.1002/mrm.25038. [DOI] [PubMed] [Google Scholar]
- 33.Nguyen C, Fan Z, Xie Y, Pang J, Speier P, Bi X, et al. In vivo diffusion-tensor MRI of the human heart on a 3 tesla clinical scanner: An optimized second order (M2) motion compensated diffusion-preparation approach. Magn Reson Med. 2016;76(5):1354–1363. DOI: 10.1002/mrm.26380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Parrish T, Hu X. A new T2 preparation technique for ultrafast gradient-echo sequence. Magn Reson Med. 1994;32(5):652–657. DOI: 10.1002/mrm.1910320515. [DOI] [PubMed] [Google Scholar]
- 35.Haldar JP, Liang Z-P. Spatiotemporal imaging with partially separable functions: A matrix recovery approach. In Proceedings of the 7th IEEE International Symposium on Biomedical Imaging: From Naono to Macro, Rotterdam, The Netherlands, 2010. p. 716–719. [Google Scholar]
- 36.Liang Z-P. Spatiotemporal imaging with partially separable functions. In Proceedings of the 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Arlington, Virginia, USA, 2007. p. 988–991. [Google Scholar]
- 37.Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn Reson Med. 2012;67(5):1355–1366. DOI: 10.1002/mrm.23128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McGivney DF, Pierre E, Ma D, Jiang Y, Saybasili H, Gulani V, et al. SVD Compression for Magnetic Resonance Fingerprinting in the Time Domain. IEEE Trans Med Imaging 2014;33(12):2311–2322. DOI: 10.1109/TMI.2014.2337321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhao B, Setsompop K, Adalsteinsson E, Gagoski B, Ye H, Ma D, et al. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn Reson Med. 2018;79(2):933–942. DOI: 10.1002/mrm.26701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.De Lathauwer L, De Moor B, Vandewalle J. A multilinear singular value decomposition. Siam J Matrix Anal A. 2000;21(4):1253–1278. DOI: 10.1137/S0895479896305696. [DOI] [Google Scholar]
- 41.Zhao B, Haldar JP, Christodoulou AG, Liang Z-P. Image Reconstruction From Highly Undersampled (k,t)-Space Data With Joint Partial Separability and Sparsity Constraints. IEEE Trans Med Imaging. 2012;31(9):1809–1820. DOI: 10.1109/TMI.2012.2203921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med. 2017;77(1):180–195. DOI: 10.1002/mrm.26102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mehta BB, Ma D, Pierre EY, Jiang Y, Coppo S, Griswold MA. Image reconstruction algorithm for motion insensitive MR Fingerprinting (MRF): MORF. Magn Reson Med. 2018;80(6):2485–2500. DOI: 10.1002/mrm.27227. [DOI] [PubMed] [Google Scholar]
- 44.Yu Z, Zhao T, Asslander J, Lattanzi R, Sodickson DK, Cloos MA. Exploring the sensitivity of magnetic resonance fingerprinting to motion. Magn Reson Imaging. 2018;54:241–248. DOI: 10.1016/j.mri.2018.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Morozov VA. On the solution of functional equations by the method of regularization. Soviet Math Dokl. 1966; 7:414–417. [Google Scholar]
- 46.Wansapura JP, Holland SK, Dunn RS, Ball WS Jr. NMR relaxation times in the human brain at 3.0 tesla. J Magn Reson Imaging. 1999;9(4):531–538. DOI: . [DOI] [PubMed] [Google Scholar]
- 47.Deoni SCL, Rutt BK, Peters TM. Rapid Combined T1 and T2 mapping Using Gradient Recalled Acquisition in the Steady State. Magn Res Med. 2003;49(3):515–526. DOI: 10.1002/mrm.10407. [DOI] [PubMed] [Google Scholar]
- 48.Helenius J, Soinne L, Perkio J, Salonen O, Kangasmaki A, Kaste M, et al. Diffusion-weighted MR imaging in normal human brains in various age groups. AJNR Am J Neuroradiol. 2002;23(2):194–199. PMID: 11847041. [PMC free article] [PubMed] [Google Scholar]
- 49.Sener RN. Diffusion MRI: apparent diffusion coefficient (ADC) values in the normal brain and a classification of brain disorders based on ADC values. Comput Med Imaging Graph. 2001;25(4):299–326. DOI: 10.1016/S0895-6111(00)00083-5. [DOI] [PubMed] [Google Scholar]
- 50.Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, et al. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med. 2005;54(3):507–512. DOI: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- 51.Cicchetti DV. Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychological assessment. 1994;6(4):284 DOI: 10.1037/1040-3590.6.4.284. [DOI] [Google Scholar]
- 52.Chen Y, Panda A, Pahwa S, Hamilton JI, Dastmalchian S, McGivney DF, et al. Three-dimensional MR Fingerprinting for Quantitative Breast Imaging. Radiology. 2019;290(1):33–40. DOI: 10.1148/radiol.2018180836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hattingen E, Jurcoane A, Daneshvar K, Pilatus U, Mittelbronn M, Steinbach JP, et al. Quantitative T2 mapping of recurrent glioblastoma under bevacizumab improves monitoring for non-enhancing tumor progression and predicts overall survival. Neuro Oncol. 2013;15(10):1395–1404. DOI: 10.1093/neuonc/not105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jiang Y, Ma D, Keenan KE, Stupic KF, Gulani V, Griswold MA. Repeatability of magnetic resonance fingerprinting T1 and T2 estimates assessed using the ISMRM/NIST MRI system phantom. Magn Reson Med. 2017;78(4):1452–1457. DOI: 10.1002/mrm.26509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magn Reson Med. 2003;50(2):343–353. DOI: 10.1002/mrm.10531. [DOI] [PubMed] [Google Scholar]
- 56.O'Halloran RL, Holdsworth S, Aksoy M, Bammer R. Model for the correction of motion-induced phase errors in multishot diffusion-weighted-MRI of the head: are cardiac-motion-induced phase errors reproducible from beat-to-beat? Magn Reson Med. 2012;68(2):430–440. DOI: 10.1002/mrm.23245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jeong HK, Gore JC, Anderson AW. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn Reson Med. 2013;69(3):793–802. DOI: 10.1002/mrm.24320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52(6):1388–1396. DOI: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- 59.Ordidge RJ, Helpern JA, Qing ZX, Knight RA, Nagesh V. Correction of motional artifacts in diffusion-weighted MR images using navigator echoes. Magn Reson Imaging. 1994;12(3):455–460. DOI: 10.1016/0730-725X(94)92539-9. [DOI] [PubMed] [Google Scholar]
- 60.Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage. 2013;72:41–47. DOI: 10.1016/j.neuroimage.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chu ML, Chang HC, Chung HW, Truong TK, Bashir MR, Chen NK. POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): A general algorithm for reducing motion-related artifacts. Magn Reson Med. 2015;74(5):1336–1348. DOI: 10.1002/mrm.25527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med. 2017;78(2):494–507. DOI: 10.1002/mrm.26382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wang N, Christodoulou AG, Xie Y, Wang Z, Deng Z, Zhou B, et al. Quantitative 3D dynamic contrast-enhanced (DCE) MR imaging of carotid vessel wall by fast T1 mapping using Multitasking. Magn Reson Med. 2019;81(4):2302–2314. DOI: 10.1002/mrm.27553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kickingereder P, Burth S, Wick A, Gotz M, Eidel O, Schlemmer HP, et al. Radiomic Profiling of Glioblastoma: Identifying an Imaging Predictor of Patient Survival with Improved Performance over Established Clinical and Radiologic Risk Models. Radiology. 2016;280(3):880–889. DOI: 10.1148/radiol.2016160845. [DOI] [PubMed] [Google Scholar]
- 65.Zhou M, Scott J, Chaudhury B, Hall L, Goldgof D, Yeom KW, et al. Radiomics in Brain Tumor: Image Assessment, Quantitative Feature Descriptors, and Machine-Learning Approaches. AJNR Am J Neuroradiol. 2018;39(2):208–216. DOI: 10.3174/ajnr.A5391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Xie Y, Christodoulou AG, Wang N, Li D. Quantitative Multi-Contrast Atherosclerosis Characterization (qMATCH): Comprehensive Quantitative Evaluation of Atherosclerosis in a Single-Scan. In Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, HI, 2017. p. 3122. [Google Scholar]
- 67.Prakkamakul S, Witzel T, Huang S, Boulter D, Borja MJ, Schaefer P, et al. Ultrafast Brain MRI: Clinical Deployment and Comparison to Conventional Brain MRI at 3T. J Neuroimaging. 2016;26(5):503–510. DOI: 10.1111/jon.12365. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Figure S1. The sequence diagram and the corresponding signal evolution of the transverse magnetization (Mxy) and the longitudinal magnetization (Mz). Mxy experiences a T2/T2+diffusion decay during the preparation, and is sufficiently dephased by the crusher gradient. The spoiler gradient removes all the transverse magnetization after the tip-up pulse, resulting in a half signal loss. Mxy reappears due to the rephasing of the subsequent crusher gradients immediately after each FLASH RF pulse, and follows a T1 decay pattern. The decay component of Mz originates from Mxy that is encoded with the phase of the preparation and tipped onto the z-axis, which is refocused subsequently by the crusher gradients and forms the imaging echo. The recover component of Mz arises from zero towards the FLASH steady state, which does not experience the preparation and is fully dephased by the crusher gradients in each FLASH TR. The gap allows sufficient signal recovery towards the thermal equilibrium for SNR purposes.
Supporting Information Table S1. Phantom and in vivo imaging protocols.
Supporting Information Table S2. Reconstruction parameters.
Supporting Information Table S3. Phantom T1 measurements.
Supporting Information Table S4. Phantom T2 measurements.
Supporting Information Table S5. Phantom ADC measurements.
Supporting Information Figure S2. The comparison of the multi-parametric SNR efficiency of T1, T2, and ADC measurements between the reference and Multitasking for each vial. T1 and T2 show the results of the NIST phantom, and ADC shows the combined results of the NIST phantom and the diffusion phantom. The SNR of each measurement of each vial is assessed as the respective mean value over standard deviation in the vial. The multi-parametric SNR efficiency for Multitasking is assessed as SNR per (Tmultitasking/3)1/2, where Tmultitasking represents the Multitasking scan time. The multi-parametric SNR efficiency for one reference method is assessed as SNR per (Treference)1/2, where Treference represents the specific reference scan time. The factor for the Multitasking SNR efficiency accounts for all three parameters being of interest but acquired in one single scan. On average, simultaneous acquisition of T1/T2/ADC using Multitasking provides 2.41x, 1.59x, and 0.72x multi-parametric SNR efficiency compared to separate acquisition using the respective reference methods.
Supporting Information Figure S3. Phase maps at n=1 of the 1st, 10th, and 20th shot of the 4 T2preps and 6 diffusion preps extracted from the full time-resolved phase map. For T2preps, little phase inconsistency can be observed between shots or between different T2preps. For diffusion-preparations, substantial phase inconsistency can be observed between shots or between different diffusion preparations.
Supporting Information Figure S4. Representative T1/T2/ADC mapping using reference protocols, Multitasking with the proposed time-resolved phase correction (PC), and Multitasking without phase correction (No PC). White arrows point to regions where substantial elevation of ADC can be observed without phase correction.
Supporting Information Table S6. Three-way repeated measures ANOVA table for T1, T2, and ADC indicating nonsignificant differences between regions and significant differences between tissues and acquisition methods.
Supporting Information Figure S5. Example clean motion-free image with clear brain tissue, motion-corrupted image with blurring artifacts and significant signal loss, and clean motion-removed image with restored tissue structures corresponding to the sequence parameter combination (n, τ, b, d) = (50,1,1,1).
Supporting Information Video S1. The intra-shot phase variation observed from the time-resolved phase map. Top row: time-resolved phase maps of 4 T2 preps. Bottom row: time-resolved phase maps of 6 diffusion-preparations. The 320 frames in the video correspond to the 320 time points within the shot. Although the crusher gradient scheme aims to maintain magnitude consistency and provide the same phase pattern within the shot, some practical factors such as eddy currents and physiological motion may contribute to the intra-shot phase variation.