Cardiovascular Risk Prediction in Ankylosing Spondylitis: From Traditional Scores to Machine Learning Assessment

Abstract

Introduction

The performance of seven cardiovascular (CV) risk algorithms is evaluated in a multicentric cohort of ankylosing spondylitis (AS) patients. Performance and calibration of traditional CV predictors have been compared with the novel paradigm of machine learning (ML).

Methods

A retrospective analysis of prospectively collected data from an AS cohort has been performed. The primary outcome was the first CV event. The discriminatory ability of the algorithms was evaluated using the area under the receiver operating characteristic (ROC) curve (AUC), which is like the concordance-statistic (c-statistic). Three ML techniques were considered to calculate the CV risk: support vector machine (SVM), random forest (RF), and k-nearest neighbor (KNN).

Results

Of 133 AS patients enrolled, 18 had a CV event. c-statistic scores of 0.71, 0.61, 0.66, 0.68, 0.66, 0.72, and 0.67 were found, respectively, for SCORE, CUORE, FRS, QRISK2, QRISK3, RRS, and ASSIGN. AUC values for the ML algorithms were: 0.70 for SVM, 0.73 for RF, and 0.64 for KNN. Feature analysis showed that C-reactive protein (CRP) has the highest importance, while SBP and hypertension treatment have lower importance.

Conclusions

All of the evaluated CV risk algorithms exhibit a poor discriminative ability, except for RRS and SCORE, which showed a fair performance. For the first time, we demonstrated that AS patients do not show the traditional ones used by CV scores and that the most important variable is CRP. The present study contributes to a deeper understanding of CV risk in AS, allowing the development of innovative CV risk patient-specific models.

Digital Features

This article is published with digital features to facilitate understanding of the article. To view digital features for this article go to https://doi.org/10.6084/m9.figshare.12887285.

Key Summary Points

Why carry out this study?

Cardiovascular disease (CVD) represents an important cause of morbidity and mortality among patients with Ankylosing Spondylitis (AS), so of cardiovascular (CV) risk prediction has a pivotal role in these patients.

The currently available cardiovascular risk algorithms demonstrate only fair or moderate discriminative ability in patients with AS.

In this study, the performance of seven cardiovascular risk predictors is evaluated in a multicentric cohort of AS patients from Italian Rheumatology Units. Moreover, for the first time in literature, performance and calibration of traditional CV predictors have been here compared with the novel paradigm of machine learning (ML).

What was learned from the study?

All the CV risk algorithms evaluated exhibit a poor discriminative ability, except for Reynold’s Risk Score (RRS) and Systematic Coronary Risk Evaluation (SCORE) which showed a fair performance.

The adaptation of CV risk algorithms according to European League Against Rheumatism (EULAR) recommendations did not provide a significant improvement in discriminative ability.

Patients with AS do not present, among the top features, the traditional ones used by FRS and other traditional methods; the most important variable is C-reactive protein (CRP). This is consistent with the result regarding RRS, which shows the best discriminative ability, probably because it includes CRP as a variable.

Machine-learning algorithms can be helpful in a better cardiovascular assessment in patients with Ankylosing Spondylitis and demonstrate that C-reactive protein can be a key feature of an increased risk in these patients.

Taking into account this variable in future ML studies could increase classification performances on AS patients.

Introduction

Ankylosing spondylitis (AS) is a spondyloarthritis (SpA) that deeply affects physical function and quality of life, and comorbidities contribute to the prognosis of this disease [1]. Patients with rheumatoid arthritis (RA) and psoriatic arthritis (PsA) show an increased risk of cardiovascular disease (CVD) [2, 3] and traditional CV risk algorithms perform poorly in these populations [4–6]. AS patients show a 20–40% increase of mortality due to CVD compared to general population [7–9]. Many traditional and disease-related factors contribute to the CVD risk in AS [10–13].

The European League Against Rheumatism (EULAR) recommended that physicians conduct an annual assessment of CV risk in AS patients [14]. The identification of high CV risk AS patients is particularly important in order to improve preventive strategies. Several CV risk algorithms have been proposed over time [15]. The performance and calibration of algorithms for calculating CV risk in RA patients can still be considered a conundrum. In particular, different scores (Framingham Score (FRS), Systematic Coronary Risk Evaluation (SCORE), Reynold’s Risk Score (RRS), and QRISK2), tend to underestimate CV risk in RA patients; the risk observed exceeds the predicted one; the different scores appear slightly calibrated for RA subjects [16, 17]. EULAR recommended to adapt the general population risk algorithms with a multiplication by the factor of 1.5 in RA patients and other inflammatory arthritis, except for QRISK2, QRISK3, and ASSIGN, which are characterized by a multiplication factor intrinsic to the algorithm for RA [18]. Recently, it has been shown that the above-mentioned risk predictor algorithms provide a less accurate prediction of CV risk in PsA patients compared to general population [4, 5].

In this study, the performance of FRS, SCORE, QRISK2, QRISK3, RRS, ASSIGN, and the Italian Progetto CUORE individual score is evaluated in a multicentric cohort of AS patients from Italian Rheumatology Units. Moreover, for the first time in the literature, performance and calibration of traditional CV predictors have been compared with the novel paradigm of machine learning (ML).

ML was recently introduced in cardiology to face challenges that cannot be solved by traditional statistical methods [24, 25]. A comparative study between Framingham and quantum neural network-based approach showed how Framingham is outdated and the outstanding potential of ML applied to CV risk prediction [20].

ML belongs to the field of artificial intelligence and it was designed for developing intelligent systems able to learn how to solve a specific problem without being explicitly programmed for it. The learning process is made possible by deriving knowledge from the huge quantity of data present in almost every field (i.e., “big data”) and has the objective of making predictions. The two biggest subsets of ML are supervised learning (SL) and unsupervised learning. In the first case, the model is built from a database that already contains the desired output, such as CVD outcome. In the second case, there is no prior knowledge about the event inside the dataset, therefore the model aims at finding subgroups of the original dataset that have common features. ML does not present the same limitations as in the case of traditional statistical methods. Particularly, not many assumptions must be made on the underlying data and non-linearities can be addressed easily. Also, ML can identify hidden variables of a model by inferring them from other variables.

In this work, SL classification approach was adopted to predict the CV risk from a database of AS patients for which the final event was already known.

Methods

A retrospective analysis of prospectively collected data from AS cohort of six Italian Rheumatology Units was conducted in November 2018. At baseline (November 2008), patients fulfilled the 1984 Modified New York Criteria and without a personal history of CV disease (CVD) were consecutively included in this study. Only patients with fully available information allowing the calculation of all the CV risk at baseline from historical datasets has been recruited.

The study was approved on 19/6/18 by the Ethics Committee of University Campus Bio-Medico di Roma (approval number: 60/18 OSS), and it was conducted in conformity with the Declaration of Helsinki and its later amendments. Written informed consent for the anonymous use of data was obtained from all participants. Baseline characteristics extracted from the cohort database were: age (years), gender (male/female), weight (kg), height (cm), CRP (mg/l), erythrocyte sedimentation rate (ESR) (mm/h), axial arthritis (grade of radiographic sacroiliitis and no-radiographic sacroiliitis Y/N), peripheral arthritis (Y/N), Bath Ankylosing Spondylitis Disease Activity Index (BASDAI), Bath Ankylosing Spondylitis Functional Index (BASFI), enthesitis (Y/N), dactylitis (Y/N), psoriasis (Y/N), history of IBD (Y/N), history of uveitis (Y/N), family history of CVD (Y/N), smoking status (Y/N/previous), hypertension (Y/N), use of antihypertensive medication (Y/N), use of statins and aspirin (Y/N), diabetes mellitus (Y/N), atrial fibrillation (Y/N), chronic kidney disease stage IV–V (Y/N), angina or heart attack in a 1st degree relative < 60 years (Y/N), systolic blood pressure (SBP) (mmHg), total cholesterol (mg/dl), and high-density lipoprotein cholesterol (HDL-C) (mg/dl).

The primary outcome was the first CV event (fatal and non-fatal), as reported by electronic patient files. Considered CV events were: sudden cardiac death, coronary artery diseases (CAD) (stable and unstable angina pectoris, myocardial infarction), cerebral vascular accident (CVA), transient ischemic attack (TIA), peripheral artery disease (PAD), and heart failure (HF).

The 10-year general FRS for CVD [21], QRISK2 [22], QRISK3 [23], CUORE [24], RRS [25], and ASSIGN [26] were calculated using already-published algorithms. SCORE algorithm for low-risk countries was used [27]. Cut-off values that mark the difference between low-to-intermediate risk and intermediate-to-high risk were 10% and 20%, respectively, except for SCORE in which cut-off values were 1% and 5% and for ASSIGN in which cut-off value that marks the difference between low to high risk is 20%.

The default median value 15.89 for the Scottish Index of Multiple Deprivation (SIMD) was used to calculate the ASSIGN score.

In order to calculate individual risk for CV within 10 years for all seven algorithms, baseline medical data were used.

The area under the receiver operating characteristic (ROC) curve, which is like the concordance-statistic (c-statistic), was used for the evaluation of the discriminatory ability of all seven algorithms.

The comparison of the agreement between observed and predicted number of CV events in stratified groups by deciles, sextiles, or septiles of the predicted risk, as appropriate, using the Hosmer–Lemeshow (HL) test allowed the assessment of calibration.

Fisher’s exact test and Mann–Whitney test were used for analysis of contingency table and comparison between ranks, respectively. Stata V.14 was used for statistical analysis.

Machine Learning

SL classification was adopted to predict the CV risk from a database of AS patients, for which the final event was already known. SL algorithms contain previous knowledge about data (i.e., labels describing the desired output of the model) and need to be trained using this knowledge before being applied to completely new data. The main goal was to build a model from a dataset (that already contains desired outputs) and to use it to make predictions on future data or data for which desired outputs are not present.

The activity flow of the work was divided in the following phases, typical of ML pipelines:

Phase 1: Training and Validation Database

Two databases were employed:

1. American patients (3658) from the Framingham Heart Study, retrieved from the Kaggle website (https://www.kaggle.com/datasets). Risk factors included in this dataset were: gender (0: female, 1: male), age (years), smoking status (0: nonsmoker, 1: smoker), hypertension treatment (0: not treated, 1: treated), total cholesterol (mg/dl), SBP (mmHg), body mass index (BMI, kg/m²), diabetes (0: without diabetes, 1: with diabetes) and CVD event (0: without CVD, 1: with CVD). In this dataset, 557 patients had a CVD and 3101 did not. This dataset is considered representative for a general population. From now on, this dataset will be indicated as the general dataset.

2. AS patients (133) were included in the study. Some risk factors included in this dataset were the same as those included in the general dataset: gender, age, smoking status, hypertension treatment, total cholesterol, SBP, BMI, diabetes and CVD event. Other non-traditional risk factors were also used: pathology time window (PTW, years), CVD family history (0: no, 1: yes), atrial fibrillation (AF, 0: no, 1: yes), HDL-C (mg/dl), use of cardio aspirin (0: no, 1: yes), CRP (mg/l), peripheral arthritis (0: no, 1: yes), enthesitis (0: no, 1: yes), dactylitis (0: no, 1: yes), IBD (0: no, 1: yes), uveitis (0: no, 1: yes), diabetes (0: no, 1: yes), comorbidity (0: no, 1: yes), use of statins (0: no, 1: yes) and CVD event (0: no, 1: yes). In this dataset, 18 patients had a CVD and 115 did not. From now on, this dataset will be indicated as the AS dataset.

It is worth noting that about 15% of patients of each database had a CVD event, therefore this is a case of classes’ imbalance.

Phase 2: Algorithm Selection and Development

Three ML techniques were considered to calculate the CV risk: Support vector machine (SVM), random forest (RF), and k-nearest neighbor (KNN) [28–31]. All ML algorithms were developed in Python 3.7.2, with the help of the following scientific computation libraries: NumPy, to manipulate data; Scikit-learn, to implement ML pipelines; Pandas, to manipulate data at a higher level than with NumPy, and Matplotlib, to visualize data.

Phase 3: Dataset Preprocessing and Feature Analysis

Data were always standardized to take them on the same scale. ML techniques were first applied to the general dataset, using only six traditional features (i.e., age, sex, SBP, total cholesterol, smoking status, and hypertension treatment). The same traditional features were used also on AS dataset to make results comparable with the traditional ones. The general dataset does not contain missing values, while the AS contain several missing values in rheumatic features. Therefore, features with more than 40 missing values were removed, while the others were imputed, because by removing them there was the possibility to remove important information from the dataset or, for small dataset like the one we have, to compromise model’s reliability. Imputation followed this strategy: in binary attributes missing values were substituted by 0 (absence of event), while in numeric attribute they were substituted by the normal value over the general Italian population.

In case of continuous features, we imputed the feature from the general database (non-rheumatic patients) and in case of binary features we imputed 0 (= no pathological event). Therefore, in general, we imputed non-recorded features as “non-pathological” thus following a conservative approach toward a more robust model with minimized biases. Moreover, concerning imputation of continuous variables, it is worth saying that, since the AS dataset was very small in size, estimating missing values by the mean value over these patients, might have low statistical significance. Concerning imputation of binary variables, the very vast majority of the patients presented 0 as binary value in those variables. Finally, it is worth mentioning that Framingham features employed to train and test the ML predictor were in the vast majority present for patients in the AS dataset.

Phase 4: Classifier Training and Validation

To train the classifiers, a balanced dataset was used (i.e., equal number of patients with and without CVD event, about 600 samples). This dataset contained patients from the general dataset because they were enough to successfully train an ML algorithm. Then, the classifier was tested on an unbalanced dataset (about 15% of patients which had a CVD event), composed by the remaining data not used during training (about 3100 samples). Bootstrap technique was used to assess model performance, with 25 random splits with replacement. This sampling technique, by means of the iterative dataset’s random splits, gives the possibility to calculate different times algorithms performances on different patients’ subsets, making performance evaluation more reliable. The trained model was also validated over the SpA population, i.e., the AS dataset. The models’ hyperparameters (SVM: C in the case of a linear kernel and C and γ in the case of a radial basis function kernel; RF: number of trees and splitting criterion; KNN: number of neighbors, i.e., k) were optimized by means of grid search, setting AUC as the scoring function and performing a fourfold cross validation. ML classifiers presented the following optimized parameters after grid search:

• SVM: radial basis function kernel, C = 0.1 and γ = 0.01;

• RF: entropy as splitting criterion and 500 trees;

• KNN: Minkowski distance metrics and K = 25.

Phase 5: Classifier Evaluation Metrics and Evaluation

Discriminatory ability for the algorithms was assessed by ROC curves and AUC values, sensitivity, specificity, accuracy, positive predictive value, and negative predictive value. Calibration between predicted and observed events was evaluated by Hosmer–Lemeshow tests by comparing the agreement of CV events in groups stratified in deciles. A comparison between traditional (FRS, CUORE, and SCORE risk scores) and novel techniques (SVM, RF, and KNN) was performed to explore performances of traditional risk predictors on AS, with and without EULAR correction coefficient. Performance metrics were calculated for the two cut-offs: low-to-intermediate (10% in the case of Framingham and CUORE, 1% in the case of SCORE) and intermediate-to-high (20% in the case of FRS and CUORE, 5% in the case of SCORE). ML output is binary; therefore, it does not present different cut-off values, but only one threshold (equal to 50%) used to binarize the output.

First, traditional algorithms (FRS, CUORE, and SCORE) were evaluated on the general population and on the AS database. Second, ML techniques were applied the general population by means of bootstrap technique and performances were compared with FRS as reference for traditional methods. Finally, obtained models trained on the general population were validated on the AS dataset.

Feature importance analysis was performed on AS dataset through importance of RF, pre-trained on balanced datasets using all AS features. This step had the aim of evaluating each variable’s role and importance as CV risk predictive parameters.

Results

Data from 133 Caucasian AS patients (1330 patient-years) were analyzed. During follow-up, 18 patients had a CV event (1.35 events per 100 patient/years): eight cases of myocardial infarction, one case of stable angina pectoris, three cases of stroke, two cases of TIA, two cases of PAD, and two cases of HF. No fatal events were reported. The primary outcome was adjusted to fit each CV risk algorithm, leaving 18 for Framingham, 13 for SCORE (38), and 11 CV events for QRISK2, RRS, CUORE, and ASSIGN. As the RRS is not applicable to patients with diabetes or those younger than 45 years, these patients (n = 70) were excluded, and only 63 patients were included in the analysis of RRS. Patient’s characteristics are summarized in Table 1.

Table 1.

Patients’ characteristics at baseline

	AS tot (n = 133)	AS without CVD ( n = 115)	AS with CVD ( n = 18)	p
Age (years)	46 (39–54)	45 (38–53)	55 (46–64)	0.003
Females (%)	45.11	46.96	33.33	Ns
Disease duration (years)	13.34 (11.34–17.89)	12.73 (11.09–15.93)	16.76 (13.34–21.34)	0.007
HLA-B27 (%)	42.86	43.48	38.89	Ns
BASDAI	4.25 (2.62–6.2)	4.1 (2.6–5.64)	6.5 (4–7.2)	0.04
BASDAI < 4 (%)	50	54.67	23.08	0.06
BASFI	3 (1.25–5.25)	2.5 (0.8–4.7)	5.4 (2.1–6)	0.03
MRI sacroiliitis (%)	90.74	90.53	92.31	ns
MRI spondylitis (%)	34.95	32.97	50	ns
Syndesmophytes (%)	31.62	28	52.94	0.04
Enthesitis (%)	32.58	31.58	38.89	ns
CRP (mg/l)	3.2 (1.6–8)	3 (1.36–7)	4.4 (3–12.2)	0.03
ESR (mm/h)	21 (11–32)	19.5 (11–31)	24 (12–45)	ns
Smokers (%)	33.83	32.17	44.44	ns
CVD family history (%)	27.07	24.35	44.44	Ns
Atrial fibrillation (%)	1.50	0.87	5.56	ns
Diabetes (%)	7.52	6.96	11.11	ns
Stage 3–5 of chronic kidney disease (%)	1.50	0	11.11	0.02
Migraine (%)	12.03	13.91	0	ns
Antipsychotics (%)	0.75	0.87	0	ns
Systolic blood pressure (mmHg)	125 (120–140)	127.5 (120–135)	125 (120–140)	ns
SCORE	1 (0–2)	0 (0–1)	2 (1–3)	0.001
CUORE	1.54 (0.06–4.54)	1.06 (0.06–4)	5.01 (2.01–8.06)	0.034
FRS	6.53 (2.08–13.53)	6.01 (2.07–12.03)	13.06 (8.03–17.07)	0.037
QRISK2	4.01 (1.01–10.06)	3.06 (1–8.03)	12.06 (6.01–17)	0.003
QRISK3	5.1 (1.4–11.4)	4.6 (1.1–9.45)	12 (3.5–17.1)	0.006
RRS	3 (1–5)	3 (1–5)	9 (4–12)	< 0.001
ASSIGN	6 (3–12)	6 (3–10)	13 (6–18)	0.003

Data are expressed as median (25–75th percentile), unless otherwise indicated

Bold numbers indicate significant p-values

AS ankylosing spondylitis, BASDAI Bath Ankylosing Spondylitis Disease Activity Index, BASFI Bath Ankylosing Spondylitis Functional Index, CRP C-reactive protein, CVD cardiovascular disease, FRS Framingham Risk Score, MRI magnetic resonance imaging, ESR erythrocyte sedimentation rate, RRS Reynold’s Risk Score, SCORE Systematic Coronary Risk Evaluation

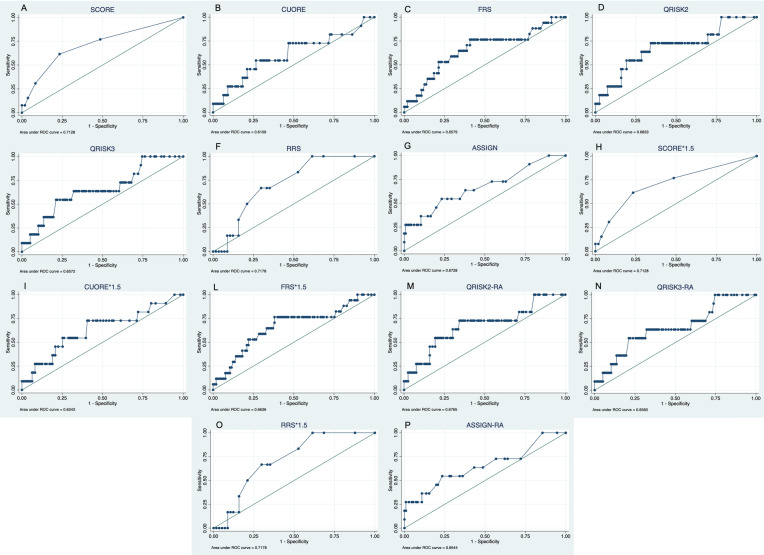
c-statistic scores of 0.71 (95% CI 0.55–0.87), 0.61 (95% CI 0.41–0.81), 0.66 (95% CI 0.51–0.81), 0.68 (95% CI 0.50–0.86), 0.66 (95% CI 0.48–0.84), 0.72 (95% CI 0.55–0.89) and 0.67 (95% CI 0.48–0.86) were found for SCORE, CUORE, FRS, QRISK2, QRISK3, RRS, and ASSIGN, respectively (Fig. 1a–g).

Fig. 1.

ROC curves of traditional cardiovascular risk algorithms. c-statistics scores: 0.71 (95% CI 0.52–0.87), 0.61 (95% CI 0.41–0.81), 0.66 (95% CI 0.51–0.81), 0.68 (95% CI 0.50–0.86), 0.66 (95% CI 0.48–0.84), 0.72 (95% CI 0.55–0.89), 0.67 (95% CI 0.48–0.86), 0.71 (95% CI 0.52–0.87), 0.63 (95% CI 0.44–0.83), 0.66 (95% CI 0.51–0.81), 0.68 (95% CI 0.49–0.86), 0.66 (95% CI 0.48–0.83), 0.72 (95% CI 0.55–0.89) and 0.65 (95% CI 0.46–0.85) for SCORE (a), CUORE (b), FRS (c), QRISK2 (d), QRISK3 (e), RRS (f), ASSIGN (g), SCORE*1.5 (h), CUORE*1.5 (i), FRS*1.5 (l), QRISK2-RA (m), QRISK3-RA (n), RRS*1.5 (o), and ASSIGN-RA (p)

Overall, the multiplicative factors did not seem to improve the performances of any of the algorithms: c-statistic scores of 0.71 (95% CI 0.52–0.87), 0.63 (95% CI 0.44–0.83), 0.66 (95% CI 0.51–0.81), 0.68 (95% CI 0.49–0.86), 0.66 (95% CI 0.48–0.83), 0.72 (95% CI 0.55–0.89) and 0.65 (95% CI 0.46–0.85) were found for SCORE*1.5 (p = ns vs. SCORE), CUORE*1.5 (p = ns vs. CUORE), FRS*1.5 (p = ns vs. FRS), QRISK2-RA (p = ns vs. QRISK2), QRISK3-RA (p = ns vs. QRISK3), RRS*1.5 (p = ns vs. RRS) and ASSIGN-RA (p = ns vs. ASSIGN), respectively (Fig. 1h–p).

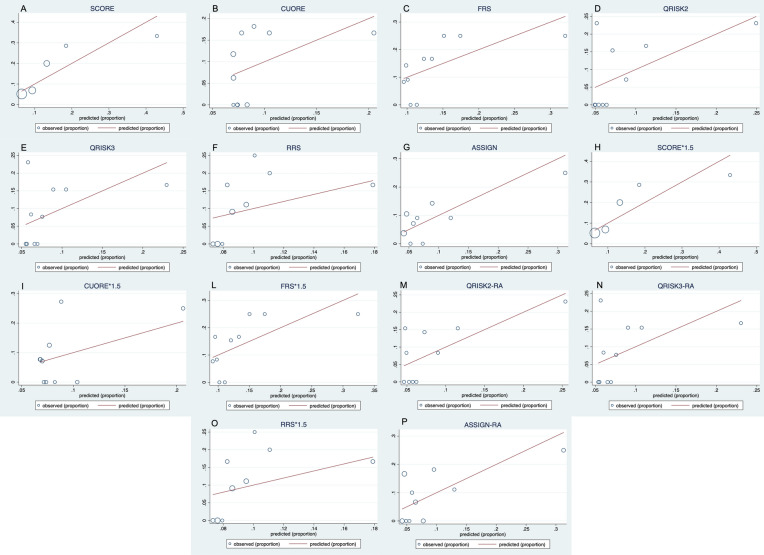
Calibration plots are reported in Fig. 2a–p. The Hosmer–Lemeshow test did not demonstrate a poor model for any of the CV risk algorithms: SCORE p = 0.6; SCORE*1.5 p = 0.6; CUORE p = 0.54; CUORE*1.5 p = 0.32; FRS p = 0.74; FRS*1.5 p = 0.69; RRS p = 0.74; RRS*1.5 p = 0.38; QRISK2 p = 0.079; QRISK2-RA p = 0.45; QRISK3 p = 0.15; QRISK3-RA p = 0.15; ASSIGN p = 0.8; ASSIGN-RA p = 0.25. Overall, we found a trend towards increased CV events compared to the expected, especially at low- and middle-risk levels.

Fig. 2.

Calibration plots comparing observed vs. predicted risk for SCORE (a), CUORE (b), FRS (c), QRISK2 (d), QRISK3 (e), RRS (f), ASSIGN (g), SCORE*1.5 (h), CUORE*1.5 (i), FRS*1.5 (l), QRISK2-RA (m), QRISK3-RA (n), RRS*1.5 (o), and ASSIGN-RA (p)

Sensitivity and specificity of the 10% and 20% cut-off points for CV risk for FRS, QRISK2, QRISK3, CUORE, RRS, and ASSIGN and of the 1% and 5% cut-off points for CV risk for SCORE are reported in Table 2.

Table 2.

Sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and accuracy of cut-off values in traditional and adapted according to EULAR recommendations CV risk scores

Variable	Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)	Accuracy (%)
SCORE > 1%	76.92 (46.19–94.96)	51.40 (41.54–61.18)	16.13 (11.87–21.54)	94.83 (86.98–98.05)	54.17 (44.83–63.29)
CUORE > 10%	18.18 (2.28–51.78)	93.58 (87.22–97.38)	22.22 (6.32–54.77)	91.89 (89.52–93.77)	86.67 (79.25–92.18)
Qrisk2 > 10%	54.55 (23.38–83.25)	76.47 (67.82–83.76)	17.65 (10.25–28.68)	94.79 (90.43–97.23)	74.62 (66.24–81.84)
Qrisk3 > 10%	54.55 (23.38–83.25)	73.73 (64.83–81.40)	16.22 (9.44–26.43)	94.57 (90.03–97.10)	72.09 (63.52–69.73)
FRS > 10%	58.82 (32.92–81.56)	66.99 (57.03–75.94)	22.73 (15.35–32.3)	90.79 (84.61–94.65)	65.83 (56.62–74.24)
RRS > 10%	33.33 (4.33–77.72)	84.21 (72.13–92.52)	18.18 (5.82–44.44)	92.31 (87.08–95.53)	79.37 (67.30–88.53)
SCORE 1.5 > 1%	76.92 (46.19–94.96)	51.40 (41.54–61.18)	16.13 (11.87–21.54)	94.83 (86.98–98.05)	54.17 (44.83–63.29)
CUORE 1.5 > 10%	27.27 (6.02–60.97)	82.88 (74.57–89.37)	13.64 (5.24–31.05)	92 (88.8–94.34)	77.87 (69.46–84.88)
Qrisk2-RA > 10%	63.64 (30.79–89.07)	69.75 (60.65–77.83)	16.28 (10.33–24.71)	95.40 (90.39–97.86)	69.23 (60.54–77.02)
Qrisk3-RA > 10%	54.55 (23.38–83.25)	70.34 (61.23–78.39)	14.63 (8.55–23.93)	94.32 (89.58–96.97)	68.99 (60.25–77.84)
FRS 1.5 > 10%	76.47 (50.10–93.19)	55.24 (45.22–64.95)	21.67 (16.47–27.96)	93.55 (85.82–97.20)	58.20 (48.93–67.06)
RRS 1.5 > 10%	66.67 (22.28–95.67)	66.67 (52.94–78.6)	17.39 (9.69–29.24)	95 (85.79–98.35)	66.67 (53.66–78.05)
SCORE > 5%	15.38 (1.92–45.45)	96.26 (90.7–98.97)	33.33 (9.2–71.17)	90.35 (88.1–92.21)	87.5 (80.22–92.83)
CUORE > 20%	9.09 (0.23–41.28)	99.08 (94.99–99.98)	50 (6.29–93.71)	91.53 (89.95–92.87)	90.83 (84.19–95.33)
Qrisk2 > 20%	18.18 (2.28–51.78)	92.44 (86.13–96.48)	18.18 (5.18–47.45)	92.44 (90.20–94.19)	86.15 (79–91.58)
Qrisk3 > 20%	18.18 (2.28–51.78)	92.37 (86.01–96.45)	18.18 (5.18–47.45)	92.37 (90.12–94.14)	86.05 (78.85–91.52)
FRS > 20%	25.53 (6.81–49.9)	89.32 (81.69–94.55)	26.67 (11.56–50.28)	87.62 (84.35–90.28)	80 (71.72–86.75)
RRS > 20%	0 (0–45.93)	92.98 (83–98.05)	0	89.83 (89.16–90.46)	84.13 (72.74–92.12)
ASSIGN > 20%	27.27 (6.02–60.97)	91.38 (84.72–95.79)	23.08(8.82–48.21)	92.98 (90.18–95.03)	85.83 (78.53–91.38)
SCORE 1.5 > 5%	15.38 (1.92–45.45)	96.26 (90.7–98.97)	33.33 (9.2–71.17)	90.35 (88.1–92.21)	87.5 (80.22–92.83)
CUORE 1.5 > 20%	9.09 (0.23–41.28)	96.40 (91.03–99.01)	20 (2.96–67.16)	91.45 (89.84–92.83)	88.52 (81.5–93.58)
Qrisk2-RA > 20%	27.27 (6.02–60.97)	89.08 (82.04–94.05)	18.75 (7.18–40.77)	92.98 (90.17–95.03)	83.85 (76.37–89.71)
Qrisk3-RA > 20%	27.27 (6.02–60.97)	89.83 (82.91–94.63)	20 (7.65–42.99)	92.98 (90.18–95.03)	84.5 (77.08–90.27)
FRS 1.5 > 20%	52.94 (27.81–77.02)	78.10 (68.97–85.58)	28.13 (18.04–41.03)	91.11 (85.97–94.49)	74.59 (65.91–82.04)
RRS 1.5 > 20%	16.67 (0.42–64.12)	91.23 (80.70–97.09)	16.67 (2.7–59.05)	91.23 (87.81–93.75)	84.13(72.74–92.12)
ASSIGN-RA > 20%	36.36 (10.93–69.21)	89.19 (81.88–94.29)	25 (11.45–46.26)	93.4 (90.01–95.69)	84.43 (76.75–90.36)

Data are expressed as percentage

FRS Framingham Score, SCORE Systematic Coronary Risk Evaluation; RRS Reynold’s Risk Score

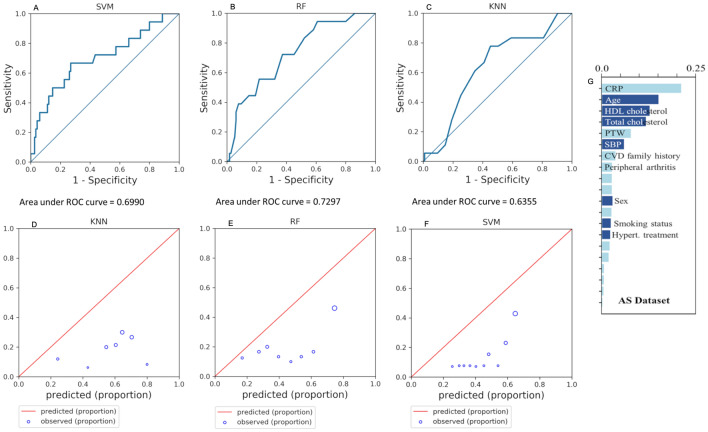
ML techniques were applied on AS patients. Models were built on the general population and validated over the rheumatic one. ML was trained with only six Framingham features (gender, age, SBP, hypertension treatment, smoking status, and total cholesterol). AUC values in the case of AS population are: 0.70 (95% CI 0.55–0.85) for SVM, 0.73 (95% CI 0.61–0.85) for RF and 0.64 (95% CI 0.50–0.77) for KNN. The correspondent ROC curves are reported in (Fig. 3a–c).

Fig. 3.

ROC curves of machine learning-based cardiovascular risk algorithms. c-Statistics scores: 0.70 (95% CI 0.55–0.85) for SVM (a), 0.73 (95% CI 0.61–0.85) for RF (b), and 0.64 (95% CI 0.50–0.77) for KNN (c). Calibration plots comparing observed vs. predicted risk for KNN (d), RF (e), and SVM (f). g Random forest’s importance

Overall, calibration plots demonstrated that observed CV risk is lower than the predicted one (Fig. 3d–f). Sensitivity, specificity, accuracy, positive predictive value, and negative predictive value are reported in Table 3.

Table 3.

Sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and accuracy of cut-off values in machine-learning CV risk scores

Variable	Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)	Accuracy (%)
KNN	77.78 (52.36–93.59)	54.78 (45.23–64.08)	21.21 (11.35–31.08)	94.03 (88.36–99.7)	57.89 (49.03–66.4)
SVM	66.67 (40.99–86.66)	60 (50.45–69.02)	20.69 (10.26–31.11)	92 (85.86–98.14)	60.90 (52.07–69.24)
RF	61.11 (35.75–82.70)	66.09 (56.67–74.65)	22 (10.52–33.48)	91.57 (85.59–97.54)	65.41 (56.68–73.44)

Data are expressed as percentage

KNN k-nearest neighbor, RF random forest, SVM support vector machine

Feature analysis was performed in this study by means of RF’s importance. RF was pre-trained in an AS dataset using all rheumatic features and it ranked features based on their relative importance. Results are represented in Fig. 3g. It is evident from the plot that in the case of AS, CRP has the highest importance, while SBP and hypertension treatment have lower importance. Feature importance analysis might be crucial to select variables to be included in further risk predictor development.

Concerning ML algorithms, a single threshold equal to 50% necessary to binarize the output (subjects above the threshold are considered at risk of developing a CVD) has been used instead of considering a cut-off, which is in the ML case meaningless. Therefore, among patients with CV events, 22.2% were under the threshold according to KNN, 27.8% were under the threshold according to SVM, and 27.8% were under the threshold according to RF.

Discussion

CVD represents an important cause of morbidity and mortality among patients with AS [32]. Only an accurate prediction of CV risk in these patients can allow the achievement of preventive strategies. All of the CV risk algorithms evaluated in the present study exhibit a poor discriminative ability, except for RRS and SCORE, which showed a fair performance. Intriguingly, only RRS includes CRP as a key variable in the assessment of CV risk. The adaptation of CV risk algorithms according to EULAR recommendations did not provide a significant improvement in discriminative ability. Notably, the Hosmer–Lemeshow test did not demonstrate a poor model fit for any of the CV algorithms considered in the present study; this is probably due to a low power of the test because of a small sample size. Regarding the cut-off point that marks the difference between low- and medium–high risk and the difference between low-medium and high risk, FRS*1.5 showed the best sensitivity, 76.47% (95% CI 50.1–93.19) and 52.94% (95% CI 6.02–60.97), respectively, and CUORE the best specificity, 93.58% (95% CI 87.22–97.38) and 99.08% (95% CI 93.53–99.98). The incidence of CVD in the present cohort may appear slightly increased as compared with other studies [33–37]; it should be noted that in the present study, a broad spectrum of CVDs has been taken into account, including TIA, PAD, and HF. Broadly, the analysis of the present study demonstrated the huge limitations of both traditional and adapted according to EULAR recommendations CV risk algorithms in patients with AS. Therefore, an ML approach has been carried out to better predict CV risk in these patients.

Considering the lack of substantial differences in performance among the algorithms examined in the present study and the availability of data from patients retrieved from the Kaggle website, we chose FRS as the reference for comparison in ML analysis. AS patients had 58.82% sensitivity and 66.99% specificity with the cut-off that marks the difference between low and medium–high risk and 25.53% sensitivity and 89.32% specificity with the cut-off that marks the difference between low-medium and high risk. Therefore, sensitivity drastically decreased when predicting CV risk in AS patients and the EULAR multiplication factor did not present an acceptable improvement. These results lead to hypothesize that an increase in sensitivity occurs with a correspondent reduction of specificity when growing the cut-off. However, accuracy remained the same or slightly decreased. EULAR multiplication factor acts in a similar way to the cut-off strategy.

For this reason, we explored the application of ML methods as new CV risk models for rheumatic patients. The general dataset was used to evaluate ML performances and to develop stable models, thanks to the large number of patients contained in it. Better results were obtained using a balanced dataset (i.e., with the same number of patients who experienced a CV event and patients who do not) to train the ML algorithms, since ML methods learn from data, therefore if the input data is asymmetric, the model will learn a consequent asymmetric decision rule. Parameter optimization has always been performed only on training datasets, otherwise performances would have been too optimistic. SVM has 66.67% sensitivity and 60% specificity; RF 61.11% sensitivity and 66.09% specificity, and KNN 77.78% sensitivity and 54.78% specificity. These results outperformed sensitivity with respect to FRS, but they tend to overestimate the risk. Therefore, future work is necessary to overcome this limitation.

Recently, it has been demonstrated that deep belief networks performed better than other prediction methods on CV risk assessment using six variables (age, SBP, diastolic blood pressure, HDL cholesterol, smoking status, and diabetes) [38]. SVM had 100% specificity, 71.8% sensitivity, and 71.8% accuracy, hence it was effective in identifying low risk, but it could not correctly predict high risk. RF had 61.4% specificity, 82.2% sensitivity, and 77.2% accuracy. Statistical deep belief networks outperformed all methods, with 73.3% specificity, 87.6% sensitivity, and 83.9% accuracy. However, a better result was obtained by Narain and coworkers who did a comparison between FRS and quantum neural network-based approach, with 98.57% accuracy [20]. This result shows that different ML methods could be used in CV risk prediction and potentially in the specific field of rheumatic patients.

Future models should also consider the great number of variables associated with CV risk in rheumatic patients. For this purpose, RF could represent a useful technique to better understand the variables most informative within a bigger dataset. Unfortunately, this method does not consider the possible correlation between two variables. In the present study, we demonstrated that patients with AS do not present, among the top features, the traditional ones used by FRS and other traditional methods; the most important variable is CRP. This is consistent with the result regarding RRS, which shows the best discriminative ability, probably because it includes CRP as a variable. Moreover, CRP plays a key role in AS, as reported elsewhere [39]. Taking into account this variable in future ML studies could increase classification performances on AS patients.

Several weaknesses of this study should be considered. The main limitation of this study is the dataset’s dimensions. Basing on this preliminary study, we suggest that a dataset of about 500 or 1000 patients (15% CV events) might be enough to allow training and validation of solid ML algorithms specific for AS. Moreover, RRS calculation was possible only in 63 patients. Furthermore, only Caucasic Italian patients have been enrolled in the present study. In addition, no information about the possible role of the different medications approved for AS on CVD can be inferred.

Conclusions

The present study contributes to a deeper understanding of CV risk in AS, with a particular focus on CV risk algorithms. Despite the small sample size, it can be concluded that RRS and SCORE has a fair performance in predicting CVD and it can be hypothesized that CRP might play a pivotal role in patients with AS. Moreover, ML could allow the development of innovative patient-specific CV risk models.