A multiscale coarse-grained model of the SARS-CoV-2 virion

Abstract

The severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is the causative agent of the COVID-19 pandemic. Computer simulations of complete viral particles can provide theoretical insights into large-scale viral processes including assembly, budding, egress, entry, and fusion. Detailed atomistic simulations are constrained to shorter timescales and require billion-atom simulations for these processes. Here, we report the current status and ongoing development of a largely “bottom-up” coarse-grained (CG) model of the SARS-CoV-2 virion. Data from a combination of cryo-electron microscopy (cryo-EM), x-ray crystallography, and computational predictions were used to build molecular models of structural SARS-CoV-2 proteins, which were then assembled into a complete virion model. We describe how CG molecular interactions can be derived from all-atom simulations, how viral behavior difficult to capture in atomistic simulations can be incorporated into the CG models, and how the CG models can be iteratively improved as new data become publicly available. Our initial CG model and the detailed methods presented are intended to serve as a resource for researchers working on COVID-19 who are interested in performing multiscale simulations of the SARS-CoV-2 virion.

Significance

This study reports the construction of a molecular model for the SARS-CoV-2 virion and details our multiscale approach toward model refinement. The resulting model and methods can be applied to and enable the simulation of SARS-CoV-2 virions.

Introduction

The onset of the global coronavirus disease 2019 (COVID-19) pandemic has brought intense investigation into the molecular components of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) encoded by the virus’s 30-kb genome. Structural biology efforts using cryo-electron microscopy (cryo-EM) and x-ray crystallographic techniques are currently reporting new structures of viral proteins every week (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12), and computational structure prediction efforts are targeting unresolved sections of the genome using a variety of protein folding algorithms. Computational and experimental studies are underway to find new molecular therapeutics that can inhibit viral activity or further elucidate the mechanisms of action of SARS-CoV-2 proteins (13, 14, 15, 16). The computer simulation of large-scale SARS-CoV-2 processes such as virion assembly, budding, entry, and fusion will remain intrinsically challenging to investigate using all-atom (AA) molecular dynamics (MD), owing to the computational cost of meaningfully simulating the hundreds of millions to billions of atoms involved.

A holistic model of the SARS-CoV-2 virion can provide insight into the mechanisms of large-scale viral processes and the collective behavior of macromolecules involved in viral replication and infectivity. SARS-CoV-2 virions contain four main structural proteins: the spike (S), membrane (M), nucleocapsid (N), and envelope (E) proteins (17). S proteins are glycosylated trimers that mediate fusion and entry, in part by attaching enclosed fusion peptide sequences into the membranes of host cells (18). M proteins appear as dimeric complexes embedded within the virion envelope and are believed to anchor ribonucleoprotein complexes to the envelope (19,20). N proteins associate with and organize RNA into ribonucleoprotein structures found in the interior of virions (21,22). Lastly, E proteins are thought to form pentameric ion channels that are found at the lipid bilayers of virion membranes and contribute to viral budding (23).

In this work, we construct a largely “bottom-up” coarse-grained (CG) model of the SARS-CoV-2 virion from the currently available structural and atomistic simulation data on SARS-CoV-2 proteins. In general, this model serves as a resource for researchers working on COVID-19 and as a platform to incorporate computational and experimental data. This model also enables new multiscale studies of SARS-CoV-2 processes to possibly help find treatment and prevention strategies against COVID-19. Atomistic trajectory and experimental structural data deposited in the National Science Foundation (NSF) Molecular Sciences Software Institute (MolSSI) will be incorporated as they become publicly available (24). In this work, we detail several of our CG methods used to iteratively develop a CG model for the full SARS-CoV-2 virion, in which molecular interactions between CG particles are derived using a combination of phenomenological, experimental, and atomistic simulation approaches.

Methods

Building models from structural data

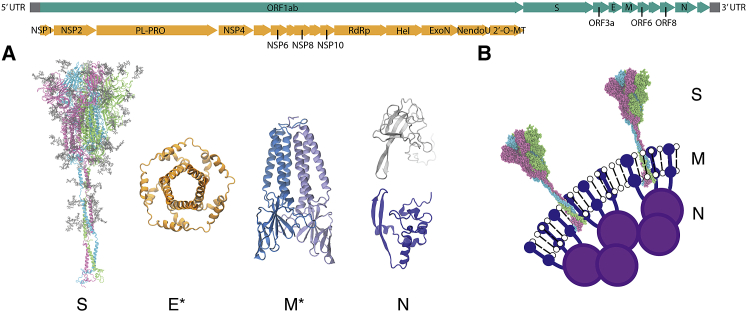
We first constructed atomic models of the structural proteins of the SARS-CoV-2 virion (Fig. 1). AA models of the open and closed state of the S protein were built based on the cryo-EM structures of the spike ectodomain (Protein Data Bank, PDB: 6VYB, 6VXX) (5), respectively, and atomic models of the N protein were constructed based on the x-ray crystallographic structure of the nucleocapsid N-terminal domain (NTD) (PDB: 6M3M) (27). Glycosylation sites were modeled using Glycan Reader & Modeler in CHARMM-GUI (28) and the site-specific glycoprofile derived from mass spectrometry and cryo-EM analysis (29,30). Homology models for the S-protein stalk, including the HR2 and TM domains, were assembled as α-helical trimeric bundles using MODELER (31) on the basis of secondary structure assignments in JPred4 (32). Homology models for the SARS-CoV-2 N protein C-terminal domain (CTD) were created from the x-ray crystallographic structure of the SARS-CoV N protein CTD (PDB: 2CJR) (33). Missing amino acid backbones in loop regions were built in MODELER, and side chain rotamers were built using SCWRL4 (34). We used atomic models for the M-protein dimer (25) and the pentameric E ion channel (26) that were developed by homology.

Figure 1.

Viral proteins of SARS-CoV-2. The genome of SARS-CoV-2 is shown in the top panel. Nonstructural proteins (NSPs) encoded in the open reading frame (ORF) 1ab are colored in orange, and the full genome is in teal. (A) AA models of the structural proteins of SARS-CoV-2 consisting of the S, E, M, and N proteins are given. Asterisks indicate homology-modeled protein structures for M and E (25,26). (B) A schematic of the virion surface from cryo-EM images of the virion is given, adapted from (19). To see this figure in color, go online.

AA protein models (see discussion below) were subsequently simulated and coarse grained to generate the CG models (see Fig. 2 and sections below). A previously developed CG model for lipids was used, consisting of three CG beads per lipid and distinct bead types for lipid headgroups and hydrophobic tails (35). A single-component CG lipid bilayer was generated in a spherical configuration and equilibrated using CG MD simulations under constant NVT conditions in LAMMPS (36). We note that in the future, more complex CG lipid models (37) can be added. Transmembrane segments of component membrane proteins were visually identified and assigned based on secondary structure motifs. Individual lipids on the outer leaflet of the spherical bilayer were randomly selected and used as initial positions for embedding spike, membrane, and envelope proteins. For each initial position, the center of mass of the transmembrane domain was aligned with the center of the lipid bilayer, and the principal axis of the protein was aligned with the vector normal to the lipid bilayer. Transmembrane regions were then substituted for the overlapping CG lipids to embed the proteins. The procedure was iterated until a spike, membrane, and envelope protein density on the virion surface was achieved that was approximately consistent with current available experimental estimates of ∼25, 1000, and 20 per virion, respectively, from cryo-EM and biochemical data (38, 39, 40). The diameters of the membrane envelope are ∼100 and 140 nm including the S proteins on the virion surface. As higher-resolution experimental data are released, the overall structure of this model can be refined.

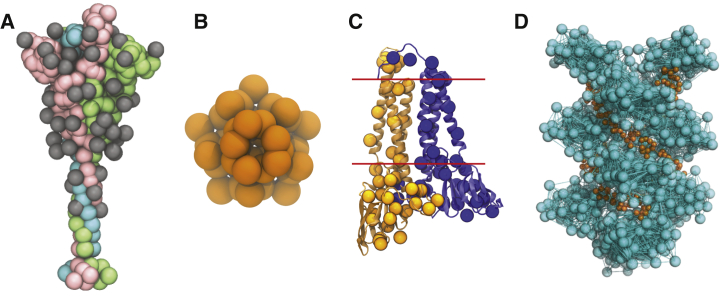
Figure 2.

CG models of the SARS-CoV-2 structural proteins. (A) The CG model of the S-protein trimer in the open state is shown. The protein monomers are depicted as pink, green, and cyan beads, respectively; the monomer in pink has an exposed receptor binding domain. Each of the 22 (× 3) N-linked glycans are depicted as gray beads. (B) The CG model of the pentameric E protein is depicted as orange beads. (C) The CG M dimer model is depicted as yellow and blue spheres, overlaid on top of the AA model of the M dimer. Each monomer has 36 CG sites, and the red lines indicate the approximate positions of the transmembrane region. (D) The CG model of the N protein CTD helix in complex with viral RNA is shown. The N protein helix and bonds derived from the hENM are depicted in cyan, and the RNA is depicted as orange beads. To see this figure in color, go online.

AA MD simulations of the S protein

Two glycosylated models of the open and closed spike were inserted into a symmetric 225 Å × 225 Å lipid bilayer mimicking the composition of the endoplasmic reticulum (ER)-Golgi intermediate compartment (41,42). The lipid patch was built using CHARMM-GUI. The complete protein-membrane system was solvated using the TIP3P water model (43) and neutralized with chloride and sodium ions to maintain a 150-mM concentration. Each system contained ∼1.7 million atoms. Minimization and equilibration were performed using the CHARMM36 force field (44,45) and NAMD 2.14 (46). Production runs were performed in the NPT ensemble using a Langevin thermostat at 310 K and Nosé-Hoover Langevin barostat at 1 atm. All production runs used a 2-fs timestep and the SHAKE algorithm. Multiple replicas of AA MD simulations of the open (3×) and closed (3×) systems were performed on NSF Frontera at the Texas Advanced Computing Center (TACC), achieving an aggregate sampling of 3.0 and 1.8 μs, respectively.

CG model of the S protein

The CG model of the glycosylated S protein (Fig. 2 A) was parameterized from the AA MD simulations described above (47). Reference statistics used conformations sampled equally from both open and closed states, with AA trajectories spanning 3.0 and 1.8 μs, respectively. First, the protein was mapped to CG beads using essential dynamics coarse graining (EDCG) (48). We used 60 and 50 CG beads for the S₁ and S₂ domains, respectively, and the 22 N-linked glycans were each mapped to a single bead. Intraprotein interactions were represented as a heteroelastic network model (hENM) with bond energies k(r − r₀)², where k is the spring constant of a particular CG bond and r₀ is the equilibrium bond length. These parameters were optimized using the hENM method (49). Interprotein interactions within the S-trimers were composed of excluded volume, attractive, and screened electrostatic terms. For excluded volume interactions, a phenomenological soft cosine potential, A[1 + cos$\frac{\pi r}{r_c}$], was used, where A = 25 kcal/mol and r_c is the onset for excluded volume. Attractive, nonbonded interactions between interprotein contacts were modeled as the sum of two Gaussian potentials, $A_1\exp \left[-\frac{{\left(r_{ij}-r_1\right)}^2}{2{\sigma }_1^2}\right]+A_2\exp \left[-\frac{{\left(r_{ij}-r_2\right)}^2}{2{\sigma }_2^2}\right]$, where r₁ and σ₁ are the mean and standard deviation determined by a fit to the pair correlation between CG sites i and j through least-squares regression. The constants A₁ and A₂ were optimized using relative-entropy minimization (REM). Screened electrostatics were modeled using Yukawa potentials, $q_i{q}_j/\left(4\pi {\epsilon }_r{\epsilon }_0{r}_{ij}\right)$exp(-κr_ij), where q_i is the aggregate charge of CG site i, κ = 1.274 nm⁻¹ is the inverse Debye length for 0.15 M NaCl, and ɛ_r is the effective dielectric constant of the protein environment, approximated as 17.5 (50).

CG models of the M and E proteins

AA simulations of the M-protein dimer were performed using homology models and a membrane model based on the ER. The membrane model included PC:PE:PI:PS:Chol lipids (0.45:0.10:0.23:0.10:0.12 mol fraction) as an initial approximation to the ER-Golgi intermediate compartment (ERGIC). The protein-membrane systems were solvated and neutralized in a similar fashion as described previously. The simulations were equilibrated for 400 ns before a 4-μs production run on Anton 2. All simulations were run in the constant NPT ensemble at 310 K and 1 atm using the CHARMM36m force field. A CG model containing ∼5 residues per CG bead was mapped from the reference statistics of the AA MD simulations using the EDCG (Fig. 2 C), and hENM approaches. A CG model for the E protein was developed by linearly mapping the amino acid sequence to particles at a resolution of 1 CG bead per five amino acids (Fig. 2 B).

CG model of the N protein

Several studies suggest that the CTD of the N protein assembles into a helix that contains two RNA binding grooves (21,51). Based on these studies, we constructed atomic and CG models of the viral ribonucleoprotein complex (vRNP) by iterating between CG and AA simulations. We first constructed an atomic model of the N protein CTD helix with two RNA binding grooves by stacking three copies of the CTD octamer structure (PDB: 2CJR), which is composed of four CTD dimers and homology modeled from the x-ray crystallographic structure of the SARS-CoV N protein CTD (33). The CTD helix was simulated in the CHARMM36m force field for 400 ns. We then constructed the CTD helix model using EDCG combined with hENM, followed by manually placing CG RNA beads into the groove of the helix (Fig. 2 D). The positions of the CG beads were used as restraints to build an atomic model of the vRNP complex. Finally, the vRNP model was relaxed and simulated in the CHARMM36m force field for 400 ns. It is important to note that recent cryo-EM studies have found granule-like densities within the virion for the vRNP complex (22). Structural detail into how CTD oligomers (including the previously proposed helical model) and RNA fit into these densities will likely require higher-resolution images.

Deriving CG molecular interactions from AA simulations

Several computational approaches have been developed to build or refine CG models using data from AA or fine-grained simulations. Our approach to coarse-graining the SARS-CoV-2 virion is to couple several CG methods in a hierarchical fashion. CG sites or “beads” are mapped from atomic structures using EDCG, a method designed to preserve the principal modes of motion sampled during atomic-level simulations (48). In EDCG, a given CG mapping operator, ${\mathit{M}}_{\mathbf{R}}^N:$ rⁿ → R^N, that relates the configurations of the atomistic trajectory (rⁿ) to that of the CG model (R^N) is variationally optimized using simulated annealing. Typically, the mapping is constructed so that contiguous segments of a protein’s primary amino acid sequence are mapped to distinct CG sites. For a fixed number of CG beads, N, the sets of atoms that are mapped to CG sites are adjusted to minimize the target residual:

$${\chi }^2=\frac{1}{3N}\sum _{I=1}^N{\langle \sum _{i,j}{\left|{\mathit{r}}_i-{\mathit{r}}_j\right|}^2\rangle }_t:i,j\epsilon I,j\ge i,$$ (1)

where I = 1, …, N is the CG site index; the brackets, ${\langle \cdot \rangle }_t$, denote a time-averaged quantity; the sum over i, j is a sum over all unique pairs in the set of atoms belonging to the CG site, I; and r_i = x_i − $⟨{\mathit{x}}_i⟩{}_t$ is the displacement of atom i from the atom’s mean position, $⟨{\mathit{x}}_i⟩{}_t$. Note that the residual is small when the displacements, r_i and r_j, are similar, i.e., the motions of atoms in the same CG site are correlated. A new map is constructed and either accepted or rejected according to a Metropolis-Hastings criterion (i.e., accepted if ${\chi }_n^2<{\chi }_{n+1}^2$; otherwise, accepted or rejected such that the new map has probability ρ = exp[−$\left({\chi }_{n+1}^2-{\chi }_n^2\right)$/T], where n is the number of iterations for simulated annealing and $T$ is the coupling to a fictitious temperature that is gradually lowered during optimization).

After defining the AA ↔ CG map, intramolecular interactions within a single polypeptide chain are treated using elastic network models (ENMs) to capture protein flexibility. In the hENM method (49), effective harmonic bonds are assigned to all pairs of particles in the CG model within a tunable distance cutoff that all initially have the same force constant, k_ij, between particles i and j to construct the bonded topology of the CG model. The harmonic force constants are optimized by first computing the normal modes of this model. In other words, solving the eigenvalue problem,

$$\mathit{H}{\mathit{v}}_{\mathit{k}}={\omega }_{\mathit{k}}^2\mathit{M}{\mathit{v}}_{\mathit{k}},$$ (2)

where H is the Hessian H_i,j = ${\frac{{\partial }^{2}V}{\partial q_i\partial q_j}|}_m$, M is the diagonal matrix for the masses of the particles, and ω_k the frequency for the mode of motion. Note that this is the solution to the equation of motion

$$\mathit{M}\frac{{\text{d}}^2\mathit{q}}{\text{d}{t}^2}+\mathit{Hq}=0,$$ (3)

where q is the generalized coordinate, and that for N classically interacting particles near the potential energy minimum, q_m,

$$V\left(\mathit{q}\right)=V\left({\mathit{q}}_m\right)+\sum _i{\frac{\partial V}{\partial q_i}|}_m\left(q_i-q_{i,m}\right)+\frac{1}{2}\sum _{i,j}{\frac{{\partial }^{2}V}{\partial q_i\partial q_j}|}_m\left(q_i-q_{i,m}\right)\left(q_j-q_{j,m}\right)+O{\left(\mathit{q}-{\mathit{q}}_m\right)}^3,$$ (4)

V(q_m) is a constant, and ${\frac{\partial V}{\partial q_i}|}_m$is zero. Using the normal modes, mean-squared fluctuations $\langle r_{ij}^2\rangle =\langle {\left(x_{ij}-\langle x_{ij}\rangle \right)}^2\rangle$ for each i, j pair can be computed by rescaling the amplitudes according to an equipartition of energy that reflects the temperature of the atomistic data. Harmonic force constants for each bond in the CG ENM are then iteratively adjusted so that fluctuations in the CG model, match that of the atomistic data, i.e.,

$$\frac{1}{k_{ij}^{n+1}}=\frac{1}{k_{ij}^n}-\alpha \left({\langle r_{ij}^2\rangle }_{\text{CG}}-{\langle r_{ij}^2\rangle }_{\text{AA}}\right),$$ (5)

where n is the number of iterations and α is a parameter that controls the magnitude of the adjustment for each iteration.

For the intermolecular interactions between proteins, nonbonded CG interactions are determined either using force matching (a.k.a. multiscale CG) (52,53) or REM approaches (54,55). In multiscale CG, the CG potential is constructed from a linearly independent basis set

$$U\left({\mathit{R}}^N\right)=\sum _{D=1}^{{\mathit{N}}_{\mathit{D}}}{\varphi }_D{U}_D\left({\mathit{R}}^N\right),$$ (6)

where the functional forms for the basis potentials, U_D (e.g., B-splines, Lennard-Jones, etc.), and the number of them, N_D, are determined by the user. The coefficients {ϕ_D} are variationally optimized such that the following residual is minimized:

$${\chi }^2=\frac{1}{3N}{\langle \sum _{I=1}^N{\left|{\mathit{f}}_{\mathit{I}}\left({\mathit{r}}^n\right)-{\mathit{F}}_{\mathit{I}}\left({\mathit{M}}_{\mathbf{R}}^N\left({\mathit{r}}^n\right)\right)\right|}^2\rangle }_t,$$ (7)

where F_I(R^N) = −$\nabla$U(R^N) is the CG force and f_I(rⁿ) is the atomistic force on the CG site I. Similarly, in the REM approach, the objective function for minimization is the Kullback-Liebler divergence, which provides a metric for the differences between the atomistic and CG probability distributions

$$S_{\text{rel}}=\int {\rho }_{\text{AA}}\left({\mathit{r}}^{\mathit{n}}\right)\text{log}\left(\frac{{\rho }_{\text{AA}}\left({\mathit{r}}^{\mathit{n}}\right)}{{\rho }_{\text{CG}}\left({\mathit{R}}^{\mathit{N}}\right)}\right)d{\mathit{r}}^{\mathit{n}}+{\langle S_{\text{map}}\rangle }_{\text{AA}},$$ (8)

where ρ_AA(rⁿ) = $Z_{\text{AA}}^{-1}{e}^{-\beta U_{\text{AA}}\left({\mathit{r}}^{\mathit{n}}\right)}$ and ρ_CG(R^N) = $Z_{\text{CG}}^{-1}{e}^{-\beta U_{\text{CG}}\left(R^N\right)}$ in the canonical ensemble and Z is the configurational partition function. Furthermore, the relative entropy can be expressed as a difference between the potential energy and free energy of the atomistic and CG ensembles:

$$S_{\text{rel}}={\beta \langle U_{\text{CG}}-U_{\text{AA}}\rangle }_{\text{AA}}-\beta \left(A_{\text{CG}}-A_{\text{AA}}\right)+{\langle S_{\text{map}}\rangle }_{\text{AA}},$$ (9)

where A = −k_BTlogZ. Minimization of the relative entropy is performed using iterative Newton-Raphson techniques. It is important to note, however, that the quality and fidelity of such CG models are determined by the molecular behavior sampled in the underlying AA simulations.

Incorporating new behavior in CG simulations

Macromolecular complexes such as virions undergo a wide range of behavior, including physical and chemical transitions, that will be difficult to capture through AA simulations alone or even with experimental techniques. This is especially true for processes that involve large conformational changes that are not sampled effectively in AA simulations, whether because of the long timescales required, free energy barriers, or inherent limitations of the simulation force field. For instance, the S protein of SARS-CoV-2 has two proteolytic cleavage sites (at the S1-S2 and S2′ locations), and binds to the host cell receptor, angiotensin-converting enzyme 2 (ACE-2). Cleavage and binding events trigger dramatic conformational changes in the spike that result in the insertion of the fusion peptide into the host cell membrane. High-resolution structural studies of the S-ACE-2 complex have made protein binding simulations amenable to enhanced sampling techniques at the AA level (4,56). The proteolytic cleavage of the spike and large-scale conformational shift toward fusion peptide insertion, however, are more difficult to sample in atomistic simulations. To address these issues, one can use CG molecular simulation techniques that allow CG particles to adaptively switch discrete “states” and interactions, such as ultra-coarse-graining (UCG) (57, 58, 59). In the limit of infrequent internal state switches, UCG implements microscopically reversible state changes that are coupled to a Metropolis-Hastings-like criterion:

$$K_{i\to j}=k_{i\to j}\text{min}[\frac{k_{j\to i}}{k_{i\to j}}{e}^{-\beta \left(U_j-U_i\right)},1]$$ (10)

where K_{i → j} is the instantaneous switching rate from state i to j, U_j − U_i is the CG effective potential energy difference between states j and i, and the rates k_{i → j} and k_{j → i} are model parameters either treated as input or calculated from atomistic simulations. This approach is similar to hybrid kinetic Monte Carlo and MD methods but with a spatial kinematic component, and it can be used to examine the transitions of the spike (i.e. “states”) that lead to the fusion of SARS-CoV-2 with host cells.

Experiments can probe longer timescales than are available from AA MD simulations. In recent cryo-EM images of SARS-CoV-2 particles, the S1 domain of the S protein was found to transiently open and close to bind the ACE-2 receptor (3,5), which are subtle conformational changes that are difficult to sample in atomistic simulations. For these conformational changes—in the case that they cannot be treated as discrete state switches—plastic network models (60) or multiconfiguration coarse graining (MCCG) methods (61) can be used to construct a CG model that continuously transitions from one state to the next. For plastic network models, two known experimental configurations of the protein are used to build a multibasin ENM that represents deviations away from each of the individual conformational minima. A phenomenological interaction Hamiltonian is constructed that couples and mixes the ENMs between the two structural endpoints. In MCCG, the primary difference is that the coupling terms in the Hamiltonian are constructed from a two-state mixing approach, derived on the basis of a mapped potential of mean force that is explicitly computed from AA simulation data along collective variables that distinguish between the two (or more) conformational states at a CG level.

Phenomenological CG models

An alternative (and sometimes necessary “top-down”) route to deriving CG models is to construct a model Hamiltonian and then analyze the model’s resulting behavior in the context of the assumed interactions. Typically, parameterization of such models is designed to fit or reproduce particular observables measured in experimental data and perhaps particular sets of AA simulation data. These can be performed based on variational optimization of some system-specific functional that depends on the experimental observable. Model Hamiltonian approaches have the advantage that physical intuition is clearer but are not systematic because each new problem requires a different treatment for the set of interactions involved. Furthermore, these approaches often require orthogonal experiments to validate the underlying model. Such coarse-graining methods are, however, especially useful in cases for which atomistic simulation is difficult or infeasible to obtain on the system or if the bottom-up methods described above are not expected to yield converged results for the effective CG potential, owing to limited atomistic sampling.

Results and discussion

Here, we present results from the first CG simulations of the SARS-CoV-2 virion (Fig. 3). It should be noted that these are early results, and we can thus expect additional simulations to become available from this model as more experimental data and AA simulations become available for the various virion components. In addition, the overall CG methodology and modeling of the virion will continue to evolve and are works in progress.

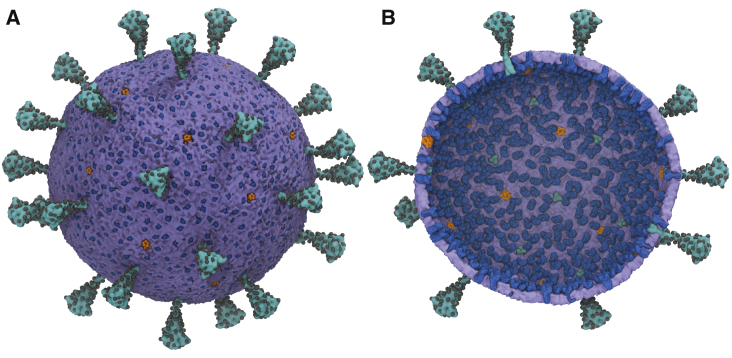
Figure 3.

A multiscale model of the SARS-CoV-2 virion. (A) Exterior view of the SARS-CoV-2 virion is given. (B) Interior view of the SARS-CoV-2 virion is given. S-protein trimers are depicted in teal, with the glycosylation sites represented as black spheres. M-protein dimers are in blue, with pentameric E ion channels in orange. The density of S, M, and E proteins was chosen to be consistent with experiments (38, 39, 40). The diameters of the membrane envelope are ∼100 and 140 nm including the S proteins on the virion surface. To see this figure in color, go online.

A CG MD simulation was performed on the complete CG virion model using LAMMPS for 10 × 10⁶ CG time steps (see Video S1). The system was energy minimized using conjugate gradient descent. A temperature of 300 K was maintained with a Langevin thermostat, with a damping constant (t_damp = 10 ps) and 100-fs timestep. Statistics were collected every 100 CG time steps. Several radial distribution functions (RDFs) or pair correlations between CG particles were computed for the MD trajectories of individual S proteins and compared to the mapped AA reference statistics from which the models were derived (Fig. 4 A). In general, the CG model captured the positions and peaks in the pair correlation functions; however, error in the fine structure of the peaks was also present, indicating that refinement involving the addition of more expressive CG basis potentials (e.g., splines) may be necessary.

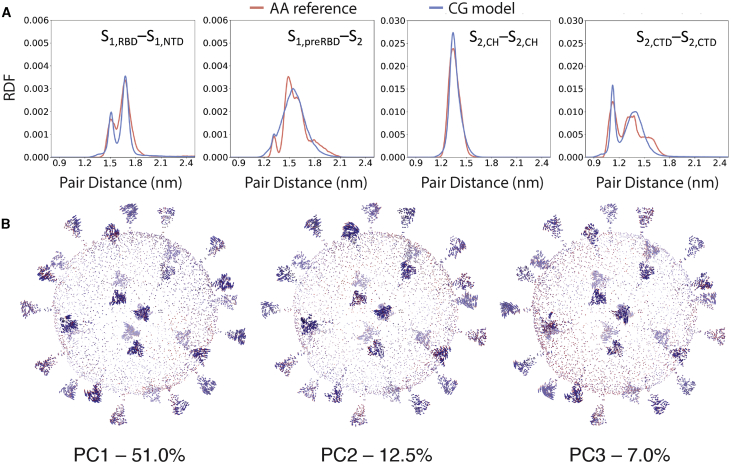
Figure 4.

Analysis of the CG MD simulations of the SARS-CoV-2 virion. (A) RDFs showing the comparison between mapped AA reference statistics and the CG spike model during the MD simulations are given. The measured RDFs are for CG particles that were mapped from the following AA residues of 1) S_1,RBD [S459-D467] and S_1,NTD [W104-L118], 2) S_1,preRBD [E309-R319] and S₂ [A852-L861], 3) S_2,CH [A1015-K1028], and 4) S_2,CTD [Y1215-V1228]. (B) Principal modes of motion of the SARS-CoV-2 virion computed from the CG MD simulation are shown. Arrows are colored from blue to red, indicating the direction of movement (see Videos S2, S3, and S4 for PC1–3, respectively). The first principal component (PC1) accounts for 51% of the total variation observed during simulation, whereas the second (PC2) and third (PC3) account for 12.5 and 7%, respectively. To see this figure in color, go online.

We performed principal component analysis (PCA) on a subset of the CG particles to examine collective modes of motion of the virion (Fig. 4 B). The Cartesian coordinates of one particle for every 15 CG lipids, one for every M and E protein, and one for every 3 S particles were extracted from the trajectory data and used to compute the covariance matrix, c_i,j = $\frac{1}{N-1}\sum _{t=1}^N{r}_i\left(t\right)r_j\left(t\right)$, where r_i(t) is the mean-free position vector, r_i(t) = x_i − ${\langle x_i\rangle }_t$ of particle i. The highest-variance eigenmode, PC1 (see Video S2), corresponds to splaying motions in the S1-S2 domain of the S protein and accounts for 51% of the total variance seen during the simulations. Similarly, PC2 (see Video S3) accounts for 12.5% of the variance and corresponds to rocking motions of the S1-S2 domain, whereas PC3 (see Video S4) accounts for 7.0% of the total variance and corresponds to twisting of the S1-S2 during CG MD. In general, there was a high degree of variance in the S protein, and these correlated modes of motion are likely informative of how the virion collectively utilizes spike proteins to explore and detect receptors. Longer CG simulations with more expressive CG models will likely be required to uncover additional modes of motion in the virion, including modes that involve the structural M, N, and E proteins.

Conclusions

This work provides an initial CG molecular model of the SARS-CoV-2 virion and details a bottom-up CG approach capable of further refining the model as new atomistic and experimental data become available. Currently, the lipid envelope is described using a particle-based phenomenological model with a soft tunable bending modulus well suited for large-scale membrane deformations, whereas the M and E proteins are modeled as rigid bodies. Intraspike interactions were developed using REM approaches on the basis of extensive, microsecond AA simulations of the spike protein. The N protein is modeled on the basis of AA simulations of helical oligomers in complex with RNA. Cross-interactions between the lipids and structural proteins used attractive Gaussian potentials between the hydrophobic lipid tails and the transmembrane domains of membrane proteins. This virion model will be iteratively refined and improved as structural, biochemical, and AA trajectory data are publicly released. The construction of an integrated CG model from individual atomistic simulations will also benefit from new developments in systematic methods for ensuring consistency between CG models developed from the reference statistics of those simulations. In particular, methods that variationally optimize in a “divide and conquer” fashion on the basis of joint statistics will likely improve model fidelity. Nonetheless, despite these noted challenges, we find that the behavior of SARS-CoV-2 structural proteins is coupled in the virion.

CG simulations of viral processes have helped elucidate a wide range of mechanisms in viruses. For example, in HIV, CG simulations contributed to the understanding of the self-assembly of the capsid (62) and innate immune sensor recognition and block of viral activity (63), as well as its inhibition by drug molecules (64). Atomistic simulations of ligand binding have also revealed a variety of unexpected, drug-targetable protein-ligand interaction sites (65, 66, 67, 68, 69, 70, 71). It is likely that molecular probes into the processes involving a holistic model of the SARS-CoV-2 virion can help reveal new routes to combat the virus by exploiting viral mechanisms involving large-scale behavior.

The CG virion model is available at https://doi.datacite.org/dois/10.34974%2Fq8ya-wh69 and https://github.com/alvinyu33/sars-cov-2-public. The model will be periodically updated with new versions as data are added and the model refined.

Author contributions

A.Y., A.J.P., P.H., V.M.-G., and G.A.V. designed research. A.Y. performed modeling and analysis on the virion. A.Y. and A.J.P. performed modeling and analysis on the S protein. A.Y. and P.H. performed modeling and analysis on the N protein. A.Y. and V.M.-G. performed modeling and analysis on the M protein. L.C., Z.G., A.C.D., and R.E.A. contributed AA simulation data on the S protein. A.Y., A.J.P., P.H., V.M.-G., L.C., Z.G., A.C.D., R.E.A., and G.A.V. wrote the manuscript.

Editor: Tamar Schlick.