Mechanochemical Function of Myosin II: Investigation into the Recovery Stroke and ATP Hydrolysis

Abstract

Myosin regulates muscle function through a complex cycle of conformational rearrangements coupled with the hydrolysis of adenosine triphosphate (ATP). The recovery stroke reorganizes the myosin active site to hydrolyze ATP and cross bridge with the thin filament to produce muscle contraction. Engineered mutations K84M and R704E in Dictyostelium myosin have been designed to specifically inhibit the recovery stroke and have been shown to indirectly affect the ATPase activity of myosin. We investigated these mutagenic perturbations to the recovery stroke and generated thermodynamically correct and unbiased trajectories for native ATP hydrolysis with computationally enhanced sampling methods. Our methodology was able to resolve experimentally observed changes to kinetic and equilibrium dynamics for the recovery stroke with the correct prediction in the severity of these changes. For ATP hydrolysis, the sequential nature along with the stabilization of a metaphosphate intermediate was observed in agreement with previous studies. However, we observed glutamate 459 being utilized as a proton abstractor to prime the attacking water instead of a lytic water, a phenomenon not well categorized in myosin but has in other ATPases. Both rare event methodologies can be extended to human myosin to investigate isoformic differences from Dictyostelium and scan cardiomyopathic mutations to see differential perturbations to kinetics of other conformational changes in myosin such as the power stroke.

Graphical Abstract

1. INTRODUCTION

ATPases are a broad class of enzymes that are important to biological life. Hydrolysis of adenosine triphosphate (ATP) within the binding sites of these proteins catalyzes a plethora of functions from intracellular transport of protein and lipid aggregates to ionic transport across cell membranes.^1,2 The class of ATPases associated with locomotion are often referred to as motor proteins; they couple the hydrolysis of ATP with force generation. The myosin superfamily is a class of motor proteins that are largely associated with intracellular transport (unconventional myosins) as well as muscle function (conventional myosins) and others.^3,4 Myosin II is a conventional myosin that exists as a dimer, with each monomer consisting of a heavy chain and two light chains. The heavy chain is structurally defined with a large globular head and an alpha helical tail, while the two light chains, also globular in motif, bind to the heavy chain near the transition of the head with the tail. The myosin head is the functional unit of myosin, consisting of the nucleotide binding site and structural regions that interact with actin filaments for force generation. Understanding of the interplay between the ever-changing actin-myosin interactions and ATP hydrolysis is vital to understand myosin function.

Myosin regulates muscle function through its kinetic cycle.^5,6 The Lymn-Taylor cycle⁷ describes the biochemical processes undergone by myosin where conformational changes as well as ATP hydrolysis modulate how myosin interacts with the actin filament in what is described to be the sliding filament model⁸ of muscle function. When nucleotides are missing from the binding site within myosin, it is held fixed on the actin surface in its strongest interacting state, often referred to as the rigor state. When ATP binds, it deviates from its rigor state to its lowest affinity state for actin, denoted as postrigor (PR) myosin. ATP hydrolysis must occur to increase myosin’s affinity for actin, but before that, the myosin head must reorganize to prepare the active site. The recovery stroke is the conformational change that primes the myosin head for ATP hydrolysis and subsequent interaction with the actin filament. Both the recovery stroke^9–11 and ATP hydrolysis^12–17 have been explored extensively as major regulators to the cross-bridge cycle between myosin and actin. Specifically, engineered point mutations have been designed to monitor their effect on the recovery stroke and subsequently ATP hydrolysis, while quantum mechanics/molecular mechanics (QM/MM) simulations have explored how the residues in the active site of myosin couple to the decomposition of ATP to adenosine diphosphate (ADP) and phosphate ion.

In this study, we expand on previous explorations of the recovery stroke and ATP hydrolysis within myosin to develop computational models for these phenomena. Though computational observations have been made previously for the recovery stroke,^18–21 our aim is to be able to calculate the free-energy profile (FEP) for the conformational change and model deviations in these profiles due to point mutations. Engineered mutations K84M and R704E, which lie at the interface between the N-terminal domain and the converter region of myosin, have been shown to decrease the rate constant and equilibrium constant for the recovery stroke.¹¹

Previous QM/MM studies have been utilized to study ATP hydrolysis within the myosin II active site.^12–17 Kiani and Fischer²² summarized their work and others in which mechanisms and barriers for ATP hydrolysis were determined by sampling the minimum potential energy surface between myosin in a pre-power stroke (PPS) conformation with ATP and ADP + Pi bound, respectively, in the nucleotide binding site. They observed that the overall mechanism proceeds sequentially, with the terminal phosphoanhydride bond of ATP breaking before a hydrating water attacks the newly formed metaphosphate intermediate. Glutamate 459 was shown to polarize the attacking water to allow the transfer of a proton from the aforementioned water to another lytic water, forming a hydronium ion that transfers the proton to nearby serines and finally to the phosphate to form the final product H₂PO₄⁻. However, in a more recent study by Lu et al.,¹⁷ metadynamics with the string method sampled and determined the minimum free energy pathway (MFEP) for ATP hydrolysis in various myosin II conformations. In their calculations, the MFEP observed Glu459 directly abstracting the proton, forming a Glu-OH⁺ intermediate that then shuttled the proton to the phosphate through a secondary water. The use of a glutamate to abstract a proton from a hydrating water has been observed in other ATPases,^23–25 but it is still unclear whether this mechanism is also inherent to myosin or proceeds as described by Kiani et al.

However, the limitations of both methodologies that produced these competing mechanisms are apparent, with refinement on a potential energy surface lacking proper thermodynamic sampling and metadynamics requiring a definition of appropriate degrees of freedom a priori that may contribute to the overall mechanism. Transition path sampling (TPS)²⁶ along with QM/MM simulations can accurately sample the transition between the reactant and product states without prior definition of the mechanism, producing an ensemble of trajectories with a large density in the trajectory space around the MFEP. Here, we implement metadynamics^27,28 and TPS as enhanced sampling methods for the recovery stroke and hydrolysis, respectively, to further enlighten the behavior behind both of these phenomena.

2. SIMULATION METHODS

2.1. Metadynamics Simulation of the Recovery Stroke.

Molecular dynamics simulations were carried out to determine the effect of mutations to the myosin structure and how the thermodynamics of the recovery stroke is therefore affected. Initially, structures that represent the beginning and final conformations of the recovery stroke had to be created as inputs for the simulations. X-ray diffraction structures for PR (PDB ID: 1FMW)²⁹ and PPS (PDB ID: 1VOM)³⁰ myosin were utilized with the preparation of each structure following a similar scheme. First, any unresolved residues within the myosin head from the X-ray images were filled in with the SWISSMODEL³¹ program. Any other missing atoms, such as hydrogens, were added to each structure with the CHARMM42³² program. Modification of the original substrates was also performed at this point to contain only ATP and a magnesium ion bound in the active site of both the PR and PPS structures. Each system was solvated in a box of TIP3 waters with a 15 Å barrier between the edge of the water box and the surface of the protein. Counterions of K and Cl were also added to a set concentration of 0.15 mol/L to neutralize the whole system.

Once prepared, PR and PPS myosin structures were subject to minimization, heating, and equilibration protocols with the NanoScale Molecular Dynamics (NAMD)³³ program. All simulations were performed with the CHARMM32 force field to simulate the protein environment. Five thousand steps of minimization were performed with the conjugate gradient method followed by a slow heating phase in which the system energy was increased at a rate of 1 K/ps until a final temperature of 300 K was reached. A final equilibration of 2 ns was run in an isobaric-isothermal (NPT) ensemble at 1 atm and 300 K. For the metadynamics simulation, the equilibrated PR structure was subjected to the calculation, with the equilibrated PPS structure acting as the target. In metadynamics, a collective variable (CV) is a physical representation of all changes as one proceeds from one stable state to the other. It needs to be chosen such that (1) it clearly distinguished the states of interest and (2) contains the relevant degrees of freedom correlated with the phenomenon that is to be observed. Since it would be difficult to correctly identify all relevant degrees of freedom a priori for such a large conformational change, this second condition can be less strict; a convenient CV may be chosen. In this study, the CV of choice is the projection of the difference vector (p) between the two coordinate systems as shown below

$$p=\sum _{i=1}^n\left(x_i^{\prime }-x_i^{\text{ref}}\right)\cdot \left(U\left(x_i\left(t\right)-x_{cog}\left(t\right)\right)-\left(x_i^{\text{ref}}-x_{\text{cog}}^{\text{ref}}\right)\right)$$

where x^ref and x_cog are the generalized coordinates for the reference and center of geometries of the group of atoms, respectively, U is the optimal rotation matrix, and x′ is a second set of coordinates. The optimal rotation matrix minimizes the root-mean-squared deviation (rmsd) between Ux^ref and x′ and, along with the monitoring of the center of geometry for the group of atoms, allows the CV to be invariant to rotations and translations as a rigid body. This CV is analogous to a rmsd between two coordinate sets but is not bounded at 0 and therefore can take on negative values. This CV and others are natively supported in NAMD through the CV module.³⁴ When normalized, p is a measure in the difference between two coordinate states (x^ref and x′) from state “A” and state “B.” When the two states are maximally apart, as designated from the initial coordinates, p returns a value of 1. However, when the two states are minimally apart and therefore overlapping, p returns a value of 0. In this case, a value of 1 designates the PR structure, while a value of 0 denotes the PPS state. In conventional metadynamics, convergence criteria must be specified, as the algorithm has been shown to not approach the estimate for the potential of mean force asymptotically but oscillates about the mean.³⁵ In this study, we monitored the evolution of the CV along the desired range (from 0 to 1), and the determined convergence was reached when this distribution was its flattest, in that all areas have been explored with the underlying potential energy surface filled completely and evenly. Determination of overall required time to convergence and error estimation of the free-energy calculation for metadynamics has been discussed previously³⁶ but in general has been difficult to categorize for biological systems and can only be accomplished for toy systems. Minor constraints are imposed on the protein to remove translation and rotation degrees of freedom that do not contribute to the observation of interest. Implementation of metadynamics calculations was performed within NAMD with the CV module.³⁴

2.2. Simulation of Myosin-Mediated ATP Hydrolysis.

For this investigation, we began with the already prepared structure for PPS myosin, with ATP + MG bound as described previously. Since there is no classical description of bond breakage, ATP along with its surrounding protein environment had to be treated quantum mechanically, while the remaining atoms were treated classically according to the CHARMM32 force field to reduce the overall computational cost. The QM/MM regions were partitioned according to previous investigations on ATP hydrolysis within Dictyostelium myosin II.²² Specifically, the included residues are as listed: Ser181, Thr186, Asn233, Ser236, Ser237, Arg238, and Glu459. Additionally, four water molecules along with the magnesium ion and the triphosphate chain of ATP were included in the QM region. Boundaries between the QM and MM regions were treated with the generalized hybrid orbital (GHO) method³⁷ with carbon atoms being used as link atoms. Figure 1 shows the partition of the QM region from the classical region. The PM3 method was used as implemented in the CHARMM program to treat the QM atoms. Though previous studies were performed at the DFT level,^12–16 a previous study demonstrated that QM/MM studies with semiempirical and ab initio methods are capable of reproducing comparable transition states within a methyltransferase.³⁸

Figure 1.

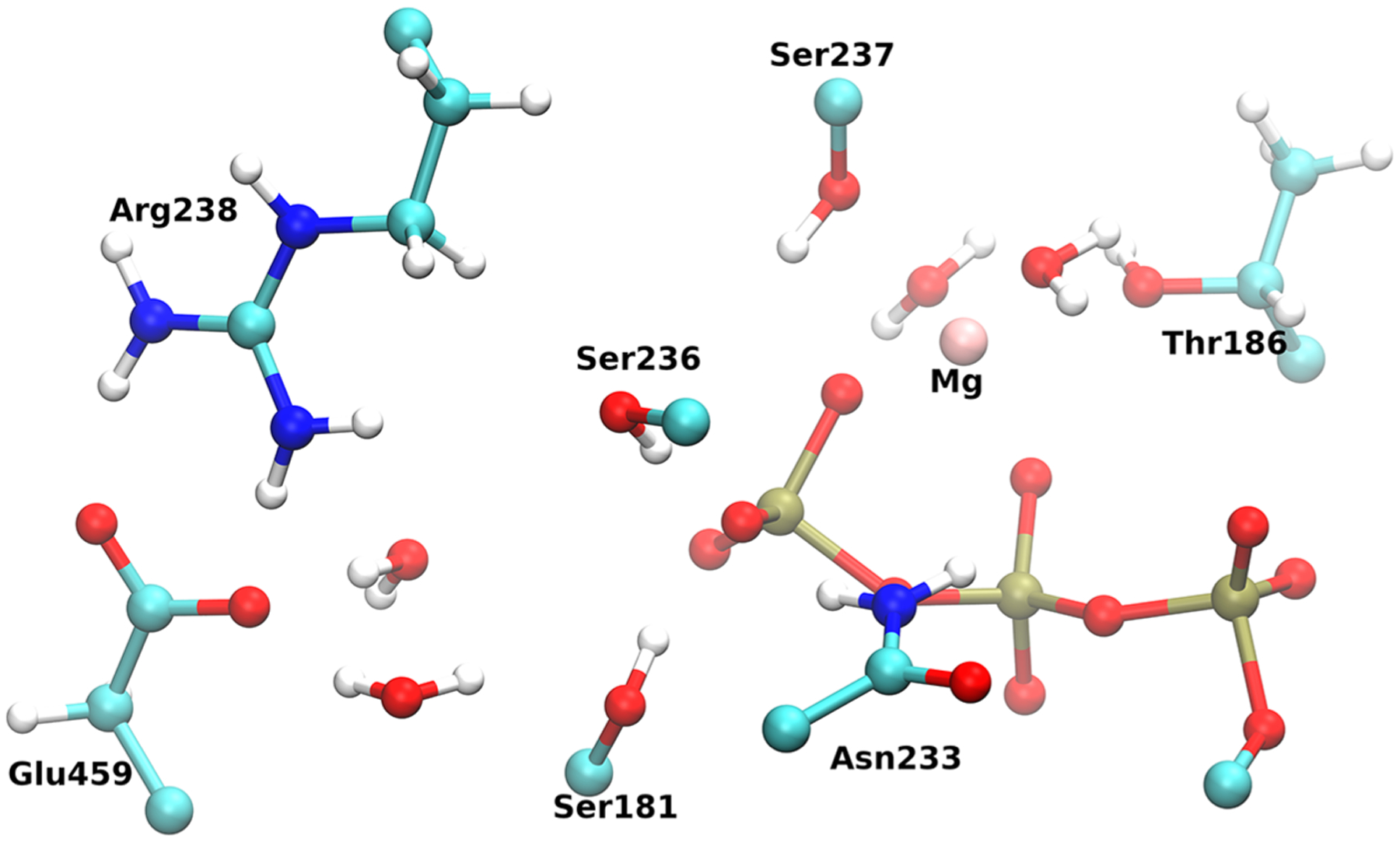
Arrangement of the QM region with the triphosphate chain (red and gold) of ATP and surrounding residues. 4 waters along with the magnesium ion were also treated quantum mechanically.

After the partitioning of the system, the protein was solvated in a water droplet extending 15 Å barrier from the protein surface, and potassium ions were added to neutralize the system. The following system was minimized initially with 50 steps of steepest descent, followed by 200 steps, with the adopted basis Newton-Raphson method with 10 kcal/mol constraints being exerted on the QM region. Following minimization, the system was heated slowly to 300 K with velocities being reassigned at the rate of 5 K every 100 steps. This heating cycle was repeated with decreasing constraints on the QM region (10, 7, 5, 3, 1, and 0 kcal/mol). A final, unconstrained equilibration was performed at 300 K for 20 ps. Treatment of the specified atoms with QMs was held throughout minimization, heating, and equilibration.

TPS²⁶ was used to generate statistically unbiased trajectories in the reactive space. Initially, order parameters need to be established to distinguish the reactive state, myosin + ATP, from the product state, myosin + ADP + Pi. These parameters included the distance between the γ oxygen and γ phosphate of ATP, and the other was the distance between the γ phosphate and the oxygen of the attacking water. The distances were specified to be less than and greater than 1.9 Å in the reactant state, while the opposite was true in the product state. An initial constrained trajectory was created to bias the system from the reactant state to the product state, and then further trajectories were created from this initial seed by selecting a random slice from the previous trajectory, perturbing its momenta and propagating the system forward and backward in time for 250 fs. A total of 150 trajectories were created, with the initial 60 trajectories being excluded from analysis to allow decorrelation from the initial bias trajectory.

Once an ensemble of reactive trajectories is created, committor analysis was performed to identify the transition states. Committor values are determined by picking a slice within a trajectory and creating further trajectories from this initial point, each with random momenta, and determining the overall probability of committing to the product state. Next, we wish to specify the reaction coordinate that contains degrees of freedom responsible for the barrier crossing. These degrees of freedom are orthogonal to the stochastic separatrix, which is the ensemble of transition states previously specified. Constrained trajectories are initiated from the transition states with those constraints being applied to degrees of freedom suspected of contributing to the barrier crossing, and committor probabilities are determined for these trajectories. If the degrees of freedom are chosen correctly, the system does not deviate from the stochastic separatrix, and the committor distribution remains peaked at 0.5, while flat distributions or those peaked at other values suggest that contributing degrees of freedom are being omitted.

3. RESULTS AND DISCUSSION

3.1. Recovery Stroke.

Metadynamics simulations sampled the underlying potential energy surface to determine the overall free-energy change when transitioning from PR myosin to PPS myosin and how changes to the myosin structure, K84M and R704E, alter the observations. To determine how any mutagenic perturbations perforate through the subdomains of the myosin head, a unique CV was defined for each subdomain of myosin: NTerm (residues 1–130), U50 (131–453), RelayHelix (454–498), L50 (499–693), and converter (694–747). Therefore, five one-dimensional contributions to the overall free-energy change were determined concurrently, with their combination detailing the overall effect as seen in Figure 2.

Figure 2.

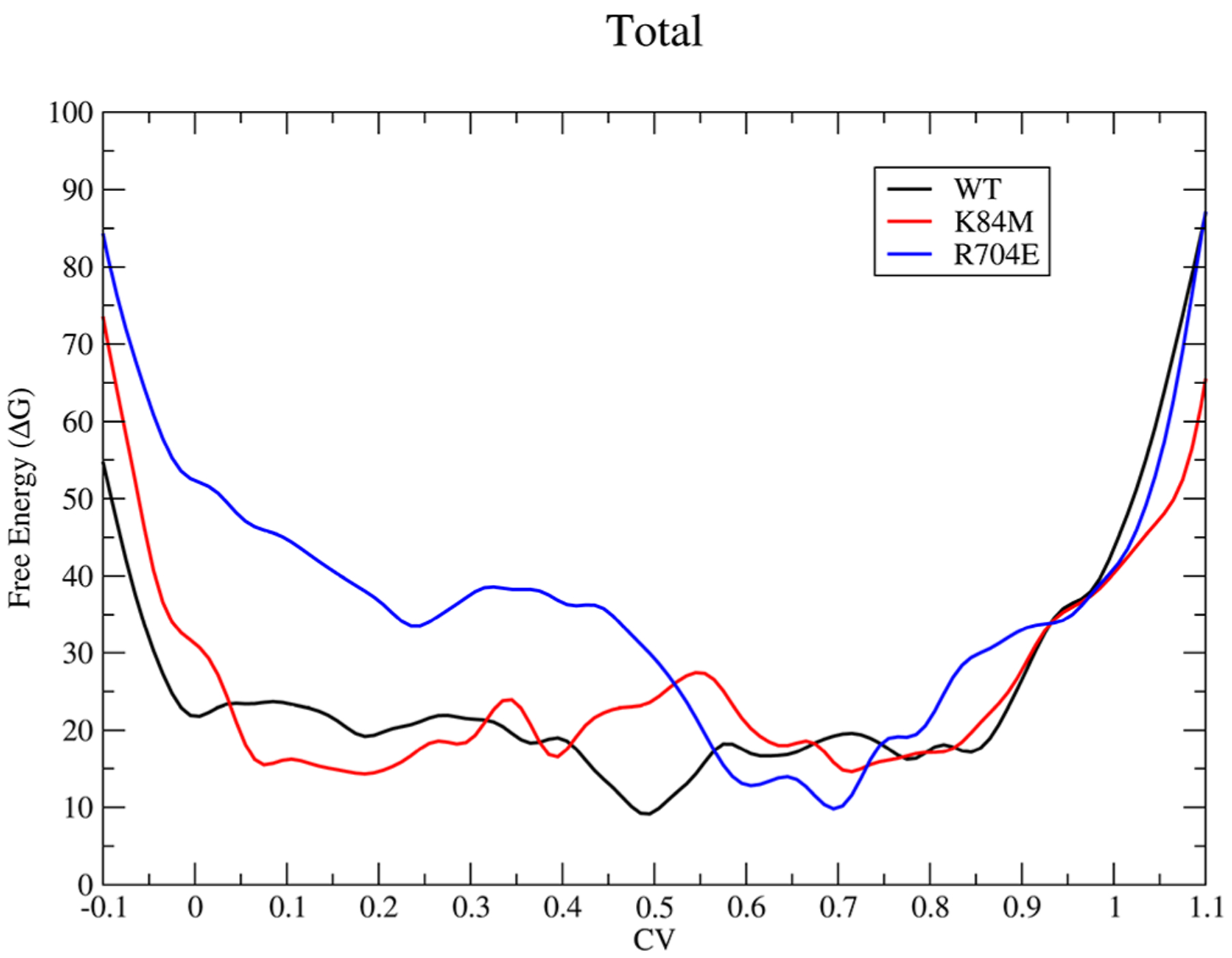
Total free-energy change, in kcal/mol, for wildtype (black), K84M (red), and R704E (blue) for the recovery stroke. The graph should be read from right to left.

For the recovery stroke, transitioning from a CV value of 1–0, there is an increase in the free-energy barrier when residues 84 and 704 are replaced with the specified residues, methionine and glutamate, respectively. In the wildtype, residues K84 and R704 have the same charge in the PR structure and lie right next to each other in very close contact.¹¹ Replacement of these residues with opposing charged residues creates a new electrostatic contact that stabilizes the PR structure and therefore requires more energy to break and therefore deviate from the PR structure. This was observed experimentally,⁶ with both the equilibrium constant as well as the rate constant for the recovery stroke decreasing due to the amino acid substitutions with a greater effect due to R704E than K84M; the same effect is observed in this study. The wildtype free-energy surface is rather flat and smooth after the initial move away from the PR structure (0.8–1.0) with a small well around the PPS state, suggesting a small stabilization at that conformation. However, both K84M and R704E deviate from the wildtype FEP, raising the overall free energy at the PPS structure, and have large changes in the surface to reach this point with a large climb from approximately 0.1–0.0 for K84M and 0.6–0.0 for R704E. These changes suggest an overall destabilization away from the PPS structure toward the PR structure. This is further observed in the FEP for just the N-terminal domain contribution in Figure 3.

Figure 3.

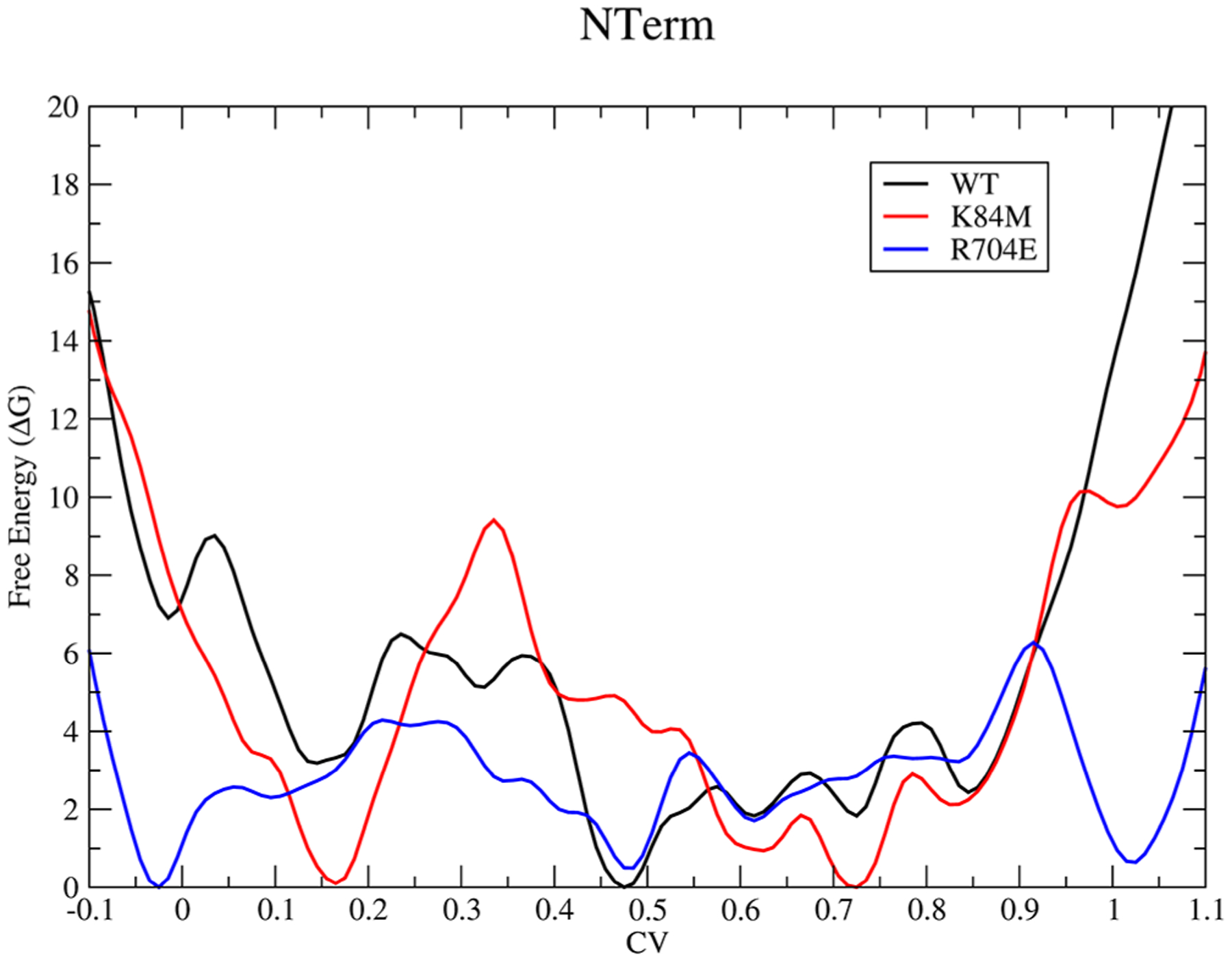
Free-energy surface for the N-terminal (residues 1–130) subdomain of myosin during the recovery stroke.

Near the PR structure, for the wildtype, the FEP moves sharply downward as the N-terminal domain along with the converter moves away from each other. In the case of the mutants, however, with the addition of the additional electrostatic interaction, a free-energy well appears around the PR structure with the depth correlated with the strength of this new contact. A similar effect can be observed in the converter contribution to the FEP (Figure S1), but the effect is not as clear, most likely due to an overall greater entropic contribution to the rearrangement of the converter region as opposed to the N-terminal subdomain. There are additional features that appear along the transition for the wildtype and mutant simulations, such as a free-energy well around a CV value of 0.5 in Figure 2 for the wildtype simulation, but since the definition of the CV is a general walk along the free-energy surface and not the optimal pathway, it is hard to determine whether these features are biologically relevant or not. However, it is clear that even with the use of a general pathway, the methodology is able to resolve the experimentally observed effects of these mutations to the recovery stroke.

3.1.1. ATP Hydrolysis: Formation of HPO₄²⁻.

When the initial bias trajectory was being created, it was observed that the proton from the attacking water was abstracted by the nearby glutamate, residue 459, to prime the newly formed hydroxide for a nucleophilic attack of the γ phosphate of ATP. Previous studies have suggested that an additional water performs this polarizing function of the attacking water,^12–16 but our attempts to replicate this mechanism led to unstable trajectories that could not be probed any further. The highly charged nature of the glutamate would have a greater effect on polarizing the attacking water and therefore deprotonating it, so it is unclear whether the other observed mechanism is an artifact due to the nature of their calculations, which were based on minimum potential energy pathways that do not provide accurate thermodynamic sampling. There have been other studies in similar systems where a glutamate performs a similar function^23–25 and abstracts a proton from the attacking water, so we included it as an order parameter.

In examining the ensemble of trajectories, it is apparent that the mechanism precedes sequentially as discussed previously,^17,22 with the phosphoandydride bond of ATP breaking before the bond formation between the metaphosphate intermediate and the attacking water. Figure 4 illustrates the bond breaking-forming events from a representative trajectory.

Figure 4.

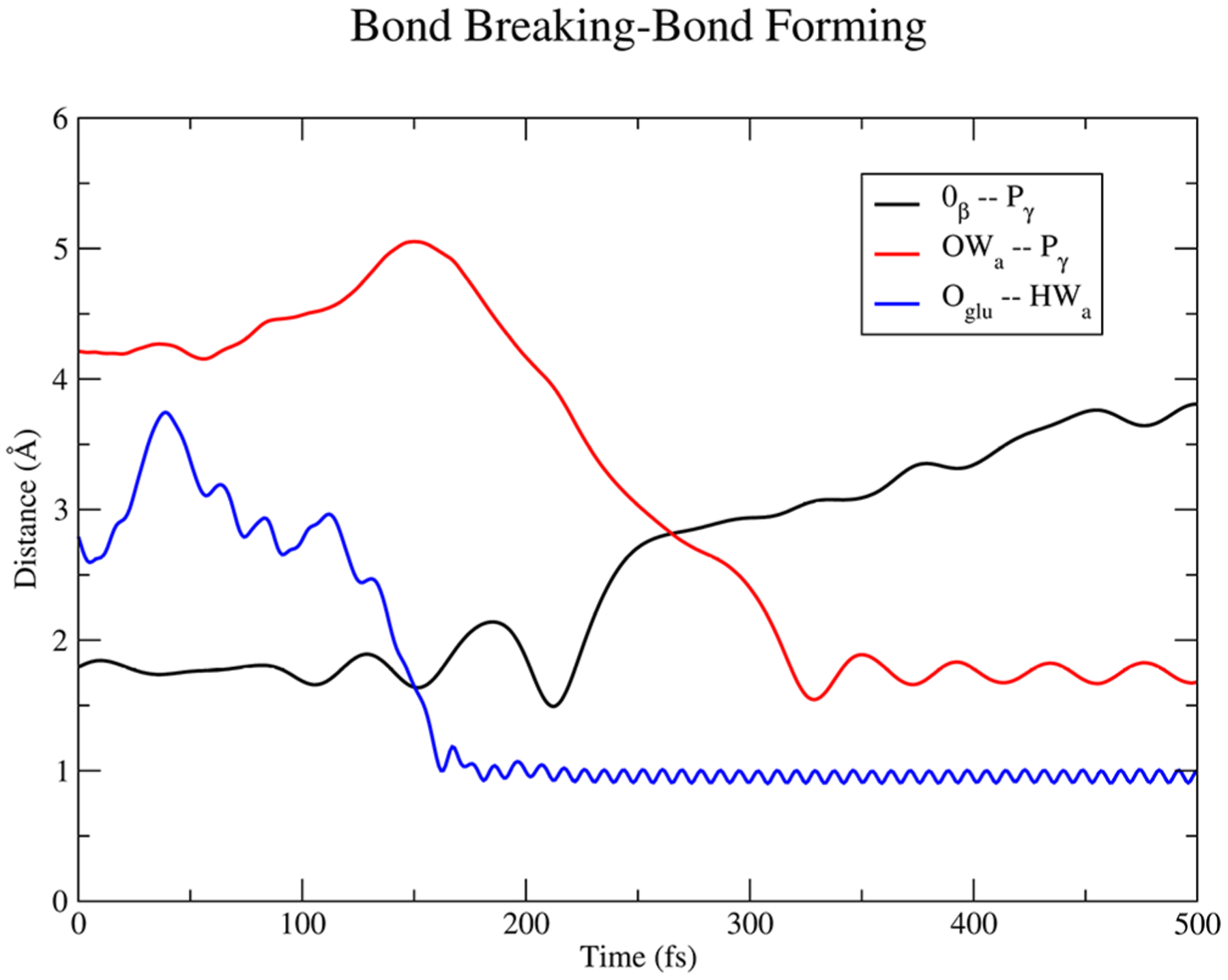
Plot of atomic distances for the γ phosphate (P_γ), β oxygen (O_β) bond of ATP along with the deprotonation of the attacking water (HW_a) by GLU459 (O_glu), and subsequent attack of the newly formed hydroxide (OW_a) to the γ phosphate from a representative trajectory.

Initially, Glu459 abstracts the proton from the attacking water, while the beta phosphoanhydride bond of ATP fluctuates with increasing amplitude until the bond breaks over 150 fs. Superseding the formation of ADP + PO₃⁻, the attacking hydroxide comes in and forms the HPO₄²⁻ intermediate about 75 fs after the initial phosphoanhydride bond-breaking event. Figure 5 shows a mechanistic summary of the formation of HPO₄²⁻ observed throughout the ensemble of trajectories.

Figure 5.

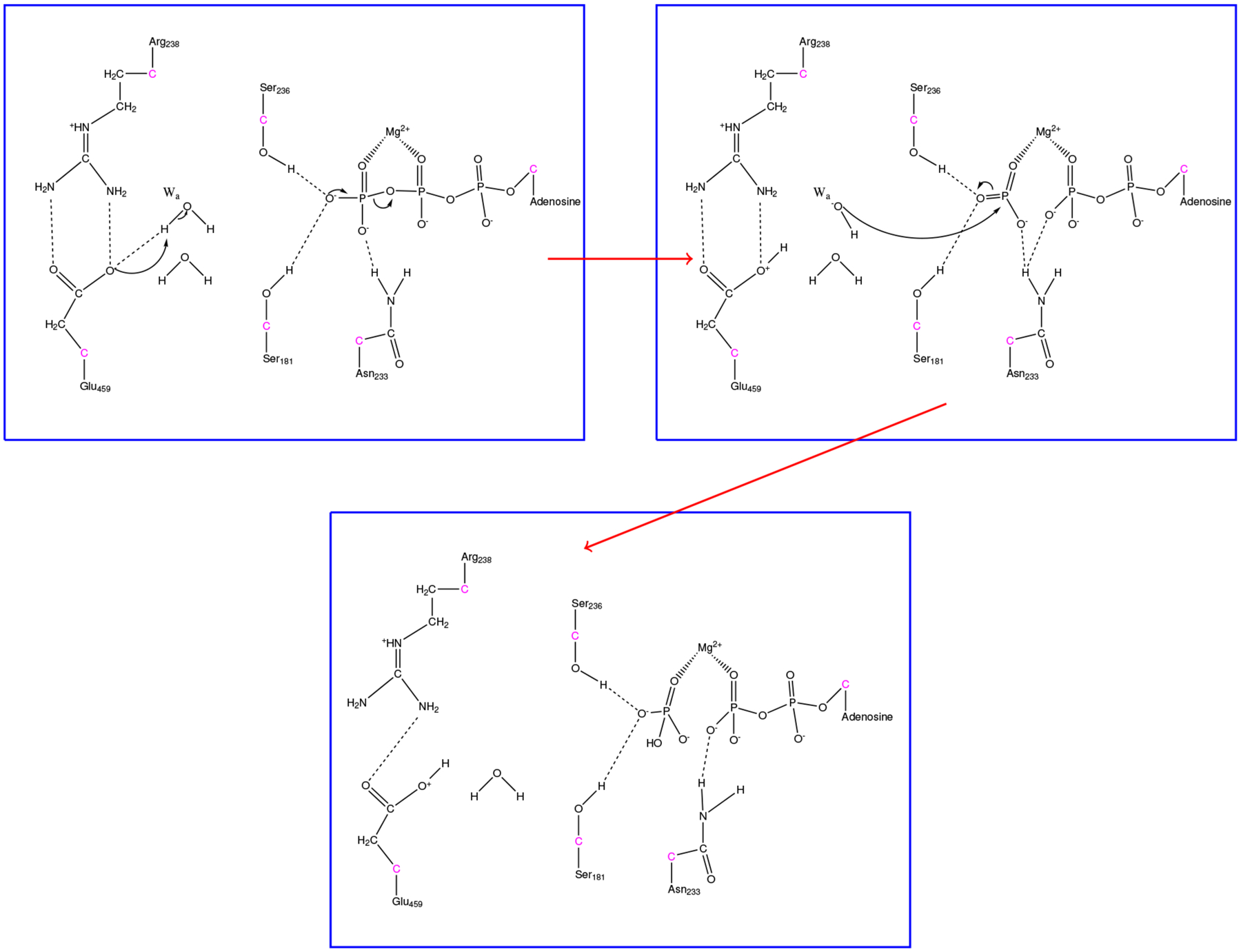
Illustration for the formation of HPO₄²⁻ in myosin. Hydrogen bonds are shown as dashed lines to demonstrate protein-substrate interactions.

The calculated transition states from these trajectories show the stabilization of the metaphosphate intermediate. Figure 6 illustrates that residues Ser181, Ser236, Ser237, and Gly 457 stabilize the PO₃⁻ in a trigonal planar conformation, well separated from ADP but before the primed hydroxide attacks. A total of four transition states were determined, each with very similar conformations for the QM region with very little geometric variation.

Figure 6.

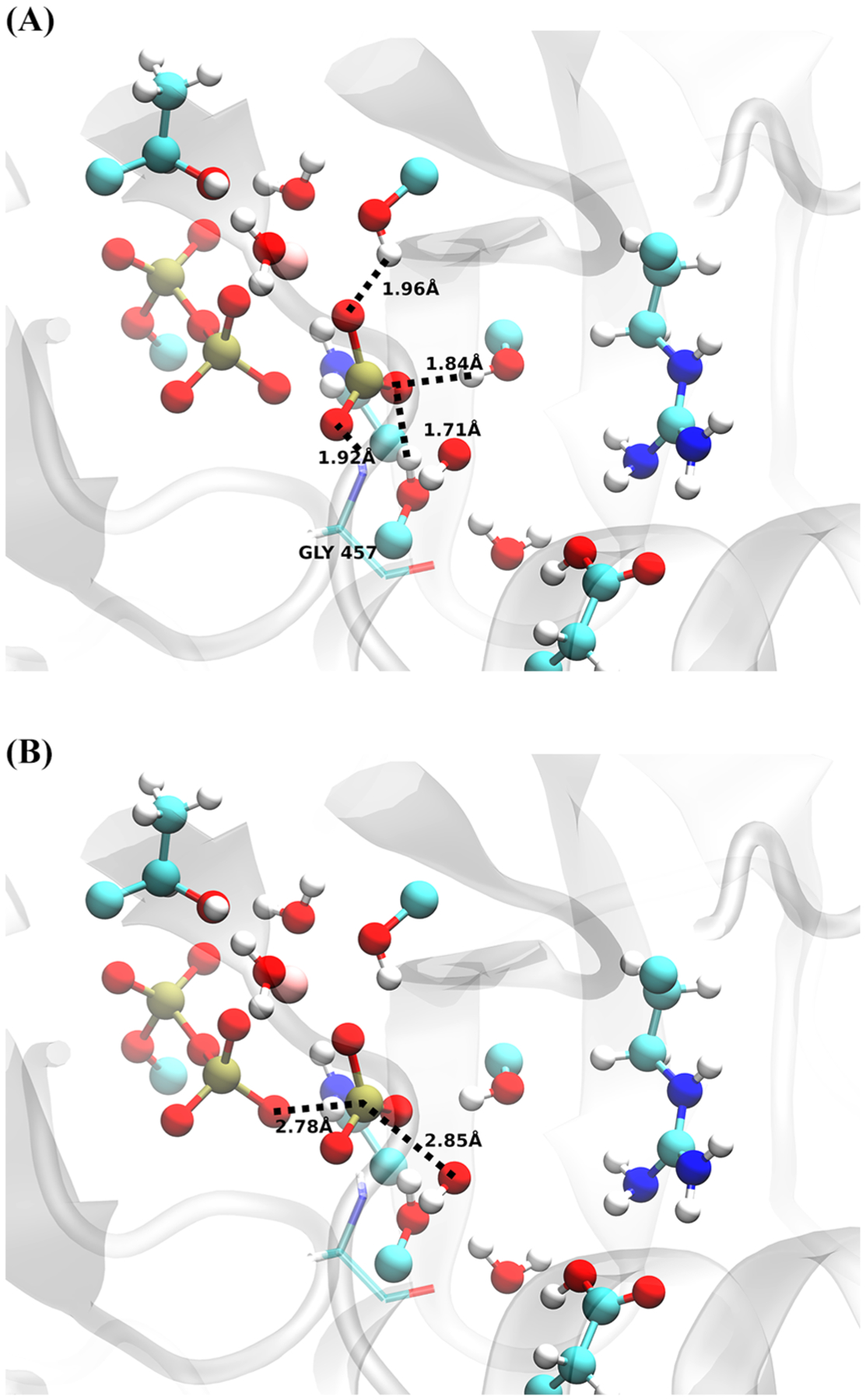
Transition-state distances from a representative structure. (Top) Residues stabilizing PO₃⁻ intermediate and (Bottom) attacking OH⁻–P_γ and O_β–P_γ distance. QM-treated atoms are shown with a ball and stick representation, with an additional classical residue, glycine 457, shown in transparent.

In determining the important degrees of freedom responsible for the reaction-to-product barrier, we initially ran constrained trajectories in which all degrees of freedom associated with the QM region were frozen and another ensemble where only degrees of freedom for the triphosphate chain and the hydroxide were constrained. These ensembles produced very different results, which are summarized in Figure 7. The distribution is largely peaked around 0.5 when the entire QM region is constrained, while the distribution is more diffuse with a lot of committance to the product state when only the triphosphate atoms along with the hydroxide were constrained. This demonstrates that the degrees of freedom associated with the entire QM region are largely correlated with the barrier crossing event, while the minimal degrees of freedom for the ATP-OH ensemble were not sufficient to remain on the stochastic separatrix. The residues that were included in the QM region have been shown previously to be important for ATP hydrolysis in myosin,^12–17 and their effect is observed here as well. We further expanded on this to determine their overall effect on the chemical event by producing other ensembles in which we remove constraints from the QM region and see the overall effect. We produced two additional ensembles with one containing constraints on the entirety of the QM region, but Glu459 was exempt, and another where Glu459, Arg238, Ser181, and a water that resides between the glutamate and serine were removed. These were chosen to demonstrate whether the rate enhancement of ATP hydrolysis by myosin was governed by electrostatic stabilization or whether there were specific protein motions that lower the free-energy barrier for the reaction. Both ensembles, see Figure S2, have shifted distributions relative to Figure 7, shifting toward products and reactants. However, the histograms still have a large weighting around 0.5, suggesting the degrees of freedom associated with the remaining residues from the QM region, Thr186, Ser236, Ser237, and Arg238, as well as the magnesium and its hydrating waters have a large contribution to the barrier crossing event by stabilizing the charge distribution along the phosphate chain. As observed from the calculated transition states, Ser236 and Ser237 stabilize the PO₃⁻ intermediate, while Thr186 and Asn233 stabilize the charge on the bisphosphate of ADP. Arg238 and Ser181 further contribute by stabilizing Glu459 in the active site to accept the proton from the attacking water since it is the apparent incorrect placement of Glu459 that causes the committor distributions to shift, as shown in Figure S2. Therefore, it is the organization of the active site that leads to catalytic efficiency, without protein motions being directly coupled to the mechanism.

Figure 7.

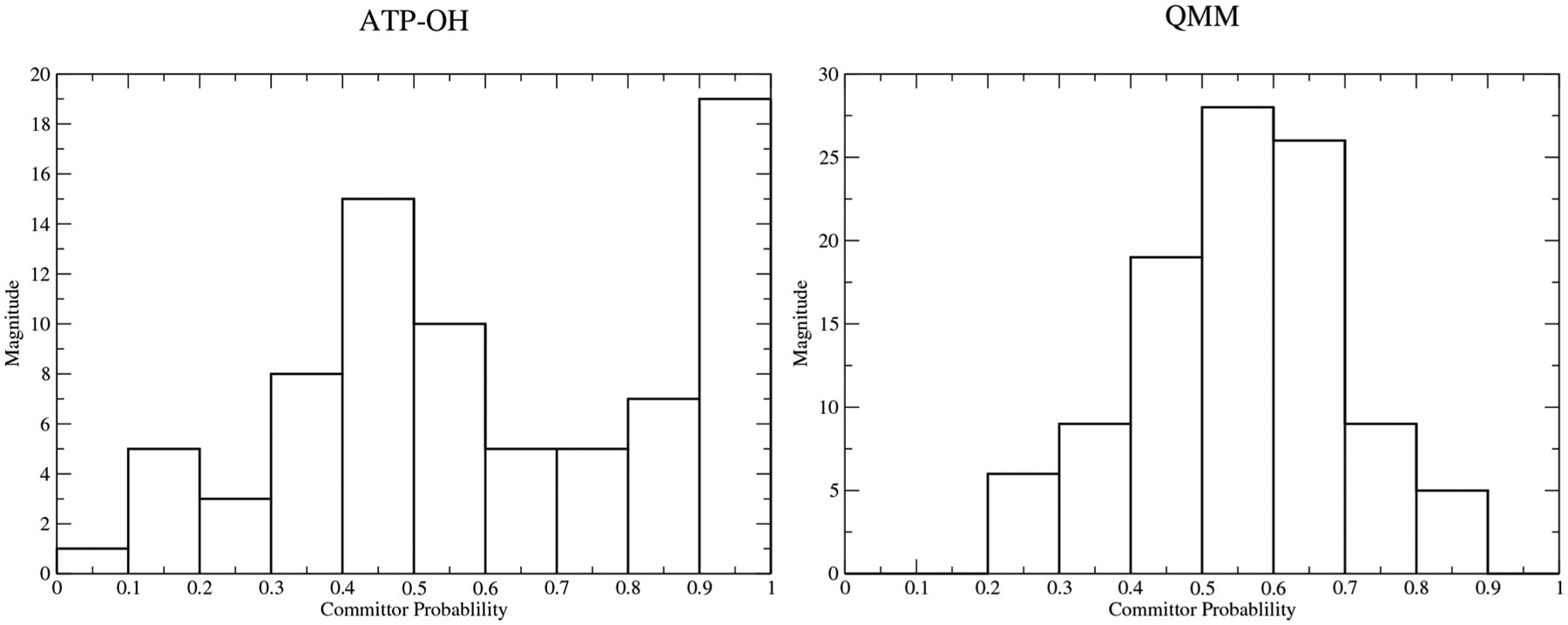
Committor distributions of constrained ensembles in which (Left) only triphosphate atoms and the attacking hydroxide were constrained and (Right) where the entire QM region was constrained.

3.2. ATP Hydrolysis: Formation of H₂PO₄⁻ with Proton Wires.

The previously described mechanism includes important residues stabilizing different parts of the substrate to perform chemistry, yielding the HPO₄²⁻ intermediate with a proton on Glu459. To form the final product, H₂PO₄⁻, this proton needs to be shuttled back toward the phosphate intermediate. The presence of proton wires within myosin has been discussed previously,²² with residues Ser181 and Ser236 allowing for two possible pathways the proton may “hop” to on its way to the HPO₄²⁻ intermediate. Therefore, we created two ensembles of trajectories, which we will refer to as the Ser181 ensemble and Ser236 ensemble, in which the proton must move away from Glu459 to HPO₄²⁻ utilizing either Ser181 or Ser236 as an intermediate. The same initial structure was utilized for both ensembles from the previous HPO₄²⁻ trajectories, and order parameters used to define the reactant state were Glu459 and the respective serines having protons bound, an oxygen-hydrogen bond distance of less than 1.3 Å, while the product state was defined by the existence of H₂PO₄⁻. Both mechanisms progressed in a similar fashion, with Figure 8 showing the overall mechanism.

Figure 8.

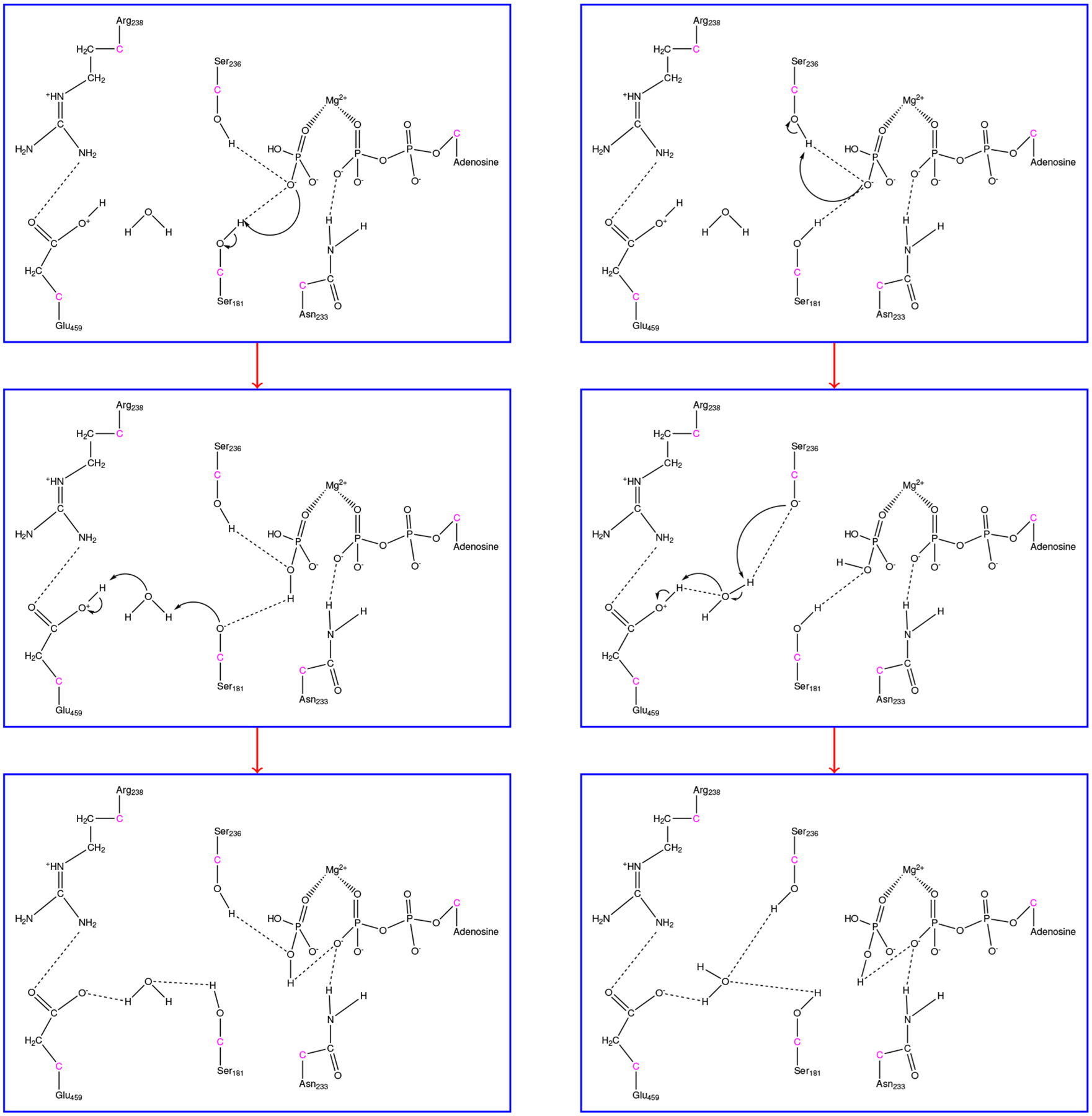
Formation of H₂PO₄⁻ with direct utilization of either (Left) Ser181 or (Right) Ser236. GHO atoms are shown in pink with only QM atoms visualized.

In both cases, HPO₄²⁻ abstracts a proton initially from either Ser181 or Ser236 that interacts with the phosphate through hydrogen bonds. Very quickly afterward, the deprotonated serines grab a proton from a nearby water, forming a hydroxide that finally deprotonates Glu459. These three events vary slightly in each of the ensembles because of the tumbling of the water, but the deprotonation of the serine usually occurs about 100 fs before the deprotonation of the water, with the reformation of Glu to its original protonation state occuring within 50 fs of the formation of the hydroxide. Figure S3 shows the timing of these events from a representative trajectory. Overall, there is little to differentiate the Ser181 ensemble from its Ser236 counterpart. The only differentiation between the two ensembles is that the hydrogen bonding network is slightly different at the product state, with the Ser236 interacting with the water when it is taking part in the mechanism with the remaining interacting with the phosphate when it is not. Attempts to determine a transition state for each of these ensembles were unsuccessful, suggesting either this second step is a diffuse process and therefore occurs on timescales longer than can be observed with the TPS methodology or metastable intermediates exist along these paths. We note that a metastable intermediate that resides between the formation of HPO₄²⁻ and H₂PO₄⁻ has been observed for ATP hydrolysis in an ABC transporter.²⁵

3.3. Overall ATPase Mechanism: Lytic Water or Glutamate?

Discussions over how ATP hydrolysis occurs within ATPases are extensive. A recent review by Kiani and Fischer²² summarized efforts to monitor the chemical reaction in myosin II. Many of the key observations made by the authors as well as others are in agreement with what is observed in this study, but the main divide occurs when describing where the proton goes from the attacking water. Kiani and Fischer and others describe a lytic water deprotonating the attacking water that then shuttles the proton through the various “wires” that exist in the active site; therefore, two waters actively participate in the initial bond-breaking event. In this study, we observe that a second water only participates in the proton shuttling after the formation of HPO₄²⁻, and Glu459 takes the role of the lytic water described by Kiani and Fischer. As stated previously, we attempted to generate trajectories utilizing two waters in the manner they described, but this led to unstable trajectories.

The question remains: does the mechanism require one or two waters to progress and why are we observing a different mechanism than other previous studies of ATP hydrolysis in myosin? We believe it ultimately comes down to the method utilized to sample the reactant to the product state. Kiani and Fischer utilize the conjugate peak refinement method³⁹ that samples the potential energy surface between two states, such as reactant and product, by optimizing saddle points along an initially guessed path on the aforementioned hypersurface, generating a new path and then again optimizing the new saddle points. This method generates a trajectory from the individual sampled points on the potential energy surface which has known energies, and therefore relative barriers may be calculated between these points. In another paper, they demonstrate this method to calculate trajectories for ATP hydrolysis in myosin II, initially generating a trajectory with the two-water mechanism, and then created another trajectory in which only one is used with the protonation of Glu459.¹⁶ One of their justifications for why the utilization of glutamate for proton extraction is unlikely was that the potential energy difference was much larger for the non-lytic water mechanism than that for the lytic and that the barrier they calculated for the lytic water mechanism was close to the experimental value (10.3 kcal/mol enthalpy of activation).²⁹ However, sampling only potential energies can be misleading since atoms are effectively frozen in space, and no thermodynamic sampling can occur. In fact, it is actually the free-energy barrier for myosin-catalyzed ATP hydrolysis that is relevant, which has been measured to be 14.5 kcal/mol.⁴⁰

TPS indirectly samples the free-energy surface between states by performing samplings in the trajectory space. This generates a collection of paths in the trajectory space with a large density of paths that produce the least “action” on the system and therefore follow the MFEPs. Though TPS does not directly provide free-energy barriers, we observed only the protonation of the glutamate. To test whether there was another more probable path we were not observing, we utilized trajectories from the initial HPO₄²⁻ ensemble and removed the order parameter for the protonation of the glutamate and generated a new ensemble. This can be observed as removing a constraint from the system as we no longer require this protonation to occur. However, we never observed any deviation from the previous trajectories, and the protonation of Glu459 continued to be present.

Another possible reason for this protonation event being nonexistent in Kiani and Fischer and other studies is the possible conformation bias. All previous QM/MM studies^12–16 determined the mechanism from stationary points, with the attacking water positioned close to the terminal end of ATP. However, proteins and their environment are inherently mobile and can sample multiple conformations around the reactant and product states. Kiani and Fischer theorize one of the possible reasons that a high barrier for the protonation of the glutamate is due to the large distance, but changing the position of the water closer to the glutamate might cause their observed mechanism to shift. A more recent study examined ATP hydrolysis in several myosin conformations to determine the overall mechanism and free-energy barrier in each case. In Lu et al.,¹⁷ metadynamics was utilized to sample the free-energy surface for the recovery stroke, with the string method used to determine the most optimal path along the computed free-energy surfaces. In the PPS conformation, the MFEP observed the formation of HPO₄²⁻ with Glu459 abstracting the proton from the attacking water and the sequential breaking/formation of the γ phosphate-β oxygen bond and attacking water-γ phosphate bond, respectively, both of which are observed in this study. For the formation of H₂PO₄⁻, the MFEP transferred the proton to HPO₄²⁻ with a hydronium intermediate from a secondary hydrating water. Though there is a clear improvement over sampling potential energy surfaces, utilizing metadynamics requires defining the degrees of freedom coupled to the chemical reaction a priori. If one were to choose slightly different degrees of freedom and/or a different CV to bias over, a completely different free-energy surface will be sampled and may lead to different computed free-energy barriers and/or changes to the overall mechanism. The advantage of TPS is that the degrees of freedom for the barrier crossing do not need to be known or defined. Also, glutamate protonation has been observed in numerous studies in other ATPases,^23–25 so it is conceivable that the same may occur within myosin motors as well. This study and others^17,23–25 highly suggest that a mechanism with the protonation of Glu459 is thermodynamically feasible within myosin and is the most probable path.

4. CONCLUSIONS

We have utilized enhanced sampling methods to sample rare events important for the function of myosin II. Metadynamics simulations generated trajectories of the recovery stroke of the cross-bridge cycle while monitoring mutagenic perturbations to kinetic and equilibrium dynamics. Both K84M and R704E increased the overall free-energy barrier in the transition of PR myosin to the PPS conformation with the same magnitude of severity that was observed experimentally. For ATP hydrolysis, TPS generated unbiased, thermodynamically correct trajectories of the conversion. We observed the formation of the HPO₄²⁻ through the stabilization of a PO₃⁻ intermediate and the final creation of H₂PO₄⁻ through two different proton wires within the myosin active site. These methods can be extended to model other states⁴¹ and transitions within the myosin cross-bridge cycle that are currently too fast for experimental observation, such as the power stroke. Additionally, this approach may be extended to make observations for human myosin and determine isoformic differences between the two myosin II variants as well as determine specific perturbation of mutations associated with cardiomyopathies to the individual steps of the myosin kinetic cycle. This may shed light on how other cardiomyopathic mutations may affect thin filament regulation of muscle contraction as well.^42,43