The Mystery of the Benzene‐Oxide/Oxepin Equilibrium—Heavy‐Atom Tunneling Reversed by Solvent Interactions

Abstract

The equilibrium between benzene oxide (1) and oxepin (2) is of large importance for understanding the degradation of benzene in biological systems and in the troposphere. Our studies reveal that at cryogenic temperatures, this equilibration is governed by rare heavy‐atom tunneling. In solid argon at 3 K, 1 rearranges to 2 via tunneling with a rate constant of approximately 5.3×10⁻⁵ s⁻¹. Thus, in a nonpolar environment, 2 is slightly more stable than 1, in agreement with calculations at the CCSD(T) level of theory. However, if the argon is doped with 1 % of H₂O or CF₃I as typical hydrogen or halogen bond donors, respectively, weak complexes of 1 and 2 are formed, and now 2 is tunneling back to form 1. Thus, by forming non‐covalent complexes, 1 becomes slightly more stable than 2 and the direction of the heavy‐atom tunneling is reversed.

Matrix‐isolation studies reveal a long‐standing misconception about the benzene‐oxide/oxepin equilibrium by confirming the intrinsic greater stability of oxepin. They also find that this equilibration proceeds via a rare heavy‐atom tunneling process at cryogenic temperatures. Finally, the solvent control of heavy‐atom tunneling is demonstrated for the first time as the direction of the reaction is inverted in the presence of Lewis acids.

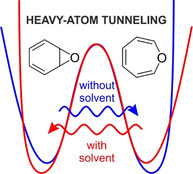
Benzene oxide (1) is the primary product of the cytochrome P450 oxidation of benzene in eukaryotic cells. ^[1] Its high reactivity leads to a number of secondary metabolites which are linked to the toxicity of benzene. ^[2] 1 has also been suggested as an intermediate in the tropospheric benzene oxidation. ^[3] The fundamental importance of 1 for the biological and environmental benzene degradation has triggered a large number of studies on this molecule. Most important for the understanding of the chemistry of 1 is the rapid equilibration with its valence tautomer oxepin (2) via a disrotatory electrocyclic rearrangement (Scheme 1). ^[4]

Scheme 1.

Equilibrium between 1 and 2, thermochemical data from ref. [5].

The first synthesis of 1 and 2 as an equilibrium mixture was reported in 1965 by Vogel, Böll, and Günther. ^[6] From the analysis of the UV spectra at room temperature, these authors concluded that the equilibrium is strongly solvent‐dependent. In water—methanol mixture 90 % of 1 and only 10 % of 2 was observed, whereas in the nonpolar isooctane the equilibrium was shifted, and oxepin 2 was now the major constituent with 70 %. The equilibrium was also studied by low‐temperature NMR spectroscopy in CF₃Br/pentane mixtures.[ ⁵ , ⁷ ] These studies revealed that in this solvent 1 is energetically more stable than 2 by 1.7 kcal mol⁻¹. However, the entropy favors 2, and at room temperature ΔG is approximately −1.3 kcal mol⁻¹, thus shifting the equilibrium towards 2 (Scheme 1). The rearrangement is very rapid at room temperature, and temperatures below −120 °C were necessary to sufficiently slow down the rearrangement to resolve individual spectra of 1 and 2 by NMR.

Calculations at the CCSD(T)/def2‐TZVP level of theory suggest that the energies of 1 and 2 are nearly degenerate with 2 being only 0.89 kcal mol⁻¹ more stable than 1. This small energy difference is below the accuracy of these calculations, and therefore it is not clear which of the two valence tautomers is more stable in the gas phase. Moreover, since the experimental equilibrium constant is strongly solvent‐dependent, it does not reflect the intrinsic stabilities of 1 and 2. The same is true for the kinetics of the 1 ⇌ 2 rearrangement, where the activation barrier of 7.2 kcal mol⁻¹ measured in CF₃Br/pentane might be solvent‐dependent and not reflect the gas phase barrier.

The opening of the C(1)‐C(6) bond in 1 to form 2 requires only small displacements of the C(1) and C(6) atoms. The largest geometrical change is the increase of the C(1)‐C(6) bond distance from 1.50 Å in 1 to 2.29 Å in 2 (CCSD(T)/def2‐TZVP), while the displacement of the other atoms, including the H atoms, is very small. Since both the activation barrier and the barrier width are small, the 1 ⇌ 2 rearrangement is a viable candidate for a rare heavy‐atom tunneling process. Prerequisite for efficient heavy‐atom tunneling is a low activation barrier, but even more important is a small barrier width. ^[8]

Heavy‐atom tunneling has been experimentally observed in a small number of examples, ^[8] many of those involving the opening or the closing of a bond in three‐membered rings (Scheme 2). Thus, bicyclopentane 3 is formed from cyclopentanediyls 4 and bicyclobutanes 5 from cyclobutanediyls 6 via heavy‐atom tunneling. ^[9] The highly strained cyclopropenes 7 and 9 undergo a tunneling reaction to give the corresponding carbene 8 and nitrene 10, respectively.[ ¹⁰ , ¹¹ ] All these reactions involve heavy‐atom tunneling in the direction determined by the thermodynamics of the rearrangement. The Cope rearrangement in semibullvalene 11 is a degenerate tunneling rearrangement, so there is no driving force. To become observable a small thermodynamic driving force had to be introduced by asymmetric deuterium substitution.[ ¹² , ¹³ ]

Scheme 2.

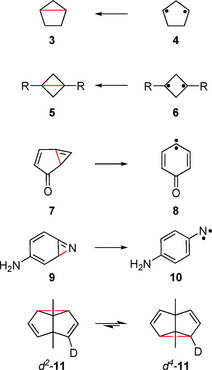
Examples of rearrangements of cyclopropane derivatives involving heavy‐atom tunneling. The bonds in red are opening or closing.

To shed light on the benzene oxide 1–oxepin 2 rearrangement and to provide evidence for heavy‐atom tunneling, the kinetics of the rearrangement were measured at temperatures below 30 K in rare gas matrices. At these temperatures, the available thermal energy is far too low to overcome an activation barrier of 7.2 kcal mol⁻¹, and thus any observable rearrangement could be attributed to tunneling. In addition, rare gases are weakly interacting cryo‐solvents, and therefore are not expected to introduce large changes in the thermodynamics and kinetics compared to the gas phase. The equilibrium mixture of 1 and 2 was sublimed at −40 °C through a tube at room temperature and deposited together with a large excess of argon on a CsI window at 3 K. Under these conditions, the room temperature equilibrium is rapidly quenched, and thus the initial ratio measured in the matrix at 3 K resembles the room temperature equilibrium. From the matrix IR spectra, the ratio between 1 and 2 was determined to be 1:13 which corresponds to ΔG ²⁹⁸=−1.51 kcal mol⁻¹, in reasonable agreement with our calculations at the CCSD(T)/def2‐TZVP level of theory which predict ΔG ²⁹⁸=−1.20 kcal mol⁻¹ (Table 1).

Table 1.

Thermodynamic parameters (given in kcal mol⁻¹ and cal mol⁻¹ K⁻¹) for the ring expansion 1→2 as determined by experimental and computational studies.

	ΔE 0 K	ΔG 298 K	ΔH 298 K	ΔS 298 K	Ratio 1/2
					298 K	3 K
calc. (DFT)[a]	−0.17	−0.47	+0.14	2.03	1:2	1:1012
calc. (CC)[b]	−0.89	−1.20	−0.59	2.05	1:8	1:1064
exp. (IR)[c]	−0.02[e]	−1.51[f]	/	/	1:13[f]	1:20[e]
exp. (lit.)[d]	/	−1.28	+1.7	10	1:8	/

[a] M06‐2X‐D3/def2‐TZVP. [b] CCSD(T)/def2‐TZVP. [c] IR in solid argon. [d] NMR in CF₃Br/pentane, refs. [5, 7]. [e] Determined at the “end” of the reaction, i.e. after >10 half‐lives (s. SI). [f] Determined immediately after deposition under the assumption that this ratio reflects the ratio in the gas phase at 298 K (s. SI).

Keeping the argon matrix in the dark at 3 K leads to the disappearance of the peaks assigned to 1 and the concomitant rise of signals assigned to 2 with a first order rate constant of approximately 5.3×10⁻⁵ s⁻¹ (Figure 1). Raising the matrix temperature from 3 K to 25 K did not change the kinetics within the error limit. Thus, the kinetics of the rearrangement is temperature‐independent even after increasing the absolute temperature by a factor of 8 which suggests that the Arrhenius activation barrier is zero. This is in contradiction to an activation barrier of 7.2 kcal mol⁻¹ measured in solution, ^[5] which strongly indicates that the rearrangement is dominated by tunneling at cryogenic temperatures.

Figure 1.

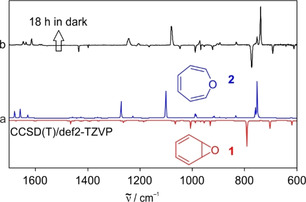
Heavy‐atom tunneling in the interconversion of 1 and 2. a) CCSD(T)/def2‐TZVP computed IR spectra of 1 (pointing downwards) and 2 (pointing upwards). b) IR difference spectrum obtained after keeping an argon matrix containing 1 and 2 in the dark at 3 K for 18 h.

Oxepin 2 is calculated to be 0.89 kcal mol⁻¹ more stable than benzene oxide 1 (CCSD(T)/def2‐TZVP, Table 1), and therefore, at 3 K the equilibrium should be completely shifted towards 2. However, even after more than 10 half‐lives, the ratio between 1 and 2 drops only from 1:13 to 1:20, much less than expected from the calculated energy difference. A similar behavior was also observed for the tunneling rearrangement of the deuterated semibullvalene 11, where the tunneling was observed, but the expected ratio of the isotopomers never reached. ^[13] An explanation for this could be that trapping of 1 and 2 in an argon matrix leads to a distribution of matrix sites with slightly different geometries and interaction patterns resulting in a distribution of energy differences between 1 and 2. Thus, the relative stability of 1 and 2 might depend on the matrix environment and even be reversed for a small fraction of molecules.

Since the early reports on the 1 ⇌ 2 rearrangement already reported strong solvent effects, ^[5] we studied the influence of hydrogen and halogen bonding on the rearrangement. H₂O and CF₃I are typical hydrogen bond and halogen bond donors, respectively, that could interact with the lone pairs at the oxygen atoms of 1 and 2. According to DFT calculations (M06‐2X‐D3/def2‐TZVP), benzene oxide 1 is slightly more stabilized by hydrogen or halogen bonding than oxepin 2. For the most stable molecular complexes, the relative stabilization of 1 compared to 2 is 0.6 kcal mol⁻¹ for the interaction with H₂O, and 0.9 kcal mol⁻¹ for the interaction with CF₃I (Figure 2). An explanation for the slightly larger stabilization of 1 might be its larger dipole moment of 1.9 D compared to 1.3 D of 2 (M06‐2X‐D3/def2‐TZVP). Since the complexes of 1 with the Lewis acids (LA) H₂O and CF₃I (1⋅⋅LA) are slightly more stabilized than 2⋅⋅LA, the equilibrium should be shifted towards 1⋅⋅LA after complex formation.

Figure 2.

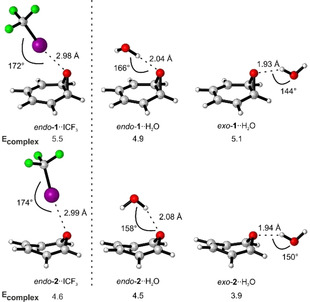
Most stable structures of H₂O and CF₃I complexes of 1 and 2 and corresponding complexation energies calculated at the M06‐2X‐D3/def2‐TZVP level of theory. For other complexes potentially being formed see SI.

This hypothesis was tested by depositing matrices at 3 K containing the room temperature equilibrium of 1 and 2 with a large excess of argon doped with 1 % H₂O or CF₃I, respectively. Under these conditions, most molecules of 1 and 2 are isolated in argon without interacting with the Lewis acids, since, statistically, interactions with the additional dopant are rare, and at 3 K diffusion even of small molecules is inhibited in the rigid low temperature matrix. Benzene oxide 1 reacts partially to 2 via a tunneling rearrangement as described above in pure argon. If the matrix is subsequently annealed at temperatures between 20 and 25 K, H₂O and CF₃I can diffuse in the solid argon and form aggregates with themselves (e.g. water oligomers) but also form the Lewis acid—Lewis base complexes 1⋅⋅LA and 2⋅⋅LA (Scheme 3). For these complexes, the equilibrium between 1⋅⋅LA and 2⋅⋅LA is shifted slightly towards 1⋅⋅LA, and thus excess 2⋅⋅LA rearranges via tunneling to 1⋅⋅LA. Thus, the 1/2 ratio in the doped matrices changes from 1:13 directly after deposition of the matrices (before complexes are formed) to >9:1 after formation of the LA complexes via annealing for several minutes and subsequent cooling to 3 K for several hours to allow for the tunneling rearrangement. The 1/2 ratios after tunneling are similar for both H₂O and CF₃I. However, since the IR spectra of 1 and 2 are very similar to those of their corresponding complexes 1⋅⋅LA and 2⋅⋅LA, the integration of IR signals is prone to large errors and the 1/2 ratio can be only roughly estimated. The IR spectra clearly reveal that the direction of the heavy‐atom tunneling is reversed by the formation of weakly bound complexes (Figure 3), thus confirming the predictions from our calculations.

Scheme 3.

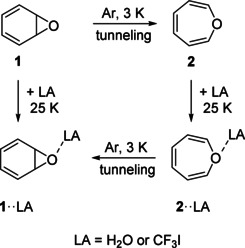
Reversible tunneling rearrangement between 1 and 2. After deposition of the matrix at 3 K, 1 rearranges slowly (hours) to 2 via tunneling. Subsequent annealing at 25 K results in the fast (minutes) formation of complexes of 1 and 2 with H₂O or CF₃I, respectively. After cooling back to 3 K, the complexes of 2 slowly (hours) rearrange to 1.

Figure 3.

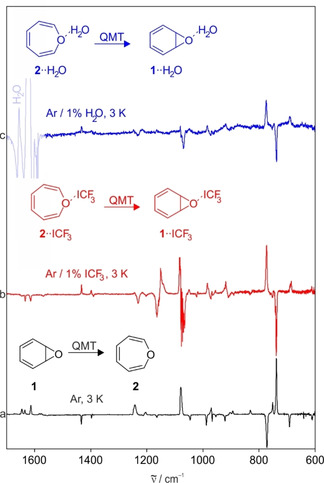
Inversion of the direction of the tunneling equilibrium between 1 and 2 upon complexation with Lewis acids. a) IR difference spectrum obtained after keeping an argon matrix containing 1 and 2 in the dark at 3 K for 18 h. b) IR difference spectrum obtained after keeping an argon matrix containing complexes 1⋅⋅ICF₃ and 2⋅⋅ICF₃ in the dark at 3 K for 66 h. c) IR difference spectrum obtained after keeping an argon matrix containing complexes 1⋅⋅H₂O and 2⋅⋅H₂O in the dark at 3 K for 40 h.

Both the experiments in weakly interacting argon matrices and the CCSD(T) calculations reveal that oxepin 2 is energetically slightly more stable than benzene oxide 1. Since the entropy also favors 2, the equilibrium should be shifted towards 2 at all temperatures. The 1 ⇌ 2 rearrangement proceeds via heavy‐atom tunneling with a half‐life of several hours if the available thermal energy does not allow to surmount the thermal activation barrier. Thus, the equilibration between 1 and 2 cannot be prevented even by cooling to cryogenic temperatures. Since this rearrangement is energetically nearly degenerate, the direction of the tunneling rearrangement is controlled by small changes in the relative stability of 1 and 2 induced by solvent interactions.

The previous findings that 1 is the more stable isomer have to be attributed to solvent effects. Both hydrogen and halogen bonding stabilize 1 slightly more than 2 and shift the equilibrium towards 1. This agrees with the earlier findings that in water—methanol mixtures 1 is the prevalent species, whereas in isooctane 2 is dominant. ^[5] It also explains the findings from NMR studies in CF₃Br/pentane mixtures. ^[7] This solvent mixture was selected since it has a very low melting point which allowed to record NMR spectra at −120 °C. However, CF₃Br is a strong halogen bond donor, comparable to CF₃I that we used in our matrix studies (see SI). Therefore, in the presence of CF₃Br, halogen bonding shifts the equilibrium towards 1, as was observed in the NMR studies (Table 1).

In summary, in non‐interacting environments, oxepin 2 is slightly more stable than its isomer, benzene oxide 1. However, the relative stability can be reversed by solvent effects. At cryogenic temperatures, the equilibration is dominated by heavy‐atom tunneling.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

T. Schleif, M. Prado Merini, W. Sander, Angew. Chem. Int. Ed. 2020, 59, 20318.