Stabilization of Linear C₃ by Two Donor Ligands: A Theoretical Study of L‐C₃‐L (L=PPh₃, NHC^Me, cAAC^Me)

Abstract

Quantum chemical studies using density functional theory and ab initio methods have been carried out for the molecules L‐C₃‐L with L=PPh₃ (1), NHC^Me (2, NHC=N‐heterocyclic carbene), and cAAC^Me (3, cAAC=cyclic (alkyl)(amino) carbene). The calculations predict that 1 and 2 have equilibrium geometries where the ligands are bonded with rather acute bonding angles at the linear C₃ moiety. The phosphine adduct 1 has a synclinal (gauche) conformation whereas 2 exhibits a trans conformation of the ligands. In contrast, the compound 3 possesses a nearly linear arrangement of the carbene ligands at the C₃ fragment. The bond dissociation energies of the ligands have the order 1<2<3. The bonding analysis using charge and energy decomposition methods suggests that 3 is best described as a cumulene with electron‐sharing double bonds between neutral fragments (cAAC^Me)₂ and C₃ in the respective electronic quintet state yielding (cAAC^Me)=C₃=(cAAC^Me). In contrast, 1 and 2 possess electron‐sharing and dative bonds between positively charged ligands [(PPh₃)₂]⁺ or [(NHC^Me)₂]⁺ and negatively charged [C₃]⁻ fragments in the respective doublet state.

C₃ stabilization: Quantum chemical studies using density functional theory and ab initio methods have been carried out for the molecules L‐C₃‐L with L=PPh₃ (1), NHC^Me (2, NHC=N‐heterocyclic carbene), and cAAC^Me (3, cAAC= cyclic (alkyl)(amino) carbene). The calculations predict that 1 and 2 have equilibrium geometries where the ligands are bonded with rather acute bonding angles at the linear C₃ moiety.

Introduction

The stabilization of transient species, small clusters, and bare atoms through coordination with Lewis bases has become a highly prolific discipline in modern chemistry. ^[1] Stable singlet carbenes like cyclic (alkyl)(amino) carbene (cAAC) ^[2] and N‐heterocyclic carbene (NHC) ^[3] have turned out to be excellent ligands for this purpose ^[4] besides the well‐known phosphine groups. Focusing on the carbon atoms as the species to be stabilized, the first divalent carbon(0) complex, carbodiphosphorane C(PPh₃)₂ was synthesized by Ramirez et al. ^[5] in 1961, followed by a proper structural characterization through X‐ray analysis in 1978 by Hardy et al. ^[6] Later, theoretical studies on the bonding situation revealed that this complex can be best described in terms of donor–acceptor interactions Ph₃P→C(0)←PPh₃ between the phosphine ligands and a bare carbon atom in the excited ¹D state. ^[7] This finding led to the theoretical prediction of stable carbodicarbene C(NHC)₂ in 2007, ^[8] a benzoannulated derivative C(NHC^Bz)₂ that was shortly afterwards synthesized by the groups of Bertrand and Fürstner. ^[9] Then, gradually the bonding concept of carbones ^[10] L→C(0)←L was extended for other donor ligands L. ^[11] The notion of dative bonding in carbones was not undisputed, ^[12] but it has been generally accepted now as a valid description of main‐group compounds. ^[13] It should be noted that the use of arrows for dative bonds was originally introduced by Sidgwick in the 1920s ^[14] and that the suggestion of divalent carbon(0) compounds L→C←L was suggested already by Varshavskii in 1980. ^[15]

The bonding analysis also showed that molecules like (R₂N)₂C=C=C(NR₂)₂ and (cAAC)=C=(cAAC) can be better represented with classical electron‐sharing double bonds rather than dative bonds.[ ^11d , ¹⁶ ] It should be noted that the donor–acceptor interactions comprise σ donation L→C(0)←L as well as π back‐donation L←C(0)→L, where the extent of back‐donation depends on the availability of low‐lying π acceptor orbitals of the ligand L. For example, a strong π acceptor such as CO induces strong π back‐donation, which means that the dative bonds in the bent equilibrium structure of carbon suboxide C₃O₂ ^[17] should be described with the formula OC⇄C(0)⇄CO.[ ^12b , ^13b ]

Regarding its next larger carbon homolog, Bestmann and co‐workers prepared in 1989 a push–pull molecule, R₃P‐C₂‐BR₃, with a dicarbon core. ^[18] In retrospect, it is interesting that the authors suggested in that paper that carbodiphosphorane C(PPh₃)₂ can be formally regarded as a “complex” consisting of two donor molecules and an electron‐rich, excited carbon atom citing earlier work with similar suggestions, ^[19] which were then thought to be a purely hypothetical formulation. The authors postulated that carbon chains with an even number n of carbon atoms would be stabilized by a push–pull mechanism D→C_n→A with a donor ligand D and acceptor ligand A at either end, whereas carbon chains with an odd number of carbon atoms are stabilized by two donor ligands D→C_n+1←D. The hypothesis was later confirmed by the synthesis of the C₃ complex Ph₃P‐C₃‐PPh₃ and the C₄ adduct Ph₂(Me)P‐C₄‐B(CH₂Ph)₃. ^[20] The latter species could be structurally characterized by X‐ray analysis whereas the former C₃ complex could only be identified by NMR and IR spectroscopy, which were interpreted in terms of a trans‐bent geometry.

The possibility of stabilizing C₂ by two donor NHC ligands was theoretically explored in 2012 by Dutton and Wilson. ^[21] They also considered the PMe₃ ligand in their study and reported that, although in (NHC)₂C₂ the central C₄ unit is almost linear, in (PMe₃)₂C₂, P‐C‐C‐P has a trans‐bent geometry. More recently, successful attempts to synthesize cAAC‐stabilized C₂ as neutral species (cAAC)C₂ were reported independently by the Roesky and Bertrand groups. ^[22] A similar effort to synthesize NHC^Bz‐stabilized C₂, by the deprotonation of a doubly protonated precursor, [(NHC^Bz)₂C₂H₂]²⁺, failed presumably because of the small HOMO–LUMO energy gap of (NHC^Bz)₂C₂. ^[23] Similar to its calculated NHC analog, the C₄ core in (cAAC)C₂ only slightly deviates from linearity. Although a comparative bonding analysis for donor–acceptor versus electron‐sharing is still missing, the linear C₄ core moiety suggests an electron‐sharing C₄ unit with electron‐sharing double bonds in (NHC)=C=C=(NHC) and (cAAC)=C=C=(cAAC) rather than dative bonds (NHC)→C₂←(NHC) and (cAAC)→C₂←(cAAC). Later, Wu et al. ^[24] isolated the 4‐pyridylidene‐supported C₂ species, which exhibits a more significant deviation from linearity by 24.2° than that observed in NHC or cAAC analogs.

The stabilization of longer carbon chains C_n where n>2 in compounds R‐C_n‐R′ with various groups R has been the topic of numerous studies. The synthetic efforts to isolate polyynes that are stabilized by metal or non‐metal end groups R has been summarized in a seminal review by Szafert and Gladys in 2003. ^[25] Research about longer cumulenes has been reviewed more recently by Tykwinski and co‐workers. ^[26] Very little is known about ligand‐stabilized C_n species with donor ligands beyond the C₂ unit. As mentioned above, the complex Ph₃P‐C₃‐PPh₃ has been synthesized in the equilibrium geometry and the bonding situation is not known so far. ^[20] Free C₃ is known as an interstellar species having ¹Σ_g ⁺ ground state, ^[27] which was spectroscopically studied in the gas phase. ^[28]

In the present study, we carried out a density functional theory (DFT) study on (L)₂C₃ complexes where L=PPh₃, NHC^Me, and cAAC^Me. The bonding situation is analyzed through natural bond orbital (NBO) and charge and energy decomposition analyses (EDA‐NOCV). The present results suggest that the phosphine complex Ph₃P‐C₃‐PPh₃ unexpectedly has a synclinal (gauche) conformation and not a trans conformation as originally assumed. ^[20] The calculations also suggest that the title molecules L‐C₃‐L with L=NHC^Me and cAAC^Me are also viable to be realized experimentally at ambient conditions. The complex (NHC^Me)₂C₃ has a trans‐bent equilibrium geometry whereas the adduct (cAAC^Me)₂C₃ possesses a nearly linear arrangement of the central C₄ core. The bonding situation of the latter complex is distinctively different from the other two adducts.

Computational Details

The geometry optimization followed by the vibrational frequencies calculations of (L)₂C₃ molecules where L=NHC^Me, cAAC^Me, and PPh₃ in their respective singlet and triplet electronic states were performed at the BP86‐D3(BJ)/def2‐TZVPP level. ^[29] All the molecules are minima on the potential energy surfaces as ensured by the absence of any imaginary frequencies. For some molecules, additional calculations were carried out with the M06‐2X functional developed by Truhlar and co‐workers. ^[30] These calculations were carried out with the Gaussian 16 program package. ^[31] The NBO analysis ^[32] was performed to evaluate the partial charge, Wiberg bond indices (WBI), and natural bond orbitals by using the NBO 6.0 program. ^[33] Unless otherwise noted, we discuss geometries and energies at the BP86‐D3(BJ)/def2‐TZVPP level. Some ab initio calculations were carried out with the DLPNO‐CCSD(T) approach ^[34] in conjunction with the cc‐pVTZ basis set ^[35] by using the program package ORCA. ^[36]

The bonding situations were analyzed by means of an energy decomposition analysis (EDA) ^[37] together with the natural orbitals for chemical valence (NOCV) ^[38] method by using the ADF 2018.105 program package. ^[39] The EDA‐NOCV calculations were carried out at the BP86‐D3(BJ)/TZ2P level ^[40] by using the BP86‐D3(BJ)/def2‐TZVPP optimized geometries. In this analysis, the intrinsic interaction energy (ΔΕ _int) between two fragments can be divided into four energy components as follows [Eq. 1]:

$${\displaystyle \Delta E{}_{\mathrm{int}}=\Delta E{}_{\mathrm{elstat}}+\Delta E{}_{\mathrm{Pauli}}+\Delta E{}_{\mathrm{orb}}+\Delta E{}_{\mathrm{disp}}}$$ (1)

Although the electrostatic ΔE _elstat term represents the quasi‐classical electrostatic interaction between the unperturbed charge distributions of the prepared fragments, the Pauli repulsion ΔE _Pauli corresponds to the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments to the wavefunction, which properly obeys the Pauli principle through explicit antisymmetrization and renormalization of the production wavefunction. As we included D3(BJ), it provides us with the dispersion interaction energy between two interacting fragments ΔE _disp. The orbital term ΔE _orb originates from the mixing of orbitals, charge transfer, and polarization between the isolated fragments, which can be further decomposed into contributions from each irreducible representation of the point group of the interacting system as follows [Eq. 2]:

$${\displaystyle \Delta E_{\mathrm{o}\mathrm{r}\mathrm{b}}={\sum }_r\Delta E_r}$$ (2)

The combination of the EDA with NOCV enables the partition of the total orbital interactions into pairwise contributions of the orbital interactions, which is vital to get a complete picture of the bonding. The charge deformation Δρ_k(r), resulting from the mixing of the orbital pairs ψ _k(r) and ψ _−k(r) of the interacting fragments presents the amount and the shape of the charge flow owing to the orbital interactions [Eq. 3], and the associated energy term ΔE _orb provides the size of stabilizing orbital energy originating from such interactions [Eq. 4].

$${\displaystyle \Delta {\rho }_{\mathrm{o}\mathrm{r}\mathrm{b}}\left(r\right)={\sum }_k\Delta {\upsilon }_k\left(r\right)=\sum _{k=1}^{N/2}{\nu }_k[-{\psi }_{-k}^2\left(r\right)+{\psi }_k^2\left(r\right)]}$$ (3)

$${\displaystyle \Delta E_{\mathrm{o}\mathrm{r}\mathrm{b}}={\sum }_k\Delta E_{\mathrm{o}\mathrm{r}\mathrm{b}}^k={\sum }_k{\nu }_k[-F_{-k,-k}^{\mathrm{T}\mathrm{S}}+F_{k,k}^{\mathrm{T}\mathrm{S}}]}$$ (4)

More details about the EDA‐NOCV method and its application are given in recent review articles. ^[41]

Results and Discussion

Figure 1 shows the optimized geometries of the three (L)₂C₃ molecules with L=PPh₃ (1), NHC^Me (2), cAAC^Me (3), and the three free ligands L and the C₃ moiety in the electronic singlet ground states. The three compounds show distinct differences in their equilibrium geometries. The molecules 1 and 2 have rather acute bonding angles L‐C1‐C2 of 124° and 139° whereas 3 exhibits a nearly linear arrangement with a bending angle L‐C1‐C2 of 171°. Another difference between the carbene complexes concerns the planes of the ligands in 2 and 3. The two NHC^Me ligands in 2 are in the same plane as C₃, whereas the two cAAC^Me ligands in 3 are perpendicular to each other, as can be seen from the torsional angle, t(N′‐C′‐C′′‐N′′) of 178.7° in the first molecule and 99.9° in the second complex.

Figure 1.

Optimized geometries of (L)₂C₃ (L=PPh₃, NHC^Me, and cAAC^Me) and fragments at the BP86‐D3(BJ)/def2‐TZVPP level. Bond lengths are given in Å, angles in degrees. Calculated bond dissociation energies D _e and free energies ΔG ²⁹⁸ for the reactions (L)₂C₃→2 L+C₃.

The phosphine ligands L around the central C₃ component in the energetically lowest lying form of 1 unexpectedly have a synclinal (gauche) conformation and not a trans conformation as originally suggested. ^[20] The calculations at the BP86‐D3(BJ)/def2‐TZVPP level predict that the trans conformation 1 a is 8.9 kcal mol⁻¹ higher in energy than the gauche form 1. The optimization of both isomers without the dispersion term at the BP86/def2‐TZVPP level suggests that 1 is only 0.4 kcal mol⁻¹ lower in energy than 1 a, which suggests that dispersion interactions significantly contribute to the stability of 1. We further optimized both conformations by using the meta‐hybrid functional M06‐2X using a def2‐TZVPP basis set with and without explicit consideration of dispersion interactions using the D3 term of Grimme. ^[42] The calculations at the M06‐2X‐D3/def2‐TZVPP level also predict that 1 is 7.0 kcal mol⁻¹ lower in energy than 1 a whereas M06‐2X/def2‐TZVPP favors 1 over 1 a by 6.0 kcal mol⁻¹. According to the DFT calculations, (PPh₃)₂C₃ (1) has a gauche equilibrium geometry whereas (NHC^Me)₂C₃ (2) has a trans‐bent conformation as the energetically lowest‐lying form. The same energy ordering is predicted by ab initio calculations at the DLPNO‐CCSD(T)/cc‐pVTZ level using the BP86‐D3(BJ)/def2‐TZVPP optimized geometries, which give the gauche isomer 1 as being 7.7 kcal mol⁻¹ lower in energy than the trans isomer 1 a. For all three molecules, the corresponding triplet state is considerably higher in energy by 30.8–41.7 kcal mol⁻¹ than the singlet state (see Figure S1 in the Supporting Information)

The experimental work on (PPh₃)₂C₃ (1) reported the ³¹P NMR spectrum of the complex, which has a signal at δ=−10.4 ppm. ^[20] We calculated the ³¹P NMR chemical shift values of 1 and 1 a by using the GIAO approach at the BP86/def2‐TZVPP level. The calculated chemical shifts for the ³¹P NMR spectrum are δ=+11.3 and +17.5 ppm for the non‐degenerate P atoms of 1 and δ=−5.6 ppm for the degenerate P of 1 a. The latter value is in much better agreement with the experimental result, which was recorded in C₆D₆. It is possible that in solution 1 a prevails over 1 or that a fast equilibrium between the gauche conformations leads to a ³¹P NMR spectrum that mimics a trans form. The calculation of 1 and 1 a with inclusion of the solvent effect of C₆D₆ by using the CPCM ^[43] approach at the BP86‐D3(BJ)/def2‐TZVPP level even showed a slightly higher preference of 1 over 1 a by 9.2 kcal mol⁻¹.

The comparison of the equilibrium geometries of 1–3 with the free ligands shows that the C−C bonds of the central C₃ moiety in 1 (1.299/1.305 Å) and 2 (1.299 Å) have essentially the same length as in free C₃ (1.301 Å) whereas 3 possesses somewhat shorter bonds (1.282 Å). The geometries suggest that the l−C₃ bonds in 1 and 2 may have a different character than in 3. This is supported by the calculated bond strength of the three different ligands to the C₃ fragment, which is also given in Figure 1. The cAAC^Me ligands in 3 are much more strongly bonded (D _e=263.9 kcal mol⁻¹; ΔG ²⁹⁸=233.5 kcal mol⁻¹) than the NHC^Me ligands in 2 (D _e=166.9 kcal mol⁻¹; ΔG ²⁹⁸=137.6 kcal mol⁻¹) and the PPh₃ ligands in 1 (D _e=126.5 kcal mol⁻¹; ΔG ²⁹⁸=92.7 kcal mol⁻¹). The calculated bond dissociation energies suggest that 2 and particularly 3 are thermodynamically more stable than 1.

We analyzed the electronic structure and bonding situation of the three molecules with charge and energy decomposition methods. Table 1 shows the NBO results of the adducts. The NBO method finds a single P−C1 σ‐bond between the phosphine ligands and C₃ in 1 whereas double bonds C_L=C1 are calculated for the ligands in 2 and 3. The P−C1 σ‐bond in 1 is polarized toward the carbon end whereas the C_L=C1 σ‐bonds in 2 and 3 are slightly polarized toward the ligand atom. The C_L=C1 π‐bonds in 2 and 3 exhibit a small polarization in the opposite direction towards C₃. The charge distribution suggests that the central carbon atom C2 of the central C₃ moiety is essentially neutral whereas the terminal carbon atoms carry negative charges, which indicates the total charge donation L→C₃←L in the order 1>2>3.

Table 1.

NBO results of the compounds (L)₂C₃ at the BP86/def2‐TZVPP level of theory. Occupation number ON, polarization, and hybridization of the L−C1 bonds and partial charges q.

Complex	Bond	ON	l−C1 polarization		q
			and hybridization [%]		C1	C2	C3
1	P−C1 σ	1.96	P: 40.6 s(30.0), p(69.4)	C1: 59.4 s(49.0), p(51.0)	−0.80	0.09	−0.79
2	CL−C1 σ	1.97	CL: 52.6 s(42.1), p(57.9)	C1: 47.4 s(47.6), p(52.4)	−0.42	0.05	−0.42
	CL−C1 π	1.65	CL: 46.7 s(0.1), p(99.9)	C1: 53.3 s(0.1), p(99.9)
3	CL−C1 σ	1.97	CL: 51.2 s(38.6), p(61.4)	C1: 48.8 s(50.1), p(49.9)	−0.19	−0.01	−0.19
	CL−C1 π	1.80	CL: 46.1 s(0.1), p(99.9)	C1: 53.9 s(0.1), p(99.9)

Detailed insight into the nature of the ligand–C₃ interactions is provided by the EDA‐NOCV approach. The versatility of the method makes it possible to distinguish (a) between the total interactions of the isolated fragments in their original electronic states, charges, and equilibrium geometries, and (b) between the interactions of the fragments in the electronic states, charges, and geometries that are present in the finally formed molecule. For example, the electronic structure of diatomic LiF can be analyzed either by using the neutral atoms Li and F as interacting fragments in the EDA‐NOCV calculations, taking into account the charge migration Li→F during bond formation. Alternatively, one can use the finally formed ions Li⁺ and F⁻ as fragments, which are better suited to calculate the interactions in the eventually formed bond. Those fragments that give the smallest change in the orbital interactions ΔE _orb are best suited to describe the final bond. This approach has proven to be very useful in cases where the electronic state or charge of the fragments is not directly apparent. ^[44]

In the present case of the molecules l‐C₃‐L, we focus on the best description of the l−C bonds in 1–3, which can be sketched with dative or electron‐sharing bonds between neutral or charged fragments. We considered four different pairs of interacting species L₂ ^q and C₃ ^q in different electronic states, which may be considered as chemically reasonable species, which lead to the molecules l‐C₃‐L. These are (a) the neutral fragments L₂ and C₃ in the electronic singlet (S) state forming dative bonds; (b) the neutral fragments L₂ and C₃ in the electronic quintet (Q) state forming electron‐sharing double bonds; (c) the singly charged fragments L₂ ⁺ and C₃ ⁻ in the electronic doublet (D) state forming electron‐sharing and dative bonds; (d) the doubly charged fragments L₂ ²⁺ and C₃ ²⁻ in the electronic triplet (T) state forming electron‐sharing and dative bonds. Table 2 gives the numerical results of the EDA‐NOCV calculations of 1–3 using the four fragments pairs (a)–(d) as interacting species.

Table 2.

EDA‐NOCV results of (L)₂C₃ molecules using four different sets of fragments with different charges and electronic states (S=singlet, D=doublet, T=triplet, Q=quintet) and associated bond types at the BP86‐D3(BJ)/TZ2P level. Energies are in kcal mol⁻¹. The most favorable fragmentation scheme and bond type is given by the smallest ΔE _orb value written in bold.

Molecule	Bond type[a]	Fragments	ΔE int	ΔE Pauli	ΔE elstat	ΔE disp	ΔE orb
(PPh3)2C3	D	(PPh3)2(S)+C3 (S)	−488.5	674.6	−428.1	−16.3	−718.6
	E	(PPh3)2(Q)+C3 (Q)	−461.1	630.4	−371.4	−16.3	−703.7
	D+E	[(PPh3)2]+(D)+[C3]− (D)	−493.8	766.5	−565.5	−16.3	−678.5
	D+E	[(PPh3)2]2+(T)+[C3]2− (T)	−824.4	967.8	−918.8	−16.3	−857.4
(NHCMe)2C3	D	(NHCMe)2(S)+C3 (S)	−541.0	634.7	−466.2	−9.4	−700.1
	E	(NHCMe)2(Q)+C3 (Q)	−544.8	506.4	−373.8	−9.4	−667.9
	D+E	[(NHCMe)2]+(D)+[C3]− (D)	−551.9	621.5	−517.2	−9.4	−646.7
	D+E	[(NHCMe)2]2+(T)+[C3]2− (T)	−875.9	659.2	−798.2	−9.4	−727.5
(cAACMe)2C3	D	(cAACMe)2(S)+C3 (S)	−594.2	419.5	−359.6	−10.6	−643.5
	E	(cAACMe)2(Q)+C3 (Q)	−407.7	519.1	−348.5	−10.6	−567.6
	D+E	[(cAACMe)2]+(D)+[C3]− (D)	−586.8	555.8	−445.4	−10.6	−686.5
	D+E	[(cAACMe)2]2+(T)+[C3]2− (T)	−930.1	873.0	−819.7	−10.6	−972.7

[a] D=Dative bond; E=electron‐sharing bond.

The results in Table 2 suggest that the best description of the l‐C₃‐L bonds for L=PPh₃ (1) and L=NHC^Me (2) comes from the interactions of the singly charged fragments L₂ ⁺ and C₃ ⁻ in the electronic doublet (D) state forming electron‐sharing and dative bonds. In contrast, the smallest ΔE _orb value and thus the best description of the l‐C₃‐L bonds for L=cAAC^Me (3) is provided by the neutral fragments L₂ and C₃ in the electronic quintet (Q) state forming electron‐sharing double bonds. This agrees with the NBO charges in Table 1, which suggest that the partial charges of the interacting fragments in 1 and 2 are clearly higher than in 3. We further analyzed the orbital interactions ΔE _orb of 1–3 by using the most favorable fragments and studied the main pairwise orbital contributions ΔE _orb(n). The numerical results are given in Table 3.

Table 3.

The EDA‐NOCV results at the BP86‐D3(BJ)/TZ2P level of L₂C₃ molecules 1–3 using (L₂)⁺ and (C₃)⁻ in the electronic doublet (D) states as interacting fragments for 1 and 2 and neutral L₂ and C₃ in the quintet (Q) states as interacting fragments for 3. Energies are in kcal mol⁻¹.

Energy	Interaction[c]	[(PPh3)2]+(D) +[C3]−(D)	[(NHCMe)2]+ (D) +[C3]−(D)	(cAACMe)2(Q) +C3 (Q)
ΔE int		−493.8	−551.9	−407.7
ΔE Pauli		766.5	621.5	519.1
ΔE disp [a]		−16.3 (1.2 %)	−9.4 (0.8 %)	−10.6 (1.1 %)
ΔE elstat [a]		−565.5 (44.8 %)	−517.2 (44.0 %)	−348.5 (37.6 %)
ΔE orb [a]		−678.5 (53.8 %)	−646.7 (55.1 %)	−567.6 (61.2 %)
ΔE orb(1) [b]	l‐C3‐L σ e− sharing (+,+)			−187.6 (33.1 %)
	L→C3←L σ donation (+,+)	−286.3 (42.1 %)	−235.1 (36.3 %)	–
ΔE orb(2) [b]	l‐C3‐L σ e− sharing (+,−)	−231.3 (34.1 %)	−208.7 (32.2 %)	−180.3 (31.8 %)
	L→C3←L σ donation (+,−)			–
ΔE orb(3) [b]	l‐C3‐L π/σ e− sharing			−77.7 (13.7 %)
	L←C3→L σ back donation	−51.8 (7.6 %)	−88.3 (13.6 %)	–
ΔE orb(4) [b]	l‐C3‐L π e− sharing			−76.7 (13.5 %)
	L←C3→L π back‐donation	−40.4 (5.9 %)	−52.9 (8.1 %)	–
ΔE orb(5) [b]	L←C3→L π back‐donation	−25.0 (3.6 %)	−18.4 (2.8 %)	–
ΔE orb(rest) [b]		−43.6 (6.4 %)	−43.3 (6.6 %)	−45.3 (8.0 %)

[a] The values in the parentheses show the contribution to the total attractive interaction ΔE _elstat+ΔE _orb+ΔE _disp. [b] The values in parentheses show the contribution to the total orbital interaction ΔE _orb.

There are five relevant orbital interactions ΔE _orb(1)–ΔE _orb(5) for molecules 1 and 2 and four terms ΔE _orb(1)–ΔE _orb(4) for complex 3. The nature of the orbital terms and the involved fragments orbitals can be identified with the help of the associate deformation densities Δρ_n and connected MOs that are shown in Figure 2, Figure 3, and Figure 4. The strongest orbital interaction ΔE _orb(1) in 1 and 2 is due to the σ donation of the HOMO of the ligands L₂ ⁺ into the LUMO of C₃ ⁻. It is remarkable and counter‐intuitive that the cation serves as donor and the anion as acceptor. However, this must be seen as only one part of the total orbital interactions. The slightly weaker orbital term ΔE _orb(2) in 1 and 2 comes from the electron‐sharing interactions of the unpaired electrons in the SOMO of the fragments. The remaining three orbital terms ΔE _orb(3)–ΔE _orb(5) in the two molecules are due the π back‐donation of the degenerate HOMO and the HOMO−1 of C₃ ⁻ to vacant orbitals of L₂ ⁺. ^[45] The strength of the π back‐donation is much less than that of the σ donation ΔE _orb(1) but the amount of charge migration, which is given by the eigenvalues υ_n, shows that π back‐donation has a similar magnitude as the σ donation, which is consistent with the NBO charges (Table 1). The amount of charge migration given by υ_n does not correlate with the associated stabilization energy ΔE _orb(n).

Figure 2.

The shape of the deformation densities Δρ _(1)–(5) that correspond to ΔE _orb(1)–(5), and the associated MOs of (PPh₃)₂C₃ and the fragments orbitals of [(PPh₃)₂]⁺ and [C₃]⁻ in the doublet state at the BP86‐D3(BJ)/TZ2P level. Isosurface values are 0.003 au. The eigenvalues |ν_n| give the size of the charge migration in e. The direction of the charge flow of the deformation densities is red→blue.

Figure 3.

The shape of the deformation densities Δρ _(1)–(5) that correspond to ΔE _orb(1)–(5), and the associated MOs of (NHC^Me)₂C₃ and the fragments orbitals of [(NHC^Me)₂]⁺ and [C₃]⁻ in the doublet state at the BP86‐D3(BJ)/TZ2P level. Isosurface values are 0.003 au. The eigenvalues |ν_n| give the size of the charge migration in e. The direction of the charge flow of the deformation densities is red→blue.

Figure 4.

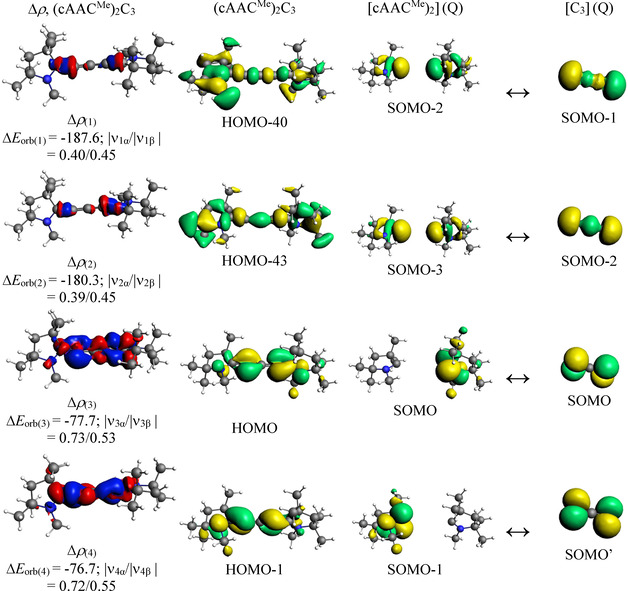
The shape of the deformation densities Δρ _(1)–(5) that correspond to ΔE _orb(1)–(5), and the associated MOs of (cAAC^Me)₂C₃ and the fragments orbitals of (cAAC^Me) and C₃ in the quintet state at the BP86‐D3(BJ)/TZ2P level. Isosurface values are 0.003 au. The eigenvalues |ν_n| give the size of the charge migration in e. The direction of the charge flow of the deformation densities is red→blue.

The four significant orbital terms ΔE _orb(1)–ΔE _orb(4) between the neutral fragments in the quintet states in complex 3 are easily recognized as the strong in‐phase (+,+) and out‐of‐phase (+,−) electron‐sharing interactions ΔE _orb(1) and ΔE _orb(2) and the weaker but still rather strong orthogonal π interactions ^[45] ΔE _orb(3) and ΔE _orb(4), which are slightly different, because the molecular planes of the cAAC^Me ligands are not perfectly orthogonal to each other.

Summary and Conclusion

The present study may be summarized as follows. Quantum chemical calculations suggest that the molecules l‐C₃‐L with L=PPh₃ (1) and NHC^Me (2) have equilibrium geometries where the ligands are bonded with rather acute bonding angles at the linear C₃ moiety. The phosphine adduct 1 has a synclinal (gauche) conformation whereas 2 exhibits a trans conformation of the ligands. In contrast, the complex with L=cAAC^Me (3) possesses a nearly linear arrangement of the carbene ligands at the C₃ fragment. The bond dissociation energies of the ligands have the order 1<2<3. The bonding analysis using charge and energy decomposition methods suggests that 3 is best described as a cumulene with electron‐sharing double bonds between neutral fragments (cAAC^Me)₂ and C₃ in the respective electronic quintet state yielding (cAAC^Me)=C₃=(cAAC^Me). In contrast, 1 and 2 possess electron‐sharing and dative bonds between positively charged ligands [(PPh₃)₂]⁺ or [(NHC^Me)₂]⁺ and negatively charged [C₃]⁻ fragments in the respective doublet state.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

S. M. N. V. T. Gorantla, S. Pan, K. C. Mondal, G. Frenking, Chem. Eur. J. 2020, 26, 14211.