A mathematical model to examine the effect of quarantine on the spread of coronavirus

Abstract

In this study, we propose a mathematical model about the spread of novel coronavirus. This model is a system of fractional order differential equations in Caputo’s sense. The aim is to explain the virus transmission and to investigate the impact of quarantine on decreasing the prevalence rate of the virus in the environment. The unique solvability of the presented COVID-19 model is proved. Also, the equilibrium points and the reproduction number of the proposed model are discussed in two cases with and without considering the quarantine factor. Using the Adams-Bashforth-Moulton predictor-corrector method, some numerical simulations are implemented to survey the behavior of the considered model.

1. Introduction

The current crisis that many countries are facing is a new virus called coronavirus. In late December 2019, an unknown virus was reported in the city of Wuhan, China. The main concern of Chinese officials was that the number of infected people was increasing exponentially, and this created an epidemic issue in Wuhan [1]. Chinese immunologists who have dealt with this emerging phenomenon believe that the new virus can easily spread in public. The main way to the transmission of coronavirus is through respiratory droplets when people are near to each other [2], [3]. Therefore, quarantine and social distancing seem to be the only appropriate control mechanisms, until a vaccine or some drugs are found for coronavirus disease 2019 (COVID-19).

Mathematical biology is one of the most interesting research areas for applied mathematicians. Many theoretical and computational studies are done by the scientists in this field [4], [5], [6], [7], [8]. In recent years, using fractional order operators have provided new aspects for describing mathematical models in biomathematics. The definition of fractional order operators can preserve hereditary and memory traits of a considered variable in a real problem [9], [10], [11], [12], [13], [14]. In many cases of natural biological processes, the present and next state of a system are dependent on its all previous states. Thus, fractional operators are suitable and valuable mathematical tools to a better understanding the behavior of natural systems. This helps researchers to propose more accurate models of various biological phenomena. Authors in literature employed different types of fractional derivatives for these purposes. Caputo and Riemann-Liouville fractional derivatives are the most used definitions by researchers [15], [16], [17], [18], [19], [20], [21]. In recent years, some new definitions of fractional derivatives have been proposed. Caputo and Fabrizio in [22] presented a fractional derivative without singular kernel. Models introduced in [23], [24], [25] are some practical applications of this fractional derivative. Based on Caputo and Fabrizio fractional derivative definition, Atangana and Baleanu [26] developed a new fractional derivative with Mittag-Leffler kernel. Researchers in [27], [28] used this fractional operator to study some other natural phenomena.

COVID-19 causes significant damage to the economies of many countries. Therefore, it is vital to find a working solution to prevent the spread of this virus and to control this disease. That is why many people around the world are working in different disciplines looking for a useful way to control the virus efficiently. In recent months, the main focus of mathematical biology specialists has been on the problems related to this pandemic. These researchers presented some models to study the important factors of virus transmission. By studying these factors, they are trying to take an essential step in this field. Thus, many mathematical models are presented to survey the dynamics of COVID-19 infection [29], [30], [33], [34], [35], [36], [37].

In this study, we introduce two fractional order models to analyze the behavior of COVID-19 in society. The main difference between these models is the quarantine factor. First, the model is surveyed according to this factor. Afterwards, the model is investigated without considering this factor.

The rest of this paper has the following organization. In Section 2, we provide an initial model of COVID-19 in the presence of the quarantine process and analysis of the model will be examined. This model consists seven compartments, each of them is somehow involved in the virus. In Section 3 we analyze a sub-model of the previous section without considering the quarantine factor. Some numerical simulations are implemented in Section 4 to investigate the effect of quarantine restrictions on the spread of coronavirus. Finally, the main findings and conclusions are presented in Section 5.

2. COVID-19 model with considering quarantine

In this section, we propose a fractional order model for studying the quarantine factor on coronavirus prevalence. Therefore, at first, we review the definition of Caputo fractional derivative [9] as

$${}_0^C{\mathrm{D}}_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma (n-\alpha )}{\int }_0^t(t-\xi ){}^{(n-\alpha -1)}{f}^{\left(n\right)}\left(\xi \right)d\xi ,n-1<\alpha <n.$$ (1)

In the following, we use ${\text{D}}^{\alpha }$ insted of ${}_0^C{\mathrm{D}}_t^{\alpha }$ for simplicity.

In the survey conducted, we will have seven compartments. People who are susceptible or exposed to the virus are shown by $S$. These individuals are divided into the following categories:

• •infected but do not yet have symptoms $\left(A\right),$
• •infected with symptoms $\left(I\right),$
• •infected who are quarantined $\left(E_q\right),$
• •infected who are hospitalized $\left(H\right),$
• •people who have recovered from the disease $\left(R\right),$
• •the quarantined susceptible individuals $\left(S_q\right),$

and

$$N\left(t\right)=S\left(t\right)+I\left(t\right)+A\left(t\right)+R\left(t\right)+H\left(t\right)+E_q\left(t\right)+S_q\left(t\right).$$

To present the model, the following parameters are introduced. $\Lambda$ is the birth rate of the population. $c$ is the contact rate. $\theta$ shows the transmission rate and $\beta$ is the probability of transmission per contact. $q$ indicates quarantined rate of susceptible individuals. ${\delta }_I$ and ${\delta }_q$ represent transition rates of symptomatic infected individuals and quarantined susceptible individuals to the quarantined infected compartment, respectively. ${\gamma }_I,$ ${\gamma }_A$ and ${\gamma }_H$ are the recovery rates of infected people with symptoms, infected people without symptoms and quarantined infected individuals, respectively. $\mu$ shows naturally death rates. $\rho$ is the probability of having symptoms among infected individuals. $\lambda$ shows the release rate of the quarantined uninfected contacts into the community. Finally, ${\alpha }_I,$ ${\alpha }_A,$ ${\alpha }_E$ and ${\alpha }_R$ represent the rates at which the virus removes from the compartments $I,$ $A,$ $E$ and $R$.

According to the above defined parameters and the relations between the considered human categories, we get the following system:

$$\{\begin{array}{c}{D}^{\alpha }S=\Lambda -(c\beta (1-q)(1-\rho )+c\beta (1-q)\rho +\beta \mathit{cq}\hfill \\ +(1-\beta )\mathit{cq})(I+\theta A)S+\lambda S_q-\mu S,\hfill \\ D^{\alpha }I=\beta c\rho (1-q)S(I+\theta A)-({\delta }_I+{\gamma }_I+{\alpha }_I)I,\hfill \\ D^{\alpha }A=\beta c(1-\rho )(1-q)S(I+\theta A)-({\gamma }_A+{\alpha }_A)A,\hfill \\ D^{\alpha }{S}_q=(1-\beta )\mathit{cqS}(I+\theta A)-(\lambda +\mu )S_q,\hfill \\ D^{\alpha }{E}_q=\beta cqS(I+\theta A)-({\delta }_q+{\alpha }_E)E_q,\hfill \\ D^{\alpha }H={\delta }_{I}I+{\delta }_q{E}_q-({\alpha }_A+{\gamma }_H)H,\hfill \\ D^{\alpha }R={\gamma }_{I}I+{\gamma }_{A}A+{\gamma }_{H}H-{\alpha }_{R}R.\hfill \end{array}$$ (2)

The right-hand side of the system (2) has the physical dimension ${\left(time\right)}^{-1}$ whereas the other side has the dimension ${\left(time\right)}^{-\alpha }$. To correct this mismatch, we use the approach proposed in [15]. So, we get the modified system as

$$\{\begin{array}{c}{D}^{\alpha }S=\Lambda -(c^{\alpha }{\beta }^{\alpha }(1-q)+c^{\alpha }q)(I+{\theta }^{\alpha }A)S+{\lambda }^{\alpha }{S}_q-{\mu }^{\alpha }S,\hfill \\ D^{\alpha }I={\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q)S(I+{\theta }^{\alpha }A)-({\delta }_I^{\alpha }+{\gamma }_I^{\alpha }+{\alpha }_I^{\alpha })I,\hfill \\ D^{\alpha }A={\beta }^{\alpha }{c}^{\alpha }(1-{\rho }^{\alpha })(1-q)S(I+{\theta }^{\alpha }A)-({\gamma }_A^{\alpha }+{\alpha }_A^{\alpha })A,\hfill \\ D^{\alpha }{S}_q=(1-{\beta }^{\alpha })c^{\alpha }\mathit{qS}(I+{\theta }^{\alpha }A)-({\lambda }^{\alpha }+{\mu }^{\alpha })S_q,\hfill \\ D^{\alpha }{E}_q={\beta }^{\alpha }{c}^{\alpha }\mathit{qS}(I+{\theta }^{\alpha }A)-({\delta }_q^{\alpha }+{\alpha }_E^{\alpha })E_q,\hfill \\ D^{\alpha }H={{\delta }_I}^{\alpha }I+{\delta }_q^{\alpha }{E}_q-({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })H,\hfill \\ D^{\alpha }R={\gamma }_I^{\alpha }I+{\gamma }_A^{\alpha }A+{\gamma }_H^{\alpha }H-{\alpha }_R^{\alpha }R.\hfill \end{array}$$ (3)

To examine the unique solvability of system (3), first we recall the following lemma.

Lemma 1

[38] (Generalized mean value theorem) Suppose that $w\left(t\right)\in C[a,b]$ and $D_t^{\alpha }w\left(t\right)\in C[a,b]$ for $0<\alpha \le 1,$ then

$$w\left(t\right)=w\left(a\right)+\frac{1}{\Gamma \left(\alpha \right)}{D}_t^{\alpha }w\left(\zeta \right).{(t-a)}^{\alpha },$$ (4)

where $a\le \zeta \le t,\forall t\in (a,b]$ .

Corollary 1

Assume that $w\left(t\right)\in C[a,b]$ and $D_t^{\alpha }w\left(t\right)\in C[a,b]$ for $0<\alpha ⩽1$ . It follows from Lemma 1 that if $D_t^{\alpha }w\left(t\right)⩾0,\forall t\in (a,b),$ then $w\left(t\right)$ is non-decreasing $\forall t\in [a,b]$ and if $D_t^{\alpha }w\left(t\right)⩽0,\forall t\in (a,b),$ then w(t) is non-increasing on $[a,b]$ .

Theorem 1

The system (3) has a unique positive solution for $t⩾0$ .

Proof

The existence and uniqueness of solution for system (3) on $[0,\infty )$ is a direct result of Theorem 3.1 and Remark 3.2 from Lin [39]. Now, on the region

$$\begin{array}{ccc}\hfill {\Omega }_{+}& =& \left\{\right(S,I,A,S_q,E_q,H,R);\hfill \\ & & S>0,I⩾0,A⩾0,S_q⩾0,E_q⩾0,H⩾0,R⩾0\},\hfill \end{array}$$

we have

$$\begin{array}{c}{D}_t^{\alpha }S{\mid }_{S=0}=\Lambda +{\lambda }^{\alpha }{S}_q\ge 0,\hfill \\ D_t^{\alpha }I{\mid }_{I=0}={\theta }^{\alpha }{\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q)\mathit{AS}\ge 0,\hfill \\ D_t^{\alpha }A{\mid }_{A=0}={\beta }^{\alpha }{c}^{\alpha }(1-{\rho }^{\alpha })(1-q)\mathit{SI}\ge 0,\hfill \\ D_t^{\alpha }{S}_q{\mid }_{S_q=0}=c^{\alpha }q(1-{\beta }^{\alpha })S(I+{\theta }^{\alpha }A)\ge 0,\hfill \\ D_t^{\alpha }{E}_q{\mid }_{E_q=0}=c^{\alpha }q{\beta }^{\alpha }S(I+{\theta }^{\alpha }A)\ge 0,\hfill \\ D_t^{\alpha }H{\mid }_{H=0}={\delta }_I^{\alpha }I+{\delta }_q^{\alpha }{E}_q\ge 0,\hfill \\ D_t^{\alpha }R{\mid }_{R=0}={\gamma }_I^{\alpha }I+{\gamma }_A^{\alpha }A+{\gamma }_H^{\alpha }H\ge 0.\hfill \end{array}$$

Thus, on each hyperplane bounding the nonnegative orthant, the vector field points to ${\Omega }_{+}$. So, Corollary (1) results ${\Omega }_{+}$ is a positive invariant set. □

2.1. Stability of the disease-free equilibrium

Now, we explore the stability for the model (3) by considering the disease free equilibrium (DFE) point and the basic reproduction number. Let the right hand side of the four differential equations in (3) are equal to zero. Then, the DFE for the model (3) will be as

$$E_0=(\frac{\Lambda }{{\mu }^{\alpha }},0,0,0,0,0,0).$$

To verify the stability of $E_0,$ the basic reproduction number denoted by $R_0$ should be computed. For this aim, the next generation matrix method [5] will be employed. First, based on this method, we define the matrices $F$ and $V$ associated with the model (3) as

$$\begin{array}{c}F=\left(\begin{array}{cccc}{\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q)S& {\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q){\theta }^{\alpha }S& 0& 0\\ {\beta }^{\alpha }{c}^{\alpha }(1-{\rho }^{\alpha })(1-q)S& {\beta }^{\alpha }{c}^{\alpha }(1-{\rho }^{\alpha })(1-q){\theta }^{\alpha }S& 0& 0\\ {\beta }^{\alpha }{c}^{\alpha }\mathit{qS}& {\beta }^{\alpha }{c}^{\alpha }q{\theta }^{\alpha }S& 0& 0\\ 0& 0& 0& 0\end{array}\right),\hfill \\ V=\left(\begin{array}{cccc}\eta & 0& 0& 0\\ 0& \xi & 0& 0\\ 0& 0& ({\delta }_q^{\alpha }+{\alpha }_E^{\alpha })& 0\\ -{\delta }_I^{\alpha }& 0& -{\delta }_q^{\alpha }& ({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })\end{array}\right).\hfill \end{array}$$

The required basic reproduction number of model $\left(3\right)$ is the spectral radius of the matrix $F{V}^{-1}$. Hence, we get

$$R_0=\frac{\psi (\eta {\theta }^{\alpha }-\eta {\theta }^{\alpha }{\rho }^{\alpha }+\xi {\rho }^{\alpha })}{\xi \eta },$$ (5)

in which

$$\begin{array}{c}\psi :={\beta }^{\alpha }{c}^{\alpha }(1-q)\frac{\Lambda }{{\mu }^{\alpha }},\eta :={\delta }_I^{\alpha }+{\gamma }_I^{\alpha }+{\alpha }_I^{\alpha },\hfill \\ \xi :={\gamma }_A^{\alpha }+{\alpha }_A^{\alpha },\hfill \end{array}$$

Theorem 2

If $R_0<1$ then the DFE point $E_0$ is locally asymptotically stable.

Proof

First, we get the Jacobian matrix related to (3) at $E_0$ as:

$$\begin{array}{c}J\left(E_0\right)=(\begin{array}{cccc}-{\mu }^{\alpha }\hfill & -\psi -c^{\alpha }q\frac{\Lambda }{{\mu }^{\alpha }}\hfill & -\psi -c^{\alpha }q{\theta }^{\alpha }\hfill & \lambda \hfill \\ 0\hfill & \psi {\rho }^{\alpha }-\eta \hfill & \psi {\rho }^{\alpha }{\theta }^{\alpha }\hfill & 0\hfill \\ 0\hfill & \psi (1-{\rho }^{\alpha })\hfill & \psi (1-{\rho }^{\alpha }){\theta }^{\alpha }-\xi \hfill & 0\hfill \\ 0\hfill & (1-{\beta }^{\alpha })c^{\alpha }q\frac{\Lambda }{{\mu }^{\alpha }}\hfill & (1-{\beta }^{\alpha })c^{\alpha }q\frac{\Lambda }{{\mu }^{\alpha }}{\theta }^{\alpha }\hfill & -({\lambda }^{\alpha }+{\mu }^{\alpha })\hfill \\ 0\hfill & {\beta }^{\alpha }{c}^{\alpha }q\frac{\Lambda }{{\mu }^{\alpha }}\hfill & {\beta }^{\alpha }{c}^{\alpha }q\frac{\Lambda }{{\mu }^{\alpha }}\hfill & 0\hfill \\ 0\hfill & {\delta }_I^{\alpha }\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\gamma }_I^{\alpha }\hfill & {\gamma }_A^{\alpha }\hfill & 0\hfill \end{array}\\ \begin{array}{cccc}& 0\hfill & 0\hfill & 0\hfill \\ & 0\hfill & 0\hfill & 0\hfill \\ & 0\hfill & 0\hfill & 0\hfill \\ & 0\hfill & 0\hfill & 0\hfill \\ -({\delta }_q^{\alpha }+{\alpha }_E^{\alpha })\hfill & 0\hfill & 0\hfill & \\ {\delta }_q^{\alpha }\hfill & -({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })\hfill & 0\hfill & \\ 0\hfill & {\gamma }_H^{\alpha }\hfill & -{\alpha }_R^{\alpha }\hfill \end{array}).\end{array}$$

The DFE is stable if all eigenvalues of the Jacobian matrix $J\left(E_0\right)$ be negative. The eigenvalues of this matrix are as follows:

$$\begin{array}{c}{\lambda }_1=-{\lambda }^{\alpha }-{\mu }^{\alpha },{\lambda }_2=-{\mu }^{\alpha },{\lambda }_3=-{\delta }_q^{\alpha }-{\alpha }_E^{\alpha },\hfill \\ {\lambda }_4=-{\alpha }_R^{\alpha },{\lambda }_5=-{\alpha }_A^{\alpha }-{\gamma }_H^{\alpha },\hfill \\ {\displaystyle {\lambda }_6=-\frac{1}{2}(K(\eta ,\psi ,\theta ,\xi ,\rho )}\hfill \\ +\sqrt{{\left(K(\eta ,\psi ,\theta ,\xi ,\rho )\right)}^2-4(-\psi \eta {\theta }^{\alpha }+\eta \xi +\psi \eta {\theta }^{\alpha }{\rho }^{\alpha }-\psi \xi {\rho }^{\alpha })}),\hfill \\ {\displaystyle {\lambda }_7=\frac{1}{2}(-K(\eta ,\psi ,\theta ,\xi ,\rho )}\hfill \\ +\sqrt{{\left(K(\eta ,\psi ,\theta ,\xi ,\rho )\right)}^2-4(-\psi \eta {\theta }^{\alpha }+\eta \xi +\psi \eta {\theta }^{\alpha }{\rho }^{\alpha }-\psi \xi {\rho }^{\alpha })}),\hfill \end{array}$$

where

$$\mathrm{K}(\mathrm{\eta },\mathrm{\psi },\mathrm{\theta },\mathrm{\xi },\mathrm{\rho }):=\eta -\psi {\theta }^{\alpha }+\xi -\psi {\rho }^{\alpha }+\psi {\theta }^{\alpha }{\rho }^{\alpha }.$$ (6)

Since the first five eigenvalues are negative, so it suffices to prove that ${\lambda }_6<0,$ and ${\lambda }_7<0$. Thus

$${\lambda }_6=-\frac{1}{2}(\mathrm{K}+\sqrt{{\mathrm{K}}^2+4\eta \xi ({\mathrm{R}}_0-1)}),$$ (7)

if $R_0<1$ then ${\mathrm{K}}^2>{\mathrm{K}}^2+4\eta \xi (R_0-1)$ and

$$K>\sqrt{{\mathrm{K}}^2+4\eta \xi (R_0-1)}>0,$$ (8)

so, it can be concluded ${\lambda }_6<0$ if $R_0<1$. According to (6) and (8), for ${\lambda }_7,$ we get

$${\lambda }_7=\frac{1}{2}(-\mathrm{K}+\sqrt{{\mathrm{K}}^2+4\eta \xi (R_0-1)}),$$ (9)

and the proof is complete. □

3. COVID-19 model without quarantine factor

In this section, we consider a sub-model of (3) without considering the quarantine factor and discuss its properties. In fact, we want to see what happens for the basic reproduction number of COVID-19 model in the absence of quarantine. It helps us to better realize the impact of quarantine on the spread of disease. Thus, we can get an apparent comparison between two cases, with and without considering quarantine facilities. For this end, by deleting the variables and parameters related to the quarantine process from (3), we get

$$\{\begin{array}{c}{D}^{\alpha }S=\Lambda -c^{\alpha }{\beta }^{\alpha }(1-q)(I+{\theta }^{\alpha }A)S-{\mu }^{\alpha }S,\hfill \\ D^{\alpha }I={\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q)S(I+{\theta }^{\alpha }A)-({\delta }_I^{\alpha }+{\gamma }_I^{\alpha }+{\alpha }_I^{\alpha })I,\hfill \\ D^{\alpha }A={\beta }^{\alpha }{c}^{\alpha }(1-{\rho }^{\alpha })(1-q)S(I+{\theta }^{\alpha }A)-({\gamma }_A^{\alpha }+{\alpha }_A^{\alpha })A,\hfill \\ D^{\alpha }H={\delta }_I^{\alpha }I-({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })H,\hfill \\ D^{\alpha }R={\gamma }_I^{\alpha }I+{\gamma }_A^{\alpha }A+{\gamma }_H^{\alpha }H-{\alpha }_R^{\alpha }R.\hfill \end{array}$$ (10)

The category $S_q$ of (3) is a subset $S$. Also, $E_q$ in (3) is a subset from the union of $A$ and $I$. So, the model (3) and the sub-model (10) have the similar main compartments. As a result, the reproduction numbers of these models are the same and obtained as (5).

Let $E^{*}=(S^{*}\left(t\right),I^{*}\left(t\right),A^{*}\left(t\right),H^{*}\left(t\right),R^{*}\left(t\right))$ is the endemic equilibrium of this model. This point can be determined by solving the system

$$\{\begin{array}{c}\Lambda -c^{\alpha }{\beta }^{\alpha }(1-q)(I+{\theta }^{\alpha }A)S-{\mu }^{\alpha }S=0,\hfill \\ {\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q)S(I+{\theta }^{\alpha }A)-({\delta }_I^{\alpha }+{\gamma }_I^{\alpha }+{\alpha }_I^{\alpha })I=0,\hfill \\ {\beta }^{\alpha }{c}^{\alpha }(1-{\rho }^{\alpha })(1-q)S(I+{\theta }^{\alpha }A)-({\gamma }_A^{\alpha }+{\alpha }_A^{\alpha })A=0,\hfill \\ {\delta }_I^{\alpha }I-({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })H=0,\hfill \\ {\gamma }_I^{\alpha }I+{\gamma }_A^{\alpha }A+{\gamma }_H^{\alpha }H-{\alpha }_R^{\alpha }R=0.\hfill \end{array}$$ (11)

The third equation leads to

$$A^{*}=\frac{{\beta }^{\alpha }{c}^{\alpha }(1-q)(1-{\rho }^{\alpha })S^{*}(I^{*}+{\theta }^{\alpha }{A}^{*})}{\xi },$$ (12)

Put $y=I^{*}+{\theta }^{\alpha }{A}^{*}$. Then, we get

$$A^{*}=\frac{{\beta }^{\alpha }{c}^{\alpha }(1-q)(1-{\rho }^{\alpha })S^{*}y}{\xi },$$

so

$$y=\frac{A^{*}\xi }{{\beta }^{\alpha }{c}^{\alpha }(1-q)(1-{\rho }^{\alpha })S^{*}}.$$ (13)

The first equation in (11) results

$$S^{*}=\frac{\Lambda }{{\mu }^{\alpha }+{\beta }^{\alpha }{c}^{\alpha }(1-q)(I^{*}+{\theta }^{\alpha }{A}^{*})}=\frac{\Lambda }{{\mu }^{\alpha }+{\beta }^{\alpha }{c}^{\alpha }(1-q)y}.$$ (14)

Substituting (14) into (13) and some direct calculations give

$$y=\frac{A^{*}\xi {\mu }^{\alpha }}{\Lambda {\beta }^{\alpha }{c}^{\alpha }(1-q)(1-{\rho }^{\alpha })-A^{*}\xi {\beta }^{\alpha }{c}^{\alpha }(1-q)}.$$ (15)

Now, from the second equation in (11), we have

$$I^{*}=\frac{{\beta }^{\alpha }{c}^{\alpha }\rho (1-q)S^{*}(I^{*}+{\theta }^{\alpha }{A}^{*})}{\eta }=\frac{{\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q)S^{*}y}{\eta }.$$ (16)

This relation leads to

$$y=\frac{\eta {\mu }^{\alpha }{I}^{*}}{{\beta }^{\alpha }{c}^{\alpha }{\rho }^{\alpha }(1-q)\Lambda -{\beta }^{\alpha }{c}^{\alpha }(1-q)\eta I^{*}}.$$ (17)

Hence, due to (15) and (17), the following result can be obtained

$$A^{*}=\frac{(1-{\rho }^{\alpha })\eta }{{\rho }^{\alpha }\xi }{I}^{*}.$$ (18)

With substituting (17) into (14)

$$S^{*}=\frac{{\rho }^{\alpha }\Lambda -\eta I^{*}}{{\mu }^{\alpha }{\rho }^{\alpha }}.$$ (19)

Now, the fourth equation in (11) results

$$H^{*}=\frac{{\delta }_I^{\alpha }}{{\alpha }_A^{\alpha }+{\gamma }_H^{\alpha }}{I}^{*}.$$ (20)

Finally, from the fifth equation in (11) and Eqs. (18), and (20), we can conclude

$$R^{*}=(\frac{{\gamma }_A^{\alpha }(1-{\rho }^{\alpha })\eta }{{\alpha }_R^{\alpha }{\rho }^{\alpha }\xi }+\frac{{\gamma }_H^{\alpha }{\delta }_I^{\alpha }}{{\alpha }_R^{\alpha }({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })}+\frac{{\gamma }_I^{\alpha }}{{\alpha }_R^{\alpha }})I^{*}.$$ (21)

Therefore, all the components of $E^{*}$ can be displayed in terms of $I^{*}$.

Theorem 3

The model (10) has an unique endemic equilibrium if and only if $R_0>1$ .

Proof. According to (17) and (19), from (16) and with doing some simple calculations, we have

$$I^{*}=\frac{\Lambda {\rho }^{\alpha }}{\eta }-\frac{{\rho }^{\alpha }\xi \Lambda }{\psi \left({\rho }^{\alpha }\xi +(1-{\rho }^{\alpha })\eta {\theta }^{\alpha }\right)}.$$

Hence, rewriting this equation due to the obtained reproduction number $R_0$ in (5) results

$$I^{*}=\frac{\Lambda {\rho }^{\alpha }}{\eta }(1-\frac{1}{R_0}).$$ (22)

So, substituting (22) into Eqs. (18)–(21) gives

$$\begin{array}{c}{\displaystyle S^{*}=\frac{\Lambda }{{\mu }^{\alpha }{R}_0},}\hfill \\ {\displaystyle A^{*}=\frac{\Lambda (1-{\rho }^{\alpha })}{\xi }(1-\frac{1}{R_0}),}\hfill \\ {\displaystyle H^{*}=\frac{\Lambda {\rho }^{\alpha }{\delta }_I^{\alpha }}{\eta ({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })}(1-\frac{1}{R_0}),}\hfill \\ {\displaystyle R^{*}=\left({\displaystyle \frac{{\gamma }_A^{\alpha }(1-{\rho }^{\alpha })\eta }{{\alpha }_R^{\alpha }{\rho }^{\alpha }\xi }+\frac{{\gamma }_H^{\alpha }{\delta }_I^{\alpha }}{{\alpha }_R^{\alpha }({\alpha }_A^{\alpha }+{\gamma }_H^{\alpha })}+\frac{{\gamma }_I^{\alpha }}{{\alpha }_R^{\alpha }}}\right)\frac{\Lambda {\rho }^{\alpha }}{\eta }(1-\frac{1}{R_0}).}\hfill \end{array}$$

The above equations show that $E^{*}$ is the endemic point of (10) if and only if $R_0>1$. $\square$

4. Results and discussion

In this section, some numerical simulations are provided to better understanding the dynamical behaviors of the fractional order COVID-19 model (3) and to investigate the impact of quarantine on this pandemic. For this goal, the Adams-Bashforth-Moulton predictor-corrector method [40], [41] will be employed to solve this nonlinear system of fractional order. To perform these simulations we need some initial values for the variables and the parameters of the model (3). For this work, we use the estimated data of confirmed coronavirus disease cases that occurred in Wuhan City and Hubei Province of China [31], [32]. The parameter estimations are observed in Table 1 . Also, we suppose the following initial conditions:

$$\begin{array}{ccc}& & S\left(0\right)=11081000,I\left(0\right)=27.679,A\left(0\right)=53.839,\hfill \\ & & S_q\left(0\right)=739,E_q\left(0\right)=1.1642,H\left(0\right)=1,R\left(0\right)=2.\hfill \end{array}$$

Table 1.

Parameters values for the model (3).

$\Lambda$	6931614.27	[32]
$\beta$	$2.1011\times {10}^{-8}$	[31]
$c$	14.781	[31]
$\theta$	0.5944	[32]
q	$1.8887\times {10}^{-7}$	[31]
${\delta }_I$	0.13266	[31]
${\delta }_q$	0.1259	[31]
${\gamma }_I$	0.33029	[31]
${\gamma }_A$	0.13978	[31]
${\gamma }_H$	0.11624	[31]
${\alpha }_A$	$1.7826\times {10}^{-5}$	[31]
$\mu$	$\frac{1}{69.5}$	[32]
$\rho$	0.86834	[31]
$\lambda$	$\frac{1}{14}$	[31]
${\alpha }_E$	$\frac{1}{68.5}$	Estimated
${\alpha }_R$	0.0144	Estimated
${\alpha }_I$	0.00723	Estimated

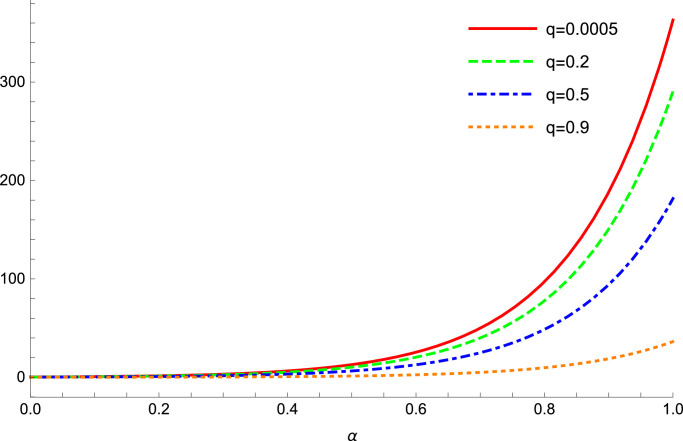
The basic reproduction number plays a crucial role in controlling COVID-19 prevalence. Thus, at first, we investigate the obtained values for this parameter. Fig. 1 shows the variations of $R_0$ with respect to the order $\alpha ,$ for numerous values of the quarantine rate $q$. It can be observed that, when we assign a small value to the quarantine rate, such as $q=0.0005,$ for $0\le \alpha \le 0.1,$ $R_0<1$ and the virus does not spread. But, when $q$ get a large value, such as $q=0.9,$ then for $0\le \alpha \le 0.45,$ the reproduction number is less than 1. So, for smaller values of $q,$ the bifurcation from a disease free equilibrium $(R_0<1)$ to a stable endemic equilibrium $(R_0>1)$ occurs for smaller values of the fractional order $\alpha$. Also, for smaller values of the quarantine rate, when $\alpha >0.5,$ it follows from this figure that the values of the reproduction number will increase severely and higher levels of prevalence can be expected. So, the graphs of Fig. 1 confirm the impact of the fractional order and the quarantine rate parameters in the fractional order model of COVID-19.

Fig. 1.

Variations of the reproduction number for several values of $0\le q\le 1$ and $0\le \alpha \le 1$.

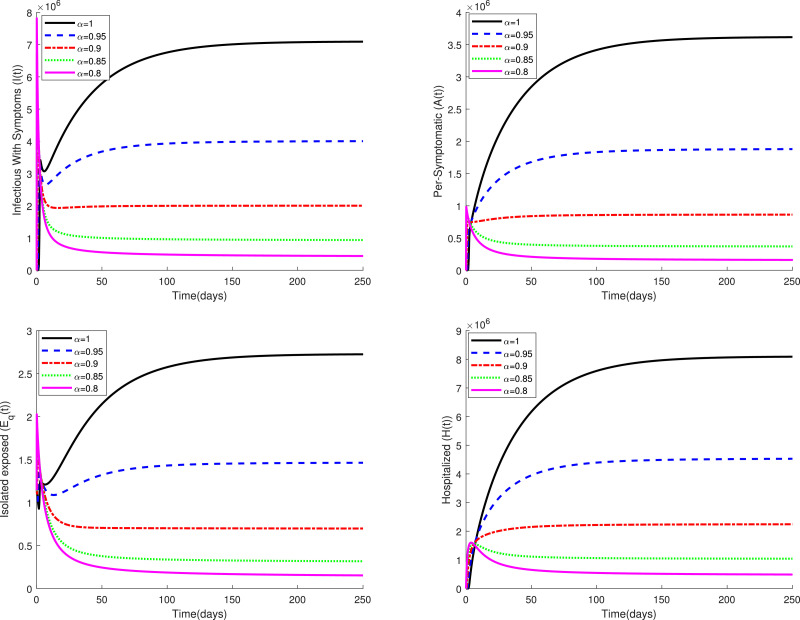
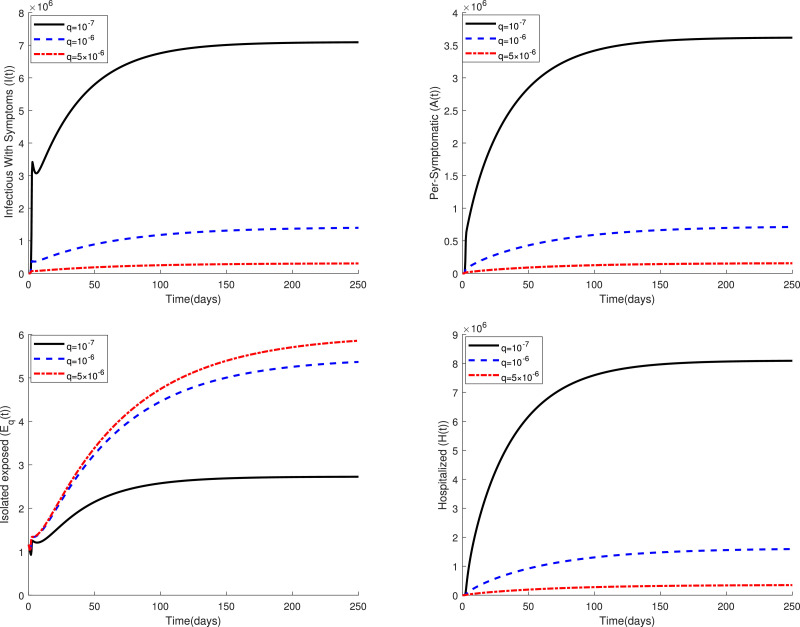
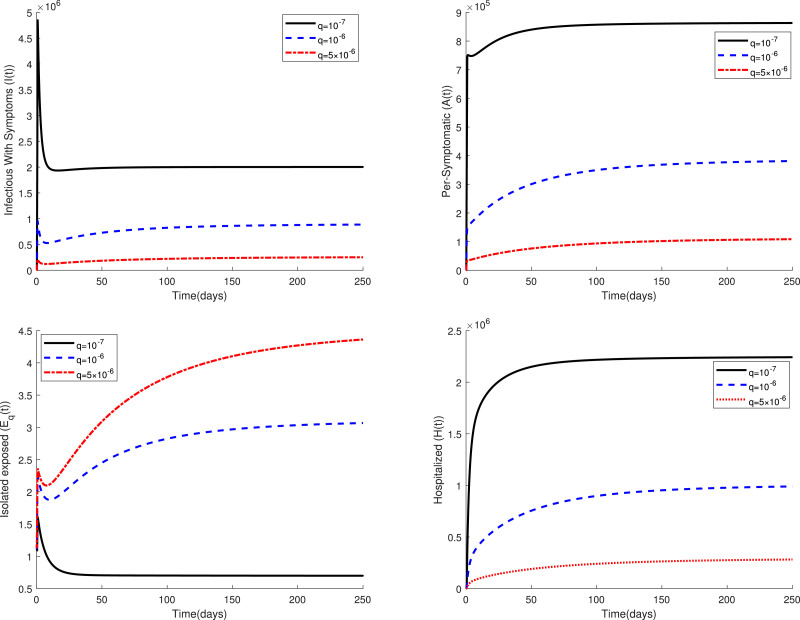
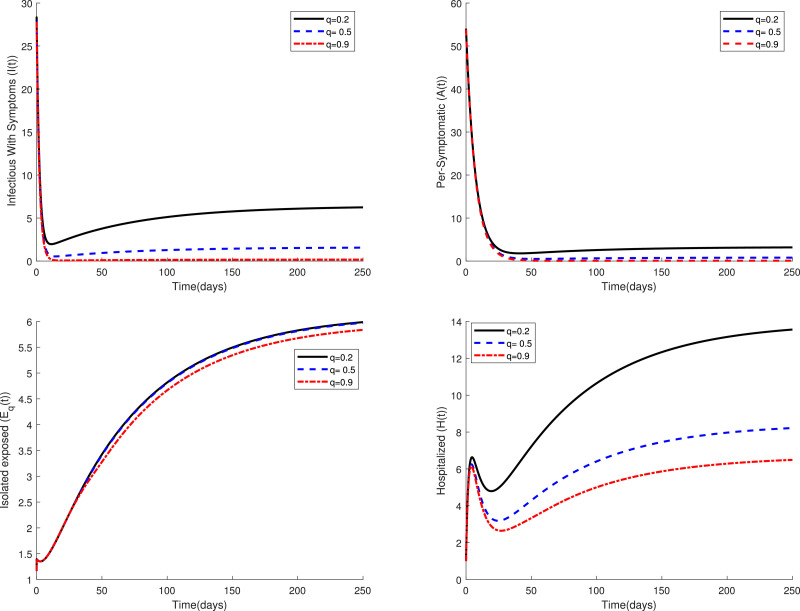
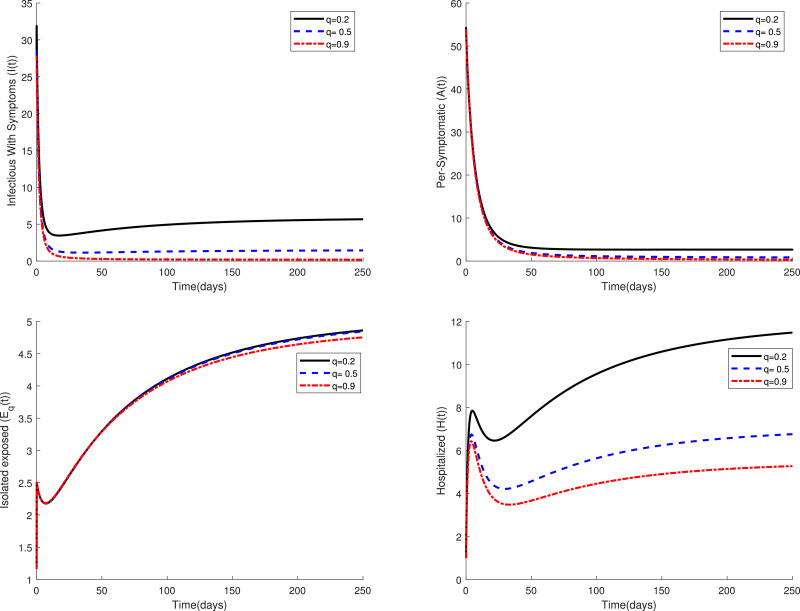
Fig. 2 displays the variations of four categories $A\left(t\right),$ $I\left(t\right),$ $E_q\left(t\right),$ and $H\left(t\right)$ of the fractional model (3) in a period of time for several values of the parameter $\alpha$ when $q={10}^{-7}$. This figure confirms that the fractional model shows a different behavior of the disease in comparison to the classical model, i.e. in the case $\alpha =1$. Figs. 3 and 4 compare the dynamics of model (3) in the classical case $\alpha =1$ and the fractional case $\alpha =0.9$ for three small values of the quarantine parameter $q$. Also, Figs. 5 and 6 present a similar comparison for larger values of $q$. The obtained results in these figures indicate that the variations in the parameter $q$ have a significant effect on the spread of the disease in the community. Also, these comparative studies highlight the role of fractional order in the mathematical modeling of COVID-19. Using fractional order models figure out new patterns for this pandemic that unseen in the integer order model.

Fig. 2.

Dynamics of system (3) for several values of $\alpha$ when $q={10}^{-7}$.

Fig. 3.

Dynamics of system (3) for several values of $q$ when $\alpha =1$.

Fig. 4.

Dynamics of system (3) for several values of $q$ when $\alpha =0.9$.

Fig. 5.

Dynamics of system (3) for $q=0.2,0.5,0.9$ when $\alpha =1$.

Fig. 6.

Dynamics of system (3) for $q=0.2,0.5,0.9$ when $\alpha =0.9$.

5. Conclusions

In the present article, a model for coronavirus disease was proposed to show the effect of quarantine on the spread of the virus. Existence of a positive solution for this model was proved and the stability of the proposed model was studied. Afterwards, to investigate the impact of quarantine, a sub-model was obtained without considering this factor. It was shown that for the reproduction numbers larger than one an endemic equilibrium point exists for this sub-model. The graph of the reproduction number versus the fractional derivative order was plotted for different values of quarantine rate. It was concluded that for smaller values of quarantine rate, the reproduction number has very significant growth. Also, we can observe that the basic reproduction number tends to the values less than 1 when the fractional order decreases. So, for smaller values of $\alpha ,$ we get a bifurcation from a pandemic state to a disease-free state. Also, the figures related to variations of the main categories of the introduced model versus time was displayed according to different values of the quarantine rate. From the performed studies it can be seen that quarantine as one of the ways to prevent COVID-19, has a great impact on its control. For future research works, it may be possible to investigate the impact of other safety strategies such as social distancing and using mask on the control of COVID-19 pandemic. Also, according to the randomness of connections between individuals, considering stochastic models for this disease could be the subject of some future researches.

CRediT authorship contribution statement

A. Babaei: Conceptualization, Methodology, Software, Writing - review & editing. M. Ahmadi: Data curation, Writing - original draft. H. Jafari: Visualization, Investigation, Writing - review & editing, Supervision. A. Liya: Writing - original draft, Software, Validation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.