Abstract
Distinct scientific theories can make similar predictions. To adjudicate between theories, we must design experiments for which the theories make distinct predictions. Here we consider the problem of comparing deep neural networks as models of human visual recognition. To efficiently compare models’ ability to predict human responses, we synthesize controversial stimuli: images for which different models produce distinct responses. We applied this approach to two visual recognition tasks, handwritten digits (MNIST) and objects in small natural images (CIFAR-10). For each task, we synthesized controversial stimuli to maximize the disagreement among models which employed different architectures and recognition algorithms. Human subjects viewed hundreds of these stimuli, as well as natural examples, and judged the probability of presence of each digit/object category in each image. We quantified how accurately each model predicted the human judgments. The best-performing models were a generative analysis-by-synthesis model (based on variational autoencoders) for MNIST and a hybrid discriminative–generative joint energy model for CIFAR-10. These deep neural networks (DNNs), which model the distribution of images, performed better than purely discriminative DNNs, which learn only to map images to labels. None of the candidate models fully explained the human responses. Controversial stimuli generalize the concept of adversarial examples, obviating the need to assume a ground-truth model. Unlike natural images, controversial stimuli are not constrained to the stimulus distribution models are trained on, thus providing severe out-of-distribution tests that reveal the models’ inductive biases. Controversial stimuli therefore provide powerful probes of discrepancies between models and human perception.
Keywords: visual object recognition, deep neural networks, optimal experimental design, adversarial examples, generative modeling
Convolutional deep neural networks (DNNs) are currently the best image-computable models of human visual object recognition (1–3). To continue improving our computational understanding of biological object recognition, we must efficiently compare different DNN models in terms of their predictions of neuronal and behavioral responses of human and nonhuman observers. Adjudicating among models requires stimuli for which models make distinct predictions.
Here we consider the problem of adjudicating among models on the basis of their behavior: the classifications of images. Finding stimuli over which high-parametric DNN models disagree is complicated by the flexibility of these models. Given a sufficiently large sample of labeled training images, a wide variety of high-parametric DNNs can learn to predict the human-assigned labels of out-of-sample images. By definition, models with high test accuracy will mostly agree with each other on the classification of test images sampled from the same distribution the training images were sampled from.
Even when there is a considerable difference in test accuracy between two models, the more accurate model is not necessarily more human-like in the features that its decisions are based on. The more accurate model might use discriminative features not used by human observers. DNNs may learn to exploit discriminative features that are completely invisible to human observers (4, 5). For example, consider a DNN that learns to exploit camera-related artifacts to distinguish between pets and wild animals. Pets are likely to have been photographed by their owners with cellphone cameras and wild animals by photographers with professional cameras. A DNN that picked up on camera-related features might be similar to humans in its classification behavior on the training distribution (i.e., highly accurate), despite being dissimilar in its mechanism. Another model that does not exploit such features might have lower accuracy, despite being more similar to humans in its mechanism. To reveal the distinct mechanisms, we need to move beyond the training distribution.
There is mounting evidence that even DNN models that exhibit highly human-like responses when tested on in-distribution stimuli often show dramatic deviations from human responses when tested on out-of-distribution (OOD) stimuli (6).
Prominent examples include images from a different domain [e.g., training a DNN on natural images and testing on silhouettes (7, 8)], as well as images degraded by noise or distortions (9–11), filtered (4), retextured (12), or adversarially perturbed to bias a DNN’s classifications (13). Assessing a model’s ability to predict human responses to OOD stimuli provides a severe test of the model’s inductive bias, i.e., the explicit or implicit assumptions that allow it to generalize from training stimuli to novel stimuli. To correctly predict human responses to novel stimuli, a model has to have an inductive bias similar to that employed by humans. Universal function approximation by itself is insufficient. Previous studies have formally compared the responses of models and humans to distorted (9, 10) and adversarially perturbed images (14, 15), demonstrating the power of testing for OOD generalization. However, such stimuli are not guaranteed to expose differences between different models, because they are not designed to probe the portion of stimulus space where the decisions of different models disagree.
Controversial Stimuli.
Here we suggest testing and comparing DNN models of vision on controversial stimuli. A controversial stimulus is a sensory input (here, an image) that elicits clearly distinct responses among two or more models. Collecting human responses to stimuli that are controversial between two models gives us great power to adjudicate between the models. The human responses are guaranteed to provide evidence against at least one of the models, since they cannot agree with both models.
Once we define a controversiality score, we can search for such stimuli in large corpora or, more flexibly, synthesize them by optimization (Fig. 1). Stimulus synthesis need not be limited to any particular stimulus prior. If the candidate models differ mostly in how they classify in-distribution examples, an appropriate synthesis procedure, guided by the models’ responses, will push the resulting controversial stimuli toward the training distribution. However, if out-of-distribution stimuli evoke considerably different responses among the candidate models, then stimulus synthesis can find them.
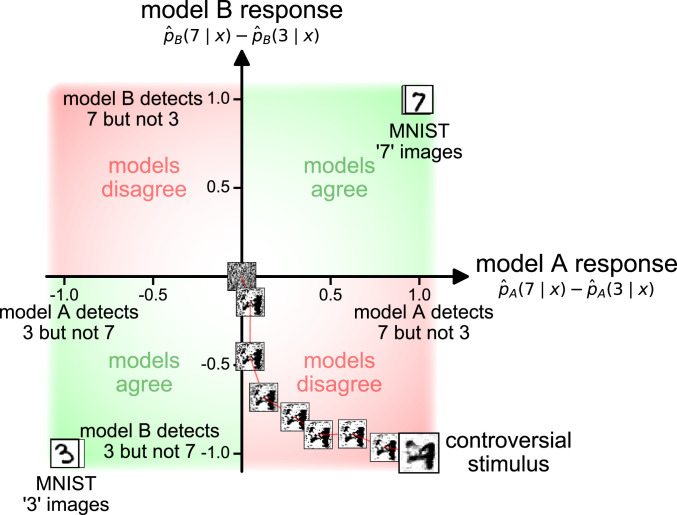
Fig. 1.
Synthesizing a single controversial stimulus. Starting from an initial noise image, one can gradually optimize an image so two (or more) object recognition models disagree on its classification. Here, the resulting controversial stimulus (Bottom Right) is classified as a 7 by model A and as a 3 by model B. Testing such controversial stimuli on human observers allows us to determine which of the models has decision boundaries that are more consistent with the human decision boundaries. Often, “natural” examples (here 50 randomly selected test MNIST examples) cause no or minimal controversy among models and therefore lack the power to support efficient comparison of models with respect to human perception. Model A here is the Capsule Network reconstruction readout, and model B is small . The stimulus synthesis optimization path (373 steps long) was sampled at nine roughly equidistant points.
Controversial Stimuli vs. Adversarial Examples.
Controversial stimuli generalize the notion of adversarial examples. An adversarial example is a stimulus controversial between a model and an oracle that defines the true label. A stimulus that is controversial between two models must be an adversarial example for at least one of them: Since the models disagree, at least one of them must be incorrect (no matter how we choose to define correctness). However, an adversarial example for one of two models may not be controversial between them: Both models may be similarly fooled (13, 16, 17). Controversial stimuli provide an attractive alternative to adversarial examples for probing models because they obviate the need for ground-truth labels during stimulus optimization. When adversarially perturbing an image, it is usually assumed that the perturbation will not also affect the true label (in most cases, the class perceived by humans). This assumption necessarily holds only if the perturbation is too small to matter (e.g., as in ref. 13). When the bound on the perturbation is large or absent, human observers and the targeted model might actually agree on the content of the image (14), making the image a valid example of another class. Such an image does not constitute a successful adversarial attack. The validity and power of a controversial stimulus, by contrast, are guaranteed given that the stimulus succeeds in making two models disagree.
Previous Work.
Our approach is conceptually related to maximum differentiation (MAD) competition (18). MAD competition perturbs a source image in four directions: increasing the response of one model while keeping the response of the other fixed, decreasing the response of one model while keeping the response of the other fixed, and the converse pair. In contrast, a single controversial stimulus manipulates two (or more) models in opposite directions. Yet crudely speaking, our approach can be viewed as a generalization of MAD competition from univariate response measures (e.g., perceived image quality) to multivariate response measures (e.g., detected object categories) and from local perturbation of natural images to unconstrained search in image space.
Results
We demonstrate the approach of controversial stimuli on two relatively simple visual recognition tasks: the classification of hand-written digits [the MNIST dataset (19)] and the classification of 10 basic-level categories in small natural images [the CIFAR-10 dataset (20)]. From an engineering perspective, both tasks are essentially solved, with multiple, qualitatively different machine-learning models attaining near-perfect performance. However, this near-perfect performance on in-distribution examples does not entail that any of the existing models solve MNIST or CIFAR-10 the way humans do.
Synthesizing Controversial Stimuli.
Consider a set of candidate models. We want to define a controversiality score for an image . This score should be high if the models strongly disagree on the contents of this image.
Ideally, we would take an optimal experimental-design approach (21, 22) and estimate, for a given image, how much seeing the response would reduce our uncertainty about which model generated the data (assuming that one of the models underlies the observed human responses). An image would be preferred according to the expected reduction of the entropy of our posterior belief. However, this statistically ideal approach is difficult to implement in the context of high-level vision and complex DNN models without relying on strong assumptions.
Here we use a simple heuristic approach. We consider one pair of models ( and ) at a time. For a given pair of classes, and (e.g., the digits 3 and 7, in the case of MNIST), an image is assigned with a high controversiality score if it is recognized by model as class and by model as class . The following function achieves this:
| [1] |
where is the estimated conditional probability that image contains an object of class according to model , and is the minimum function. However, this function assumes that a model cannot simultaneously assign high probabilities to both class and class in the same image. This assumption is true for models with softmax readout. To make the controversiality score compatible also with less restricted (e.g., multilabel sigmoid) readout, we used the following function instead:
| [2] |
If the models agree over the classification of image , then and will be either both high or both low, so either or will be a small number, pushing the minimum down.
As in activation–maximization (23), we can use gradient ascent to generate images. Here we maximize Eq. 2 by following its gradient with respect to the image (estimated numerically for experiment 1 and symbolically for experiment 2). To increase the efficiency of the optimization and to avoid precision-related issues, the optimization was done on Eq. 4 (Materials and Methods), a numerically favorable variant of Eq. 2. We initialized images with uniform white noise and iteratively ascended their controversiality gradient until convergence. A sufficiently controversial resulting image (e.g., ) is not guaranteed. A controversial stimulus cannot be found, for example, if both models associate exactly the same regions of image space with the two classes. However, if a controversial image is found, it is guaranteed to provide a test stimulus for which at least one of the models will make an incorrect prediction.
Experiment 1: Adjudicating among MNIST Models
Candidate MNIST Models.
We assembled a set of nine candidate models, all trained on MNIST (SI Appendix, Table S1 and section A). The nine models fall into five families: 1) discriminative feedforward models, an adaptation of the VGG architecture (24) to MNIST, trained on either the standard MNIST dataset (“small VGG”; SI Appendix, section A.1) or on a version extended by nondigit images (“small ”; SI Appendix, Fig. S1); 2) discriminative recurrent models, the Capsule Network (25) (“CapsuleNet”) and the Deep Predictive Coding Network (26) (“Wen-PCN-E4”); 3) adversarially trained discriminative models, DNNs trained on MNIST with either (“Madry ”) or (“Madry ”) norm-bounded perturbations (27); 4) a reconstruction-based readout of the Capsule Network (28) (“CapsuleNet Recon”); and 5) class-conditional generative models, models classifying according to a likelihood estimate for each class, obtained from either a class-specific, pixel-space Gaussian kernel density estimator (“Gaussian KDE”) or a class-specific variational autoencoder (VAE), the “Analysis by Synthesis” model (29) (“Schott ABS”).
Many DNN models operate under the assumption that each test image is paired with exactly one correct class (here, an MNIST digit). In contrast, human observers may detect more than one class in an image or, alternatively, detect none. To capture this, the outputs of all of the models were evaluated using multilabel readout, implemented with a sigmoid unit for each class, instead of the usual softmax readout. This setup handles the detection of each class as a binary classification problem (30).
Another limitation of many DNN models is that they are typically too confident about their classifications (31). To address this issue, we calibrated each model by applying an affine transformation to the preactivations of the sigmoid units (the logits) (31). The slope and intercept parameters of this transformation were shared across classes and were fitted to minimize the predictive cross-entropy on MNIST test images. For pretrained models, this calibration (as well as the usage of sigmoids instead of the softmax readout) affects only the models’ certainty and not their classification accuracy (i.e., it does not change the most probable class of each image).
Synthetic Controversial Stimuli Reveal Deviations between MNIST Models and Human Perception.
For each pair of models, we formed 90 controversial stimuli, targeting all possible pairs of classes. In experiment 1, the classes are the 10 digits. Fig. 2 shows the results of this procedure for a particular digit pair across all model pairs. Fig. 3 shows the results across all digit pairs for four model pairs.
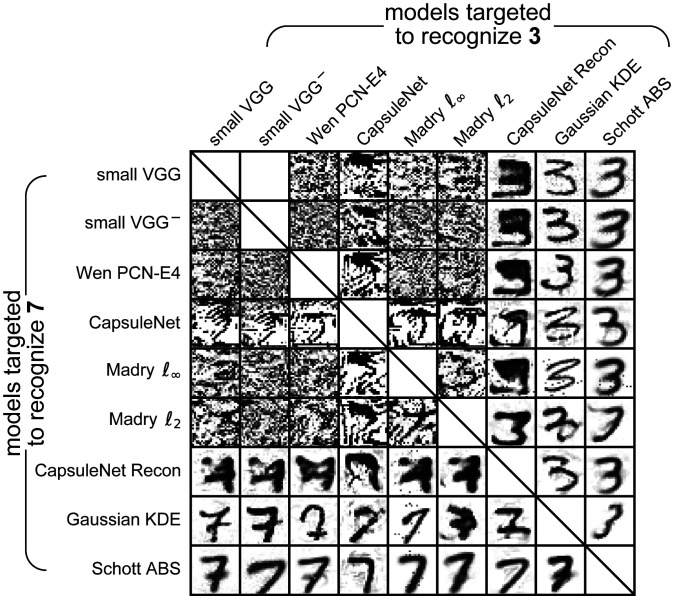
Fig. 2.
Synthetic controversial stimuli for one digit pair and all pairs of MNIST models (experiment 1). All these images result from optimizing images to be recognized as containing a 7 (but not a 3) by one model and as containing a 3 (but not a 7) by the other model. Each image was synthesized to target one particular model pair. For example, the bottom-left image (seen as a 7 by us) was optimized so that a 7 will be detected with high certainty by the generative ABS model and the discriminative small VGG model will detect a 3. All images here achieved a controversiality score (Eq. 2) greater than 0.75.
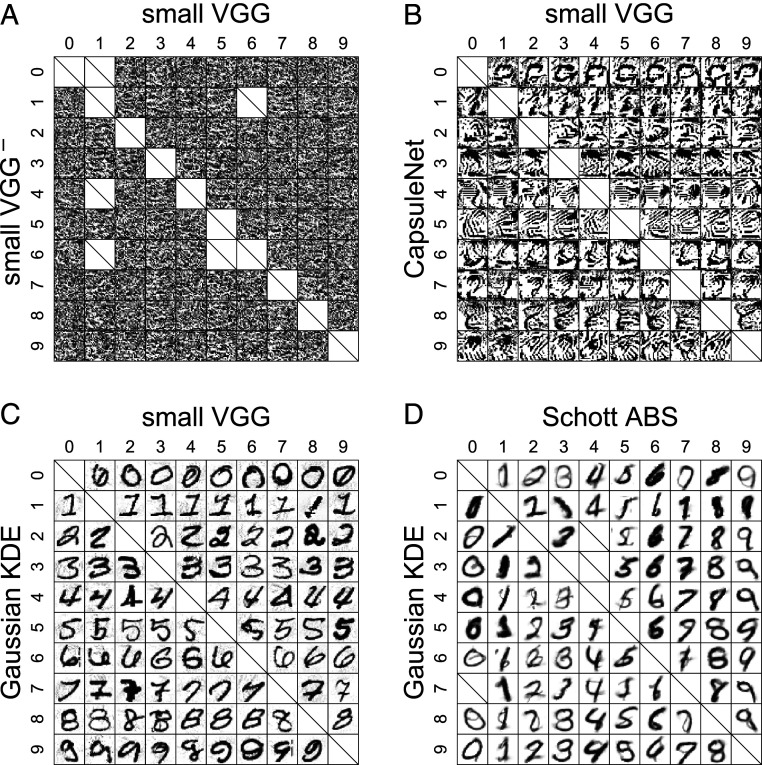
Fig. 3.
(A–D) Synthetic controversial stimuli for all digit pairs and four different MNIST model pairs (experiment 1). The rows and columns within each panel indicate the targeted digits. For example, the top-right image in D was optimized so that a 9 (but not a 0) will be detected with high certainty by the Schott ABS model and a 0 (but not a 9) will be detected with high certainty by the Gaussian KDE model. Since this image looks like a 9 to us, it provides evidence in favor of Schott ABS over Gaussian KDE as a model of human digit recognition. Missing (crossed) cells are either along the diagonal (where the two models would agree) or where our optimization procedure did not converge to a sufficiently controversial image (a controversiality score of at least 0.75). See SI Appendix, Fig. S2 for all 36 model pairs.
Viewing the resulting controversial stimuli, it is immediately apparent that pairs of discriminative MNIST models can detect incompatible digits in images that are meaningless to us, the human observers. Images that are confidently classified by DNNs, but unrecognizable to humans are a special type of an adversarial example [described by various terms including “fooling images” (32), “rubbish class examples” (16), and “distal adversarial examples” (29)]. However, instead of misleading one model (compared to some standard of ground truth), our controversial stimuli elicit disagreement between two models. For pairs of discriminatively trained models (Fig. 3 A and B), human classifications are not consistent with either model, providing evidence against both.
One may hypothesize that the poor behavior of discriminative models when presented with images falling into none of the classes results from the lack of training on such examples. However, the small model, trained with diverse nondigit examples, still detected digits in controversial images that are unrecognizable to us (Fig. 3A).
There were some qualitative differences among the stimuli resulting from targeting pairs of discriminative models. Images targeting one of the two discriminative recurrent DNN models, the Capsule Network (25) and the Predictive Coding Network (26), showed increased (yet largely humanly unrecognizable) structure (e.g., Fig. 3B). When the discriminative models pitted against each other included a DNN that had undergone -bounded adversarial training (27), the resulting controversial stimuli showed traces of human-recognizable digits (Fig. 2; Madry ). These digits’ human classifications tended to be consistent with the classifications of the adversarially trained discriminative model (see ref. 33, for a discussion of adversarial training and perception).
And yet, when any of the discriminative models was pitted against either the reconstruction-based readout of the Capsule Network or either of the generative models (Gaussian KDE or ABS), the controversial image was almost always a human-recognizable digit consistent with the target of the reconstruction-based or generative model (e.g., Fig. 3C). Finally, synthesizing controversial stimuli to adjudicate between the three reconstruction-based/generative models produced images whose human classifications are most similar to the targets of the ABS model (e.g., Fig. 3D).
The ABS model is unique in having one DNN per class, raising the question of whether this, rather than its generative nature, explains its performance. However, imitating this structure by training 10 small VGG models as 10 binary classifiers did not increase the human consistency of the small VGG model (SI Appendix, Fig. S3). Another possibility is that a higher-capacity discriminative model with more human-like visual training on natural images might perform better. However, MNIST classification using visual features extracted from the hidden layers of an Imagenet-trained VGG-16 did not outperform the ABS model (SI Appendix, Fig. S4). Finally, the advantage of the ABS model persisted also when the optimization was initialized from MNIST test examples instead of random noise images (SI Appendix, Fig. S5).
Human Psychophysics Can Formally Adjudicate among Models and Reveal Their Limitations.
Inspecting a matrix of controversial stimuli synthesized to cause disagreement among two models can provide a sense of which model is more similar to us in its decision boundaries. However, it does not tell us how a third, untargeted model responds to these images. Moreover, some of the resulting controversial stimuli are ambiguous to human observers. We therefore need careful human behavioral experiments to adjudicate among models.
We evaluated each model by comparing its judgments to those of human subjects and compared the models in terms of how well they could predict the human judgments. For experiment 1, we selected 720 controversial stimuli (20 per model-pair comparison; SI Appendix, section D) as well as 100 randomly selected MNIST test images. We presented these 820 stimuli to 30 human observers, in a different random order for each observer. For each image, observers rated each digit’s probability of presence from 0 to 100% on a five-point scale (SI Appendix, Fig. S6A). The probabilities were not constrained to sum to 1, so subjects could assign high probability to multiple digits or zero probability to all of them for a given image. There was no objective reference for correctness of the judgments, and no feedback was provided.
For each human subject and model , we estimated the Pearson linear correlation coefficient between the human and model responses across stimuli and classes,
| [3] |
where is the human-judged probability that image contains class , is the model’s corresponding judgment, is the mean probability judgement of subject , and is the mean probability judgment of the model. The overall score of each model was set to its mean correlation coefficient, averaged across all subjects: , where is the number of subjects.
Given the intersubject variability and decision noise, the true model (if it were included in our set) cannot perfectly predict the human judgments. We estimated a lower bound and an upper bound on the maximal attainable performance (the noise ceiling; SI Appendix, section F). The lower bound of the noise ceiling (“leave one subject out”; black bars in Fig. 4 A and B) was estimated as the mean across subjects of the correlation between each subject’s response pattern and the mean response pattern of the other subjects (34). The upper bound of the noise ceiling (“best possible model”; dashed lines in Fig. 4 A and B) is the highest across-subject-mean correlation achievable by any possible set of predictions.
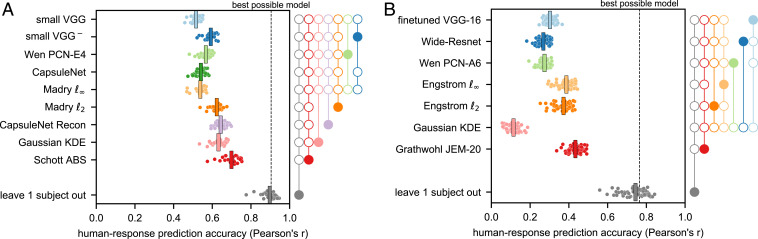
Fig. 4.
The performance of the candidate MNIST (A) and CIFAR-10 (B) models in predicting the human responses to the entire stimulus set. Each dot marks the correlation coefficient between the responses of one individual human participant and one model (Eq. 3). The vertical bars mark across-subject means (). The gray dots mark the correlation between each participant’s responses and the mean response pattern of the other participants. The mean of the gray dots (a black bar) is the lower bound of the noise ceiling. The dashed line (“best possible model”) marks the highest across-subject mean correlation achievable by any single model (upper bound of the noise ceiling). Significance indicators (A and B, Right): A solid dot connected to a set of open dots indicates that the model aligned with the solid dot has significantly higher correlation than any of the models aligned with the open dots (P 0.05, subject-stimulus bootstrap). Testing controlled the familywise error rate at 0.05, accounting for the total number of model-pair comparisons (45 for experiment 1, 28 for experiment 2). For equivalent analyses with alternative measures of human-response prediction accuracy, see SI Appendix, Fig. S7. See SI Appendix, Fig. S8 for the models’ prediction accuracy evaluated separately on controversial and natural stimuli and SI Appendix, Fig. S9 for an evaluation on different ratios of controversial to natural stimuli. The deep generative model (ABS, experiment 1) and the deep hybrid model (JEM-20, experiment 2) (both in red) explain human responses to the combined set of controversial and natural stimuli better than all of the other candidate models. And yet, none of the models account for all explainable variance: Predicting each subject from the subject’s peers’ mean response pattern achieves significantly higher accuracy.
The results of experiment 1 (Fig. 4A) largely corroborate the qualitative impressions of the controversial stimuli, indicating that the deep generative ABS model (29) is superior to the other models in predicting the human responses to the stimulus set. Its performance is followed by that of the Gaussian KDE, the reconstruction-based readout of the Capsule Network, and the adversarially trained model. The other models (all discriminative) performed significantly worse. All models were significantly below the lower bound of the noise ceiling (the black bar in Fig. 4A), indicating that none of the models fully explained the explainable variability in the data.
We also evaluated the models separately for controversial stimuli and natural stimuli (i.e., MNIST test images; SI Appendix, Fig. S8C). The ABS and Gaussian KDE models were not as good as the discriminative models in predicting the human responses to the natural MNIST test images, indicating that the discriminative models are better at achieving human-like responses within the MNIST training distribution.
Experiment 2: Adjudicating among CIFAR-10 Models
The MNIST task has two obvious disadvantages as a test case: 1) its simplicity compared to visual object recognition in natural images and 2) the special status of handwritten characters, which are generated through human movement. In experiment 2, we applied the method of controversial stimuli to a set of models designed to classify small natural images from the CIFAR-10 image set. The purely generative ABS model is reported to fail to scale up to CIFAR-10 (29). We therefore included the Joint Energy Model (JEM) (35), which implements a hybrid discriminative–generative approach to CIFAR-10 classification.
Candidate CIFAR-10 Models.
We assembled a set of seven CIFAR-10 candidate models (SI Appendix, Table S2 and section B). The seven models fall into five model families largely overlapping with the model families tested in experiment 1: 1) discriminative feedforward models, a VGG-16 (24) first trained on ImageNet and then retrained on upscaled CIFAR-10 (“finetuned VGG-16”) and a Wide-Resnet trained exclusively on CIFAR-10 (36) (“Wide-Resnet”); 2) a discriminative recurrent model, a CIFAR-10 variant of the Deep Predictive Coding Network (26) (“Wen-PCN-A6”); 3) adversarially trained discriminative models, Resnet-50 DNNs trained on CIFAR-10 with either (“Engstrom ”) or (“Engstrom ”) norm-bounded perturbations (37); 4) a class-conditional generative model, the pixel-space Gaussian kernel density estimator (“Gaussian KDE”); and 5) a hybrid discriminative–generative model, the Joint Energy Model (35) (“Grathwol JEM-20”).
The hybrid JEM has the same WRN-28-10 architecture (36) as the discriminative Wide-Resnet model mentioned above, but its training combines a discriminative training objective (minimizing the classification error) with a generative training objective. The generative objective treats the LogSumExp of the DNN’s logits as an unnormalized image likelihood estimate and encourages high-likelihood assignments to in-distribution images. Including the generative objective in the training improves the model’s robustness to adversarial attacks (35). The model’s robustness can be further improved by refining the input-layer representation during inference, nudging it to have higher likelihood. We have tested the JEM model with 20 refinement steps (hence we refer to it here as “JEM-20”).
As in experiment 1, we used sigmoid readout to allow for more flexible responses, such as detecting multiple or none of the categories. Since the candidate models had a wide range of test accuracies (SI Appendix, Table S2), the sigmoid readout was calibrated for each model such that negative examples would be assigned a median probability of 0.1 and positive examples a median probability of 0.9.
Synthetic Controversial Stimuli Reveal Deviations between CIFAR-10 Models and Human Perception.
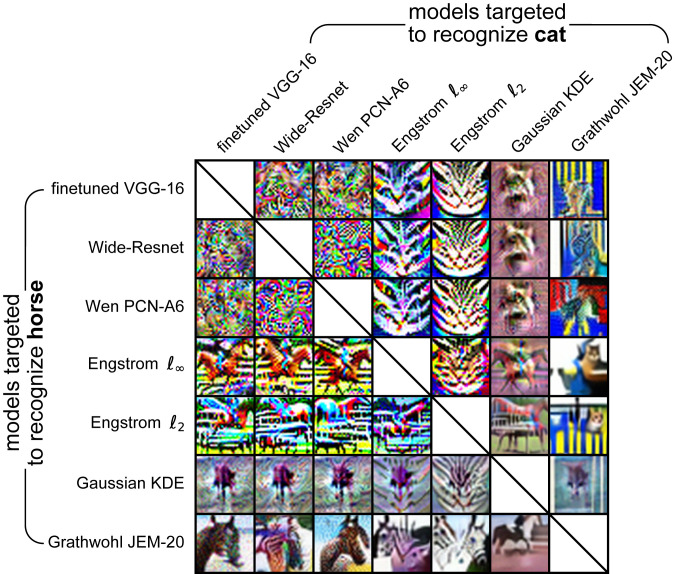
Examples of the resulting controversial stimuli appear in Fig. 5 and SI Appendix, Fig. S10. When DNNs trained with a nonadversarial discriminative objective (i.e., the finetuned VGG-16, the discriminatively trained Wide-Resnet, and the Predictive Coding Network) are paired with each other, the resulting controversial stimuli do not appear to humans to contain objects of any of the categories. These results bear strong resemblance to those in experiment 1. In contrast to experiment 1, however, the target categories for the Gaussian KDE were, by and large, not discernible to humans, indicating that this shallow-generative model, which worked surprisingly well on MNIST, does not scale up to CIFAR-10. Pitting the Gaussian KDE against the JEM-20 model (SI Appendix, Fig. S10C) produced almost naturally looking images, in which the target categories of JEM-20 are discernible. In some of these images, low-level features suggestive of the target category of the Gaussian KDE can also be recognized. Also, the target categories of the adversarially trained models were more discernible than in experiment 1 (SI Appendix, Fig. S10 A and B). Finally, pitting the JEM-20 model against one of the adversarially trained models (SI Appendix, Fig. S10D) often produced images in which the target category for JEM-20 was discernible. In some images, however, the human-perceptible category was the target of the adversarially trained DNN or both or neither of the categories were perceptible. These ambiguities suggest deviations of both JEM-20 and the adversarially trained DNNs from human perception and emphasize the importance of quantitative behavioral experiments.
Fig. 5.
Synthetic controversial stimuli contrasting the seven different CIFAR-10-classifying models. Each stimulus results from optimizing an image to be detected as a cat (but not as a horse) by one model and as a horse (but not as a cat) by another model. For example, the image at Bottom Left (seen as a horse by us) was optimized so that the hybrid discriminative–generative JEM-20 model will detect a horse and the discriminative, finetuned VGG-16 model will detect a cat. All images here achieved a controversiality score (Eq. 2) greater than 0.75. The images are shown in upsampled format as presented to the human subjects. See SI Appendix, Fig. S11 for all class combinations.
We ran a behavioral experiment similar to experiment 1, presenting 420 controversial stimuli (20 per model-pair comparison) as well as 60 randomly selected CIFAR-10 test images. We ran two replications of the experiment on 30 subjects each, using a new, independent batch of controversial stimuli for each replication. The results pooled over both replications (60 subjects) are presented in Fig. 4B, whereas the (virtually identical) results of each individual replication are presented in SI Appendix, Fig. S12.
On average across the stimulus set, JEM-20 was significantly more accurate at predicting the human perceptual judgments than all other models. Similarly to experiment 1, none of the models reached the lower bound of the noise ceiling (the leave-one-subject-out estimate). The two adversarially trained models (trained on and bounded perturbations) were second to the JEM-20 model in their human-response prediction accuracy. Next was the finetuned VGG-16 model and then the discriminatively trained Wide-Resnet and the Predictive Coding Network. The Gaussian KDE had the lowest human-response prediction accuracy.
Measuring the human response-prediction accuracy separately for controversial stimuli (SI Appendix, Fig. S8B) showed no significant difference between the JEM-20 model and the adversarially trained DNNs. For the natural images, however, the JEM-20 model significantly outperformed the adversarially trained DNNs (SI Appendix, Fig. S8D). The model that best predicted the human responses to the natural images was the finetuned ImageNet-trained VGG-16, indicating that no single model in our candidate set was uniformly dominant, as would be expected of the true model.
Discussion
In this paper, we introduce the method of synthetic controversial stimuli, and we demonstrate its utility for adjudicating among DNNs as models of human recognition in the context of two simple visual recognition tasks, MNIST and CIFAR-10. Controversial stimuli reveal model differences and empower us to find failure modes, capitalizing on the fact that if two models disagree, at least one of them must be wrong.
The method of controversial stimuli can be useful to two groups of scientists. The first group is cognitive computational neuroscientists interested in better understanding perceptual processes, such as object recognition, by modeling them as artificial neural networks. The second group is computer scientists interested in comparing the robustness of different DNN models to adversarial attacks.
Controversial Stimuli Offer a Severe Test for DNNs as Brain-Computational Models.
Natural stimuli will always remain a necessary benchmark for models of perception. Moreover, at the moment it is still feasible to compare and reject DNNs as models of human vision on the basis of their classifications of natural, nonmodel-driven stimuli (e.g., refs. 38–42). As DNN models become better at fitting the training distribution, such informative errors on natural examples are expected to diminish. Scientists designing experiments comparing the human consistency of models can search for natural controversial stimuli to increase the power of model comparison. However, even for the models we have today, natural stimuli (including controversial ones) do not provide a severe test. In particular, a mechanistically incorrect model with many parameters that has been trained on natural images can achieve high performance at predicting human-assigned labels of images sampled from the same distribution. Synthetic controversial stimuli that are not limited to the training distribution provide a severe test of a model’s inductive bias because they require the model to generalize far beyond the training distribution. Synthetic controversial stimuli ensure that we do not favor models that are higher-capacity function approximators regardless of their functional consistency with human perception. Here, the considerably different model rank orders observed when considering synthetic controversial stimuli and when considering natural stimuli (SI Appendix, Figs. S8 and S9) indicate that these two benchmarks shed light on complementary facets of model–human consistency.
Controversial Stimuli Generalize Adversarial Attacks.
Engineers use adversarial examples to test the robustness of models. Adversarial examples can be viewed as a special case of controversial stimuli. An ideal adversarial example is controversial between the targeted model and ground truth. In principle, therefore, adversarial examples require the evaluation of ground truth in the optimization loop. However, the evaluation of ground truth is often difficult, because it may be costly to compute or may require human judgment. In practice, adversarial attacks usually use a stand-in for ground truth, such as the assumption that the true label of an image does not change within a pixel-space ball of radius .
Controversial stimulus synthesis enables us to compare two models in terms of their robustness without needing to evaluate or approximate the ground truth within the optimization loop. We require only a single ground-truth evaluation once the optimization is completed to determine which of the models responded incorrectly. Hence, controversial stimuli enable us to use more costly and compelling evaluations of ground truth (e.g., human judgments or a computationally complex evaluation function), instead of relying on a surrogate measure.
The most common surrogate measure for ground truth is robustness. A model is said to be robust if perturbations of the image confined to some distance in image space (defined by an norm) do not change the model’s classification. The notion of robustness has led to analytical advances and enables adversarial training (5, 27). However, since robustness is a simple surrogate for a more complicated ground truth, it does not preclude the existence of adversarial examples and so does not guarantee robustness in a more general sense. This is particularly evident in the case of object recognition in images, where the ground truth is usually human categorization: A model can be robust for a large and yet show markedly human-inconsistent classifications, as demonstrated by controversial stimuli (here), distal adversaries (29), and “invariance attacks” (43), in which a human subject manually changes the true class of an image by making modifications confined to an ball in image space. The motivating assumption of robustness is that the decision regions are compact and their boundaries are far from the training examples. This does not hold in general. Controversial stimuli allow us to find failure modes in two or more models by studying differences in their decision boundaries instead of relying on assumptions about the decision boundaries.
Controversial Stimuli: Current Limitations and Future Directions.
Like most works using pretrained models (1, 2), this study operationalized each model as a single trained DNN instance. In this setting, a model predicts a single response pattern, which should be as similar as possible to the average human response. To the extent that the training of a model results in instances that make idiosyncratic predictions, the variability across instances will reduce the model’s performance at predicting the human responses. An alternative approach to evaluating models would be to use multiple instances for each model (44), considering each DNN instance as an equivalent of an individual human brain. In this setting, each model predicts a distribution of input–output mappings, which should be compared to the distribution of stimulus–response mappings across the human population. Instance-specific idiosyncrasies may then be found to be consistent (or not) with human idiosyncratic responses.
Another limitation of our current approach is scaling up: Synthesizing controversial stimuli for every pair of classes and every pair of models is difficult for problems with a large number of classes or models. A natural solution to this problem would be subsampling, where we do not synthesize the complete cross-product of class pairs and model pairs.
Future research should also explore whether it is possible to replace the controversiality index with an optimal experimental design approach, jointly optimizing a stimulus set to reduce the expected entropy of our posterior over the models. Finally, adaptive measurement between or within experimental sessions could further increase the experimental efficiency.
Generative Models May Better Capture Human Object Recognition.
One interpretation of the advantage of the best-performing models (the VAE-based analysis by synthesis model in experiment 1 and the Joint Energy Model in experiment 2) is that, like these two models, human object recognition includes elements of generative inference. There has recently been considerable progress with DNNs that can estimate complex image distributions (e.g., VAEs and normalizing-flow models). However, such approaches are rarely used in object recognition models, which are still almost always trained discriminatively to minimize classification error. Our direct testing of models against each other suggests that DNN classifiers that attempt to learn the distribution of images (in addition to being able to classify) provide better models of human object recognition.
However, none of the tested models approached the noise ceiling, and while the ABS and JEM models performed better than all of the other models on average, they were worse than some of the discriminative models when the natural examples were considered in isolation (SI Appendix, Fig. S8 C and D). Each of these two outcomes indicates that none of the models were functionally equivalent to the process that generated the human responses.
Generative models do not easily capture high-level, semantic properties of images (45, 46). In particular, this problem is evident in the tendency of various deep generative models to assign high likelihood to out-of-distribution images that are close to the mean low-level statistics of the in-distribution images (45). Hybrid (discriminative–generative) approaches such as the joint energy model (35) are a promising middle ground, yet the particular hybrid model we tested (JEM-20) was still far from predicting human responses accurately. An important challenge is to construct a generative or hybrid model that 1) reaches the noise ceiling in explaining human judgments, 2) scales up to real-world vision (e.g., ImageNet), and 3) is biologically plausible in both its architecture and training. The method of controversial stimuli will enable us to severely test such future models and resolve the question of whether human visual judgments indeed employ a process of generative inference, as suggested by our results here.
Materials and Methods
Further details on training/adaptation of candidate models, stimulus optimization and selection, human testing, and noise-ceiling estimation appear in SI Appendix.
Controversial Stimuli Synthesis.
Each controversial stimulus was initialized as a randomly seeded, uniform noise image (, where 0 and 1 are the image intensity limits). To efficiently optimize the controversiality score (Eq. 2), we ascended the gradient of a more numerically favorable version of this quantity:
| [4] |
where (an inverted LogSumExp, serving as a smooth minimum), is a hyperparameter that controls the LogSumExp smoothness (initially set to 1), and is the calibrated logit for class (the input to the sigmoid readout). Experiment-specific details on stimulus optimization appear in SI Appendix, sections C.1 and C.2.
Human Subjects.
Ninety participants took part in the online experiments and were recruited through prolific.co. All participants provided informed consent at the beginning of the study, and all procedures were approved by the Columbia Morningside ethics board.
Statistical Inference.
Differences between models with respect to their human response prediction accuracy were tested by bootstrapping-based hypothesis testing. For each bootstrap sample (100,000 resamples), subjects and stimuli were both randomly resampled with replacement. Stimuli resampling was stratified by stimuli conditions (one condition per model pair, plus one condition of natural examples). For each pair of models and , this bootstrapping procedure yielded an empirical sampling distribution of , the difference between the models’ prediction accuracy levels. Percentages of bootstrapped accuracy differences below (or above) zero were used as left-tail (or right-tail) P values. These P values were Holm–Šídák corrected for multiple pairwise comparisons and for two-tailed testing.
Supplementary Material
Acknowledgments
This material is based upon work supported by the National Science Foundation under Grant 1948004. T.G. acknowledges Edmond and Lily Safra Center for Brain Sciences (ELSC) Postdoctoral Fellowships for Training Abroad. NVIDIA donated a Titan Xp used in this research. We thank Máté Lengyel for a helpful discussion and Raphael Gerraty, Heiko Schütt, Ruben van Bergen, and Benjamin Peters for their comments on the manuscript.
Footnotes
The authors declare no competing interest.
This paper results from the Arthur M. Sackler Colloquium of the National Academy of Sciences, “Brain Produces Mind by Modeling,” held May 1–3, 2019, at the Arnold and Mabel Beckman Center of the National Academies of Sciences and Engineering in Irvine, CA. NAS colloquia began in 1991 and have been published in PNAS since 1995. From February 2001 through May 2019, colloquia were supported by a generous gift from The Dame Jillian and Dr. Arthur M. Sackler Foundation for the Arts, Sciences, & Humanities, in memory of Dame Sackler’s husband, Arthur M. Sackler. The complete program and video recordings of most presentations are available on the NAS website at http://www.nasonline.org/brain-produces-mind-by.
This article is a PNAS Direct Submission. J.B.T. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1912334117/-/DCSupplemental.
Data Availability.
Optimization source code, synthesized images, and anonymized, detailed behavioral testing results are available at GitHub, https://github.com/kriegeskorte-lab/PNAS_2020_Controversial_Stimuli.
References
- 1.Kriegeskorte N., Deep neural networks: A new framework for modeling biological vision and brain information processing. Annu. Rev. Vis. 1, 417–446 (2015). [DOI] [PubMed] [Google Scholar]
- 2.Yamins D. L. K., DiCarlo J. J., Using goal-driven deep learning models to understand sensory cortex. Nat. Neurosci. 19, 356–365 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Kietzmann T. C., McClure P., Kriegeskorte N., “Deep neural networks in computational neuroscience” in Oxford Research Encyclopedia of Neuroscience, (Oxford University Press, 2019). [Google Scholar]
- 4.Jo J., Bengio Y., Measuring the tendency of CNNs to learn surface statistical regularities. arXiv:1711.11561 (30 November 2017).
- 5.Ilyas A., et al. , Adversarial Examples Are Not Bugs, They Are Features in Advances in Neural Information Processing Systems 32, Wallach H., et al., Eds. (Curran Associates, Inc., 2019), pp. 125–136. [Google Scholar]
- 6.Geirhos R., et al. , Shortcut learning in deep neural networks. arXiv:2004.07780 [cs, q-bio] (20 May 2020).
- 7.Kubilius J., Bracci S., Op de Beeck H. P., Deep neural networks as a computational model for human shape sensitivity. PLoS Comput. Biol. 12, e1004896 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Baker N., Lu H., Erlikhman G., Kellman P. J., Deep convolutional networks do not classify based on global object shape. PLoS Comput. Biol. 14, e1006613 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dodge S., Karam L., “A study and comparison of human and deep learning recognition performance under visual distortions” in 2017 26th International Conference on Computer Communication and Networks (ICCCN, Vancouver, Canada, 2017), pp. 1–7.
- 10.Geirhos R., et al. , “Generalization in humans and deep neural networks” in Advances in Neural Information Processing Systems 31, Bengio S., et al., Eds. (Curran Associates, Inc., 2018), pp. 7538–7550. [Google Scholar]
- 11.Hendrycks D., Dietterich T. et al. , “Benchmarking neural network robustness to common corruptions and perturbations” in 7th International Conference on Learning Representations (ICLR, New Orleans, LA, 2019).
- 12.Geirhos R., et al. , “ImageNet-trained CNNs are biased toward texture; Increasing shape bias improves accuracy and robustness” in 7th International Conference on Learning Representations (ICLR, New Orleans, LA, 2019).
- 13.Szegedy C., et al. , Intriguing properties of neural networks. arXiv:1312.6199 [cs] (19 February 2014).
- 14.Zhou Z., Firestone C., Humans can decipher adversarial images. Nat. Commun. 10, 1334 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Elsayed G., et al. , “Adversarial examples that fool both computer vision and time-limited humans” in Advances in Neural Information Processing Systems 31, Bengio S, et al., Eds. (Curran Associates, Inc., 2018), pp. 3910–3920. [Google Scholar]
- 16.Goodfellow I. J., Shlens J., Szegedy C., “Explaining and harnessing adversarial examples” in 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA (2015).
- 17.Liu Y., Chen X., Liu C., Song D., “Delving into transferable adversarial examples and black-box Attacks” in 5th International Conference on Learning Representations, ICLR 2017, Toulon, France (2017).
- 18.Wang Z., Simoncelli E. P., Maximum differentiation (MAD) competition: A methodology for comparing computational models of perceptual quantities. J. Vis. 8, 1–13 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lecun Y., Bottou L., Bengio Y., Haffner P., Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324 (1998). [Google Scholar]
- 20.Krizhevsky A., “Learning multiple layers of features from tiny images” (Tech. Rep., University of Toronto, Toronto, ON, Canada, 2009).
- 21.Lindley D. V., On a measure of the information provided by an experiment. Ann. Math. Stat. 27, 986–1005 (1956). [Google Scholar]
- 22.Houlsby N., Huszár F., Ghahramani Z., Lengyel M., Bayesian active learning for classification and preference learning. arXiv:1112.5745 (24 December 2011).
- 23.Erhan D., Bengio Y., Courville A., Vincent P., “Visualizing higher-layer features of a deep network” (Tech. Rep. 13411, University of Montreal, Montreal, QC, Canada, 2009). [Google Scholar]
- 24.Simonyan K., Zisserman A., Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556 (10 April 2015).
- 25.Sabour S., Frosst N., Hinton G. E., “Dynamic routing between capsules” in Advances in Neural Information Processing Systems 30, Guyon I, et al., Eds. (Curran Associates, Inc., 2017), pp. 3856–3866. [Google Scholar]
- 26.Wen H., et al. , “Deep predictive coding network for object recognition” in Proceedings of the 35th International Conference on Machine Learning, Dy J., Krause A., Eds. (PMLR, Stockholmsmässan, Stockholm, Sweden, 2018), vol. 80, pp. 5266–5275. [Google Scholar]
- 27.Madry A., Makelov A., Schmidt L., Tsipras D., Vladu A., “Toward deep learning models resistant to adversarial attacks” in 6th International Conference on Learning Representations (ICLR, Vancouver, Canada, 2018).
- 28.Qin Y., et al. , “Detecting and diagnosing adversarial images with class-conditional capsule reconstructions” in 8th International Conference on Learning Representations (ICLR, 2020).
- 29.Schott L., Rauber J., Bethge M., Brendel W., “Toward the first adversarially robust neural network model on MNIST” in 7th International Conference on Learning Representations (ICLR, New Orleans, LA, 2019).
- 30.Zhang M.-L., Zhou Z.-H., Multilabel neural networks with applications to functional genomics and text categorization. IEEE Trans. Knowl. Data Eng. 18, 1338–1351 (2006). [Google Scholar]
- 31.Guo C., Pleiss G., Sun Y., Weinberger K. Q., “On calibration of modern neural networks” in Proceedings of the 34th International Conference on Machine Learning, Precup D., The Y. W., Eds. (Association for Computing Machinery, 2017), vol. 70, pp. 1321–1330. [Google Scholar]
- 32.Nguyen A., Yosinski J., Clune J., “Deep neural networks are easily fooled: High confidence predictions for unrecognizable images” in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR, 2015).
- 33.Tsipras D., Santurkar S., Engstrom L., Turner A., Madry A., “Robustness may Be at odds with accuracy” in 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA (2019).
- 34.Nili H., et al. , A toolbox for representational similarity analysis. PLoS Comput. Biol. 10, 1–11 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Grathwohl W., et al. , “Your classifier is secretly an energy based model and you should treat it like one” in 7th International Conference on Learning Representations (ICLR, New Orleans, LA, 2019).
- 36.Zagoruyko S., Komodakis N., Wide residual networks. arXiv:1605.07146 (14 June 2017).
- 37.Engstrom L., Ilyas A., Santurkar S., Tsipras D., Robustness (Python Library, 2019). [Google Scholar]
- 38.Jozwik K. M., Kriegeskorte N., Storrs K. R., Mur M., Deep convolutional neural networks outperform feature-based but not categorical models in explaining object similarity judgments. Front. Psychol. 8, 1726 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rajalingham R., et al. , Large-scale, high-resolution comparison of the core visual object recognition behavior of humans, monkeys, and state-of-the-art deep artificial neural networks. J. Neurosci. 38, 7255–7269 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Peterson J. C., Abbott J. T., Griffiths T. L., Evaluating (and improving) the correspondence between deep neural networks and human representations. Cogn. Sci. 42, 2648–2669 (2018). [DOI] [PubMed] [Google Scholar]
- 41.Battleday R. M., Peterson J. C., Griffiths T. L., Capturing human categorization of natural images at scale by combining deep networks and cognitive models. arXiv:1904.12690 (26 April 2019). [DOI] [PMC free article] [PubMed]
- 42.Schrimpf M., et al. , Brain-Score: Which artificial neural network for object recognition is most brain-like?. bioRxiv:407007 (5 September 2018).
- 43.Jacobsen J. H., Behrmannn J., Carlini N., Tramèr F., Papernot N., Exploiting excessive invariance caused by norm-bounded adversarial robustness. arXiv:1903.10484 [cs, stat] (25 March 2019).
- 44.Mehrer J., Spoerer C. J., Kriegeskorte N., Kietzmann T. C., Individual differences among deep neural network models. bioRxiv:2020.01.08.898288 (9 January 2020). [DOI] [PMC free article] [PubMed]
- 45.Nalisnick E., Matsukawa A., Whye Teh Y., Gorur D., Lakshminarayanan B., “Do deep generative models know what they don’t know?” in 7th International Conference on Learning Representations (ICLR, New Orleans, LA 2019).
- 46.Fetaya E., Jacobsen J. H., Grathwohl W., Zemel R., “Understanding the limitations of conditional generative models” in The International Conference on Learning Representations (ICLR, 2020).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Optimization source code, synthesized images, and anonymized, detailed behavioral testing results are available at GitHub, https://github.com/kriegeskorte-lab/PNAS_2020_Controversial_Stimuli.