Representations of common event structure in medial temporal lobe and frontoparietal cortex support efficient inference

Abstract

Prior work has shown that the brain represents memories within a cognitive map that supports inference about connections between individual related events. Real-world adaptive behavior is also supported by recognizing common structure among numerous distinct contexts; for example, based on prior experience with restaurants, when visiting a new restaurant one can expect to first get a table, then order, eat, and finally pay the bill. We used a neurocomputational approach to examine how the brain extracts and uses abstract representations of common structure to support novel decisions. Participants learned image pairs (AB, BC) drawn from distinct triads (ABC) that shared the same internal structure and were then tested on their ability to infer indirect (AC) associations. We found that hippocampal and frontoparietal regions formed abstract representations that coded cross-triad relationships with a common geometric structure. Critically, such common representational geometries were formed despite the lack of explicit reinforcement to do so. Furthermore, we found that representations in parahippocampal cortex are hierarchical, reflecting both cross-triad relationships and distinctions between triads. We propose that representations with common geometric structure provide a vector space that codes inferred item relationships with a direction vector that is consistent across triads, thus supporting faster inference. Using computational modeling of response time data, we found evidence for dissociable vector-based retrieval and pattern-completion processes that contribute to successful inference. Moreover, we found evidence that these processes are mediated by distinct regions, with pattern completion supported by hippocampus and vector-based retrieval supported by parahippocampal cortex and lateral parietal cortex.

Understanding of real-world experiences is often supported by abstract knowledge. For instance, when going to a restaurant, you might first have an appetizer, then a main course, and finally dessert. Through similar experiences in multiple restaurants, you can abstract knowledge about the general sequence of events to expect. Your general knowledge about restaurants may then help you remember visits to specific restaurants and infer what to expect during upcoming visits. For example, to remember what you previously ordered for dessert at a specific restaurant, your general knowledge will guide you to focus on what occurred toward the end of dinner at that restaurant. Similarly, when visiting a French restaurant, you might predict which dessert you will have before seeing a menu based on past visits to French restaurants. While research has provided insight into how memories of individual events are formed, less is known about how abstract knowledge of common event structure is represented in the brain or how such knowledge supports memory-based inference. Here, we test whether hippocampus and prefrontal cortex represent similar events in a way that encodes common features with a consistent geometry to support efficient memory-based decisions (1).

Recent work shows that hippocampus and prefrontal cortex form representations, often referred to as cognitive maps, of both spatial and nonspatial relationships within a given context (2–6). These cognitive maps are thought to aid inference of relationships that have not been observed directly (2). Prior studies have found evidence that representational overlap, or memory integration (7), in hippocampus and medial prefrontal cortex (MPFC) mediates inference behavior (8–10). While studies of memory integration have focused on how pairs of related events become integrated in memory (11, 12), recent work in monkeys suggests that cognitive maps may also represent multiple task-relevant dimensions simultaneously (1). Such work suggests that hippocampus and prefrontal cortex may represent task features in a low-dimensional format, wherein individual task elements are represented with a common geometry that is consistent regardless of how other task features vary. For example, in monkeys, the direction between low- and high-reward value trials in hippocampal representational space is the same regardless of the specific stimulus being presented (1). This consistent vector relationship across trials has been proposed to be a form of abstraction—learned through feedback—that optimizes generalization to new events. However, real-world learning is often unsupervised and requires recognizing both specific and abstract properties, for example learning about a specific restaurant while also learning the series of events restaurants share.

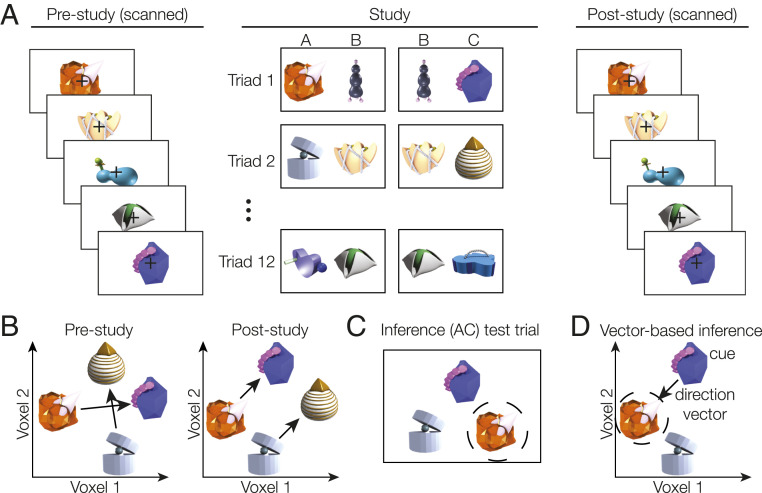
To test how the brain represents the abstract, common structure shared across events, we examined data from a study in which participants learned pairs of items (13); each pair (AB, BC) was drawn from a triad of three items (ABC), and there were 12 distinct triads in the task (Fig. 1A). Within each triad, the AB pair was always presented first and later followed by the BC pair. While participants were only instructed to learn about the individual pairs, previous analysis of this study demonstrated that indirectly related items (A and C) that share a common associate (B) show increased pattern similarity in hippocampus and prefrontal cortex after learning, suggesting that they have become integrated in memory (11). Memory integration has been proposed to facilitate inference about indirectly associated items (2). However, while it is possible to learn each triad separately, the triads share a common structure comprising A, B, and C items; the common structure among triads may promote formation of neural codes, particularly in hippocampus and prefrontal cortex, that represent all of the triad relationships with a common geometry (Fig. 1B). In such a common geometric representation, there would be a shared direction vector between indirectly associated items (A and C), regardless of their specific triad membership. To illustrate how common geometric representations may be formed without explicit feedback, we show that a simple back-propagation network learns to represent an abstract direction vector across triads while maintaining distinctions between individual triads in a single hierarchical representation (see Fig. 4).

Fig. 1.

(A) Participants learned associations between pairs of objects during the study phase. Unbeknownst to participants, objects were organized into triads of A, B, and C items. Within each triad of objects, an initial pair (AB) was learned first, followed by an overlapping (BC) pair. The left/right position of objects on the screen was randomized across presentations. Triads were learned in either a blocked order, for which all AB pairs were learned first followed by the BC pairs, or an intermixed condition, wherein AB and BC pairs were intermixed. Before and after learning, participants viewed each object in isolation, allowing us to measure how neural object representations changed as a result of learning. (B) We hypothesized that learning would cause items to become organized within a common cross-triad geometry, with a consistent direction between A and C items for all triads. (C) After scanning, participants performed an inference test; they were cued with a C item and asked to choose the A item that shared an indirect relationship with the cue. (D) We predicted that a common neural geometry across triads would support a vector-based inference process. The cue item representation could be combined with the direction vector representing the relevant relationship (here, C to A) to target the correct item in memory.

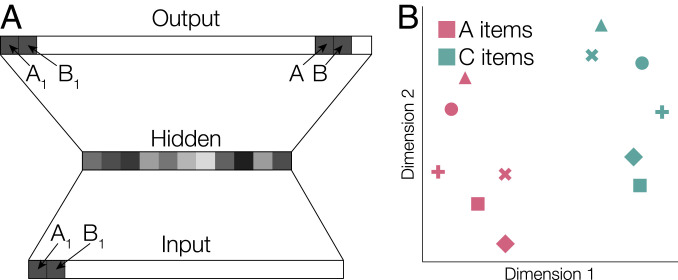
Fig. 4.

(A) We simulated learning in our task using a simple three-layer network. The network was trained to take item pairs as input and produce an output of that same item pair and the abstract identity of an item within the triad (i.e., either the A, B, or C element). Example input and target output patterns are shown for one simulated pair, A₁B₁. The network learns to associate each item with both the other item in the pair and its abstract identity in the triad. (B) After training, we simulated the postlearning item display task by presenting individual items to the network. We then used multidimensional scaling to characterize representations of A and C items in the hidden layer. Item representations reflected both abstract item identity (shown as different colors) and triad (shown as different symbols).

We further tested how a common geometric representation across triads supports efficient inference behavior. After learning, participants completed a surprise inference test of the associations between indirectly related A and C items (Fig. 1C). They were presented with a C item as a cue and had to select the corresponding A item. If the indirect association between A and C is coded with a consistent direction vector across triads, then this vector could be used to quickly infer unobserved relationships among events. In the case of an AC inference, by adding the C-to-A direction vector to a given C item cue, the correct A item could be predicted quickly from the common geometry (Fig. 1D). Such vector-based inference derived from a common neural geometry contrasts with a more effortful process, whereby multiple individual associations (i.e., A→B, B→C) are iteratively retrieved via pattern completion before an inference judgment can be made (14, 15). We therefore predicted that individuals who formed common geometric relationships among the triads would be faster at inference than participants with less geometrically aligned representations of the individual triad relationships. Furthermore, we used computational modeling to isolate how the distinct mechanisms of pattern completion and vector-based inference based on shared geometry contribute to inference.

Results

Medial Temporal Lobe and Frontoparietal Cortex Represent the Common Structure across Events.

We predicted that learning of the initial (AB) and overlapping (BC) pairs from each triad would result in the formation of neural geometries reflecting the common structure of relationships across triads (Fig. 2A). We focused on neural representations of the A and C items, as we hypothesized that representation of common structure would be particularly important for inferring the indirect relationships among items that were never seen together directly. We predicted that the common neural geometry would represent the grouping of items within a triad, with a consistent vector direction for indirectly associated (A and C) items across triads (Fig. 2A).

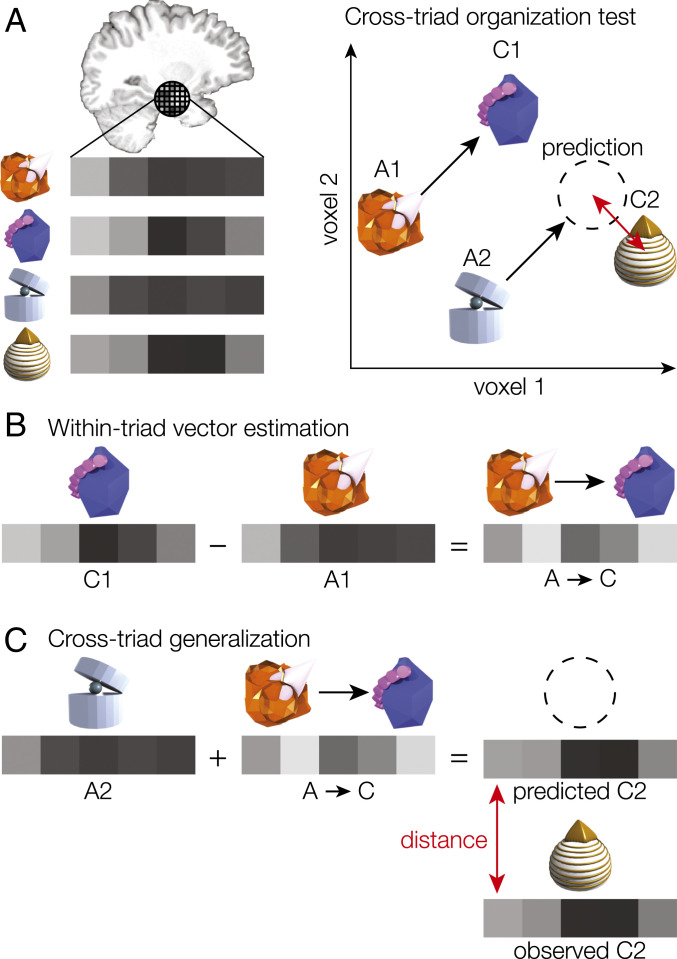
Fig. 2.

(A) For a given brain region, we measured activation estimates for each voxel to obtain an activation vector for each item. We tested for a common neural geometry across triads by using the patterns from one triad to predict the pattern associated with a different triad (dotted circle). If the triads share consistent representational vectors between the elements, then the difference between the predicted and observed patterns for the left-out item (red arrow) should be small. (B) We first estimated the average vector from A to C by subtracting the A pattern from the C pattern for all triads in a training set and averaging the difference vectors. (C) We then added the estimated A→C vector to the A item of a left-out triad, forming a prediction of what the pattern of activation should be for the corresponding C item. Finally, we evaluated the prediction by calculating the Euclidean distance between the prediction and the activation pattern observed for that item. We compared distance error to a chance distribution estimated by randomly swapping A and C items within each triad.

After the study phase, participants viewed each item in isolation, allowing us to measure the neural activation pattern associated with each item. We tested for representation of a common geometry across triads using a cross-validation procedure. On each cross-validation fold, we estimated the average direction vector between A and C across a set of triads (Fig. 2B) and used this vector to predict the relation between A and C items in a left-out triad (Fig. 2C). We added the A→C vector to the left-out A item pattern to form a prediction of what the activation pattern should be for the corresponding C item. We then evaluated this prediction by calculating the Euclidean distance between the predicted pattern and the pattern observed for that item; if there were a common geometry across triads, this distance error would be small relative to chance (estimated using a permutation test).

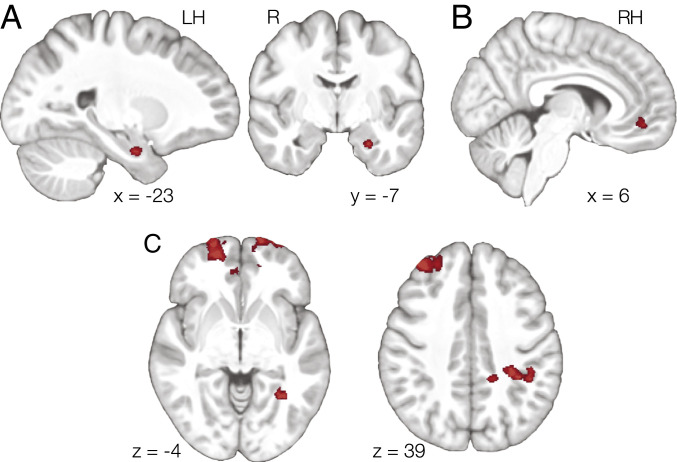
Consistent with our predictions, left anterior hippocampus (Fig. 3A) and right MPFC (Fig. 3B) exhibited representational geometries that were common across triads. A whole-brain analysis further revealed common geometry in left lateral parietal cortex (LPC), left parahippocampal cortex (PHC), bilateral frontopolar cortex, and right dorsolateral prefrontal cortex (DLPFC; Fig. 3C). The LPC cluster extended into medial areas but was primarily located on the lateral surface. Critically, these regions represented the common structure across triads even though participants were not instructed to learn the abstract properties of the task and received no reinforcement during learning that would explicitly cue them to the abstract task properties.

Fig. 3.

(A) We found evidence of a common neural geometry across triads in anterior hippocampus. Results were cluster-corrected within hippocampus. (B) We also found evidence of common neural geometry within MPFC (cluster corrected within MPFC). (C) Whole-brain analysis revealed additional clusters in bilateral frontopolar cortex, left PHC, right DLPFC, and LPC.

While we found evidence that medial temporal and frontoparietal areas formed a common geometry across triads, hierarchical representations that code both abstract commonalities among events and distinctions between them might be particularly efficient at supporting memory-based decisions. Therefore, we tested whether regions exhibiting cross-triad organization also distinguished between individual triads. We used the same cross-validation statistic as before but compared the observed prediction error to a permutation distribution estimated by scrambling items across triad to obtain a z-statistic for each participant and region. We found that PHC representations significantly distinguished between individual triads [$t\left(25\right)=2.94$, $P=0.017$, false discovery rate Benjamini–Hochberg (FDR-BH)–corrected one-sided test], while the other regions did not [$t\left(25\right)<2.08$, $P>0.05$, FDR-BH–corrected one-sided test]. However, we did not observe a significant difference in triad separation between PHC and the other regions ($P>0.05$, FDR-BH–corrected) and therefore do not conclude that triad separation is necessarily selective to PHC.

A Neural Network Model of Learning Predicts Formation of a Hierarchical Task Representation.

After learning, we observed abstract representations of common event structure and hierarchical representations that represented both event commonalities and differences. To examine how hierarchical representations might emerge during learning, we trained a three-layer neural network model on our task (cf. ref. 1). We trained the network to associate each item with both the specific item(s) to which it was paired and with a representation of its abstract identity within a triad (i.e., whether each item was an A, B, or C item; Fig. 4A and SI Appendix, Fig. S2 A–C). After training, presentation of individual items (similar to the poststudy scans) elicited hierarchical patterns in the hidden layer of the network that represented the full structure of the task (Fig. 4B and SI Appendix, Fig. S2 D–F). These results suggest that a hierarchical representation of the task can be learned without explicit feedback. Abstract representations of common triad structure (as we observed in frontoparietal cortex and hippocampus) may guide formation of hierarchical representations that reflect commonalities among multiple events while maintaining distinctions between individual episodes (as we observed in PHC).

Common Geometric Representations in Hippocampus and Parietal Cortex Predict Faster Inference.

We hypothesized that common geometric relationships would facilitate performance on the AC inference test. Participants had near-ceiling accuracy on the AC inference test and the direct AB and BC tests (SI Appendix, Fig. S1A). Thus, we focused on individual differences in response time for correct trials on the inference test (SI Appendix, Fig. S1B). Response times were significantly slower on the inference test compared to the direct tests [$t\left(25\right)=6.63$, $P=2.24\times {10}^{-8}$]. During the study phase, triads were learned in either a blocked or intermixed schedule (Materials and Methods). Response times did not differ between schedules for either the direct [$t\left(25\right)=1.97$, $P=0.055$] or inference [$t\left(25\right)=0.60$, $P=0.56$] tests.

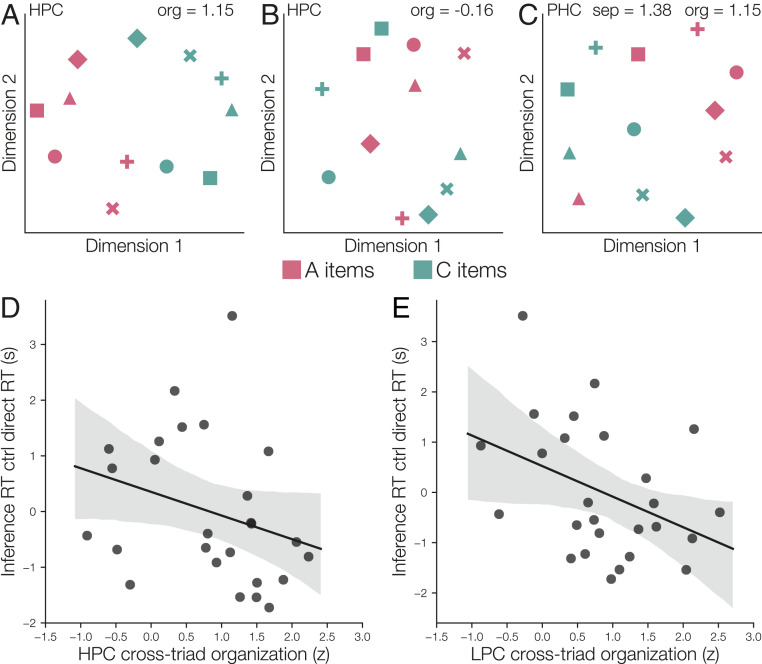
For each region exhibiting a common geometry across triads, we calculated an organization score for each participant. Organization was measured as the z-statistic of prediction accuracy based on common geometry, relative to chance. For the triads learned in each schedule (blocked or intermixed), we visualized individual differences in neural organization using multidimensional scaling of average item patterns. Fig. 5 A and B shows examples for two participants, illustrating hippocampus representations for items learned through the intermixed schedule. Fig. 5C shows an example, taken from the intermixed schedule of one participant, of PHC patterns exhibiting both cross-triad geometric structure and separation between different triads. The degree of cross-triad organization did not differ between the blocked and intermixed learning schedules in any region ($P>0.05$, FDR-BH–corrected). In PHC, we observed no difference in triad separation between schedules [$t\left(25\right)=0.19$, $P=0.85$]. Therefore, we averaged across learning schedule for all subsequent analyses.

Fig. 5.

(A) Average hippocampus (HPC) item patterns in a participant with relatively strong cross-triad geometric organization (as indicated by the z-statistic of organization relative to chance). Multidimensional scaling (MDS) was used to reduce the dimensionality of mean hippocampal activity patterns for visualization. Colors indicate within-triad position (A or C), and symbols indicate which triad each item belonged to. Note that A and C items can be cleanly divided by drawing a line. The plot shows A and C item patterns for the six triads learned in the intermixed condition; similar organization was observed in the blocked condition. (B) MDS plot of mean hippocampus activation patterns for items learned in the intermixed condition, for a participant with less-coherent cross-triad organization. (C) MDS plot of mean PHC activation patterns for items learned in the intermixed condition, for a participant with both high cross-triad organization and high triad separation. (D) The degree of cross-triad organization in hippocampus (relative to organization expected by chance) was predictive of faster response times on the later surprise inference test, after controlling for direct test response time. Shaded area is a 95% confidence interval based on a bootstrap procedure. (E) Cross-triad organization in LPC also predicted individual differences in response time.

We hypothesized that participants who exhibited greater geometric organization after learning (e.g., Fig. 5A) would make faster inference decisions. To test this hypothesis, we examined the relationship between the organization z-statistic for each participant after learning and their subsequent mean response time on correct inference trials (Fig. 5 D and E). In hippocampus and LPC, we found that increased geometric organization after learning predicted faster inference response times, after controlling for individual differences in response time on the direct tests (hippocampus: $r=-0.52$, $P=0.018$; LPC: $r=-0.42$, $P=0.046$; Spearman correlation, FDR–corrected one-sided permutation test). There was no significant correlation for any of the other regions ($P>0.05$, FDR–corrected one-sided permutation test). We also examined whether triad separation in PHC was related to individual differences in response time. There was a trend toward a negative relationship ($r=-0.327$, $P=0.052$, Spearman correlation, one-sided permutation test). Our results suggest that formation of common geometric structures within hippocampus and LPC may facilitate inference about object relationships that have not been directly observed.

Hippocampus, PHC, and Parietal Cortex Support Dissociable Retrieval Processes.

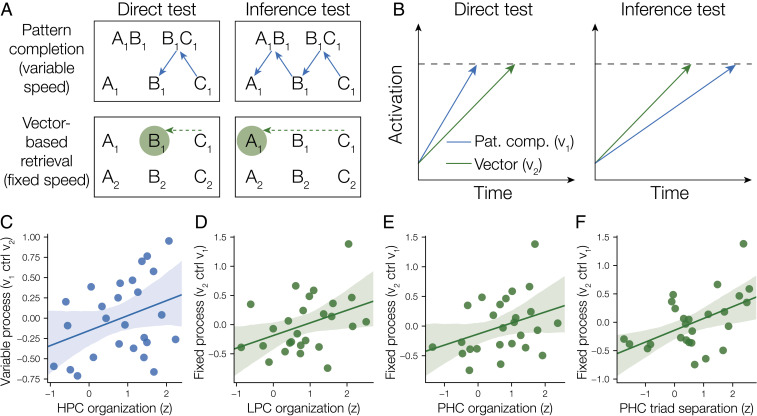
We hypothesized that representation of common geometric structure may facilitate faster inference by supporting targeted retrieval of memories, through use of the common vector coding A→C direction across triads. The common geometry among indirectly related items in each triad could be used to speed inference decisions by targeting the position of the probed item relative to the test cue in the geometric structure. For example, when presented with a retrieval cue such as item C₁ (the C item from triad 1) and asked to retrieve the corresponding A item (A₁), common geometry could guide targeted retrieval of the indirectly related item, allowing for more efficient inference (Fig. 6A). In contrast, previous work suggests that participants could also perform inference through an iterative retrieval process, whereby a cue (e.g., C₁) triggers pattern completion to the associated pair (B₁C₁), and then the retrieved intermediate item (B₁) triggers pattern completion to its other associated pair (A₁B₁; Fig. 6A) (14). However, this process would require multiple retrievals, and therefore inference based on this process would be slower than pattern completion of directly learned associations.

Fig. 6.

(A) We hypothesized that retrieval during both the direct memory and inference tests could be accomplished either through pattern completion of individual associations or through a vector-based retrieval process guided by common geometric representation across triads. We hypothesized that pattern completion would be fast but would take longer than the vector-based retrieval process for the inference test as more retrieval steps (depicted by individual arrows) are necessary to infer that A and C are related. In contrast, common representational geometry could be used to guide vector-based retrieval of a specific memory. The common geometry could be used to calculate a vector (dotted arrow) pointing to where the targeted memory should be in the representation (circle), thus providing a means to infer indirect relationships. This vector-based retrieval approach does not require multiple retrieval steps and may thus have an advantage over the pattern-completion process for the inference test in particular. (B) We simulated the retrieval process using the LBA model of response time. Different retrieval processes were simulated as trajectories from some starting point to a threshold. Response time is modeled as the time that the first retrieval process hits the threshold. The model predicts that the pattern completion process will finish first more often on direct test trials, but that the vector-based retrieval process will win more often on inference trials. We used the model to estimate the speed of the variable-speed pattern completion $\left(v_1\right)$ and fixed-speed vector-based retrieval $\left(v_2\right)$ processes for each participant, based on their response times on the direct and inference tests. (C) Hippocampus (HPC) geometric representation tracked individual differences in the speed of the pattern completion process ($v_1$ parameter after controlling for $v_2$). Shaded area is a 95% confidence interval based on a bootstrap procedure. (D) LPC geometric organization tracked individual differences in the speed of the vector-based retrieval process ($v_2$ parameter after controlling for $v_1$). (E and F) In PHC, both common geometry across triads and separation between triads were related to the fixed-speed process ($v_2$ parameter after controlling for $v_1$).

To better understand how common geometric representation relates to response time, we developed a formal model of how retrieval processes may contribute to both memory for direct associations and inference. Our model hypothesizes that there are two distinct processes that may contribute to memory and inference in our task: pattern completion, which is fast for retrieval of direct associations but slower for inference of indirect associations (i.e., variable speed), and a vector-based retrieval process leveraging the shared geometry across triads that takes the same amount of time regardless of whether a direct or indirect association is being retrieved (i.e., fixed speed; Fig. 6A). We used the linear ballistic accumulator (LBA) model of decision making (16) to model response times produced by the combination of the two hypothesized processes to the direct and inference tests (Fig. 6B). Critically, we found that our proposed dual-process model predicts distinct patterns of response time data when compared to a single-process model and that the dual-process model provides a better account of individual differences in response time (SI Appendix, Fig. S3). We used the dual-process model to estimate individual differences in the speed of the pattern completion and vector-based retrieval processes for the direct and inference tests. We used Bayesian inference to estimate model parameters for both the variable-speed process (with base speed $v_1$) and fixed-speed process (with speed $v_2$) for each participant, based on their response time distributions and accuracy on the direct and inference tests (SI Appendix, Figs. S4–S8).

To test whether neural geometry in hippocampus, PHC, and LPC was related to the pattern completion or vector-based retrieval processes, we examined whether the speed parameter estimates $v_1$ and $v_2$ were related to neural organization in each region. We predicted that participants with more coherent geometries would demonstrate faster drift rates in either $v_1$ or $v_2$, both of which influence inference response times according to the model. Using a regression model including $v_1$ and $v_2$ to predict organization, we found that $v_1$ (variable speed) explained unique variance in hippocampal geometric organization [$t\left(23\right)=1.83$, $P=0.040$, one-sided test] but $v_2$ (fixed speed) did not [$t\left(23\right)=0.48$, $P=0.32$, one-sided test]. Conversely, $v_2$ explained unique variance in LPC geometric organization [$t\left(23\right)=2.10$, $P=0.024$, one-sided test] but $v_1$ did not [$t\left(23\right)=0.26$, $P=0.80$]. Next, we examined how both common geometry across triads and triad separation in PHC relate to the $v_1$ and $v_2$ model parameters. We found that the $v_2$ parameter explained unique variance in both aspects of PHC organization after controlling for $v_1$ [organization: $t\left(23\right)=1.76$, $P=0.046$; triad separation: $t\left(23\right)=2.90$, $P=0.004$, one-sided tests], but $v_1$ did not explain unique variance [organization: $t\left(23\right)=-0.74$, $P=0.77$, triad separation: $t\left(23\right)=-0.32$, $P=0.63$, one-sided tests], suggesting that hierarchical representations in PHC may support vector-based retrieval. Furthermore, we found that common geometry across triads predicted decision speed even when controlling for the degree to which neural representations were clustered by type (e.g., two A items being more similar than an A item and a C item; SI Appendix, Fig. S9), suggesting that common geometry is specifically predictive of inference performance.

Our results provide evidence that common geometric structure in hippocampus is related to efficient pattern completion, while geometric structure in LPC and hierarchical representations in PHC support vector-based retrieval. To test the hypothesis that LPC and PHC support a distinct process from hippocampus, we examined whether organization in each region explains unique variance in the model parameters. Hippocampal geometric organization explained unique variance in the $v_1$ parameter (residualized with respect to $v_2$) after controlling for LPC and PHC geometric organization and PHC triad separation [$t\left(21\right)=2.02$, $P=0.029$, one-sided test]. We also found that the signals related to $v_2$ parameter residuals (LPC and PHC geometric organization and PHC triad separation) explained unique variance after controlling for hippocampal geometric organization [$F\left(3,\hspace{0.17em}21\right)=4.12$, $P=0.0191$]. Our results thus provide evidence of distinct hippocampal and LPC/PHC contributions to memory retrieval and inference.

Discussion

We show that hippocampus, PHC, and frontoparietal regions represent common structure across events. Activation patterns in these regions reflected a common task geometry, wherein the relationships between elements of individual triads were represented with common directions across triads. This abstract representation emerged even though participants were only instructed to attend to and learn individual pairs. Furthermore, common geometry in hippocampus, PHC, and LPC predicted faster inference decisions about indirectly related A and C items, even after controlling for clustering of items by type (e.g., two A items being more similar than an A item and a C item). During the inference test, participants were given a C item and asked to select the corresponding A associate. Critically, both choices were associated with the same element within each triad (i.e., both were A items); therefore, making a correct response required retrieving a specific A–C association. Thus, our results provide evidence that abstract representations of common structure facilitate inference about specific associations.

Previous computational models of associative memory have proposed that pattern completion may support inference about overlapping events (17, 18); however, these models do not address how representations of common event structure might further guide inference. We hypothesized that abstract representations may support a vector-based retrieval process that allows efficient retrieval of indirectly associated items. To test this hypothesis, we developed a formal model of memory-based decisions in which responses may be driven by either pattern completion to directly experienced event relationships or vector-based retrieval of both directly experienced and inferred relationships. We found that a dual-process model, in which both pattern completion and vector-based retrieval processes contribute to inference, explained individual differences in response times more accurately than a simpler model based on pattern completion alone. Furthermore, we found evidence of a dissociation between the roles of different regions: Common geometry in hippocampus predicted the speed of the pattern completion process, while PHC and LPC common geometries predicted the speed of the vector-based retrieval process. In PHC, separation between triads also predicted the speed of vector-based retrieval. This finding suggests that hierarchical representations in PHC may help connect abstract representation of commonalities with the specific features of events.

Together with MPFC and LPC, PHC is a component of a hypothesized posterior medial network that is proposed to represent abstract structure, for example the general sequence of events that occurs when one visits a restaurant (19, 20). Here, we provide evidence for this theoretical proposition, showing that abstract information about commonalities among events is represented in posterior medial areas in the form of a consistent neural geometry. The posterior medial network is functionally connected with hippocampus (19, 21), which has also been implicated in representing abstract knowledge of task-relevant features (2–4). Here, we found that anterior hippocampus representations not only link pairs of related events (11, 22) but further abstract commonalities across a number of events that share a common structure. Moreover, we found that prefrontal areas, including MPFC, DLPFC, and frontopolar cortex, formed common geometric representations of task structure after learning. Recent evidence suggests that MPFC performs dimensionality reduction (23), a mechanism that may facilitate formation of abstract representations (1). DLPFC and frontopolar cortex have been proposed to support learning about inferred task structure in the context of reinforcement learning paradigms that require learning of complex rules through feedback (24–28). Together with such work, the present findings suggest that MPFC, DLPFC, and frontopolar cortex may be involved in inferring relevant features of the task and forming low-dimensional abstract representations.

Our findings parallel recent primate work showing that abstract neural geometries are formed in hippocampus and DLPFC during reinforcement learning (1). We extend those findings by demonstrating that abstract neural representations are formed in the human brain in the absence of feedback. Furthermore, we find that in addition to hippocampus and DLPFC, LPC and PHC also represent abstract commonalities. In the primate study, abstract neural representations reflected the current task context, which monkeys learned by monitoring the temporal regularities of reward outcomes. In the current study, we find that medial temporal lobe and frontoparietal regions distinguish between A and C items, which only differ from each other in their temporal regularities. It is notable that similar common geometries were observed in the blocked condition, in which all AB pairs were learned before all BC pairs, and in the intermixed condition, in which AB and BC pairs were intermixed. The lack of differences in neural geometries between these very different learning schedules suggests that the abstract representations reflect the specific temporal regularities of the task (i.e., that AB pairs were always presented before their corresponding BC pairs across both conditions) rather than broad differences in temporal context, which are present only in the blocked condition. Our findings thus complement prior work showing that abstract temporal statistics are reflected in hippocampal and prefrontal responses (29, 30) and build upon that work by showing how representation of abstract temporal properties in medial temporal and parietal regions promote inference.

Our model-based analyses suggest that organization in PHC and LPC guides a vector-based retrieval process, whereby inferred associations are accessed directly rather than through iterative retrieval of individual pairings. While LPC activity tracks successful retrieval of episodic memories (31), its specific role in memory processing is controversial (32). For instance, LPC lesions do not substantially impact memory retrieval (33). However, several theories suggest that LPC contributes to memory by directing attention to retrieved memory contents to guide decision making (34). Our results provide a more mechanistic explanation of how LPC may control movement between memories in an efficient way; given a relationship, encoded in a direction vector through a learned neural geometry, and a cue, encoded as a position within the common geometric space, LPC may compute a new position within the learned geometry to target specific memories. In other words, LPC may support predictive inference by navigating through the shared geometric structure. Our findings thus suggest that LPC may be more important for navigating relational maps of memories than for retrieving details about individual memories. LPC has been implicated in transitive reasoning (35), mathematical operations such as approximate addition (36), and numerical inductive inference (37), raising the possibility that it may play a domain-general role in vector-based navigation through different types of cognitive maps.

LPC and PHC are highly interconnected regions (38), suggesting they may work together to guide vector-based retrieval using both abstract and specific features of events in memory. The present findings indicate that PHC simultaneously represents commonalities among and distinctions between triads. Through interactions with LPC, the multidimensional geometry in PHC may allow for translation between the abstract and specific features to promote inference. PHC has been implicated in processing of spatial stimuli (39–41) and representing geometric features of spatial layouts such as distance and angle (42, 43). While PHC has been proposed to have an important role in spatial cognition, recent work has demonstrated that nonspatial memories may become organized within cognitive maps with similar properties to spatial cognitive maps (2–4, 44, 45). Our results suggest that PHC may play a domain-general role in representing abstract task geometries through formation of multidimensional cognitive maps.

While LPC and PHC representations predicted individual differences in the vector-based retrieval process, hippocampus tracked a pattern-completion process that is slower for inference of indirect associations than for retrieval of directly learned associations. Recent evidence suggests that hippocampus may support inference through an iterative process of retrieving individual memories (14, 15, 46). For simplicity, in our model, we assumed that the pattern completion process is always an iterative process of retrieving separate memories of the AB and BC pairs. However, recent studies have found evidence that related events may become integrated in overlapping memory traces during encoding, facilitating efficient flexible retrieval (8–10, 47). It is difficult to examine the contribution of memory integration in this study, however, as a prior investigation of this dataset demonstrated that memory integration did not occur consistently across the blocked and intermixed conditions (7). However, the present findings indicate that hippocampal abstraction of common task geometries may be more robust than integration of elements of individual pairs. The fact that common geometric coding was localized to anterior hippocampus is consistent with leading theories (48) which propose that anterior hippocampal coding emphasizes commonalities among rather than differences between events.

In conclusion, we find evidence that individual memories are organized into a common geometric representation in hippocampus, PHC, LPC, and prefrontal cortex that reflects the abstract structure shared across events, even in the absence of explicit task demands to attend to this structure. Such organized representational geometries further predict individual differences in the speed of flexible retrieval. We propose that neural representations with common geometric structure may provide an efficient way of accessing memories that are not easily accessible via pattern-completion mechanisms, while also making it possible to infer associations between events that have not been directly observed. Importantly, representations with consistent geometric structure are efficient at coding multiple dimensions (1), making them well-suited for learning complex hierarchical structures that reflect abstract relationships between contexts with similar structure. These mechanisms may be critical for building mental models of real-world situations for which structure is not directly learned but instead must be inferred based on limited experience.

Materials and Methods

Participants and Procedures.

Data from the study were previously reported in ref. 11. Data from 26 participants were included in all analyses (14 women; ages 18 to 27 y; $21.6\pm 0.5$ y). Stimuli consisted of 36 novel objects (11, 49) that were arranged into 12 ABC triads. Triads were presented to participants as overlapping AB and BC pairs; each pair was presented 12 times. Triads were divided into two learning conditions. In the blocked learning condition, all AB pair presentations occurred before the presentation of any BC pairs. In the intermixed learning condition, AB and BC pairs were presented in alternation. The left/right position of stimuli on the screen was randomized across presentations. Participants were not made aware of the overlap between AB and BC pairs before beginning the experiment. Participants were exposed to single items both immediately before and following study during functional MRI scanning while performing an orthogonal change-detection task (Fig. 1A). See SI Appendix for details of scanning parameters and preprocessing. In each of the four prestudy runs and four poststudy runs, each of the 36 items was presented in isolation twice. Following scanning, it was explained to participants that A and C items could be indirectly related through their common association with a single item, B. Participants were then tested on their memory for indirectly (AC) and directly (AB, BC) related associations (Fig. 1D). See SI Appendix for full task details.

Measuring Neural Geometry.

Patterns of activation associated with individual items were estimated under the assumptions of the general linear model using a least squares–separate approach (50). To test whether there was a consistent A-to-C direction across triads, we used a cross-validation procedure that estimated the average direction vector from A to C on one set of triads and evaluated that vector on a left-out triad. On each fold of the cross-validation, we first estimated the average vector between A and C items for all triads except one. We then added this vector to the A item of a left-out triad to obtain a prediction of what the pattern of activation should be for the corresponding C item and tested whether prediction accuracy was greater than expected due to chance. We calculated an organization score z-statistic by comparing the observed prediction accuracy with a chance distribution determined by randomly permuting item type (A vs. C) within each triad separately.

We quantified representation in searchlight spheres (radius three voxels) across the brain by calculating cross-triad prediction accuracy separately for each learning condition, averaging across conditions, and calculating a z-statistic of average prediction accuracy relative to chance. Participant z-statistic images were transformed to a group template using ANTs. Group results were cluster-corrected within hippocampus and MPFC a priori regions of interest (ROIs) and at the whole-brain level with a familywise alpha of 0.05. Group-level clusters were reverse-normalized to the space of individual participants and organization z-statistics were calculated for each participant and ROI. To measure between-triad separation, we used the same prediction accuracy statistic as in the original test for cross-triad organization but compared it to a chance distribution determined by randomly permuting C items across triads while leaving A items fixed. See SI Appendix for further details.

Network Model of Learning.

To simulate the study phase, we used a three-layer back-propagation network (Fig. 4A). For each pair, we trained the network to take the items as input (e.g., A₁ and B₁, the A and B items from triad 1) and output both the same items (A₁ and B₁) and their corresponding item types (e.g., A and B; see SI Appendix, Fig. S2 B and C). We simulated learning of six triads (as in each of the individual learning conditions) by presenting AB and BC pairs to the network. After training, we simulated the postlearning display task by presenting individual items to the network and recording the state of the hidden layer (SI Appendix, Fig. S2 D–F), which we analyzed using metric multidimensional scaling (Fig. 4B). See SI Appendix for full details.

Response Time Model.

We simulated response time on direct and inference test trials using the LBA framework (16). LBA assumes that evidence for each available option accumulates until a decision threshold is reached. The first accumulator to reach the decision threshold determines which option is selected. In our model, each choice was represented by two accumulators: one for the variable-speed pattern-completion process and one for the fixed-speed vector-based retrieval process (Fig. 6A). We used a hierarchical Bayesian model to obtain estimates of the pattern completion process speed $\left(v_1\right)$ and the vector-based retrieval process speed $\left(v_2\right)$ for each participant, fitting responses for all triads regardless of learning condition. Finally, we used regression to test whether common geometry across triads or separation of individual triads in each region was related to unique variance in the $v_1$ and $v_2$ parameter estimates for each participant. See SI Appendix for full details.

Code Availability.

Code implementing the searchlight analysis, network model, and response time model is available at https://osf.io/6eqbf/.