Improved physiological noise regression in fNIRS: A multimodal extension of the General Linear Model using temporally embedded Canonical Correlation Analysis

Abstract

For the robust estimation of evoked brain activity from functional Near-Infrared Spectroscopy (fNIRS) signals, it is crucial to reduce nuisance signals from systemic physiology and motion. The current best practice incorporates short-separation (SS) fNIRS measurements as regressors in a General Linear Model (GLM). However, several challenging signal characteristics such as non-instantaneous and non-constant coupling are not yet addressed by this approach and additional auxiliary signals are not optimally exploited. We have recently introduced a new methodological framework for the unsupervised multivariate analysis of fNIRS signals using Blind Source Separation (BSS) methods. Building onto the framework, in this manuscript we show how to incorporate the advantages of regularized temporally embedded Canonical Correlation Analysis (tCCA) into the supervised GLM. This approach allows flexible integration of any number of auxiliary modalities and signals. We provide guidance for the selection of optimal parameters and auxiliary signals for the proposed GLM extension. Its performance in the recovery of evoked HRFs is then evaluated using both simulated ground truth data and real experimental data and compared with the GLM with short-separation regression. Our results show that the GLM with tCCA significantly improves upon the current best practice, yielding significantly better results across all applied metrics: Correlation (HbO max. +45%), Root Mean Squared Error (HbO max. −55%), F-Score (HbO up to 3.25-fold) and p-value as well as power spectral density of the noise floor. The proposed method can be incorporated into the GLM in an easily applicable way that flexibly combines any available auxiliary signals into optimal nuisance regressors. This work has potential significance both for conventional neuroscientific fNIRS experiments as well as for emerging applications of fNIRS in everyday environments, medicine and BCI, where high Contrast to Noise Ratio is of importance for single trial analysis.

1. Introduction

Functional Near-Infrared Spectroscopy (fNIRS) is a non-invasive, nonionizing optical imaging technique that measures the hemodynamic changes associated with brain activity (Boas et al., 2014; Ferrari and Quaresima, 2012; Villringer and Chance, 1997). It uses light in the near-infrared region to measure the concentration changes in oxygenated and deoxygenated hemoglobin (HbO and HbR respectively) in the cerebral cortex, a signal that is spatially and temporally comparable to blood oxygenation level dependent (BOLD) signals measured by functional Magnetic Resonance Imaging (fMRI) (Huppert et al., 2006, 2005; Kleinschmidt et al., 1996). Despite its low penetration depth and spatial resolution, the technique has found widespread use both in the research and clinical field due to its portability, safety, low-cost and the ecological validity that it provides in experimental and real-life settings (Boas et al., 2014; Yücel et al., 2017).

The fNIRS signal is an integration of the brain signals arising from the cerebral cortex as well as the systemic physiological signals from superficial layers (i.e. scalp and skull), which often has a larger magnitude. This systemic interference is driven by blood pressure fluctuations related to heart rate, respiration, and low-frequency oscillations (Gregg et al., 2010; Saager and Berger, 2008) or body movement and posture (von Lühmann et al., 2019). Due to its dominance over brain signals, one critical step in fNIRS data processing is to remove the contribution of superficial layers to the fNIRS signal and various approaches for the removal of confounding signals have been proposed. Among them are band-pass filtering (Huppert et al., 2009), adaptive filtering (Kamran and Hong, 2013), and autoregressive modeling (Barker et al., 2013b), to name a few. See (Scholkmann et al., 2014) for a review. The current best practice is to simultaneously measure scalp hemodynamics using additional detectors, typically called “short-separation detectors”, located approximately 10 mm apart from each source (Saager and Berger, 2008). This scalp-only measurement can then be used as a regressor to remove the scalp contamination from the brain signal measured with standard-separation source-detector pairs (Gregg et al., 2010; Saager and Berger, 2008; Zhang et al., 2009).

Motion can generate confounding signals both of physiological and non-physiological origin, as discussed in more detail in (von Lühmann et al., 2019). It can, indirectly and non-instantaneously, induce both local and systemic physiological interference, affecting brain as well as scalp signals. Examples are blood pressure changes or blood pooling following a change in head and body posture. Direct motion artifacts due to optical decoupling between the optode (source/detector) and the scalp (Cooper et al., 2012) lead to instantaneous or slow changes in the signal that do not reflect changes in physiology. Motion artifact detection and removal or correction algorithms are commonly used to deal with this second type of decoupling artifacts in the data (Brigadoi et al., 2014; Cooper et al., 2012). More recently, fNIRS has become relatively robust to optode decoupling artifacts by the use of novel fiberless and lightweight wearable instruments (Safaie et al., 2013; von Lühmann et al., 2017; von Lühmann et al., 2015; Zhao and Cooper, 2017). These new technologies enable the use of fNIRS in more challenging populations, e.g. infants/toddlers (Cristia et al., 2013), and in more natural settings and environments, e.g. walking or bicycling outdoors (Holtzer et al., 2011; Piper et al., 2014). In turn, however, signal contamination with motion-induced systemic interference increases.

Conventionally, an fNIRS signal-processing pipeline involves steps that tackle both types of confounding signals: systemic fluctuations and motion artifacts. While one can filter and perform correction prior to the estimation of the hemodynamic response function (HRF) and then perform conventional block averaging, a more preferred approach is to use a General Linear Model which allows for simultaneous extraction of the HRF while filtering the confounding signals using nuisance regressors (Cohen-Adad et al., 2007; Friston et al., 1994). As the observed hemodynamic signal is a combination of both the brain response to experimental stimuli as well as the additional confounding signals, a priori knowledge about these components allows a more accurate and robust estimation of the HRF when a GLM approach is implemented (Diamond et al., 2006; Kirilina et al., 2013). Among the signals that are commonly used for this purpose are auxiliary measurements of systemic physiology (short-separation measurements, blood pressure, cardiac oscillations, respiration) or head motion (accelerometers). In particular, the use of short-separation detector measurements as a regressor in the GLM has been previously shown to statistically improve HRF estimation (Gagnon et al., 2011; Yücel et al., 2015).

There are several challenging characteristics present in fNIRS signals which are not directly addressed by the standard GLM approach. Among them are I) non-instantaneous and non-constant coupling (both between fNIRS channels as well as between fNIRS signals and other modalities), II) pronounced correlation of physiological nuisance signals and III) statistical dependencies of the underlying physiological processes. Typical examples are I) cardiac or movement induced blood pressure variations spreading along the vascular path underneath the fNIRS sensors and thus interfering with the signal at each sensor with varying time delays, II) oscillatory signals from cardiac, respiration and Mayer waves which are highly correlated across all measurement channels, and III) interdependent regulation of these and other functions by the autonomous nervous system. To tackle these challenges outside of the GLM, we have recently introduced a new methodological framework for the multivariate analysis of fNIRS signals using Blind Source Separation (BSS), and its application in the unsupervised accelerometer-based identification and rejection of indirect motion-induced physiological hemodynamic artifacts, a method called BLISSA²RD (von Lühmann et al., 2019). In that work, we extensively explored the aforementioned challenges and incorporated three approaches as a remedy: A) Independent Component Analysis methods that exploit both higher order statistics and sample dependency (Adali et al., 2014; Fu et al., 2014), B) utilization of multiple modalities, i.e., fNIRS, accelerometer signals and short-separation measurements and C) Canonical Correlation Analysis (Anderson, 1958; Hotelling, 1936) with temporal embedding (Bießmann et al., 2010).

However, these remedies are not only limited to unsupervised applications. Here, we propose a new approach “GLM with temporally embedded CCA” (GLM with tCCA) that integrates the above-mentioned BSS framework with the current best practice for analysis of fNIRS signals - the supervised General Linear Model with short-separation regression (GLM with SS) - to combine the strengths of both domains. The purpose of this manuscript is threefold:

Firstly, we show how to incorporate the advantages of multimodality and temporally embedded CCA into the conventional supervised GLM in a straight-forward way. It allows the flexible integration of any number of auxiliary modalities and signals, while orthogonality of the provided regressors is ensured.

Secondly, we provide guidance for the selection of optimal parameters and auxiliary signals for the proposed GLM with tCCA approach. We have found these by challenging the model with the estimation of single trial HRFs (necessary in Brain Computer Interface (BCI) type applications) as well as HRF estimation from many trials (relevant for research in neuroscience and psychology), using three different simulated HRF amplitude levels added onto resting-state fNIRS data.

Lastly, we have compared the new approach with the standard GLM with short-separation regression. We show that the GLM with tCCA significantly improves upon the current standard by providing more optimal nuisance regressors, which leads to a significantly reduced physiological noise floor, and consequently to a significantly enhanced performance in the detection and extraction of evoked HRFs. Performance of the method is quantified with the metrics F-Score, Correlation (Corr) and Root Mean Squared Error (RMSE), calculated with respect to a known HRF synthetically added to resting data. We also evaluate performance using experimental data from a visual stimulation paradigm.

2. Methods

In this section, firstly, we introduce relevant aspects of the General Linear Model and Canonical Correlation Analysis with temporal embedding. Please refer to Appendix A and B for more background. In Section 2.2, we lay out a description of the proposed GLM with tCCA approach. In Section 2.3, we elaborate on the exploration of optimal parameters for GLM with tCCA and its performance evaluation and comparison to the standard GLM with SS approach. Finally, in Section 2.4, we briefly describe the experimental paradigm and acquisition of the data used for evaluation.

2.1. Mathematical background

2.1.1. The General Linear Model in fNIRS/fMRI

An established model for analysis in fMRI and fNIRS studies is the “General Linear Model (GLM)”. It is a special case of the generative linear mixing model for neuroimaging data, implemented for supervised linear regression. Please see Appendix A where we provide a short mathematical introduction to the concept of generative linear mixing models. The GLM incorporates a priori knowledge such as stimulus onset timing and hemodynamic response function models for the estimation of evoked hemodynamic responses (Calhoun et al., 2001; Josephs et al., 1997; Ye et al., 2009). It is typically expressed as

$$\mathit{Y}=\mathit{G}\mathit{\beta }+E$$ [1]

where $Y\in {ℝ}^{T\times N}$ is the observation matrix with measurement data from all time points T and recorded channels N. In the following, we will denote observed data samples of modality y at time point t and channel n with scalars y_n(t), the column vectors of the observation matrix as $y_n\in {ℝ}^T$ and its row vectors as $y(t)\in {ℝ}^N$. $G\in {ℝ}^{T\times M}$ is called the design matrix that incorporates a priori knowledge about the expected shape of the evoked hemodynamic response, time structure of the experiment and regressors for drifts and/or physiological nuisance signals. $\beta \in {ℝ}^{M\times N}$ is the set of coefficients/weights for the M functional and cofounding components that are to be estimated, and $E\in {ℝ}^{T\times M}$ is the residual. Under the GLM assumption and for all time points t, the observed hemodynamic signal y_n(t) in each of the N channels is given by a combination of functional, physiological, and drift signals as well as a residual as follows:

$$y_n(t)=y_n^{\mathit{\text{functional}}}(t)+y_n^{\mathit{\text{physiology}}}(t)+{\mathit{\text{drift}}}_n(t)+{\epsilon }_n.$$ [2]

The evoked hemodynamic signal $y_n^{\mathit{\text{functional}}}$ is typically reconstructed either with

A) K gamma-variant functions Γ(t) (Abdelnour and Huppert, 2009) or B) with a weighted set of temporal basis functions b_i(t made from a linear combination of H normalized Gaussian functions b_i = N (Δt · h,σ), with a standard deviation σ and means separated by Δt, both typically on the order of 0.5s:

$$\mathit{\text{hrf}}(t)=\sum _{h=1}^H{b}_i(t-\Delta t\cdot h){\beta }_h$$ [3]

hrf (t) is then repeated at each stimulus onset δ_k

$$y_n^{\mathit{\text{functional}}}(t)=\sum _{k=0}^K\mathit{\text{hrf}}\left(t-{\delta }_k\right).$$ [4]

The current state of the art fNIRS GLM approach uses short-separation (SS) fNIRS channels as regressors to model $y_n^{\mathit{\text{functional}}}$ and 3^rd order polynomials to model drift_n. All regressors are then combined to form the design Matrix G and the GLM Equation [1] is solved for each regressor’s contribution, the coefficients $\widehat{\beta }$, in a least squares approach:

$$\widehat{\mathit{\beta }}={\left({\mathit{G}}^{\top }\mathit{G}\right)}^{-1}{\mathit{G}}^{\top }\mathit{Y}$$ [5]

2.1.2. Canonical Correlation Analysis with temporal embedding

Canonical Correlation Analysis (CCA) is a generative linear mixing model based method for finding co-modulating components in multivariate data (Anderson, 1958; Hotelling, 1936). Please see Appendix B for a brief formal introduction and a formulation of the CCA objective function. If the correlation between two modalities y and z that are to be investigated with CCA is not instantaneous, optimal extraction filters w depend on a — usually unknown — time lag τ. One solution is to temporally embed one modality with a given set of D time lags {τ₀, …, τ_D}, thus optimizing time-lag-dependent projections

$$\underset{{\mathit{w}}_y,{\mathit{w}}_z(\tau )}{\text{max}}\mathit{\text{Corr\hspace{0.17em}}}\left(\sum _i^D\mathit{y}(t){\mathit{w}}_y,\mathit{z}(t-\tau ){\mathit{w}}_z\left({\tau }_i\right)\right).$$ [6]

This method has been applied to medical imaging in various forms, for instance with temporal kernel CCA (tkCCA) for multimodal fMRI analysis (Bießmann et al., 2010) or in our previous work to identify movement-induced physiological artifacts in the fNIRS signal (von Lühmann et al., 2019).

2.2. Proposed method using tCCA

In the conventional GLM, the physiological nuisance regressors in Equation [2] are constructed using J_SS weighted short-separation fNIRS measurements $\left(y_j^{SS}(t)\right)$, and are expressed as

$$y_n^{\mathit{\text{physiology}}}(t)=\sum _j^{J_{SS}}{\beta }_{n,j}^{SS}{y}_j^{SS}(t).$$ [7]

We propose the extension of the current GLM by using latent components found by temporally embedded Canonical Correlation Analysis (tCCA) instead, and to model the physiological nuisance regressors as

$$y_n^{\mathit{\text{physiology}}}(t)=\sum _j^{J_{\mathit{\text{CCA}}}}{\beta }_{n,j}^{CCA}{\widehat{s}}_j^{CCA}(t).$$ [8]

Here, ${\widehat{s}}_j^{\mathit{\text{CCA}}}$ are latent components in the auxiliary signals found by tCCA. J_CCA observed auxiliary signals are concatenated into the observation matrix $Z\in {ℝ}^{T\times J}$. By appending D time-shifted copies of Z, the original data is temporally embedded into the new observation matrix $Z_t=\left[Z_{{\tau }_0},+Z_{{\tau }_1},\dots ,Z_{{\tau }_D}\right]\in {ℝ}^{T\times (D+1)J}$. For the time shifts τ_d = d · Δt, d ∈ {0, 1, …, D} the number of copies D and the step width Δt have to be selected. Regularized CCA is then performed between Z_t and the observed fNIRS signals Y, yielding latent components for both fNIRS $\left({\widehat{S}}_Y\right)$ and auxiliary signals $\left({\widehat{S}}_{Z_t}\right)$ that correlate maximally in CCA space. We regularize CCA by shrinking the empirical covariance matrices C_yy and C_zz in the generalized eigenvalue formulation of the CCA objective function (see Equation [B.2] in Appendix B) as follows:

$${\mathit{C}}_{**}^{\mathit{\text{shr}}}\left({\lambda }_{*}\right)=\left(1-{\lambda }_{*}\right){\mathit{C}}_{**}+{\lambda }_{*}{\nu }_{*}\mathit{I}.$$ [9]

Here λ_* ∈ [0, 1] is the shrinking hyper parameter, and ν_* is the average eigenvalue of C_**. We identify the optimal shrinkage parameter analytically, as was shown in (Blankertz et al., 2011; Ledoit and Wolf, 2004).

Finally, the subset of the resultant latent auxiliary components whose canonical correlation with latent fNIRS components exceeds a predetermined correlation threshold ρ_thesh (denoted as ${\check{S}}_{Z_t}\subseteq {\widehat{S}}_{Z_t}$) are used as physiological nuisance regressors in the GLM.

The approach is summarized in Fig. 1. The GLM with tCCA enables the integration and exploitation of any type and number of available physiological auxiliary signals, such as short-separation (SS) fNIRS, blood pressure (BP), respiration (RESP), photo plethysmography (PPG) and movement/accelerometer (ACCEL) measurements. Temporal embedding of all available auxiliary signals helps alleviate effects due to non-instantaneous coupling. Lastly, using a correlation threshold, overfitting and computational cost can be reduced. These steps improve the fit of nuisance components in the measured fNIRS data, which consequently leads to a better Contrast to Noise Ratio.

Fig. 1.

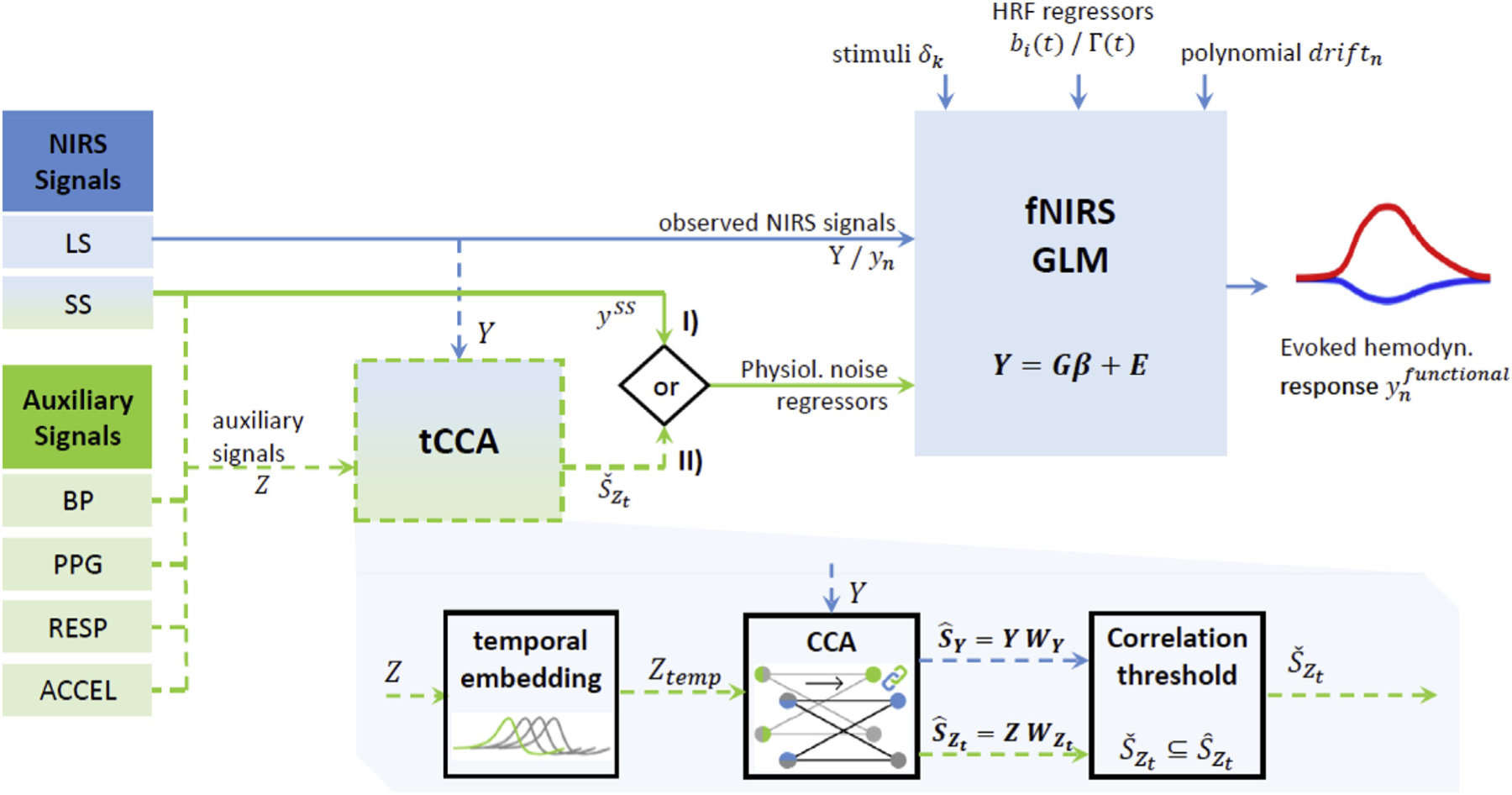
Extension of conventional GLM with SS regression (I) to GLM with tCCA (II). GLM recovers hemodynamic response function (HRF) estimates from observed Long-Separation (LS) fNIRS signals Y, using a priori knowledge of stimulus onsets and HRF and drift regressors. In the conventional GLM with SS (I), Short-Separation (SS) signals are used as physiological noise regressors to gain better HRF estimates $y_n^{\mathit{\text{funct}}}$. In the expanded GLM with tCCA, SS signals as well as other available auxiliary signals Z (BP: Blood Pressure, PPG: PhotoPlethysmogram, RESP: Respiration, ACCEL: Accelerometer) are exploited using temporally embedded Canonical Correlation Analysis (tCCA). Applying tCCA and a correlation threshold ρ_thesh yields physiological nuisance regressors ${\check{S}}_{Z\text{t}}$ in the tCCA source space that are superior to the standard SS approach. This improves contrast to noise ratio of the recovered HRF.

2.3. Parameter selection and performance evaluation

In order to obtain the optimal parameters (step size Δt, maximum time lag τ_D and correlation threshold ρ_thesh) for the proposed GLM with tCCA approach, we investigate the performance of the method with each possible combination in a predefined parameter space. Using each set, we recover HRFs from fNIRS resting data augmented with synthetic HRFs. We define an optimum parameter set that results in low root-mean square error (RMSE), high correlation (Corr) and high F-score (see Equation [14] in the following section). After obtaining the optimum parameter set, we evaluate the performance of the new method by comparing it with the traditional GLM with SS in terms of (1) the noise removal in the power spectrum; (2) RMSE, Corr and F-score obtained for the estimated HRF from the synthetic-HRF-added data; and 3) the statistical significance of the brain activation in response to a visual stimulus paradigm. Lastly, we investigate the contribution of different combinations of auxiliary measurements to the optimal performance.

2.3.1. Synthetic HRF

We generate synthetic HRFs with three different amplitudes for our simulations using a gamma function with a time-to-peak of 6 s and a total HRF duration of 16.5 s resulting in signal changes documented in Table 1. “HRF 100” is obtained by introducing a signal change of +1% and −2% in the raw signal at 690 nm and 830 nm respectively. “HRF50” and “HRF 20” correspond to 50% and 20% of a change in “HRF 100”. For each participant in our dataset (see Section 2.4), 5 min of resting state fNIRS data is divided into two halves (folds) for training and testing in a two-fold cross-validation approach (see following Section 2.3.3). The synthetic HRF is convolved with an onset vector with random inter-stimulus interval between 0 and 3.5 s and is then added onto a randomly selected half of the channels in the testing fold of the resting data, creating 6 to 8 trials.

Table 1.

Parameter for synthetic HRF.

	Change from Baseline		HRF peak Amplitude
	690 nm	830 nm	HbO	HbR
HRF 100	+1%	−2%	0.66 μMol	−0.23 μMol
HRF 50	+0.5%	−1%	0.33 μMol	−0.11 μMol
HRF 20	+0.2%	−0.4%	0.13 μMol	−0.05 μMol

2.3.2. Metrics

We used the following metrics to evaluate the performance of the GLM with tCCA over the conventional GLM with SS:

1. The root mean squared error (RMSE) between the estimated $(\widehat{\mathit{\text{HRF}}})$ and true HRF (HRF) time series across the activation time window of length T is calculated as

   $$\mathit{\text{RMSE}}=\sqrt{\frac{1}{T}\sum _{t=1}^T{(\mathit{\text{HRF}}[t]-\widehat{\mathit{\text{HRF}}}[t])}^2}.$$ [10]

2. The Pearson’s Correlation Coefficient between the estimated $(\widehat{\mathit{\text{HRF}}})$ and true HRF (HRF) is obtained over the window spanned by T by using the “corr” function in MATLAB (MathWorks Inc., Natick, MA).

3. F-score is calculated as

   $$\mathit{\text{F-Score}}=2\times \frac{\mathit{\text{Precison\hspace{0.17em}}}\times \mathit{\text{\hspace{0.17em}Recall}}}{\mathit{\text{Precision\hspace{0.17em}}}+\mathit{\text{\hspace{0.17em}Recall}}}\text{\hspace{0.17em}\hspace{0.17em}with}$$ [11]

   $$\mathit{\text{Precision}}=\frac{TP}{TP+FP}\mathit{\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and}}$$ [12]

   $$\mathit{\text{Recall}}=\frac{TP}{TP+FN},$$ [13]

   where TP, FP and FN are true positives, false positives and false negatives respectively. In order to determine whether a given channel is a TP, FP, TN, or FN, a paired t-test was performed to evaluate statistically significant differences in hemodynamic response during baseline (from 2 s prior to onset of the stimulus until the onset of the stimulus) and during the HRF peak activation (from 5 s to 10 s after the onset of the stimulus) (p-value threshold set to 0.05). For instance, when a synthetic-HRF-added channel shows a significant change from baseline, it is considered as TP (see Fig. 2B). Fig. 2A shows a demonstrative example of the RMSE and correlation of HRFs recovered with both GLM methods.

Fig. 2.

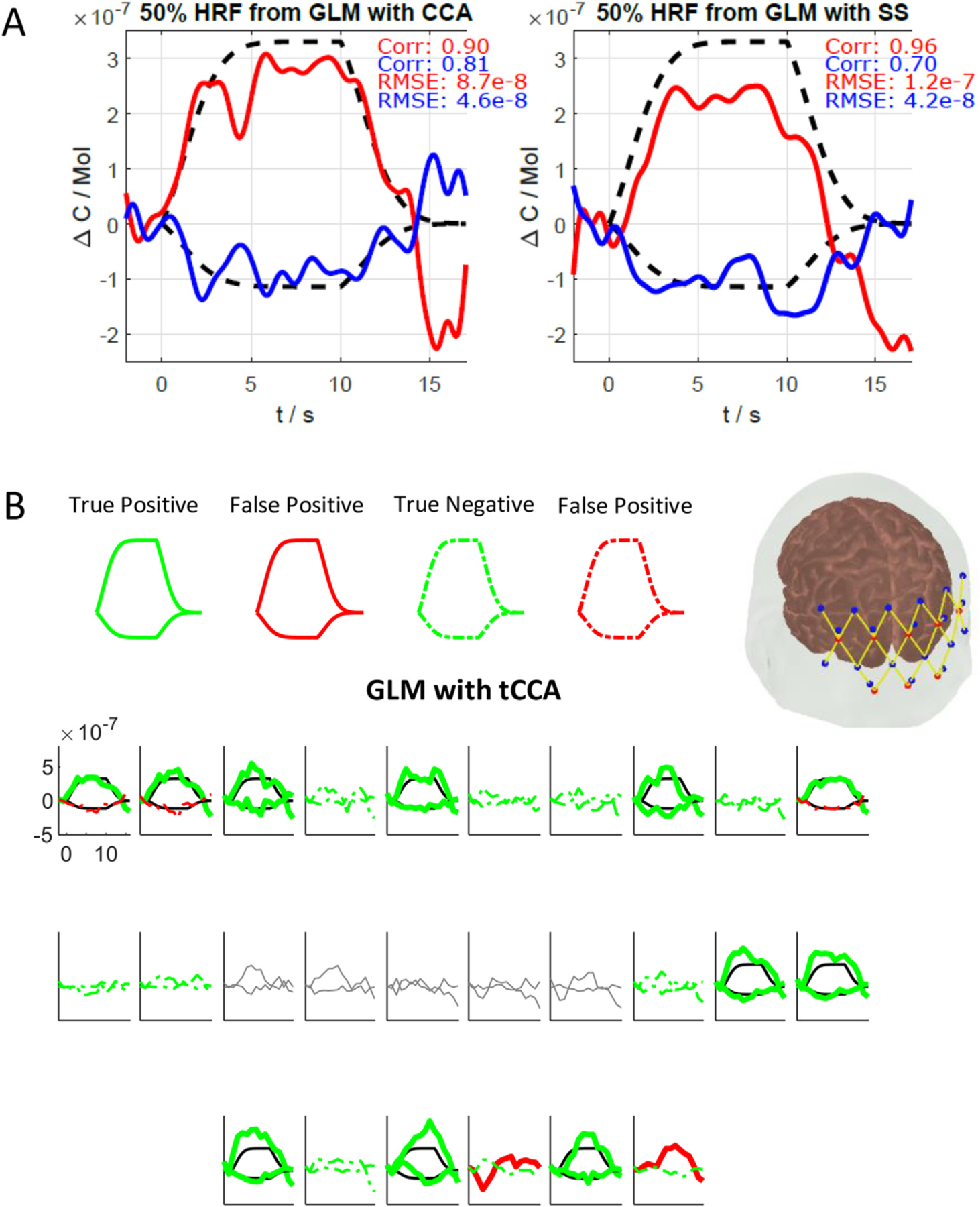
(A) Single channel across trial average HRF example from subject 4, Ch34 (HbO: red, HbR: blue) and ground truth (black dashed). Left: new tCCA GLM, right: conventional SS GLM. (B) Estimated HRF and corresponding statistics obtained using GLM with tCCA. The channels that are true positive (bold) and true negative (dashed) are shown in green. Channels that are false positive (bold) and false negative (dashed) are shown in red. The true HRF (black lines) and pruned channels (grey lines) are also shown.

2.3.3. Parameter selection and evaluation pipeline

Three parameters have to be selected for the extended GLM with tCCA. The temporal embedding of the auxiliary signals depends on the step (=shift) size Δt and the maximum absolute time lag τ_D or the maximum number of shifts D. After the tCCA step, the correlation threshold parameter ρ_thesh determines the subset of all available physiological regressors that are used as input to the GLM. The choice of these three parameters affects how well the regressors fit the confounding signals within the measured fNIRS signals – and therefore affect the performance and generalization of the overall method. The optimal parameter set depends on the characteristics of the dataset to be analyzed, and can be individually identified in an offline analysis. A priori knowledge can be used to narrow down the available parameters to physiologically reasonable ranges. The aim of this section is to provide guidance for the parameter selection by identifying generally robust regions in parameter space, and to use a single identified optimal set to compare the performance of the proposed approach with that of the current gold standard. To do so, we perform GLM based HRF recovery with the established HOMER2 fNIRS data analysis package (Huppert et al., 2009) in a two-fold cross validation scheme, using ground truth data from 2.3.1.

In the following section, we describe the corresponding analysis pipeline for parameter selection and performance evaluation, also summarized in Fig. 3. In a first step, noisy fNIRS channels are identified and removed using the HOMER2 function hmrPruneChannels (dRange = 10⁴–10⁷ (corresponding to 80 and 140 dB for a TechEn System), SNRthresh = 5). Auxiliary and fNIRS data are downsampled and interpolated to the same time base, resulting in a sample rate of 25 Hz for all signals. Both sets of data are then split into two halves (folds) of 150s each. Each half is subsequently used once for training and once for testing during the two-fold cross validation. All fNIRS data is then converted into optical densities and motion artifacts are identified and the corresponding trials are rejected using the HOMER2 function hmrMotionArtifact (tMotion = 0.5, tMask = 1, STDEVthresh = 30, AMPthresh = 5). Both fNIRS and auxiliary data are zero-phase low pass filtered to 0.5 Hz. fNIRS optical densities are then converted to concentration changes with the modified Beer-Lambert law with a partial pathlength factor of 6 (Boas et al., 2004; Delpy et al., 1988), and auxiliary signals are z-scored. Using the training data, regularized CCA is performed between fNIRS signals Y and the temporally embedded auxiliary signals Z_t. The resulting CCA filter matrix $W_{Z_t}$ is then used to project the temporally embedded auxiliary test data into CCA space. The projected auxiliary signals in ${\widehat{S}}_{Z_t}$ whose canonical correlation with their corresponding fNIRS counterparts ${\widehat{S}}_Y$ does not exceed the threshold ρ_thesh, are discarded. All others are subsequently used as physiological regressor inputs to the GLM (Fig. 3A). In the standard SS approach, short-separation fNIRS signals are used as regressors instead (Fig. 3B). We assumed that the signal changes at the two short-separation channels in our design are representative of the systemic changes in scalp over the visual cortex covered by our probe. GLM-based HRF deconvolution is performed using the HOMER2 function hmrDeconvHRF_DriftSS, with Gaussian HRF basis functions (Equation [3]) and a 3^rd order polynomial drift regression (trange = [−2 17], glmSolveMethod = 1, idx-Basis = 1, paramsBasis = [0.5 0.5], rhoSD_ssThresh = 0 (for GLM with tCCA) and 15 (for GLM with SS), flagSSmethod = 0 (for GLM with tCCA) and 1 (for GLM with SS), driftOrder = 3, flagMotionCorrect = 0). For each channel and chromophore (HbO and HbR), using the estimated HRFs by the GLM and the ground truth HRF, evaluation metrics (MSE, Correlation and F-Score) are then calculated 1) for each single trial and are then averaged, and 2) for the average HRF across all trials.

Fig. 3.

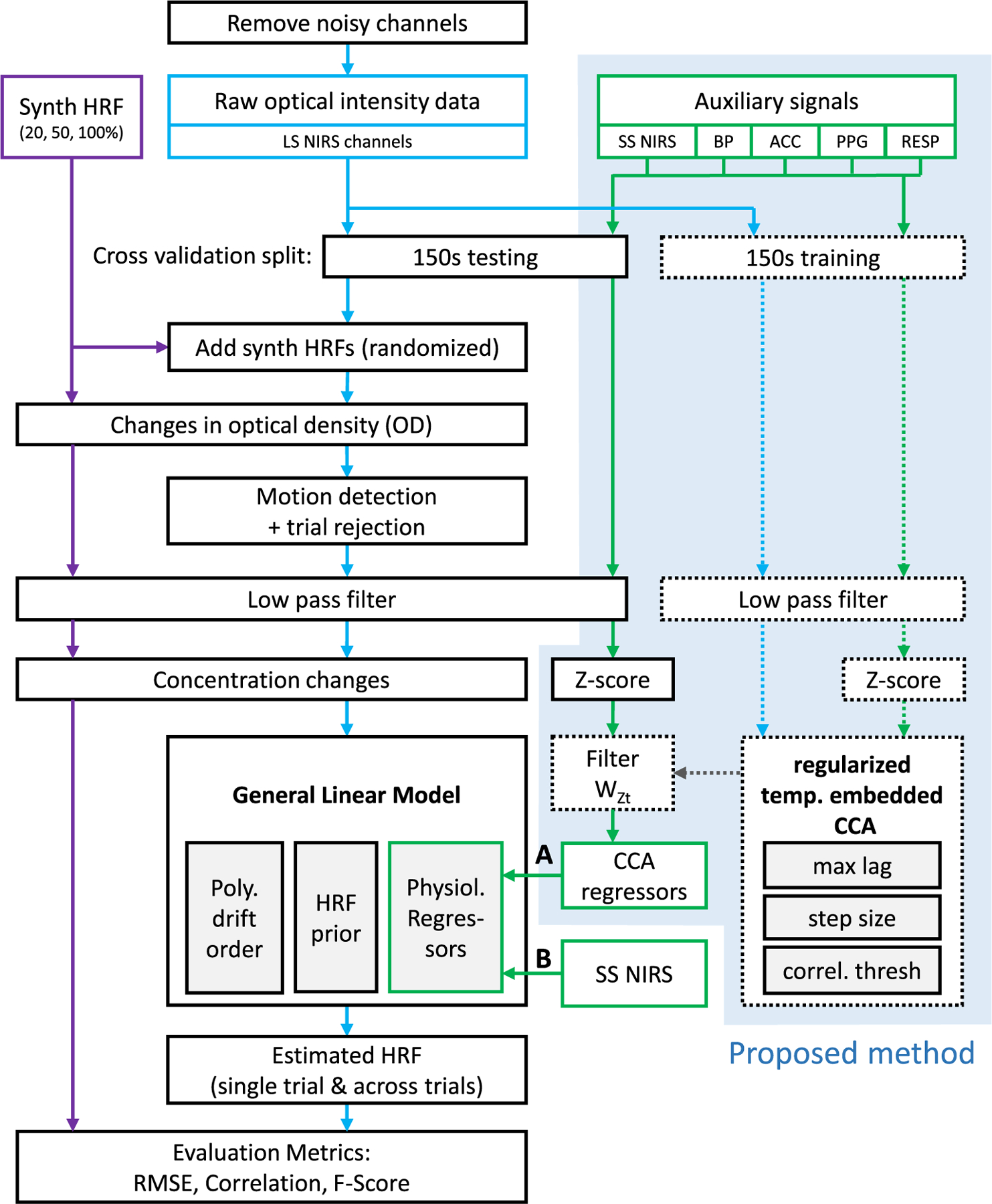
Diagram of evaluation pipeline. Blue: fNIRS signals. Green: Auxiliary signals. Solid lines: testing data. Dashed lines: training data. Blue box: proposed method (A). We use temporally embedded CCA with a variety of auxiliary signals to provide physiological nuisance regressors for the GLM. (B) state of the art approach using short-separation NIRS signals only. HRF: Hemodynamic Response Function, SS: Short Separation, LS: Long Separation, BP: Blood Pressure, ACC: Acceleration, PPG: Photo plethysmography, RESP: Respiration. Please note that SS NIRS signals fed into GLM with SS and with tCCA were previously converted to concentration changes analogous to LS NIRS channels.

We perform this evaluation for three different simulated HRF levels (20, 50 and 100%, see Section 2.3.1) and for each of the 1320 possible points {Δt, τ_D, ρ_trsh} in the parameter space, which is spanned by step length Δt ∈ {0.08s, 0.16, …0.96s}, overall maximum lag τ_D ∈ {0s, 1s, …10s} and correlation threshold ρ_thesh ∈ {0, 0.1, …0.9}. These ranges were chosen under the following restrictions and assumptions about the non-instantaneous coupling between auxiliary signals and fNIRS signals: 1) causality: the former precede the latter (time embedding by delaying auxiliary signals), 2) coupling delays are limited to 10 s, 3) the smallest feasible step length is limited by the instrument’s sample rate, which is typically not higher than 25 Hz.

For each performance metric, chromophore, and point in parameter space, the results are averaged across all participants, folds and channels (F-Score: n = 14×2 = 28, RMSE/Corr: n = 14×2×13 = 364). To identify the optimal parameter set for a given HRF amplitude h ∈ {20, 50, 100%} and recovery approach r ∈ {single trial, across trials}, the average values for each performance metric and chromophore are then min-max normalized across all points in parameter space. This way we ensure an equal contribution of each metric in the objective function J_h,r, which we define as follows:

$$J_{h,r}\left(\Delta t,{\tau }_D,{\rho }_{\mathit{\text{trsh}}}\right)={\widehat{\mathit{\text{RMSE}}}}_{\mathit{\text{HbO}}}+{\widehat{\mathit{\text{RMSE}}}}_{\mathit{\text{HbR}}}-{\widehat{\rho }}_{\mathit{\text{HbO}}}-{\widehat{\rho }}_{\mathit{\text{HbR}}}-{\widehat{F}}_{\mathit{\text{HbO}}}-{\widehat{F}}_{\mathit{\text{HbR}}}$$ [14]

For a globally optimal parameter set across all conditions (h, r), we define the global objective function as the overall sum of all objective functions: ∑J_h,r.

2.3.4. Contribution of auxiliary signals

The proposed tCCA GLM extension exploits all provided auxiliary signals. In our dataset, these are short-separation fNIRS channels (SS), respiration (RESP), blood pressure (BP), photo plethysmography (PPG) and accelerometer (ACCEL). While the use of multiple auxiliary physiological signals is advantageous, it will not always be feasible to acquire them all – and for prioritization, it would be desirable to know the contribution of each to the overall achievable performance. Therefore, the previous analysis pipeline is repeated as before, but with the provided auxiliary signals limited to 1) a single auxiliary modality (e.g. only SS fNIRS) and 2) all possible combinations of two modalities (e.g. SS fNIRS and ACCEL; ACCEL and PPG and so on). We perform the analysis for the identified optimal parameter set. For all performance metrics and chromophores, we investigate the percent difference between the best achievable result using all modalities, and the result using only single/dual auxiliary modalities. We also investigate the performance difference between GLM with tCCA and GLM with SS under the exact same conditions, when both methods are provided only with SS signals.

2.3.5. Performance evaluation

The optimal parameter set for the GLM with tCCA was identified as {step size Δt = 0.08s, absolute timelag τ_D = 3s, and correlation threshold ρ_thresh = 0.3} (see Fig. 6) by optimizing the performance metric from Equation [14]. This set is used for the following evaluation.

1. Comparison of noise floor reduction: We obtain the power spectrum of the raw, unfiltered 50 Hz intensity signal at each channel, after applying GLM with tCCA and GLM with SS, using the pwelch function in MATLAB (Mathworks, Natick, MA) with a 100-s rectangular windowing of the data and 50% overlap of successive segments. The mean power at each channel is calculated for four different frequency bands: (1) low frequency oscillations (0.01–0.1 Hz), (2) respiration (0.1–0.5 Hz), (3) cardiac (0.5–1.5 Hz) and (4) cardiac harmonics (1.5–10 Hz). Both methods are then statistically compared in terms of their reduction of spectral noise power in each band.

2. Comparison of HRF recovery performance using the simulated data: Synthetic HRFs are added to resting state fNIRS data and recovered using GLM with tCCA and GLM with SS using the cross validation approach explained in the previous Section 2.3.3. The efficiency of the two methods is compared using MSE, Corr and F-score.

3. Comparison of HRF recovery performance using visual stimulation data: We estimate hemodynamic responses evoked by a real visual stimulation task applying GLM with tCCA and GLM with SS. The methods are compared in terms of the number of channels with evoked responses significantly different than baseline i.e. “activated channels”, as determined conventionally by a t-test between peak activation and baseline periods, and the significance of activation (p-value).

Fig. 6.

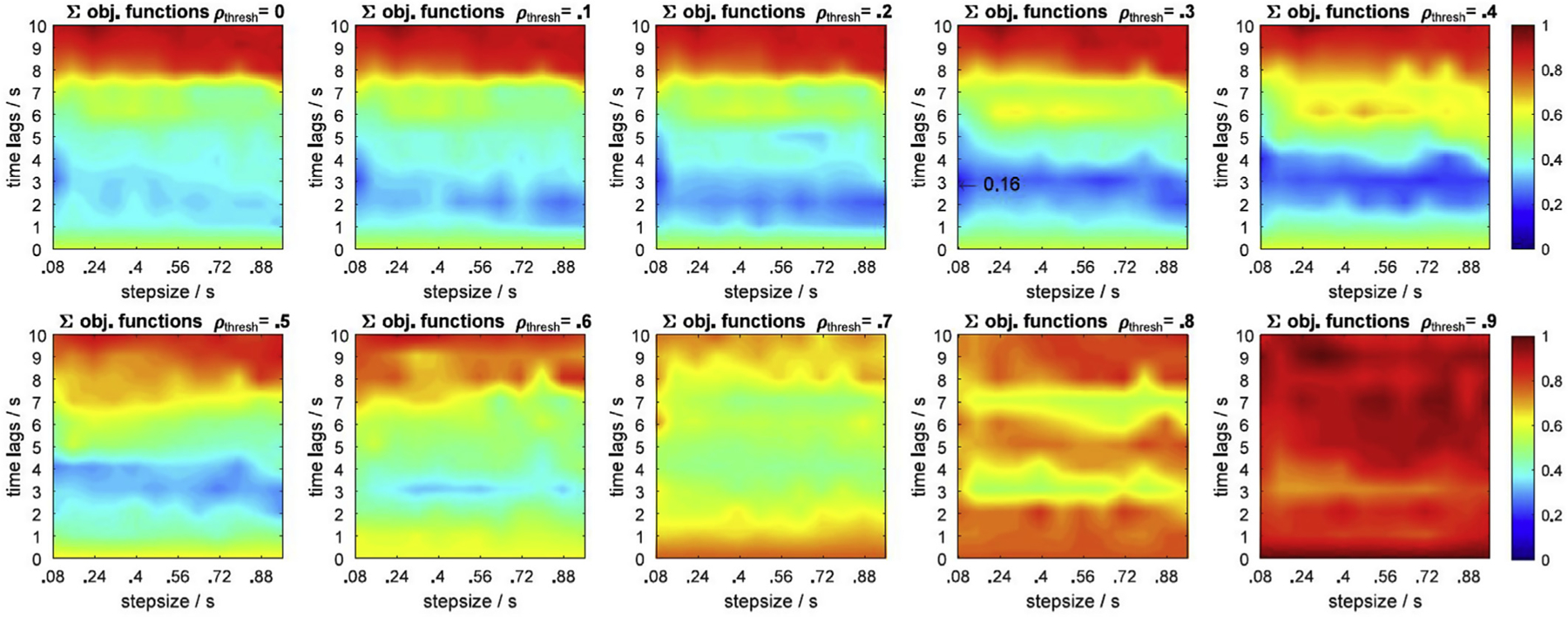
Sum over all objective functions for HRF = 20, 50, 100% and single trial and across trial HRF recovery. ρ_thresh: correlation threshold. Blue regions indicate the smallest (optimal) value of the global objective function. Arrow: global optimum across all parameter dimensions, metrics, chromophores, HRF amplitudes and recovery approaches. Optimal parameter set is step size 0.08s, time lag 3s, and correlation threshold 0.3.

2.4. Experiment and dataset

2.4.1. Participants

Fourteen healthy subjects were recruited for this study (age: 21 ± 2 years; 11 male/3 female). The study was approved by and carried out in accordance with the regulations of the Institutional Review Board of Boston University. Each subject provided a signed written informed consent form prior to the experiment. Subjects had no neurological or psychological disorders. Ten subjects were right-handed and four were left-handed.

2.4.2. Experimental paradigm

During the experiment, subjects were seated in a comfortable chair. Signal quality was checked for all devices. After a 5-min resting state recording, a visual stimulus was presented on a 23” monitor with 60 Hz refresh rate using Psychtoolbox, a MATLAB toolbox for generating visual and auditory stimuli for neuroscience experiments (Brainard, 1997; Kleiner et al., 2007) (MathWorks, Natick, MA). Each run started with a 14s baseline (grey screen) followed by a 10s duration counter-phase radial visual checkerboard with a 12 Hz inversion rate, interleaved by a rest period of 5–10 s of grey screen (Fig. 4). The number of trials was 24 for the first five subjects (total duration: ~470s) and 10 for the remaining subjects (total duration: ~230s). A red dot appeared in the center of the monitor during the rest as well as visual stimulus periods.

Fig. 4.

Visual paradigm: The visual task consisted of a counter-phase radial visual checkerboard with a 12 Hz inversion rate, interleaved by resting periods with a grey screen.

To follow the performance of the subjects, the brightness of the dot was randomly varied and the subjects were asked to press a button whenever there was a change in its brightness.

2.4.3. fNIRS system and probe

fNIRS data were acquired using a CW6 fNIRS system (TechEn Inc. MA, USA) operating at 690 and 830 nm wavelengths. The system is a multichannel continuous wave optical imager with 32 frequency-encoded lasers (half at 690 and half at 830 nm) and 32 avalanche photo-diode detectors. The light is carried from the CW system to the head probe and back via optical fiber bundles. The head probe was designed utilizing AtlasViewer software (Aasted et al., 2015) and consisted of an elastic cap (EasyCap, Herrsching, Germany) with 8 sources and 12 long-separation detectors (~3 cm apart from the source). Two of the eight sources have a short-separation detector ~1 cm apart from the source location. In total, our probe configuration consisted of 26 long-separation and 2 short-separation channels covering the occipital lobe (Fig. 5). The spatial sensitivity map in Fig. 5 right panel represents the sensitivity of the probe to cortical absorption changes and is obtained by Monte Carlo simulations of photon migration in tissue as described in detail by Aasted et al. (2015). fNIRS data was acquired with a sample rate of 50 Hz.

Fig. 5.

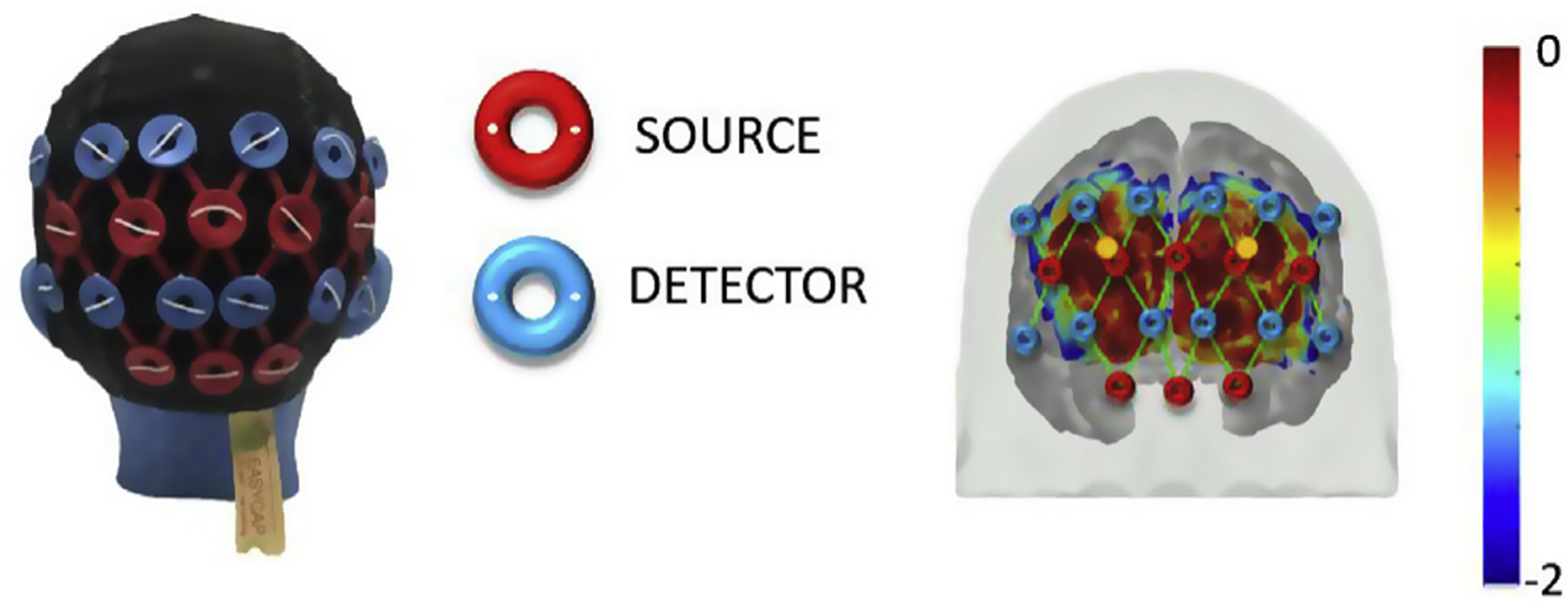
fNIRS head probe over occipital region: head cap with sources (red) and detectors (blue) is shown on the left; sensitivity profile of the probe is shown on the right. The long-separation channels (green lines) and the location of short-separation detectors (circles in gold) are displayed on the brain map. The color scale spans the sensitivity logarithmically.

2.4.4. Auxiliary recordings

Systemic physiological changes and head motions of the subjects were simultaneously recorded along with the fNIRS data. An MP160 data acquisition and analysis system was used to record auxiliary physiological changes (BIOPAC Systems Inc., Goleta, CA). The pulse waveform was recorded using a PPG100C amplifier and TSD200 Photo Plethysmogram (PPG) pulse transducer placed on the subject’s right index finger (BIOPAC Systems Inc., Goleta, CA). Respiration data was collected via measuring the abdominal (or thoracic) expansion and contraction using a RSP100C amplifier and a TSD201 respiration transducer (respiration belt) (BIOPAC Systems Inc., Goleta, CA) around the subject’s chest. The blood pressure waveform was recorded using a DA100C amplifier and a TSD110 pressure transducer (BIOPAC Systems Inc., Goleta, CA) placed on the subject’s right thumb. Head motions in x, y, z directions were collected using an accelerometer (ADXL335, Analog Devices Inc., Norwood, MA) secured on the head with a headband. Respiration, blood pressure waveform, PPG and accelerometer data were simultaneously acquired at 50 Hz throughout the experiment.

3. Results

In this section, we initially report the results from the investigation of the optimum parameter set and the minimum required auxiliary signal set for the best performance of the proposed method. Subsequently, we present the results of the performance comparison between the standard best practice GLM with SS and the proposed GLM with tCCA with respect to 1) noise reduction in the power spectrum, 2) HRF recovery using simulated data and 3) HRF recovery using real data from the visual stimulation experiment. All significance tests are paired t-tests.

3.1. Parameter selection

The optimum parameter set for the best performance of GLM with tCCA was determined using the defined objective function J that optimizes Corr, RMSE and F-Score (Equation [14]). Performance depends on the parameters step size Δt, time lag τ_D, and correlation threshold ρ_thresh, as well as on the Contrast to Noise Ratio (CNR) which is modulated by the amplitude of the synthetic HRF (20, 50, 100%), and the recovery approach (single trial and across trials). Fig. 6 provides a summary of the main result: It shows the sum of all objective functions across HRF levels and recovery approaches in all three parameter dimensions. Generally, optimal regions, indicated in blue in the plots, are Δt ≥ 0.08s, 1.5s ≤ τ_D ≤ 4s, and ρ_thresh ≤ 0.5. The global optimum is at Δt = 0.08s, τ_D = 3s, and ρ_thresh = 0.3. Optimality starts decaying beyond a correlation threshold of 0.5 and for long time lags τ_D ≥ 7s.

More details on each performance metric in 2D parameter space at the identified globally optimal parameter set are provided in Appendix C for the different CNRs (varying HRF amplitudes) in single trial recovery (Fig. C.1) and across trial recovery (Fig. C.2). The observable general trends can be summarized as follows: For Corr and RMSE and both chromophores, optimal parameter regions are similar. When CNR is low, as in the single trial HRF recovery case, very short and very long overall time lags are less optimal. For higher CNR, in the across trial HRF recovery case, this trend is more distinct for long overall time lags and less distinct for short overall time lags. As CNR increases, the location of optimal regions determined by the F-Score become more similar to those regions determined by the Corr and RMSE for both chromophores.

3.2. Contribution of auxiliary signals

Fig. 7 shows the result from the comparative investigation of HRF recovery performance metrics when the GLM with tCCA was provided one, two or all auxiliary signal types. Here we show results for the 50% single trial HRF as a representative example. The optimal performance (max Corr and F-Score, min RMSE) is achieved when all auxiliary signals are provided to the model. When only one auxiliary modality is available, short-separation (SS) fNIRS channels provide the most valuable information for regression, with a max performance decrease of 11% in correlation and 14% in F-Score, and a 19% RMSE increase when compared to the achievable optimum using all auxiliary signal types. Notably, this performance of GLM with tCCA using only SS measurements is still significantly better than the one achieved by the standard GLM estimation with SS measurements: Corr (+13%/+5%), RMSE (−29%/−14%) and F-Score (+31%/+34%) for HbO/HbR respectively in 50% single trial HRF recovery. When only two auxiliary modalities are available for GLM with tCCA, the use of accelerometer signals as a second modality combined with any other single modality yields a significant performance increase over all other single modalities. The same observation holds when SS fNIRS is used as the second modality. Together, SS fNIRS and ACCEL yield a performance that is only 4% below the optimum that is achieved when all available auxiliary measures are used.

Fig. 7.

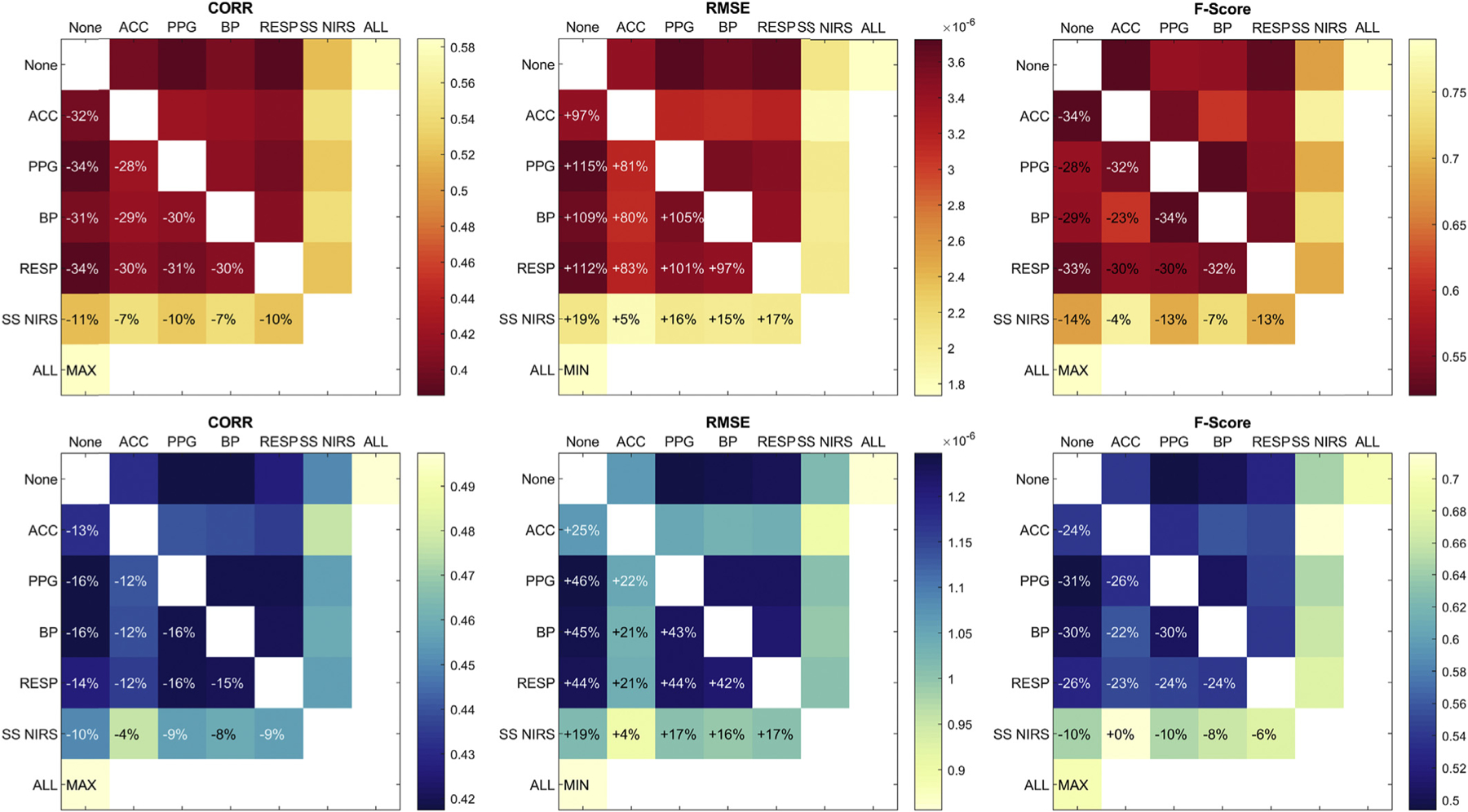
Contributions of auxiliary signals in GLM with tCCA using optimal parameter set with Δt = 0.08s, τ_D = 3s, and ρ_thresh = 0.3. None: Single modality, combination with no other, ACC: Accelerometer, PPG: Photo Plethysmogram, BP: Blood Pressure, RESP: Respiration, SS fNIRS: Short-Separation fNIRS. Red (top row): HbO, blue (bottom row): HbR. Results shown are for the 50% single trial HRF case.

3.3. Performance evaluation & comparison: GLM with tCCA vs GLM with SS

The following subsection presents the performance evaluation results from the comparison between the proposed method GLM with tCCA (using all available auxiliary signals), and the conventional GLM with SS (using SS signals), via three different approaches: Power spectral noise removal, HRF recovery from simulated data and HRF recovery from real visual stimulus data.

3.3.1. Comparison of noise floor reduction

Power spectral noise removal with GLM with tCCA using the identified optimal parameter set was compared to that of GLM with SS by getting the mean power spectrum of the raw intensity signal at each channel for four different frequency bands after the noise regression with each method. Fig. 8 left panel shows the mean power spectrum of a representative subject after the noise removal using GLM with tCCA (red line) and GLM with SS (blue line). Overall and across subjects, a higher reduction of physiological noise power by GLM with tCCA was observed. Most evident is the almost complete rejection of the cardiac peak at 1 Hz. Depending on the selected parameters, additional noise can be introduced at higher frequencies. This effect will be discussed in Section 4.

Fig. 8.

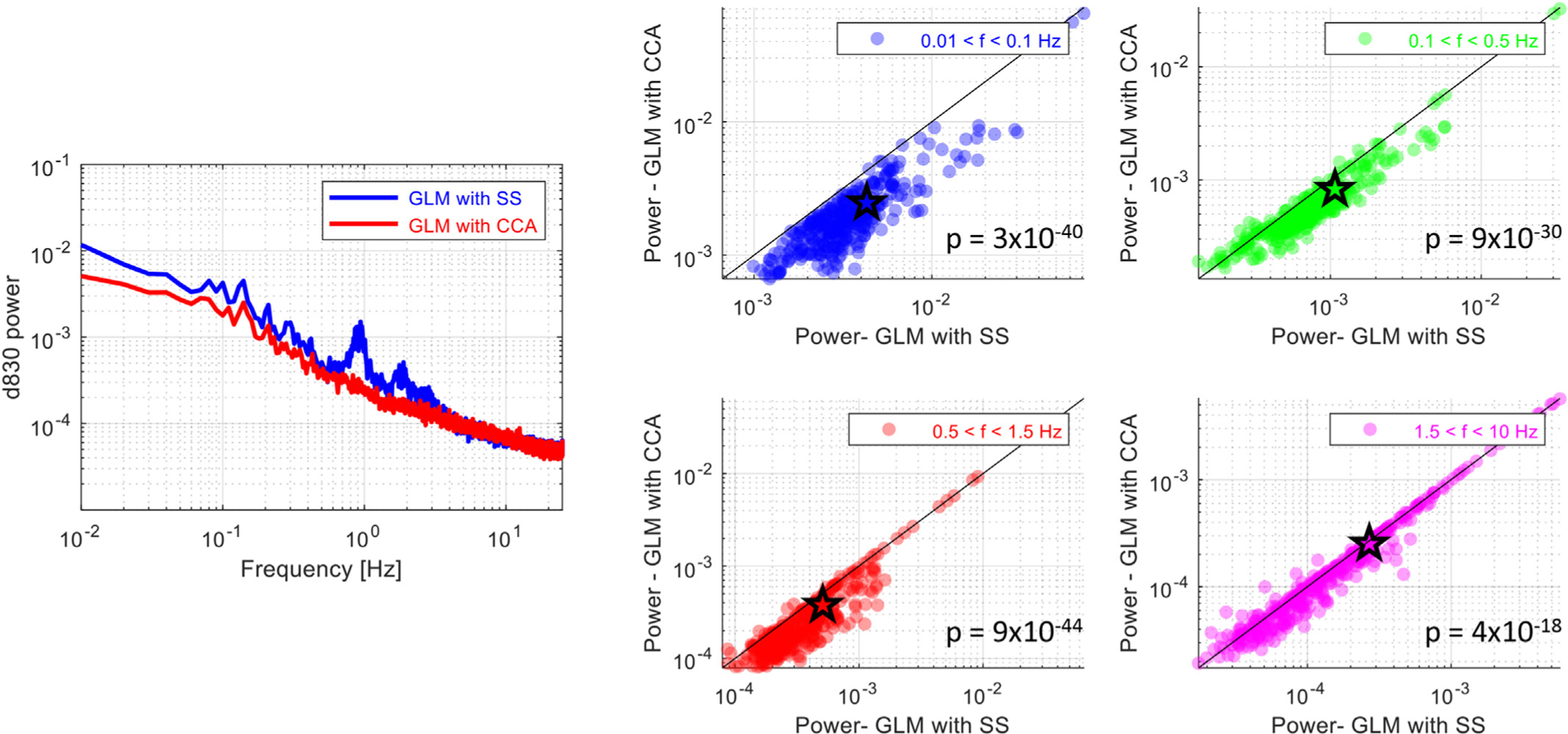
Left panel: Comparison of power spectra: The normalized power at 830 nm averaged across all long-separation channels shown for GLM with tCCA (red line) and for GLM with SS (blue line) for one subject. Parameter set used: Δt = 0.08s, τ_D = 3s, and ρ_thresh = 0.3. Right panel: Comparison of noise removal at different frequency bands: Mean power of the raw intensity (830 nm) at each channel and subject for four different frequency bands: (1) low frequency oscillations (0.01–0.1 Hz) (blue), (2) respiration (0.1–0.5 Hz) (green), (3) cardiac (0.5–1.5 Hz) (red) and (4) cardiac harmonics (1.5–10 Hz) (magenta). P-values are obtained via a statistical comparison of the mean power obtained after GLM with tCCA and GLM with SS at each channel using a paired t-test.

To quantify the difference in the noise level between the methods, the mean power of the raw intensity at each channel was obtained for four different frequency bands: low frequency oscillations (0.01–0.1 Hz), respiration (0.1–0.5 Hz), cardiac (0.5–1.5 Hz) and cardiac harmonics (1.5–10 Hz). The two methods, then, were statistically compared in terms of their rejection of noise power in each band. The scatter plots that contrast the two methods are shown for 830 nm in Fig. 8, right panel. A statistically significant reduction in both power at 830 and at 690 nm was observed at all frequency bands with GLM with tCCA (paired t-test, p ≪ 0.001).

3.3.2. Comparison of HRF recovery performance using simulated data

In this section, we summarize the results of the comparative investigation of HRF recovery performance of both methods as quantified by correlation, RMSE and F-Score using simulated ground truth data. For GLM with tCCA, the identified optimal parameter set with Δt = 0.08s, τ_D = 3s and, ρ_thresh = 0.3 was used. Fig. 9 shows representative results for 50% HRF amplitude and single trial recovery. GLM with tCCA significantly outperformed GLM with SS across all these metrics both for HbO and HbR. A corresponding typical single trial average HRF as recovered by both methods is depicted in Fig. 2 in Section 2.3.2.

Fig. 9.

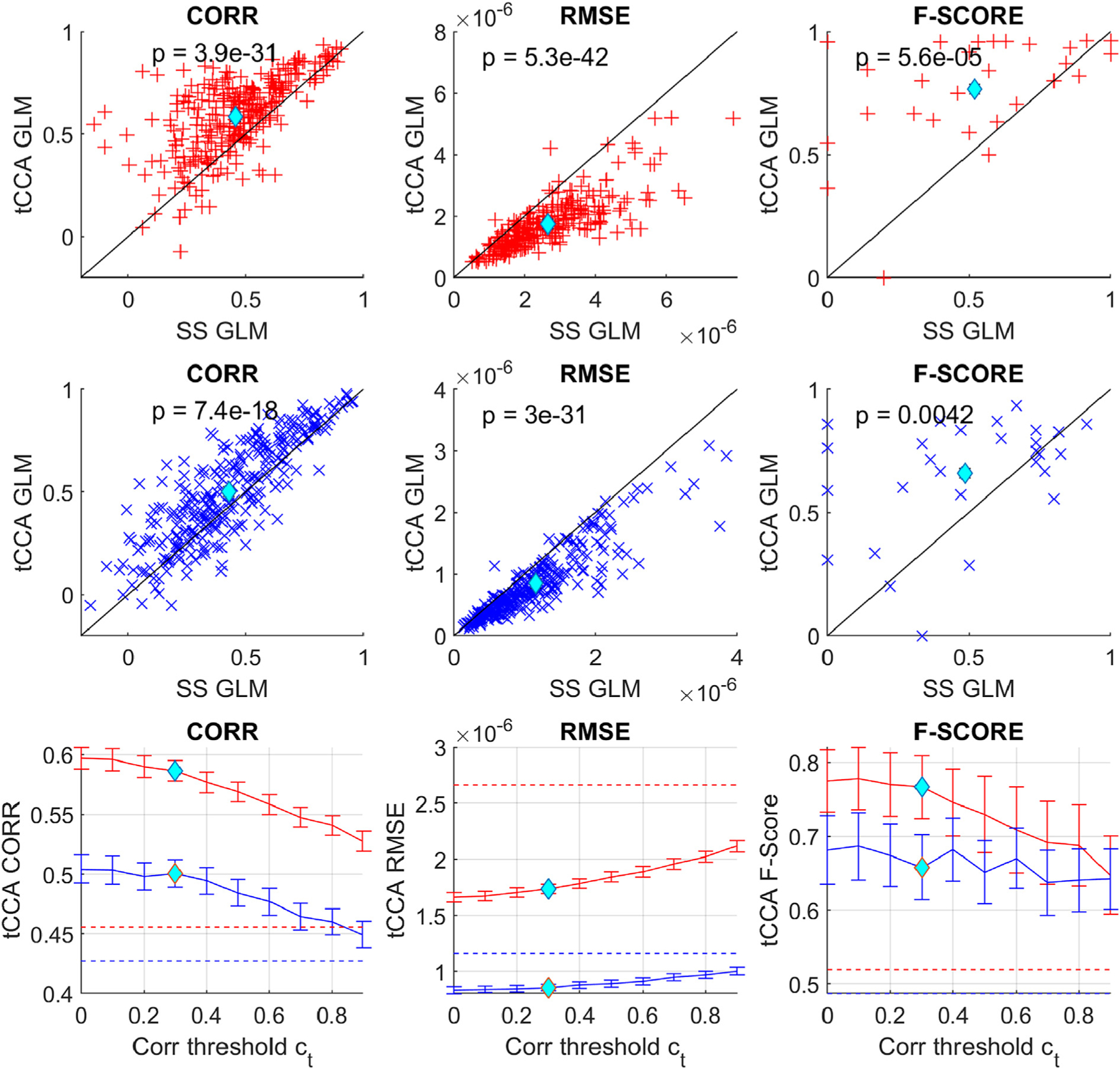
First two rows: Scatter plots comparing MSE/Corr/F-score performance metrics for GLM with SS and GLM with tCCA using 50% HRF amplitude data. Each data point marks the average result of all recovered single trial HRFs across a single channel and subject, as depicted in Fig. 2. Red: HbO, blue: HbR, cyan diamond: average. Bottom row: solid line shows grand average and standard error of all metrics for GLM with tCCA with fixed optimal time lag and time steps vs. the correlation threshold. Dotted lines are the results for the standard GLM with SS.

Table 2 summarizes all results for the different performance metrics, chromophores, HRF amplitudes and single trial / across trial recovery. GLM with tCCA outperformed GLM with SS in almost all cases. In Correlation and RMSE, improvement was highly statistically significant (p ≪ 0.001) for both chromophores in single trial recovery and for all HRF amplitude levels. When HRFs were recovered across trials, RMSE of HbO was significantly improved for all HRF amplitude levels. F-Score was significantly improved for both HbO and HbR for 20 and 50% HRF amplitudes and single and across trial recovery (p ≪ 0.001).

Table 2.

Summary of statistics for performance comparison using ground truth. GLM SS: Conventional GLM with SS regression. GLM tCCA: proposed extension with tCCA. CORR: Correlation, RMSE: Root Mean Square Error, F1: F-Score, ST: Single Trial, AT: Across Trials. Blue: statistically significant improvement offered by the GLM tCCA method.

			20% HRF			50% HRF			100% HRF
			GLM SS	GLM tCCA	t-test p =	GLM SS	GLM tCCA	t-test p =	GLM SS	GLM tCCA	t-test p =
CORR	HbO	ST	.20 ± .18	.29 ± .20	5e-15	.46 ± .20	.59 ± .18	4e-31	.71 ± .16	.81 ± .12	3e-36
		AT	.49 ± .36	.51 ± .32	0.21	.80 ± .22	.83 ± 0.15	0.07	.93 ± .10	.95 ± .06	0.14
	HbR	ST	.20 ± .19	.25 ± .22	1e-7	.43 ± .23	.50 ± .24	7e-18	.64 ± .22	.70 ± .21	2e-18
		AT	.45 ± .36	.43 ± .35	0.28	.73 ± .27	.73 ± .24	0.6	.88 ± .15	.88 ± .14	0.34
RMSE	HbO	ST	26.6 ± 1.59	17.2 ± 9.2	5e-43	26.6 ± 1.6	17.3 ± 9.2	5e-42	26.8 ± 15.9	17.8 ± 8.6	1e-39
	x1e-7	AT	1.5 ± .97	1.3 ± .85	3e-4	1.4 ± .10	1.3 ± .85	5e-3	1.5 ± 1.0	1.3 ± .80	0.13
	HbR	ST	11.6 ± .85	8.5 ± 6.3	8e-32	11.6 ± .85	8.5 ± 6.3	3e-31	11.6 ± 8.5	9.0 ± 6.3	2e-29
	x1e-7	AT	.7 ± .6	.65 ± .49	0.60	.66 ± .60	.65 ± .49	.68	.67 ± .59	.68 ± .48	0.55
F1	HbO		.12 ± .18	.39 ± .29	2e-5	.52 ± .30	.77 ± .22	6e-5	.88 ± .13	.90 ± .10	0.71
	HbR		.17 ± .21	.36 ± .24	3e-4	.48 ± .30	.66 ± .23	4e-3	.82 ± .16	.85 ± .11	0.29

The improvement of GLM with tCCA over GLM with SS in terms of RMSE and F-Score was more distinct with lower Contrast to Noise Ratio of the data, which was modulated by HRF amplitude and number of trials used for recovery. For HbO at the lowest CNR (HRF 20% single trial) the use of GLM with tCCA resulted in an increase of 45% in Corr, a decrease of 55% in RMSE and a 3.25-fold increase in F-Score.

Fig. 10 displays the average true positive rate (TPR) versus average false positive rate (FPR) across subjects and splits for the HRF recovery in HbO (red dots) and HbR (blue dots) with different synthetic HRF amplitudes (20, 50 and 100%) for each possible combination of step size Δt, time lag τ_D and correlation threshold ρ_thesh in the pre-defined parameter space that spans Δt ∈ {0.08s, 0.16, …0.96s}, τ_D ∈ {0s, 1s, … 10s} and ρ_thesh ∈ {0, 0.1, …0.9}. Also shown are average TPR and FPR at 1) the previously identified global optimal parameter (cyan diamond: Δt = 0.08s, τ_D = 3s, and ρ_thresh = 0.3), and 2) at the global optimum when additionally considering FPR in the objective function in Equation (14) (yellow diamond: Δt = 0.64s, τ_D = 2s and ρ_thresh = 0.4), and 3) for GLM with SS (green square). Note that similar to a conventional ROC-curve, the accuracy of the statistical test results increases towards the top left-hand border of the plots which gives a high TPR (sensitivity) and low FPR (1-specificity).

Fig. 10.

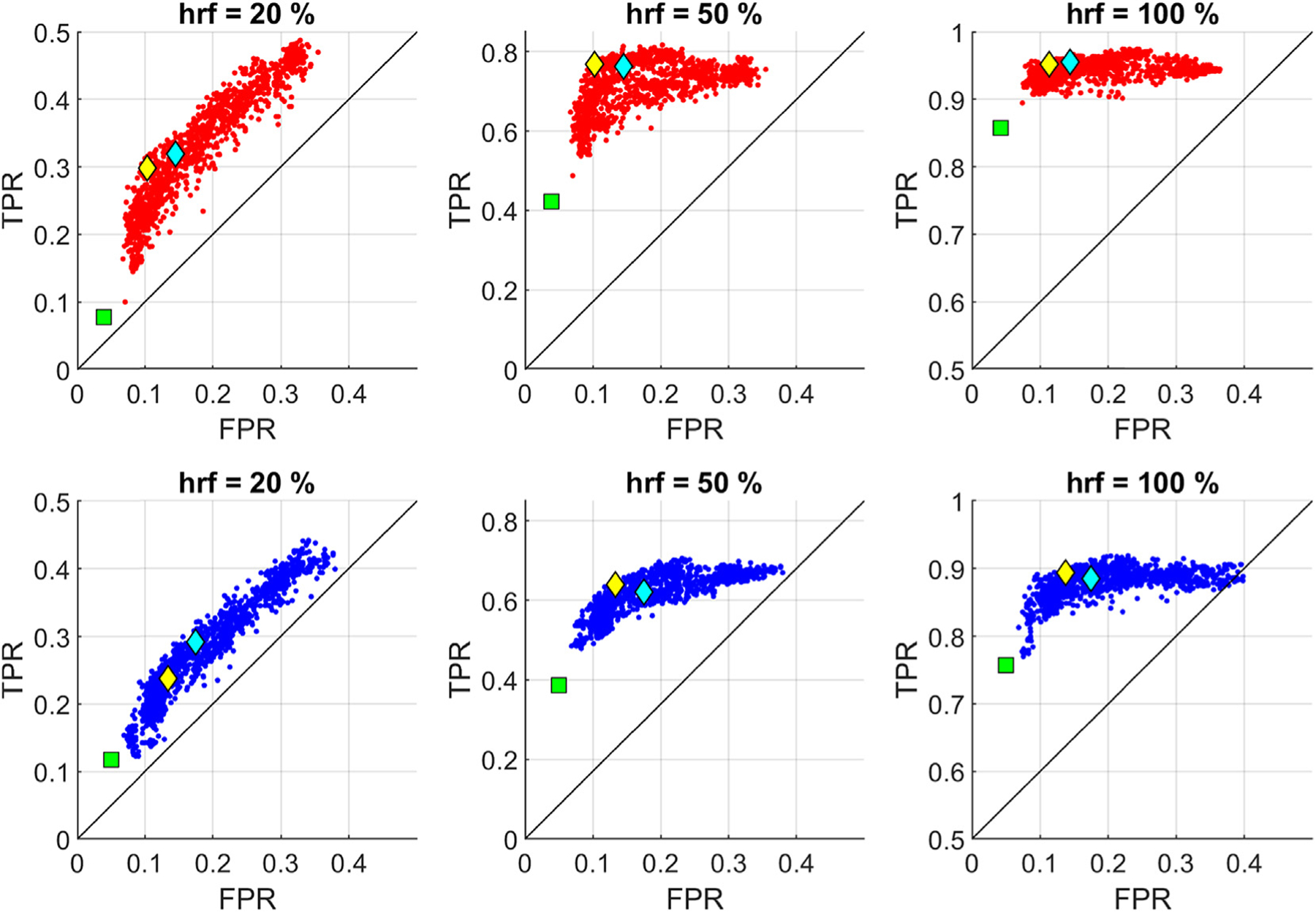
TPR versus FPR: Each point in the graph provides the average TPR and FPR across subjects and splits for a given parameter set {Δt, τ_D, ρ_trsh} spanning Δt ∈ {0.08s, 0.16, …0.96s}, τ_D ∈ {0s, 1s, …10s} and ρ_thesh ∈ {0, 0.1, …0.9} for HbO (red dots) and HbR (blue dots) using 20, 50 and 100% HRF amplitude data. Cyan diamond: Set 1, previously identified global optimum for the objective function in Equation [14]. Yellow diamond: Set 2, global optimum under additional consideration of FPR. Green square: TPR versus FPR for GLM with SS.

For both chromophores and different HRF amplitudes, GLM with tCCA with the original optimum parameter (cyan diamond) yields either optimal or close to optimal accuracy. When FPR is also considered in the objective function (yellow diamond), there is a trade-off between a slight improvement in FPR and a reduced TPR especially for the 20% HRF case. GLM with SS provides the lowest FPR, however, it dramatically reduces the TPR at the same time (e.g. more than 3-fold decrease in HbO TPR when GLM with SS is used for the 20% HRF case). Note that the false positive rate is the same for different HRF amplitudes, as both FPs and TNs are calculated based on the results from the channels on which no HRF is added.

3.3.3. Comparison of HRF recovery performance using real visual stimulation data

As a third performance evaluation, we compared the GLM with tCCA to GLM with SS using visual stimulation data. The hemodynamic response to a real visual stimulation task was estimated and the number of significantly activated channels was compared for both methods (Fig. 11). The number of active channels was significantly higher for the GLM with tCCA (paired t-test, p-value = 0.02), while the p-values for the active channels were significantly lower for HbO (paired t-test, p-value = 5.4 × 10⁻⁶) (Table 3). No significant difference in these metrics was observed for HbR.

Fig. 11.

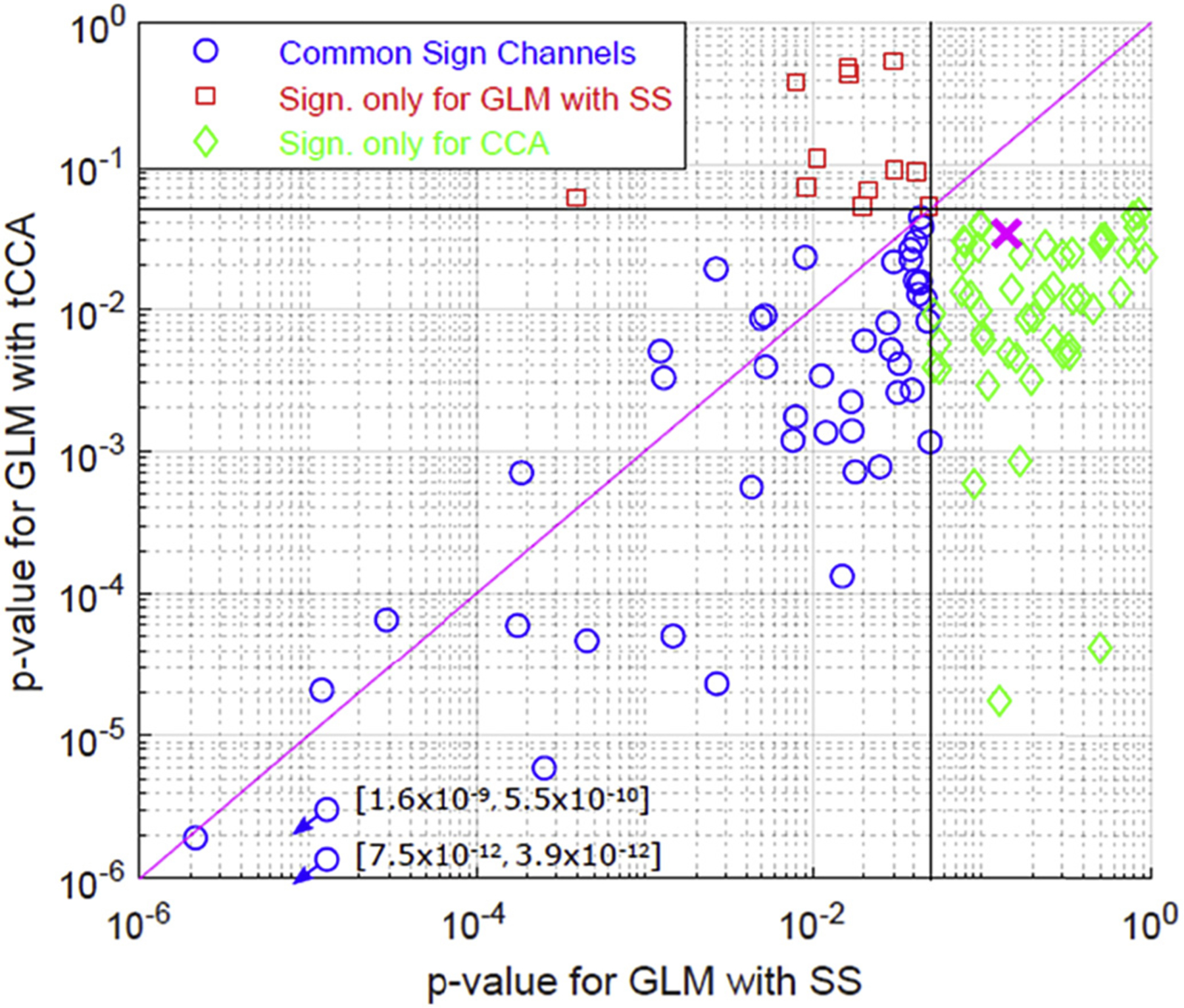
Comparison of active channels in visual stimulation data: Channels found significantly active only for GLM with tCCA (green) and only for GLM with SS (red). Blue circles show the channels that were found active with both methods. Magenta cross is the mean p-value for GLM with SS vs GLM with CCA across the combined set of channels that show significance using either of the methods.

Table 3.

Number and p-values of significantly activated channels SS GLM vs tCCA GLM.

(mean ± std)		GLM with SS	GLM with tCCA	t-test
# of significant channels	HbO	4.2 ± 4.9	6.9 ± 5.2	p = 0.02
	HbR	3.8 ± 4.2	5.2 ± 3.3	ns
p-value (union of significant channel set for both methods)	HbO	0.14 ± 0.21	0.03 ± 0.09	p = 5.4 × 10−6
	HbR	0.14 ± 0.24	0.08 ± 0.18	ns

4. Discussion

For the robust estimation of evoked brain activity from functional Near Infrared Spectroscopy signals, it is crucial to filter confounding contributions from systemic physiology and motion induced signal fluctuations. The current best practice incorporates short-separation fNIRS measurements as regressors in a General Linear Model. In this manuscript, we presented an extension that improves the standard approach by incorporating regularized temporally embedded CCA to create more optimal nuisance regressors. This way, both non-instantaneous and non-constant coupling and signals from multiple auxiliary modalities are more optimally incorporated, and physiological interference is more strongly rejected, improving the overall estimation accuracy of the brain activity.

Parameter selection for the proposed method:

We investigated the parameter space and identified cross-validated optimal regions using simulated ground truth data and RMSE, Correlation and F-Score as performance metrics. Across all tested conditions, the region with Δt ≥ 0.08s, 1.5s ≤ τ_D ≤ 4s, and ρ_thresh ≤ 0.5 was identified as optimal, with a global optimum at Δt = 0.08s, τ_D = 3s, and ρ_thresh = 0.3 (see Fig. 6). The maximum delay of ≤ 4s is physiologically plausible, as we are currently not aware of any systemic processes with a non-instantaneous coupling longer than a few seconds (Tong et al., 2012). A second optimum (Δt = 0.64s, τ_D = 2s and ρ_thresh = 0.4) was identified by additionally considering FPR in the objective function of our evaluation pipeline (see Fig. 10). These findings are also in line with previous investigations of movement induced artifacts using accelerometer and fNIRS signals where simple cross-correlation analysis in channel space yielded optimal lags of Δt < 2s, with a peak around Δt = 0.6s(von Lühmann et al., 2019). In the same work, a saturation of canonical correlation coefficients of the co-modulating components was observed in tCCA space for τ_D > 3s, and a step width Δt = 0.36s and correlation threshold of ρ_thresh = 0.4 were selected.

Across all tested conditions, two regions in parameter space were identified as non-optimal (or “keep-out”) regions: A) temporal embedding with long absolute time lag τ_D > 7s and B) correlation thresholds ρ_thresh > 0.5. The latter results in a strongly decreasing number of signals provided for regression in the GLM. We cross-validated (CV) the performance for the whole parameter space and across subjects to increase robustness against overfitting. Consequently, optimality of regions is determined by the method’s performance – but constrained by generalizability. Two implications follow from this CV approach: 1) The identified regions provide a robust rule of thumb for good performance across subjects and datasets, but 2) the performance of GLM with tCCA can be further enhanced for subject and dataset-specific offline analysis by identifying the optimal parameters in each individual case. Therefore, our evaluation and comparison results can be understood as pessimistic lower bound estimates of the method’s performance.

Choice and contribution of auxiliary signals:

The tCCA GLM extension enables flexible incorporation of any auxiliary signals available. As opposed to providing these signals directly to the GLM, the use of tCCA simultaneously 1) ensures orthogonality of regressors, 2) allows for dimensionality reduction and 3) enables denoising of the regressors using a correlation threshold. While it is often desirable to have as much physiological information from as many different modalities as possible, it is not always feasible or even necessary to acquire all of those signals. Our investigation of the contribution of single and paired auxiliary modalities to the overall reduction of physiological interference in the enhanced GLM showed that short-separation fNIRS and accelerometer signals taken together provide almost all information required for obtaining the optimally performing regressors (see Fig. 7). The contribution of single modalities will also depend on paradigm and application as, for instance, accelerometer signals are especially important in studies with moving subjects (von Lühmann et al., 2019). While our comparative investigation confirmed that short-separation channels are the most useful modality among those typically available, the additional use of accelerometer signals significantly increased performance beyond that of short-separation channels only. This observation is especially noteworthy, as the data in this study was acquired in a conventional experiment with subjects sitting with minimal head motion where accelerometer signals have so far rarely been considered to add value. We attribute this added value to the accelerometer picking up additional, complementary information from the head movements as well as posture/orientation changes, which can lead to non-stationarities in the fNIRS signals that are not identified as abrupt motion artifacts in the fNIRS signals.

Performance Evaluation and Comparison:

As a first performance evaluation metric, we investigated the benefit of GLM with tCCA in terms of the noise reduction in the power spectrum of the raw NIRS signal (see Fig. 8). GLM with tCCA reduces power of nuisance signals with high statistical significance at all frequency bands, which cover low frequency oscillations, Mayer waves, respiration, cardiac and its harmonics. The performance gain in high frequency bands can be diminished 1) when auxiliary signals with a white noise power above the noise level of the fNIRS signals are weighted strongly in the CCA step, and 2) when the choice of Δt introduces artificial periodicity (see paragraph “Additive noise and amplification of estimation errors” below for the details). In the majority of fNIRS studies, the focus lies on changes in lower frequency bands, typically around 0.1 Hz and the data is usually low pass filtered at 0.5 Hz or below. These effects do therefore not affect the quality of conventional HRF estimation.

Overall, the performance evaluation of the GLM with tCCA resulted in a significant improvement in all metrics when compared to the GLM with SS (see Table 2). While the evaluation metrics were also better than the GLM with SS for across trial HRF recovery, the strength of the proposed approach showed itself more dramatically at lower Contrast to Noise Ratios, especially in “single trial HRF recovery”. These results gain importance in view of the recent advances in the BCI/Neuroergonomics field and an increasing number of domains that incorporate fNIRS in ambulatory and monitoring applications (Ayazetal., 2013; Piper etal., 2014; von Lühmann etal., 2017). The most substantial improvement was observed in the F-score, especially for the lowest signal to noise ratio case (20% peak HRF amplitude) with a 3.25-fold increase for HbO and 2.12-fold increase for HbR. F-score is a weighted mean of precision and recall and thus carries information on all crucial metrics related to the robustness of the HRF estimation: true positives, false positives (Type I error) and false negatives (Type II error). For the 50 and 100% peak HRF amplitude simulations, there was still an increase in F-score but less dramatic, as with higher HRF amplitudes, contrast to noise ratio increases and the HRF estimation becomes more trivial for GLM with SS as well (1.48-fold increase for HbO and 1.37-fold increase for HbR for 50% peak HRF amplitude and no significant improvement for 100% peak HRF amplitude). While using GLM with tCCA there were >30% and 25% reduction in RMSE for single trial recovery for HbO and HbR respectively. The reduction was ~10% for HbO for across trial recovery (no significant reduction for HbR for across trial recovery). On the other hand, while there was a significant increase in Corr with the GLM with tCCA (ranging from ~14 to 45% for single trial HbO recovery and from ~9 to 25% for single trial HbR recovery), the reductions were not statistically significant for across trial HbO/HbR recovery. Similar to RMSE scores, correlation improves by averaging across many trials, thus reducing the difference in performance across methods. It is noteworthy, that there is a significant improvement over the standard GLM with SS even when only short-separation signals are used as auxiliary inputs and without making use of any additional auxiliary modalities: Corr (+13%/+5%), RMSE (−29%/−14%) F-Score (+31%/+34%) for the exemplary case of 50% peak HRF amplitude, single trial recovery and and HbO/HbR respectively.

In addition to F-score, we compared sensitivity (TPR) and 1-specificity (FPR) of the methods. For both HbO and HbR with different peak amplitudes (20, 50 and 100%), using the previously identified original parameter set and the second parameter set that is obtained via additional consideration of FPR in the objective function, GLM with tCCA provided the optimal or close to optimal performance (evident from Fig. 10, see cyan diamond towards the top left-hand border of the plot i.e. higher TPR and lower FPR). The FPR were modest at the original optimum parameter set compared to GLM with SS. Barker et al. previously reported FPR (Type I error rate) on the order of 5–9% with their proposed autoregressive model, a great reduction from that of regular GLM without SS regression (FPR = 37%) (Barker et al., 2013a). With a similar synthetic HRF peak amplitude as in Barker et al., ((0.05 −0.66 μM) vs (0.01 − 0.1 μM)), our original optimum parameter set (Δt = 0.08s, τ_D = 3s, and ρ_thresh = 0.3) achieves slightly higher FPRs (FPR_HbO = 14%%, FPR_HbR = 17%). The FPR got lower for the optimum parameter set obtained when additionally considering FPR as one of the weighted metrics (Δt = 0.64s, τ_D = 2s, and ρ_thresh = 0.4) (FPR_HbO = 10%, FPR_HbR = 13%). While GLM with SS provided better FPR (FPR_HbO = 4%, FPR_HbR = 5%) than both of these optima as well as the autoregressive model, it comes with a trade-off of greatly reduced TPR. Depending on the objectives of any given study, one can choose the best parameter set to adjust for the trade-off between TPR and FPR.

We also compared the new method with GLM with SS in terms of statistical significance of activated channelsusing real visual stimulation fNIRS data with blocks of visual checkerboard interleaved by rest periods. For HbO, the number of channels that are significantly different than baseline i.e. “activated channels”, was greater and the corresponding p-values were lower for our new method (see Fig. 11). Although there was an improvement in both metrics for HbR as well, the results were not statistically significant. These results are consistent with our simulation results which showed less dramatic improvement in HbR estimation. It is known that physiological fluctuations including low frequency oscillations, Mayer waves, cardiac and respiratory oscillations are more pronounced in the HbO signal than the HbR signal (Zhang et al., 2015), thus any filtering that will regress out such physiological contaminations would be expected to improve the estimation of HbO more than HbR. The difference in the number of active channels between methods should be interpreted with caution, as the ground truth for the visual stimulation data is not known. Some of the channels that show significant activation can be false positives for both methods, and more likely so for GLM with tCCA for the optimal parameter set being used. Our simulation results are indicative of such a behavior (see cyan diamond versus green square in Fig. 10).

Additive noise and amplification of estimation errors:

The following considerations should be taken into account to ensure that no additional noise or estimation errors are introduced by the use of tCCA:

1. Artificial periodicity: tCCA regressors are weighted combinations of all temporal embedded inputs. Due to the temporal embedding, signals are repeated after each time shift Δt, which artificially introduces periodicity within the mixed signal used for regression at f_O = 1/Δt and its higher harmonics. For instance, for Δt = 0.16s, this effect leads to peaks in the power spectrum at 6.25 Hz (= 1 /0.16s) and its higher harmonics. The power of such artificial peaks increases with the number of employed temporally embedded signals (the longer the absolute time lags for fixed step size) as this increases periodicity within the mixed signal. These effects occur outside of the typical band of interest in fNIRS, and can thus be removed by subsequent low pass filtering without interfering with HRF estimation. However, if higher frequency components of the fNIRS signal are to be investigated, e.g., the heartbeat, the choice of Δt and the other windowing approaches should be considered accordingly.

2. White noise: The approach finds regressors by linear combination of the temporally embedded auxiliary signals, which will always lead to a reduction of physiological 1/f noise in the GLM regression. However, if the power of uncorrelated (white) noise in the weighted signals that construct the tCCA regressors is higher than the white noise in the fNIRS signals, the GLM regression will lead to an increase in white noise in the recovered signals: Subtraction/addition of two zero-mean white noise signals with different power always results inwhite noisepower equal to the larger of both signals. This observation becomes most apparent in higher frequency bands where 1/f noise does not dominate. In the tCCA step, auxiliary signals with components that lead to a high canonical correlation with the projected fNIRS signals are included with relatively larger weights. These weights equally scale white noise components. Consequently, there is a trade-off in the cleaning approach when regressors are based on auxiliary signals with both strongly correlated physiological components and a pronounced white noise component. It is therefore recommended to discard very noisy auxiliary signals from the set provided for tCCA. The higher the number of temporal embeddings and thus the larger the number of input signals to the CCA, the more similar signals / redundant physiological information is provided for the construction of the regressors. Beyond a certain point, especially periodic components (e.g. the heart beat) can be modeled with multiple time shifts of the same signal, which has an averaging effect and therefore increases CNR of physiological signals to white noise. Consequently, more time lags lead to a better fit of the physiological nuisance signals, a reduction in white noise addition if auxiliary signals were noisy, and also rejection of more (physiological) interference during HRF estimaton.

3. High dimensional signal embeddings: While the use of more time lags (smaller time steps Δt) is potentially beneficial with respect to 1) and 2) above, a higher number of temporal embeddings also increases the risk of overfitting and the likelihood of the CCA data covariance matrices to be ill-conditioned. To address these risks, we performed cross-validation and regularization using shrinkage. In fNIRS, temporal embedding typically does not lead to high dimensional problems, as signals are acquired at sample rates not much higher than 25 Hz (limiting the smallest Δt), and the maximum overall delay τ_D is not larger than a few seconds. Notably, the use of a kernel, which can be linear or nonlinear (Müller et al., 2003) makes the problem virtually insensitive to very high dimensional time lag representations (Scholköpf et al., 1998). Therefore, in special cases with high dimensional signal embeddings, our approach can be extended by using a (linear) kernel, and performing temporal kernel CCA (tkCCA) instead (Bießmann et al., 2010).

5. Conclusion

In this study, we introduced the fNIRS “GLM with temporally embedded CCA” (GLM with tCCA), an approach that integrates blind source separation methods into the current best practice for analysis of fNIRS signals – the supervised General Linear Model with short-separation regressors. Overall, the new method significantly outperforms the conventional GLM with SS regression on all evaluation metrics (RMSE, Corr, F-score, p-value). The new approach increases the robustness of HRF estimation without introducing any notable additional computational load while allowing flexible integration of any number of auxiliary modalities, by generating more optimal nuisance regressors. This has potential significance both for conventional neuroscientific fNIRS experiments as well as in emerging applications of fNIRS in everyday environments. The method will be implemented in the HOMER3 toolbox (https://github.com/BUNPC/Homer3) to allow easy access for the fNIRS community. All the relevant code is currently available on https://github.com/avolu/tCCA-GLM with open public access.

Appendix A. The Generative Linear Model

The generative linear model is a commonly used abstract mathematical model for the generation of macroscopic neuroimaging data such as EEG, MEG, fMRI, and fNIRS. It represents the measured data as a linear mixture of functionally distinct processes (Haufe et al., 2014; Parra et al., 2005). These generative or forward models factorize observed measurement data into latent factors (components) with a temporal signature and their corresponding spatial activation patterns. The factorization result depends on the selected optimization criteria and models are often unsupervised. We express the generative linear forward model of physiological data by

$$\mathit{Y}=\mathit{S}\mathit{A}+E$$ [A.1]

Where, as in the General Linear Model, $Y\in {ℝ}^{T\times N}$ is the observation matrix with measurement data from all time points T and recorded channels N. In the linear mixing model, observations are assumed to be a linear combination of M components ${\mathit{s}}_m\in {ℝ}^T$, accumulated in the matrix $S\in {ℝ}^{T\times M}$, which are mapped into channel space by the mapping matrix $A\in {ℝ}^{M\times N}$. The generative linear model can contain the additional residual/noise term $E\in {ℝ}^{T\times N}$. The corresponding discriminative or backward model is given by

$$\widehat{S}=YW.$$ [A.2]

It is used to estimate the latent components $\widehat{S}\in {ℝ}^{T\times M}$ from the observed data using a set of extraction filters $W\in {ℝ}^{N\times M}$. In machine learning driven blind-source separation (BSS) approaches, no a priori knowledge about stimulus onset timings or class labels is used. Hence, without additional constraints, the factorization of W and $\widehat{S}$ are not unique and further assumptions about spatial and temporal dynamics are required. These assumptions distinguish different blind-source separation methods (PCA, ICA, CCA, etc.) and their suitability for the respective application (Bießmann et al., 2011).

The General Linear Model (GLM) in Section 2.1.1 is a special supervised case of the generative linear mixing model, and Equation [A.1] is typically expressed with G instead of S, and β instead of A, a notation we follow in our expression of the GLM in Equation [1].

Appendix B. Canonical Correlation Analysis

A generative linear model based method for finding co-modulating components in multivariate data is Canonical Correlation Analysis (CCA) (Anderson, 1958; Hotelling, 1936). For observations of each modality y and z, it estimates normalized linear extraction filters ${\mathit{w}}_y\in {ℝ}^{N_y}$ and ${\mathit{w}}_z\in {ℝ}^{N_z}$, the canonical variates, that maximize the canonical correlation between the projections of each modality into latent component space:

$$\underset{w_y,w_z}{\text{max}}\mathit{\text{\hspace{0.17em}Corr\hspace{0.17em}}}\left(y(t)w_y,z(t){\mathit{w}}_z\right)$$ [B.1]

Using centered data y and z and their empirical auto-covariance matrices C_yy and C_zz and cross-covariance matrices C_yz and C_zy, the CCA objective function [B.1] can be reformulated in block matrix form

$$\left[\begin{array}{cc}0& C_{y\mathit{z}}\\ C_{z\mathit{y}}& 0\end{array}\right]\left[\begin{array}{l}{w}_y\hfill \\ w_z\hfill \end{array}\right]=\lambda \left[\begin{array}{cc}{C}_{y\mathit{y}}& 0\\ 0& C_{z\mathit{z}}\end{array}\right]\left[\begin{array}{l}{\mathit{w}}_y\hfill \\ {\mathit{w}}_{\mathit{z}}\hfill \end{array}\right],$$ [B.2]

which is a generalized eigenvalue equation. To solve [B.2] without amplifying estimation errors, covariance matrices must be invertible and well-conditioned. Consequently, C_yy and C_zz should be regularized - especially when data is high dimensional, when only limited observations are available, or when all measurement channels within the same modality are highly correlated, as is the case in fNIRS (Bießmann et al., 2010).

Appendix C. Parameter Selection - Performance Metric Details

In this section, using the identified globally optimal parameter set, more details on each performance metric in 2D parameter space are provided for a fixed correlation threshold ρ_thresh = 0.3, for the different CNRs resulting from varying HRF amplitudes, and for single trial recovery (Fig. C.1) and across trial recovery (Fig. C.2). In each subfigure, all three average performance metrics are displayed for each chromophore together with the summarizing objective function result. Summing up all 6 objective function plots from Figs. C.1 and Fig. C.2 yields the global objective function plot at ρ_thresh = 0.3 in Fig. 6 in results Section 3.1. In all plots, the location of the identified globally optimal parameter set is marked with an arrow and the corresponding value of the performance metric at this point is given. The results for F-Score remain constant for both single and across trial recovery, as the F-Score is calculated using all trials.

Fig. C.1.

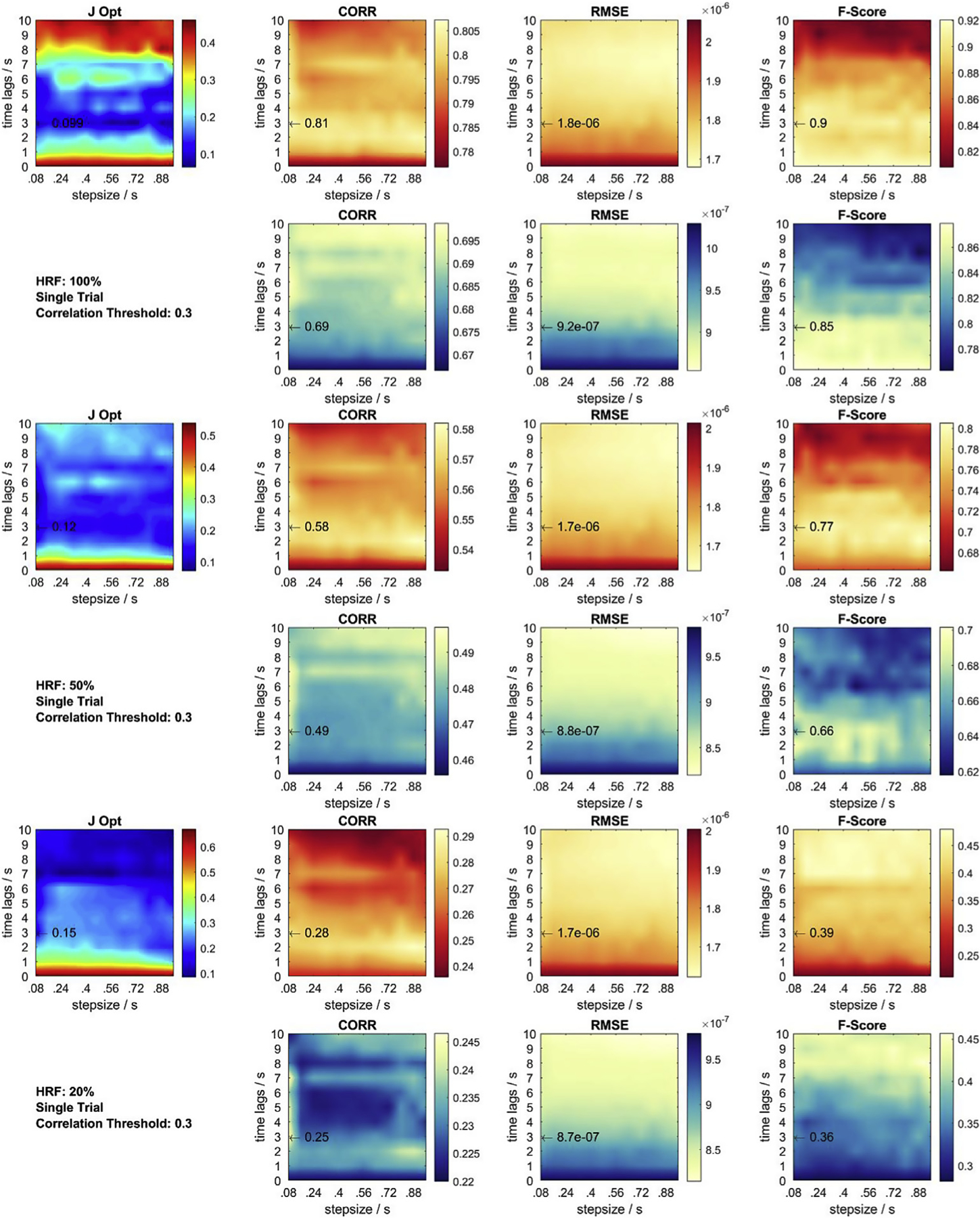
Metrics and objective function at correlation threshold 0.3 for single trial HRF = 20, 50, 100% recovery. Red contour plots: HbO. Cyan contour plots: HbR. Black arrow: Previously identified global optimum across all objective functions and conditions. J Opt displays the sum of each set of 6 normalized contour plots.

Fig. C.2.

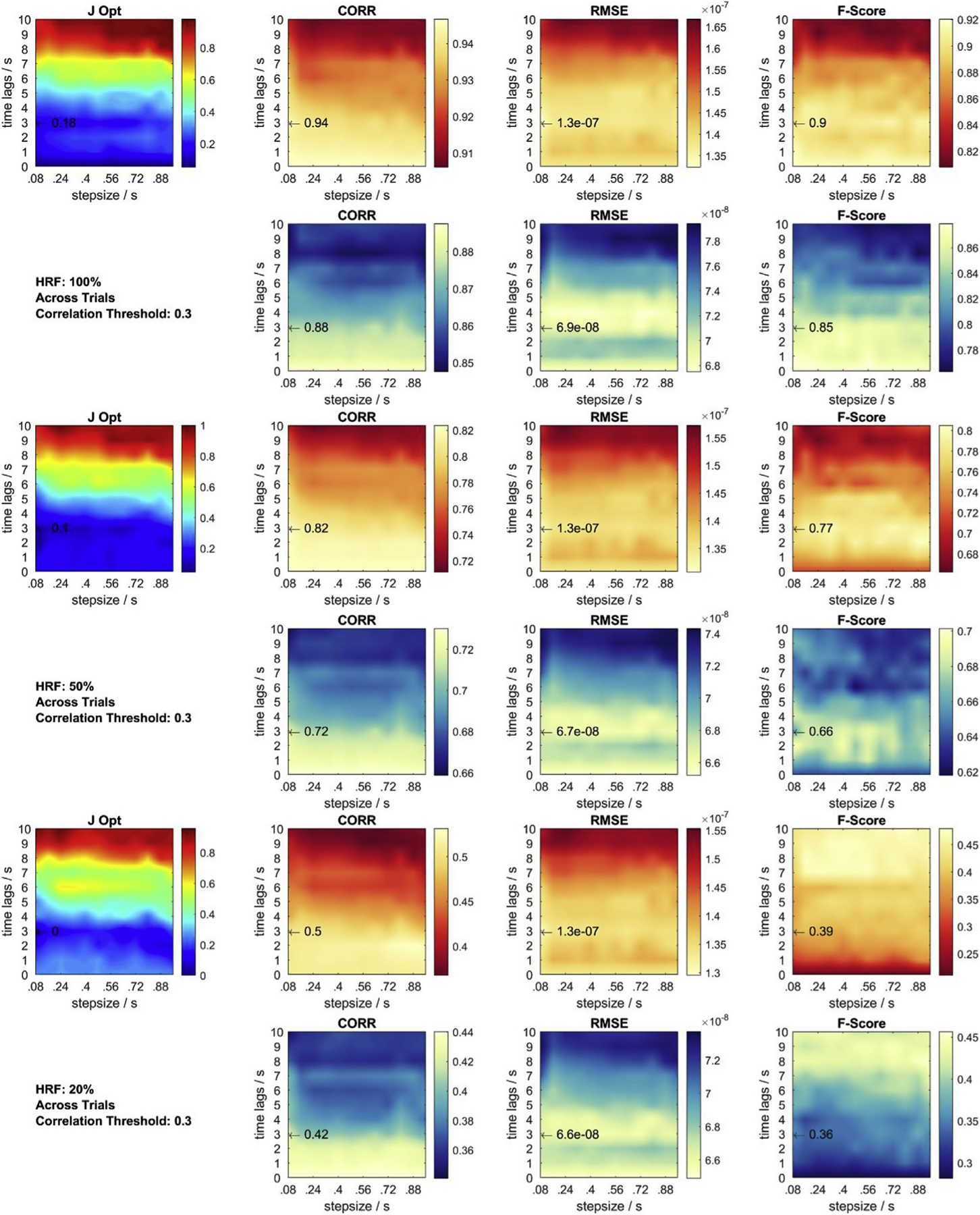
Metrics and objective function at correlation threshold 0.3 for across trial HRF = 20, 50, 100% recovery. Red contour plots: HbO. Blue contour plots: HbR. Black arrow: previously identified global optimum across all objective functions and conditions. J Opt displays the sum of each set of 6 normalized contour plots.