A spatial hierarchical model for integrating and bias-correcting data from passive and active disease surveillance systems

Abstract

Disease surveillance data are important for monitoring disease burden and occurrence, and for informing a wide range of efforts to improve population health. Surveillance for infectious diseases may be conducted passively, relying on reports from healthcare facilities, or actively, involving surveys of the population at risk. Passive surveillance typically provides wide spatial coverage, but is subject to biases arising from differences in care-seeking behavior, diagnostic practices, and under-reporting. Active surveillance minimizes these biases, but is typically constrained to small areas and subpopulations due to resource limitations. Methods based on linkage of individual records between passive and active surveillance datasets provide a means to estimate and correct for the biases of each system, leveraging the size and coverage of passive surveillance and the quality of data in active surveillance. We develop a spatial Bayesian hierarchical model for bias-correcting data from both systems to yield an improved estimate of disease measures after adjusting for under-ascertainment. We apply the framework to data from a passive and an active surveillance system for pulmonary tuberculosis (PTB) in Sichuan, China, and estimate the average sensitivity of the active surveillance system at 70% (95% credible interval: 62%, 78%), and the passive system at 30% (95% CI: 24%, 35%). Passive surveillance sensitivity exhibited considerable spatial variability, and was positively associated with a site’s gross domestic product per capita. Bias-corrected estimates of county-level PTB prevalence in the province in 2010 identified regions in the southeast with the highest PTB burden, yielding different geographic priorities than previous reports.

1. Introduction

Disease surveillance systems provide critical public health information that can be used for the timely detection of disease outbreaks, evaluation of the impact of interventions, monitoring of trends in disease burden, and estimation of important epidemiologic parameters (Sell, 2010). Surveillance data are also routinely leveraged to examine associations between disease occurrence and potential risk factors (Yip et al., 1995). At the same time, surveillance data are fundamentally limited with respect to completeness and accuracy, owing in part to resource constraints that result in under-ascertainment or biased sampling across geographical regions, time periods and sub-populations. As a result, epidemiologic parameters or disease measures estimated or extrapolated from surveillance data are widely known to be subject to some level of bias (Declich and Carter, 1994; Gibbons et al., 2014; Lee et al., 2010; Souty et al., 2014).

Over the last two decades, the transition from paper-based to electronic surveillance systems has increased the timeliness and volume of disease surveillance data available for analysis in many parts of the world (Bansal et al., 2016). One important opportunity arising from this transition has been to combine data from multiple surveillance systems and from multiple locations, motivating the use of increasingly sophisticated statistical techniques and models capable of integrating and jointly analyzing multi-source data. Two broad classes of disease surveillance – passive and active – are of interest with respect to opportunities for data integration and analysis. Passive surveillance systems are generally structured around data collection, storage and transmission from healthcare facilities. These systems rely on encounters between patients and healthcare providers. For example, hospitals participating in a passive surveillance network may report the diagnosis of a particular disease at a regular schedule, or within a certain number of hours or days after the diagnosis is confirmed. Passive disease surveillance is generally less costly, allowing for information to be collected in continuous time across the extent of the network of participating facilities, but is widely acknowledged to suffer from under-ascertainment (not all diseased individuals present at a reporting facility), under-diagnosis (not all cases at the facility are correctly identified, depending on the quality of diagnostic routines available), and under-reporting (not all identified cases are reported). Notably, factors related to the completeness of passive surveillance data, such as care-seeking behavior, access to health-care, and diagnostic rigor, may be expected to vary spatially across participating facilities and their population catchments.

Active surveillance systems, by contrast, employ survey methods to estimate the prevalence of disease in defined sub-populations. For example, passive surveillance of hepatitis C in the United States occurs through mandatory reporting of cases diagnosed during healthcare encounters to the National Notifiable Disease Surveillance System, while testing serum samples collected every 2 years by the US National Health and Nutrition Examination Survey is a form of active surveillance for the disease (Rosenberg et al., 2018). Active surveillance data collection is resource-intensive, and therefore usually limited in extent and duration, but can provide data that is more representative of sampled populations, and may be of higher quality due to standardization of diagnostic methods.

In the present work, we develop and evaluate a statistical framework for integrating data from active and passive surveillance of infectious diseases in order to estimate and adjust for under-ascertainment of surveillance systems. Our approach builds on prior methods that model the probability of being reported by individual or multiple systems to estimate the hidden population not captured by any system. Classical log-linear models (Cormack, 1989) for analyzing such multi-source surveillance data have been widely used in the literature and have been extended to allow for Bayesian inference (Basu and Ebrahimi, 2001), to accommodate individual heterogeneity (Fode and Rivest, 2015), and to incorporate novel approaches to improve parameter estimation (Arnold et al., 2010; Manrique-Vallier and Fienberg, 2008). These methods focus on the estimation of ascertainment probability without accounting for the underlying count process. As a result, when multi-source surveillance data are collected at different spatial locations, these methods cannot directly incorporate spatial dependence and covariates in modeling the unobserved count process to improve inference. N-mixture models address this problem by treating site-specific counts as a Poisson process, and inference is carried out using the marginal likelihood of counts by integrating the binomial likelihood over a set of possible values of counts for each site (Dail and Madsen, 2011; Royle, 2004; Royle et al., 2007). While N-mixture models have been implemented to provide estimates of the total number of diseased individuals across sites with multi-source surveillance data, they have not previously been adapted to the scenario in which a limited set of multi-source surveillance data exist along side a more extensive set of data collected from sites where only one system operates, which is a common situation in practice. By extending the N-mixture model to jointly estimate disease occurrence and ascertainment processes across multi- and single-surveillance sites, we propose a framework that better leverages available spatial information on disease outcomes and relevant covariates, and provides a direct means of estimating the true occurrence of disease throughout a spatial extent.

The remainder of the paper is organized as follows. In Section 2, we introduce the motivating surveillance data of active and passive pulmonary tuberculosis (PTB) in western China. In Section 3, we describe a Bayesian spatial hierarchical model for jointly analyzing multi-source surveillance data from multiple spatial locations to estimate disease prevalence across a larger region. This is accomplished by combining estimated ascertainment probabilities of a passive surveillance system with a spatially kriged surface of true case counts. In Section 4, we describe a simulation study to evaluate the proposed model and compare with binomial mixture model (Fode and Rivest, 2015) that does not explicitly model the true case as a latent variable. In Section 5, we apply our model framework to the motivating dataset. To our knowledge, this is the first application of a spatial model capable of analyzing multi-source disease surveillance reports.

2. Motivating data

We collected pulmonary tuberculosis (PTB) surveillance data from Sichuan Province, China, from a passive and an active surveillance system. The passive National Infectious Disease Reporting System (NIDRS) was established in 2004 in China, encompassing virtually all healthcare facilities. It covers 39 mandatory notifiable infectious diseases, including PTB, and operates across a real-time network linking the Chinese Centers for Disease Control and Prevention (China CDC), regional CDCs, and reporting facilities (Liang et al., 2014). We hereinafter denote this passive PTB surveillance system as PTBS1. In parallel with NIDRS, an active national cross-sectional PTB prevalence survey is carried out periodically by public health officials and local agencies with household surveys for PTB conducted within representative samples of communities. The survey, which we denote PTBS2 from here forward, was carried out nationally in 1979, 1985, 1990, 2000 and 2010, and follows the guidelines for population-based tuberculosis prevalence surveys put forward by the World Health Organization (Wang et al., 2014; World Health Organization. Regional Office for the Western Pacific, 2007).

We obtained individual level PTB surveillance data from PTBS1 between 2009–2010 and PTBS2 in 2010 Wang (2011). To identify individuals reported by both PTBS1 and PTBS2, a record linkage procedure was implemented based on name, date of birth, sex, and residential address identifiers. PTBS1 surveillance was continuous in 2009–2010, and covered every county in the province. PTBS2 surveillance was conducted from May 10 to June 22, 2010 in 24 sites where record identifiers enabled linkage to PTBS1data (Fig. 1). We assume a temporally closed-population by only considering PTBS1 data from August 1, 2009 to July 31, 2010, allowing the joint analysis of continuous-time passive data with discrete-time active surveys under the assumption that the samples draw from the same underlying population. Within this time interval, this assumption is viewed as reasonable given that the average recovery time for PTB is 6 to 18 months if treated. Covariates for population, gross domestic product (GDP) per capita, and longitude/latitude were obtained from government sources (Sichuan Bureau of Statistics, 2011).

Fig. 1.

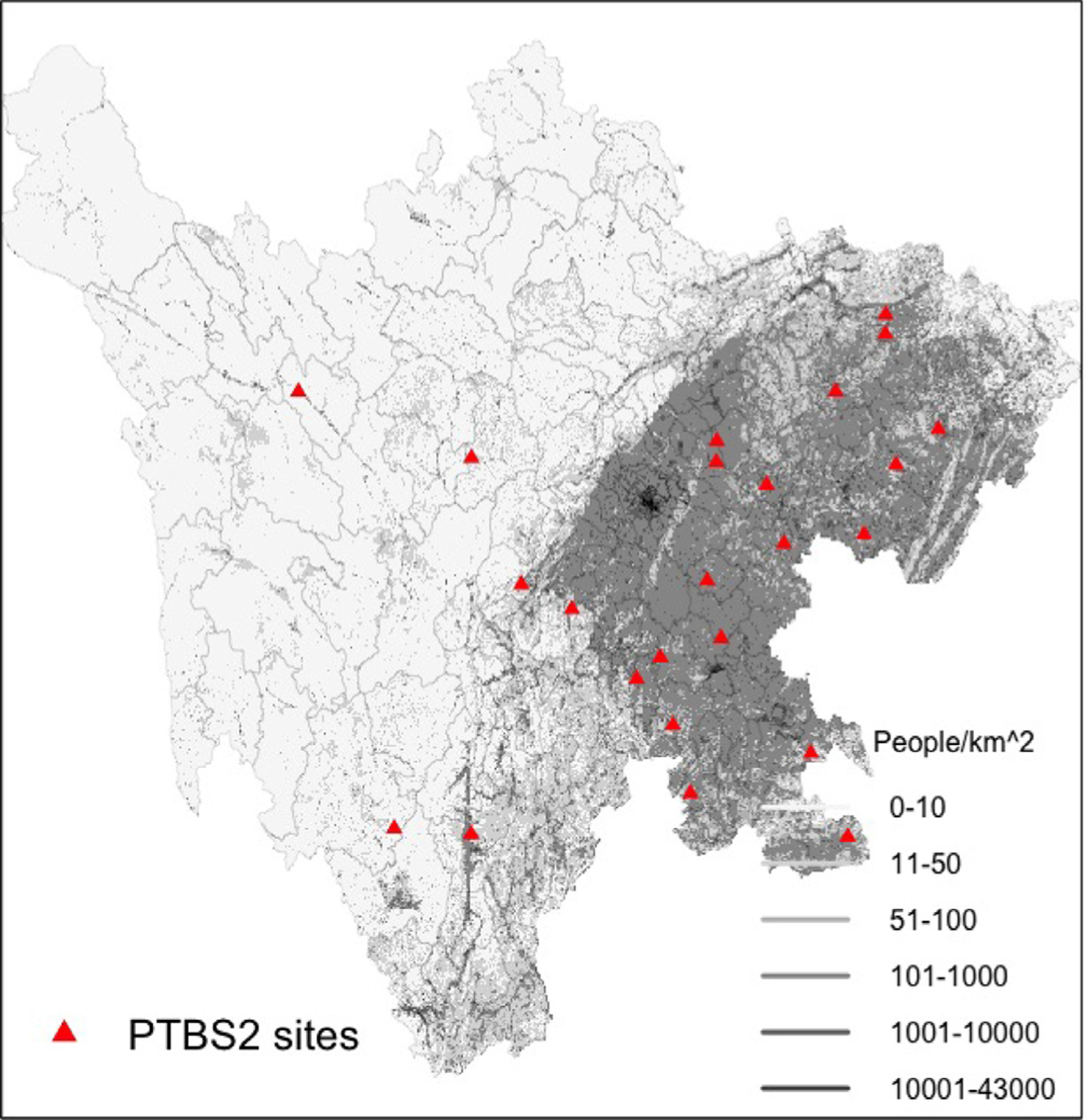
A map of the study region where the framework was tested, showing population density (Dobson et al., 2000)(grey shading), county borders (thin black boundaries), and location of 24 surveillance sites in Sichuan Province where linkage of PTBS1 and PTBS2 data was conducted.

3. Spatial hierarchical ascertainment model

Assume there are T surveillance systems under consideration. Let N_s be the unknown number of cases at the sth surveillance site, and n_s (≤N_s) be the unique number of cases ascertained by any of the systems at the sth site. For an individual i at site s, if they are ascertained by system t, then y_it,s = 1, otherwise, y_it,s = 0. Now, if the ascertainment probability for individual i under system t at site s is p_it,s, Y_it,s follows a Bernoulli distribution with probability density function $f(y_{it,s},p_{it,s})=p_{it,s}^{y_{it,s}}{(1-p_{it,s})}^{1-y_{it,s}}$. Assuming individuals and systems are independent of each other, the data likelihood is obtained by multiplying the individual probabilities together accounting for all combination of being ascertained by each system or not. We begin by specifying the data likelihood for a single site where s. The likelihood for N individuals and T systems is

$$\begin{gathered} L(N_s,\{p_{it,s}\};\{y_{it,s}\}) \\ =\frac{N_s!}{({\prod }_h{y}_h!)(N_s-n_s)!}\prod _{i=1}^{N_s}\prod _{t=1}^T[p_{it,s}^{y_{it,s}}{(1-p_{it,s})}^{1-y_{it,s}}], \end{gathered}$$ (1)

where {y_it,s} and {p_it,s} denote a set of binary values and corresponding ascertainment probabilities for each individual, system and location; y_h represents the number of cases which share the same ascertainment history h. The likelihood in Eq. (1) is also called a single cell likelihood. For the multi-source case of two systems, the ascertainment histories are: cases ascertained only by system t = 1, cases ascertained only by system t = 2, cases ascertained by both systems t = 1 and t = 2 and cases ascertained neither by systems t = 1 nor t = 2. We note that the our ability to estimate N_s using the above likelihood relies on the assumption that systems are independent and that we observe some cases captured by both systems.

Assuming that variability in ascertainment probability depends only on different survey systems and different locations, Eq. (1) can be represented by a multinomial distribution,

$$\begin{gathered} L(N_s,\{p_{t,s}\};\{y_h\})=\frac{N_s!}{({\prod }_h{y}_h!)(N_s-n_s)!}{\pi }_{0,s}{(\{p_{t,s}\})}^{N_s-n_s} \\ \prod _{h=1}^{2^T-1}[{\pi }_{h,s}{(\{p_{t,s}\})}^{y_h}], \end{gathered}$$ (2)

where y_h denotes case count for ascertainment history h, and π_h,s(·) represents the probability of each ascertainment history h at each location. For two systems assuming system independence, we can define π_h,s as given in Table 1. The number of cases for ascertainment history h = 1, 2, 3 is known and corresponds to the number of cases ascertained by both systems t = 1 and t = 2, system t = 1 only, and system t = 2 only. However, the h = 0 case is unobserved, and thus it will be estimated by the model.

Table 1.

The probability π_h for each ascertainment history.

h	πh,s
0	(1 - p1,s) * (1 – p2,s)
1	p1,s * p2,s
2	p1,s * (1 – p2,s)
3	(1 - p1,s) * p2,s

The likelihood in Eq. (2) includes an unknown parameter N_s at each location. One technique to borrow information across locations is to assume a distribution for N_s and integrate out N_s as a nuisance parameter. We assume N_s at each location follows a Poisson distribution with a mean parameter λ_s. Thus, the joint likelihood is expressed in λ_s as,

$$L({\lambda }_s,\{p_{t,s}\};\{y_h\})={\int }_{N_s}L(N_s,\{p_{t,s}\};\{y_h\})\times p(N_s\mid {\lambda }_s)d{N}_s.$$ (3)

Because N_s is discrete, we have

$$\begin{gathered} L({\lambda }_s,\{p_{t,s}\};\{y_h\})=\sum _{N_s=n_s}^{\infty }\frac{N_s!}{({\prod }_h{y}_h!)(N_s-n_s)!}{\pi }_{0,s}{(\{p_{t,s}\})}^{N_s-n_s} \\ \prod _{h=1}^{2^T-1}\{{\pi }_{h,s}{(\{p_{t,s}\})}^{y_h}\}\times \frac{{\lambda }_s^{N_s}\mathit{\text{exp}}({\lambda }_s)}{N_s!}. \end{gathered}$$ (4)

The integrated likelihood in Eq. (4) sums up to N_s = ∞. In practice, one can choose a large upper bound for N_s after which any change in likelihood is negligible. This choice should be based on the maximum number of observations and an approximate estimate of the ascertainment probability. Sensitivity analyses should also be conducted to ensure that inference is robust. For example, we chose an upper bound of 150 in the application, where the maximum site-specific count n_s is 34 and found there was no difference in likelihood compared to an upper bound of 200. Finally, the constant term, ∏_hy_h! can also be removed from the likelihood as it does not depend on unknown parameters.

The likelihood in Eq. (4) is constructed for a single site. For S sites, the joint likelihood is shown in Eq. (5), and assumes observations among all sites are conditionally independent given λ_s at each location.

$$L(\{{\lambda }_s\},\{p_{t,s}\};\{Y_h\})=\prod _{s=1}^{S}L({\lambda }_s,\{p_{t,s}\};\{y_h\}).$$ (5)

We can further introduce structure on the vector of latent variable λ_s to account for spatial dependence. Let

$$\text{log}({\lambda }_s)=\alpha +e_s,$$ (6)

where α denotes an intercept and e_s follows a mean-zero Gaussian process with an exponential covariance structure for a finite set of S locations, i.e., (e₁,…,e_s)′ ~ N(0, ∑), ${\Sigma }_{ij}={\sigma }^2\text{exp}(-\frac{D_{ij}}{\varphi })$, D_ij represents the Euclidean distance between site i and j, and ϕ is the range parameter. Similar to disease mapping applications, it is also common to include in Eq. (6) an offset of the logarithmic of the at-risk population at site We use covariates to model site-specific detection probabilities p_t,s:

$$\mathit{\text{logit}}(p_{t,s})={\mathit{\text{Z}}}_{t,s}{\beta }_{t,p},$$ (7)

where Z_t,s is a set of covariates for system t. Note that the transformations on p and λ are familiar canonical link functions from generalized linear mixed models and ensure the range for p and λ can be modeled with covariates and Gaussian processes. One may encounter identifiability issues when N and p in a binomial distribution are estimated simultaneously and both parameters include flexible random effects (DasGupta and Rubin, 2005).

A Bayesian hierarchical formulation is a natural approach to performing inference in the present context. Latent processes are put on N_s to form three layers of hierarchy in the proposed model. The data layer is given in Eq. (5) where the integrated data likelihood is constructed. The process layer is given in Eq. (6), where the latent process λ_s is described by the transformed mean structure and covariance structure for the Poisson count process N_s. We define vague priors for model parameters, chosen to provide as little information as possible and maintain conjugacy when possible to facilitate estimation. Specifically, the covariate effects β_t,p and α follow N(0, 100²⁾, and logit(p) follows N(0, 100²⁾, respectively. The spatial range parameter ϕ follows Gamma (5, 0.025), and the marginal variance of spatial random effect σ² follows inverse-Gamma (1.01,0.01). The posterior distributions of β_t,p, ϕ and λ can be sampled using Metropolis-Hastings algorithms.

For estimating true case counts at out-of-sample locations with no surveillance data, the posterior predictive distribution of N_s is given by

$$[N_s\mid \Omega ]=\mathit{\text{Pois}}({\tilde{\lambda }}_s)\times [{\tilde{\lambda }}_s\mid \Omega ]\times [\Omega ],$$ (8)

where [Ω] is the posterior distribution of all model parameters denoted by Ω, and λ_s is the spatially interpolated Poisson mean from in-sample locations. At locations with surveillance data, we use the conditional posterior distribution given the number of unique cases n_s. For example, at in-sample locations with data from both surveillance systems, the posterior distribution is given by

$$[N_s\mid \Omega ]=n_s+\mathit{\text{Pois}}({\lambda }_s(1-p_{1,s})(1-p_{2,s}))\times [{\lambda }_s\mid \Omega ]\times [\Omega ],$$ (9)

where p₁ and p₂ are the system ascertainment probabilities. Similarly, at out-of-sample locations with only data from the first surveillance system, the posterior predictive distribution is given by

$$[N_s\mid \Omega ]=n_s+\mathit{\text{Pois}}({\tilde{\lambda }}_s(1-p_{1,s}))\times [{\tilde{\lambda }}_s\mid \Omega ]\times [\Omega ].$$ (10)

4. Simulation

To evaluate the performance of the spatial hierarchical ascertainment model, a simulation study was conducted. At each round of simulation, we simulated 40 random locations from a 100 × 100 square area. A spatial Poisson process was generated on this field as the underlying true counts with log mean α = 3 and a spatially correlated residual with σ² = 0.2 and ϕ = 30 for the exponential covariance function. Two independent systems were assumed to ascertain subjects. The first passive system (S1) has an ascertainment probability p₁ = 0.269 and the second active system (S2) has p₂ = 0.881, corresponding to logit(p₁) = −1 and logit(p₂) = 2. Among the 40 locations, 25 were randomly chosen as in-sample study sites with linked active and passive surveillance data. The remaining 15 locations were used to evaluate out-of-sample prediction performance when only the passive surveillance S1 data are available.

A binomial mixture (BM) model is one recent approach to analyze multi-source linked dataset. The BM approach only uses likelihood of the ascertained subjects and does not explicitly model the unobserved latent count process. The BM model assumes a truncated binomial distribution and the log-likelihood is proportional to

$$L(p_1,p_2)=\sum _{i=1}^n\text{log}\frac{p_1^{y_{i1}}{(1-p_1)}^{(1-y_{i1})}{p}_2^{y_{i2}}{(1-p_2)}^{(1-y_{i2})}}{1-(1-p_1)(1-p_2)},$$ (11)

where y_i1 and y_i2 are observed binary indicators for whether the ith individual was ascertained by S1 or S2. Because

$$n_s~\text{Binom}(N_s,1-(1-p_1)(1-p_2)),$$

the true count at the location s can be estimated as,

$${\widehat{N}}_s=\frac{n_s}{1-(1-p_1)(1-p_2)}$$ (12)

where n_s is total unique counts at location s. At locations where there is only S1 data, Eq. (12) reduces to n_s/p₁. The variance of ${\widehat{N}}_s$ is $E[Var({\widehat{N}}_s\mid p_1,p_2)]+Var[E({\widehat{N}}_s\mid p_1,p_2)]$, where both components can be estimated using posterior samples of p₁ and p₂.

The BM model serves as the baseline for comparison to (1) the proposed spatial ascertainment (SA) model we introduced in Section 2, and (2) an independent ascertainment (IA) model where the random effects in log(λ_s) are assumed to be independent. At the 15 sites without linked S1-S2 data, we considered two types of prediction: assuming no surveillance data is available using Eq. (8), and assuming only S1 data is available using Eq. (9). We refer these two scenarios as Pois-NA and Pois-S1, respectively.

The simulation was repeated 100 times. We used R (version 3.5.1 Feather Spray) to implement the Markov chain Monte Carlo (MCMC) algorithm. We performed both in-sample prediction at 25 S1-S2 linked sites and out-of-sample prediction at the remaining 15 sites. We also estimated the total count summed across 40 sites. Root mean square error (RMSE), 95% empirical coverage probability (CVG) and posterior standard deviation (SD) were computed by averaging over sites and simulations for each scenario.

Simulation results are given in Table 2. For estimating true case counts at the 25 in-sample locations, all models perform similarly. However, for predictions at locations with only S1 data, the spatial ascertainment model (SA, Pois-S1) is superior than the BM model in RMSE and posterior SD. We also observe a considerable reduction in uncertainty as measured by SD comparing the SA and BM models. This is likely because the BM model is based solely on observed counts and does not borrow information on N_s from neighboring locations. Having partial data from S1 (scenario Pois-S1) reduced the RMSE by 20% compared to the scenario where no surveillance is available (Pois-NA). Finally, the independent ascertainment (IA) model is a mis-specified model in this simulation since the true case counts were simulated with spatial correlation. The importance of capturing spatial dependence is demonstrated by the decrease in RMSE and increase in coverage comparing SA to IA models.

Table 2.

Results of simulation study comparing 3 different models: Binomial mixture (BM), independent ascertainment (IA), and spatial ascertainment (SA). For predictions at locations without both S1 and S2 data, Pois-NA assumes no surveillance data and Pois-S1 assumes only S1 data. Root mean square errors (RMSE), 95% empirical coverage probabilities (CVG) and averaged posterior standard deviation (SD) are reported.

Location	Measure	BM	IA model		SA model
			Pois-NA	Pois-S1	Pois-NA	Pois-S1
S1-S2	RMSE	1.55		1.53		1.52
linked	CVG	0.95		0.99		0.99
sites	SD	1.51		1.49		1.49
S1-only	RMSE	7.95	10.84	7.91	8.34	6.46
sites	CVG	1.00	0.70	0.75	0.84	0.87
	SD	14.45	4.64	3.98	5.26	4.29
Total	RMSE	39.90	56.06	43.35	41.78	34.95
sites	CVG	1.0	0.92	0.81	0.99	0.92
	SD	65.99	56.06	28.73	53.66	31.05

5. Application

Using the spatial hierarchical ascertainment model framework developed in Section 2, we estimated the prevalence of PTB at the county-level across the province using linked data from PTBS1 and PTBS2. We assumed the ascertainment probability of PTBS2 did not vary by location, i.e., p_2,s = p₂, since all surveys were conducted simultaneously by the same organization. However, we allow ascertainment probabilities of PTBS1 to vary spatially in order to adjust for variable ascertainment bias across sites; these passive systems are expected to be subject to care and reporting differences across facilities, and differences in access and care-seeking behaviors among the populations served. Moreover, by allowing variability between locations, we have the means with which to extrapolate the ascertainment probability across the whole province. This is accomplished via three covariates chosen to reflect geographic and economic information as shown in Eq. (13): standardized longitude (Z_1,s), standardized latitude (Z_2,s), and standardized GDP per capita (Z_3,s). The model for ascertainment probability of PTBS1 is

$$\mathit{\text{logit}}(p_{1,s})={\beta }_{p0}+Z_{1,s}{\beta }_{p1}+Z_{2,s}{\beta }_{p2}+Z_{3,s}{\beta }_{p3},$$ (13)

where β_p’s are coefficients of covariates above. Since the true count is assumed to be a Poisson process, we included an at-risk population offset in modeling N_s as shown in Eq. (14).

$$\text{log}({\lambda }_s)=\text{log}({\text{ population }}_s)+\alpha +e_s.$$ (14)

To examine the performance of the spatial process, we compared two residual processes, a white noise process (i.e., e ~N(0, σ²⁾) and a Gaussian process with exponential covariance structure as described in Section 2. The MCMC procedure was run for 25,000 iterations with 5,000 as burn-in. Convergence was assessed using trace-plots of key model parameters. To evaluate the performance of the spatial effect model, deviance information criterion (DIC) was computed (Spiegelhalter et al., 2002). The spatial model exhibited better fit than the non-spatial model (DIC = 353 and 364, respectively), and the parameter estimates of the spatial model are shown in Table 3. The estimated mean ascertainment probability of PTBS1 across sites was 0.30 (95% Credible Interval (CI): 0.24, 0.35), and mean ascertainment probability of PTBS2 was 0.70 (95% CI: 0.62, 0.78). We found a significant effect of latitude on the ascertainment probability of PTBS1 (point estimate 0.32, 95% CI: 0.10, 0.54), with substantial increases observed from south-to-north. The effect of GDP per capita was 0.15 (95% CI: −0.07, 0.37), suggesting an increase in ascertainment probability of PTBS1 in areas with higher GDP.

Table 3.

Parameter estimates and their 95% credible intervals in the spatial model.

Parameter	Posterior Mean	Posterior 95% CI
βp0	−0.87	(−1.13 −0.62)
βp1	−0.08	(−0.32, 0.15)
βp2	0.32	(0.10,0.54)
βp3	0.15	(−0.07,0.37)
p2	0.70	(0.62, 0.78)
α	−5.09	(−5.56 −4.52)
ϕ	116	(31, 254)
σ2	0.34	(0.12, 0.83)

To assess model fit, we used the spatial ascertainment model to conduct an in-sample prediction for the 24 sites. The observed count of a particular ascertainment history at each location followed a Poisson distribution, with mean parameters λ_s multiplied by corresponding ascertainment probability using Eq. (9). Fig. 2 shows the 95% posterior predictive interval for all sites and all ascertainment histories compared with observed data. 67 observed data points out of 72 cells fell inside of the posterior interval (about 93% coverage probability).

Fig. 2.

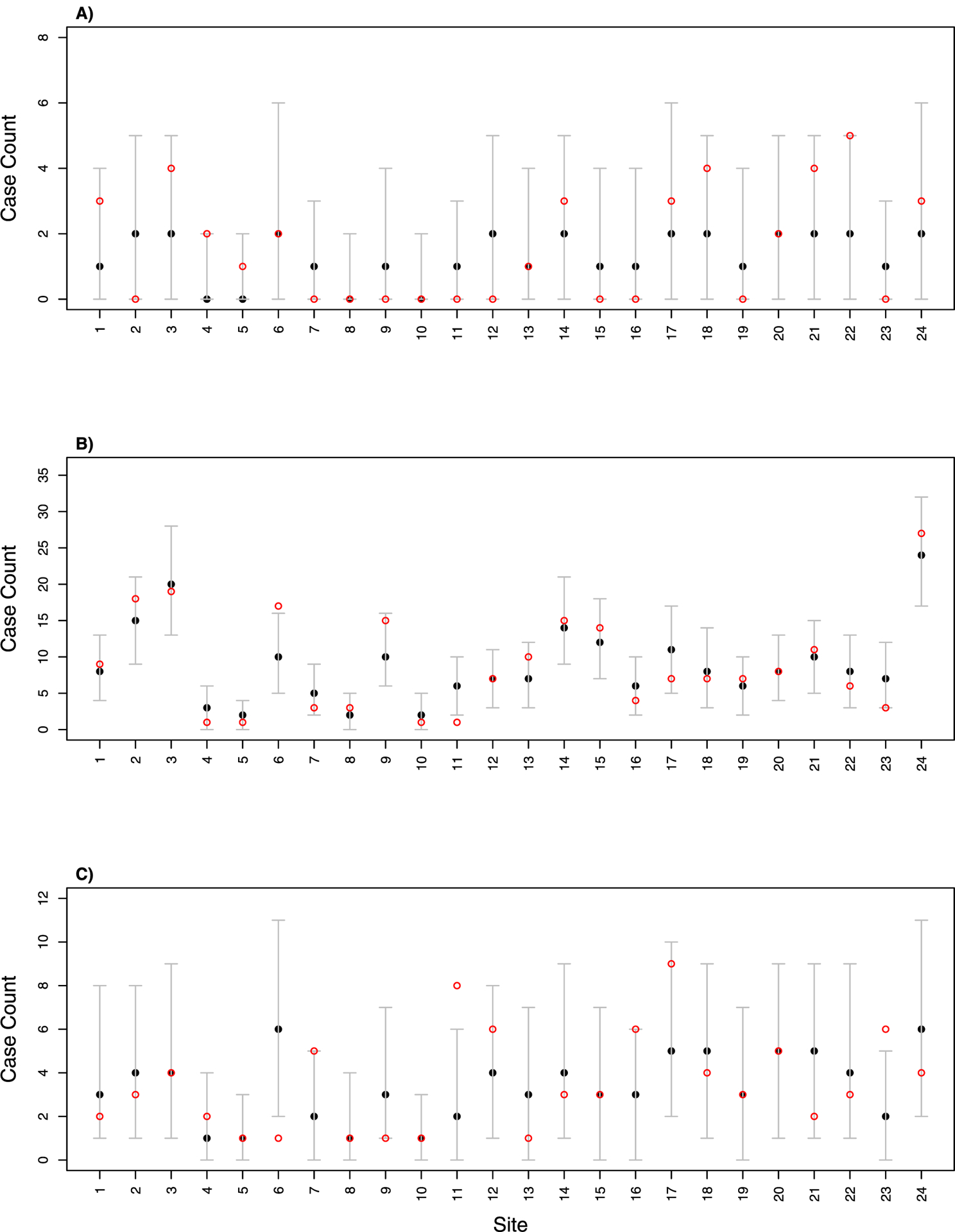
The in-sample prediction of: (A) PTBS1 only, (B) PTBS2 only, and (C) joint PTBS1/PTBS2 across the 24 sites. Figures show the true counts (red hollow points) and 2.5%, 50% and 97.5% percentile of posterior distributions (black dots and error bars).

We also conducted leave-one-out cross-validation to assess the out-of-sample prediction ability of the model. For each round of cross-validation we left one site out and used the other 23 sites to predict the left-out site. We used the conditional posterior predictive distribution given in Eq. (10). Once we obtain N_s, the posterior distribution of counts in each cell category can be sampled using a multinomial distribution with N_s size and π_h({p_1,s}) probabilities for each ascertainment history. Fig. 3 demonstrates the performance of the cross-validation, showing 65 out of the 72 cells falling inside of 95% prediction interval. Most of the missed cell counts are in the PTBS2 only category, possibly a consequence of using p₁’s information to construct N at each location. Of course, out-of-sample prediction of PTBS2 is not of practical interest, being as most locations have no PTBS2 information.

Fig. 3.

The out-of-sample prediction of: (A) PTBS1 only, (B) PTBS2 only, and (C) joint PTBS1/PTBS2 across the 24 sites. Figures show the true counts (red hollow points) and 2.5%, 50% and 97.5% percentile of posterior distributions (black dots and error bars).

During the study period, 72,318 cases were reported by PTBS1 and PTBS2. We estimated the total PTB case count for the province in 2010 to be 374,000 cases (95% Confidence Interval: (320,000, 436,000)). Fig. 4 shows the quantile of reported cases (Fig. 4a) and estimated cases (Fig. 4b) for each county in 2010; and the reported prevalence rate per 10,000 people (Fig. 4c) and the estimated prevalence rate (Fig. 4d) for 2010 across the province. Compared with reported cases, the estimated number of cases exhibits notable differences in spatial heterogeneity. While bias-corrected PTB case counts are higher than unadjusted data throughout the province, PTB cases in southeastern counties, in particular, appear to have been sharply underestimated by unadjusted PTBS1 reports. As a consequence, these areas are among those with the highest PTB prevalence rates in the province when using the bias-corrected estimator, while several northern counties fall into the lower quantiles of TB prevalence after adjustment.

Fig. 4.

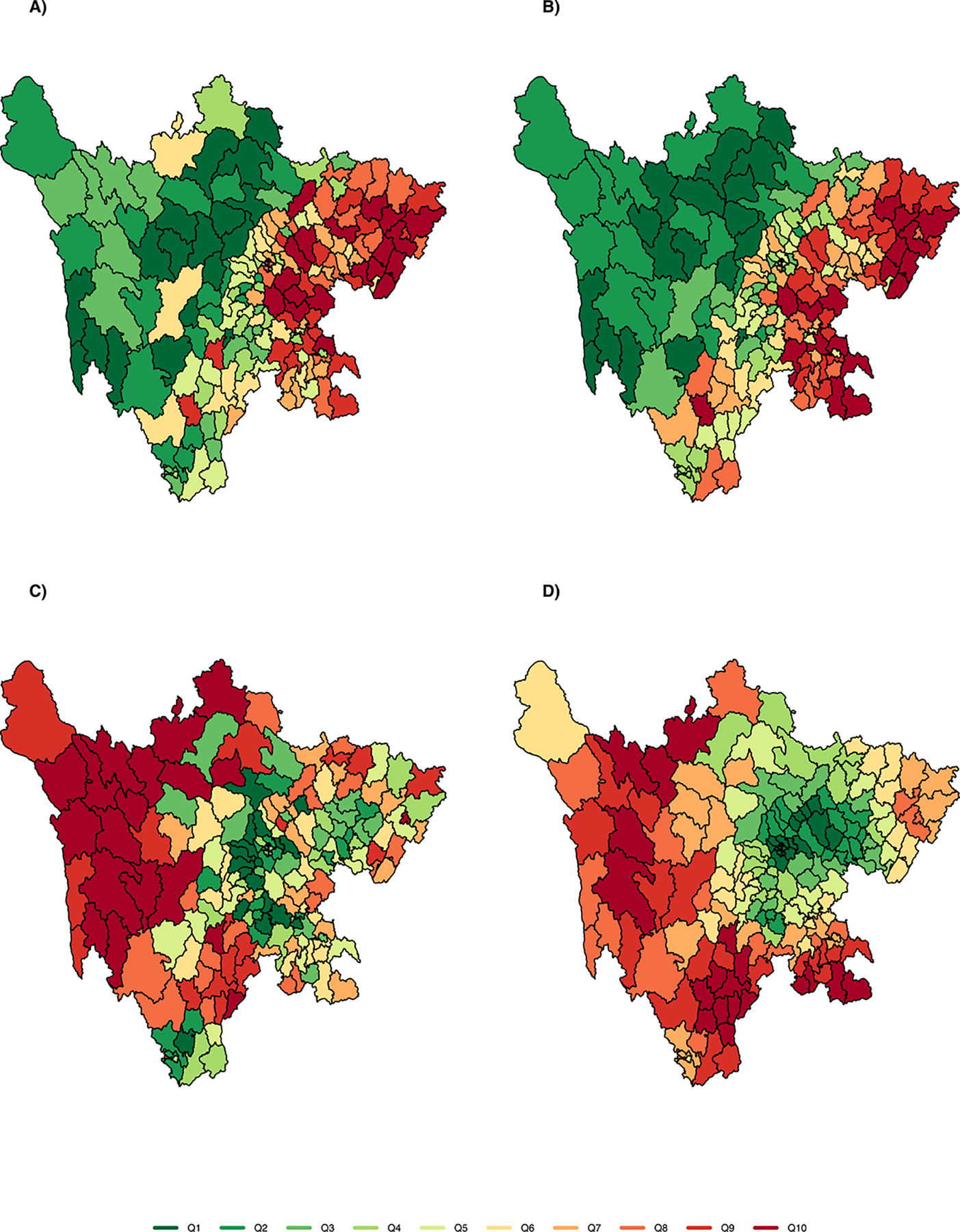
Maps of study region showing county-level estimates in 2010 of: A) unadjusted counts of ascertained PTB cases; B) adjusted counts (i.e., estimated true number); C) unadjusted population prevalence; and D) adjusted population prevalence (i.e., estimated true prevalence). PTB counts and prevalence are shown in 10 quantiles to aid visualization, from low (green) to high (red).

6. Discussion

We have developed a framework for analysis of surveillance systems that is capable of integrating active and passive surveillance data and estimating ascertainment probability and true case numbers and prevalence by location. Compared to other frameworks, we demonstrate how jointly modeling spatial multi-source surveillance data can improve estimates of disease measures, and provide the means to extrapolate and bias-correct measures over wide coverages typical of passive surveillance systems. A key objective of collecting infectious disease surveillance data is understanding spatial patterns of disease, which are critical in the detection of disease emergence, identification of transmission hotspots, and estimation of disease burden across populations. Improved estimates of the spatial distribution of disease can guide public health interventions, and can be used to better structure surveillance systems so as to fill key data gaps that impede progress on disease control, particularly in settings with limited resources to conduct public health surveillance.

With local estimates of ascertainment probability in hand, data providers can be evaluated as to their reporting performance, and targeted, active surveillance can be planned so as to achieve improved estimates where under-ascertainment is expected to be most severe. Furthermore, bias-corrected estimates of disease prevalence can suggest re-allocation of disease control efforts to areas where case-ascertainment substantially underestimates the true burden of disease. Analysis of bias-corrected estimates may yield more accurate estimation of known risk factors, as well as the identification of previously unrecognized risk factors.

Through the integration and analysis of multi-source data on PTB in Sichuan, China, we were able to bias-correct passive surveillance reports, which exhibit wide spatial and temporal coverage. Surveillance systems are of course incapable of perfectly ascertaining all cases within a region, and systems in resource-limited settings are particularly constrained in the data they collect and the inference that can be drawn from them. The passive surveillance system investigated here exhibited an average 30% ascertainment probability, lower than WHO’s estimate for the whole China (87%, 95% confidence interval: 75–100%) (World Health Organization, 2018). Our estimated ascertainment probability varied both by local economic conditions and by geographic location. Substantial underreporting within passive systems is commonly observed, and underreporting probability is known to be spatially heterogeneous (Alter et al., 1987; Gibbons et al., 2014; Held et al., 2006; Shepard et al., 2012; Thacker et al., 1983).

The active surveillance system exhibited an average 70% ascertainment probability, and through the integration of passive and active surveillance data we derived a bias-corrected estimate of disease prevalence across the province, adjusting passive counts according to spatially varying ascertainment probability. Bias-corrected estimates suggest that the prevalence of PTB in Sichuan Province in 2010 may have been up to five times higher than previously reported, and our analyses identified new areas of high burden in the southeast (Fig. 4b). The estimated lower performance of passive surveillance in the southeast that is associated with the region’s latitude and GDP may be related to cultural practices influencing care-seeking behavior and treatment compliance. Notably, the affected region includes the Liangshan Yi autonomous region, which is experiencing ongoing TB and HIV/AIDS epidemics, and where reporting capacity is known to be limited (Liu et al., 2009).

Limitations of the methods presented here include relying on successful record linkage between systems, and adherence to the closed population assumption within the study region and period. Because the passive surveillance system operates continuously while the active system is intermittent, to better approximate a closed population we adopted a criterion that allowed for inclusion of passive cases that occurred up to 12 months before the end of the active survey, based on the typical duration of treatment for PTB. Additionally, we treated active surveys as representative of the areas covered by passive systems. To bias-correct the passive reporting, we used ascertainment probabilities estimated in areas where active reporting was available, and extended these probabilities to regions without active data. We attempted to address this limitation by incorporating spatially-varying covariates in modeling passive ascertainment probabilities.

Several analytic and methodological directions warrant further investigation. First, like previous frameworks for the analysis of multi-system data, the model introduced in this paper cannot directly accommodate individual-level covariates in the system-specific ascertainment probabilities. This is because individuals that are not ascertained by either system do not have covariate information recorded. Future work may stratify ascertained cases by covariates (e.g., gender or age groups) to examine how ascertained probability varies across sub-populations. Second, the modeling approach warrants further extension to consider more than two systems by specifying the corresponding ascertainment histories and their probabilities, as in Table 1. One key assumption of our modeling framework is the independence between the active and the passive surveillance system. It is possible that in areas with active surveillance, the ascertainment probability is also higher in passive reporting due to better awareness and testing. With more than two systems, bivariate dependence between systems may be estimated, allowing the framework to provide more robust estimates of system ascertainment probabilities for most real-world scenarios. Another approach to account for dependence with only two systems may be to construct more informative priors for system-specific ascertainment probabilities based on expert knowledge (Stoner et al., 2019). Finally, further work could fruitfully extend the likelihood to model multi-source data that are spatiotemporal or multi-disease in nature, by introducing random effects in λ_s that are dependent between time points or between diseases. Extending the model to include temporal effects would allow the framework to be used to help disentangle trends in disease epidemiology from trends in reporting and ascertainment, which is a common problem when interpreting longitudinal disease surveillance data. Meanwhile, specifying a multi-disease hierarchical model would allow integration of more extensive surveillance data, leveraging commonalities in the occurrence, common risk factors for, and coincident surveillance of multiple outcomes.