Towards predicting the product quality in hot-melt extrusion: Small scale extrusion

Abstract

In product development, it is crucial to choose the appropriate drug manufacturing route accurately and timely and to ensure that the technique selected is suitable for achieving the desired product quality. Guided by the QbD principles, the pharmaceutical industry is currently transitioning from batch to continuous manufacturing. In this context, process understanding and prediction are becoming even more important. With regard to hot melt extrusion, the process setup, optimization and scale-up in early stages of product development are particularly challenging due to poor process understanding, complex product-process relationship and a small amount of premix available for extensive experimental studies. Hence, automated, quick and reliable process setup and scale-up requires simulation tools that are accurate enough to capture the process and determine the product-process relationships. To this end, the effect of process settings on the degradation of the active pharmaceutical ingredient (API) in a lab-scale Leistritz ZSE12 extruder was investigated. As part of the presented study, the limitations of traditional process analysis using integral process values were investigated, together with the potential that simulations may have in predicting the process performance and the product quality. The results of our investigation indicate that the average melt temperatures and the exposure times in specific zones along the screw configuration correlate well with the API degradation values and can be used as potent process design criteria to simplify the process development.

Graphical abstract

1. Introduction

Hot melt extrusion (HME) is increasingly applied in the pharmaceutical industry, mostly for solubilization of poorly soluble active pharmaceutical ingredients (McFall et al. 2019; Monschke et al. 2020; Schittny et al. 2018; Steffens and Wagner 2020; Vasoya et al. 2019) (APIs) in immediate release, control release (Fukuda et al. 2006; Vo et al. 2016; Zhu et al. 2006) and nano (Baumgartner et al., 2016, Baumgartner et al., 2014; Bhagurkar et al. 2017; Patil et al. 2015; Silva et al. 2018) formulations, as well as for the manufacturing of specific drug delivery devices (Bode et al. 2019; Cossé et al. 2017; Eder et al. 2017; Koutsamanis et al. 2019). This trend calls for fast, reliable and inexpensive product and process development (Breitenbach 2002; Crowley et al. 2007; Dadou et al. 2020; Evans et al. 2018; Huang et al. 2017; Kohlgrüber 2007; Matić et al. 2020; Patil et al. 2016; Rauwendaal 2014; Repka et al. 2007; Saerens et al. 2013). Typically, formulation and process development are disconnected, i.e., during the formulation development the formulation's processability is not considered. If at all, the formulation is only tested in a table-top-scale extruder, making it extremely challenging to transfer the product to the pilot and production scales. With that regard, the flexibility of HME in terms of process settings and screw configurations (the significant width of processing window) is of advantage, since a variety of formulations can be processed and various product goals can be fulfilled (e.g., immediate or controlled release formulations).

However, defining the optimal setting within this wide process window is challenging, especially across different scales. Thus, many tests are conducted to optimize the process performance. In addition, there are no universally applicable scale-up laws and the screw designs are not necessarily directly transferable (especially when multiple extruder vendors are involved). The process windows can vary so significantly that certain formulations are simply not processable on a bigger extruder. Lastly, few people in the pharmaceutical industry are trained to design, scale and optimize HME processes. All of this contributes to a significant increase in the development costs and risks, making HME an unlikely production choice. In light of that, significant effort has been made to better understand the technology and the process-product relationships, which is in alignment with the FDA Quality by Design (QbD) guidelines for pharmaceutical processes (Gupta and Khan 2012; ICH Q8 2017; Islam et al. 2014; Kumar and Gupta 2015; Mishra et al. 2018; Yu et al. 2014).

In terms of process development and transfer, the HME process is still mostly viewed as a black-box, and subtle differences in the screw geometry, screw configuration and processing conditions between the various extruder scales are been neglected or disregarded. The reason is relatively simple: although crucial for process understanding, experimental methods cannot offer insights into the extruder operation since only global parameters can be determined (e.g., the overall specific mechanical energy (SMEC), residence time distribution (RTD) of the process and the melt pressure and temperature at the die) for a given screw configuration and process settings. Resolved and detailed information (local fill rates, temperature inhomogeneity in the melt, shear distributions, pressures, etc.) are generally not available and cannot be obtained even using sophisticated PAT (Process Analytical Technology) equipment. Simulation methods can tackle these challenges and provide a much deeper process understanding. Considering the costs and complexity of process setup, it would be desirable to estimate the potential process windows and product quality ranges early on in the formulation phase, during which small amounts of API are typically available. This way, it would be possible to choose candidate formulations adequately and early on in the development stage.

Essentially, a model-based process design for a specific formulation requires three components:

• 1.a small-scale measurement methodology sufficiently similar to HME that requires small amounts of the formulation, with the goal of testing the formulation's response to various mechanical stress conditions,
• 2.a solid process understanding, i.e., a process model that predicts the process response (filling degree, melt temperature, RTD, SMEC, etc.) as a function of input parameters (screw configuration, screw speed, throughput, barrel temperature, etc.), and
• 3.a link between the critical material attributes (CMAs), the critical process parameters (CPPs) and the formulation responses (i.e., critical quality attributes, CQAs), in order to map out regions where the in-spec quality product is obtained. This is also known as the Design Space (DS) according to the QbD terminology.

To date, our group has worked intensively on the first two issues, developing a vacuum compression molding tool for rapid sample preparation (Eder et al. 2017; Treffer et al. 2015) and creating a high-fidelity Lagrangian simulation environment that is based on a combination of Smoothed Particle Hydrodynamics (SPH) and 1D mechanistic modelling as a tool for the HME process understanding, design and scale-up (Eitzlmayr et al., 2017, Eitzlmayr et al., 2014, Eitzlmayr et al., 2013; Eitzlmayr and Khinast, 2015a, Eitzlmayr and Khinast, 2015b). In our framework, SPH was used for a detailed 3D characterization of individual screw element pairs commonly found in co-rotating intermeshing twin screw extruders. The focus was on determining the dimensionless pressure build-up and power consumption (Kohlgrüber 2007; Pawlowski 1971) of the element pairs, as well as their distributive mixing action. The knowledge gained was subsequently applied for our 1D HME simulation code developed in-house, which accurately computes axial distributions of filling degree, pressure, melt temperature, SMEC, and local and overall RTDs. Details on the internals of the 1D HME code, the assumption, connections to the SPH simulation results, melt temperature calculation procedure, heat transfer coefficient calculations and so on, can be found in papers published earlier from our group (Eitzlmayr et al., 2014, Eitzlmayr et al., 2013). Unlike the commercially available 1D codes for extrusion, to calculate the melt flow 1D HME utilizes the dimensionless pressure and power characteristics and the distributive mixing action as the descriptor of individual screw performance, rather than simplified screw geometries. This is particularly advantageous when using nonstandard, complex mixing and/or kneading elements with discontinuous screw geometries, where the pressure and power characters can easily be calculated by means of high-fidelity 3D SPH simulations.

The underlying assumption of our approach is that the product quality is the result of the formulation's thermo-mechanical exposure during the process. If the thermo-mechanical history can be mirrored on various scales, so can be the resulting quality. With that regard, considering the full complexity of the process is crucial, rather than treating the process as a black-box problem (i.e., analyzing it based on integral values of SMEC and RTD and, occasionally, die melt temperature and pressure). The influence of every screw element in the screw configuration has to be examined, and the screw setup has to be addressed adequately in order to reach appropriate states of thermo-mechanical load on the product on various extruder scales.

The present study addresses the third point on the list by examining the influence of process conditions on the API degradation in a lab scale 12 mm (ZSE12) intermeshing co-rotation twin screw extruder from Leistritz. It included the process setup for the small-scale extruder (ZSE12), a comparison between the predicted (via 1D HME) and experimentally obtained process responses and an investigation of the product quality as a response to the process settings selected. First, the link between the product quality, the process settings and the readily available process variables, such as torque, SMEC and mean residence time distribution (mRTD) was investigated. This attempt resulted in limited success. However, the investigation was extended to include the possible correlations between the product quality and the process variables that are not easily available to an average process engineer, e.g., the melt temperature in a specific zone along the screw configuration and the mean residence time associated with that zone (local exposure time a certain local temperature peak). This is the novelty of the presented study and can be considered a step forward in extruder process setup, scale-up and design.

The overall goal of this study was to achieve a better understanding of the relation between the product quality attributes selected (i.e., degradation) and the HME settings in order to achieve a more reliable process setup and scale-up based on modelling.

2. Materials and methods

2.1. Equipment and process setup

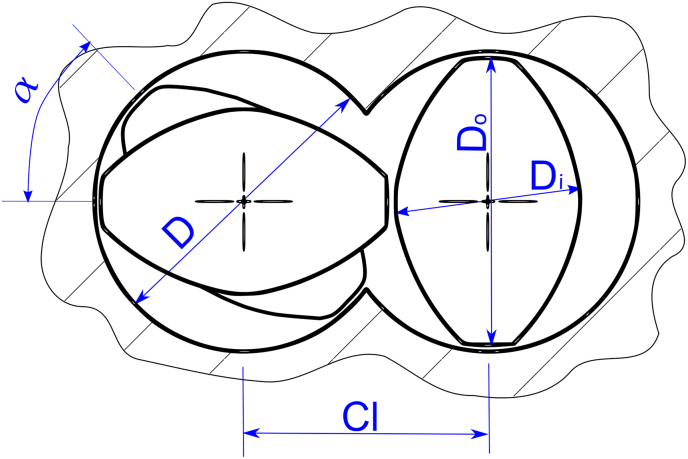
As mentioned above, in this study the ZSE12 12 mm extruder from Leistritz was used. This choice is in line with the initial product development phase that generally begins with the formulation screening and involves a small-scale extruder to minimize the amount of material requested and keep the process uncomplicated. The general extruder dimensions and a cross section of the ZSE12 extruder are presented in Table 1 and Fig. 1.

Table 1.

General characteristics of Leistritz lab-scale 12 mm ZSE12 HP-PH extruders.

ZSE12 HP-PH
D – Barrel diameter	12 mm
Do – Outer screw diameter	11.85 mm
Di – Inner screw diameter	7.85 mm
Cl – centerline distance	10 mm
τmax – Maximal available torque	20 Nm
Theoretical throughput range	0.05–1 kg/h
n – Screw speed	up to 1000 rpm

Fig. 1.

Details of the twin-screw extruder screw cross section showing the barrel diameter (D), screw outer and inner diameters (Do and Di, respectively), screw centerline distance (Cl) and the angle between the kneading discs for kneading elements (α).

The used screw configuration was the only one available at the time since the equipment was still in its prototype state. Six screw elements make up the entire configuration, of which three are standard conveying elements with pitches of 10 mm, 16 mm and 20 mm. The other three screw elements are kneading elements with angles (α in Fig. 1) of 30°, 60° and 90° between the individual kneading blocks. The full screw configuration has a length of 480 mm (standard 40 L/D), as shown in Table 2 and Fig. 2, and various processing zones. The powder intake zone consists of a series of conveying elements with a pitch of 20 mm, ending with two 16 mm pitcher elements before the melting zone. High-pitched conveying elements in the beginning of the powder intake zone are used for increasing the available free volume of the powder feed and achieving the maximum throughput for the extruder. Reducing the pitch before the kneading zone serves two purposes: (1) the powder is compacted, eliminating air pockets that might have formed; and (2) the lower pitch elements are more suitable for pressure build-up before the first kneading zone. The first kneading zone (also melting zone) contains a combination of 30° and 60° kneading elements. Its process function is to fully melt the polymer-API mixture. The setup involving two angles of the kneading elements results in different inherent conveying capabilities, which creates a “soft” back-conveying zone. As a result, a small section with an increased fill degree can be expected. The kneading zones following the initial melting zone consist of three sections and ensuring the various stages of distributive and dispersive mixing action and increased mechanical energy input: the first one with a 90° kneading element, the second one with a combination of 30° and 60° kneading elements and the third one with a 60° kneading element. Note that the first and third kneading section have the same configuration (i.e., a combination of 30° kneading element followed by a 60° kneading element) but different process functions (i.e., melting and mixing, respectively). Three mixing zones are not required for the formulation examined and such a screw setup is normally used when liquid and/or secondary powder feeding in employed in the remaining conveying sections (which is not the case in this study). Before the die, a pressure build-up zone is set up by reducing the conveying element pitch: first, from 20 mm to 16 mm and then to 10 mm. The goal is to build up enough pressure to force the extrudate through the die. The die has a cylindrical length of 3.75 mm and a cylindrical diameter of 2 mm. The same screw configuration with the inherent conveying and pressure build-up numbers of the individual screw element pairs was also used as a basis for the screw discretization in the 1D HME simulations.

Table 2.

The screw configuration for the trials on the ZSE12 prototype extruder, with A₁ and A₂ parameters for 1D HME simulations.

Official Name	Short Name	Screw Length [mm]	Pitch/Angle [mm/°]
GFA-2-20-30-A	C20	30	20
GFA-2-20-30	C20	30	20
GFA-2-20-30	C20	30	20
GFA-2-20-10	C20	10	20
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
KB4-2-10-30°-Re	K30	10	30°
KB4-2-10-60°-Re	K60	10	60°
GFA-2-16-10	C16	10	16
KB4-2-10-90°	K90	10	90°
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
KB4-2-10-30°-Re	K30	10	30°
KB4-2-10-60°-Re	K60	10	60°
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
KB4-2-10-60°-Re	K60	10	60°
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
GFA-2-16-20	C16	20	16
GFA-2-16-10	C16	10	16
GFA-2-10-20	C10	20	10
GFA-2-10-20	C10	20	10
GFA-2-10-20	C10	20	10
Total length:		480 mm

Nomenclature: C-conveying element; K-kneading element.

Fig. 2.

Prototype screw configuration used for the ZSE12 extruder experiments and 1D HME simulations. The screw configuration is assembled from three conveying elements with pitches for 20 mm, 16 mm and 10 mm (C20, C16 and C10 respectively) and kneading elements.

The process settings (screw speed, throughput and barrel temperature) were chosen to cover the broadest processing window possible, disregarding the possible ramifications for the product quality. The goal of any formulation and process development step is the production of an in-spec product (in our case, amorphous API without any degradation). However, assuming that in-spec product can be achieved within a process window (i.e., the design space), it may be even more interesting to study under which process conditions the product fails and why (i.e., the envelope of failure). Hence, the process throughput was set from 0.1 kg/h to 0.4 kg/h; the screw speed was set to 100 rpm, 300 rpm and 500 rpm. The two barrel temperature settings were 120 °C and 140 °C, ensuring a broad process window for our study. Details of process settings are provided in Table 3, Table 4.

Table 3.

Throughputs, screw speeds and barrel temperature profiles used for the ZSE12 trials and 1D HME simulations.

Exp. Nr.	Throughput [kg/h]	Screw speed [rpm]	Barrel temperature profile
PN 1	0.1	100	I
PN 2	0.4
PN 3	0.1	100	II
PN 4	0.4
PN 5	0.1	300	I
PN 6	0.4
PN 7	0.1	300	II
PN 8	0.4
PN 9	0.1	500	I
PN 10	0.4
PN 11	0.1	500	II
PN 12	0.4

Table 4.

Barrel temperature settings used in the ZSE12 trials and simulations.

Profile	B. 1	B. 2	B. 3	B. 4	B. 5	B. 6	B. 7	B. 8	Die
I	40 °C	60 °C	120 °C	120 °C	120 °C	120 °C	120 °C	120 °C	120 °C
II	40 °C	60 °C	140 °C	140 °C	140 °C	140 °C	140 °C	140 °C	140 °C

2.2. Formulation

The model formulation was a simple two-component system comprising Eudragit RL PO with a 20% mass loading of Famotidine. Famotidine is prone to thermal degradation. Eudragit RL PO is an established polymer applied in hot-melt-extruded formulations (Maniruzzaman et al. 2013; Mustafin 2011; Perpétuo et al. 2013). Famotidine commercially available as polymorph B (Haihang Industry Co., Ltd., China) and Eudragit RL PO (Evonik Industries, Germany) were the materials used in the extrusion experiments. Pre-blends with 20% of Famotidine content were prepared in 2 L containers (1 kg) and mixed with the Turbula T2F (WAB-Group, Switzerland) for 10 min at 60 rpm.

Research shows that the two components do not interact with each other (Chordiya et al. 2011). They are suitable candidates for the preparation of solid dispersions since the melting point of Famotidine (form B, 166°) and the expected extrusion temperature window of Eudragit RL (165–170 °C) (Parikh et al. 2014) are within a similar temperature range. Furthermore, Famotidine is a thermolabile drug, which begins to degrade shortly after melting (Viciosa et al. 2016), making degradation a probable event in the chosen process settings.

To model the process via our 1D HME simulation tool, the used formulation had to be parametrized. Heat capacity, thermal conductivity, specific volume and viscosity of the selected formulation were measured, analyzed and fitted with suitable models. The PVT behavior of the formulation was measured using a PVT100 device in accordance with the ISO 17744 guidelines. The measurements were performed at 40 °C-220 °C and 200 bar-1200 bar. The data obtained were fitted to the Schmidt model (Schmidt 1986) in order to be used in the 1D HME simulations to calculate specific volume v [cm³/g]:

$$v_{\left(p,T\right)}=\frac{K_1}{p+K_4}+\frac{K_2\bullet T}{p+K_3}$$ (1)

Two sets of K₁ to K₄ parameters are used, one for the solid phase (if temperature T is below the transition temperature) and one for the liquid phase (if temperature T [°C] is above the transition temperature). The transition temperature T_tr [°C] is a function of pressure p [bar] and is calculated as:

$$T_{\mathit{tr}\left(p\right)}=K_8+K_9\bullet p$$ (2)

The relevant K₁ to K₉ parameters can be found in Table 5.

Table 5.

K parameters for calculating the specific volume according to the Schmidt model.

	Solid state	Melt state
K1 [bar cm3/g]	28,811	35,221
K2 [bar cm3/(g°C)]	1.0731	1.2637
K3 [bar]	3050.1	2650.9
K4 [bar]	35,556	44,179
K8 [°C]	106.12
K9 [°C/bar]	0.002816

Rheology of the formulation was measured with a standard plate-plate rheometer (MCR 301 from Anton-Paar). The sample preparation for the rheology measurements was performed using the vacuum compression molding tool, that was specifically developed for such purposes (Treffer et al. 2015). The frequency range measured spans between 0.1 s⁻¹ to 628 s⁻¹ for three probe temperatures of 100 °C, 115 °C and 130 °C. The data points obtained were subsequently fitted via a simplified variant of the Carreau-Yassuda model for non-Newtonian fluids:

$$\eta \left(\dot{\gamma },T\right)=\frac{{\eta }_0{a}_T}{{\left(1+\frac{\left|\dot{\gamma }\right|a_T}{{\dot{\gamma }}_{\mathit{crit}}}\right)}^m}$$ (3)

where η ist the viscosity in [Pa ∙ s], T[°C] is the melt temperature, $\dot{\gamma }\left[s^{-1}\right]$ is the shear rate, ${\dot{\gamma }}_{\mathit{crit}}\left[s^{-1}\right]$ is the critical shear rate, η₀[Pa ∙ s] the zero-shear-rate viscosity and a_T [−] is the Williams-Landel-Ferry temperature shift factor calculated as:

$$a_T=\mathit{exp}\left[-\frac{C_1\left(T-T_r\right)}{C_2+T-T_r}\right]$$ (4)

with T_r[°C] being the reference temperature. The viscosity parameters used for the fit are shown in Table 6. The heat capacity and thermal conductivity were approximated via linear temperature-dependent fits. Both were measured via modulated differential scanning calorimetry (mDSC) using the DSC 2014 F1 Phoenix® with an automated sampling unit (NETZSCH-Geraetebau GmbH, Selb, Germany). The heat capacity [J/m³K] below glass transition temperature T_g = 65 ° C is:

$$c_{p,s}=-273.04+38.22\bullet T$$ (5)

and above the glass transition temperature:

$$c_{p,\mathrm{m}}=2095.35+1.55\bullet T$$ (6)

Table 6.

Parameters for the Carreau-Yassuda viscosity fit.

η0 [Pas]	50,250
${\dot{\mathrm{\gamma }}}_{\text{crit}}$ [s−1]	0.64
m [−]	0.5703
Tr [°C]	130
C1 [−]	15.1378
C2 [°C]	132.0361

The thermal conductivity λ[W/mK] was modeled as:

$$\lambda =0.15633+4.704\bullet {10}^{-4}\bullet T$$ (7)

where T is the melt temperature.

2.3. Mean residence time measurements

In the course of the process, the residence time distribution (RTD) was measured, evaluated and compared to the results obtained via 1D HME. The measurements were executed after a steady state was reached and samples for product-quality measurements were obtained. A blue pigmented tracer pellet of approximately 10-20 mg was inserted into the extruder's powder inlet. At the same time a camera (Fujifilm Fine Pix HS25EXR) began recording the die's strand outlet. The resulting videos were post-processed in Matlab® (Mathworks, Natick, MA, USA) using the script developed earlier (Kruisz et al., 2018, Kruisz et al., 2017; Wahl et al. 2018). Each video frame was analyzed to determine the average values assigned to the RGB color space within a specified mask, which deliberately included only the portion of strand where the color change was observed. For a better signal, the score of 1st Principal Components (PC1) of RGB values was computed and accessed. The PC1 signals obtained were fitted to an analytical solution of the Fokker-Planck equation for twin-screw extruders, where the exit age distribution E(τ) is a function of the Peclet number Pe and the dimensionless time τ = t/θ, with t being the actual time and θ being the mean residence time (mRT):

$$\text{color values}=\mathrm{k}\mathrm{f}\left(\mathrm{Pe},\mathrm{\tau }\right)$$ (8)

$$\mathrm{E}\left(\mathrm{\tau }\right)=\mathrm{f}\left(\mathrm{Pe},\mathrm{\tau }\right)=\sqrt{\frac{\mathrm{Pe}}{\mathrm{\pi \tau }}}exp\left(-\frac{\mathrm{Pe}}{4}\frac{{\left(1-\mathrm{\tau }\right)}^2}{\mathrm{\tau }}\right)-\frac{\mathrm{Pe}}{2}exp\left(\mathrm{Pe}\right)erfc\left(\sqrt{\frac{\mathrm{Pe}}{4}}\frac{1+\mathrm{\tau }}{\sqrt{\mathrm{\tau }}}\right)$$ (9)

2.4. API degradation

The extrudate's samples consisted of pellets from the strand granulator collected after reaching a steady process. Triplicates of randomly-sampled pellets were weighed in volumetric flasks and dissolved in methanol in an ultrasound bath for 10 min. The resulting solutions were transparent, ranging from colorless to red, correlating with the extrudate's color. This suggests that the impurity responsible for the color may be soluble in methanol. The percent of degradation f was calculated based on the difference between initial pre-blend content C₀ and final extrudate content C_extrudate from the UPLC measurements.

$$f=\frac{C_0-C_{\mathit{extrudate}}}{C_0}\bullet 100\%$$ (10)

The content of Famotidine from the extrudates Famotidine solutions was obtained via UPLC using an Acquity UPLC™ HSS T3 (100 × 2.1 mm²) 1.8-μm column at 40 °C and a detection wavelength of 266 nm. Gradient elution was applied to separate FAM from its impurities, with a mobile phase of ACN (acetronytril) and TFA (trifluoroacetic acid) in water, a variable composition over time and a constant flow rate of 0.4 mL/min. Full specifications are provided in Table 7.

Table 7.

HPLC method for Famotidine detection.

Column	Waters Acquity UPLC T3 1.8 μm × 100 mm
Calibration Range	50-700 ppm
Flow	0.400 mL/min
Wavelength	266 nm
Column Temperature	40 °C
Sample Temperature	20 °C
Injection Volume	1 μL
Duration	10 min
Mobile Phase Flow
Time [min]	Volume [%]
	0.03% TFA in Water	ACN
0.0	97	3
0.5	97	3
1.0	20	80
8.0	20	80
8.1	97	3
10.0	97	3

ACN = acentonitrile; TFA = trifluoroacetic acid

3. Results and discussion

3.1. Effect of process settings on extruder state

As part of the process control and simulation validation efforts, the process torque, SMEC and RTD were captured, analyzed and compared to the values obtained in the 1D HME simulations. A detailed analysis can provide valuable insights into the process, showing the effect of the process settings on the filling degree, the melt temperature and the pressure profile (see our earlier work (Matić et al. 2019)). A comparison between the experimental and in silico values is important for validating the simulations, including the A1 and A2 values used to parametrize the screws, and the parametrization of the formulation obtained via the material's measurements. Note that the A1 and A2 values represent the inherent conveying and pressure build-up capacities of individual screw element pairs, respectively. They are a dimensionless representation of the conveying and pumping action of the screw geometries and are discussed in more detail in our earlier work (Eitzlmayr et al. 2017; Eitzlmayr and Khinast 2015b) and the literature (Kohlgrüber 2007; Pawlowski 1971). The experimental and modeled torque and SMEC values are shown in Table 8, Fig. 3, Fig. 4, respectively.

Table 8.

Process and product response in the settings applied.

Trial Nr.	Throughput [kg/h]	Screw speed [rpm]	Barrel temp.	Torque [Nm]	SMEC [kWh/kg]	mRT1D [s]	API Degradation
PN 1	0.1	100	I	3.91	0.410	530	7%
PN 2	0.4			4.25	0.112	164	3%
PN 3	0.1	100	II	2.82	0.295	527	18%
PN 4	0.4			3.30	0.087	163	7%
PN 5	0.1	300	I	3.72	1.170	503	27%
PN 6	0.4			4.42	0.347	136	9%
PN 7	0.1	300	II	3.01	0.947	499	44%
PN 8	0.4			3.73	0.292	135	19%
PN 9	0.1	500	I	3.60	1.884	498	61%
PN 10	0.4			4.29	0.562	131	24%
PN 11	0.1	500	II	2.82	1.477	494	81%
PN 12	0.4			3.39	0.444	130	36%

Fig. 3.

Influence of process settings on the extruder torque obtained experimentally and in silico (1D).

Fig. 4.

Influence of process settings on the process SMEC obtained experimentally and in silico (1D).

Although the model does not capture the torque exactly, it captures the torque and SMEC trends well. The ZSE12 extruder has a maximal available torque of 20 Nm. An increase in the throughput results in an increase in the torque needed for the rotation of the shaft. This is expected since there is more material in the system to be processed. In contrast, an increase in the barrel temperature results in a decrease of the torque needed for processing. This can be attributed to overall higher melt temperature that is achieved due to an equilibrium between the heat dissipation and the higher barrel temperature settings. Higher melt temperature also means a reduced overall melt viscosity and since it lowers the resistance of the processed melt to deformation, it also reduces the torque needed for the screw rotations.

A change in screw speed does not seem to change the process torque in this example, most likely due to relatively low throughputs, i.e., low overall filling degree of the extruder. The torque and SMEC [kWh/kg] are functionally connected as:

$$\mathit{SMEC}=\frac{2\bullet \pi \bullet n\bullet \tau }{60000\bullet \dot{m}}$$ (11)

Here, n is the rotation rate in [rpm] and τ the torque in [Nm] and $\dot{m}\left[\mathit{kg}/h\right]$. SMEC represents the energy the screws provide to process the material per kilogram of material. Therefore, an increase in the screw speed directly translates into more energy per kilogram of processed material. Similarly, an increase in the throughput or the barrel temperature reduces the energy consumed from the screws since the amount of material increases (increased throughput) or energy is provided by the increased barrel heat.

In addition to the torque and SMEC, experimental and in silico mRT values were obtained and analyzed. Experiments determining the mRT were performed using only pure Eudragit RL. Due to excessive clogging of the material in the powder intake zone it was impossible to run extrusions in the high-throughput-low-screw-speed setting (0.4 kg/h and 100 rpm). Thus, for both barrel temperatures and 0.4 kg/h throughput settings, experiments were run at higher screw speeds, i.e., 250 rpm instead of 100 rpm. The results are summarized in Fig. 5.

Fig. 5.

Influence of the process settings on the mean RTD (mRT) obtained experimentally and in silico (1D).

The 1D HME model captures well the measured mRT and the influence of the throughput, screw speed and barrel temperature on the mRT. A reduction in the mRT can be expected in response to an increase in the screw speed, at least in this screw configuration. A more drastic change in the mRT can be expected due to a change in the throughput. In contrast, a change in the barrel temperature has a minor effect on the mRT. The reason is could be that the mRT is also a measure of extruder filling, i.e., a higher screw speed empties the extruder until the lowest possible fill level is reached at a given throughput, after which it remains constant. On the other hand, an increase in the throughput forces the material to move faster at a given screw speed.

In one setting (0.1 kg/h @ 300 rpm and Barrel temp. II), the difference between the experimental and in silico mRT values was more pronounced. It was most likely an outlier caused by an error in the RTD measurement since it does not follow the expected mRT behavior, i.e., the difference between the mRT obtained at barrel temperatures I and II in otherwise identical settings (0.1 kg/h @ 300 rpm) was higher than expected and higher than observed in any other settings. Moreover, it is implausible that the mRT is lower at 0.1 kg/h @ 300 rpm than at a screw speed of 500 rpm in the same setting.

3.2. The effect of process settings on the degradation

As stated before, the HME process settings were chosen such that in some settings the API degradation would be observed. To that end, API degradation was analyzed as a function of the independent process variables: the screw speed, the throughput and the barrel temperature.

The influence of screw speed, throughput and barrel temperature on the API degradation is shown in Fig. 6. With other process variables constant, an increase in the screw speed clearly leads to an increase in the API degradation. Since the shear rates in the extruder increase linearly with the screw speed, the viscous dissipation and the melt temperature are higher. Hence, the increase in degradation is linear to the screw speed. An increase in the throughput has the opposite effect on the API degradation due to a decrease in the residence time of the melt inside the extruder. Moreover, increasing the barrel temperature increases the API degradation. Since the melt temperature is simply a balance between the viscous dissipation and the barrel's cooling power, it is clear that, with all other process variables constant, an increase in the barrel temperature will result in higher melt temperatures and a higher API degradation. Interestingly, the 0.4 kg/h-Barrel temp. II setting results in an equal or lower API degradation compared to the 0.1 kg/h-Barrel temp. I setting, i.e., an increase in the API degradation that is only due to the barrel temperature increase (from Barrel temp. I to II) is lower than that due to a reduction in throughput (from 0.4 kg/h to 0.1 kg/h) in the studied system. Although it is possible to establish the limits within which the process variables can vary to yield an acceptable product quality (DS), the throughput and the barrel temperature cannot be used as a unique descriptor of the expected product quality (in our case, quantified as the extent of API degradation). This is an important result of this work.

Fig. 6.

API degradation versus the process screw speed, throughput and barrel temperature.

In order to identify a unique descriptor of API degradation, the process state variables that can be measured during the process, e.g., mRT and SMEC, were investigated. The contribution of mRT to understanding the effect of process settings on the API degradation is illustrated in Fig. 7. Since two throughputs are considered, the mRT results are clustered around 150 s for 0.4 kg/h throughput and around 500 s for 0.1 kg/h throughput at 3 screw speeds. The results suggest that the API degradation cannot be sufficiently explained based on the overall process mRT alone since relatively similar mRT values result in drastic variations in the API degradation. Hence, relying on the mRT as a sole process descriptor for setup and scale-up does not seem to be a good approach if consistent product quality is the goal.

Fig. 7.

API Degradation as a function of process mRT_1D, throughput and barrel temperature.

Another dependent variable often used as a setup and scale-up criteria is the SMEC consumed during the process. Fig. 8 shows the obtained API degradation as a function of the process SMEC. SMEC increases with an increase in the screw speed, but decreases with increased throughput and barrel temperature, provided that all other process variables are constant.

Fig. 8.

API Degradation versus process SMEC, with cases A, B, C and D showing either similar API degradation for different SMEC values or different API degradation for similar SMEC values.

This was expected since, as discussed above, an increase in the barrel temperature leads to an increase in the melt temperature, lowering the melt viscosity and the viscous dissipation. Moreover, the throughput is in the denominator in the SMEC equation (Eq. 11). At first glance, SMEC seems to be a good predictor/descriptor of API degradation, which rises steadily together with the rising SMEC. In processes with a throughput of 0.4 kg/h, the SMEC and the API degradation do not exceed ~0.6 kWh/kg and 40%, respectively. At 0.1 kg/h, a maximal SMEC of around 1.88kWh/kg and an API degradation of above 80% are achieved. It should be noted that this SMEC input is exceptionally high and most likely would not be considered a viable process setup in the traditional sense. Fig. 8 shows that multiple process settings can result in different SMEC values but similar API degradation levels, and vice versa. In our case, it is possible to form at least three pairs of settings that result in a similar degradation:

• •A: PN 1 (0.1 kg/h, 100 rpm, temp I, 0.410kWh/kg) and PN 4 (0.4 kg/h, 100 rpm, temp. II, 0.087kWh/kg) with an API degradation of 7%
• •B: PN 3 (0.1 kg/h, 100 rpm, temp. II, 0.295kWh/kg) and PN 8 (0.4 kg/h, 300 rpm, temp. II, 0.292kWh/kg) with API degradations of 18% - 19%, respectively.
• •C: PN 5 (0.1 kg/h, 300 rpm, temp. I, 1.170kWh/kg) and PN 10 (0.4 kg/h, 500 rpm, temp. I, 0.562kWh/kg) with API degradations of 27% and 24%, respectively.

In addition to case B, there is one more case with a similar SMEC and a different API degradation:

• •D: PN 1 (0.1 kg/h, 100 rpm, temp. I, 0.410kWh/kg) and PN 12 (0.4 kg/h, 500 rpm, temp. II, 0.444kWh/kg) with API degradations of 7% and 36%, respectively.

Clearly, similar API degradation and similar SMEC values are only achieved in case B. In the others cases, although the corresponding SMEC values are similar, the resulting API degradations vary significantly (e.g., settings A and C) or the SMEC values are similar but the API degradations are significantly different (e.g., case D).

This is an important result: although higher SMEC values generally result in higher API degradations, SMEC does not seem to be a good descriptor of the process and product quality equivalence. Therefore, it is not advisable to use it for scale-up, as suggested by many authors and discussed in one of our previous papers (Matić et al. 2019). Moreover, even in case C with the same barrel temperature profile (profile I), the resulting SMEC values differ by a factor of two while the API degradation is similar. However, assuming that the maximal throughput is desirable, this is a good example of achieving the same product quality at two throughputs on the same machine.

In light of the above, rather than SMEC, the process mRT and the SMEC divided by the process mRT were considered as possible descriptors of API degradation, using integral process values (Fig. 9). The SMEC is divided by the process mRT in order to eliminate the time variable from the SMEC values since the SMEC value indirectly contains the mRT.

Fig. 9.

API degradation as a function of process SMEC/mRT_1D and mRT_1D.

Fig. 9 shows that at a constant exposure time (mRT), an increase in the SMEC/mRT value results in an increased API degradation at constant barrel temperature. Furthermore, the results for the same barrel temperature settings indicate that similar SMEC/mRT values with a higher mRT result in a higher API degradation (i.e., if the formulation is exposed to the amount of power per kilogram for a longer time period, the API degradation is likely to increase). Since increasing the barrel temperature decreases the SMEC of the process while having no significant impact on the mRT, the comparability between the settings with different barrel temperatures is not provided. The example above indicates that same SMEC and mRT values can be obtained in different process settings (screw speed, throughput and barrel temperature settings) while similar SMEC and mRT values can be achieved using different screw configurations. This implies that the product quality (in this case, API degradation) is not uniquely correlated with any of the independent or state variables that can be easily obtained and controlled during the process. Hence, process setup and scale-up methods whose goal is to maintain similar values of SMEC and mRT are fundamentally flawed and will inevitably result in extensive process optimization efforts.

To find more suitable product quality descriptors results from the 1D HME simulations were analyzed in more detail. The distribution of filling degree and melt temperature of one exemplary setting obtained in 1D HME reduced-order simulations is shown in Fig. 10. The shown setting is the 0.1 kg/h throughput at 100 rpm screw speed with the two barrel temperature settings. The filling degree of the extruder is a function of screw configuration (location and combination of screw elements with different melt conveying capacities), throughput and screw speed. A screw configuration with kneading elements that typically have lower conveying capacities than conveying elements (Eitzlmayr et al. 2017; Matić et al. 2019) will result in a higher filling degree or a fully filled section. This can be observed in the location of 90° kneading element (location 2 in Fig. 10). An increase in the screw speed leads to a decrease in the overall filling degree, and an increase in the throughput has the opposite effect on the overall filling degree. It is important to note that a change in the barrel temperature generally does not result in a change in the extruder's filling degree. Examining the effect of increasing the barrel temperature on the melt temperature indicates that, when all other parameters are constant, the melt temperature also increases by the same degree (about 20 °C in our example). The location of high temperature peaks does not change since it is primarily a function of screw configuration. Fully filled sections with kneading elements tend to create melt temperature peaks due to higher energy inputs and longer residence times in these regions, as illustrated below. Based on the melt temperature distribution, it was possible to investigate the (cross section-averaged) melt temperature and the local mRT (lmRT) values in various zones along the extruder screw configuration. To calculate the lmRT values, the lengths of individual kneading zones were taken as the representative lengths. Given the screw configuration used (Fig. 2) and the location of melt temperature peaks, five possible zones of interest were defined: four kneading sections (from 1 to 4 in Fig. 10) and the die section (5 in Fig. 10). In Fig. 11, Fig. 12, Fig. 13, Fig. 14, the relative API degradation (i.e., relative to the initial amount of API) is shown as a function of average melt temperature and lmRT in particular zones.

Fig. 10.

Melt temperature and filling degree obtained in the 1D HME simulations for the 0.1 kg/h throughput at 100 rpm screw speed and both barrel temperature settings.

Fig. 11.

API degradation as a function of local mRT_1D and average melt temperature in the 1^st and in the 3^rd kneading zones, (assembled from 30° and 60° kneading elements). The amount of API degradation is shown in the boxes for every combination of local mRT_1D and averaged local melt temperature.

Fig. 12.

API degradation as a function of local mRT_1D and average melt temperature in the second kneading zone with a 90° (K90) kneading element. The degree of API degradation is shown in boxes for every combination of local mRT_1D and averaged local melt temperature.

Fig. 13.

API degradation as a function of local mRT_1D and average melt temperature at the 4rd kneading zone, assembled from one 60° kneading element. The amount of API degradation is shown in the boxes for every combination of local mRT_1D and averaged local melt temperature.

Fig. 14.

API degradation as a function of local mRT1D and average melt temperature in the die zone. The degree of API degradation is shown in boxes for every combination of local mRT1D and averaged local melt temperature.

The first and the third kneading zone have the same configuration, the same lmRT values of ~0.5 s- 2.8 s and the same average melt temperatures of ~140 °C - ~155 °C (Fig. 11). The second kneading zone is the most ‘aggressive’ kneading zone with 90° kneading elements, lmRT values of ~8 s - ~33 s and average melt temperatures of ~159 °C-185 °C (Fig. 12). The fourth kneading zone section consisting of one 60° kneading element has lmRT values of ~0.4 s- ~ 2.9 s and average temperatures of ~140 °C - ~158 °C (Fig. 13). As stated above, the die section has the longest lmRT (~145 s - ~460 s), accounting for most of the overall lmRT, with temperatures ranging from ~139 °C to ~157 °C (Fig. 14). Although the die section has the highest lmRT of all, the melt temperature is relatively low, with a low energy input (no dissipation from the screw). Note that there are different lmRTs in different locations along the screw. Whereas the fully filled sections in the location of 90° kneading element and the die section have two distinct lmRT values (~8 s and ~ 33 s for the 90° element and ~ 145 s and ~ 460 s for the die section), the partially filled kneading element section has three distinct lmRT values. This is due to the different forces driving the residence time in the fully and partially filled zones. In the former, the dominant RTD driving force is the throughput of the system (two distinct lmRT values resulting from two throughput settings), whereas in the latter the screw speed drives the transport of material and the RTD (three distinct lmRT values resulting from three screw speed settings).

Analyzing the lmRT and average melt temperature plots in terms of API degradation predictability shows that the average melt temperature and lmRT in the 90° kneading element zone correlate closely with the API degradation (Fig. 12). Note that the residence time in this kneading zone is not a function of rpm since the screw is fully filled. All other zones do not provide a clear link between the API degradation and the melt temperature and lmRT. Fig. 11, Fig. 13, Fig. 14 indicate that a lower melt temperature results in a higher degradation despite a constant exposure time (constant lmRT) and that at constant melt temperature a shorter exposure time will result in a higher API degradation, which cannot be true. Thus, at least in the presented case, the average melt temperatures and lmRT in the die and other kneading sections (except of the 90° kneading element zone) cannot be key drivers of the API degradation. Nevertheless, Fig. 12 clearly shows the API degradation as a function of local mRT and average melt temperature. At a constant exposure time (constant lmRT), a higher average temperature will always result in a higher API degradation. The effect of barrel temperature is also inherently included. In the case of constant (or similar) average melt temperature, longer exposure time at a certain temperature will result in a higher API degradation. Moreover, Famotidine has been reported to be a thermolabile drug substance that degrades at or slightly above the melting point of ~165 °C (Viciosa et al. 2016), which is the temperature expected in the 90° kneading element zone, according to the simulation results. Hence, the temperature and time of exposure in certain zones along the screw configuration could be used a predictor of API degradation.

4. Summary and conclusion

Developing roadmaps and tools for quick, safe and efficient pharmaceutical process setup and scale-up of continuous pharmaceutical processes is crucial for cost-efficient drug production. HME is especially interesting since it provides solubility enhancement to poorly soluble pharmaceutical APIs. What is more, it is a modular process with a variety of screw elements to choose from while designing the screw configuration. However, modularity can hinder the process design (e.g., the process may have to be developed from scratch for a new API and/or carrier combination), and, in addition to being poorly soluble, APIs are often temperature-sensitive and available in low quantities during the initial development phase. Hence, the HME process development and scale-up for pharmaceutical purposes has to be accomplished in a manner that is different from traditional pharma manufacturing. Process simulations and investigations of process-product relationships are essential for achieving a quick and reliable process setup.

In this work the degradation of Famotidine (in the 20% Famotidine and 80% Eudragit RL formulation) as a function of extruder settings was examined. A Leistritz ZSE12 12 mm extruder was used, representing a small-scale extruder typically applied in product development. The API degradation was chosen as the relevant product response. The process settings selected assured a wide process window to elicit a significant degradation and reduce the product quality. The resulting API degradation was evaluated as a function of process SMEC and SMEC/mRT ratio. SMEC alone was not a good descriptor of process adequacy in terms of API degradation since a similar degradation was achieved at different SMEC values and similar SMEC values lead to different API degradation levels. Analyzing the API degradation as a function of mRT and SMEC/mRT was a better process descriptor in one barrel temperature setting. At similar SMEC/mRT values, a higher API degradation was achieved with higher mRT. Assuming that the combination of melt temperature and mRT is responsible for the API degradation, zones of interest (zones of high stress) were defined along the screw. The most relevant zones are zones in kneading elements and the die section where overall higher residence times are expected. The API degradation was investigated as a function of local mRT and local average melt temperature obtained in the 1D HME simulations for all the relevant zones. It was established that the 90° kneading element zone has the highest average melt temperature peaks and correlates with the API degradation best, i.e., a higher API degradation is achieved at higher averaged melt temperature in this zone and a higher local mRT. The influence of screw speed, throughput and barrel temperature was taken into account. The above insights can be used in the HME process development according to the QbD framework prior to any actual extrusion trials. By analyzing the API degradation as a function of time and temperature, various screw configurations, screw speeds, throughputs, barrel temperatures and die designs can be evaluated in terms of resulting SMEC values, mRT values, local mRT values and melt temperatures in order to predict the product response. This can greatly simplify the pharmaceutical HME process setup and scale-up and eliminate a number of assumptions in the process design.

In summary, it means that future formulation quality charts could be developed that show the formulation quality as a function of temperature and exposure time. This way, the process could first be designed in silico to remain within the desired temperature and exposure time boundaries (i.e., the design space) along the entire screw configuration to guarantee adequate product quality. In the end of the process design phase, the in silico design space could be experimentally validated, significantly reducing empiricism, waste and energy demand during process and product development.

Nomenclature

Latin symbols
aT [−]	Williams-Landel-Ferry temperature shift factor
cp, s and cp, m [J/kgK]	Heat capacity of solid and melt, respectively
cv [J/m3K]	Specific heat capacity at constant volume
c0 and cextrudate	Initial API content and API content in the Extrudate, respectively
C1 and C2 [−,°C]	Fitting parameters for the WLF temperature shift factor
D [m]	Barrel diameter
Di [m]	Inner screw diameter
Do [m]	Outer screw diameter
f [%]	Percentage of degradation
K1, K2, K3, K4, K8, K9 [bar cm3/g, bar cm3/g°C, bar, bar, °C, °C/bar]	Menges density factors
$\dot{m}$ [kg/h]	Throughput
n [rpm]	Screw speed
p [bar]	Pressure
Pe [−]	Peclet number
T, Tr and Ttr [°C]	Melt temperature, reference temperature and transition temperature
t [s]	Time
Greek symbols
α [°]	Cross section/kneading block tilt angle
$\dot{\gamma }$ and ${\dot{\gamma }}_{\mathit{crit}}$ [s−1]	Shear rate and critical shear rate, respectively
η and η0 [Pas]	Fluid viscosity and zero-shear-viscosity, respectively
Θ [s]	mRT
λ [W/mK]	Thermal conductivity
v [cm3/g]	Specific volume
τ [s]	Dimensionless time
ω, ψ, ε, χ, κ, ξ [−]	Exponents of the Menges and Feistkorn scale-up method

Abbreviations

A1	Inherent Conveying Capacity
A2	Inherent Pressure Build-Up Capacity
API	Active Pharmaceutical Ingredient
ACN	Acentonitrile
DS	Design Space
HME	Hot-Melt Extrusion
mRT	mean Residence Time
lmRT	local mean Residence Time
PAT	Process Analytical Technology
PC1	1st Principal Components
PVT	Pressure Volume Temperature
QbD	Quality by Design
RTD	Residence Time Distribution
SMEC	Specific Mechanical Energy Consumption
SPH	Smoothed Particle Hydrodynamics
TFA	Trifluoroacetic Acid
TSE	co-rotating Twin-Screw Extruder
ZSE12	Leistritz 12 mm co-rotating twin-screw extruder

Declaration of Competing Interest

None.