Boundary Element Fast Multipole Method for Enhanced Modeling of Neurophysiological Recordings

Abstract

Objective:

A new numerical modeling approach is proposed which provides forward-problem solutions for both noninvasive recordings (EEG/MEG) and higher-resolution intracranial recordings (iEEG).

Methods:

The algorithm is our recently developed boundary element fast multipole method or BEM-FMM. It is based on the integration of the boundary element formulation in terms of surface charge density and the fast multipole method originating from its inventors. The algorithm still possesses the major advantage of the conventional BEM - high speed - but is simultaneously capable of processing a very large number of surface-based unknowns. As a result, an unprecedented spatial resolution could be achieved, which enables multiscale modeling.

Results:

For non-invasive EEG/MEG, we are able to accurately solve the forward problem with approximately 1 mm anatomical resolution in the cortex within 1–2 min given several thousand cortical dipoles. Targeting high-resolution iEEG, we are able to compute, for the first time, an integrated electromagnetic response for an ensemble (2,450) of tightly packed realistic pyramidal neocortical neurons in a full-head model with 0.6 mm anatomical cortical resolution. The neuronal arbor is comprised of 5.9 M elementary 1.2 μm long dipoles. On a standard server, the computations require about 5 min.

Conclusion:

Our results indicate that the BEM-FMM approach may be well suited to support numerical multiscale modeling pertinent to modern high-resolution and submillimeter iEEG.

Significance:

Based on the speed and ease of implementation, this new algorithm represents a method that will greatly facilitate simulations at multi-scale across a variety of applications.

I. Introduction

Electroencephalography (EEG) [1]–[2] and magnetoencephalography (MEG) [3] record electric potentials and magnetic fields due to neural currents non-invasively. These methods are used as tools in basic neuroscience, in clinical research, and as diagnostic and monitoring tools in clinical practice.

Several excellent open-source software packages for EEG/MEG analysis are available, including Brainstorm [4], FieldTrip [5], and MNE [6]. However, the corresponding forward-problem solution offers significant room for improvement. All three packages offer the analytical spherical conductor model and the boundary-element method (BEM) as options for the solution of the forward problem. The BEM implementation employs three low-resolution layers extracted from the subject’s MRI: scalp, outer skull, and inner skull. The resolution of these layers is limited to approximately 7,000 triangles per compartment (with 2,000 default) when Brainstorm is used [7]. Furthermore, the cortical compartments - cerebrospinal fluid (CSF), gray matter (GM), and white matter (WM) - are not routinely included. As a result, significant errors may be generated for the forward solution [8].

To overcome this issue, better solutions have been proposed including recent FEM (finite element method) development [9] resulting in software duneuro [10].

In this study, we propose a new high-resolution numerical approach which solves the problem described above. The algorithm is our recently developed boundary element fast multipole method or BEM-FMM. It is based on the integration of the boundary element formulation in terms of surface charge density and the fast multipole method originating from its inventors [12]–[13]. The algorithm is capable of processing a very large number of surface-based unknowns. As a result, an unprecedented spatial resolution could be achieved, which enables multiscale modeling.

Note that there have been attempts to employ the fast multipole method (FMM) for the solution of the MEG/EEG forward problem already about 15 years ago [11]. Perhaps surprisingly, these early attempts did not generate convincing results. There were probably two reasons: an insufficient performance of an in-house FMM and a sub optimal BEM formulation. The main challenge here is to select the proper BEM formulation and devise an accurate numerical integration scheme for the solution, as well as to couple these with the proper FMM algorithm in an efficient way.

The study is organized as follows. Section 2 (Theory) describes the BEM-FMM approach. The mathematical formulation and method realization (software) are described in the supplementary sections (Supplements A and B, respectively). Section 3 (Method Performance for EEG/MEG Dipoles) reports BEM-FMM performance for head models with 1.1 mm and 0.6 mm cortical resolution, respectively, and for conventional current dipoles. The traditional BEM is simply unable to solve such problems while the finite element method (FEM) may become somewhat slower for a large number of cortical dipoles [14]–[16].

For the first time, Section 4 (Response of a Realistic Neuronal Arbor) computes the integrated electromagnetic response for an ensemble (2,450) of tightly packed realistic pyramidal neocortical neurons. The neuronal arbor is comprised of 5.9 M individual elementary dipoles with the average length of 1.2 μm each. Field resolutions of 20 μm (for near fields) and 350 μm (at macroscale) are demonstrated.

Our second aim is therefore to support the modern high-resolution intracranial recording technique - intracranial electroencephalography or iEEG - which is blossoming in various fields of human neuroscience [17]. iEEG includes electrocorticography (ECoG), stereoencephalography (SEEG), and local field potential (LFP) recordings. Typical electrode spacings have been 4–10 mm while the diameter of subdural plate electrodes (ECoG) is often 1.2 – 3 mm and the diameter of depth electrodes (SEEG) is 0.86 – 1.1 mm with 2.29 or 2.41 mm height [17]. At present, arrays with electrodes as small as 20 μm in size and with 25 – 100 μm electrode spacings are designed and tested [18]. LFP electrodes are, for example, 50 μm-diameter tungsten microwires [19]. The same is valid for more accurate MEG measurement techniques [20]–[21]. Our initial results indicate that the BEM-FMM may be the best technique to support numerical modeling pertinent to iEEG and other intracranial recordings at any scale.

II. Theory

A. Integrating boundary element method and fast multipole method

Fig. 1 shows the flowchart of BEM-FMM [22]–[23] proposed in this study for EEG/MEG modeling and described in detail in the Supplement. Compared to the conventional BEM formulation presently used in EEG/MEG studies [24]–[29], our method has two distinct features.

Fig. 1.

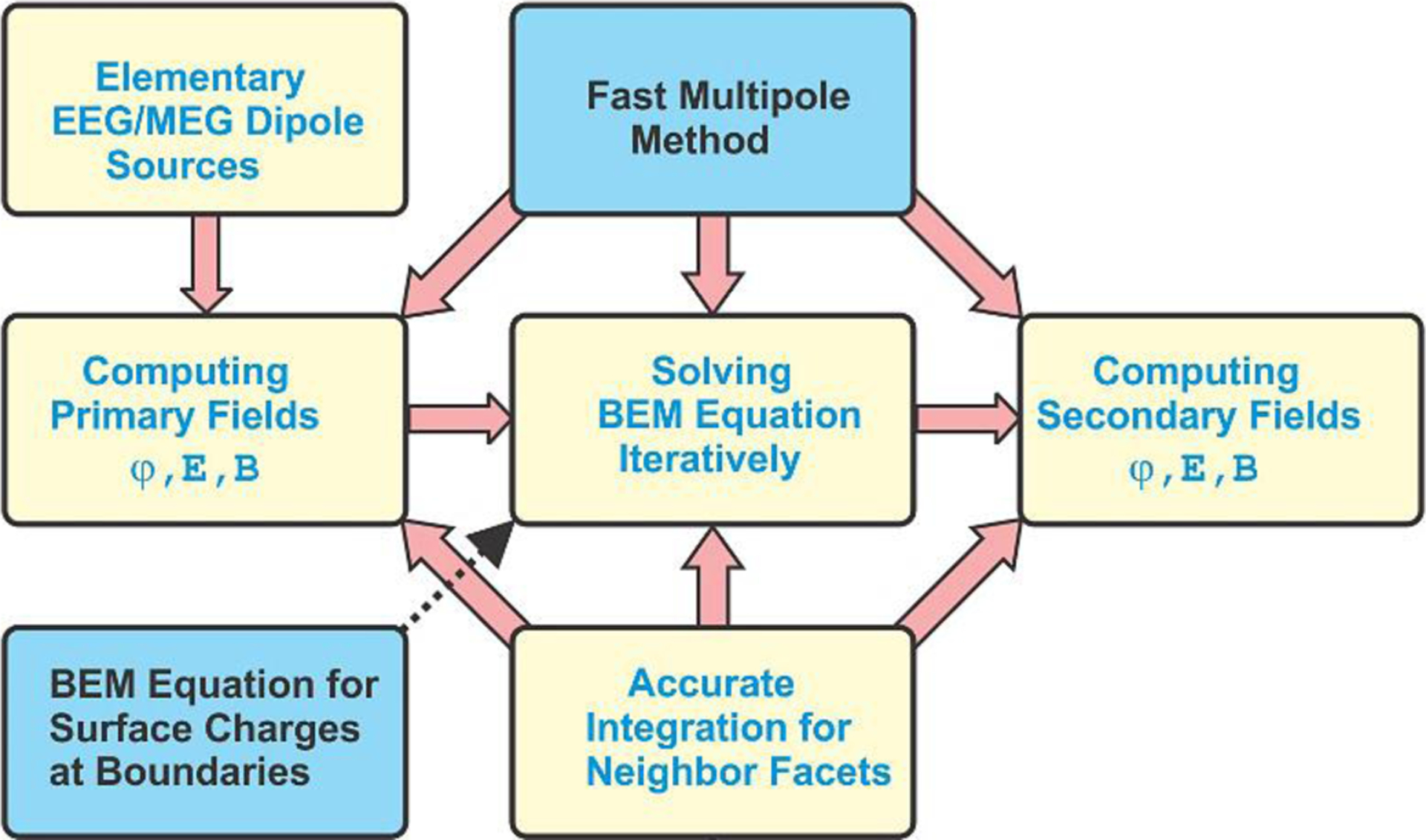
High-level flowchart of boundary element fast multipole method for EEG/MEG/iEEG modeling along with its major features.

First, we employ the fast multipole method or FMM [12]–[13], [30] through the entire solution process as shown in Fig. 1. It starts with computing primary fields – electric potential φ^p(r), electric field intensity E^p(r), and magnetic flux density B^p(r) - due to dipole sources at tissue boundaries and everywhere in space. In this way, the number of elementary dipole sources becomes practically unlimited: the FMM-based primary field computations with over 5 M dipole sources for 2.8 M target points run under 15 seconds or faster on a typical server. In contrast to FEM, BEM-FMM does not need to perform the singularity extraction [14]–[16] since there are no volumetric elements containing the sources themselves.

However, when the sources are very close to the triangulated boundaries, we compute the primary fields by accurate integration over the triangle area and the spatial averaging using the Galerkin method [22]–[23]. This feature is discussed in Supplement A.

Next, FMM is applied to solve the resulting boundary integral equation iteratively since it speeds up computation of a matrix-vector product by several orders of magnitude. This approach does not require the BEM matrix to be formed and inverted explicitly; it results in a very significant reduction of solution time and memory resources. Finally, once the charge density solution at the boundaries is obtained, we again use FMM to compute secondary fields - electric potential φ^s(r), electric field intensity E^s(r), and magnetic flux density B^s(r) - in a high-resolution grid everywhere in space.

B. Charge-based integral equation of the boundary element method

The conventional BEM formulation for EEG/MEG modeling used today [4]–[6] employs the integral equation written in terms of surface electric potential φ(r). In contrast to this, we employ the integral equation written in terms of electric charge density ρ(r) at the boundaries [31]–[33] as described in Supplement A. Apart from the fact that the surface-charge formulation is a natural foundation for the fast multipole method, it is directly applicable to the conductivity boundaries with junctions (described in Supplement A) that previously have required adhering to the finite element method or have required a separate BEM formalism [29].

III. Method Performance for EEG/MEG Dipoles

A. Results for 1.1 mm cortical resolution

A triangular surface-based head model for subject #101309 from the Population Head Model Repository [33]–[35] originating from the Human Connectome Project [36] was solved via BEM-FMM. The model includes the following seven compartments: cerebellum, CSF, GM, skin (or scalp), skull, ventricles, and WM, and results in about 700,000 triangular facets in total. The average mesh resolution (edge length) is 1.5 mm for scalp and skull and 1.1 mm for CSF, GM, and WM. Tissue conductivities are adopted from the IT’IS database [37] with the average scalp conductivity chosen as 0.333 S/m. With the BEM-FMM approach, an EEG forward computation executes in approximately one minute. The number of dipoles is insignificant. This estimate is for an Intel Xeon E5–2698 v4 CPU (2.20 GHz) server, 256 Gb RAM, MATLAB 2018a.

To demonstrate the importance of the anatomical detail and accuracy of the head model, a single finite-length (1.8 mm) cortical dipole with a moment Q = 1.8 nA · m is placed in the vicinity of the right motor cortex at two different orientations, as shown in Fig. 2a,b. The scalp potential was computed with all brain compartments present and with only three brain compartments present, respectively, which is similar to OpenMEEG software [7], [38]. There are clear differences in the scalp potential distribution (Fig. 2 c–f), especially in the amplitude. Quantitative measures are given in Table I. They are the relative difference measure (RDM) or topographical error, RDM = ‖φ₁/‖φ₁‖ − φ₂/‖φ₂‖‖, and the logarithmic magnitude (lnMAG) error, lnMAG = ln (‖φ₁‖/‖φ₂‖). The topographical error in Table I may be as large as 67%.

Fig. 2.

Electric potential distribution in V over the scalp surface for nearly radial (a) and nearly tangential (b) cortical dipoles (Q = 1.8 nA · m) at the primary motor cortex (coronal plane). c), d) Solutions with all brain compartments included. e), f) Approximate solutions with only three brain compartments (scalp, inner skull, outer skull) included. Note the differences in the maximum amplitudes of the on-skin voltage in every case.

TABLE I.

Topographical error and magnitude error in the electric potential for the scalp and inner skull surfaces, respectively, between the complete anatomical model computed with BEM-FMM and the common BEM model used today [38], [7] that omits the CSF, GM, and WM interfaces.

Surface where the electric potential is computed	RDM error, %	lnMAG error
Scalp for nearly vertical dipole in Fig. 2a	67	−1.0
Scalp for nearly horizontal dipole in Fig. 2b	29	−0.6
Inner skull(dura) for nearly vertical dipole in Fig. 2a	29	−1.7
Inner skull(dura) for nearly horizontal dipole in Fig. 2b	38	−1.1

B. Results for 0.6 mm cortical resolution

In addition to the extracranial EEG/MEG fields, the BEM-FMM method can be utilized to model the intracranial fields in the vicinity of the neuronal sources. This can be beneficial for analyzing ECoG and/or SEEG, especially when the speed of this method is used as an advantage in solving the forward problem. Once this method is implemented in an inverse solution algorithm, BEM-FMM could greatly expand the use of iEEG for accurate source imaging, even in intraoperative settings.

To evaluate this possibility, the surface mesh from the previous example was refined using a 1×4 barycentric triangle subdivision and then surface-preserving Laplacian smoothing [39], [40] was applied. This results in a model that has an average oversampled mesh resolution of 0.6 mm in the cortex and 2.8 M triangular facets in total. The high-resolution model runs reasonably fast, in approximately 200 seconds using an Intel Xeon E5–2698 v4 CPU (2.20 GHz) server, 256 Gb RAM, MATLAB 2018a. To demonstrate field distributions, a 1.8 mm long and nearly radial dipole with the moment Q = 1 nA · m, directed outwards is placed near the primary motor cortex, as shown in Fig. 3a,b in both coronal and sagittal planes. Figs. 3c, d show the resulting electric and magnetic fields, respectively. Every field plot is based on 500×500 observation points at a uniform spacing of 100 μm.

Fig. 3.

Single-dipole EEG and MEG field distributions computed with the BEM-FMM algorithm for a head model with 2.8 M facets. The dipole moment is Q = 1 nA · m. a), b) Problem geometry in two planes. c) The electric field magnitude in the coronal plane using a logarithmic scale vs 1 μV/m. d) The absolute value of dominant tangential magnetic-field component B_x in the sagittal plane using a logarithmic scale vs 1 aT. A magnetic field lacuna is seen in Fig. 3d.

The total electric field magnitude is given in the coronal plane in Fig. 3c while Fig. 3d shows the absolute value of the dominant tangential magnetic-field component B_x in the sagittal plane. In order to display large field variations, we use the decibel scale as noted in the respective figures. The electric field is indeed observed to be discontinuous at the interfaces between the tissue compartments while the magnetic field is not. Fig. 3c clearly demonstrates how the electric field of the current dipole is attenuated and smeared by the scalp; both the amplitude and the spatial specificity of the recordings would greatly increase if the electrodes could be attached to the skull instead of skin. On the other hand, Fig. 3d illustrates a magnetic-field lacuna that is typical for a nearly radial dipole (which in the spherically symmetric model would produce no extracranial field). However, this lacuna is bent and is shifted quite significantly due to the intricate geometry of the anatomically realistic conductivity boundaries resulting in a diminished yet non-zero field outside the head.

Note that in Fig. 3, EEG and MEG responses have been compared, but only for the radial dipole. Since MEG, unlike EEG, behaves fundamentally different for tangential and radial dipoles, the MEG comparison between radial and tangential dipoles is additionally discussed in Supplement B (Example 2).

C. Results for a cortical equivalent dipole layer with the cortical area of 360 mm²

A spatially extended cortical equivalent dipole layer [41] was simulated using the same high-resolution model. For comparison purposes, this extended source was created around the single dipole from the previous example. To generate the source, we selected all triangular facets of the white matter shell within a distance of 10 mm from the original dipole and assigned to every such facet a 1.6 mm long dipole. All the individual dipoles were directed along the outer normal vectors of the white matter facets and were directed outwards as shown in Fig. 4a,b.

Fig. 4.

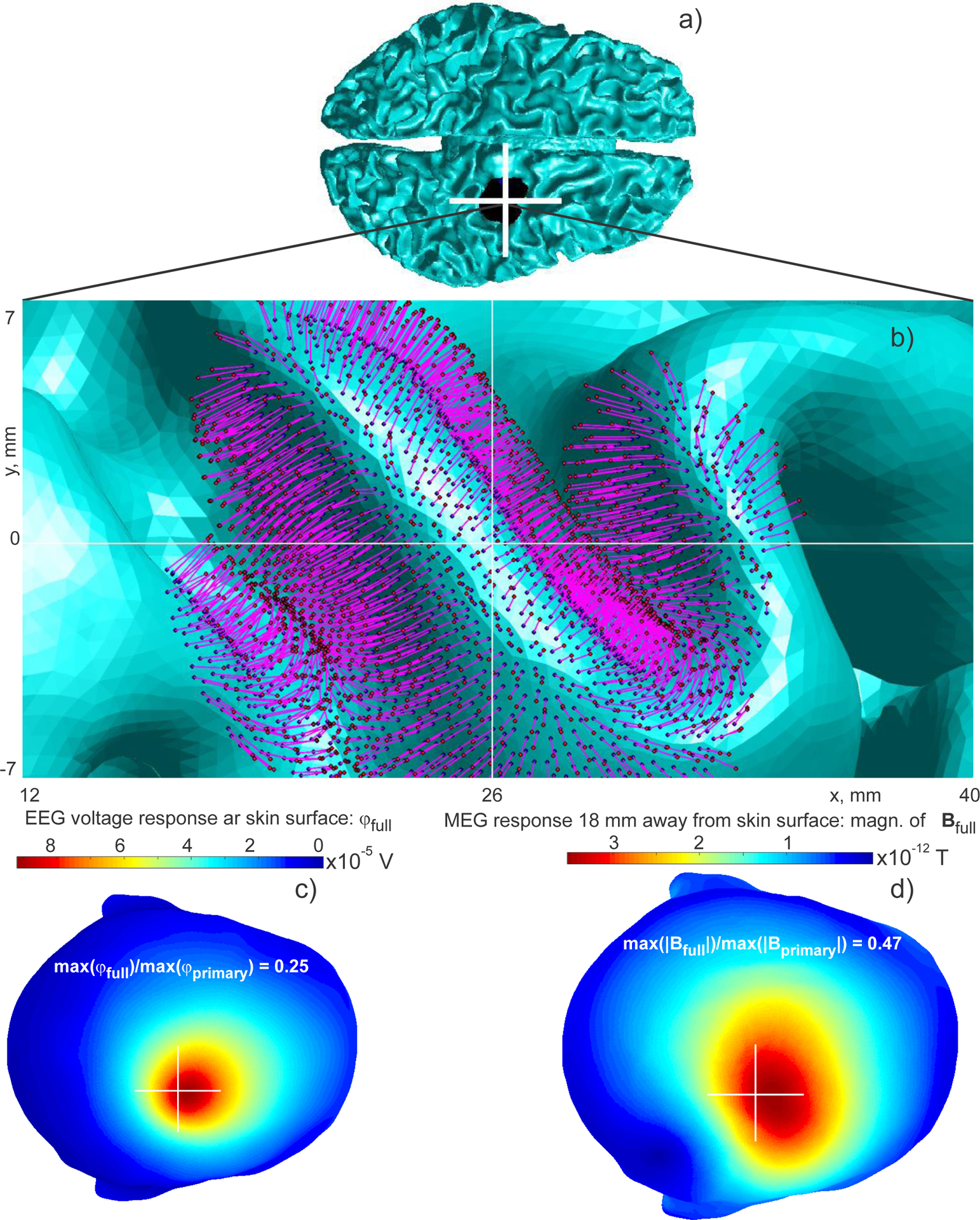
EEG/MEG responses of a cortical equivalent dipole layer computed via BEM-FMM. The total area of the cortical layer is 360 mm². Current dipole moment density q₀ (current dipole moment per unit cross sectional area of the active cortex) in the source region is given by the value q₀ = 1 nA · m/mm² (Okada-Murakami constant). a) Problem geometry. b) Close-up view of the dipole layer. c) The electric potential on the skin surface using a linear scale; d) The magnitude of the total magnetic field 18 mm away from the skin surface using a linear scale. The center of the white cross coincides with projection of the geometrical center of the layer onto a transverse plane.

The distance of each current dipole from the white matter shell was 0.2 mm. Fig. 4b depicts the corresponding dipole distribution to scale. The number of individual dipoles in the present example is ~2,000 although numbers as large as 200,000 were also tested.

To choose a realistic value of current dipole moment density q₀ (current dipole moment per unit cross sectional area of the active cortex) in the source region, we used the value q₀ = 1 nA · m/mm² [42]. This value is invariant across the cerebral cortex, hippocampus and cerebellum across a wide phylogenetic scale from reptiles to humans. This value also agrees with the dipole moment density estimated from a neural current MRI study [43]. When the dipole length is d and the area of the dipole layer is A, an expression for the dipole current I₀ follows from q₀ = I₀d/A, which yields I₀ = q₀A/d. The total area of the macroscopic cortical dipole layer is 360 mm². The overall simulation times are nearly the same as for the single dipole in Section 3.2 illustrating another computational advantage of the BEM-FMM approach.

The convergence rate is initially very fast, but it slows down after the relative residual reaches 10⁻³. Fig. 4c shows the resulting surface electric potential on the skin surface and Fig. 4d shows the magnitude of the total magnetic field 18 mm away from the skin surface. A quite significant change in the MEG response pattern is observed as compared to the case of the single dipole located at the cluster center. This is likely due to the presence of multiple horizontal dipoles whose contributions add up. As to the EEG response pattern, it becomes a bit wider and spatially shifted, but its shape remains nearly the same as for the single dipole.

IV. Response of a Realistic Neuronal Arbor

A. Multiscale modeling for a smaller cortical area of 15.8 mm²

The microscopic neural origin of the primary currents in EEG/MEG is thought to be the aggregate of postsynaptic longitudinal currents flowing inside the apical dendrites of the large, spatially aligned neocortical pyramidal neurons or PNs [45]–[46]. As a realistic PN model, we choose a digital morphological reconstruction of a neocortical pyramidal neuron H16–03-001–01-09–01_559391771_m, ID NMO_86955 from the NeuroMorpho.Org inventory Version 7.5 [47]. The wire reconstruction contained a total of 81 compartments: 23 axonal branches, 40 dendritic branches, 18 apical dendrite branches, and a (spherical, 6.3 μm radius) soma. The total number of individual straight geometrical segments or edges in the neuron wire model was 9237 and the total number of nodal points was 9318. The neuron length was approximately 900 μm, with the longest apical dendrite branch of approximately 500 μm. The neuron morphology is illustrated in Fig. 5b; the apical dendrite branches are shown blue.

Fig. 5.

Construction of a layer of realistic neocortical pyramidal neurons. a,b) Neocortical pyramidal neuron ID NMO_86955 from the NeuroMorpho.Org inventory. The apical dendrite arbor is shown blue. c) Conformal cloning the PN in layer II/III with the density of 6.2 per mm². Only two cortical surfaces (WM and GM) are shown here.

To estimate the fields of a single neuron, its apical dendrite branches have been divided into 2387 individual straight segments - the elementary current dipoles - each with an average length of 1.2 μm. Such dipoles are seen in Fig. 5a. This detailed model is somewhat superfluous for EEG or iEEG purposes since all intermediate current sources along a branch will cancel out and only the end sources (two per branch) will remain significant. However, it is still meaningful for MEG purposes since the entire current path along the neuronal arbor will be reflected in the measurements.

We clone the neuron model for a large number of locations in the primary motor cortex and in between WM and GM surfaces of the model used previously as illustrated in Fig. 5c.

For every triangular facet of WM, we aligned the neuron with its normal vector and then move it toward a position that was approximately 1 mm away from the WM triangular surface in the direction of its outer normal vector. Fig. 5c shows the corresponding neuron cluster with one neuron per triangle and with the normal vector drawn from the triangle center. To construct this cluster of neurons, all triangular facets of the white matter shell have been selected, which are within a distance of 3 mm from a given observation point. This resulted in a cortical area of 15.8 mm² and in 98 neurons in total. The neuron density in Fig. 5c is only 6.2 per mm².

We targeted layer II/III and attempted to increase the PN density to at least 150 per mm² (for more detailed density estimates see, for example, [48]). We indeed realize that this value can still be far too low. For this work, we did not study the field originating in layer V even though the large PNs in this layer can also produce strong electric and magnetic fields locally inside the brain. For every selected triangle, we therefore introduced 25 inner nodal points corresponding to a Gaussian quadrature of 10^th order of accuracy [49] and then performed neuron cloning for every such point. This operation resulted in 2,450 neurons in total over the cortical area of 15.8 mm² and in the PN density of 155 per mm². The final result is shown in Fig. 6a. Due to the high arbor density, individual neurons are not easy to distinguish visually even after magnification, as expected.

Fig. 6.

a) Conformal cloning PNs in layer II/III with the density of 155 per mm². The apical dendrite arbor (5.9 M elementary dipoles) is shown blue; b) Computed total induced electric potential in the coronal plane passing through the cluster center. The log-modulus transformation scale given by Eq. (A15) of Supplement A has been used with φ₀ = 0.1 μV; c) Distribution of the magnitude of the total magnetic field in the same coronal plane, also using a logarithmic scale normalized to 10 fT; d) Distribution of the magnitude of the total electric field in the same coronal plane, also using a logarithmic scale normalized to 1 μV/m.

The BEM-FMM simulations involve 5.9 M elementary dipoles. A current of 6.45 nA is assigned to every elementary dipole. Given the apical dendrite length of 500 μm and taking into account all the peripheral branches, this leads to the PN longitudinal dipole moment of approximately Q = 6.5 pA · m. Note that this value is higher than the typical values of neurons [42, 45] since the current in each compartment was chosen to match the dipole moment density to the Okada-Murakami constant of 1 nA · m/mm² for this neuron density. The average transverse dipole moment of the neuron was found to be negligibly small.

The method converges fast and reaches the relative residual of 10⁻³ in ten iterations, with about 26 seconds per iteration.

B. Response at microscale

Figs. 6b–d show near fields (1 cm² total observation area, 500 × 500 observation points, 20 μm spatial resolution) elicited by an ensemble of cortical neurons. Computed total induced electric potential in the coronal plane passing through the cluster center is shown in Fig. 6b. Here, the log-modulus transformation scale given by Eq. (A15) of Supplement A has been used with φ₀ = 10 μV. The potential distribution is becoming rather smooth in the immediate vicinity of the neuron cluster. Figs. 6c, d show the distributions of the magnitude of the total magnetic and electric fields, respectively, in the same coronal plane, also using a logarithmic scale. The electric field is more strongly confined within the cluster. Local field variations associated with the cluster curvature are observed all the way up to the gray matter surface.

C. Comparison with experimental data and other computational data

In [43], the local B field inside an active neuronal tissue based on the phase shift detected with Gradient Echo (GE) MRI was measured in intact cerebellum of turtle in vitro. The phase shift can be used to compute the local field from a simple basic equation (ΔΦ = γΔB_zTE, where ΔΦ is the phase shift, γ is the gyromagnetic ratio, ΔB_z is local magnetic field and TE is echo time). That gave a local B field ΔB_z of 0.6–0.9 nT in individual tissues. The value of ΔB_z averaged across 7 tissue samples was 0.2–0.3 nT. The local B field inside the cluster predicted in Fig. 6c is ~94 dB or 10⁻¹⁴ × 10^94/20 = 0.50 nT, which is within the range of measured values.

In Ref. [44], a realistic single cell model of a pyramidal neuron was used to compute the local B field and the phase shift in the GE MRI. They found a ΔB_z of as much as 10 pT in the vicinity of a single neuron. It is unfortunately not possible to directly compare their values with values from our simulation study since the neuron models and assumed conditions of activation differ. Nevertheless, in our case we obtained a local field of around 1 pT for a single neuron.

D. Response at macroscale

The same solution has been used to generate the response at macroscale shown in Fig. 7. Fig. 7a shows the relative position of the cluster in the right hemisphere. The voltage and magnetic field were computed over the skin surface, and over the inner skull (dura) surface, respectively. The results are shown in Fig. 7b–e. The inner-skull voltage in Fig. 7b varies from 0 to 450 μV and is spatially strongly localized. In contrast, the on-skin voltage in Fig. 7d varies from 0 to approximately 37 μV only, and the response is spread over a much wider area. In Fig. 7c, the magnitude of the total magnetic field at the inner skull surface reaches its maximum of 55 pT whereas the magnitude of the magnetic field at the skin surface shown in Fig. 7e is again spread over a much wider area and has a maximum of only 6 pT. This value is stronger than the values normally measured with MEG on humans probably due to the short distance between the source volume and the measurement surface among other factors.

Fig. 7.

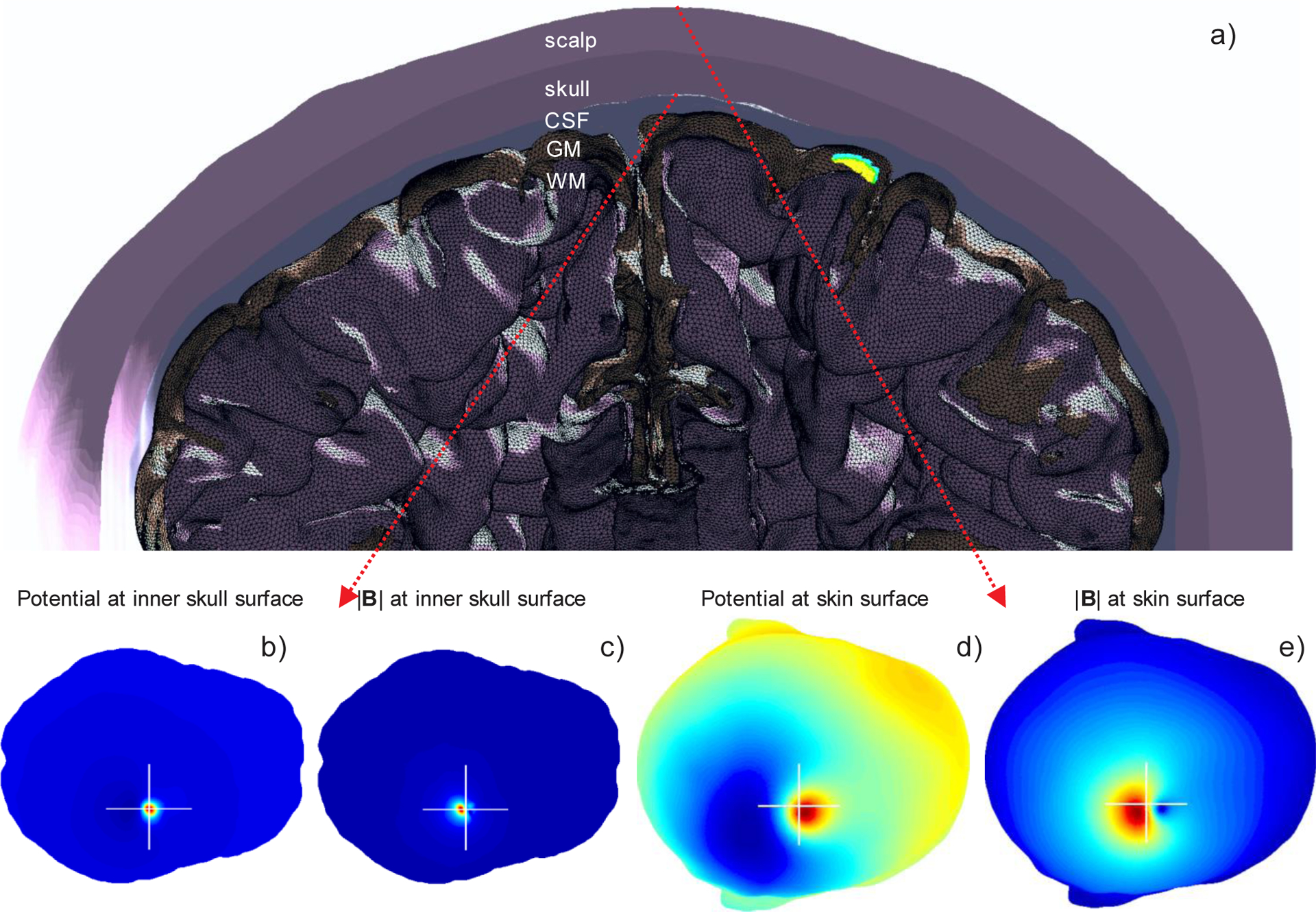
a) Ensemble of neurons from Fig. 6a shown in the coronal plane of the entire macroscopic head model with 2.8 M facets. The apical dendrite arbor (5.9 M elementary dipoles) is shown blue. b) Inner-skull voltage changes from 0 to 450 μV and is strongly localized. c) Magnitude of magnetic field at the inner skull surface reaches its maximum of 55 pT and is strongly localized. d) On-skin voltage changes from 0 to approximately 37 μV; the response is spread over a much wider area. e) Magnitude of magnetic field at the skin surface has the maximum of 6 pT; the response is spread over a much wider area.

E. Comparison with the cortical equivalent dipole layer of the same area (15.8 mm²)

The numbers given above were compared to the simulations performed for the single equivalent current dipole and a cortical equivalent dipole layer of the same size, position, and with the same dipole moment per unit area. Two observations were made:

1. The dipole results strongly depend on the dipole length and position between white and gray matter. Longer dipoles give higher potentials and stronger magnetic field responses as expected. The local magnetic field and the external field outside the brain are both sensitive to the location of the dipole sheet relative to the brain-CSF and the CSF-skull boundaries.

2. The local magnetic field B_tissue within and around the active tissue depends on the geometry and net dipole moment of the neurons and equivalent magnetic field generators. The single equivalent current dipole of 1 nA·m produced a tangential B_tissue of ~0.1 nT near the dipole (Fig. 3d). The sheet of current dipoles with a dipole moment density of 1 nA·m/mm² produced a tangential B_tissue of ~0.2 nT (not shown), whereas the sheet of realistic neurons with the same current dipole moment density produced a total B_tissue of ~0.5 nT (Fig. 6c). These values are all within the range of the local magnetic fields estimated with MRI [43].

V. Summary of Computational Performance

For the case studies included in this paper and for the relevant studies of Supplement B, approximate execution times necessary to obtain an accurate solution are (using an Intel Xeon E5–2698 v4 CPU (2.20 GHz) server, 256 Gb RAM, and accessible multithreading MATLAB 2018a/2019a platform, Windows):

• Head models with 0.7–0.9 M facets and with 1–5000 elementary dipoles: 50–150 sec;

• Head models with 2.8 M facets and with 10⁶–10⁷ elementary dipoles (basic neuronal arbor): 300–500 sec.

A new FMM library was released in the spring of 2019 [50] and it was included into the redistributable software package described in Supplement B. This library enables vectorized computation of dipole distributions with the same positions but with different individual weights and for the same head models, resulting in significant reduction in computational cost by using the same FMM space partitioning

VI. Discussion

A. Method advantages

Some advantages of the BEM-FMM modeling approach established in this study are its high speed while maintaining a low computational error and high field resolution as demonstrated both in the study as well as in the software application examples of Supplement B. Furthermore, the method is well suited for a very large number of dipoles; the dipoles are also permitted to have a finite length, which makes the method well suited for modeling sources of laminar LFP recordings arising from synaptic activities at different cortical layers.

The numerical leakage through surfaces that are very close to each is not an issue for BEM-FMM as long as these small gaps are well localized in space. In this case, the potential integrals for interacting neighbor facets are simply pre-computed analytically (Supplements A, B), which enables a separation distance approaching zero.

A non-nested head topology is permitted for EEG since the underlying derivation of the charge-based integral equation [51] uses only the local boundary conditions ([51], see also Supplement A). The non-nested topology, e.g., fontanels in the incompletely ossified skull, implies the proper treatment of manifold objects with coincident boundaries ([51], see also Supplement A): every inter-object boundary must be counted only once.

However, the secondary magnetic field computation (the Geselowitz formula in Supplement A) is still based on the Stokes theorem, and would perhaps require an additional revision for non-nested geometries.

B. Method limitations

In general, while highlighting the computational power of the BEM-FMM, the problem geometry is still relatively simple, and a uniform current is assigned to each segment of each apical dendrite branch. A significantly more realistic multilayer multiscale cortical model could be developed for further analysis illuminating the relationship between the microscopic and macroscopic MEG/EEG measures. The BEM-FMM algorithm should be in position to readily simulate and process substantially more complex multiscale models.

Neurons in the brain exhibit complex intrinsic dynamics over a wide frequency range. In particular, the time courses of individual neuronal currents can be faster than that of the postsynaptic currents of the ensemble which are usually used as the sources. This observation questions the limits of the quasistatic approximation. Fortunately, the macroscopic conductivities of the brain compartments do not vary significantly in the frequency band from 0 Hz to approximately 3–5 kHz [37]. Therefore, the solution obtained should in principle hold at sub-millisecond scales as well. However, in such a situation there is a risk of inaccuracies in the model. One open problem might be the increasing effect of displacement currents.

On the other hand, responses of different neurons and their arbor are not necessarily synchronized, which was the major simplifying assumption of the present calculations. It is possible in principle to separate the responses of every single neuron or responses of the dendritic arbor vs responses of the axonal arbor, and then combine them into a temporal pattern, with certain weights. This difficult task is beyond the scope of this study.

Additionally, we mention that previous modeling studies have shown that the contribution to the magnetic field from the current inside the membrane is two orders of magnitude larger than that from the external current [53]. The contribution from current within the membrane is negligible [53]. A relevant discussion is also provided in Ref. [54] - cf., e.g., Fig. 5 - as well as in Ref. [55].

Despite significant advantages quantified in this study, the BEM-FMM algorithm itself is not without its limitations. It is not able to handle anisotropic materials, at least in its present form. The FMM part of the BEM-FMM algorithm is a very non-trivial mathematical engine. Therefore a general-purpose FMM library is used [50]. Furthermore, the largest gains in computational efficiency are obtained for problems where high-resolution models are desired.

We also note that the present method depends on the surface mesh quality, the type of basis functions used, and seems to work best for large-scale high-quality smooth manifold meshes. The above-mentioned limitations are shared by many iterative solvers and their practical significance is expected to be small. More research is required to establish standard convergence criteria as well as to quantify the numerical robustness of the results. Even more research is required to establish a set of clinical examples where the method advantage becomes critical.

VII. Conclusions

Here, we present a computational framework for high-resolution modeling of neuroelectromagnetic fields, which is based on efficient utilization of the FMM acceleration of the boundary element method. In contrast to existing approaches, our novel method is equally well suited for modeling extracranial and intracranial fields and the possible applications include high-resolution modeling of both non-invasive (EEG, MEG) and intracranial (ECoG, depth-electrode LFP) recordings. This progress may provide significant advances in both clinical and basic neuroscience.

In the most demanding clinical evaluations, such as presurgical mapping in epileptic patients, the initial evaluation that starts with EEG and/or MEG is followed by direct recordings with subdural (ECoG) or intraparenchymal depth electrodes. However, despite its vastly improved SNR, ECoG provides only indirect information of the majority of underlying cortical areas, i.e., cortical sulci. In particular, the peaks in ECoG patterns for tangential sources do not coincide with the location of the source. On the other hand, the EEG depth electrodes may provide only very limited sparse coverage. Therefore, in principle, the same procedures that are developed for MEG/EEG source modeling could also be applied to greatly improve the value of invasive recordings, which contain more detailed spatial information, but the locations of the current sources still need to be computationally inferred from the electric/magnetic field data. Unfortunately, due to the inherent limitations, and most crucially due to the surgical penetrations in the skull, no widely accepted application for source modeling for both invasive and non-invasive EEG data still exists.

In conclusion, the present BEM-FMM approach has the potential to become a useful computational tool for high-resolution forward modeling of electric and magnetic fields of electrophysiological origin. An open-source BEM-FMM software is released along with the present paper [52]. Supplement B provides the reference manual with three application examples.