Sensitivity analysis based on the random forest machine learning algorithm identifies candidate genes for regulation of innate and adaptive immune response of chicken

Abstract

Two categories of immune responses—innate and adaptive immunity—have both polygenic backgrounds and a significant environmental component. The goal of the reported study was to define candidate genes and mutations for the immune traits of interest in chickens using machine learning–based sensitivity analysis for single-nucleotide polymorphisms (SNPs) located in candidate genes defined in quantitative trait loci regions. Here the adaptive immunity is represented by the specific antibody response toward keyhole limpet hemocyanin (KLH), whereas the innate immunity was represented by natural antibodies toward lipopolysaccharide (LPS) and lipoteichoic acid (LTA). The analysis consisted of 3 basic steps: an identification of candidate SNPs via feature selection, an optimisation of the feature set using recursive feature elimination, and finally a gene-level sensitivity analysis for final selection of models. The predictive model based on 5 genes (MAPK8IP3 CRLF3, UNC13D, ILR9, and PRCKB) explains 14.9% of variance for KLH adaptive response. The models obtained for LTA and LPS use more genes and have lower predictive power, explaining respectively 7.8 and 4.5% of total variance. In comparison, the linear models built on genes identified by a standard statistical analysis explain 1.5, 0.5, and 0.3% of variance for KLH, LTA, and LPS response, respectively. The present study shows that machine learning methods applied to systems with a complex interaction network can discover phenotype-genotype associations with much higher sensitivity than traditional statistical models. It adds contribution to evidence suggesting a role of MAPK8IP3 in the adaptive immune response. It also indicates that CRLF3 is involved in this process as well. Both findings need additional verification.

Introduction

Immune response is a complex trait that is controlled by multiple interacting genes with different magnitudes of phenotypic effects, as well as the environment. Genomic regions related to the complex traits are defined as quantitative trait loci. Deciphering genetic bases of complex traits leads from defining of the QTL toward pointing at a single mutation responsible for a considerable amount of the genetic trait variations called a quantitative trait nucleotide (QTN). An active part of the innate immunity is expressed by the presence of natural antibodies (NAbs). NAbs are immunoglobulins that does not need any external stimulation of the immune system to be secreted by B-1 cells in large quantities (Ochsenbein et al., 1999). NAbs are very effective as a first barrier to pathogen invasion. They are polyreactive and present in high abundance in the host organism (Frank, 2002). All of that makes them crucial for the initial steps of the immune response, before the acquired antibodies are generated (Siwek and Knol, 2005).

The other type of immune response, adaptive immunity, is a targeted specific response to antigens that appear in the environment. The presence of significant amount of an antigen triggers production of antibodies that are specific to this particular antigen.

The present study takes into account both types of immune responses in chickens. In addition to response to LPS and LTA representing the innate response, the specific antibody response toward keyhole limpet haemocyanin (KLH), representing an adaptive immune response, was examined. KLH is a high-molecular-weight protein antigen collected from the hemolymph of the sea mollusk, Megathura crenulata. KLH induces Th2-like type of immune response. This protein is commonly used as a soluble model protein in biological studies (Bliss et al., 1996).

The present study is an extended analysis of the data already described by Siwek et al. (2015). The original study was conducted using standard statistical methods, and while it revealed connection between the genetic traits, the effect was week. The linear models based on the QTNs identified in the original study explain no more than 1% of variance in the immune response.

The original analysis was performed using the assumption that QTNs are independent and have a simple additive influence on the immune response. The present study goes beyond these assumptions and uses machine learning–based sensitivity analysis that can detect nonadditive and nonlinear effects (Saltelli et al., 2000; Sobol, 2001; Helton et al., 2006). Therefore, within this approach, the effect of a single QTN is therefore not analysed in isolation but in the context of its interactions with other QTNs.

To this end, we apply a novel protocol of analysis which is based on machine learning (ML). ML methods are used preferentially when one has no a priori knowledge about the relationships between the variables describing the system. These methods are particularly useful when the relationships are complex and nonlinear. There are multiple methods and learning algorithms that fall under this general term. They are broadly divided into supervised and unsupervised learning. In the first class, one is interested in building a predictive model for one of the properties of the system under scrutiny, which is often called a decision variable, using other properties as descriptive variables. ML model is developed to predict the decision variable based on the descriptors, using a set of examples for which both descriptors and responses are known. On the other hand, in the unsupervised learning, no special variable is defined, and the goal of the analysis is identification of a deeper structure in the data. The present study aims at finding relationships between genetic variables and the immune response; hence, it belongs to the area of supervised learning. Numerous methods have been developed and used for building such models. A recent study compared performance of 179-ML algorithms belonging to 17 classes (Fernández-Delgado et al., 2014). It only included the most popular algorithms for which implementation exists in R, WEKA, or Matlab. The algorithm that was recommended as best overall by the authors is random forest (RF) (Breiman, 2001). RF is a general purpose machine learning algorithm for classification and nonparametric regression, that is, widely across multiple disciplines, with many applications in bioinformatics, for example, in gene expression studies (Díaz-Uriarte and De Andres, 2006; Kursa, 2014), discovering protein-protein interactions (Qi et al., 2006; You et al., 2015), or genetic association studies (Chen et al., 2007; Goldstein et al., 2011; Botta et al., 2014).

RF is an ensemble of decision or regression trees, which is used both as a tool for classification and for feature selection. This is possible because RF provides a robust, internally cross-validated, estimate of the importance of variable Imp(V) that is obtained using sensitivity analysis. Each tree in an ensemble is built using different samples of the data, and each split of the tree is built on a variable selected from a subset of all variables. The randomness injected in the process of tree construction has 2 effects. On one hand, it decreases the classification accuracy of an individual tree significantly, on the other, it decorrelates individual classifiers and helps to decrease overfitting. What is more, for each tree, there is a subset of objects not used for construction of this tree, the so-called out-of-bag (OOB) objects. This allows for unbiased estimate of the classification error and Imp(V). To estimate the latter, the following procedure is used. For a given variable X, a subset S_X of trees that used X is identified. Then for each tree from S_X, the prediction error on the OOB objects is measured. Then the values of X are randomly permuted among OOB objects, thus removing any information on the true values of X, and the prediction error for these objects is measured. The average increase of the prediction error on the OOB objects, due to removal of the information on X, is a measure of its importance.

Unfortunately, in most cases, it is not easy to find the threshold of importance that separates relevant variables from the irrelevant ones. This is particularly difficult when the number of objects is small and the number of variables is very large. To this end, the Boruta algorithm for all-relevant feature selection (Kursa et al., 2010) has been proposed. It uses the importance score from multiple runs of the RF algorithm to discover the informative variables. In each iteration, the original data set is extended by adding a randomized copy of each variable. The importance of each variable is compared with a maximal importance achieved by a random variable. Only these variables that have importance higher than the maximal importance of randomized variables in a sufficiently numerous iterations are deemed relevant. Boruta is used as an equivalent of the ordinary statistical test of significance in systems with complex, nonlinear relationships between descriptors and decision variables. For example, it has been used in the study of microbial influence on neurodevelopmental disorders (Hsiao et al., 2013), for identification of gastrointestinal microbiome signatures of pediatric patients with irritable bowel syndrome (Saulnier et al., 2011), or study of immune response to HIV (Ackerman et al., 2013). The algorithm is used by a protocol for analysis of genetic polymorphism (Salehe et al., 2017), identification of genetic markers of obesity (Montañez et al., 2017), or analysis of genetic variance in populations or subpopulations of a Mediterranean shrub (Herrera and Bazaga, 2016).

The protocol implemented in the present study is based on that used earlier for investigation of causes of crashes of climatic models (Paja et al., 2015). It uses RF classification algorithm to build nonparametric regression between descriptive variables (single nucleotide polymorphisms [SNPs]) and decision variables (immune response) and to estimate importance of variables. Boruta algorithm for all-relevant feature selection is used for establishing hyperparameters of the algorithm, namely the number of relevant variables in the system.

Materials and methods

For brevity, only a brief summary of the experimental design is reported here; the more detailed description can be found in the original article (Siwek et al., 2015). This allows us to concentrate on the analytical protocol, which is the main contribution of the present study.

Experimental Design

Experimental Population

Biological material has been obtained from the experimental population, created by crossing 2 breeds of hens: Zk (Green-legged Partridgelike) and WL (White Leghorn). All birds were kept on a floor system on a farm at the University of Life Sciences in Lublin. Chickens obtained routine vaccines against the Salmonella, Gumboro disease, bronchitis, Bourse Fabricius disease, and encephalomyelitis. Population details are given in the previous study (Siwek et al., 2010). The final F2 generation, which was mostly used in the current analysis, consisted of 506 birds which were obtained in 6 hatches. Immune responses were defined as NAbs to KLH and environmental antigens LPS and LTA and specific antibody response to KLH. Phenotypic data were expressed by titers as the log2 values of the highest dilution giving a positive reaction for KLH (Siwek et al., 2003) and for LTA and LPS (Siwek et al., 2006), respectively.

SNP Genotyping

For the SNP genotyping, an Illumina custom 384-plex oligonucleotide pool assay was designed, and the GoldenGate Genotyping assay (Illumina Inc., San Diego, CA) was conducted. Detailed description of the SNP selection and genotyping and the quality control is given in the original analysis study (Siwek et al., 2015). After removal of the SNPs of low quality and zero variance, 218 SNPs were used in the present study as descriptive variables.

The results of the experiments are 4 independent data sets:

• 1.level of NAbs for LPS,
• 2.level of NAbs for LTA,
• 3.level of NAbs for KLH, measured immediately after exposure (further referred to as KLH0),
• 4.level of antibodies specific to KLH, measured 7 d after exposure (further referred to as KLH7).

After removing observations with incomplete data, data sets 1 to 3 consist of 412 individual chickens, whereas data set 4 consists of 413 birds. For further analysis, qualitative variables were converted to numeric variables (variables tagged as “AA” were changed to 1, “AB” or “BA” to 2), and missing values of SNP genotypes (or tagged as “NC”) were replaced with the mode value of the all birds.

Data Analysis

We performed a sensitivity analysis based on machine learning models of immune response. This technique is based on a simple idea. To assess the influence of a given variable on a phenomenon under scrutiny, we first build a predictive model using a full set of selected variables and then remove the tested variable from the description. The decrease of the model predictive power is a measure of influence of the tested variable on the studied phenomenon. This idea can be easily implemented to test importance of a subset of variables (e.g., all SNPs from a single gene). In such a case, one has to remove a given subset of variables from the description and measure the decrease of predictive power of the model.

The analyses performed within the present study follow the same principle that is used for establishing the importance of variables in RF—decrease of the classification accuracy due to removal of information is a measure of the relevance of this information. The protocol was implemented in R (R Core Team, 2012), using randomForest and Boruta packages (Liaw and Wiener, 2002; Kursa and Rudnicki, 2010).

The first stage of the analysis, consisting of 2 steps, is performed using all available data for each data set. In the first step, data normalisation and removal of the batch effects are performed for each data set. In the second, Boruta is used for each data set to determine the number of relevant variables. This number is used later as the meta-parameter of the simulation protocol in feature selection based directly on RF.

The remaining part of the protocol is performed using cross-validation, where a model is built using part of the data and tested on the remaining part. In the second stage, the analysis informative SNPs for each data set were determined, and predictive models were built using all relevant SNPs. Finally, the sensitivity test of the models to removal of the information corresponding to entire genes is performed, which allows to identify subsets of genes that lead to best predictive models. All the crucial steps in the analysis are described in more detail in the following sections.

Data Normalization

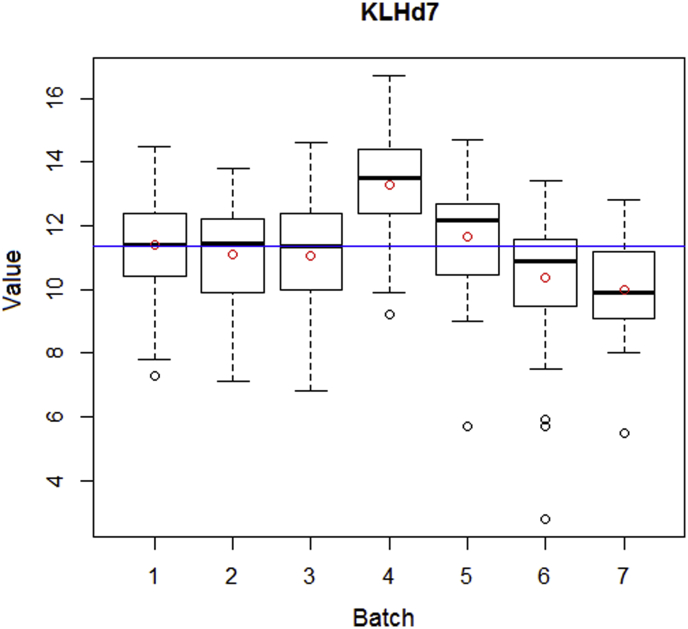
It is universally acknowledged that combining data from different batches in straightforward manner can lead to misleading results (Leek et al., 2010). Therefore, the extent of batch effects was carefully checked for all immune traits. Two possible confounding variables examined were the time of measurement and the sex of the chicken. Significant batch effects were observed for the time of measurements (Figure 1), whereas there was no difference between sexes. To remove differences between batches, the data were transformed to Z-scores within each batch and merged to a single set after the transformation.

Figure 1.

Boxplot for KLH7 data set. The blue line depicts the mean value of KLH7 response calculated for all individuals and batches, and the red dots mark the mean value of KLH7 in each batch.

Identification of the Optimal Set of Informative SNPs

The informative SNPs are identified using RF modelling and feature selection based on the RF estimate of the importance of variable Imp(V).

The core protocol is rather straightforward. First, we find the informative SNPs, by taking average ranking of SNPs' importance obtained from multiple independently built instances of RF classifier. Then, we remove iteratively the least important SNP from the list and construct RF classifier on the decreasing number of SNPs. The ranking of SNPs is performed at each step because removing of one SNP can change the ranking of the remaining ones. The procedure is repeated until the classification error starts to grow after removing SNPs. The SNPs that are used by the model with the smallest error constitute the optimal set.

The procedure described previously is rather simple, nonetheless, its implementation requires special care to avoid overfitting. It may arise when the same data are used for generation of a model and for estimation of its performance. To avoid that, one can assign half of the data for model building and remaining half for evaluation of results. Such a setup results in rather inefficient usage of data—the model is built using only half of the data. What is more, when the number of objects in the sample is low, results may strongly depend on the composition of the sample. The better solution is to apply the cross-validation procedure. In the k-fold cross-validation procedure, the sample is divided into k parts. Then k-1 parts are used to generate the model, and the remaining part is used for evaluation. The procedure is repeated k times, with each part serving once as a test set and k-1 times contributing to the training set. Such a procedure gives estimates both for average and SD of the models' error. Unfortunately, when the sample size is small, the results may still depend on a particular split of data. In effect, both estimates may be biased by a particular split. To alleviate this problem, we repeat the cross-validation several times, with independent splits of data at each iteration.

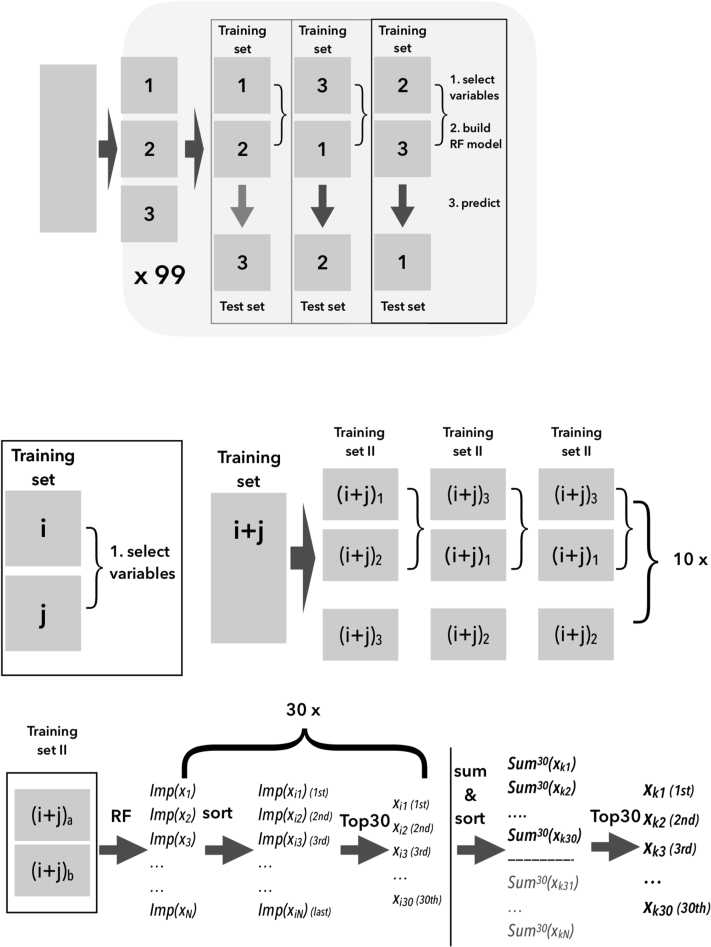
In the first step, the initial set of SNPs, that will be further optimised, is obtained. This step is performed in 99 independent repeats of the 3-fold cross-validation procedure (Figure 2). Within each iteration, first the set of relevant features is selected for the training set. Then the RF regression model is built using selected variables, and the quality of the model is tested on the test set. The feature selection is performed with the help of the resampling scheme, based on 10 repeats of 3-fold cross-validation. In each iteration, the training is split into 3 parts, and 3 different samples are created as a combination of these parts. Then the RF model is built on each sample, and the Imp(V) for each variable is collected. The sum of Imp(V) from the 30 samples is then used to rank variables. The 30 variables with the highest Imp(V) are selected. These variables are used to build a RF model for the training set and validate the prediction on the test set. The number of variables that are used for model building is a meta-parameter of the procedure, which was obtained with the help of Boruta algorithm for all-relevant feature selection. To this end, Boruta was used for the KLH7 data set, and the number of truly relevant variables was established. The number of relevant variables established for KLH7 was used as a parameter for all other data sets because we wanted to keep the number of hyperparameters in the protocol as low as possible. The initial models for KLH7 were best, and therefore, we decided to develop an entire protocol for this data set and then repeat without further optimisations for other data sets. The resampling scheme with a fixed number of features returned at each iteration is similar to one used by Boruta but has significantly lower computational cost. What is more, the number of relevant variables is subjected to verification and optimisation in the second stage; hence, potentially higher accuracy of Boruta is not necessary.

Figure 2.

Selection of the relevant variables using random forest importance in the double cross-validation scheme. The external cross-validation is used to establish good estimate of classification.

The average of the variance explained in the test set from the 99 repeats of the procedure is our reference baseline performance, used for comparisons at the later steps.

In the next step, we perform a sensitivity analysis on the SNP level. The initial set of variables consisted of the SNPs that were used at least 150 times in the first step. The redundant SNPs from this initial list were removed using recursive feature elimination algorithm (Guyon et al., 2002). At each step, 300 RF models were built on different subsamples of data for the current set of variables. The number of trees in the forest (ntree parameter) was set to 5,000, to ensure good estimate of the Imp(V). The number of variables tried for each split (mtry parameter) was set to 2. This parameter was established by trial and error to give best predictive performance of the classifier. The Imp(V), measured as the increase of mean square error after permuting values of the variable, was collected for variable for each model. Then the SNP with the lowest average Imp(V) was removed from the data set, and the procedure iteratively repeated, until the performance of the model started to drop. The model with the smallest number of SNPs that gave stable level of explained variance in the validation set was selected as a final one. This procedure was applied for KLH7, LPS, and LTA phenotypic traits only. Models built for KLH0 trait had no predictive power in cross-validation, which was anticipated as there should be no genetic contribution to KLH innate response.

Significance of Genes

The presence of an SNP in the group of optimal SNPs shows that it carries information on the immune response. Nevertheless, the informativeness may arise because of a correlation with other variables that are truly responsible for the changes in the response. In particular, the SNP in question may be identified as relevant because it is in the linkage disequilibrium with another allele that is truly responsible for the biological effect. By the same token, it may be difficult to estimate the true influence of a single SNP because the presence of multiple correlated SNPs may diminish apparent importance of the removed one. What is more, SNPs are secondary objects because they represent mutations in genes, which are primary objects of genetic analysis. Indeed, the analysis of the linkage disequilibrium among 218 SNPs indicated that 18 SNPs were in complete linkage (the Pearson coefficient of correlation r = 1), 44 SNPs were in close linkage (r ≥ 0.99), and 92 SNPs were in linkage (r ≥ 0.9). By comparison, only 2 weakly linked (r ≥ 0.28) SNPs were found in 218 random SNPs.

Therefore, in the next step, the sensitivity analysis was performed on the level of entire genes, with all SNPs located within the same gene removed or added to the feature set as a single variable. To estimate the influence of individual genes, first the reference model was built using all SNPs selected in the procedure described previously. Then the SNPs located within the gene under scrutiny were removed from the description, and the model was built on the reduced set of variables. Both models were then evaluated on the test set. The decrease of correlation between model and test set was used as a measure of genes' influence on the immune response. This procedure is designed to counteract the strong correlations between SNPs within a single gene. Removal of a single member of the set of strongly correlated variables has no influence on the classifier performance—it is necessary to remove all of them to see the effect. One should note the difference between the sensitivity analysis and standard recursive feature elimination protocol. In the latter, one iteratively removes the least relevant variable from the description of the data and stops when the quality of the model starts to drop. In the sensitivity analysis, one removes a set of variables from the predefined set of descriptive variables and measures the drop of the quality of the model. This analysis is performed for all variables, independently from their position in the importance ranking. Therefore, in the sensitivity analysis, we can see the effect of removing the set of higher ranked variables.

Three types of results of sensitivity analysis were observed. For one class of genes, a significant decrease of model quality was recorded. Another class consists of genes for which the decrease was not significantly different from zero. Finally, there was a class of genes for which removal of the SNPs located within the gene under scrutiny resulted in the improved quality of the model.

This observation led to a final procedure for selection of genes. First, the new reference set of SNPs was constructed, consisting of all genes that have a positive contribution to the mode, that is, genes belonging to the first class described previously. Then various combinations of genes were removed from the reference to examine whether models built using a smaller set of variables can achieve similar or possibly even better predictive power than that obtained for reference set of variables.

In all cases, the analysis was performed using 1,000 repeats of 3-fold cross-validation, resulting in 3,000 different models tested on 3,000 different validation sets for each immune response examined in the present study.

Results

Identification of Informative SNPs

The feature selection procedure gives fairly stable results in all data sets. Out of 218 descriptive variables present in the data set, only 56 variables have appeared at least once in the 297 optimal variable sets for KLH7 data set. Among them, 10 SNPs were present in all 297 cases, and 29 SNPs were present in at least 150 cases. In the case of the LPS data set, the number of SNPs that appeared at least once was 61, 12 SNPs were present in all cases, and 27 SNPs appeared in at least 150 cases. For the LTA data sets, the corresponding numbers were 56, 15, and 30. Finally, for the KLH0, the numbers are 59, 11, and 27. The detailed results of feature selection procedure are presented in the Supplementary Tables 1–4.

The results for the KLH0 are interesting because we do not expect any genetic component for the innate response to KLH0, nevertheless, the algorithm consistently selects nonrandom variables to build models. This can be expected because, due to random fluctuations, some variables can have random correlations with a decision variable on the training set. However, these correlations should not be carried over to the test set, hence the classifiers built on random variables should have no predictive power. This is indeed the case—models built with the help of selected SNPs have no predictive power at all; the average variance explained by models in cross-validation is 0.00 ± 0.05%.

The best predictive models were obtained for the KLH7 data set. The average over ensemble of 297 models was 11.6% of explained variance, and for the model built using 29 most representative SNPs, it was 11.2%. The procedure for elimination of SNP did not produce consistent results, and the average result varied randomly between 11 and 12% of explained variance from step to step; hence, we decided to report the value obtained from the full set of 29 SNPs.

In the case of LPS and LTA data sets, the results were similar and significantly weaker.

The average variance explained by 297 LPS models was 3.7%, and for the model built using most representative SNPs, it was 4.4%. The recursive elimination of least informative SNPs allowed for reduction of the variable set to 15 SNPs.

The average variance explained by 297 LTA models and for the model built using most representative SNPs was 4.5%. The recursive elimination of SNPs allowed for reduction of the set of variables to 20 SNPs.

The results obtained by all models built using the most representative variables fall well within the distribution of individual models because SD of all distributions is roughly 4%. One should note, however, that for KLH7, the model built using 30 most representative variables explains slightly less variance than the average of 297 models suggest. For LPS and LTA, the representative models explain slightly more variance than respective averages of individual models. It shows that feature selection did not lead to overfitting for KLH and slight overfitting for both LPS and LTA. The detailed account of results can be seen in Supplementary Table 5.

Sensitivity Analysis for Genes

The sensitivity analysis for genes was performed for 3 data sets, for which predictive models based on SNPs can be built. In the first step, the SNPs in the optimal subsets were associated with genes. In the case of KLH7, 18 genes were identified, 15 genes for LTA, and 9 genes for LPS. The results of the significance analysis varied between data sets. The most interesting results were obtained for the KLH7 data set.

KLH7

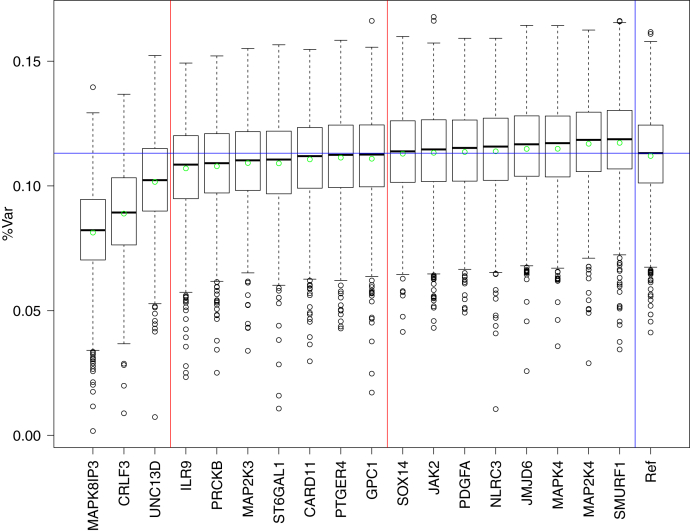
For KLH7, 3 groups appeared in the set of genes. Three genes—MAPK8IP3, CRLF3, UNC13D—have a strong association with the KLH response. The removal of SNPs associated with each of these genes led to decrease of explained variance by at least 1%. For 7 other genes, the removal of their SNPs from the description decreased the quality of the models by between 0 and 0.5%. For the last 8 genes, the model built without their SNPs were better than the reference model (Table 1 and Figure 3).

Table 1.

Sensitivity analysis of genes for KLH7.

Stage 1
Group	Gene	SNPs	Mean	Mean diff.
	Reference	All SNPs	11.2%	0
I	MAPK8IP3	15714774, 14068006, 16001483,
		14692425,16690726	8.1%	−3.1%
	CRLF3	15827424, 15826603,
		13508431, 15826598	8.9%	−2.3%
	UNC13D	15039342	10.2%	−1.0%
II	ILR9	10731333	10.7%	−0.5%
	PRCKB	15008890, 14075158	10.8%	−0.4%
	MAP2K3	15006760	10.9%	−0.3%
	ST6GAL1	15965697	10.9%	−0.3%
	CARD11	14071669, 15005804	11.1%	−0.1%
	PTGER4	16102750	11.1%	−0.1%
	GPC1	16651464	11.1%	−0.1%
III	SOX14	15947324	11.3%	0.1%
	JAK2	14777688	11.3%	0.1%
	PDGFA	14070244	11.4%	0.2%
	NLRC3	29005402	11.4%	0.2%
	JMJD6	15820319	11.5%	0.3%
	MAP2K4	15035880, 15035854, 14105858	11.7%	0.5%
		15810344
	SMURF1	14072521, 15725673	11.7%	0.5%

Stage 2
	Base group	Additional genes	Mean	Mean diff.
	I	-	12.2%	1.0%
	I	Group II (7 genes)	14.1%	2.9%
	I	PRCKB	13.7%	2.5%
	I	IL9R	13.6%	2.4%
	I	ILR9, PRCKB	14.9%	3.7%
Final model		MAPK8IP3, CRLF3, UNC13D, PRCKB, ILR9	14.9%	3.7%

Stage 1: The numbers describe the performance of the random forest models, built without the indicated gene. The reference row displays performance of model containing all the genes. Horizontal lines separate 3 group pf genes. The SNPs that were present in all 297 sets in the previous step are displayed in boldface. The SNPs that were present in more than 90% of cases are displayed in italic. Stage 2: The effect of adding selected genes and combinations of genes to the base set consisting of genes from the group I.

The SNPs that were present in all 297 sets in the previous step are displayed in boldface.

Figure 3.

Boxplot of gene sensitivity for KLH7 trait (Table 1). The red vertical lines divide genes into 3 groups by their influence on the models. The last plot describes a reference series with all the genes. The horizontal line is a reference level—median of the reference models.

In the next step, we checked the effect of removing all SNPs from genes belonging to the third group from the description. This result led to a significant increase of the model quality—the variance explained increased from 11.2 to 14.1%. What is more, even a model built using only 3 genes from the first group, with explained variance equal to 12.2%, is better than reference. In further analysis, we used genes from the group I as the base set. Then we examined effects of extending this base set by SNPs from all possible combinations of genes from the group II. For 2 sets consisting of SNPs belonging to 4 variables, the results were very close to the result obtained for the full set of 10 genes. The best results were obtained for a set consisting of 5 genes (Table 1). A more detailed presentation of results is available in Supplementary Tables 6–8.

LPS

For the LPS, all the 9 selected genes had a considerable impact on the models (Table 2). Excluding SNPs from each of these genes resulted in significantly decreased result, by at least 0.8%. Therefore, the final model consists of these 9 genes.

Table 2.

Sensitivity analysis of genes for LPS.

Group	Gene	SNPs	Mean	Mean diff.
	Reference	All SNPs	4.4	0
I	ST6GAL1	15965697	3.1%	−1.3%
	TRAF7	14072516	3.0%	−1.4%
	ITGB4	14110474,13507637	3.4%	−1.0%
	PTGER4	16102750	3.4%	−1.0%
	SPHK1	15039217	3.5%	−0.9%
	MAPK8IP3	15714774, 16001483	3.5%	−0.9%
	CRLF3	15826598, 15827424, 15040786	3.6%	−0.8%
	MAP2K4	15035880, 15810344, 14105858	3.6%	−0.8%
	PROCR	15968294	3.6%	−0.8%

The numbers describe the performance of the random forest models, built without the gene. The reference row describes the series of models containing all the genes.

LTA

For the LTA data set, the results were qualitatively similar to those obtained for KLH7 (Table 3). The genes can be divided into 3 groups. The removal of SNPs belonging to any of the 6 genes in the first group led to a significant decrease of the model quality, by at least 0.7%. For 3 genes from the second group, the removal of SNPs from the variable set resulted in a moderate decrease of model quality. For the remaining group of genes, the removal of their SNPs from the descriptive variables either had no effect or even improved model results, by up to 0.5%. In the second stage of sensitivity analysis, all possible combinations of 3 genes from group II were added to the genes from group I. The best result was obtained for a set of 7 genes from group I and gene SOX14 from group II.

Table 3.

Sensitivity analysis of genes for LTA.

Stage 1
Group	Gene	SNPs	Mean	Mean diff.
	Reference	All SNPs	4.5%	0.00%
I	CRLF3	15826598, 15040786	2.3%	−2.2%
	MAPK8IP3	15714774	3.0%	−1.5%
	TNFRSF13B	14072943	3.4%	−1.1%
	SMURF1	14072521, 15725673	3.5%	−1.0%
	PDGFA	14070244	3.6%	−0.9%
	PTGER4	16102750	3.8%	−0.7%
II	SOX14	10730793	3.9%	−0.6%
	FOXJ1	14110239	4.3%	−0.2%
	GPC1	15943775	4.3%	−0.2%
III	ITGB4	15821339, 14110474	4.5%	+0.0%
	SPHK1	15039217	4.7%	+0.2%
	IL9R	15732513	4.7%	+0.2%
	MAP2K4	15035854, 15035880, 15810344	4.9%	+0.4%
	ST6GAL1	15965697	4.9%	+0.4%
	JMJD6	15820338	5.0%	+0.5%

Stage 2
	Base group	Additional genes	Mean	Mean diff.
	I	SOX14, FOXJ1, GPC1	7.1%	2.6%
	I	SOX14, FOXJ1,	7.9%	3.4%
	I	SOX14	7.8%	3.3%

The numbers describe the performance of the random forest models, built without the gene. The reference row describes the series of models containing all the genes.

The SNPs that were present in all 297 sets in the previous step are displayed in boldface.

Discussion

As should be expected from the biological considerations, we have not discovered a genetic influence on the innate response for the KLH antibody (KLHd0). For the remaining traits, we have been able to attribute between 4.4 and 14.9% to genetic factors. The following best results were obtained:

• •KLH7: 14.9% explained variance by the model based on 13 SNPs from 5 following genes: MAPK8IP3, CRLF3, UNC13D, ILR9, and PRCKB;
• •LPS: 4.5% explained variance by the model based on 15 SNPs from 9 following genes: ST6GAL1, TRAF7, ITGB4, SPHK1, MAPK8IP3, PTGER4, CRLF3, MAP2K4, and PROCR;
• •LTA: 7.8% explained variance by the model based on 9 SNPs from 7 following genes: CRLF3, MAPK8IP3, TNFRSF13B, SMURF1, PDGFA, PTGER4, and SOX14.

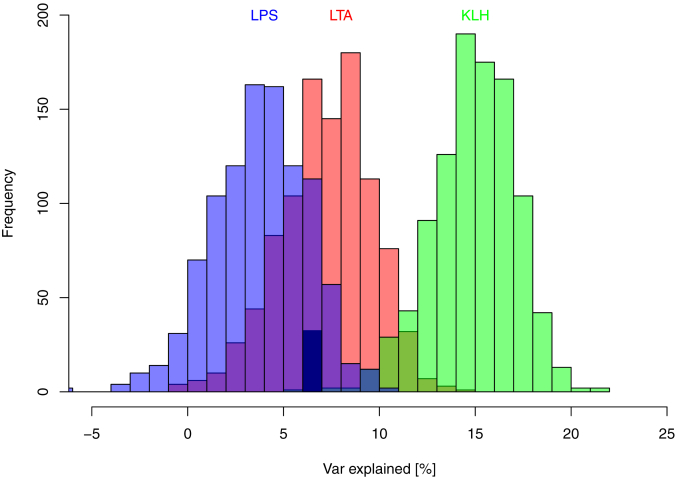
One should note that the results reported for the models are obtained as average over 1,000 repeats of the cross-validation procedure. Hence, for each response, 3,000 individual models have been built and tested on the independent data. The results of these tests are widely distributed around their respective mean values (Figure 4). One can observe that for the LPS and even the LTA models, some tests have negative predictive power. Even for KLH7, the explained variance in a significant fraction of cases was below 10%.

Figure 4.

Histograms of the performance of random forest models for KLH7, LPS, and LTA phenotypic traits. Models were built using optimal feature set for each trait. Histograms were generated using 1,000 iterations of 3-fold cross-validation.

It is worth noting that not all SNPs from these genes were used to built models. Most SNPs are rejected by a feature selection procedure, and in effect, about half of the genes are represented by one SNP only.

It is interesting to compare the decrease of the model quality in the sensitivity analysis, with the final quality of the model. For the KLH7 trait, 5 variables (MAPK8IP3, CRLF3, UNC13D, PRCKB, and ILR9) contribute to the final model. The sum of their sensitivities is 7.3% of lost explained variance, whereas the model explains 14.9% of variance (Table 1). It is clear that the difference must arise because of strong synergistic interactions between variables.

For LPS, the opposite situation can be observed—the sum of sensitivities is 8.9%, whereas the model explains only 4.5% of variance (Table 2). In this case, the model has both significant interactions and redundancy. In the case of LTA, both quantities are roughly balanced. The sum of sensitivities is 8.0%, whereas the final model explains 7.8% of variance (Table 3). Nevertheless, it is still likely that our model for LTA still has both: interactions between variables and redundancy that cancel each other. This hypothesis is supported by the observation that removal of 11 variables from the initial model nearly doubled the predictive abilities of the model. This could be achieved only by removing misguided interactions. It is unlikely that the such interactions were limited only to the variables that were finally removed from the model.

Two genes, namely MAPK8IP3 and CRLF3 are included in all 3 models. They are the 2 most important genes both in the case of KLH and LTA response but have relatively lower rank in the case of LPS. One should note, however, that the number of SNPs in the model is different in each case. MAPK8IP3 in KLH7 data series is represented by 5 SNPs, in LPS by 2 SNPs, and in LTA by one SNP. Similarly, they are 4 SNPs from CRLF3 in KLH7, 3 in LPS, and 2 in LTA; moreover, one SNP that is present in variables sets for LPS and LTA is absent in the variable set of KLH7.

One gene, namely PTGER4, represented by a single SNP is included in the final model for LPS and LTA data sets. Interestingly, this gene is also present in the initial KLH model, but it is later removed by gene-based sensitivity analysis. Initial KLH model includes also ST6GAL1 and MAP2K4 present in the LPS model as well as PDGFA, SOX14, and SMURF1 present in the LTA models. One should note that SOX14 is represented by different SNPs in KLH and LTA models, and also in the case of MAP2K4, one of 3 SNPs is different.

All these connections show that both innate and adaptive immune responses are strongly connected by a network of dependencies. The central nodes of the network observed in the experimental study are MAPK8IP3 and CRLF3, and their influence is modified by other genes. The MAPK8IP3 gene is a part of MAPK signalling pathway and has been associated with regulation of JNK1 (MAPK8) (Kuboki et al., 2000), which in turn controls T-helper-cell differentiation and cytokine production (Rincón et al., 2000; Dong et al., 2002; Jeffrey et al., 2007). MAPK8IP3 is also known to be involved in carcinogenesis (Yuan et al., 2015). The CRLF3 gene has been reported to be involved in regulation of a cell cycle (Yang et al., 2009).

The 3 genes specific to KLH are IL9R, PRKCB, and UNC13D. IL9R codes receptor of interleukin 9, which in turn is a signal molecule secreted by T-helper cells as a part of adaptive immune response. PRKCB regulates glycolysis in B cells and is essential for their long-term survival. Both these genes are involved in regulation of the adaptive immune system. The third gene unique to KLH response is UNC13D that regulates secretory activity of the neutrophiles (Shirakawa et al., 2004), which is part of the innate response. Out of 5 genes included in the model 2, namely IL9R and PRKCB, are already known to be directly involved in the regulation of adaptive immune response. MAPK8IP3 plays multiple roles in the MAPK signalling pathway, and one of them is possibly regulation of T-helper-cell actions, similar to IL9R. The function of CRLF3 is not well established, and UNC13D is involved in the innate response. Inclusion of the latter in the model does not mean that either UNC13D is involved in adaptive response or that a model is wrong. It may reflect the design of experiment and limitations of the gathered data. The original experiment was designed to maximise variance in the KLH adaptive response. Owing to technical limitations, the data were collected on the SNPs belonging to 36 out of possible hundreds of genes related to immune response.

It is likely that UNC13D plays a role of proxy for other genes with whom it is correlated, either because of the linkage disequilibrium or coregulation. What is more, we cannot exclude the possibility for any of the genes included in the model. While results from modelling are far from perfect, they are strong enough to warrant further investigation into the role of CRLF3 and MAPK8IP3 in the adaptive immune response.

We refrain from giving the biological interpretation for 2 remaining models, for several reasons. First, as mentioned previously, the experiment itself was designed to maximise adaptive response to KLH, and hence, the variance in the innate response is only a side effect. Second, the models for LTA and especially for LPS have much lower explanatory power. What is more, the complexity of the model grows with falling explanatory power—the best model for KLH is built using 5 genes, the intermediate model for LTA is built on 7 genes, and the weakest model for LPS is built on 9 genes. Finally, multiple genes included in the models are known for their role in adaptive, rather than innate, response. For example, the PTGER4 gene that is included in both LPS and LTA models is a gene for prostaglandin receptor EP4 that has multiple roles in the adaptive immune response (Woodward et al., 2011). Taking all these factors into account, it is most likely that the genes included in LPS and LTA models act as proxy for other factors that were not included in the collected data.

The genes identified in the present study as relevant are in a broad agreement with those that were found previously in S15 (Table 4). The agreement is best for the KLH7 trait, for which the genetic signal is strongest in the data. The gene CRLF3 is present in our predictive model but not in the set of genes connected with adaptive immunity to KLH found in S15. However, it has been identified as significant for innate response to LPS in S15. It is possible that CRLF3 acts by enhancing the contributions of other genes to adaptive response, and this cannot be discovered by a standard univariate analysis. The agreement between genes with weaker association with KLH response identified in both studies is poor. Also, the results for 2 remaining data sets agree between 2 studies to a lesser extent.

Table 4.

Summary of the sensitivity analysis for all traits.

Gene	Chromosome	KLH7		LPS		LTA
		P19	S15	P19	S15	P19	S15
EPHB1	9		+		++
GPC1	9	∗∗				∗∗
KLHL6	9		+		+		+
PROCR	9		+	∗∗∗	++
SOX14	9	∗				∗∗∗
ST6GAL1	9	∗∗		∗∗∗		∗
CARD11	14	∗∗	++				+
IL9R	14	∗∗∗	++		+	∗	++
MAP2K3	14	∗∗					++
MAPK8IP3	14	∗∗∗	++	∗∗∗	+	∗∗∗	++
NLRC3	14	∗
PDGFA	14	∗	++			∗∗∗
PRKCB	14	∗∗∗	++		+		++
SMURF1	14	∗				∗∗∗
SOCS1	14				+
TNFRSF13B	14					∗∗∗	+
TRAF7	14		+	∗∗∗
CRLF3	18	∗∗∗		∗∗∗	++	∗∗∗
FOXJ1	18		+		++	∗∗	++
ITGB4	18		++	∗∗∗		∗	+
JMJD6	18	∗	+			∗	++
MAP2K4	18	∗	+	∗∗∗		∗
SPHK1	18			∗∗∗		∗
UNC13D	18	∗∗∗	++
JAK2	Z	∗
PTGER4	Z	∗∗		∗∗∗	++	∗∗∗	++

The results of the present study are denoted as P19 and are compared with results from Siwek et al. (2015), denoted as S15. The following symbols are used. P19: ∗∗∗ gene included in the final model, ∗∗ positive sensitivity score, negative sensitivity score; S15: ++ gene significant both in RMM and CAR analysis, + gene significant only in CAR analysis.

The discrepancy between results of both studies is not surprising, given that the analytical methods used in both studies are very different. In particular, methods used in the present study take into account complex relationships between multiple variables, that cannot be effectively identified in simpler univariate and bi-variate analysis performed in S15. On the other hand, some variables that have statistically significant associations with response may not be discovered by the current approach because they may not be sufficiently useful for the RF classifier, to be included in the list of important variables. It is worth noting that agreement between the lists of important genes is best for the best model and worst for the worst model. This can be also expected—when the signal is strong enough, the noise becomes relatively small, and its influence on the results of the analysis is diminished.

While comparison with the S15 on the gene level gives fairly reasonable results, the comparison on the level of individual SNPs is far more divergent. Only 6 SNPs were identified as relevant in the previous study, one for KLH, rs15820324, 4 for LPS, rs14110239, rs15946185, rs16102750, and rs15731101, and one for LTA, rs14110519. The rs15820324 was included in the top 30 most important SNPs only 3 times in 297 cross-validation models; hence, it never entered further modelling stages. Instead, 29 other SNPs were used in the initial RF model, and 13 of them were used in the final model. The linear model of KLH response based on the single SNP rs15820324 explains 1.5% of variance. The linear model built on the 13 SNPs selected in our procedure explains 7.2% of variance in the response variable. For comparison, the RF model based on the same 13 SNPs explains 14.9% of variance in the cross-validation.

In the case of LPS data set, the original study identified 4 significant SNPs. The rs14110239 was never included into any feature set for LPS; however, it was included in all 297 feature sets for LTA in the initial feature selection procedure. The rs16102750 was included in all 297 feature sets for LPS, as well as KLH and LTA, in the initial feature selection procedure and was included to the final feature set in LPS and LTA models. The rs15946185 and rs15731101 were not included in any feature sets for LPS, LTA, and KLH in the initial feature selection procedure. The linear model built on these 4 variables explains 0.3% of variance in the LPS response function. For comparison, a linear model built using 15 SNPs identified by the present study explains 1.0% of variance in LPS, whereas the RF model built on the same feature set explains 4.5% of variance.

Finally, the rs14110519 identified in the original study as significant for LTA was not included in any feature sets for LPS, LTA, and KLH in the initial feature selection procedure. The linear model using this variable explains 0.5% of variance in the LTA response function. In comparison, the best model in the present study using 9 SNPs explains 7.8% of variance, and linear model built on the same feature set explains 2.5% of variance.

Conclusion

We have applied the sensitivity analysis based on the machine learning algorithm to examine the associations between genetic markers and immune response in chickens.

The genes identified by this methodology generally agree with the genes identified by a statistical approach in the original study. The agreement was best for adaptive response to KLH antibody and worst for innate response to LPS. This correlates well with the strength of the signal discovered in the data. The models obtained using RF algorithm for nonparametric and nonlinear regression were significantly better than linear models using the same variables. What is more, they are much better than linear models using SNPs that were identified as relevant by a standard statistical approach in the original study. The results obtained for innate response to the KLH antigen show that the methodology implemented in the study is relatively resistant to overfitting. Owing to careful application of the cross-validation procedure, the predictive models can be constructed only for systems where there is true link between descriptive variables and response. This is demonstrated by the negative result obtained for innate response to KLH. On the other hand, the improved performance of models of adaptive immune response to KLH, upon removal of information about some genes, shows that overfitting was nevertheless present and prevented good generalization of the models. This overfitting could be removed by treating strongly correlated variables as a single unit. We have shown that sensitivity analysis based on the machine learning approach can be much more sensitive for identification of relevant variables in the system where complex nonlinear and nonadditive interactions between variables may be present. What is more, the machine learning regression models have much better predictive power than their linear counterparts. These results may be explained by a combination of 2 effects. First, possible interactions between genetic variables in the system can be used by ML models but are inaccessible to standard linear additive models. Alternatively, the ML approach may be better for dealing with incomplete and indirect data.

The best model was built for the adaptive response to KLH antibody and the worst for the innate response to LPS. These differences are consistent with the design of the experiment and are very well rooted in our knowledge of immune response. The parental generation of the experimental population was selected for a primary antibody response toward KLH antigen. As already mentioned, KLH triggers the Th2 type of adaptive immune response, which is also connected to LTA. In particular, LTA is a ligand for TLR2 (Toll-like receptor 2) which, being a part of innate response, acts as a trigger of the adaptive response of the type Th2, which in turn is responsible for the adaptive response to nonpathogenic KLH antigen. On the other hand, LPS initiates the Th1 type of immune response via interactions with different proteins from the TLR family, namely TLR4.

All final predictive models constructed in the present study use SNPs from 2 genes, namely MAPK8IP3 and CRLF3. What is more, these 2 genes were the 2 most important genes in the model for KLH adaptive response. The KLH model contains also 2 genes that are already well known to be involved in regulation of adaptive response, namely ILR9 and PRCKB, as well as one gene involved in regulation of innate response, namely UNC13D. This result strongly suggests that both MAPK8IP3 and CRLF3 play a significant role in the adaptive immune response. The MAPK8IP3 is described in the literature and it is known that it is connected with JNK signaling pathway. We hypothesise that CRLF3 has a similar role and interacts with another signalling pathway, possibly the JAK STAT pathway. Owing to these interactions, both genes have broad action by triggering cascade of gene activations on the signaling pathways.

The procedure used in the present article is computationally demanding and can be difficult to reproduce directly for larger data sets, with thousands of animals described with 60K or even 600K SNPs. The main limiting factor is the initial feature selection step, which is performed with the Boruta algorithm. While the algorithm has been used for high-throughput omics data and, in recent review (Degenhardt et al., 2019), has been recommended as the most powerful approach, nevertheless, it was also noted as very computationally demanding. For a system with one order of magnitude larger number of objects and 2 orders of magnitude larger number of variables, the computational effort would be at least 3 orders of magnitude larger. For such systems, one may need to apply another feature selection algorithm. However, it is crucial that this algorithm should be able to identify interacting variables. One could use the Monte Carlo Feature Selection (Dramiński et al., 2008) or the MultiDimensional Feature Selection (Piliszek et al., 2019; Mnich and Rudnicki, 2020) algorithms for this purpose. The remaining part of the protocol is applied to a system with a much smaller number of informative variables and would be feasible even for much larger systems.