A combined molecular/continuum-modeling approach to predict the small-angle neutron scattering of curved membranes

Abstract

This paper develops a framework to compute the small-angle neutron scattering (SANS) from highly curved, dynamically fluctuating, and potentially inhomogeneous membranes. This method is needed to compute the scattering from nanometer-scale membrane domains that couple to curvature, as predicted by molecular modeling. The detailed neutron scattering length density of a small planar bilayer patch is readily available via molecular dynamics simulation. A mathematical, mechanical transformation of the planar scattering length density is developed to predict the scattering from curved bilayers. By simulating a fluctuating, curved, surface-continuum model, long time- and length-scales can be reached while, with the aid of the planar-to-curved transformation, the molecular features of the scattering length density can be retained. A test case for the method is developed by constructing a coarse-grained lipid vesicle following a protocol designed to relieve both the osmotic stress inside the vesicle and the lipid-number stress between the leaflets. A question was whether the hybrid model would be able to replicate the scattering from the highly deformed inner and outer leaflets of the small vesicle. Matching the scattering of the full (molecular vesicle) and hybrid (continuum vesicle) models indicated that the inner and outer leaflets of the full vesicle were expanded laterally, consistent with previous simulations of the Martini forcefield that showed thinning in small vesicles. The vesicle structure is inconsistent with a zero-tension leaflet deformed by a single set of elastic parameters, and the results show that this is evident in the scattering. The method can be applied to translate observations of any molecular model’s neutron scattering length densities from small patches to large length and timescales.

1. Introduction

Over a significant range of composition and temperature, mixing saturated and unsaturated lipids together with cholesterol leads to two-dimensional liquid-liquid coexistence [1, 2]. The physics of line tension leads to perimeter-minimizing circular domains. However, additional physical mechanisms may promote modulated phases [3] that have non-circular equilibrium structure and that arrange on sub-optical lengthscales. This work develops a new tool that combines molecular and continuum modeling to predict the scattering from sub-micron scale structures. The motivation is the hypothesis that liquid ordered (L_o) and disordered (L_d) phases have disparate curvature preferences, leading to non-circular patterning as the compositional variation couples to the wavelength of energetically favorable undulations [4]. As discussed below, continuum modeling can access a much larger range of length- and time-scales than all-atom simulation, while all-atom simulations are able to accurately predict both the strong transverse scattering from lipid bilayers and the spontaneous curvature of lipids. The combination of the two, in the framework presented here, holds the potential to describe the scattering from complex mixtures featuring strong undulations leading to modulated phases [4]. The critical first test in this paper is to model the scattering from the extreme curvature of a small vesicle.

The work of Feigenson et al. [5] describes such modulation in lipid bilayers with non-circular equilibrium structure and nanoscopic size. In the quaternary mixtures of Ref. [5], modulation occurs when the unsaturated component contains both di-oleoyl and 1-palmitoyl-2-oleoyl phosphatidylcholines (DOPC and POPC, respectively). Förster resonance energy transfer (FRET), a technique that reports nanometer-scale contacts between fluorophores, indicates that di-stearoyl phosphatidylcholine (DSPC), POPC, and cholesterol mixtures are also phase-separated, even though the domains may not be visible by optical spectroscopy [6, 7]. While FRET indicates inhomogeneity, it does not provide direct information on structure; it only indicates the co-localization of probes.

A section of the bilayer must be asymmetric to manifest a curvature preference, otherwise the stresses in the leaflets cancel. In a phase separated bilayer, the L_o and L_d can appear out of register such that the opposite phase is on the opposite leaflet. This may be driven by hydrophobic mismatch; the L_o is significantly thicker and so by arranging the phases out of register, the thickness of adjoining regions will match [8, 9, 10]. Additionally, coarse-grained simulations have attributed registration effects to curvature [11, 9]. Furthermore, the plasma membrane is known to be highly asymmetric [12] in lipid composition, and thus likely in curvature stress as well. In Ref. [13], Lorent et al. show that a third of the lipids in the outer leaflet of the plasma membrane have completely saturated acyl chains, while this is true of only a tenth of the lipids in the inner leaflet. Combined with the substantial enrichment of highly curvature-sensitive phosphatidylethanolamine (PE) on the inner leaflet, the ingredients for coupling to curvature are in place. Shlomovitz and Schick point out that while the inner leaflet of the plasma membrane does not have lipids compatible with phase separation, PE may support modulation by curvature-mediated trans-leaflet coupling [14]. Their hypothesis is supported by the instability predicted by Leibler for mixtures of curvature sensitive lipids [15], where dynamic redistribution in the leaflets supports large deformations.

Besides curvature-mediated coupling, a significant out-of-plane dipole in one phase can prohibit large-scale domains [16, 17, 18, 19, 20, 21, 22, 23]. The collective energy increases with the area of the domain (rather than its perimeter) disfavoring large domains. Amazon et al. [24, 25] employed a combined line-tension/continuum-mechanical model, similar to that of Ref. [26], to demonstrate that differences in bending energy and dipole potential can limit domains at the nanometer-scale.

The main goal of the current work is to model small-angle neutron scattering (SANS) from a particular lipid composition as the bilayer responds to lipid curvature stress. SANS operates below the spectroscopic optical limit and gives correlated positions at the nanometer scale. With selective deuteration, the signal from specific lipids can be amplified relative to the background scattering of the environment. The technique has implied the existence of 40-nm diameter membrane features in gram-positive bacteria, where selective deuteration of a targeted membrane is feasible [27]. SANS techniques have been applied to measure the thickness of isolated membrane regions to probe trans-leaflet coupling. For example, Heberle et al. demonstrated that trans-leaflet coupling reduced the thickness of a gel domain in the outer leaflet of a large unilamellar vesicle (LUV) [28]. Similarly, Eicher et al. found that the asymmetric distribution of curvature-sensitive lipids could influence trans-leaflet coupling of the melting transition, with scattering techniques reporting the transverse structure of the phases [29]. The application of SANS found that the small molecule melatonin gives rise to phase-modulating behavior in small 50 nm diameter vesicles, which the authors model with the mathematical formalism applicable to microemulsions [30].

The SANS intensity reflects large bilayer structures, including curving undulations of the bilayer. In general for a complex sample with SANS, spatial correlations are entangled and require an accurate model for interpretation. Molecular simulations provide such a model, with complete resolution in time and space. Yet computational resources limit both the duration and size of simulations; this is especially prohibitive when modeling lipid bilayer curvature. Periodic boundary conditions suppress undulations incompatible with the simulation box shape. Yet when the simulation size is extended to the tens of nanometers, simulation times must be also be extended well into the microsecond range to allow for lipid lateral redistribution. Relatively large simulations are necessary so that domains are able to take their preferred shape and size.

Continuum models are a computationally feasible approach to extend modeling well into the regime necessary to model modulated phases. The energetics of membrane shape is modeled by employing the Helfrich/Canham [31, 32] Hamiltonian. The most straightforward way to model compositional fluctuations is through a two state model built on line tension. This approach is able to reproduce the temperature-dependent dynamics and fluctuations in the size of domains [33, 34]. With these basic elements the challenge is to add to the continuum model additional physical effects leading to size and shape modulation in more complex mixtures.

The nanometer-scale hexagonal packing of L_o phases observed in the simulations of Ref. [35] approaches the range of feasible lipid spontaneous curvature where the local shape of the leaflet and composition could strongly couple. A key compositional factor is cholesterol. Not only does cholesterol partition between the two phases, but simulations predict that curvature stresses arising from cholesterol in the two phases are very different [36]. This interpretation stands in contrast to the axiom that spontaneous curvature is an intrinsic property of lipids, rather than that of domains of a particular composition. The difference is stark; given the high cholesterol content of ordered phases, and the high negative spontaneous curvature of cholesterol both from simulation and experiment, the ordered phase should itself have significant negative spontaneous curvature [37]. However, the CHARMM forcefield (which shows cholesterol’s negative spontaneous curvature in disordered phases) indicates ordered domains have positive spontaneous curvature [36]. The difference in spontaneous curvature between L_d and L_o phases supports the hypothesis that curvature preferences are a factor in promoting phase modulation.

This work addresses the need for simulation methodology to assist in the interpretation of SANS experiments of inhomogeneous bilayers, emphasizing how inhomogeneity couples to high curvature. An additional use is to predict the magnitude of coupling effects to see how they will be visible to SANS. This includes whether they will be distinguishable from competing signals, such as the distribution of vesicle sizes and composition that are inherent in any experiment. The approach is based on taking data from simulations of manageable size, i.e., small bilayer patches and, through continuum modeling, translate these into the full scattering from vesicles, including predictions of how lipid redistribution will couple to curvature.

The work here is based on previous similar efforts to compute scattering from inhomogeneous systems. Carrillo et al. applied highly coarse-grained, implicit solvent molecular modeling to model the scattering from small vesicles [38]. They point out that the scattering can be computed from the Debye formula, in which pairs of scatterers are summed over, or by using a three dimensional fast Fourier transform (FFT), the cost of which depends on the FFT grid density. With this explicit particle approach, they were able to determine the time-dependent correlation of the scattering intensity, enabling comparison to spin-echo experiments. This framework is attractive in that the underlying molecular model naturally has the full set of elastic deformations, which otherwise must be added explicitly to continuum models. However, to accurately predict the complete scattering of a vesicle at high q where molecular scale features are represented, the detail of an all-atom model is likely necessary. The reference calculation we perform here for the scattering of a Martini vesicle uses the same approach as in Ref. [38].

Vesicle scattering has been approximated by separating the vesicle form from the transverse component (the scattering length density variation along the bilayer normal). See, for example, Ref. [39] that develops a model that combines the scattering form of polydisperse distribution of vesicle sizes with an approximation for the transverse structure. Significant insights into the structure of bilayers are gained from simple forms for the transverse structure, including fitting with “three-level” or “top hat” functions [40, 41, 42], Gaussian functions [43, 44, 45], or other simple forms used to represent variations in the density. Henderson used a Monte Carlo model to sample the scattering from multiple aggregates [46]. Heberle [47] et al. developed a general theory to predict the scattering from vesicles containing phase-separated circular domains, extending Henderson’s Monte Carlo sampling to verify their theory, and the effort has been extended to model randomly distributed nanoscopic domains [48, 49]. The scattering modeled in Ref. [47] reflects both vesicle shape as well as lateral correlations due to phase separation. The hexagonal substructure observed for L_o in Ref. [35] belongs in a separate class of lateral heterogeneity not apparently driven by line tension, but by the molecular scale interactions of individual lipids. To model this very fine structure, two of the present authors designed an algorithm that separates close-ranged correlations from long range correlations to mitigate fine size effects when applied to modestly-sized simulations [50].

The approach of this paper is to develop a method capable of taking information from a small patch of Martini bilayer and employing a continuum model to predict the full scattering. Small vesicles are used as a testing ground, not simply because they are convenient to simulate, but also because strong curvature, as they exhibit, is hypothesized to contribute to the nanometer-scale modulation of domain shapes in complex mixtures. A related challenge is to characterize the stresses present in those small vesicles and parameterize that stress into the continuum model. It is unclear if the highly curved leaflets of a small vesicle can be interpreted in terms of the mechanical parameters of planar simulations. The method developed here parameterizes leaflet lateral strains so that the scattering of vesicles with strained leaflets can be predicted.

2. Methods

2.1. Coarse-grain Martini modeling

All simulations were run in GROMACS [51]. The temperature was equilibrated at 310.15 K using a combination velocity rescaling/stochastic algorithm [52]. A timestep of 20 femtoseconds was employed, as is appropriate for the soft Martini potential. The standard dielectric constant for Martini, 15, was used.

Vesicle systems were built using the Vesicle Builder component of the CHARMM-GUI Martini Maker online tool [53]. The CHARMM-GUI system is a widely used scheme for constructing all-atom and coarse-grained simulations, especially those containing bilayers [54]. The Vesicle Builder module was built recognizing the difficulty of constructing a vesicle with the correct lipid and osmotic-stress balance and takes special measures to prevent these stresses. These measures are reviewed here but originally appeared in Refs. [55, 56].

Six pores, aligned on the Cartesian poles, are formed in the vesicle by temporarily applying collective potentials that prevent lipid tails from entering the region. During this equilibration period, exceeding a microsecond, lipids are able to move between the leaflets, in some part relieving lipid imbalances. Just as importantly for achieving zero tension, water moves between the inside and the outside of the vesicle. With too much water, the vesicle bilayer will be under positive tension, expanding the bilayer area and limiting fluctuations. With too little water, the bilayer will contract or pucker inward. The external potential is then slowly removed and equilibration continues. The vesicles were built entirely of POPC, following which 10% of the inner leaflet lipids were mutated to POPE.

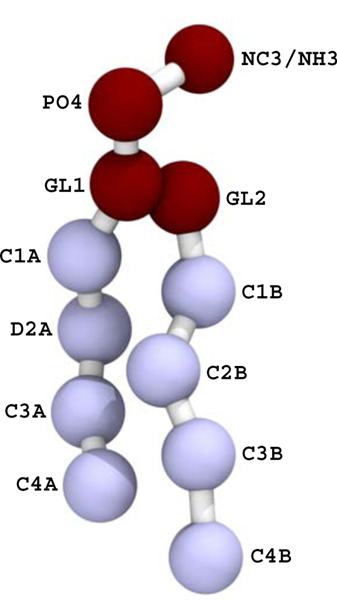
Two vesicles, consisting of POPC on the outer leaflet and a 90:10 POPC:POPE ratio on the inner leaflet, were simulated for two microseconds. A larger vesicle had a diameter of approximately 18 nm, while a smaller one had diameter approximately 13 nm (measured at the bilayer midplane). As discussed further in the conclusions, these vesicles are smaller than are typically studied with SANS and are instead intended to model the high curvature that may arise in phase modulation. Configurations were sampled every nanosecond. The scattering lengths for the groups were set to −0.5158 for NC3, −0.2649 for NH3, 2.672 for PO4, 1.888 for the GL beads, −0.3332 for the saturated acyl groups, and 0.4152 for the unsaturated sites (see Fig. 1). The scattering length density was computed on a 2 Å grid and the FFT was computed and squared. The intensity was averaged over the 2000 frames of simulation data.

Figure 1:

The POPC (with NC3) and POPE (with NH3) lipids used in the study. The interaction site names (e.g., C2B) are referred to in the text regarding the pivotal plane of bending.

Planar systems were built and simulated with GROMACS to compute the transverse neutron scattering length density (NSLD), β(z). The CHARMM-GUI bilayer builder was used [54]. The standard CHARMM-GUI equilibration procedure was used, followed by 200 nanoseconds of production dynamics. The NSLD of the asymmetric POPC/POPE mixture was computed from a small planar simulation with 100 lipids per leaflet (100% POPC in the top leaflet, 90:10 POPC:POPE in the lower leaflet). The laterally-averaged scattering length density was computed by performing a histogram in the z dimension (with length approximately 80 Å) with 250 bins.

2.2. Material deformation of the planar scattering length density to model curvature

The approach here to modeling the complete scattering from a vesicle consisting of a single liquid-ordered bilayer is to combine continuum modeling of large dynamic structures with the laterally averaged scattering length density β_LA computed from molecular simulation. Figure 3 illustrates the method for computing the contribution of shape and dynamical fluctuations to the scattering intensity. The fluctuations of the sphere are computed using a spherical harmonic representation of the (two dimensional) surface. The three-dimensional scattering length density is evaluated using the β_LA(z) distribution computed from a planar simulation. At a given point on the surface, here in general {u,v} coordinates, the position is r(u,v) and the normal is n(u,v). The lipid density at a point is computed using the square root of the metric tensor, g_uv. The normal, metric tensor, and curvature are computed using standard techniques of differential geometry, based on the first and second derivatives of r(u,v) with respect to u and v [57].

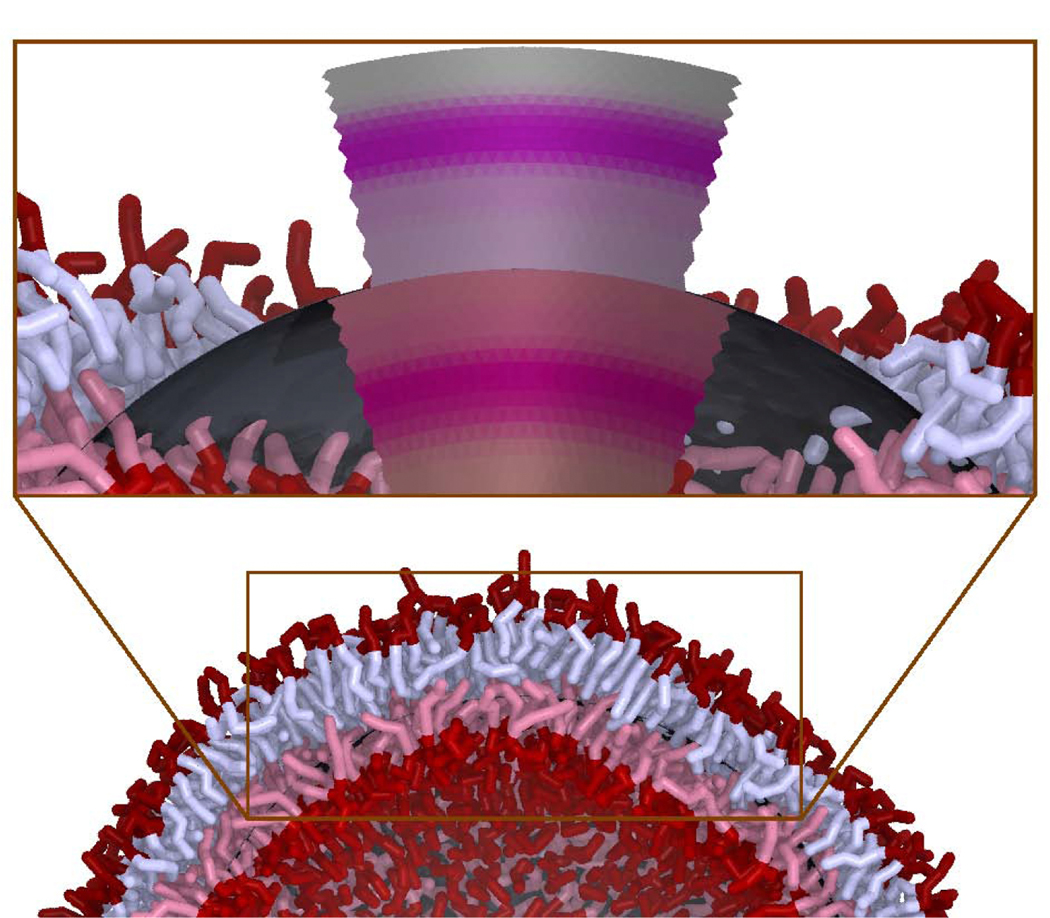
Figure 3:

An illustration of how a surface continuum model, combined with a scattering length density profile from molecular simulation, β_LA(z), is used to model the scattering centers from a dynamically fluctuating vesicle of a particular size. A frame of a simulation of a Martini vesicle is shown (water is removed from the image for clarity). In the inset, a portion of the lipids are removed and the continuum model is shown. The underlying approximately spherical continuum model is shown in dark grey while the deformed NSLD is shown for both the outer and inner leaflets. The shapes of the inner and outer leaflets are discontinuous because, in this model, the leaflets deform semi-independently (they meet at the dark grey continuum-modeled midplane). The inner leaflets of the Martini model and continuum-modeled density are both tinted red.

The basis of the continuum model is to use the bilayer midplane to evaluate the Helfrich/Canham [31, 32] curvature energy of the fluctuating bilayer:

$$E={\int }_A\frac{\kappa }{2}{\left(c-c_0\right)}^2,$$ (1)

where c is the curvature and c₀ is the spontaneous curvature. The distribution of scatterers off the midplane is then computed based on β_LA(z), itself computed from a simulation of a flat bilayer. The methodology here corrects for the change in the scattering length density of a curved bilayer according to the assumption that the area at a position in the leaflet interior is constant, z_ns, and that the volume of the bilayer is conserved everywhere up to second order in the curvature. See below for a brief discussion of the pivotal plane and neutral surface. The constant volume assumption is strongly indicated by simulations and experiment [58]. For a positively curved bilayer, for example, that of the outer leaflet of a vesicle, there is more surface area near the neutral surface (4π[R + z_ns]²) than there is at the bilayer midplane (4πR²). For this example, the ratio of these two areas is 1 + 2z_nsR⁻¹ = 1 + z_nsJ to first order in J, where J is the sum of the two principal curvatures, here R⁻¹ + R⁻¹ = 2R⁻¹ for a perfect sphere. At constant volume, the change in area is compensated for by a change in thickness, described below.

Given J computed at {u,v}, the area of lipid material occupied A(z) a distance Δz = z − z_ns from a patch of the leaflet at its neutral surface z_ns (with area A₀) is

$$A(\mathrm{\Delta }z)=A_0+A_{0}J\mathrm{\Delta }z,$$ (2)

where the lateral strain is

$${ϵ}_{\text{lateral}}(\mathrm{\Delta }z)=J\mathrm{\Delta }z$$ (3)

and z = 0 is the bilayer midplane. To preserve volume at first order in J, the leaflet deforms along the bilayer normal with transverse strain ε_transverse to cancel ε_lateral:

$${ϵ}_{\text{transverse}}(\mathrm{\Delta }z)=-J\mathrm{\Delta }z$$ (4)

For convenience the material transverse coordinate, z’ of the deformed bilayer is defined in terms of the undeformed resting coordinate z as

$$\begin{gathered} z^{\prime }={\int }_0^z\text{d}t\left[1+{ϵ}_{\text{transverse}}\left(t-z_{\text{ns}}\right)\right] \\ =z\left[1+J\left(z_{\text{ns}}-\frac{1}{2}z\right)\right] \end{gathered}$$ (5)

The two leaflets of a bilayer have local curvature with sign opposite to that of the other. For a particular point at the bilayer midplane, there will be a greater local density of lipids on the positive curvature side of the bilayer, as opposed to the negative side. Consider an arbitrary point z, the transverse coordinate of the leaflet. The scattering length of the continuum element is β_LA(z). The coordinate of the scatterer is then computed as

$$r(u,v,z)=r(u,v)+z^{\prime }(z)n(u,v)$$ (6)

where z’ is computed from Eq. 5. Eq. 5 is modified depending on which leaflet is being sampled; to switch the orientation of the leaflet, the sign of J and the normal must be reversed.

After selecting a position at the midplane by {u,v}, the number of lipids in a particular leaflet must then be adjusted for curvature. In general, a point on a surface will not be specified by a Cartesian system {x,y}, where the area element of a patch of tiny patch is dxdy and the units are unambiguous (e.g., meters). Rather, a generalization is employed, with coordinates labeled with {u,v}. The area element in the vicinity is computed via the metric, the map between the arbitrary coordinates and real space. For example, in a spherical coordinate system ({θ,φ}), this factor is r² sin(φ), where φ is the azimuthal angle. The factor is computed using the general formula |r_u × r_v|, where r_u and r_v are the derivatives of the surface position with respect to the general coordinates. To randomly select a set of scattering elements from the continuum surface, a random point {u,v} is multiplied by

$$w=\left|r_u\times r_v\right|$$ (7)

The area of the lipid is constant with curvature not at the bilayer midplane, but at z_ns. To account for this, the weight is modified on a per-leaflet basis according to curvature.

$$w^{\prime }=w\left(1+J{z}_{\text{ns}}\right)$$ (8)

where the sign of J depends on the leaflet considered.

Lateral strain can be introduced into a leaflet using the simple volume preserving transformation

$$\begin{gathered} x^{\prime }=x\left(1+\frac{1}{2}{ϵ}_{\text{lateral}}\right) \\ {y}^{\prime }=y\left(1+\frac{1}{2}{ϵ}_{\text{lateral}}\right) \\ {z}^{\prime }=z\left(1-{ϵ}_{\text{lateral}}\right) \end{gathered}$$ (9)

This strain alters the number of lipids in the continuum-modeled leaflet as:

$$w^{\prime \prime }=w^{\prime }\left(1-{ϵ}_{\text{lateral}}\right)$$ (10)

For example, if the area of the lipid is increased, fewer lipids are required to cover the surface.

The weight of the scatterer, equivalent to its probability, w”, which accounts for the change in density with curvature and strain. The transverse and lateral strains of the leaflet are zero at the neutral surface. This applies both to the inner (negative) and outer (positive) leaflets. For the positively curved leaflet, the strain at the midplane is negative; it has been compressed. For the negatively curved leaflet, the strain at the midplane is positive. Therefore, per unit midplane area, the positively curved leaflet has more lipids, by a factor of $\frac{1+J{z}_{{}_{\text{ns}}}}{1-J{z}_{{}_{\text{ns}}}}$.

2.3. Continuum modeling

The dynamics of the membrane are propagated using Brownian dynamics (see for example Ref. [59]), where the dynamical variable is the amplitude of the n = 2 to n = 6 spherical harmonic of the vesicle. The surface is evaluated using the subdivision limit surface (SLS) algorithm [60]. The SLS component of the software package is not necessary for the vesicle calculation here; the calculation could be done analytically for these simple spherical deformations. However, the SLS allows for modeling arbitrary topology surfaces, so that, for example, lipidic cubic phases, pores, and other special structures can be simulated. The mesh for the SLS consists of 162 mesh points formed by applying Loop subdivision [61, 62] twice to an icosahedron. The curvature energy (Eq. 1) of the mesh is evaluated using three point integration on each face. For faces containing an irregular mesh point (with five neighbors), a 16 point Gaussian-quadrature rule is applied to increase accuracy. With the SLS, the spherical harmonic deformations should not be applied directly to the mesh vertices, because the surface itself is a linear transformation of the those vertices. Instead, the mesh displacements for a spherical harmonic deformation are determined by solving for the linear transformation of the mesh points that best yields a particular spherical harmonic (evaluated at the integration points). The dynamics of the spherical-harmonic amplitudes evolve under the influence of the energy in Eq. 1. The bending modulus was set to 25 kcal/mol. Fluctuations in thickness beyond those controlled by curvature were not modeled.

2.4. Evaluating I(q)

The coherent SANS intensity I(q) a distance r_D from the detector is determined by

$$\psi (\mathit{q})\propto r_D^{-1}\sum _i{b}_i{e}^{ı\mathit{q}\cdot {\mathit{r}}_i}$$ (11)

$$I(q)=|\psi (q){|}^2$$ (12)

where b_i is the neutron scattering length of atom i at position r_i, and q is the scattering vector determined by the detector position relative to the sample and neutron beam. The static (large) factor r_D is irrelevant and will be dropped for convenience. There is a one-to-one correspondence of scattering vectors q and detector positions. The absolute-squared-sum can be expanded to yield:

$$I(q)=\sum _i\sum _j{b}_i{b}_j{e}^{ıq\cdot \left({\mathit{r}}_i-{\mathit{r}}_j\right)}=\sum _{ij}{b}_i{b}_j{e}^{ıq\cdot r_{ij}}$$ (13)

where the negative sign on r_j is a result of complex conjugation when computing the absolute magnitude squared, and r_ij = r_i − r_j.

Whereas with Eq. 12 the wavefunction ψ must be computed for the complete system before squaring (the sum is inside the square), with Eq. 13 many incomplete sums of scattering pairs can be computed and averaged over time.

The use of Eq. 13 also makes orientational averaging convenient. Orientational averaging of a configuration can be accomplished by averaging over each orientation of r_ij, or alternatively, over each orientation of q:

$$I_{\Omega }(q)=\sum _{ij}{b}_i{b}_j{(4\pi )}^{-1}{\int }_0^{2\pi }\text{d}{\theta }_q{\int }_0^{\pi }\text{d}{\varphi }_q{e}^{ıq\cdot r_{ij}}$$ (14)

where q = q{sin(θ_q)sin(φ_q),cos(θ_q)sin(φ_q),cos(φ_q)} and the Ω subscript indicates orientational averaging. For convenience the integration can be performed by aligning r_ij with the q_z axis (φ_q = 0) such that q · r_ij = qr_ij cos(φ_q):

$$\begin{gathered} I_{\Omega }(q)=\sum _{ij}{(4\pi )}^{-1}{\int }_0^{2\pi }\text{d}{\theta }_q{\int }_0^{\pi }\text{d}{\varphi }_q\sin \left({\varphi }_q\right)e^{ıq{r}_{ij}\cos \left({\varphi }_q\right)} \\ =b_i{b}_j\frac{\sin \left(q{r}_{ij}\right)}{q{r}_{ij}} \end{gathered}$$ (15)

The SANS intensity of the continuum model was determined by the following procedure for each of 5000 configurations of the simulation. One thousand randomly sampled points (u,v) were chosen from the bilayer midplane of the sphere. At each of these points, twenty points along the planar z coordinate were drawn. By drawing points from the distribution of NSLD in the planar simulation, it is assured that points in the material are sampled evenly. The final position of the scattering element in three dimensions is determined by first applying the lateral deformation (Eq. 9) to z, then using Eq. 5. The weight w” is determined from Eqs. 7, 8, and 10. From this set of points, 10⁵ pairs are drawn and are used to sample Eq. 15, with each pair multiplied by the product of each points’ weight, w”. The Fourier transform method yielded equivalent results, with the sampled points put onto a fine grid.

3. Results & Discussion

3.1. Deformation of the small-vesicle leaflets

The deformation predicted by Eq. 5 is predicated on pointwise conservation of volume as the material deforms. This is justified on a longer lengthscale by the area compressibility modulus (per unit height) compared to the bulk modulus of the material [63, 58] and is borne out in analysis of molecular simulation [58]. However, it is not clear that the mechanical parameters of the lipid, determined for the planar system (see, for example Ref. [64]) will be applicable to highly curved leaflets. The inverse hexagonal phase is a convenient experimental system to study very high negative curvature [65]. For the inner leaflet, all-atom simulations have shown consistency in the spontaneous curvature with hexagonal phase simulations [66]. Yet the Martini model may display different behavior at high curvature than all-atom models. As demonstrated herein, the details of the deformation of the inner and outer leaflets impact the scattering that results.

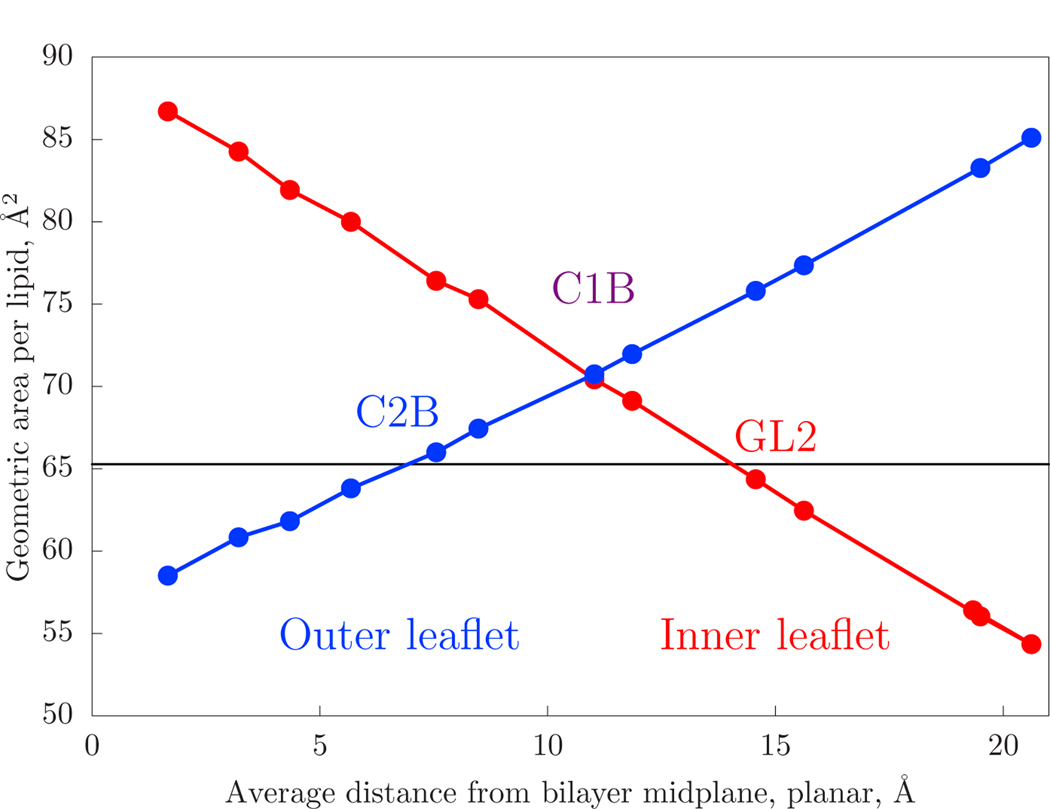
To determine the appropriate values of the neutral surface (z_ns) and lateral strain (ε_lateral), the density of coarse-grain Martini sites is examined. The area-per-lipid of the 18 nm diameter vesicle, broken down by Martini interaction site, is plotted in Fig. 4. The data are plotted against the height above the bilayer midplane for a planar simulation on the horizontal axis. The area-per-lipid of the planar system is plotted as a horizontal line in the same plot. The pivotal plane, defined by the position in a curved leaflet for which the area-per-lipid is constant as curvature is varied, is determined by the intersection of the data, including with the horizontal line. However, if the leaflet is strongly deformed, for example, by an area strain due to external tension (or that applied by the opposite leaflet and/or osmotic stress), the intersection will shift. The blue data corresponds to the outer leaflet. For the outer leaflet, the area-per-lipid matches that of the planar system at the Martini C2B site.

Figure 4:

The geometric area-per-lipid (4πR² divided by the number of lipids) of a Martini site in a ca. 18 nm diameter vesicle plotted against the same site’s height above the bilayer midplane in a planar simulation. The form is expected to be linear, as per Eq. 2. The area-per-lipid for the planar system, plotted as a horizontal line, is the projected area of the bilayer. The inner leaflet curve (red) plots both the NH3 sites of POPE as well as the NC3 sites of POPC. The outer leaflet curve (blue) has only POPC.

The pivotal plane and neutral surface are closely related. The pivotal plane reflects the fact that lipid spontaneous curvature acts to strain the leaflet as curvature energy is balanced against lateral tension. For example, lipids with extreme negative spontaneous curvature may prefer to be strained such that their radius is decreased. As shown by Leikin et al. [67], the difference is on the order of 1–2 Åfor high spontaneous curvature lipids. Given this, the two are treated as equivalent within the uncertainties at play in this work.

The parameters of the mechanical transformation (Eqs. 5 and 9) cannot strongly differentiate between a shift in the neutral surface and a latent area/thickness strain. A shift in the neutral surface would arise from, for example, a highly curved outer leaflet being unable to accommodate the thickening of the acyl chain region due to fundamental limits on molecular flexibility. In this case, the neutral surface would shift toward the middle of the bilayer. This is effectively indistinguishable from a leaflet-number imbalance between the inner and outer leaflets.

3.1.1. Comparison of the continuum and coarse-grain modeled intensity

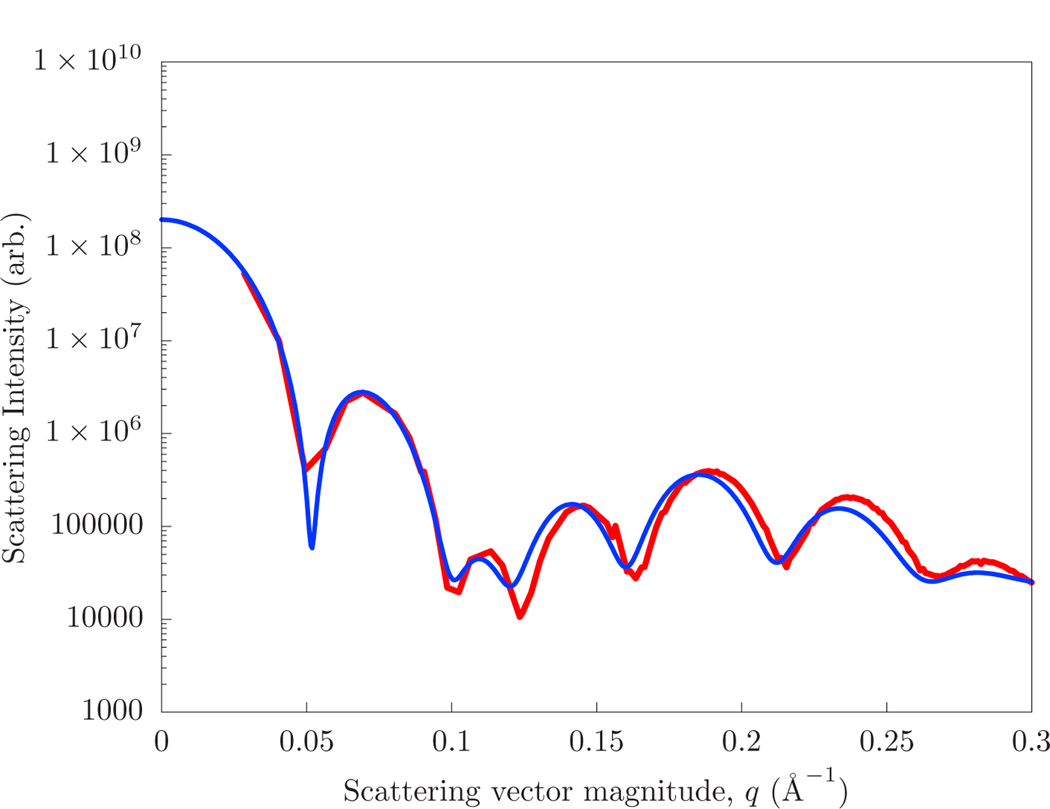
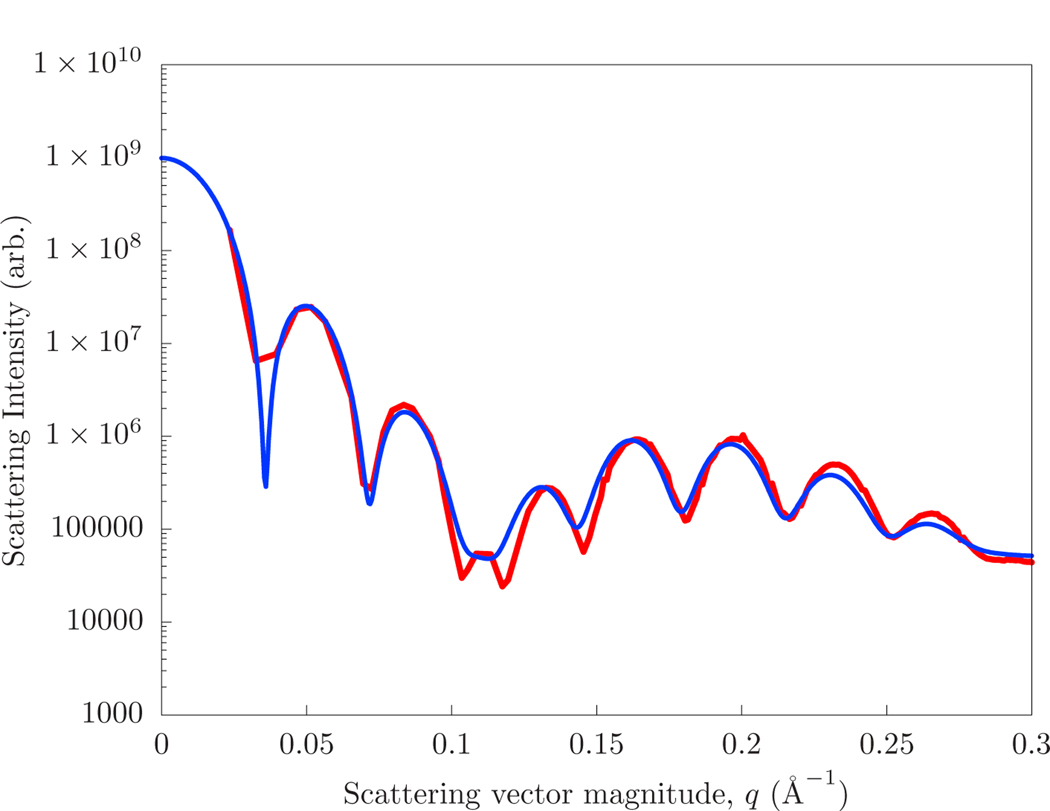
The SANS intensities of the coarse-grained model and the continuum model (with mechanical parameters matched to fit) of the 13 nm and 18 nm diameter vesicles are shown in Figs. 5 and 6, respectively. The strains (ε_lateral) and neutral surface positions (z_ns) of the inner and outer leaflet, as well as the radius of the vesicle itself, have been optimized over a rough scan of parameter space to match the average radial scattering length density. The final intensity is determined by optimizing a scaling factor and constant to the continuum intensity. The constant represents the contribution due to the finite scattering length of the Martini interaction site.

Figure 5:

The scattering computed directly from that of a ca. 13 nm diameter Martini vesicle (red) and that of a hybrid continuum/planar-molecular simulation of the same system (blue).

Figure 6:

The scattering computed directly from that of ca. 18 nm diameter Martini vesicle (red) and that of a hybrid continuum/planar-molecular simulation of the same system (blue).

The best fit scattering intensities have separate neutral surfaces for the inner and outer leaflet, with z_ns = 9 Åfor the outer leaflet and z_ns = 15 Åfor the outer leaflet. These are consistent with the plotted area-per-lipid as a function of atom type in Fig. 4. The optimal parameter set included a 10% strain in the outer leaflet in the 18 nm vesicle, although this was not differentiated from a shift in the neutral surface. The same strains and neutral surface positions were applied to both the 13 nm diameter vesicle simulations, but with an additional 10% strain to the inner leaflet. A bending modulus of 25 kcal/mol produced the best agreement of the scattering intensity. If the bending modulus is reduced to 15, the magnitude of the shape oscillations at high q are reduced by half, and are washed away for smaller values.

The accuracy of the match was most sensitive to the thickness of the bilayer (which most closely determined the transverse correlation) and the overall size of the vesicle (which determined the “beat” of oscillations at the vesicle size). Thus, the quality of the fit can be viewed as using continuum modeling to verify the overall transverse structure of the bilayer in a highly curved system. Experimentally, vesicle samples will have a distribution of size, likely making comparison with models challenging. However, the accuracy here is important for precision comparisons, including with hypotheses regarding the structure of modulated phases [4].

4. Conclusions

This paper presented a methodological framework, along with accompanying software [68], to compute the scattering of high curvature regions of leaflets. The primary targets for testing were coarse-grained (Martini) simulations of very small (13–18 nm diameter) vesicles. Although the vesicles were equilibrated in such a way as to remove osmotic and lipid-number stresses, apparent strains were observed. The accuracy of the model was excellent, where given the radius and thickness of the vesicle, a nearly quantitative model of the scattering could be determined.

Extension to all-atom simulations of lipid bilayers is warranted, considering that the observed neutral surface for highly curved Martini lipids appears to be very different from that obtained from a buckled planar bilayer [69, 70]. Maintaining the same elastic coefficients (neutral surface location) appears unbearable for the outer leaflet of small vesicles; the acyl chains must extend and narrow too far. For example, in Risselada et al. [55], the authors observed that highly flexible lipids in the outer leaflet would “backfold”, lifting a disordered tail up out of the compressed midplane space. Considering the limited resolution of the Martini forcefield, this suggests that all-atom models could be quite different, in terms of interdigitation.

Recently, Hossein and Deserno [71] pointed out that a membrane with a strong spontaneous curvature imbalance (as is apparent from the asymmetric lipid distribution of PE) should spontaneously tubulate, and that an imbalance in lipid number could counteract this. Characterization of differential stress is challenging because it must be resolved on the leaflet level, as opposed to the total bilayer tension. Scattering offers the possibility of distinguishing leaflet properties. A drawback is that the intensity of asymmetric bilayers does not typically go to zero at characteristic locations, making interpretation more challenging. The intent of this work is that precision modeling will enable the interpretation of such complex systems.

The small vesicles studied here are difficult to check directly with SANS, which typically employs larger extruded vesicles. However, in order to study the structure of curvature-modulated phases it is necessary to have an accurate method to model the small-lengthscale details of curvature embedded in large objects, be it internal to the phase or occurring at phase boundaries. As demonstrated by the computed scattering from these small vesicles, the method here is able to model very high curvature.

The natural extension of this continuum modeling approach is to combine line tension energetics that yield domain formation with spontaneous curvature and NSLD information computed from simulation [50, 36]. Many of the elements are already present in the work of Hu et al. [26] and Amazon et al. [24, 25], in which membrane deformation couples to the line tension.

Figure 2:

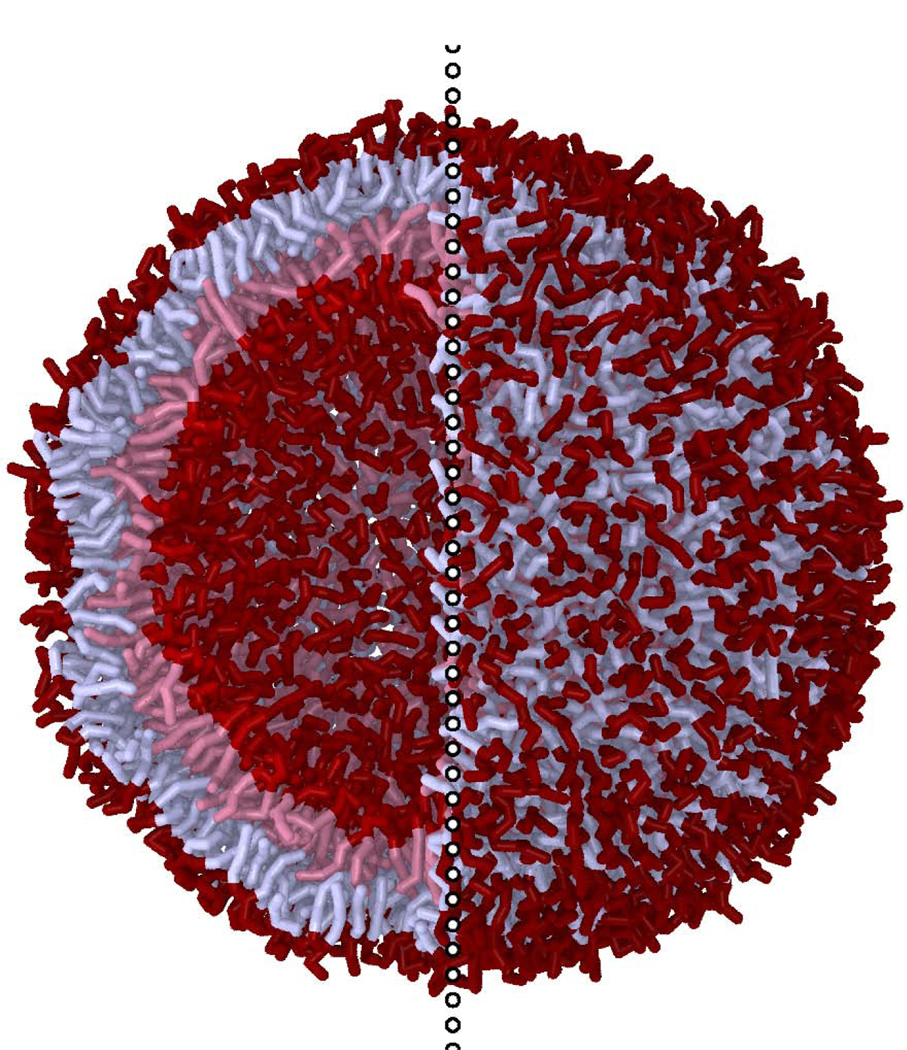
A rendering of a ca. 18 nm diameter POPC/POPE Martini vesicle the scattering from which that of the hybrid continuum/planar-molecular modeling is compared. To the left of the vertical dotted line the near lipids are hidden to show the vesicle interior. Tail interaction sites are light while surface sites are dark. The inner and outer leaflet lipids are tinted separately.