Multiple-Imputation Variance Estimation in Studies With Missing or Misclassified Inclusion Criteria

Abstract

In observational studies using routinely collected data, a variable with a high level of missingness or misclassification may determine whether an observation is included in the analysis. In settings where inclusion criteria are assessed after imputation, the popular multiple-imputation variance estimator proposed by Rubin (“Rubin’s rules” (RR)) is biased due to incompatibility between imputation and analysis models. While alternative approaches exist, most analysts are not familiar with them. Using partially validated data from a human immunodeficiency virus cohort, we illustrate the calculation of an imputation variance estimator proposed by Robins and Wang (RW) in a scenario where the study exclusion criteria are based on a variable that must be imputed. In this motivating example, the corresponding imputation variance estimate for the log odds was 29% smaller using the RW estimator than using the RR estimator. We further compared these 2 variance estimators with a simulation study which showed that coverage probabilities of 95% confidence intervals based on the RR estimator were too high and became worse as more observations were imputed and more subjects were excluded from the analysis. The RW imputation variance estimator performed much better and should be employed when there is incompatibility between imputation and analysis models. We provide analysis code to aid future analysts in implementing this method.

Abbreviations:

ADE

AIDS-defining event

AIDS

acquired immunodeficiency syndrome

ART

antiretroviral therapy

HIV

human immunodeficiency virus

MI

multiple imputation

RR

Rubin’s rules

RW

Robins and Wang

Multiple imputation (MI) is a common tool used to account for missing data and measurement error (1). While increasingly popular due to the availability of statistical software packages containing imputation functions, MI and calculation of the corresponding imputation variance estimator still involve several assumptions that require careful consideration. Notably, a popular imputation variance estimator, originally proposed by Rubin (1) and often called “Rubin’s rules” (RR), has been shown to be biased when the imputation model is misspecified or if there is incompatibility between the imputation model and the analysis model (2).

Incompatibility between imputation and analysis models, sometimes referred to as uncongeniality (3, 4), is an important consideration for many practical data analyses. Uncongeniality occurs when the assumptions of the imputation model are discordant with those of the analysis model. A practical example is subgroup analyses, where the analysis model allows for the association to differ based on group status yet no distinction is made between groups when imputing missing values.

Studies that incorporate data from large observational data sets, such as those derived from electronic health records, typically require several data processing steps prior to performing analyses. These types of data are prone to errors, often across multiple variables. These errors may lead to misclassification of whether subjects should be included in the study. For example, a study may only include patients who started using a particular medication or who had a particular clinical diagnosis, whereas data on medication use and clinical diagnoses extracted from the electronic health records may have errors. With error-prone data, it is often advisable to validate a subsample of the data to quantify error rates and to identify systemic data collection issues. Once a subsample has been validated, one can employ MI techniques to address the data errors (5–7). Specifically, records that have undergone data validation can be thought of as having complete data, whereas data are partially missing and must be imputed for those records that were not validated. MI is an excellent analysis choice in these settings because it is capable of addressing complicated error structures, including errors in which records are actually included in the study. Inclusion/exclusion status can be imputed. An important implication, however, is that records included in the imputation model may be excluded from the analysis model, resulting in uncongeniality between imputation and analysis models. Therefore, the RR variance estimator is biased.

An alternative imputation variance estimator, proposed by Robins and Wang (RW) (2), does obtain unbiased variance estimates in settings with misspecification or incompatibility. Unlike Rubin’s approach, the RW variance estimator is based on components derived directly from both the imputation and analysis models. This ensures a proper accounting of the information from the imputation procedure, which is essential for unbiased variance estimation if the analysis model assumptions are different from those in the imputation model. While this RW imputation variance is fairly well known among statisticians conducting methods research in missing data, it has been rarely implemented (8, 9) and seems to be unknown by most analysts. Compared with Rubin’s variance estimator, the RW estimator is complex and requires additional calculations by both the imputer and the analyst. In their original manuscript, Robins and Wang wrote that they “hope that, in the future, software developers will create packages” (2, p. 117) with which to implement their approach. Hughes et al. (8) implemented the RW approach for some simple scenarios and showed via simulations that the RW estimator outperformed the RR estimator with moderate sample sizes. Although their paper was helpful in clarifying the RW estimator, they provided no software code for their analyses or simulations. Twenty years after RW’s publication, no existing software packages implement the RW estimator, and to our knowledge, there is only 1 example with publicly available code (9).

Incompatibility between imputation and analysis models is an important consideration that should no longer be overlooked by analysts. While we do provide an overview of technical details regarding the RW (as well as Rubin’s) imputation variance estimator in Web Appendix 1 (available at https://academic.oup.com/aje), the goals of this paper are 1) to highlight an interesting and increasingly common setting in which inclusion/exclusion is based on error-prone variables, 2) to illustrate how MI can be used to address uncertainty in study eligibility, 3) to demonstrate the bias of the commonly used RR variance estimator with uncongeniality in this setting, and 4) to illustrate and make the RW variance estimator more accessible. Using data from a human immunodeficiency virus (HIV) cohort, we provide a motivating example in which exclusion criteria are implemented after missing data have been imputed and compare the corresponding RR and RW imputation variance estimates. We also present findings from simulations with varying levels of incompatibility between the imputation and analysis models due to exclusion criteria as well as different amounts of missingness. Finally, we share all relevant statistical code needed for facilitating future implementation.

MOTIVATING EXAMPLE

To illustrate the implications of uncongeniality due to multiply imputing misclassified inclusion criteria, we first present a motivating example using data from a cohort of HIV patients who received care at the Vanderbilt Comprehensive Care Clinic (Nashville, Tennessee) between 1998 and 2010. Data from this cohort have been described previously (10). Approval for this data analysis was obtained from the institutional review board of Vanderbilt University.

We were interested in assessing the association between CD4 cell count at enrollment (baseline) and subsequent outcomes during the first year among patients who initiated antiretroviral therapy (ART) at enrollment. A patient was classified as having a poor outcome if they died, had an acquired immunodeficiency syndrome (AIDS)-defining event (ADE), or were lost to follow-up during the first 12 months after enrollment. For this study, patients were excluded from analyses if they did not have an ART dispensation within the first month after enrollment, if they did not initiate care at the clinic (defined as having less than 3 months of follow-up), or if they enrolled at the clinic less than 12 months before the data freeze date.

Two key analysis variables, corresponding to ART dispensation and occurrence of ADEs, were error-prone. Follow-up time and death status were not error-prone. Of the 4,217 patients in the original cohort, 3,526 initiated care and enrolled in treatment at least 12 months before the study freeze date. Since follow-up time did not contain errors, we used only these 3,526 patients for subsequent analyses.

Data validation by chart review was performed for key variables for all records in the data set that had been extracted from the electronic health records. As a result, 2 data sets were available: an unvalidated data set containing records completed prior to the chart review and a validated data set containing records for the same patients completed following the chart review. The validated data were considered to be correct (i.e., the “gold standard”). For this example, we pretended that validated data were available for only a randomly selected subset of records (n = 1,000; 28%); values for the remaining records (n = 2,526; 72%) were considered missing (i.e., masked) and needed to be imputed.

Using both unvalidated and validated data for the 1,000 validated patient records, we constructed a sequence of conditional regression models to impute the true values of the 2 error-prone variables (any ART dispensation in the first month and any ADE within 12 months) conditional on the unvalidated values of these same variables and 3 additional covariates (calendar year of enrollment, baseline CD4 cell count, and baseline log viral load). Specifically, we fitted a logistic regression model for any ART dispensation conditional on the unvalidated ART dispensation variable, the unvalidated ADE variable, and the 3 additional covariates. We also fitted a logistic regression model for ADE within 12 months conditional on the unvalidated ADE variable, the unvalidated ART dispensation variable, the validated ART dispensation variable, and the 3 additional covariates. There were no missing elements for calendar year of enrollment, baseline CD4 cell count, or baseline log viral load.

We then multiply imputed (m = 50 imputation replications) the true ART dispensation and ADE indicators based on these models for the 2,526 records with masked validation data. Following each imputation replication, exclusion criteria were assessed to establish an analysis data set wherein all included patients had an ART dispensation in the first month. We then fitted a logistic regression model with a composite outcome of loss to follow-up, ADE, or death within 1 year of enrollment and the calendar year of enrollment, baseline CD4 count, and baseline log viral load as covariates of interest. The association between baseline CD4 count and subsequent poor outcomes was estimated as the mean of parameter estimates across the 50 imputation replications. The corresponding imputation variance estimate was calculated in 2 ways: using Rubin’s rules and using the approach proposed by Robins and Wang.

Across 50 imputations, the average number of patients who met study inclusion criteria was 1,012 (29%), ranging from 968 to 1,072 subjects. The estimated log odds of a poor outcome were lower by 0.113 for every 100-unit increase in CD4 cell count. The corresponding imputation variance estimate for the log odds was 29% smaller using the RW estimator (0.046) relative to the RR estimator (0.065). When calculating confidence intervals corresponding to the odds ratio (odds ratio = 0.89), the RW-based 95% confidence interval (0.82, 0.98) was narrower than the RR-based 95% confidence interval (0.79, 1.01).

In this example, the imputation model included all patients meeting follow-up criteria, whereas the analysis model required that the patients also started ART in the first month. Furthermore, the number of patients meeting inclusion criteria varied across imputation replications. Therefore, the imputation and analysis models were fitted to different populations and were incompatible; hence, the variance estimated using Rubin’s rules was not consistent for the true variance. The inflated standard error seen with the RR estimator cannot be corrected using a robust-variance estimator of RR; such an approach yielded a very similar, slightly smaller, standard error (0.064) to that seen with standard RR. However, the performance of these variance estimators cannot be fully evaluated, since the true association between CD4 count and poor outcomes was unknown. Below we use simulations to evaluate whether the RR variance estimators result in confidence intervals that are too conservative (i.e., with coverage probabilities much higher than their nominal levels) and whether they can be corrected using the RW variance estimator.

SIMULATION

We further assessed the relative performance of the imputation variance estimators by establishing scenarios where both the percentage of missing data and the percentage of observations excluded from the analysis data set varied. Suppose we had a data set containing 4,000 electronic health records with 4 key variables: 2 continuous, correlated variables, x₁ and x₂; a continuous variable, A^*; and a binary variable, D^*. For this simulation, 2 of these variables (A^* and D^*) were error-prone versions of the actual variables of interest, A and D. Our goal was to estimate the association between a predictor variable A and a binary outcome D in a subset of subjects with values of A greater than some threshold.

To generate data for this simulation, x₁ and x₂ were drawn from a bivariate normal distribution with mean 0, variance 1, and covariance −0.25; A^* was drawn from a normal distribution with mean 1 and variance 1; and D^* was drawn from a Bernoulli distribution with the logit probability of success equal to −3 + 0.5 A^*. A was drawn from a normal distribution with mean equal to − x₁ + 0.5 x₂ + 0.9 A^* + 0.5 D^* and variance 2. Finally, D was drawn from a Bernoulli distribution with the logit probability of success equal to −5.5 − 2 x₁ + x₂ + 5 D^* + 0.5 A. The mean difference between A and A^* was approximately 0.06 with variance 2.5. The percentage of subjects with discordant D and D^* was approximately 11%; 7% of subjects had an event (D = 1) that was misclassified as a nonevent (D^* = 1). Note that we assumed that there were no data errors for the other 2 variables, x₁ and x₂. Note also that we sampled A and D conditional on their error-prone counterparts, A^* and D^*, for ease of properly specifying the imputation model. For a given inclusion threshold, the true value of the association between the predictor variable A and the binary outcome D was approximated by calculating a large sample estimate from a logistic regression model based on 5,000,000 validated records.

A subset of 1,000 subjects was randomly selected to represent an audited cohort with (A, D) known; for the remaining 3,000 subjects, (A, D) were treated as missing. A^*, D^*, x₁, and x₂ were treated as known for all 4,000 subjects.

In this setting, we used a chained equations (i.e., sequential regression) approach to multiply impute missing values of A and D by first fitting a linear regression model for A conditional on A^*, D^*, x₁, and x₂ and then a logistic regression model for D conditional on A^*, D^*, x₁, x₂, and A using the subset of 1,000 audited records. For each imputation, the imputer accounted for both parameter uncertainty and random noise in the imputations. We used 50 MI replications.

Suppose our goal was to estimate the association between A and D in the subset of subjects with A > 2. Using the imputed data set, we first excluded subjects with A ≤ 2; we refer to this reduced data set as the analysis data set. Using this analysis data set, we fitted a logistic regression analysis model to estimate the association between A and D. Since the imputations were generated using observations from all subjects while the analysis model was based on just those with an imputed value of A > 2, there was incompatibility between the imputation model and the analysis model.

When we repeated the simulation for this example 2,500 times, the mean RW standard error estimate (0.0861) was smaller than the mean RR standard error estimate (0.1152). For comparison, the empirical standard error estimate (i.e., the standard deviation of the 2,500 estimates) was 0.0827. The imputation variance estimator proposed by RW yielded 95% confidence intervals with coverage closer to 95%, 0.957 versus 0.997 for the RR estimator. These findings suggest a large discrepancy between the RW and RR variance estimators when the percentage of missing (unvalidated) observations is high (75%) and a small proportion of observations are included in the analysis model (28%).

To better compare the performance of the 2 variance estimators, we expanded the simulation to include different validation subsample sizes (n = 500, 1,000, 1,500, 2,000, 2,500, 3,000, 3,500, and 4,000) as well as different inclusion thresholds (A > {−∞, −1, −0.5, 0, 0.5, 1, 1.5, 2, 2.5, 3}). For each inclusion threshold, we calculated the average size of the corresponding analysis data set that remained after subjects were excluded. The average size of the analysis data set varied from 524 to 4,000. For each simulation, we calculated 95% Wald confidence intervals using the RW and RR imputation variance estimators.

Coverage estimates for 95% confidence intervals based on 2,500 simulations using both the RR (Figure 1A) and RW (Figure 1B) estimators for all 80 combinations of validation subsample sizes and inclusion thresholds are provided in Web Tables 1 and 2. The Monte Carlo simulation error, estimated using a bootstrap method (11), was 0.5% or lower for coverage estimates.

Figure 1.

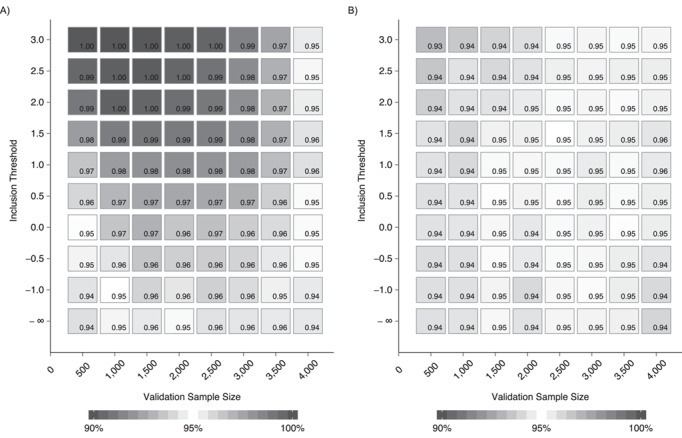
Coverage estimates for 95% Wald confidence intervals calculated using either Rubin’s rules (1) (A) or Robins and Wang (2) (B) variance estimators for different combinations of validation-subsample sizes and analysis-data-set sizes. Plots were generated for combinations of 8 validation-subsample sizes (n = 500, 1,000, 1,500, 2,000, 2,500, 3,000, 3,500, and 4,000) and 10 different inclusion thresholds (A > {−∞, −1, −0.5, 0, 0.5, 1, 1.5, 2, 2.5, 3}). For each inclusion threshold, we calculated the average data-set size of the corresponding analysis data set that was generated.

The coverage probability was higher for confidence intervals calculated using Rubin’s imputation variance estimator as more subjects were excluded from the analysis data set and more observations were imputed. Coverage was very high (i.e., > 99%) for a substantial number of simulations, demonstrating that confidence intervals constructed using the RR estimator in these settings were much too wide.

Annotated R code with which to simulate data, perform MI, obtain parameter estimates, and calculate imputation variance estimates using both the RR and RW estimators is provided in Web Appendices 2 and 3. All of our analyses were performed using R, version 3.4.1 (R Foundation for Statistical Computing, Vienna, Austria).

DISCUSSION

As the popularity of MI grows, it is important that analysts are familiar with and able to carry out best practices regarding variance calculations. We have highlighted a key situation—an analysis data set smaller than the imputation data set due to exclusion based on an imputed value—where the standard variance estimation based on RR was biased. This bias was substantial, resulting in very conservative confidence intervals.

There are many settings where uncongeniality between imputation and analysis models will result in biased variance estimates using the RR estimator. In general, uncongeniality is most concerning when the imputation model is less saturated than the analysis model (4). For example, as Hughes et al. (8) highlighted, the unnecessary inclusion of an interaction variable in the analysis model that was omitted from the imputation model will result in biased variance estimates. In this article, we focused on the setting where the subjects included in the analysis model were different from those in the imputation model. We chose this example because it clearly illustrates the problem with the RR estimator. Misclassification of inclusion status is common (but often overlooked) when using routinely collected data for research, and MI is being increasingly used to account for measurement error and misclassification (5–7).

For ease of presentation, several simplifications were made in our motivating HIV example. These included focusing on a composite endpoint and requiring the possibility of at least 1 year of follow-up. While these simplifications allowed us to focus on a simple scenario, we acknowledge that inferences regarding this particular analysis may have limited clinical relevance. Additionally, in our motivating example, the RW-based 95% confidence interval did not include 1, whereas the RR-based 95% confidence interval overlapped with 1. Of course, such discordance in statistical significance will not always occur when implementing these 2 imputation variance estimators. However, this example illustrates that it is possible. Finally, we used a chained equations (i.e., sequential regression) approach for imputation; while the conditional regression models specified in both the motivating example and the simulations were compatible with a joint distribution, in some cases there can be stability and convergence issues with this approach (12), and results may be biased if imputation models are poorly specified (4).

We are aware of at least 1 other method, arising from the survey sampling literature, for estimating the variance of the MI estimator when there is uncongeniality (13); this approach is also complex and has been rarely implemented in practice. It is clear that the complexity of RW's variance estimator (and other similar approaches) has historically served as a barrier to implementation. To allow others to reproduce our work and apply it to their specific settings, we have included our statistical software code and have provided additional details on how to calculate the RW variance estimator.

While hopefully a useful tool, the provided R code requires some modification for implementations involving the imputation of more than 2 variables or using imputation models other than logistic or linear regression. We encourage researchers to build on the existing code provided here to create functions generalizable to more settings. We are aware of at least 1 research group that has proposed constructing an R package for calculating RW imputation variance estimates, but to our knowledge the work was never finished (14). Creating software that generalized the RW estimator would be a challenging but worthy endeavor.