Prioritizing additional data collection to reduce decision uncertainty in the HIV/AIDS response in 6 US cities: a value of information analysis

Abstract

Objectives:

The ambitious goals of the US “Ending the HIV Epidemic” will require a targeted, context-specific public health response. Model-based economic evaluation provides useful guidance for decision-making while characterizing decision uncertainty. We aim to quantify the value of eliminating uncertainty about different parameters in selecting combination implementation strategies to reduce the public health burden of HIV/AIDS in 6 US cities and identify future data collection priorities.

Methods:

We used a dynamic compartmental HIV transmission model developed for 6 US cities to evaluate the cost-effectiveness of a range of combination implementation strategies. Using a metamodeling approach with nonparametric and deep learning methods, we calculated the expected value of perfect information (EVPI), representing the maximum value of further research to eliminate decision uncertainty, and the expected value of partial perfect information (EVPPI) for key groups of parameters that would be collected together in practice.

Results:

The population EVPI ranged from $59,683 (Miami) to $54,108,679 (Los Angeles). The rank ordering of EVPPI on key groups of parameters were largely consistent across cities and highest for parameters pertaining to HIV risk behaviors, probability of HIV transmission, health service engagement, HIV-related mortality, health utility weights and health care costs. Los Angeles was an exception, where parameters on retention in pre-exposure prophylaxis ranked highest in contributing to decision uncertainty.

Conclusions:

Funding additional data collection on HIV/AIDS may be warranted in Baltimore, Los Angeles and New York City. Value of information analysis should be embedded into decision making processes on funding future research and public health intervention.

Précis:

Funding additional HIV data collection may be warranted in three of the six targeted cities and should be prioritized to several key groups of parameters

Introduction

Despite over $20B of annual federal funding directed towards the domestic HIV/AIDS response, 38,000 new cases were diagnosed in 2017 in the USA (1, 2). The recently announced “Ending the HIV Epidemic: A Plan for America” initiative has set ambitious goals to reduce new HIV infections by 75% within 5 years and by 90% within 10 years (3). Achieving these goals necessitates “an infusion of resources to employ strategic practices in the right places targeted to the right people to maximize impact and end the HIV epidemic in America” (3). While a range of tools to end the HIV epidemic are available, resources – both financial and human – are scarce and compete with other priorities outside HIV (4).

As the global public health response moves towards localized combination implementation strategies to combat HIV/AIDS (4–7), economic models are increasingly used to inform health decision-making in the care and prevention of HIV/AIDS. They provide a unified framework to quantify the health and economic value of different strategies while accounting for their synergistic effects (8–10). Adequately characterizing city-level HIV microepidemics in a simulation modeling framework is data-intensive, particularly given the substantial disparities in access to services and health outcomes observed across HIV risk and race/ethnic groups in the US (11). The inherent uncertainty in estimating many of the required parameters, which span population composition and dynamics, health service engagement, disease progression, HIV transmission, cost and utility weights (11, 12), may obscure value-based recommendations and lead to potentially suboptimal decisions.

The US has invested in a range of multi-site surveillance studies that provide vital information for simulation modeling, including HIV risk behaviors from the National HIV Behavioral Surveillance (NHBS); ART surveillance data from Medical Monitoring Project from the US Centers for Disease Control and Prevention (CDC) and clinical data from the HIV Research Network (12). Nonetheless, our previous study found a paucity of representative, high-quality local administrative data, particularly on rates of HIV testing and ART engagement (12). This is in many cases due to structural barriers where data are either not systematically collected or organized in isolated silos, creating barriers to access and linkage with other data sources (13). The infrastructure to facilitate data collection is costly to construct, and not all model parameters will impact recommendations equally. Efforts to collect additional data should focus on those with the most potential to reduce uncertainty in funding allocation decisions (14).

Value of information (VoI) analysis quantifies the opportunity cost of acting on suboptimal recommendations due to uncertainty underlying model parameters. It also helps guide efforts to ensure the limited resources available for data collection are focused on the most influential parameters for a given decision (15). Expected value of perfect information (EVPI) and expected value of partial perfect information (EVPPI) estimate the value of eliminating uncertainty from all parameters jointly and from a subset of parameters respectively, providing guidance for setting research priorities. The expected value of sample information (EVSI) measures the expected value of sample (imperfect) information from a given study of a particular design with a known sample size, which can be used to inform future research design. The conventional approach to EVPPI and EVSI is based on a nested Monte Carlo procedure that is computationally costly, particularly for a complex model with many competing interventions (16–18). Metamodeling, a tool that simplifies the relationship between the inputs and outputs of a simulation model (19), has been increasingly used as an alternative method to expedite value of information analysis (16, 20). A previous EVPPI analysis using a metamodeling approach shortened the computation time from weeks to minutes while consistently yielding similar estimates (17).

On the basis of a comprehensive evidence synthesis (12); a systematic model calibration and validation (21); and an extensive economic evaluation of 16 evidence-based interventions individually (22) and in combination (23) for 6 US cities with diverse HIV microepidemics, we identified combination strategies to address the HIV/AIDS epidemic in each city along with uncertainty underlying the selection of the optimal (highest-valued) strategy. A decomposition of the sources of this uncertainty, coupled with a judgement on the value of eliminating it in each setting, can guide future research efforts focused explicitly on reducing decision uncertainty. Our objective is to quantify the value of eliminating uncertainty about different groups of parameters to reduce decision uncertainty regarding the cost-effectiveness of HIV combination implementation strategies in six US cities. We aimed to identify future research priorities through EVPPI analysis on key groups of uncertain parameters using a metamodeling approach with advanced regression techniques.

Methods

Model Description

We adapted a previously published dynamic compartmental HIV transmission model (21, 24–26) to simulate the HIV microepidemics in six US cities: Atlanta, GA; Baltimore, MD; Los Angeles (LA), CA; Miami, FL; New York City (NYC), NY; and Seattle, WA. Each city features distinct epidemiological characteristics and public health responses to HIV (6). In the model, the adult population aged 15–64 in each city was partitioned by biological sex, HIV risk group, race/ethnicity, sexual risk behavior level (high- vs. low-risk), and access to opioid agonist treatment among people who inject drugs, for a total of 42 population groups. Individuals within each group progress through 19 health states illustrated in Appendix Figure A1. We considered dynamic HIV transmission through heterosexual contact, homosexual contact or needle sharing. The model captured heterogeneity in the risk of HIV transmission, maturation, mortality, and accessing health and prevention services. Full details about the model are available in prior articles (21–23).

The model’s input parameters were grouped in seven categories: (1) Initial population estimates and population dynamics [N=1,074]; (2) parameters used to calculate the probability of HIV transmission [N=201]; (3) screening, diagnosis, treatment and HIV disease progression [N=312]; (4) HIV prevention programs [N=23]; (5) the costs of medical care [N=30]; (6) health utility weights [N=26]; and (7) intervention parameters (e.g. effect, scale of delivery and cost) [N=184]. The derivations, point estimates, uncertainty distributions and quality of evidence were reported for all model parameters in a manuscript detailing the evidence synthesis for this project (12, 22). For parameters with lower quality of evidence where little information was available, we allowed for prior distributions with higher variance (27). Although parameters were assumed to be independent, for potentially correlated parameters with an empirically established rank ordering (e.g. quality-adjusted life year (QALY) weights, costs for different health states), we used a recently-proposed method (28) to establish joint uncertainty distributions from parameters’ marginal distributions and their ordinal preferences.

Cost-effectiveness analysis

We evaluated the cost-effectiveness of 16 evidence-based HIV interventions and their combinations within three domains: HIV prevention, including Syringe Service Program, medication for opioid use disorder (MOUD), either buprenorphine or methadone, targeted PrEP for high-risk men who have sex with men (MSM); HIV testing, including opt-out testing in the hospital emergency room and in primary care, electronic medical record (EMR) testing offer reminder, nurse-initiated rapid testing, MOUD initiated rapid testing; and Treatment engagement, including case management (ARTAS) for ART initiation, care coordination for ART retention, targeted care coordination (CD4<200), EMR ART engagement reminder, RAPID ART initiation, enhanced personal contact for ART re-initiation, ART re-linkage program. We considered combinations of the 16 interventions for each city, excluding any that would not practically be implemented jointly, for a total of 23,040 unique combinations.

Consistent with our previous studies, we maintained the same evaluation time horizon of 20 years (2020–2040) to capture the long-term individual benefits of ART and 2nd-order transmission effects. All costs were reported in 2018 US dollars, and we chose a base cost-effectiveness threshold of $100,000/QALY while varying this threshold in three discrete levels ($50,000/QALY, $100,000/QALY, and $150,000/QALY) for EVPI analysis. Decisions were made by choosing the strategy i with the highest net monetary benefit (NMB), as estimated by:

$$NM{B}_i=QAL{Y}_i\times \mathit{\text{Threshold}}-Cos{t}_i$$

Probabilistic Sensitivity Analysis

The probabilistic sensitivity analysis (PSA) dataset for input parameters was constructed by randomly sampling all uncertain parameters (including initial population estimates) simultaneously from their prior distributions or fitted joint distributions. For each sample of the model inputs, corresponding costs and QALYs for the given combination implementation strategies were estimated, representing one PSA simulation. As a vast majority of the over 23,000 competing strategies we estimated had a zero or near-zero probability of being the health-maximizing strategy for a given threshold, we performed PSA only on the subset of combination implementation strategies with a non-zero probability of being selected.

Value of Information Analysis

VoI analysis provides a systematic approach to quantify the value of research in reducing decision uncertainty. EVPI represents the maximum a decision maker should be willing to pay to eliminate uncertainty from all model parameters. For a given cost-effectiveness threshold, we first evaluated and ranked the NMB of all combination strategies setting all input parameters at their point estimates as the base case (i.e. a deterministic) analysis and identified the 25 combination strategies with the highest NMB for each city. We then generated 2,000 random samples of model inputs, conducted PSA on these 25 highest-valued strategies and estimated their corresponding NMB. We chose 25 to make the problem tractable given computation limitations and the final number was determined through an iterative process: at each threshold level, we gradually expanded the inclusion of top-ranked strategies (from 5 to 25 in an increment of 5) while assessing their probabilities of being the highest-valued (i.e. with highest NMB) in the 2,000 PSA simulations. We proceeded the process until we found that strategies with NMB from the deterministic analysis ranked below 20 had nearly zero probability to be selected. We then calculated the opportunity loss for a given simulation as the difference of NMB between the optimal strategy (i.e. with highest NMB) in a given simulation and the overall optimal strategy - the combination strategy with the highest expected NMB across all simulations. Finally, EVPI was estimated by averaging the opportunity loss across all simulations. Given that our model is developed at the population level, the computed EVPI directly represents a population estimate, thus requiring no extrapolation. We also expressed this uncertainty as a cost per million residents to clarify relative differences across cities.

EVPPI provides an estimate of the value of eliminating uncertainty for specific parameters or groups of parameters. The value of collecting additional information for particular parameters depends on both their influence on the cost-effectiveness of competing strategies and the extent of uncertainty (29). Using a metamodeling approach (16, 20), we modeled the opportunity loss of each strategy (same as in EVPI) as a function of the parameters of interest at the base threshold of $100,000/QALY. We adopted two advanced metamodeling methods with a generalized additive model (GAM) and a deep learning artificial neural network (ANN) model to approximate the inner expectation of the conventional nested Monte Carlo approach (16–18). In simulation models like ours where the relationship between opportunity loss and parameters is non-linear, these methods provide highly flexible functions requiring no parametric assumptions and are found to outperform linear modeling approaches (30, 31). The GAM is efficient and more straightforward to implement with high precision, but is constrained by the size of regression parameters because the required PSA sample size increases exponentially (16). We therefore used GAM for each individual parameter and the ANN model, which can approximate complex, non-linear relationships in data with high dimensionality, to estimate the full EVPPIs for parameters in groups. Key groups of parameters were selected by having at least one parameter whose EVPPI > (0.05 × EVPI) and groupings were based on which parameters were likely to be informed by any one single study in practice. Given the large number of input parameters, we required a larger number of PSA runs to avoid overfitting and achieve more precise EVPPI estimates. The outputs from GAM for each individual parameter were used to inform the selection of key groups of parameters for ANN metamodel analysis. Following a procedure displayed in Appendix Figure A2, we expanded the PSA samples to 20,000 and performed EVPPI analysis with the two aforementioned methods. We then compared the resulting EVPPI estimates to inform targets for prioritizing future data collection. We constructed the ANN for each metamodel with 4 hidden layers and 10 hidden nodes per layer (32). To address the randomness in generating initial weights for the ANN algorithm, we repeated each estimation ten times and averaged the results for the final EVPPI values. We described the process for result validation and tuning for the ANN model in detail in the Appendix. We executed model simulation using R version 3.6.1 (www.r-project.org) and built the GAM and ANN metamodels using the R package “mgcv” (v1.8–31) (33) and “keras” (v2.2.5.0) (34), respectively.

Results

Uncertainty in cost-effectiveness

Results from our PSA demonstrate that the optimal combination implementation strategies, i.e. with the highest NMB, varied across cities (Figure 1, Figure 2). At the base threshold of $100,000/QALY, the probability of the most probable strategies to be highest-valued ranged from 30% (LA) to 56% (Atlanta). The uncertainty came from the decision on choosing between competing combinations that differed by only one or two interventions. This uncertainty may result in opportunity costs due to acting on the suboptimal decision and is strongly associated with the magnitude of EVPI and EVPPI. Results for other thresholds (Appendix Figure A4 and A5) indicated that the level of uncertainty generally decreased with higher cost-effectiveness thresholds.

Figure 1. The probabilities of competing combination strategies representing the highest value at a cost-effectiveness threshold of $100,000 per QALY.

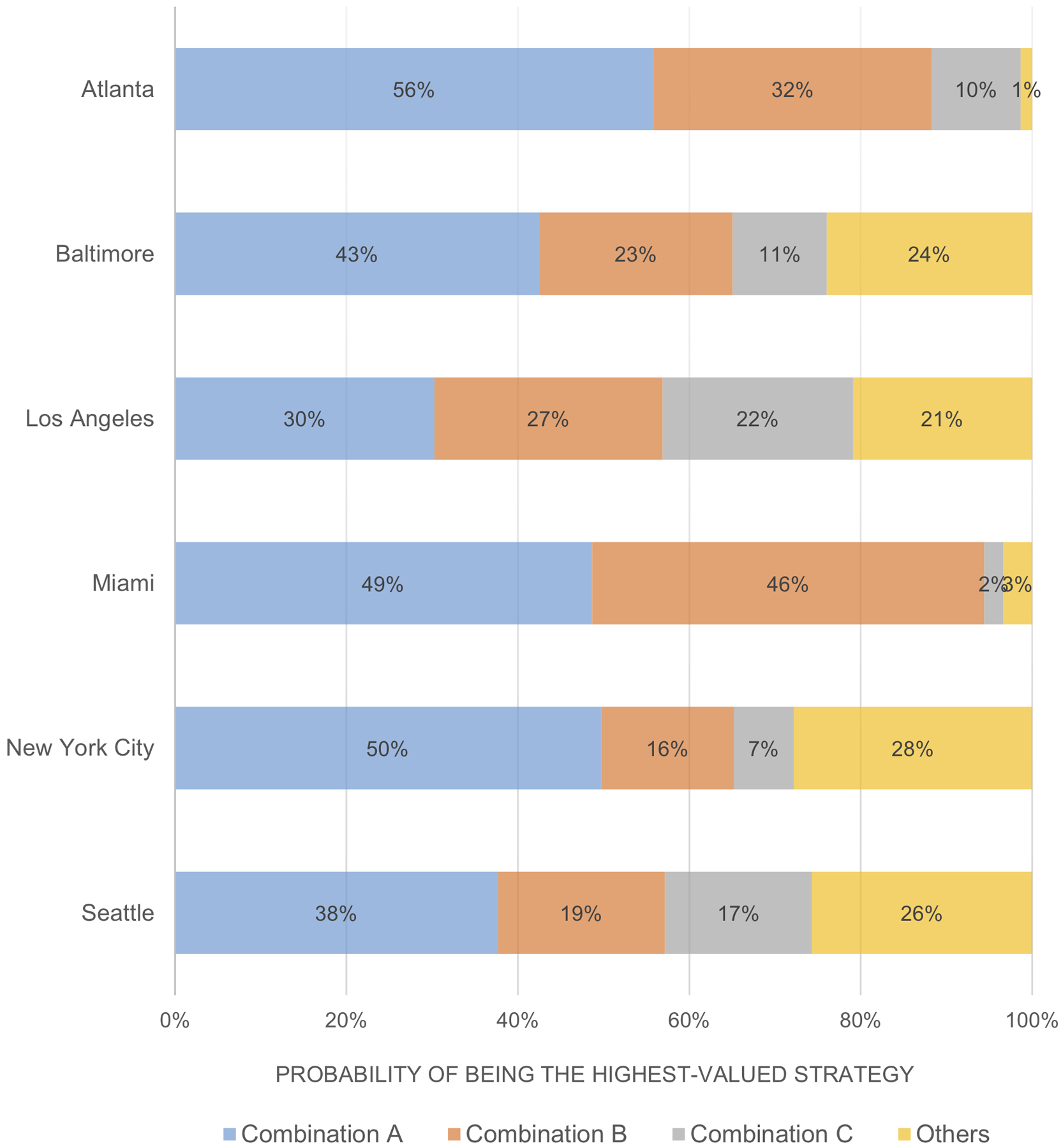
QALY: quality-adjusted life year

Figure 2. The composition of the highest-valued combination strategies at a cost-effectiveness threshold of $100,000 per QALY.

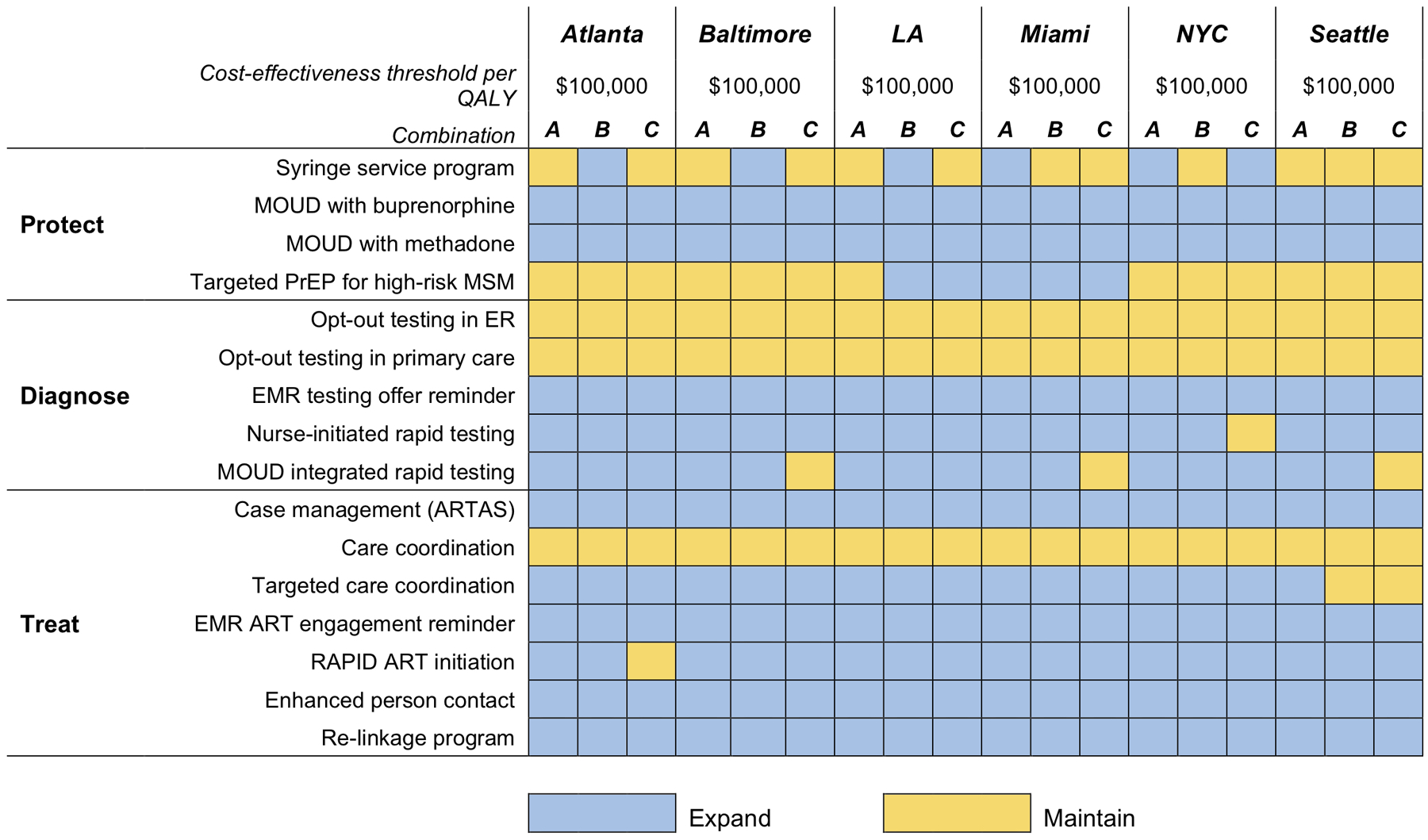
LA: Los Angeles; NYC: New York City; MOUD: Medication for opioid use disorder; PrEP: Pre-exposure prophylaxis; MSM: Men who have sex with men; ER: Hospital emergency room; EMR: Electronic medical records; ART: antiretroviral therapy.

Expected value of perfect information

Figure 3 shows the EVPI for each city at the base cost-effectiveness threshold. The city-level EVPI was found to be small in Miami ($59,683), Atlanta ($92,684), and Seattle ($340,439) and relatively greater in Baltimore ($1,348,364), NYC ($7,649,541), and LA ($54,108,679). Per individual EVPI, after standardizing with city population size, was generally consistent to the city-level results and was highest in LA ($8,009,105 per million residents) and lowest in Atlanta ($20,880 per million residents). These upper bounds on the return of future research demonstrate higher chance to exceed the costs of feasible research for improving data precision. Through estimating EVPI at different thresholds (Appendix A6), we found that values became smaller with increasing threshold levels when the decision uncertainty was reduced, except for LA. The large increase in EVPI for LA from $50,000/QALY to $100,000/QALY reflected uncertainty surrounding the inclusion of PrEP in the combination implementation strategy (an effective yet very costly strategy) at the higher threshold.

Figure 3. Expected value of perfect information (EVPI) results at a cost-effectiveness threshold of $100,000 per QALY. (A) The city-level EVPI. (B) The EVPI per million residents.

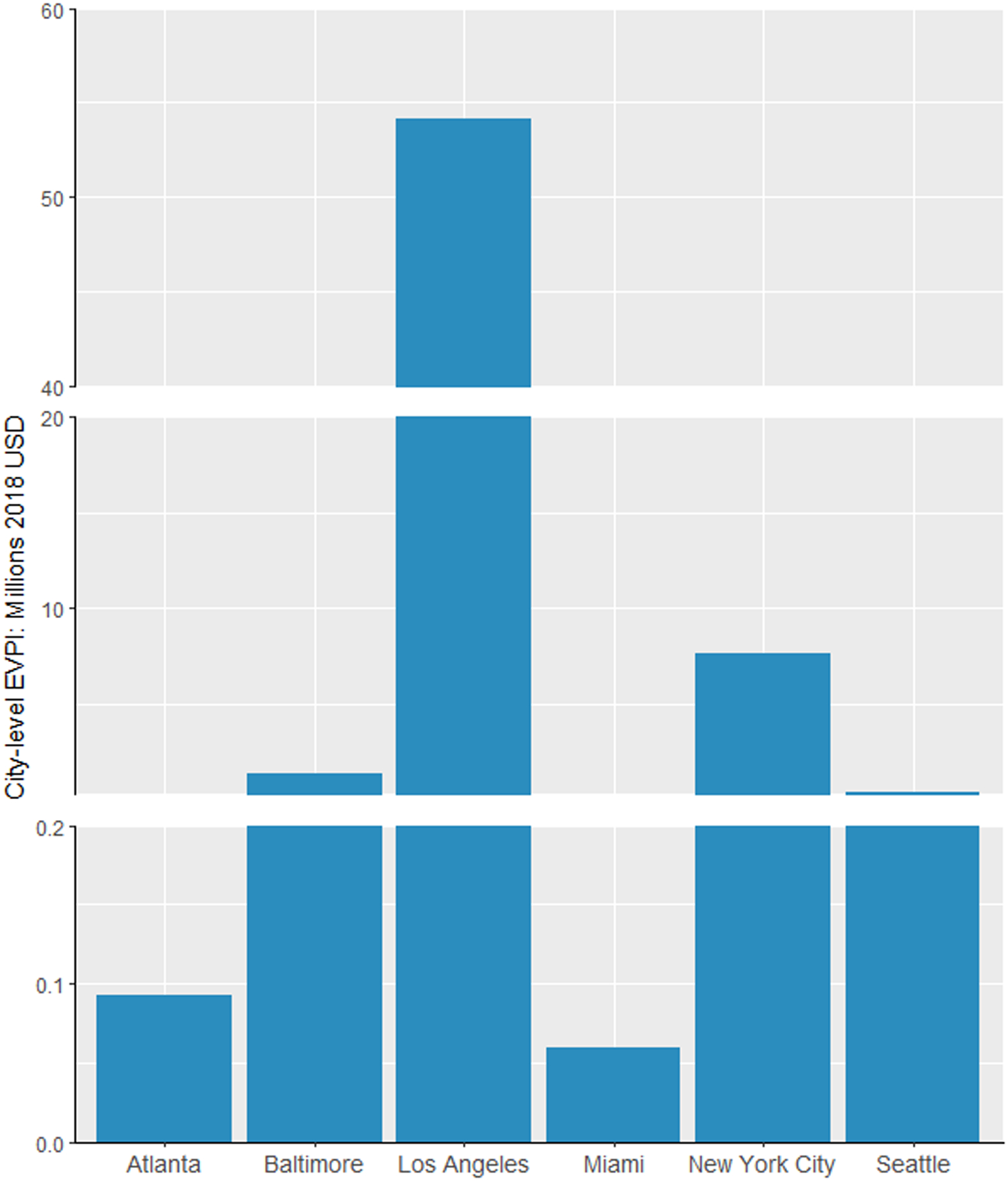
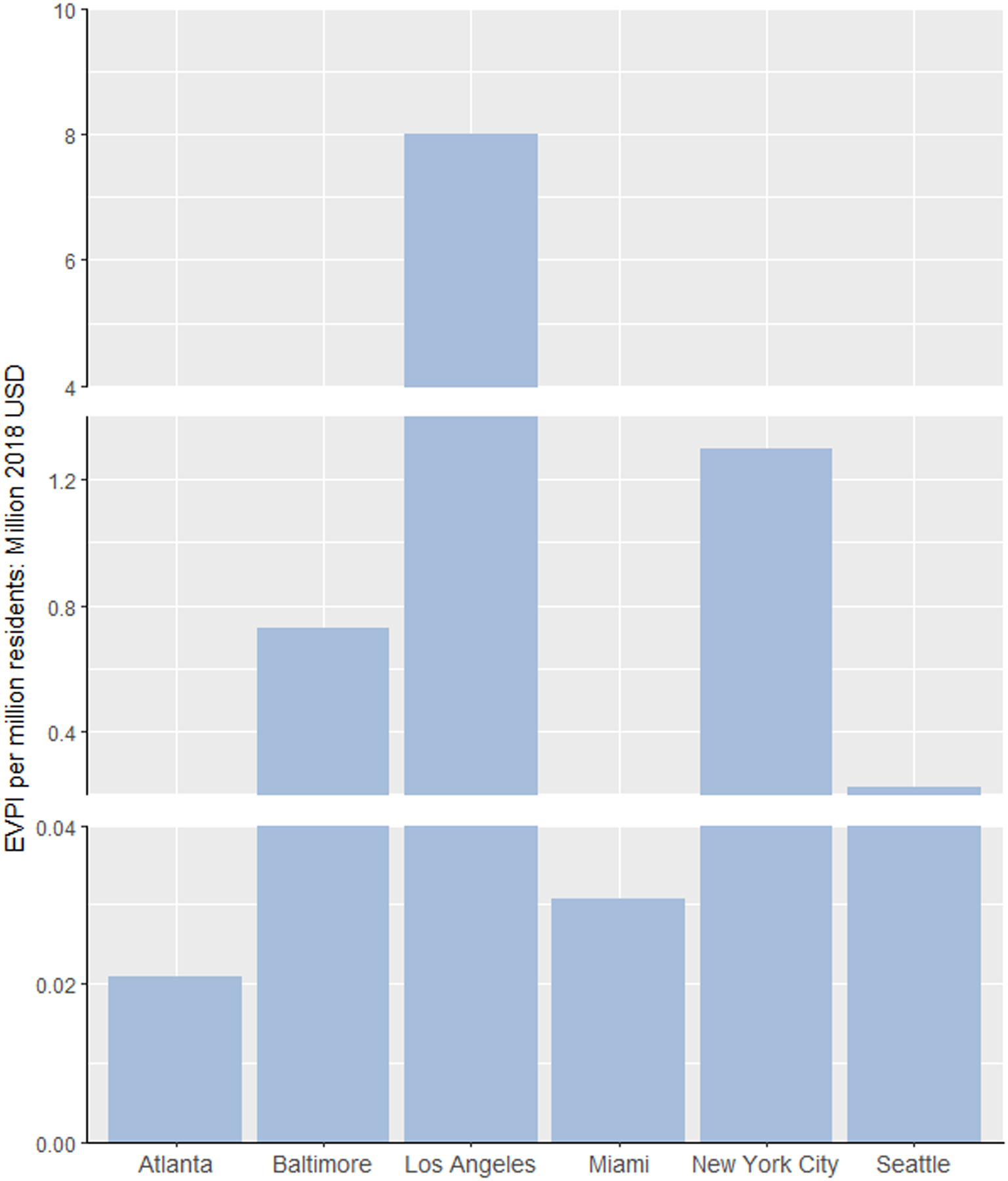
Population size (aged 15–64) used to calculate the EVPI per million residents: Atlanta: 4,447,524; Baltimore: 1,844,759; Los Angeles: 6,755,896; Miami: 1,946,897; New York City: 5,894,751; Seattle: 1,542,132.

Expected value of partial perfect information

We presented in Appendix Figure A2 the distribution of EVPPI values we estimated at a threshold of $100,000/QALY from metamodeling analysis with a GAM on each individual parameter for each city. Many parameters were found to have an EVPPI of $0, implying acquiring additional information on them is unlikely to impact the allocation decision. We found a high degree of consistency across cities on the parameters that were most influential on decision uncertainty and we grouped them accordingly: (1) mortality rate estimates for people living with HIV (PLHIV), stratified by injection drug use status and ART receipt (N=58); (2) the probability of direct ART engagement (within 1 month of diagnosis) (N=15); (3) the rate of ART initiation (N=15); (4) the rate of ART dropout (N=54); (5) the number of sexual partners, both heterosexual and homosexual (N=25); (6) HIV transmission probabilities per heterosexual partnership (N=6); (7) HIV transmission probabilities per homosexual partnership (N=3); (8) HIV transmission probabilities per shared injection contact (N=3); (9) the HIV testing rate across strata (N=30); (10) QALY weights (N=11); and (11) health care costs for individuals receiving ART (N=18) (Appendix Table A1). Some additional groups of influential parameters specific to individual cities included (12) injection frequency among people who inject drugs (N=2), (13) the effectiveness of SSP (N=1) in reducing the probability of shared injection (Atlanta, Baltimore and Miami) and (14) the PrEP retention rate (LA, N=1). Figure 4 compares the EVPPI for these key groups of parameters, showing that the value of information associated with reducing parameter uncertainty was highest for the number of sexual partners (ranged from $36,695 in Miami to $19,619,277 in LA), the probability of immediate ART engagement (ranged from $32,380 in Miami to $8,660,878 in LA), and HIV testing parameters (ranged from $34,094 in Miami to $9,665,386 in LA) except in LA where the EVPPI for PrEP retention rate ($22,861,668) exceeded all other parameters.

Figure 4. The city-level expected value of partial perfect information for identified parameter groups at a cost-effectiveness threshold of $100,000 per QALY.

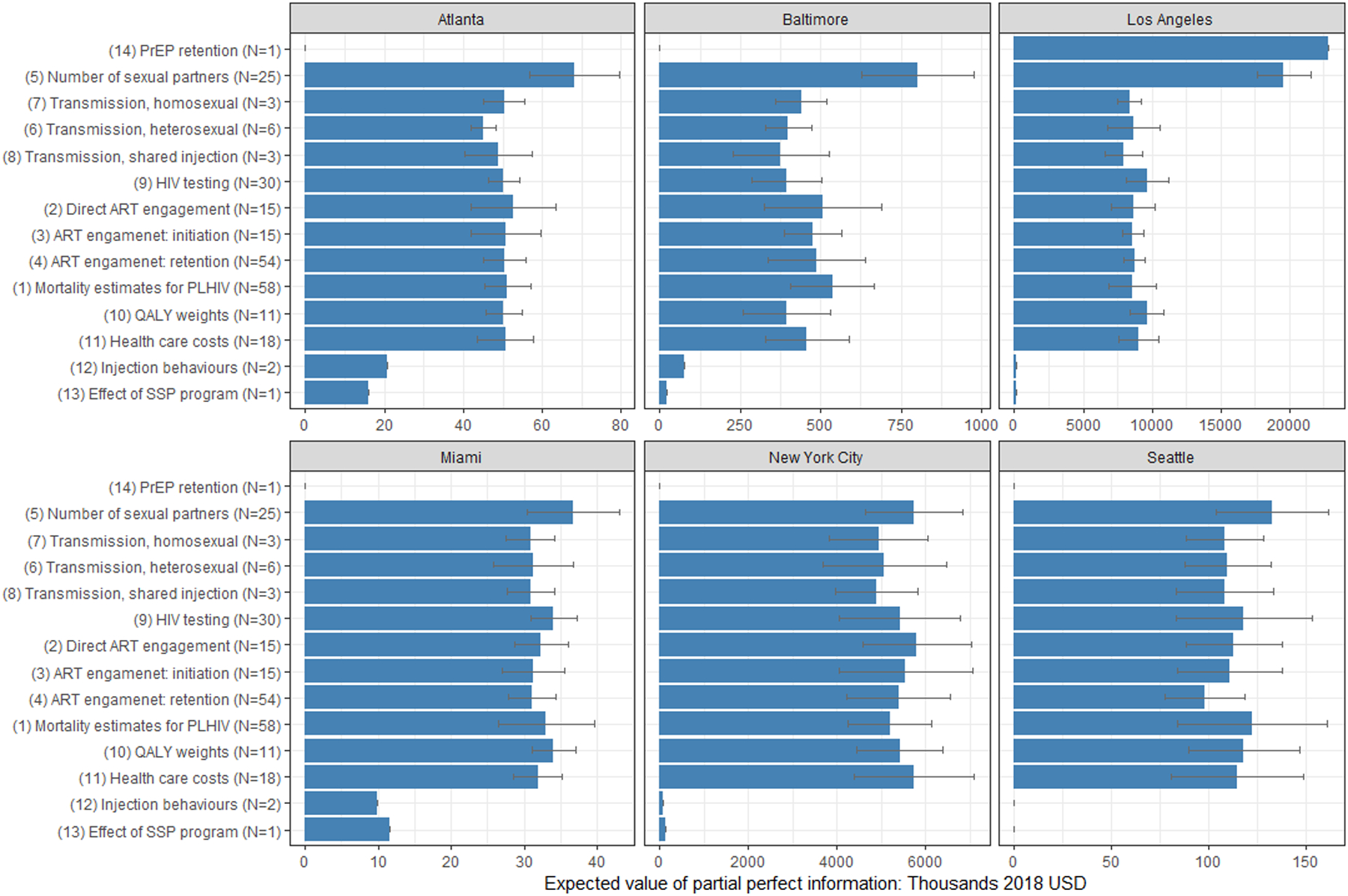
Bracketed group indexes correspond to the ones defined in Results section. Parameter groups have been ordered according to the ranking of estimated EVPPI values. The error bars represent the mean ± 1.96 x standard deviation of the estimated values from the ten repeated estimations. Parameters groups with two or fewer parameters were estimated by ANN model and thus had no error bars. N: number of parameters in the given group.

Discussion

We performed a VoI analysis to determine the potential value of additional data collection in reducing decision uncertainty on the cost-effectiveness of localized HIV combination implementation strategies in six US cities. The high EVPIs we estimated for Baltimore, New York City and LA suggest there is substantial value in further data collection to reduce decision uncertainty in these cities. Through an extensive EVPPI analysis, we identified the primary contributors to the uncertainty in these decisions and recommended further data collection on HIV risk behaviors, probability of HIV transmission per sexual partnership or shared injection contact, health service engagement, HIV-related mortality, health utility weights and health care costs. Given existing data collection infrastructure in the US for most of the identified parameters groups, improving the validity and precision of data will likely rely on enhancing current efforts rather than launching new research efforts at greater costs.

The low EVPI values we estimated for Atlanta, Miami and Seattle at a $100,000/QALY threshold were a result of their relatively smaller populations and lower levels of decision uncertainty. Although this may suggest that funding further data collection may not be justified, these findings should be interpreted with caution as they reflect the current status of a given microepidemic (and our knowledge of it) and thus may change over time. For example, the current high incidence of HIV in Miami makes most interventions highly cost-effective despite substantial uncertainty in expected costs and benefits of implementation. However, if incidence declines in the future, the probability of a suboptimal implementation decision – and accordingly, the EVPI, will increase. EVPI calculations should thus be updated alongside prospective modeling efforts.

EVPPI analysis provides insight into the value of reducing uncertainty for model parameters that are most influential to decision uncertainty. We identified several key groups of parameters that were consistently detected as potential targets across cities for future research, including HIV risk behaviors; probability of HIV transmission; health service engagement; HIV-related mortality; health utility weights; and health care costs (for PLHIV on ART). Many model parameters within these groups were also found to be highly influential on epidemiological targets in a global sensitivity analysis in our previous model calibration work (21). The value of other parameters was low or negligible. This does not mean that their uncertainty is unimportant, but that gathering more accurate information about these parameters would be unlikely to help us reduce decision uncertainty and narrow the ultimate decision. In particular, improving estimates on the rate of PrEP retention was valued at over $20 million in LA but was negligible in other cities. Though effective in preventing HIV transmission, PrEP is a costly intervention whose value is highly dependent on recipients’ persistence (35) and the evidence informing PrEP retention was characterized by a wide uncertainty range (20.6 months, range: 13.1–49.6) (12), resulting in substantial variation in PrEP persistence. However, in all cities except LA, this intervention had either 100% or 0% probability of entering as a component in the optimal strategy and thus had negligible impact on decision uncertainty, resulting in a stark contrast in valuation of EVPPI.

Collectively, parameters pertaining to the number of sexual partners contributed to a high degree of decision uncertainty across all cities. The importance of these behavioural parameters has also been noted in many prior modeling studies (36, 37). Our current model parameter values were informed by evidence from NHBS (38) and the National Survey of Family Growth (NSFG) (39). Although these population-based surveillance databases provide the best available evidence on this topic, these surveys featured several threats to internal and external validity that could potentially be improved upon with greater investments. For example, NSFG only provided regional rather than city-level data while in NHBS, where city-specific data were available, sample sizes for some population groups were small, resulting in wide uncertainty ranges. Equally importantly, the framing of the survey questions did not always correspond to how the model parameters in this particular application were encoded, which may have inevitably introduced additional uncertainty from data triangulation. Enhancing behavioural evidence on the basis of current surveillance system should focus on subpopulations with high risk behaviours (40). An ongoing project may provide an example for a multi-site community-engaged study that engages a high-coverage sample of MSM recruited using respondent-driven sampling (41). Notably, in this application researchers also applied standardized adjustment methods to generate population-representative estimates (42).

Health service engagement was another parameter category found to be influential. Good-quality evidence for population-level HIV testing rates in the US is sparse. We derived these testing parameters from NHBS (43, 44), the Behavioral Risk Factor Surveillance System (45), and other sources in the peer-reviewed literature. Further, in the absence of city-specific data, ART engagement parameters were derived from corresponding regional HIVRN data (46) and corresponding primary analysis (47). These data, available from sample-based studies in selected sites, may have been unrepresentative of the general population. Establishing a centralized public health database to systematically collect and combine surveillance and health administrative data across different jurisdictions and agencies could substantially reduce the bias and uncertainty of population-level evidence. Although CDC is making efforts to enhance the collection, analysis, visualization, and dissemination of its surveillance data, challenges exist in coordinating information sharing, developing a broader surveillance workforce, and building health information systems to integrate data collected from various parties (48–50).

Although several modern methods have been developed to replace the conventional nested Monte Carlo procedure in VoI estimation (20), few applications using dynamic transmission models have been published (17). Further, this study presents one of the few examples of applying advanced metamodeling approaches, including a deep learning method, in estimating the EVPPI for large groups of parameters and many competing strategies. We demonstrated a pragmatic approach in applying VoI analysis while maintaining a high level of rigor. We also found limited guidance on several critical steps of VoI analysis. One question we encountered was whether to include calibrated parameters with their posterior calibrated values or their prior uncertainty ranges in the PSA. We chose the latter option as we felt that the posterior ranges on calibrated parameters may arbitrarily shrink decision uncertainty and undervalue the estimated EVP(P)I. VoI analysis using calibrated values does not truly reflect our current knowledge about the uncertainty of parameters being calibrated and their impact on decision uncertainty. Further, the posterior ranges on calibrated parameters are subject to uncertainty stemming from a number of choices made in the calibration process, including the selected calibration targets, the goodness-of-fit measure, the parameters chosen for calibration, and the calibration algorithm (21). We note that this was a departure from our prior analysis (23), and explains the differences in the PSA results presented herein. Questions also remain about to what extent these VoI results are transferable beyond their current setting. For parameters that are based on common evidence and can be generalizable across locations, e.g. transmission probabilities, it may be more meaningful to sum the relevant populations across locations when computing the population-level EVPPI to inform the true value of collecting additional data on those parameters.

This analysis has several limitations. First, the procedure we undertook to only perform PSA on a subset of the highest-valued combination strategies identified in the deterministic base case might inevitably omit several strategies that had very small probabilities of being chosen as optimal. We felt these omissions had a negligible impact on the VoI while significantly improving computational efficiency in this application. Second, we did not consider potential developments in HIV interventions. Emerging evidence, which may comprise longer-acting ART and PrEP formulations or substantial cost reductions from the introduction of generic formulations could alter the VoI estimates. Third, we did not attempt to calculate the EVSI, which remains a topic for further inquiry. Finally, the structural uncertainty attributable to our model was outside the scope of this VoI analysis, which focuses explicitly on parameter uncertainty. As decisions about model structure may also influence decision uncertainty, cross-model comparisons can provide a robust validation of the recommendations of a given model and highlight additional priorities on the nature of data that should be incorporated to reduce decision uncertainty.

Conclusion

We found uncertainty on the combination implementation strategies that would be most cost-effective for HIV prevention. This uncertainty is associated with high opportunity cost where benefits are likely to outweigh the cost of future research to improve parameter precision in three out of six cities we considered in this project. To refine decision making for HIV, priority should be given to data collection on several key groups of parameters consistently found to be associated with the greatest decision uncertainty, including HIV risk behaviors, health service engagement, probability of HIV transmission, HIV-related mortality, health utility weights and health care costs. Value of information analysis, combined with other information, such as study feasibility, relevance and the cost of research, should be embedded into decision making processes on funding and identifying targets for data acquisition efforts.

Highlights.

• Achieving the ambitious goals set by the US “Ending the HIV Epidemic” initiative necessitates localized combination implementation strategies. Economic models provide useful tool to inform health decision-making. However, the inherent uncertainty underlying model parameters may propagate into decision uncertainty regarding what constitutes the optimal response. Value of information analysis estimates the value of collecting additional data to reduce decision uncertainty and helps guide efforts of data collection to focus on the most influential parameters.

• We demonstrated a pragmatic approach in applying metamodeling approach in value of information analysis in a dynamic transmission model. This study presents one of the few examples of applying advanced metamodeling approaches, including a deep learning method, in estimating the expected value of partial perfect information for large groups of parameters and many competing strategies.

• We found substantial value in further data collection to reduce decision uncertainty in Baltimore, Los Angeles, and New York City. We also identified the primary contributors to the uncertainty in the decisions and recommended further data collection on HIV risk behaviors, probability of HIV transmission, health service engagement, HIV-related mortality, health utility weights and health care costs.