Abstract
A semiquantitative risk factor has 2 components: any exposure (yes/no) and the quantitative amount of exposure (if exposed). We describe the statistical properties of alternative analyses with such a risk factor using linear, logistic, or Cox proportional hazards models. Often analyses employ the amount exposed as a single quantitative covariate, including the nonexposed with value zero. However, this analysis provides a biased estimate of the exposure coefficient (slope) and we describe the magnitude of the bias. This bias can be eliminated by adding a binary covariate for exposed versus not to the model. This 2-factor analysis captures the full risk-factor effect on the outcome. However, the coefficient for any exposure versus not does not have a meaningful interpretation. Alternatively, when exposure values among those exposed are centered (by subtracting the mean), the estimate of this coefficient represents the difference in the outcome between those exposed versus not in aggregate. We also show that the biased model provides biased estimates of the coefficients for other covariates added to the model. Proper analysis of a semiquantitative risk factor should start with a 2-factor model, with centering, to assess the joint contributions of the 2 components of the risk-factor exposure. Properties of models were illustrated using data from a multisite study in North America (1983–2019).
Keywords: modeling exposure, semiquantitative covariate, smoking and smoking intensity, variable with spike at zero
Abbreviations
- bpm
beats per minute
- CCN
confirmed clinical neuropathy
- df
degrees of freedom
- EDIC
Epidemiology of Diabetes Interventions and Complications
- LDL
low-density lipoprotein
Epidemiology research often employs a semiquantitative exposure (e.g., smoking) that is actually a mixture of a binary covariate for exposure (yes/no) and a quantitative covariate for the amount of exposure among those exposed. Methods for the analysis of such data as the outcome or dependent variable have been described (1, 2), including where the outcome variable is truncated from below (3). Herein, however, we use a semiquantitative variable as a risk factor in a regression model to assess the association of any exposure (e.g., smoking yes/no) and the exposure level (e.g., smoking intensity) with an outcome.
Often the analysis has employed a single quantitative covariate, including the nonexposed subjects with an intensity value of zero. For example, Feodoroff et al. (4) recently presented an analysis of the association of smoking with the risk of cardiovascular disease in a large cohort of subjects with type I (insulin-dependent) diabetes. Their models included separate coefficients for the smoking intensity (pack-years smoking) among current smokers and former smokers, and included the nonsmokers with value zero. However, Leffondré et al. (5), in an example (i.e., numerical computation), suggested that such analyses that do not account for the difference between smokers and nonsmokers provide a biased estimate of the coefficient or slope of the outcome regressed on the amount exposed. Herein we provide a derivation of the statistical expression for the magnitude of the bias. We also show that such analyses that include other covariates provide biased estimates of the coefficients for those covariates as well.
In some analyses the quantitative component of the exposure has been centered by subtracting the mean from each value, and the nonexposed have been included with the exposure amount zero (5–7). However, the statistical properties of a centered model have not been described. Such data have also been used to estimate a nonlinear exposure-response curve (8, 9), focusing on the goodness of fit of the nonlinear model.
Herein we describe the interpretation of the corresponding coefficients in noncentered and mean-centered linear models for a quantitative outcome, a logistic regression model for a binary outcome, and a Cox proportional hazards model for an event-time outcome. We show that a model with the quantitative exposure alone, that also includes the nonexposed with exposure value zero, provides a biased estimate of the exposure coefficient relative to that in a model restricted to those exposed. Further, if other factors are added to this model, their coefficient estimates are also biased relative to a model that includes a binary variable for those exposed versus not. Thus, preferable is a 2-factor model with centered exposure values that yields unbiased estimates of the model coefficients and those of other covariates added to the model, and provides an overall comparison of the outcome for those exposed versus not in addition to the association with the amount of exposure. We have illustrated properties of models with application to data from the Diabetes Control and Complications Trial and Epidemiology of Diabetes Interventions and Complications study (DCCT/EDIC) (clinical trials registration numbers: NCT00360893, NCT00360815), conducted in the United States and Canada. These studies span the period from 1983 to date.
LINEAR MODELS FOR A SEMIQUANTITATIVE RISK FACTOR
Suppose that a semiquantitative exposure variable is employed as a risk factor (predictor) for a quantitative outcome 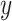 in a simple linear regression model. Let the binary variable
in a simple linear regression model. Let the binary variable  designate whether a subject was exposed
designate whether a subject was exposed  versus not
versus not  , and
, and 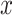 be the amount of exposure in the
be the amount of exposure in the 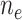 of the
of the 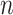 observations that were exposed, where
observations that were exposed, where 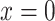 if not exposed.
if not exposed.
As examples, we have conducted analyses of smoking exposure among participants in the study of the Epidemiology of Diabetes Interventions and Complications (EDIC), an observational study of the incidence and prevalence of micro- and macrovascular complications in over 1,000 participants with type 1 diabetes mellitus, followed annually (10). Smokers included current smokers and those who quit within 3 months prior to an annual visit, and the intensity is the current average number of cigarettes smoked per day. Nonsmokers did not currently smoke or previously smoked and quit 3 or more months prior to the visit.
Consider models to assess the association of smoking with pulse rate (beats per minute (bpm)) after 2-years of follow-up in EDIC. Among the 268 smokers, the mean intensity was 15.97 cigarettes per day and the mean pulse rate 75.42 bpm, whereas for the 1,012 nonsmokers the mean intensity was 0 by definition and the mean pulse rate was 72.11 bpm. The mean difference in pulse rate among smokers versus nonsmokers is  , with standard error = 0.7113 yielding t = 4.65 and P < 0.0001. However, this ignores the potential influence of smoking intensity.
, with standard error = 0.7113 yielding t = 4.65 and P < 0.0001. However, this ignores the potential influence of smoking intensity.
Table 1 presents the coefficient estimates for additional models for the EDIC pulse rate data.
Table 1.
Linear Regression Models of the Association of the Prevalence of Smoking Versus Not 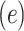 and the Smoking Intensity (
and the Smoking Intensity (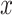 or
or 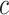 ) With Pulse Rate (Beats per Minute,
) With Pulse Rate (Beats per Minute, 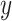 ) at 2 Years of Follow-up in the Epidemiology of Diabetes Interventions and Complications Cohort, North America, Circa 1995
) at 2 Years of Follow-up in the Epidemiology of Diabetes Interventions and Complications Cohort, North America, Circa 1995
| Model |
Coefficient (Factor) |
Estimate | SE | P Value | Model F | df | P Value |
|---|---|---|---|---|---|---|---|
Noncentereda 1: 
|
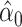
|
75.1046 | 1.1994 | <0.0001 | 0.098 | 1 | 0.7546 |

|
0.0199 | 0.0634 | 0.7546 | ||||
Noncentereda 2: 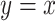
|
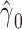
|
72.3224 | 0.3145 | <0.0001 | 15.73 | 1 | <0.0001 |
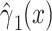
|
0.1442 | 0.0364 | <0.0001 | ||||
Noncentereda 3: 
|

|
72.1117 | 0.3256 | <0.0001 | 10.87 | 2 | <0.0001 |
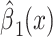
|
0.0199 | 0.0626 | 0.7511 | ||||
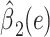
|
2.9929 | 1.2268 | 0.0148 | ||||
Centeredb 4: 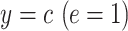
|

|
75.4216 | 0.6415 | <0.0001 | 0.098 | 1 | 0.7546 |

|
0.0199 | 0.0634 | 0.7546 | ||||
Centeredb 5: 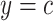
|
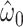
|
72.8047 | 0.2918 | <0.0001 | 0.099 | 1 | 0.7530 |
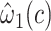
|
0.0199 | 0.0631 | 0.7530 | ||||
Centeredb 6: 
|

|
72.1117 | 0.3256 | <0.0001 | 10.87 | 2 | <0.0001 |

|
0.0199 | 0.0626 | 0.7511 | ||||
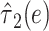
|
3.3100 | 0.7115 | <0.0001 |
Abbreviations: df, degrees of freedom; SE, standard error.
a Models with noncentered smoking intensities (x, models 1–3).
b Models with centered intensities (c, after subtracting the mean, models 4–6).
Semiquantitative variable without centering
The quantitative association of smoking intensity 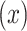 with pulse rate
with pulse rate 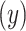 among the
among the  smokers can be directly assessed using model 1:
smokers can be directly assessed using model 1:
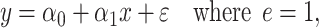 |
(1) |
where the errors  are assumed to have mean zero and constant variance for all observations. The coefficient
are assumed to have mean zero and constant variance for all observations. The coefficient  provides an unbiased estimate of the slope of pulse rate on smoking intensity—in this case not significant, with
provides an unbiased estimate of the slope of pulse rate on smoking intensity—in this case not significant, with 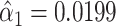 and P = 0.7546. However, this does not allow for a general association with smoking (i.e., a generally higher pulse rate among smokers vs. nonsmokers independent of the amount smoked). Also, under this model the intercept
and P = 0.7546. However, this does not allow for a general association with smoking (i.e., a generally higher pulse rate among smokers vs. nonsmokers independent of the amount smoked). Also, under this model the intercept  is the estimate of the mean of
is the estimate of the mean of 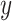 among smokers
among smokers  who smoked 0 cigarettes per day
who smoked 0 cigarettes per day  , which is a hypothetical, nonexistent value given that there are no smokers
, which is a hypothetical, nonexistent value given that there are no smokers  with intensity
with intensity 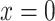 .
.
Often, however, the analysis employs all  subjects, including nonsmokers, as in model 2:
subjects, including nonsmokers, as in model 2:
 |
(2) |
where 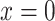 for nonsmokers. This model shows a significant association of the outcome
for nonsmokers. This model shows a significant association of the outcome 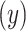 with smoking in all 1,280 subjects including the 1,012 nonsmokers with
with smoking in all 1,280 subjects including the 1,012 nonsmokers with 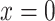 (P < 0.0001). However, Web Appendix 1 shows that the coefficient estimates
(P < 0.0001). However, Web Appendix 1 shows that the coefficient estimates 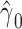 and
and 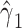 are biased relative to the coefficients
are biased relative to the coefficients 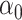 and
and 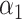 in the unbiased model 1, the slope estimate being
in the unbiased model 1, the slope estimate being  relative to
relative to  . Thus, the model estimates the pulse rate to be 0.1442-bpm higher for a smoker of 1 cigarette per day versus a nonsmoker, as well as 0.1442-bpm higher for a smoker of
. Thus, the model estimates the pulse rate to be 0.1442-bpm higher for a smoker of 1 cigarette per day versus a nonsmoker, as well as 0.1442-bpm higher for a smoker of 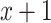 cigarettes per day versus a smoker of
cigarettes per day versus a smoker of 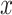 cigarettes per day for any
cigarettes per day for any  . This is implausible.
. This is implausible.
In addition, the standard error of the intensity coefficient in this biased model 2 is about half that in the unbiased model 3 (0.0364 versus 0.0634) with resulting P values of < 0.0001 versus 0.7546. This would lead to the erroneous conclusion that the smoking intensity in this case is positively associated with the pulse rate.
Alternatively, a 2-factor mixture model would assess both the association of smoking versus not 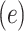 and the smoking intensity
and the smoking intensity  with the outcome
with the outcome 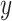 , as in model 3:
, as in model 3:
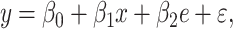 |
(3) |
with coefficient vector 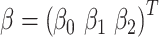 . Using least-squares estimation the coefficient estimates satisfy
. Using least-squares estimation the coefficient estimates satisfy
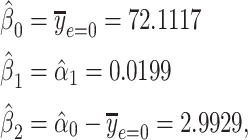 |
(4) |
so that the intercept 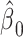 is the mean of
is the mean of 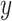 among nonsmokers,
among nonsmokers, 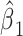 is the slope of
is the slope of 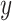 on
on 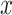 among smokers as in model 1, and
among smokers as in model 1, and 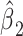 is the difference between the intercept from model 1 and the mean of
is the difference between the intercept from model 1 and the mean of  among nonsmokers. While the slope is the same
among nonsmokers. While the slope is the same 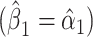 as in model 1, the standard error,
as in model 1, the standard error,  , and P are slightly different owing to the addition of the binary component with estimate
, and P are slightly different owing to the addition of the binary component with estimate  , P = 0.0148. The model test of the joint null hypothesis
, P = 0.0148. The model test of the joint null hypothesis 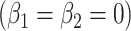 for the full influence of smoking is highly significant (F = 10.87 on 2 degrees of freedom (df), P < 0.0001), more so than either 1-df test of each component.
for the full influence of smoking is highly significant (F = 10.87 on 2 degrees of freedom (df), P < 0.0001), more so than either 1-df test of each component.
Figure 1 then depicts the relationships in model 3. The estimated intercept is 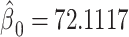 , which equals the mean pulse among nonsmokers
, which equals the mean pulse among nonsmokers  . The estimated regression line provides the estimated mean pulse rate over the range of intensity values
. The estimated regression line provides the estimated mean pulse rate over the range of intensity values 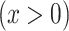 among smokers computed as
among smokers computed as  . Given that
. Given that 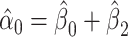 and
and 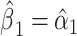 the regression line is computed as
the regression line is computed as 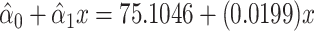 for
for 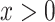 .
.
Figure 1.

Estimated mean pulse (beats per minute (bpm), 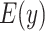 ) from the noncentered model 3 in (equation 3) as a function of the smoking intensity
) from the noncentered model 3 in (equation 3) as a function of the smoking intensity 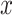 where
where 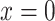 designates the nonsmoker subset of the cohort and
designates the nonsmoker subset of the cohort and 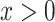 designates the smoking intensity among smokers, using data from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 1995. The point marked by the triangle is the model-estimated intercept
designates the smoking intensity among smokers, using data from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 1995. The point marked by the triangle is the model-estimated intercept 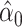 of the smokers-only model 1 in (equation 1), the diamond is the model-estimated pulse rate for a smoker with intensity = 1, the square is the mean pulse rate among smokers
of the smokers-only model 1 in (equation 1), the diamond is the model-estimated pulse rate for a smoker with intensity = 1, the square is the mean pulse rate among smokers 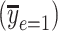 at the average intensity, and the circle is the mean pulse rate among nonsmokers
at the average intensity, and the circle is the mean pulse rate among nonsmokers  . The model 3 estimate of the coefficient for smoker versus not
. The model 3 estimate of the coefficient for smoker versus not  in (equation 3) equals the difference in pulse rate for points triangle minus circle. This figure was generated by plotting a point at (0, 72.1117) and then a line connecting the points (
in (equation 3) equals the difference in pulse rate for points triangle minus circle. This figure was generated by plotting a point at (0, 72.1117) and then a line connecting the points (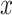 ,
, 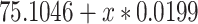 ),
), 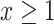 .
.
Note that the test of the hypothesis 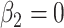 represents a test of the hypothesis that the mean of
represents a test of the hypothesis that the mean of 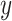 among the nonsmokers
among the nonsmokers 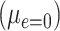 equals the intercept of the quantitative association alone
equals the intercept of the quantitative association alone 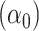 or the difference between the points marked by the triangle and circle in the figure, and is not very meaningful. Rather, it would be of greater interest to test the difference in the mean pulse between smokers versus nonsmokers (i.e., the vertical difference between the points marked by the square and circle).
or the difference between the points marked by the triangle and circle in the figure, and is not very meaningful. Rather, it would be of greater interest to test the difference in the mean pulse between smokers versus nonsmokers (i.e., the vertical difference between the points marked by the square and circle).
In summary, model 1 shows that the slope of pulse rate on the smoking intensity among smokers 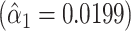 is not significantly different from a horizontal line (slope = 0). Model 2 shows that adding the 1,012 nonsmokers to the intensity data set yields a highly significant slope estimate (
is not significantly different from a horizontal line (slope = 0). Model 2 shows that adding the 1,012 nonsmokers to the intensity data set yields a highly significant slope estimate ( , P < 0.0001) but this estimate is severely biased owing to the discontinuity between the regression line among smokers and the lower average pulse rate among nonsmokers. Model 3 shows that inclusion of the nonsmokers with an additional term in the model for smoker versus not is highly significant (P < 0.0001, 2-df) with the coefficient for smoker versus not being
, P < 0.0001) but this estimate is severely biased owing to the discontinuity between the regression line among smokers and the lower average pulse rate among nonsmokers. Model 3 shows that inclusion of the nonsmokers with an additional term in the model for smoker versus not is highly significant (P < 0.0001, 2-df) with the coefficient for smoker versus not being 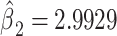 with P = 0.0148. However, this coefficient does not provide an estimate of the overall difference in the mean pulse rate among smokers versus nonsmokers.
with P = 0.0148. However, this coefficient does not provide an estimate of the overall difference in the mean pulse rate among smokers versus nonsmokers.
Semiquantitative variable with centering
Often the smoking intensity (or amount of exposure) is centered by subtracting the mean intensity among smokers from the smoking intensity values, but retaining the value  for nonsmokers. Thus,
for nonsmokers. Thus, 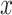 is transformed to a centered semiquantitative variable, say
is transformed to a centered semiquantitative variable, say 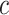 , as
, as
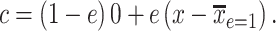 |
(5) |
Table 1 shows the centered models. The equivalent of model 1 is model 4:
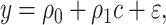 |
(6) |
where e = 1, using only the  smokers. Then,
smokers. Then, 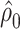 is the estimated mean pulse associated with
is the estimated mean pulse associated with  , or with the mean intensity
, or with the mean intensity 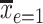 . This can be obtained as
. This can be obtained as  . Also,
. Also, 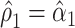 from the noncentered model 1 and is nonsignificant.
from the noncentered model 1 and is nonsignificant.
The centered equivalent to model 2 using all observations including nonsmokers is model 5:
 |
(7) |
Unlike model 2, which provided a highly significant biased estimate of the slope, model 5 provides an unbiased estimate of the slope 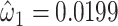 that is nonsignificant and virtually identical to that of model 4. Further, Web Appendix 2 shows that model 5 provides an unbiased estimate of the slope when the 2-factor model is correct. Thus, including nonexposed subjects with value zero in addition to the mean-centered data for those exposed also yields an unbiased estimate of the slope
that is nonsignificant and virtually identical to that of model 4. Further, Web Appendix 2 shows that model 5 provides an unbiased estimate of the slope when the 2-factor model is correct. Thus, including nonexposed subjects with value zero in addition to the mean-centered data for those exposed also yields an unbiased estimate of the slope 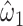 .The centered 2-factor model is model 6:
.The centered 2-factor model is model 6:
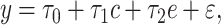 |
(8) |
where it can then be shown that the coefficient estimates satisfy
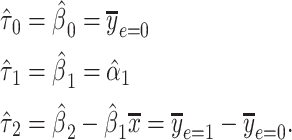 |
(9) |
The noncentered 2-factor model 3 and centered model 6 yield identical model F tests, intercepts and slopes, standard errors, and P values. However, this centered model provides a more relevant representation of the association of smoking versus not with a coefficient estimate  that is the difference in the mean pulse rate among smokers versus that among nonsmokers
that is the difference in the mean pulse rate among smokers versus that among nonsmokers 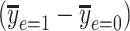 . Conversely, the coefficient from the noncentered model 3
. Conversely, the coefficient from the noncentered model 3  is the difference between the intercept of the smokers-only model 1 and the mean pulse rate among nonsmokers
is the difference between the intercept of the smokers-only model 1 and the mean pulse rate among nonsmokers  . Thus, the tests of the hypotheses
. Thus, the tests of the hypotheses 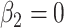 and
and 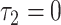 differ, the latter being more relevant, and more significant, in these data.
differ, the latter being more relevant, and more significant, in these data.
Web Appendix 2 describes the expected values of the coefficient estimates for these 3 centered models and shows that the coefficient estimate for the quantitative exposure is unbiased in each.
Figure 2 then describes these results. Using model 6, the 2 components of smoking have a significant model F test, with P < 0.0001. Among smokers the pulse rate is expected to increase by 0.0199 bpm per cigarette smoked, which is not significantly different from zero. However, the mean pulse rate between smokers and nonsmokers differs by  bpm, which is highly statistically significant.
bpm, which is highly statistically significant.
Figure 2.

Estimated mean pulse rate (beats per minute (bpm), 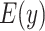 ) from the centered model 6 in (equation 8) as a function of the centered smoking intensity
) from the centered model 6 in (equation 8) as a function of the centered smoking intensity 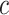 among smokers and nonsmokers
among smokers and nonsmokers 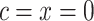 , using data from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 1995. The regression line starts from the centered intensity equivalent to an intensity of 0 (the point marked by the diamond = −
, using data from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 1995. The regression line starts from the centered intensity equivalent to an intensity of 0 (the point marked by the diamond = −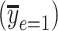 = −15.23) where the square point is the intersection of the mean pulse and the mean centered intensity (= 0) among smokers, and the circle is the mean pulse rate among nonsmokers. The model (equation 8) coefficient estimate
= −15.23) where the square point is the intersection of the mean pulse and the mean centered intensity (= 0) among smokers, and the circle is the mean pulse rate among nonsmokers. The model (equation 8) coefficient estimate 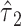 equals the difference in pulse rate for points square minus circle.
equals the difference in pulse rate for points square minus circle.
Other covariate associations
In a multivariate model, the coefficient estimate for each covariate is a function of the estimates for the other covariates. For example, consider a model with smoking (yes/no), smoking intensity, and low-density lipoprotein (LDL, in mg/dL) as predictors. Any bias in the estimates of the coefficients for the semiquantitative smoking variables will then introduce a bias in the coefficient estimate for LDL. An explicit proof is presented in Web Appendix 3.
For example, consider a model to assess the joint effects of smoking and LDL levels on pulse rate in the full cohort, not just for smokers. In this case, the addition of LDL to models 1 and 4 in smokers alone is not relevant. The LDL coefficient estimates per 10 mg/dL in a univariate (unadjusted) model, and when added to models 2, 3, 5 and 6 using all subjects, are shown in Table 2.
Table 2.
The Low-Density Lipoprotein Coefficient Estimates per 10 mg/dL in a Univariate (Unadjusted) Model and When Added to Models 2, 3, 5, and 6 (Including the Smoking Variables) With the Full Sample, Epidemiology of Diabetes Interventions and Complications Cohort, North America, Circa 1995
| Model | LDL Estimate | SE |
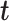 Value Value
|
P Value |
|---|---|---|---|---|
| LDL alone | 0.510 | 0.094 | 5.43 | <0.0001 |
LDL + smoking  alone alone |
0.481 | 0.094 | 5.14 | <0.0001 |
| 2: LDL + noncentered intensity | 0.480 | 0.094 | 5.12 | <0.0001 |
| 3: LDL + noncentered 2-factor | 0.481 | 0.094 | 5.13 | <0.0001 |
| 5: LDL + centered intensity | 0.510 | 0.094 | 5.42 | <0.0001 |
| 6: LDL + centered 2-factor | 0.481 | 0.094 | 5.13 | <0.0001 |
Abbreviations: LDL, low-density lipoprotein; SE, standard error.
With no adjustment for smoking, the LDL coefficient in the full cohort is 0.510. Adjusting for smoking (or any other covariate that is correlated with LDL) is expected to provide a different coefficient value (see Web Appendix 3). Adjusting for smoker versus nonsmoker alone yields an LDL coefficient of 0.481. The same coefficient is provided by the unbiased 2-factor models 3 and 6. The noncentered 1-factor model 2, which provides a biased estimate of the coefficient for 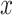 , also provides an unbiased estimate of the LDL coefficient. However, the centered, 1-factor model 5 provides a biased estimate of the adjusted LDL coefficient, being equal to that of the LDL alone with no adjustment. Thus, the centered model 5 corrects for the bias in the intensity slope in the uncentered model, but it introduces a bias in the LDL slope. Again the 2-factor model with LDL added would be preferred.
, also provides an unbiased estimate of the LDL coefficient. However, the centered, 1-factor model 5 provides a biased estimate of the adjusted LDL coefficient, being equal to that of the LDL alone with no adjustment. Thus, the centered model 5 corrects for the bias in the intensity slope in the uncentered model, but it introduces a bias in the LDL slope. Again the 2-factor model with LDL added would be preferred.
NONLINEAR REGRESSION MODELS
We now show that similar relationships apply to the logistic and Cox proportional hazards models. As is shown for linear models in Web Appendix 1, expressions for the expected values of the model coefficients can be obtained along the lines described in Emond et al. (11) and also show that the model 2 coefficients are biased.
Logistic regression model
Consider a logistic regression model where 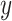 is a binary variable to indicate a positive
is a binary variable to indicate a positive 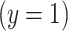 versus negative
versus negative 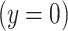 response or outcome. The model then estimates the logit of the probability that
response or outcome. The model then estimates the logit of the probability that  given smoking intensity
given smoking intensity  , designated as
, designated as  , where
, where 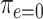 is the probability among nonsmokers
is the probability among nonsmokers  . Thus, the 3 noncentered models are
. Thus, the 3 noncentered models are
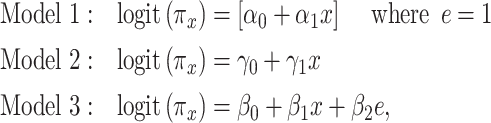 |
(10) |
and the 3 centered models 4–6 likewise as a function of parameters  ,
, 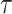 , and
, and  , respectively.
, respectively.
For illustration consider the association of smoking at EDIC year 13 with the presence or absence of confirmed clinical neuropathy (CCN) at year 13. Among the 168 smokers, the mean intensity is 15.23 cigarettes per day and the prevalence of CCN is 65 subjects (38.7%) whereas for the 984 nonsmokers the mean intensity is 0 by definition and the prevalence is 281 subjects (28.6%). The odds ratio of CCN for smokers versus nonsmokers is 1.579 (P = 0.0084) ignoring the amount smoked.
Table 3 presents the coefficient estimates for each model. In model 1, using only the smokers 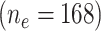 , the coefficient
, the coefficient  relating the logit of the prevalence of CCN to the quantitative smoking intensity is not significant.
relating the logit of the prevalence of CCN to the quantitative smoking intensity is not significant.
Table 3.
Logistic Regression Models of the Association of the Prevalence of Smoking Versus Not 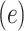 and the Smoking Intensity (
and the Smoking Intensity ( or
or  ) With the Prevalence of Confirmed Clinical Neuropathy at 13 Years of Follow-up in the Epidemiology of Diabetes Interventions and Complications Cohort, North America, Circa 2006
) With the Prevalence of Confirmed Clinical Neuropathy at 13 Years of Follow-up in the Epidemiology of Diabetes Interventions and Complications Cohort, North America, Circa 2006
| Model |
Coefficient (Factor) |
Estimate a | SE | P Value | Model χ 2 | df | P Value |
|---|---|---|---|---|---|---|---|
Noncenteredb 1: 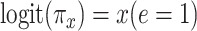
|
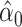
|
−0.5891 | 0.3064 | 0.0545 | 0.24 | 1 | 0.6217 |
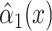
|
0.0084 | 0.0170 | 0.6217 | ||||
Noncenteredb 2: 
|
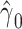
|
−0.9010 | 0.0687 | <0.0001 | 6.09 | 1 | 0.0136 |
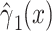
|
0.0232 | 0.0094 | 0.0136 | ||||
Noncenteredb 3: 
|
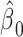
|
−0.9170 | 0.0706 | <0.0001 | 7.19 | 2 | 0.0274 |

|
0.0084 | 0.0170 | 0.6215 | ||||
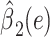
|
0.3280 | 0.3144 | 0.2969 | ||||
Centeredc 4: 
|
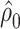
|
−0.4610 | 0.1585 | 0.0036 | 0.24 | 1 | 0.6217 |

|
0.0084 | 0.0170 | 0.6217 | ||||
Centeredc 5: 
|
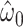
|
−0.8459 | 0.0643 | <0.0001 | 0.27 | 1 | 0.6001 |
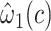
|
0.0094 | 0.0180 | 0.6001 | ||||
Centeredc 6: 
|

|
−0.9170 | 0.0706 | <0.0001 | 7.19 | 2 | 0.0274 |

|
0.0084 | 0.0170 | 0.6215 | ||||

|
0.4561 | 0.1735 | 0.0086 |
Abbreviations: df, degrees of freedom; SE, standard error.
a Estimate is the log odds ratio.
b Models with noncentered smoking intensities (x, models 1–3).
c Models with centered intensities (c, after subtracting the mean, models 4–6).
Model 2 then expresses the probability of CCN 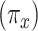 as a function of
as a function of 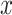 alone among all 1,152 subjects, including nonsmokers, with coefficient estimate
alone among all 1,152 subjects, including nonsmokers, with coefficient estimate 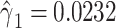 , P = 0.0136. However, as for the linear model, this coefficient estimate is biased, being almost 3-fold greater than the coefficient in model 1 owing to the inclusion of the 984 nonsmokers with intensity value zero.
, P = 0.0136. However, as for the linear model, this coefficient estimate is biased, being almost 3-fold greater than the coefficient in model 1 owing to the inclusion of the 984 nonsmokers with intensity value zero.
The mixture model 3 intercept is 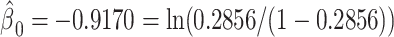 or the logit of the proportion with CCN among the nonsmokers. As in the linear model, the smoking intensity coefficient is the same,
or the logit of the proportion with CCN among the nonsmokers. As in the linear model, the smoking intensity coefficient is the same, 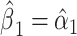 . Then,
. Then, 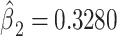 satisfies almost exactly
satisfies almost exactly 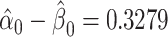 , as in the case of a linear model. Although the 2-factor model test is significant, with P = 0.0274, neither of the 1-df tests of the coefficients for the 2 components
, as in the case of a linear model. Although the 2-factor model test is significant, with P = 0.0274, neither of the 1-df tests of the coefficients for the 2 components 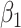 or
or 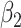 is significant, as might occasionally occur.
is significant, as might occasionally occur.
Figure 3 then shows the prevalence (probability CCN present) for nonsmokers 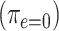 and smokers with intensity
and smokers with intensity 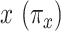 over the range of levels of intensity
over the range of levels of intensity 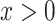 . Let
. Let 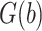 denote the inverse logit or logistic function
denote the inverse logit or logistic function 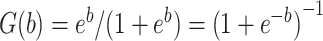 . Under the 2-factor mixture model:
. Under the 2-factor mixture model:
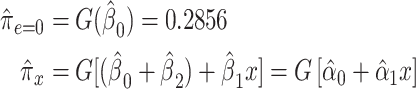 |
(11) |
for  .
.
Figure 3.

Probability of confirmed clinical neuropathy  as a logistic function of the smoking intensity
as a logistic function of the smoking intensity 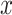 where
where 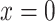 designates the nonsmoker subset of the study cohort and
designates the nonsmoker subset of the study cohort and  designates the smoking intensity among smokers, using data at 13 years of follow-up from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 2006. The figure plots the point marked by the circle = (0,
designates the smoking intensity among smokers, using data at 13 years of follow-up from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 2006. The figure plots the point marked by the circle = (0, 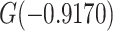 ) and the line with points (
) and the line with points ( ,
, 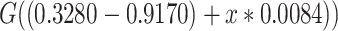 ,
,  .
.
Models 4 and 5 are nearly equivalent, as for the linear model (see Table 3). In model 6, given that the logit of the probability of CCN is the outcome, it follows that
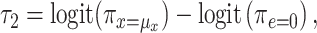 |
(12) |
which equals the log odds ratio of CCN for smokers versus nonsmokers. The model-based estimated logits of the probabilities are  and
and  with a difference that yields the estimate
with a difference that yields the estimate  . A similar computation using the logits of the simple prevalences (0.3869 versus 0.2856) yields a trivially different log odds ratio of
. A similar computation using the logits of the simple prevalences (0.3869 versus 0.2856) yields a trivially different log odds ratio of  .
.
Then a test of  is a test of the equality of the prevalence among smokers versus nonsmokers. In this example, the test of
is a test of the equality of the prevalence among smokers versus nonsmokers. In this example, the test of 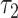 is significant whereas that of
is significant whereas that of 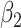 is not. As with the linear model, the coefficient
is not. As with the linear model, the coefficient 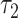 provides a more meaningful description of the difference between smokers and nonsmokers than does
provides a more meaningful description of the difference between smokers and nonsmokers than does  in the noncentered model 3.
in the noncentered model 3.
Cox proportional hazards model
Consider a Cox proportional hazards model of the association of smoking at EDIC year 2 with the time to a cardiovascular event or right censoring over 20 subsequent years of follow-up. Among the 268 smokers the mean intensity is 15.63 cigarettes per day, and 43 (16.0%) subjects were cardiovascular disease cases, whereas among the 1,026 nonsmokers the mean intensity is 0 by definition, and 107 (10.4%) were cases. The hazard ratio of cardiovascular disease for smokers versus nonsmokers is 1.63 (P = 0.007) ignoring the amount smoked.
The 3 noncentered models are:
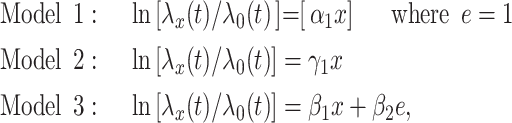 |
(13) |
and the 3 centered models 4–6 likewise as a function of parameters  ,
,  and
and 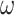 , respectively. Table 4 shows the estimated coefficients.
, respectively. Table 4 shows the estimated coefficients.
Table 4.
Cox Proportional Hazards Regression Models Relating the Prevalence of Smoking Versus Not  and the Smoking Intensity (
and the Smoking Intensity (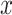 or
or  ) at 2 Years of Follow-up to the Risk (Hazard) of an Initial Cardiovascular Event in the Epidemiology of Diabetes Interventions and Complications Cohort, North America, Circa 2006
) at 2 Years of Follow-up to the Risk (Hazard) of an Initial Cardiovascular Event in the Epidemiology of Diabetes Interventions and Complications Cohort, North America, Circa 2006
| Model |
Coefficient (Factor) |
Estimate a | SE | χ 2 Value | P Value | Model χ 2 | df | P Value |
|---|---|---|---|---|---|---|---|---|
Noncenteredb 1: 
|

|
0.0109 | 0.0152 | 0.52 | 0.4726 | 0.52 | 1 | 0.4726 |
| Noncenteredb 2 |
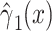
|
0.0234 | 0.0086 | 7.44 | 0.0064 | 7.44 | 1 | 0.0064 |
| Noncenteredb 3 |
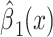
|
0.0112 | 0.0153 | 0.53 | 0.4657 | 8.08 | 2 | 0.0176 |
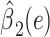
|
0.3125 | 0.3099 | 1.02 | 0.3132 | ||||
Centeredc 4: 
|

|
0.0109 | 0.0152 | 0.52 | 0.4726 | 0.52 | 1 | 0.4726 |
| Centeredc 5 |

|
0.0148 | 0.0180 | 0.68 | 0.4111 | 0.68 | 1 | 0.4111 |
| Centeredc 6 |

|
0.0112 | 0.0153 | 0.53 | 0.4657 | 8.08 | 2 | 0.0176 |
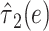
|
0.4869 | 0.1810 | 7.23 | 0.0072 |
Abbreviations: df, degrees of freedom; SE, Standard error.
a Estimate is the log hazard ratio.
b Models with noncentered smoking intensities (x, models 1–3).
c Models with centered intensities (c, after subtracting the mean, models 4–6).
As in the other analyses, the coefficient 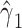 for model 2 using all subjects yields a strongly biased overestimate of the smoking intensity coefficient relative to model 1. However, this bias is reduced but not eliminated in the centered model 5.
for model 2 using all subjects yields a strongly biased overestimate of the smoking intensity coefficient relative to model 1. However, this bias is reduced but not eliminated in the centered model 5.
Because the background hazard functions for models 1 versus 3 differ, the coefficients for the smoking intensity 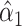 and
and 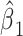 differ slightly. Centered models 4 and 6 show the same coefficient for smoking intensity as do the noncentered models 1 and 3.
differ slightly. Centered models 4 and 6 show the same coefficient for smoking intensity as do the noncentered models 1 and 3.
In models 3 and 6, the 2-factor model χ2-test yields the value 8.08 with P = 0.0176. In model 3 the tests of  and
and 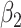 are both nonsignificant. However, in model 6, the test of
are both nonsignificant. However, in model 6, the test of 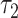 is significant, and the coefficient
is significant, and the coefficient 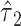 yields a hazard ratio of
yields a hazard ratio of 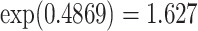 for smokers versus nonsmokers.
for smokers versus nonsmokers.
Figure 4 then presents the hazard ratio using model 6 (13) as a function of the centered smoking intensity 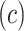 , the intercept having been absorbed into the background hazard.
, the intercept having been absorbed into the background hazard.
Figure 4.

Hazard ratio for the risk of a cardiovascular event for smokers at a given centered smoking intensity  (
(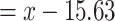 , where
, where 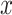 is the smoking intensity and
is the smoking intensity and 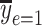 = 15.63) versus the risk among nonsmokers as an exponential function of
= 15.63) versus the risk among nonsmokers as an exponential function of 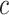 , using data at 13 years of follow-up from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 2006. This line connects the points (
, using data at 13 years of follow-up from the Epidemiology of Diabetes Interventions and Complication study, North America, circa 2006. This line connects the points (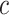 ,
, 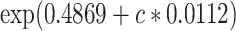 ).
).
DISCUSSION
Semiquantitative measures are often employed as risk factors in epidemiology where smoking and other exposures are common. Such variables are a mixture of a binary component (e, exposed versus not) and a quantitative component x for those exposed. Thus, statistical models should employ terms for both components to capture the full influence of the exposure variable.
However, a common approach is to use the exposure 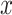 as a single covariate in a model with values zero for those not exposed (model 2 herein). For example, a recent article assessed the association of smoking intensity (packs per day) separately among current and former smokers with the risk of coronary heart disease outcomes using the Cox proportional hazards model. They reported that “One pack per day significantly increased the risk of incident coronary heart disease in current smokers compared with never smokers (HR 1.45 [95% CI 1.15, 1.84])” (4, p. 2580). However, this interpretation is incorrect. This is not the hazard ratio comparing current smokers with nonsmokers but rather an estimate of the hazard ratio of coronary heart disease per pack per day where the hazard ratio for a smoker of 1 pack per day versus a nonsmoker is assumed to be the same as the hazard ratio for a smoker of 2 versus 1 pack per day, or 11 versus 10, etc. This is implausible. Rather, one might expect that there is a fundamental difference in risk for smokers versus nonsmokers in addition to the difference in risk associated with an increase in the smoking intensity (i.e., that the 2-factor model is correct). In this case, the estimate of the coefficient for the smoking intensity (log hazard ratio per unit intensity) in a model with intensity as the only factor (with value zero for nonsmokers), that is, model 2 above, is biased compared with a model restricted to only include current smokers (model 1 above).
as a single covariate in a model with values zero for those not exposed (model 2 herein). For example, a recent article assessed the association of smoking intensity (packs per day) separately among current and former smokers with the risk of coronary heart disease outcomes using the Cox proportional hazards model. They reported that “One pack per day significantly increased the risk of incident coronary heart disease in current smokers compared with never smokers (HR 1.45 [95% CI 1.15, 1.84])” (4, p. 2580). However, this interpretation is incorrect. This is not the hazard ratio comparing current smokers with nonsmokers but rather an estimate of the hazard ratio of coronary heart disease per pack per day where the hazard ratio for a smoker of 1 pack per day versus a nonsmoker is assumed to be the same as the hazard ratio for a smoker of 2 versus 1 pack per day, or 11 versus 10, etc. This is implausible. Rather, one might expect that there is a fundamental difference in risk for smokers versus nonsmokers in addition to the difference in risk associated with an increase in the smoking intensity (i.e., that the 2-factor model is correct). In this case, the estimate of the coefficient for the smoking intensity (log hazard ratio per unit intensity) in a model with intensity as the only factor (with value zero for nonsmokers), that is, model 2 above, is biased compared with a model restricted to only include current smokers (model 1 above).
Conversely, a simple univariate regression model among those exposed (model 1 above) provides an unbiased estimate of the slope of the outcome 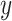 versus the level of exposure
versus the level of exposure 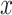 . The estimated slope is also the same in a 2-factor model with an additional binary variable for exposed versus not and an intensity value zero for the nonexposed (model 3). The coefficient
. The estimated slope is also the same in a 2-factor model with an additional binary variable for exposed versus not and an intensity value zero for the nonexposed (model 3). The coefficient 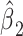 for exposure versus not in this model is the difference between the intercept of model 1 and the mean value of the outcome
for exposure versus not in this model is the difference between the intercept of model 1 and the mean value of the outcome 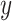 among the nonexposed (See Figure 1), and
among the nonexposed (See Figure 1), and  when the two are equal. Thus,
when the two are equal. Thus, 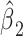 in model 3 is not a very meaningful quantity.
in model 3 is not a very meaningful quantity.
Often the quantitative component is centered by subtracting the mean of 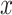 among the exposed from the value for each exposed subject, while retaining the value zero for nonexposed subjects. The resulting coefficient for the centered intensity
among the exposed from the value for each exposed subject, while retaining the value zero for nonexposed subjects. The resulting coefficient for the centered intensity 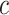 in the centered models 4 and 6 is the same as that for the noncentered intensity
in the centered models 4 and 6 is the same as that for the noncentered intensity 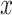 in the noncentered models 1 and 3, as are the standard error and P values. Further, the 2-df model F tests are the same in the noncentered model 3 and the centered model 6.
in the noncentered models 1 and 3, as are the standard error and P values. Further, the 2-df model F tests are the same in the noncentered model 3 and the centered model 6.
As described above, the coefficient for the intensity 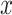 in the noncentered model 2 with all subjects (and value 0 for nonsmokers) is biased relative to the coefficient in models 1 and 3 (as well as for
in the noncentered model 2 with all subjects (and value 0 for nonsmokers) is biased relative to the coefficient in models 1 and 3 (as well as for 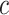 in models 4 and 6). However, the like centered model 5 provides an unbiased estimate of the coefficient for
in models 4 and 6). However, the like centered model 5 provides an unbiased estimate of the coefficient for 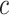 equal to that in these other models. Nevertheless, we also show that the estimated coefficients for other covariates added to this model might still be biased. Essentially, if there is an overall difference between the exposed versus nonexposed, such that the 2-factor model is correct, then fitting a model with only the centered exposure and other covariates is a misspecification with an important omitted covariate (exposed versus not) such that the estimated coefficients for the other covariates are then biased.
equal to that in these other models. Nevertheless, we also show that the estimated coefficients for other covariates added to this model might still be biased. Essentially, if there is an overall difference between the exposed versus nonexposed, such that the 2-factor model is correct, then fitting a model with only the centered exposure and other covariates is a misspecification with an important omitted covariate (exposed versus not) such that the estimated coefficients for the other covariates are then biased.
Further, the coefficient for exposure versus not  in the centered 2-factor linear model 6 equals the mean difference of the outcome
in the centered 2-factor linear model 6 equals the mean difference of the outcome  for those exposed versus nonexposed. This is a much more useful quantity than is the coefficient estimate
for those exposed versus nonexposed. This is a much more useful quantity than is the coefficient estimate 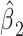 in the noncentered model 3 (see Figures 1 and 2).
in the noncentered model 3 (see Figures 1 and 2).
The same general results apply to a logistic regression model where the centered model coefficient  for the binary component is the model-based log odds ratio of the outcome for those exposed versus nonexposed, and to a Cox proportional hazards model where
for the binary component is the model-based log odds ratio of the outcome for those exposed versus nonexposed, and to a Cox proportional hazards model where 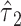 is the overall log hazard ratio for smokers versus nonsmokers.
is the overall log hazard ratio for smokers versus nonsmokers.
Thus, in general, a 2-factor model analysis with centered values for a semiquantitative variable (model 6 above) is recommended to assess the contributions of both the binary component (exposed versus not) and the quantitative component jointly, and to test the significance of the 2 components individually and jointly. Further, the coefficient 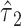 for exposure versus not has the appealing property of comparing the outcome for those exposed versus not. This model will also provide unbiased estimates of the coefficients for other covariates added to the model.
for exposure versus not has the appealing property of comparing the outcome for those exposed versus not. This model will also provide unbiased estimates of the coefficients for other covariates added to the model.
Further, the 2-df F test above in model 6 (or model 3) provides a joint test of the total association of an exposure with the outcome. If that test is significant at level 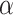 , then under the closed testing principle (12), additional tests of
, then under the closed testing principle (12), additional tests of  and
and 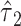 can also be tested at the same level
can also be tested at the same level  without the need for a correction for 2 tests. The same tests using the noncentered model 3 would be identical.
without the need for a correction for 2 tests. The same tests using the noncentered model 3 would be identical.
Robertson et al. (13) described 2-factor logistic models for a case-control study to capture a nonlinear association of the quantitative component with the outcome. Greenland and Poole (14) debated whether the nonexposed should be included and suggested a “practical compromise” that would fit the equivalent of models 2 and 3 above. However, we show that inclusion of the nonexposed with value zero in model 2 is ill-advised because it leads to a biased estimate of the slope.
A semiquantitative variable has also been called a variable with a “spike at zero.” Authors have described various approaches to model the association of the quantitative (nonzero) component with the outcome as nonlinear functions, such as fractional polynomials (15–17). Some have used the binary component to represent the nonexposed (=1) versus the exposed (=0). In terms of the notation herein this yields the centered 2-factor linear model
 |
(14) |
Compared to the centered model 6, 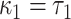 and
and  so that
so that 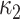 is the difference between the mean outcome among nonexposed minus exposed.
is the difference between the mean outcome among nonexposed minus exposed.
Recently Lorenz et al. (18) also compared models with linear trends versus nonlinear fractional polynomials and showed that the latter, in general, provide better fit than simple models equivalent to models 2 and 3 herein. However, their focus was on the deviance of the fit of different dose-response models, not the interpretation of the coefficients. Similar results would apply to other “model-free” methods to describe the association of the outcome with the quantitative exposure such as regression splines.
In the present work, we have assumed that the association between the outcome and the intensity among those exposed is captured by a linear risk gradient. In practice it would be prudent to also employ model-free methods to describe the pattern or nature of the risk gradient and to then employ a model with a risk gradient that best fits the observed data. In doing so, however, it is important to start with an unbiased model such as the simple model 1 restricted to those exposed, or the 2-factor model 6 (or 3). This is especially important when the analysis is attempting to establish the causal association of the exposure with the outcome.
In conclusion, we have described the properties of different simple models to assess the association of a semiquantitative exposure with an outcome, and describe the benefits of employing separate coefficients to represent the influence of the binary component for any exposure versus not and the influence of the quantitative level of exposure. Such a model provides an unbiased assessment of the overall effect of the exposure. Further, when the quantitative exposure values are centered, the coefficient for the binary component then equals the difference in the outcome between the exposed versus not, either in the means of a quantitative outcome, the logits of a probability (or log odds ratio) for a binary outcome in a logistic model, or the log hazard ratio for a Cox proportional hazards model of lifetimes. Further, in a centered 2-factor model, the coefficient estimates for other covariates are unbiased. Thus, the preferred approach is model 6 with a binary variable to represent exposure versus not and a centered quantitative covariate to represent the amount of exposure (with value zero for the nonexposed), and other covariates of interest.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: The Biostatistics Center, Department of Biostatistics and Bioinformatics, Milken Institute School of Public Health, George Washington University, Rockville, Maryland (John M. Lachin, Ionut Bebu, Barbara Braffett); Department of Biostatistics and Bioinformatics, Milken Institute School of Public Health, George Washington University, Rockville, Maryland (John M. Lachin, Ionut Bebu); and Department of Epidemiology, Milken Institute School of Public Health, George Washington University, Rockville, Maryland (Barbara Braffett).
This work was partially supported by the National Institute of Diabetes and Digestive and Kidney Diseases of the National Institutes of Health (U01-DK-094176 and U01-DK-094157) for the Diabetes Control and Complications Trial/Epidemiology of Diabetes Interventions and Complications study.
The data from the Diabetes Control and Complications Trial/Epidemiology of Diabetes Interventions and Complications study were supplied by the National Institute of Diabetes and Digestive and Kidney Diseases Central Repositories. All data files are available from the National Institute of Diabetes and Digestive and Kidney Diseases Repository database (https://repository.niddk.nih.gov/studies/edic/?query=dcct).
This manuscript was not prepared under the auspices of the Diabetes Control and Complications Trial or Epidemiology of Diabetes Interventions and Complications study and does not represent analyses or conclusions of the Diabetes Control and Complications Trial/Epidemiology of Diabetes Interventions and Complications study group, the National Institute of Diabetes and Digestive and Kidney Diseases Central Repositories, or the National Institutes of Health.
Conflict of interest: none declared.
REFERENCES
- 1. Lachenbruch PA. Analysis of data with clumping at zero. Biom Z. 1976;18(5):351–356. [Google Scholar]
- 2. Lachenbruch PA. Comparison of two-part models with competitors. Stat Med. 2001;20(8):1215–1234. [DOI] [PubMed] [Google Scholar]
- 3. Tobin J. Estimation of relationships for limited dependent variables. Econometrica. 1958;26(1):24–36. [Google Scholar]
- 4. Feodoroff M, Harjutsalo V, Forsblom C, et al. Dose-dependent effect of smoking on risk of coronary heart disease, heart failure and stroke in individuals with type 1 diabetes. Diabetologia. 2018;61(12):2580–2589. [DOI] [PubMed] [Google Scholar]
- 5. Leffondré K, Abrahamowicz M, Siemiatycki J, et al. Modeling smoking history: a comparison of different approaches. Am J Epidemiol. 2002;156(9):813–823. [DOI] [PubMed] [Google Scholar]
- 6. Pandeya N, Williams GM, Sadhegi S, et al. Associations of duration, intensity, and quantity of smoking with adenocarcinoma and squamous cell carcinoma of the esophagus. Am J Epidemiol. 2008;168(1):105–114. [DOI] [PubMed] [Google Scholar]
- 7. Kraemer HC, Blasey CM. Centering in regression analyses: a strategy to prevent errors in statistical inference. Int J Methods Psychiatr Res. 2004;13(3):141–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Royston P, Sauerbrei W. Multivariable Model-Building: A Pragmatic Approach to Regression Analysis Based on Fractional Polynomials for Modelling Continuous Variables. Chichester, United Kingdom: John Wiley & Sons Ltd.; 2008. [Google Scholar]
- 9. Becher H, Lorenz E, Royston P, et al. Analysing covariates with spike at zero: a modified FP procedure and conceptual issues. Biom J. 2012;54(5):686–700. [DOI] [PubMed] [Google Scholar]
- 10. Nathan DM, Bayless M, Cleary P, et al. Diabetes Control and Complications Trial/Epidemiology of Diabetes Interventions and Complications study at 30 years: advances and contributions. Diabetes. 2013;62(12):3976–3986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Emond MJ, Ritz J, Oakes D. Bias in GEE estimates from misspecified models for longitudinal data. Commun Stat Theory Methods. 1997;26(1):15–32. [Google Scholar]
- 12. Marcus R, Peritz E, Gabriel KR. On closed testing procedures with special reference to ordered analysis of variance. Biometrika. 1976;63(3):655–660. [Google Scholar]
- 13. Robertson C, Boyle P, Hsieh CC, et al. Some statistical considerations in the analysis of case-control studies when the exposure variables are continuous measurements. Epidemiology. 1994;5(2):164–170. [DOI] [PubMed] [Google Scholar]
- 14. Greenland S, Poole C. Interpretation and analysis of differential exposure variability and zero-exposure categories for continuous exposures. Epidemiology. 1995;6(3):326–328. [DOI] [PubMed] [Google Scholar]
- 15. Royston P, Altman D. Regression using fractional polynomials of continuous covariates: parsimonious parametric modelling. J R Stat Soc Ser C Appl Stat. 1994;43(3):429–467. [Google Scholar]
- 16. Jenkner C, Lorenz E, Becher H, et al. Modeling continuous covariates with a “spike” at zero: bivariate approaches. Biom J. 2016;58(4):783–796. [DOI] [PubMed] [Google Scholar]
- 17. Lorenz E, Jenkner C, Sauerbrei W, et al. Dose-response modelling for bivariate covariates with and without a spike at zero: theory and application to binary outcomes. Stat Neerl. 2015;69(4):374–398. [Google Scholar]
- 18. Lorenz E, Jenker C, Sauerbrei W, et al. Modeling variables with a spike at zero: examples and practical recommendations. Am J Epidemiol. 2017;185(8):650–660. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


