External validation of radiomics-based predictive models in low-dose CT screening for early lung cancer diagnosis

Abstract

Purpose:

Low-dose CT screening allows early lung cancer detection, but is affected by frequent false positive results, inter/intra observer variation and uncertain diagnoses of lung nodules. Radiomics-based models have recently been introduced to overcome these issues, but limitations in demonstrating their generalizability on independent datasets are slowing their introduction to clinic. The aim of this study is to evaluate two radiomics-based models to classify malignant pulmonary nodules in low-dose CT screening, and to externally validate them on an independent cohort. The effect of a radiomics-features harmonization technique is also investigated to evaluate its impact on the classification of lung nodules from a multicenter data.

Methods:

Pulmonary nodules from two independent cohorts were considered in this study; the first cohort (110 subjects, 113 nodules) was used to train prediction models, and the second cohort (72 nodules) to externally validate them. Literature-based radiomics features were extracted and, after feature selection, used as predictive variables in models for malignancy identification. An in-house prediction model based on artificial neural network (ANN) was implemented and evaluated, along with an alternative model from the literature, based on a support vector machine (SVM) classifier coupled with a least absolute shrinkage and selection operator (LASSO). External validation was performed on the second cohort to evaluate models’ generalization ability. Additionally, the impact of the Combat harmonization method was investigated to compensate for multicenter datasets variabilities. A new training of the models based on harmonized features was performed on the first cohort, then tested separately on the harmonized and no-harmonized features of the second cohort.

Results:

Preliminary results showed a good accuracy of the investigated models in distinguishing benign from malignant pulmonary nodules with both sets of radiomics features (i.e. no-harmonized and harmonized). The performance of the models, quantified in terms of Area Under the Curve (AUC), was >0.89 in the training set and >0.82 in the external-validation set for all the investigated scenarios, outperforming the clinical standard (AUC of 0.76). Slightly higher performance was observed for the SVM-LASSO model than the ANN in the external dataset, although they did not result significantly different. For both harmonized and no-harmonized features, no statistical difference was found between Receiver Operating Characteristic (ROC) curves related to training and test set for both models.

Conclusions:

Although no significant improvements were observed when applying the Combat harmonization method, both in-house and literature-based models were able to classify lung nodules with good generalization to an independent dataset, thus showing their potential as tools for clinical decision-making in lung cancer screening.

1. Introduction

In the past decade, several clinical trials have demonstrated the benefits of low dose CT (LDCT) screening for early detection of lung cancer, with the National Lung Screening Trial (NLST) ¹ and the Dutch-Belgian Randomized Lung Cancer Screening Trial (NELSON) studies ² demonstrating mortality reductions of 20% and 26%, respectively. These outcomes have prompted a number of medical societies to recommend LDCT screening for heavy smokers over 55 years old ^3–6. Nonetheless, questions remain about the costs of large-scale screening, the large number of images the radiologists have to deal with, and the potential over-diagnosis associated with false positive findings. Computer-aided decision support tools have been touted as a means to reduce the radiologist work-load, reduce inter-observer variation ⁷ and improve the ability of radiologists to detect pulmonary nodules ⁸.

In this context, the radiomics concept of extracting features describing tumor characteristics such as intensity, shape, and heterogeneity from medical imaging data to identify those that correlate with clinically useful outcomes, has gained prominence ^9,10. In the domain of lung cancer, radiomics-based models have been demonstrated to predict overall survival ¹¹, response to therapy ^12–15, tumor characterization ¹⁶ and malignancy identification ^17–21. Of the radiomics-based applications proposed in the literature to classify benign from malignant lesions in lung cancer ^17–21 however, few have been externally validated to evaluate their generalizability to datasets independent from the ones used for training ²². External validation is important in demonstrating the feature robustness ²³ and predictive performance of the model on independent datasets ^24,25, as these are critical determinants to clinical adoption.

The multiple sources of variability in LDCT, including differences in acquisition and reconstruction parameters as well as the scanner detectors, can indeed affect model performance and robustness ²⁶, and consequently the ability of prediction models to reach the same performance on different populations. This variability could be limited, in part, by imposing homogeneous acquisition and reconstruction protocols, but this requires extensive consensus on the best practice and is challenging to apply across different patients and scanner hardware. In consequence, post-reconstruction harmonization techniques have been proposed. The most widely used harmonization techniques involve image resampling ²⁷, however methods that act directly on features have been recently introduced. Among these is the Combat model ²⁸, which was previously exploited in the field of genomics for batch effect reduction.

The aim of this work is to evaluate prediction models based on radiomics features for early identification of pulmonary nodule malignancy. Specifically, an in-house prediction model based on artificial neural network (ANN) was implemented along with an alternative model from the literature based on a support vector machine (SVM) classifier coupled with a least absolute shrinkage and selection operator (LASSO)¹⁹. Both models were validated externally on an independent dataset and compared with the clinical standard defined on the American College of Radiology (ACR) Lung CT Screening Reporting and Data System (Lung-RADS) ²⁹. We further examine the effectiveness of the Combat model ²⁸, a state-of-the-art harmonization method, in limiting the impact of inter-scanner and acquisition setting variability.

2. Materials and Methods

2.A. Datasets

In this study, we use two independent patient cohorts.

The first cohort (Cohort-1), used as the training set, consisted of scans from a 110 patient subset of the COSMOS study dataset ^30,31 of the Istituto Europeo di Oncologia (IEO, Milano, Italy). This study was approved by the local ethical committee who waived the requirement for additional patient consent for re-analysis of this data.

The second cohort (Cohort-2), used as a testing set for external validation, was the subset of 72 cases from the publicly available LIDC dataset ³², previously reported in the work by Choi et al. ¹⁹.

In each CT scan, at least one pulmonary nodule was identified, and a binary tumor mask defined. Binary masks for Cohort-1 patients were manually contoured by a single radiologist. For Cohort-2, at least one annotation performed by an expert radiologist was available; when more than one contour per lesion was present, a consensus contour was defined by using simultaneous truth and performance level estimation^19,33.

Images had an in-plane dimension of 512 × 512 voxels for both cohorts, and while CT acquisition and reconstruction settings were different between the cohorts, similar inconsistencies were also present within each cohort. CT scans of Cohort-1 were acquired using a tube peak potential equal to 100 kV, 120 kV or 140 kV for 2, 49 and 59 subjects, respectively, whereas the tube current was fixed at 30 mA. In this cohort, all CT scans were reconstructed with a standard convolution kernel and a fixed slice thickness of 2.5 mm, while in-plane resolution ranged between 0.57 and 0.87 mm. For Cohort-2, tube current ranged between 80 and 570 mA while the tube peak potential was fixed at 120 kV, except one case that was 140 kV ¹⁹. The CT scans were reconstructed with “standard/non-enhancing” (43 subjects), “slightly enhancing” (17 subjects) or “over enhancing” (12 subjects) convolution kernels. Slice thickness ranged from 1.0 mm to 2.5 mm while in-plane pixel size ranged from 0.54 to 0.89 mm.

Distinctions between the two cohorts were also found in lesion size (maximum diameters) and attenuation characteristics (solid, part-solid and non-solid). Table I summarizes the clinical and imaging properties of pulmonary nodules in each cohort. A total of 113 lesions (58 malignant and 55 benign) were present in Cohort1 and 72 (41 malignant and 31 benign) in Cohort-2. Fig. 1 shows an example of lung nodules from Cohort-1.

Table I.

Clinical and imaging characteristics of pulmonary nodules in the training (Cohort-1) and testing (Cohort-2) cohorts, subdivided by size and type.

		Cohort-1 Training set		Cohort-2 External validation set
		Benign	Malignant	Benign	Malignant
Nodule size	<= 6 [mm]	9	0	8	4
	>6 to <=8 [mm]	5	9	10	4
	>8 to <=15 [mm]	34	31	8	7
	>15 [mm]	7	18	5	26
Nodule type	non-solid	1	6	0	0
	part-solid	6	11	4	11
	solid	48	41	27	30

Fig 1.

Representative pulmonary nodules considered from Cohort-1 illustrating the cases of solid nodules on figures a), b) and c), while examples of non-solid nodules can be observed in figures d)-e) and f). The maximum diameter of the six cases were equal to 12mm, 9mm, 12mm, 9mm, 19mm and 18mm, respectively.

As performed in Choi et al. ¹⁹ for Cohort-2, a Lung-RADS categorization was also performed for Cohort-1 relying on an expert radiologist’s annotation of lesion size, nodule type, presence/absence of calcification, internal tissue type and other imaging findings (contours irregularity).

2.B. Feature extraction

Before feature extraction, images and correspondent binary tumor masks were resampled to an isotropic voxel dimension of 1×1×1 mm.

Feature extraction was performed with a publicly available tool (https://github.com/taznux/radiomics-tools) for Cohort-1 and Cohort-2 considering the same set of 129 features used in Choi et al. ¹⁹. These features consisted of: 35 (3D) and 18 (2D) shape features, 14 (3D) and 8 (2D) shape intensity features, 9 (3D) and 9 (2D) first order histogram features, and 35 texture features. (Refer to Section 2.5 for details on feature harmonization).

For each feature, statistical power in distinguishing benign from malignant nodules was evaluated using the Wilcoxon rank sum test (alpha=5%).

2.C. ANN model definition and training

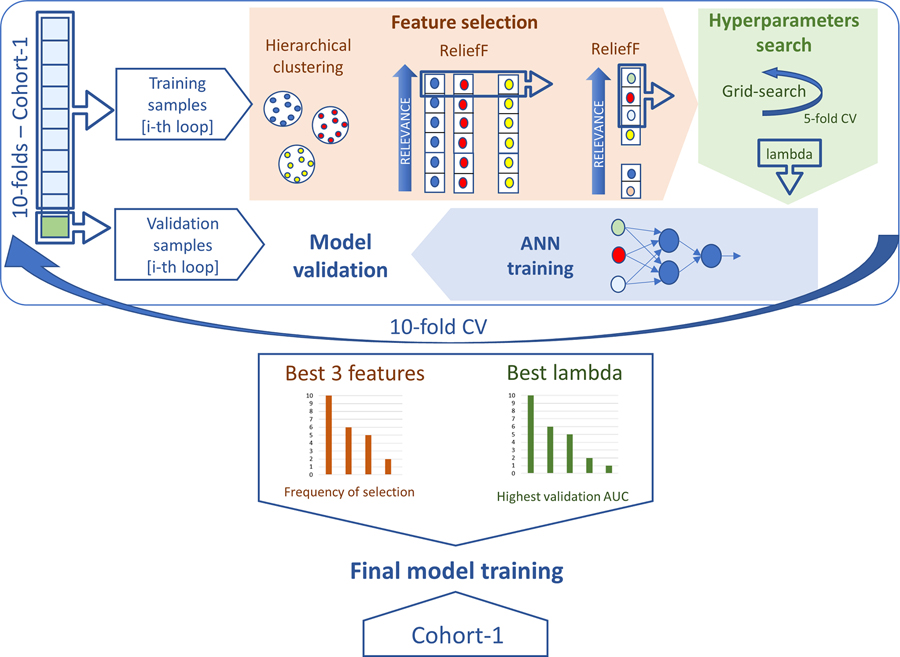
For the in-house ANN model, implemented in Matlab ® (version 2018a), we first performed feature selection and hyperparameter tuning through a 10-folds cross-validation (10-fold CV). After this, the most stable features and best hyperparameters were chosen to train the final model. An explanation of the methodology employed during 10-fold CV to train the model on Cohort-1 is given below and outlined in Fig. 2. Additional details are reported in Supplementary Material A.

Fig 2.

ANN model training. Schematic representation of the methodology adopted in the 10-fold CV to determine the most stable features and the best hyperparameters used to train the final ANN on the complete set of Cohort-1 samples.

The proposed feature selection approach entailed the combination of an unsupervised and a subsequent supervised feature selection technique. Correlation-based hierarchical clustering was first applied to the input set of 129 features, with a threshold at 0.85 ¹⁹. Then, the ReliefF supervised ranking algorithm was employed to filter correlated features inside each cluster, then the highest-ranking feature was selected. The ReliefF algorithm was chosen for its ability to distinguish features that are predictive while simultaneously take into account inter-dependency among attributes ³⁴.

The three best-performing features in the training set were then used as input for tuning the hyperparameters of a shallow neural network whose architecture was established a-priori. The feed-forward ANN ³⁵ was defined with a single hidden layer where the two inner neurons and the single output neuron were represented by a ReLU (Rectified Linear Unit) and a sigmoidal activation function, respectively. This architecture was defined experimentally by evaluating different combinations of input and hidden neurons for an ANN with a single and two hidden layers. As no relevant improvements were found increasing the net complexity with an additional hidden layer (see Supplementary Material B) the single hidden layer ANN was adopted.

To avoid overfitting of the network, large weights were penalized through L2 regularization. The regularization parameter lambda was therefore the only hyperparameter to be defined. For this purpose, a two-step grid search approach was adopted (see Supplementary Material A), consisting of a 5-fold CV repeated twice. The first 5-fold CV provided a temporary regularization lambda chosen as the value from a logarithmic scale corresponding to the best performance in terms of area under the curve (AUC) of the receiver-operator-curve (ROC). The definitive lambda value of the i-th 10-fold CV loop was established with the same metric after the second 5-fold CV, repeated for each possible lambda values chosen on a linear scale around the temporary regularization lambda.

After feature selection and hyperparameter definition, the ANN model was trained on the current set of training samples and then applied to the validation samples within the i-th 10-fold CV.

The above pipeline was performed for each loop of the 10-fold CV, after which the definitive feature set and hyperparameters were established. Definitive features corresponded to those most frequently selected among the 10-fold CV loops, while, as the overall definitive lambda value, we selected the regularization parameter that resulted in the best performance in the 10-fold CV validation sets. With the definitive features and hyperparameters, a repeated 10×10-fold CV was performed to evaluate the model in Cohort-1. The final model was finally trained on the complete set of samples involved in the 10-fold CV and then externally validated on Cohort-2.

2.D. SVM-LASSO literature model

A literature-based model was also evaluated. Specifically, the SVM-LASSO workflow proposed by Choi et al.¹⁹was adopted, as it makes use of the same set of radiomic features as for training the ANN model. The SVM-LASSO model consists in the following steps: after a preliminary feature selection with hierarchical clustering, the best feature set was established applying a repeated 10-fold CV where, inside each loop, a LASSO selector refined the search of best features, followed by the support vector machine training. The features more frequently selected in the 10-fold CV were then used to train the final model on the entire training set samples. For more details on the SVM-LASSO model, readers are referred to Choi et al.¹⁹.

2.E. Experiments

2.E.1. Feature harmonization

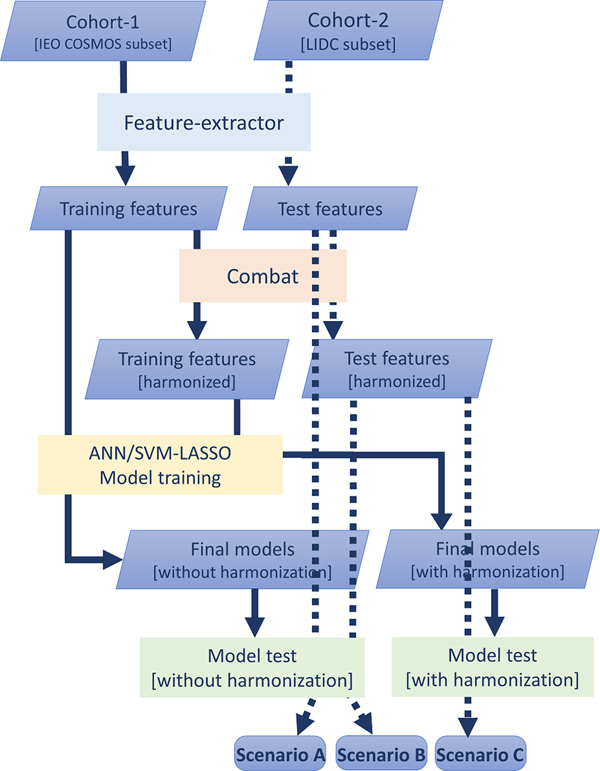
For harmonization between the training and external-validation sets, assuming the absence of inhomogeneities between samples of the same cohort, the Combat method was applied to the features, thus producing a second set of features for each cohort ²⁸ (Fig. 3, orange box). The entire procedure of feature selection, hyperparameter definition, and final model training was repeated on the harmonized features of Cohort-1 for both the ANN and SVM-LASSO model (Fig. 3, yellow box).

Fig 3.

Workflow for external validation. Features extracted from the Cohort-2 are used to externally validate the model trained with no-harmonized features of Cohort-1 (Scenario A). External-validation harmonized features, obtained after Combat application, are used to both models: scenario B refers to the external validation performed with the model trained with no-harmonized features, whereas scenario C represents the external validation of the model trained with harmonized features coming from Cohort-1. Feature extraction (blue box) made use of publicly available tools and was common to both training and external-validation data across cohorts. Model definition and training (yellow box) are described in Fig.2. The green boxes represent the external validation with the three different scenarios. The solid lines follow the training set path, while dashed lines track the external validation process.

According to the Combat method, each feature y measured in a ROI j, and related to a scanner i, can be described as follows:

$$y_{ij}=\alpha +X_{ij}\beta +{\gamma }_i+{\delta }_i{\epsilon }_{ij}$$

where α is the mean value of feature y, X_ij the design matrix of the covariates of interest, β the regression coefficients associated to each covariate, γ_i the additive effect of scanner i on features, δ_i the multiplicative scanner effect and ε_ij the error term.

The harmonization process consists in estimating, using empiric Bayes estimates, the parameters ${\gamma }_i^{*}$ and ${\delta }_i^{*}$ and applying the following transformation, based on the batch effect observed for feature y:

$$y_{ij}^{Combat}=\frac{y_{ij}-\widehat{\alpha }-X_{ij}\widehat{\beta }-{\gamma }_i^{*}}{{\delta }_i^{*}}+\widehat{\alpha }+X_{ij}\widehat{\beta }$$

where $\widehat{\alpha }$ and $\widehat{\beta }$ are estimates of parameters α and β. In our case, the only batch effect considered was the difference in cohort and the term X_ijβ was neglected, leaving out any covariate (e.g. malignancy).

To apply the Combat harmonization, we adopted the public available Matlab implementation (https://github.com/Jfortin1/ComBatHarmonization/) proposed by Fortin et al. ³⁶.

To statistically evaluate the effect of feature harmonization on models’ predictive power, Wilcoxon rank sum test (alpha=5%) was used (Section 2.2). Additionally, for features involved in final model training, Wilcoxon was applied also to compare distributions of the whole set of harmonized features with no-harmonized ones.

2.E.2. External validation

External validation of the models was performed considering the same subset of 72 nodules from the LIDC dataset³² used in Choi et al. ¹⁹. For this purpose, each model was applied considering the subset of the no-harmonized selected features, along with the harmonized features derived by the Combat feature harmonization technique ²⁸, to evaluate if an improvement in model generalizability can be appreciated using harmonized features.

Three external validation scenarios were therefore considered (Fig. 3) for both ANN and SVM-LASSO models. In the first case, the model trained on no-harmonized features of Cohort-1 was applied to the no-harmonized features of Cohort-2 (Scenario A). In the second scenario, the same model was applied to the harmonized-features of Cohort-2 (Scenario B). In the third, the model based on harmonized features for Cohort-1 was applied to the harmonized features of Cohort-2 (Scenario C).

For each validation, we evaluated AUC (95% confidence intervals, CI), accuracy (Acc), false positive rate (FPR) and true positive rate (TPR). Additionally, the difference between cross-validation and external validation was evaluated through DeLong test³⁷ (alpha=5%) and McNemar ³⁸ test (alpha=5%) for ROC curves (AUC) and frequencies comparison, respectively. The same test analyses were also used to compare the performance of the ANN model versus the SVM-LASSO model. Comparison with a clinical model

The two radiomics-based models were finally compared to a clinical model, to demonstrate the higher predictive power of radiomics features in malignancy identification with respect to the actual clinical standard. A logistic regression was applied adopting as predictors Lung-RADS categorizations. Performance was evaluated in terms of AUC, Acc, FPR and TPR. Additionally, ROC curves were statistically compared with that found for ANN and SVM-LASSO relying on De Long³⁷ test (alpha=5%), while frequencies relying on Mc Nemar³⁸ test (alpha=5%).

3. Results

3.A. ANN model performance

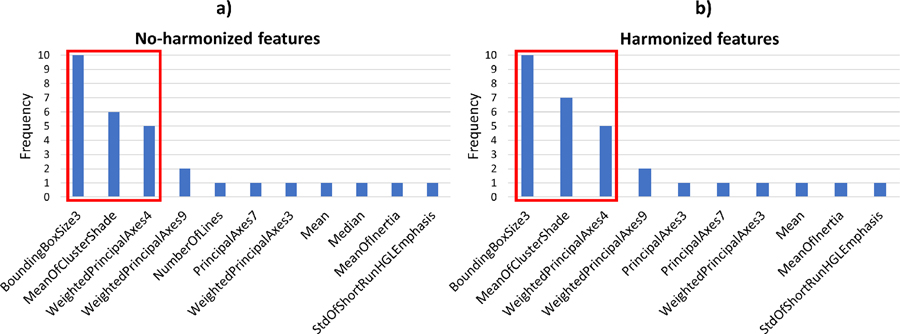
In the case of the ANN workflow, the features selected by the feature selection process were the same for training on both the no-harmonized and harmonized features. The three best-performing features (i.e. those with the highest predictive power in the feature selection phase) were statistically different for both training and external-validation cohorts when comparing their distributions without or with feature harmonization (Wilcoxon rank sum test, p<0.05). Specifically, during the 10-fold CV, “BoundingBoxSize3” (bounding box size in anterior/posterior direction), “MeanOfClusterShade” and “WeightedPrincipalAxes4” were the best-performing features and they were selected 10/10, 6/7 and 5/5 times in training without/with harmonization, respectively (Fig. 4).

Fig 4.

Selection counts of features that were selected in at least one 10-fold CV-loop for ANN model. The red box indicates the three features found to be most stable for the no-harmonized features (Fig. 4a) and harmonized features (Fig. 4b).

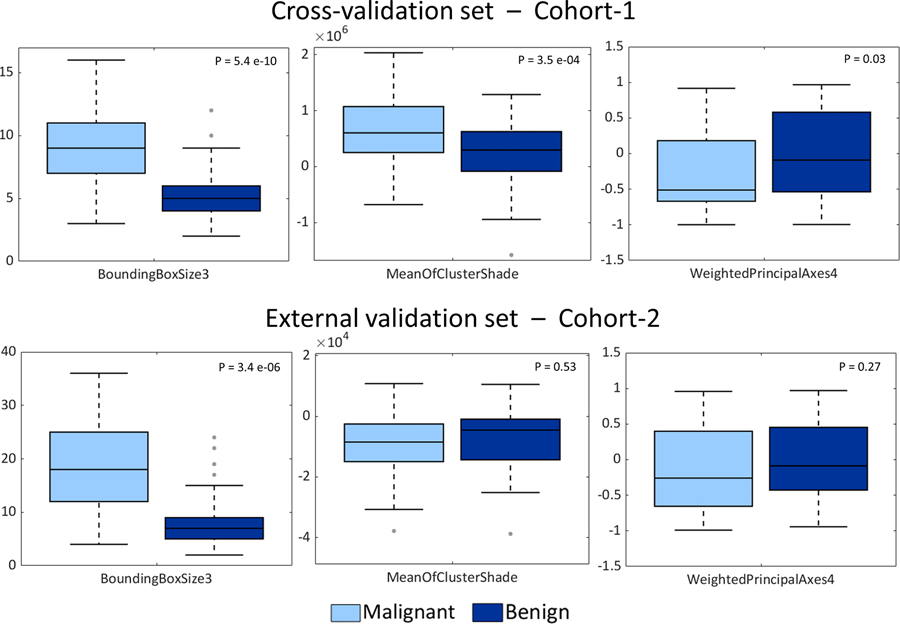
As reported in the boxplots of Fig. 5, distributions of the three no-harmonized features used to derive the final model were compared for malignant and benign nodules in both cohorts of patients. For the cross-validation set (Fig. 5, top panels), a statistical difference was found between benign and malignant nodule distributions for each of the three radiomic features. According to the Wilcoxon rank sum test (alpha=5%), p-values were <0.05 for “BoundingBoxSize3”, “MeanOfClusterShade” and “WeightedPrincipalAxes4”. However, in the external validation set, only BoundingBoxSize3 showed a statistically significant difference (p = 3.4×10⁻⁰⁶) between benign vs. malignant lesions. The same statistical test (Wilcoxon rank sum test, alpha=5%) was applied to all the 129 radiomics features considered (Supplementary Materials C).

Fig 5.

Comparison of malignant nodules and benign nodules distributions for the three selected features for ANN model: BoundingBoxSize3 (left panels), MeanOfclusterShade (central panels) and WeightedPrincipalComponent (right panels). Panels on the top are related to the cross-validation set while panels on the bottom represent distributions of external validation-set features. For each pair of distributions p-values resulted from the Wilcoxon rank sum test are reported (alpha=5%).

The ANN architecture with three input neurons and a single two-neurons hidden layer provided the best performance in malignancy identification (AUC equal to 0.89, Supplementary Materials B). The final values of regularization lambda were 0.031 (mean±std: 0.038 ±0.01) and 0.018 (mean±std: 0.03±0.01) corresponding to the highest AUC among 10-fold CV iterations for model trained on no-harmonized and harmonized features, respectively.

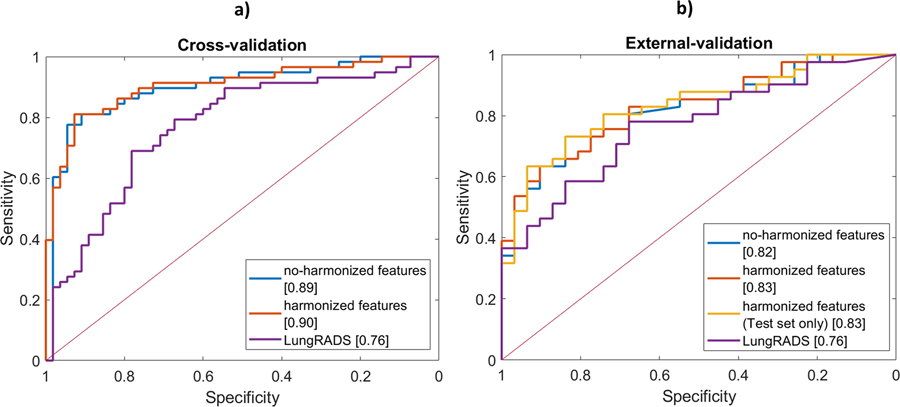
Table II reports model performance on the training and external-validation dataset in distinguishing malignant from benign nodules. ANN model performance was summarized by ROC curves for the cross-validation set (Fig. 6a), via repeated 10×10 folds CV, and for external validation set (Fig. 6b) where features and regularization lambda previously established in the 10-fold CV were kept fixed. The AUC values in 10×10 folds CV were found equal to 0.89 (CI: 0.83–0.95) with no-harmonized features, and 0.90 (CI: 0.84–0.96) with harmonized features and no significant difference was found between the two conditions^37,38.

Table II.

ANN Model prediction results in training cross-validation and the three external validation scenarios (A, B and C) in terms of area under the curve (AUC), accuracy (Acc), true and false positive rate (TPR and FPR). Performance on the training set summarizes predictions of the 10×10-fold CV loops for the model based on no-harmonized features and the one based on harmonized features.

	Cross-validation		External validation
	no-harmonized features	harmonized features	scenario A	scenario B	scenario C
AUC (95% CI)	0.89 (0.83–0.95)	0.90 (0.84–0.96)	0.82 (0.73–0.92)	0.82 (0.73–0.92)	0.83 (0.74–0.92)
Acc [%]	83.2	83.4	76.4	72.2	76.4
FPR [%]	14.9	15.8	29.0	22.6	22.6
TPR [%]	81.4	82.8	80.5	68.3	75.6

Fig 6.

ANN Model performance. ROC for training set (Cohort-1) on the left (a) and for external-validation set (Cohort-2) on the right (b).

The ROC curves were also not significantly different in the three external-validation scenarios considered. Specifically, for Scenario A (training and testing on no-harmonized features) an AUC of 0.82 (CI: 0.73–0.92) was obtained in the external dataset. Similar results were found for Scenario B (training with no-harmonized features and testing on harmonized features) and Scenario C (training and testing on harmonized features), where AUC resulted equal to 0.82 (CI: 0.73–0.92) and 0.83 (CI: 0.74–0.92), respectively. Differences in frequencies (McNemar test) were found in the external validation between Scenario A vs. Scenario B and C, as the TPR was lower (<80%) when harmonization was applied. Differences between the training set and the external-validation set for Scenario A were not significant, confirming the generalizability of the ANN model.

Compared with the Lung-RADS clinical model (Supplementary material D, Table S2), the performance of the ANN model was significantly different in cross-validation, with higher AUC and Acc (0.89 and 83.2% vs. 0.76 and 71.4%). In the external-validation set, no significant difference was found between Lung-RADS and ANN with the De Long test, although AUC improved of 8% (Acc of 14%) in the ANN model. Nevertheless, significant difference was found in terms of frequencies (McNemar test), with Lung-RADS presenting random performance for TPR (51.2% vs. 80.5% for Lung-RADS and ANN, respectively). Additional details are reported in supplementary materials D.

3.B. SVM-LASSO model performance

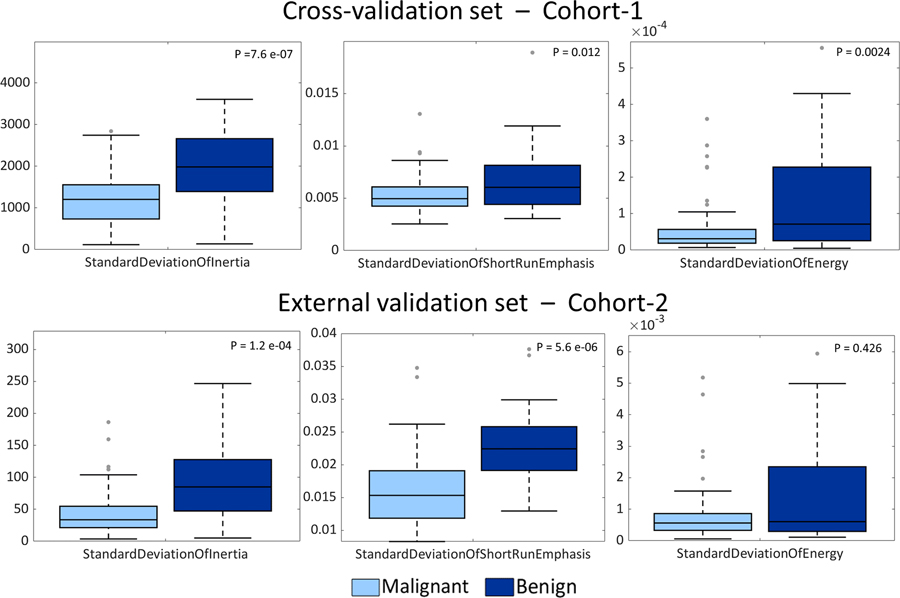
As regards the SVM-LASSO model, 5 features were selected when no feature harmonization was applied and 4 features in the case of harmonization, for the 10-folds CV. The 5 no-harmonized features selected in Scenario A were: ‘MeanOfClusterShade’, ‘WeightedPrincipalAxes4’, ‘StandardDeviationOfInertia’, ‘StandardDeviationOfShortRunEmphasis’ and ‘StandardDeviationOfEnergy’. ‘MeanOfClusterShade’ and ‘WeightedPrincipalAxes4’ were the most frequently selected features both with and without harmonization, in a fashion similar to ANN model. Excluding ‘StandardDeviationOfEnergy’, the same harmonized features were selected for Scenario C.

With respect to the ANN model, three additional features were found to have predictive power (Fig. 7). Specifically, ‘StandardDeviationOfInertia’ and ‘StandardDeviationOfShortRunEmphasis’ were statistically different for benign and malignant nodules on both Cohort-1 and Cohort-2 (Wilcoxon rank sum test, alpha=5%). ‘StandardDeviationOfEnergy’ was instead found significantly discriminative for the two groups of nodules only for Cohort-1, and it was selected for the final model training only among no-harmonized features.

Fig 7.

Comparison of malignant nodules and benign nodules distributions for the three additional features selected in the SVM-LASSO model with respect to the ANN model: StandardDeviationOfInertia (left panels), StandardDeviationOfShortRunEmphasis (central panels) and StandardDeviationOfEnergy (right panels). Panels on the top are related to the cross-validation set while panels on the bottom represent distributions of external validation-set features. For each pair of distributions p-values resulted from the Wilcoxon rank sum test are reported (alpha=5%).

SVM-LASSO model performance in terms of AUC, accuracy, FPR and TPR (Table III) was comparable with that of the proposed ANN model in the cross-validation dataset: without harmonization, AUCs were 0.90 (0.85–0.96) vs. 0.89 (0.83–0.95), whereas, with harmonized features, an AUC of 0.89 (0.84–0.95) resulted for the literature model vs. 0.90 (0.84–0.96) of the ANN.

Table III.

LASSO-SVM model prediction results in terms of area under the curve (AUC), accuracy (Acc), false positive rate (FPR) and true positive rate (TPR). Performance on the training set summarizes predictions of the 10×10-fold CV loops for the model based on no-harmonized features (“without harmonization”) and the one based on harmonized features (“with harmonization”). External-validation results are instead subdivided according to the three scenarios performed (A, B and C).

	Cross-validation		External validation
	no-harmonized features	harmonized features	scenario A	scenario B	scenario C
AUC (95% CI)	0.90 (0.85–0.96)	0.89 0.84–0.95)	0.86 (0.78–0.95)	0.86 (0.77–0.95)	0.86 (0.77–0.95)
Acc [%]	78.7	80.5	79.1	81.9	79.1
FPR [%]	21.9	20.0	35.5	25.9	32.3
TPR [%]	79.3	81.0	90.0	87.8	87.8

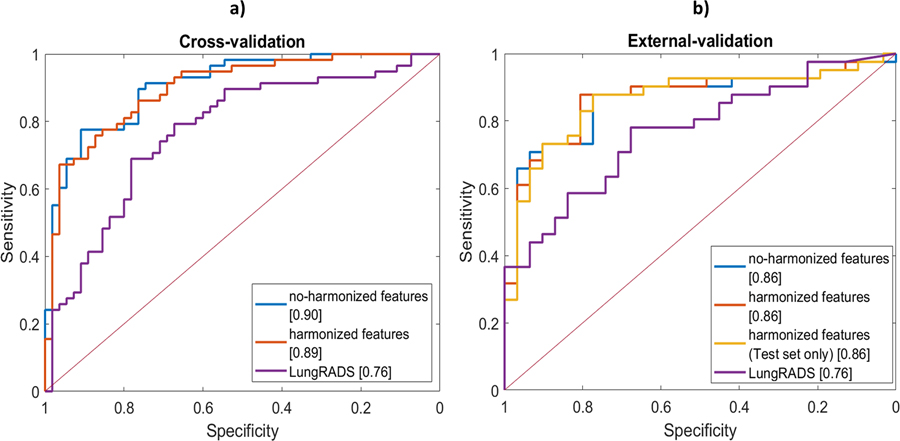
In the external validation, performance of the literature model (Table II) was slightly higher than that of the proposed ANN (Table III); both having AUCs above 0.8 and demonstrating their good generalizability. Specifically, for scenarios A, B and C, AUCs for the SVM-LASSO model improved of about 5% with respect to the ANN model. Nevertheless, for Scenario A, no significant differences (De Long and McNemar tests) were found between the two compared models (SVM-LASSO vs. ANN) in cross-validation and in external validation (Fig. 8).

Fig 8.

SVM-LASSO model performance. Comparison of ROCs with and without the use of feature harmonization for a) the training set (Cohort-1) and b) external-validation set (Cohort-2). The same ROC analysis applied to the ANN model, yielded no significant difference in ROC curves when considering harmonized features with respect to no-harmonized ones also for the SVM-LASSO model. Furthermore, no o difference was found between training set ROC curves and those related to external validation set.

In comparison with the Lung-RADS clinical model (Supplementary material D), AUC was higher for SVM-LASSO by 18% and 13% in cross-validation and external-validation, respectively. In the external validation, no significant difference was observed with the De Long test between SVM-LASSO and Lung-RADS, whereas a significant difference was found in terms of frequency (McNemar test).

4. Discussion

Differences in CT acquisition and reconstruction protocols, as well as some technical aspects that differ between scanners, can cause difficulties for the generalization of radiomics-based prediction models and their subsequent introduction in the clinical practice. This has led to increasing recognition of the importance of external validation of radiomics-based models ²⁴, and measures to transform, normalize and harmonize independent datasets, have been proposed to limit biases between scans and scanners ²⁸.

In light of these considerations, we evaluated the performance of a prediction model based on ANN, which was implemented in-house, and that of an alternative model from the literature based on a SVM-LASSO approach ¹⁹. Both models were evaluated without and with harmonization with the Combat technique of the features across the COSMOS dataset used for training the models and the LIDC dataset for their external validation. We further compared the radiomics-based ANN and SVM-LASSO models to a logistic regression based on clinical parameters using the Lung-RADS categorization criteria ²⁹.

According to the frequency with which each radiomics feature was selected, ‘BoundingBoxSize3’, i.e. the pulmonary nodule size in anterior-posterior direction, ‘MeanOfClusterShade’ and ‘WeightedPrincipalAxes4’ were chosen as features to train the ANN model. Similarly, when training the SVM-LASSO model¹⁹, ‘MeanOfClusterShade’ and ‘WeightedPrincipalAxes4’ were the features selected with the highest frequency during cross-validation, along with three additional features. Two features were therefore common to the ANN and SVM-LASSO models when trained on the same dataset. Notably, none of the features selected based on the COSMOS training data were amongst those found by Choi and colleagues ¹⁹, where the SVM-LASSO model was trained on LIDC dataset. Nevertheless, high correlation is expected between features of same type found predictive in the literature work and in the presented study (i.e. ‘BoundingBoxSize2’ with ‘BoundingBoxSize3’, ‘StardardDeviationOfInverceDifferenceMoment’ with ‘MeanOfClusterShade’ and ‘WeightedPrincipalAxes4’).

When analyzing the significance of the selected features in terms of malignant vs. benign discrimination, all the features selected in both ANN and SVM-LASSO models were able to discriminate for malignancy in the cross-validation set. However, the two most commonly selected features (i.e. ‘MeanOfClusterShade’ and ‘WeightedPrincipalAxes4’) were not significant in predicting malignancy on Cohort-2, thus resulting in (i) “BoundingBoxSize3” for ANN model and (ii) two out of five features (i.e. ‘StandardDeviationOfInertia’ and ‘StandardDeviationOfShortRunEmphasis’) for SVM-LASSO, being the most predictive features in both cohorts. This confirms the results on models’ performance, where a slightly better AUC in cross-validation was observed than in external validation, and may suggests that SVM-LASSO model can provide a more flexible feature selection than ANN model, where just one feature resulted significant in the external dataset.

Both the ANN and the SVM-LASSO model demonstrated good accuracy in predicting lung nodules malignancy for both the no-harmonized and harmonized features, achieving AUCs > 0.89 (accuracy >83% in case of no-harmonization, and >78% in case of harmonization) in the training cohort. We also examined the performance of the models on the external validation cohort, where performance was slightly reduced than the cross-validation set, with AUCs in the range of 0.82 – 0.86 (accuracy of 72–81%). The SVM-LASSO model presented slightly higher generalization ability than the ANN model, although no statistical difference was observed comparing the two models in terms of ROC curves and frequencies.

In general, this level of performance is comparable to works present in literature. Liu et al. (2017) ²² is one of the few works where validation was done considering a cohort coming from a different center; an AUC of 0.80 (accuracy = 74%) was obtained in the external validation of a model consisting of four features identified through a logistic regression model. In the NLST dataset ³⁹, divided in two cohorts for validation, different radiomics-based machine learning algorithms were compared and an AUC of 0.83 was reached combining 23 features through a Random forest model. Tu and colleagues (2018)²⁰ achieved an AUC of 0.80 but they did not perform an external validation. In the study by Choi et al.¹⁹ in which the SVM-LASSO model was trained on the LIDC dataset reported an AUC of 0.89, which was matched in our study when the model was trained on the COSMOS dataset.

Data harmonization did not yield significant improvements in the models’ performance during training, even though harmonized features were statistically different from the no-harmonized ones (Wilcoxon test, alpha=5%). Similarly resulted in the external-validation set, where no increased performance was observed in terms of AUC, Acc and TPR when harmonization was applied (Scenario A vs. Scenarios B and C). Independently from harmonization, cross-validation and external-validation (Scenario A) weren’t statistically different, attesting the models’ capability to predict lesion malignancy on both the COSMOS dataset and the independent LIDC dataset.

The comparison with the clinical model demonstrated the higher predictive power of radiomics features with respect to clinical ones. In the cross validation set, ANN and SVM-LASSO resulted significantly different from Lung-RADS, with improved AUC/Acc with respect to 0.76/71.4% for the clinical model. In the external validation, no statistical difference was found between the clinical model ROC curve and those of the three scenarios considered for both radiomics-based models (De Long test), although an improvement in AUC of 7% and 13% was quantified for ANN and SVM-LASSO. The significant difference between the radiomic-based models and the clinical one in the external validation was instead confirmed in terms of frequencies (Mc Nemar test), with the clinical model presenting a random performance in malignancies identification (TPR of 51.2% vs. > 80% for ANN and SVM-LASSO).

There are some limitations to the present work that need to be taken into consideration. The feature selection strategy of the ANN was less effective in generalizing to new data than the SVM-LASSO, suggesting that further improvements of the model are thus needed. About the number of samples considered in this work, with just 110 cases in the training set, there is scope for training the model on a greater number of cases. Nonetheless, the present training set is comparable or larger in size with respect to many in the literature for radiomics-based lung cancer prediction ^19,20,22. The use of additional external validation datasets to provide a more robust validation of the implemented models is also desirable. Further examination is also needed of the ability of the Combat and other approaches mitigating the effects of inter-scan and inter-scanner variability to increase generalizability of predictive model accuracy for multicentric studies. We further note that the compliance with emerging standards for feature definition of the publicly available tool we used for feature extraction is not certified ⁴⁰, we plan therefore to perform the analysis with a feature extraction tool that adheres to standardized feature definitions.

5. Conclusions

Two radiomics-based models were evaluated for lung cancer malignancy prediction in low-dose CT screening. An in-house ANN model was considered along with a literature model based on SVM-LASSO. The models were trained on a first cohort of patients and then successfully validated on an independent external dataset, achieving AUCs of >0.89/0.89 and >0.82/0.86 for ANN/SVM-LASSO models in training and external validation set, respectively. No improvements were observed when applying the Combat method to harmonize features coming from the two different datasets of patients, suggesting models’ robustness on data from different centers.