Model averaging methods for the evaluation of dose-response model uncertainty when assessing the suitability of studies for estimating risk

Abstract

This paper describes the use of multiple models and model averaging for considering dose–response uncertainties when extrapolating low-dose risk from studies of populations with high levels of exposure. The model averaging approach we applied builds upon innovative methods developed by the U.S. Food and Drug Administration (FDA), principally through the relaxing of model constraints. The relaxing of model constraints allowed us to evaluate model uncertainty using a broader set of model forms and, within the context of model averaging, did not result in the extreme supralinearity that is the primary concern associated with the application of individual unconstrained models. A study of the relationship between inorganic arsenic exposure to a Taiwanese population and potential carcinogenic effects is used to illustrate the approach. We adjusted the reported number of cases from two published prospective cohort studies of bladder and lung cancer in a Taiwanese population to account for potential covariates and less-than-lifetime exposure (for estimating effects on lifetime cancer incidence), used bootstrap methods to estimate the uncertainty surrounding the µg/kg-day inorganic arsenic dose from drinking water and dietary intakes, and fit multiple models weighted by Bayesian Information Criterion to the adjusted incidence and dose data to generate dose-specific mean, 2.5th and 97.5th percentile risk estimates. Widely divergent results from adequate model fits for a broad set of constrained and unconstrained models applied individually and in a model averaging framework suggest that substantial model uncertainty exists in risk extrapolation from estimated doses in the Taiwanese studies to lower doses more relevant to countries like the U.S. that have proportionally lower arsenic intake levels.

1. Introduction

1.1. Background

This paper describes an approach that involves the use of dose–response model averaging using multiple constrained and unconstrained models for evaluating model uncertainty. Published studies of the risk of bladder cancer (Chen et al., 2010b) and lung cancer (Chen et al., 2010a) within a large northeastern Taiwanese population that form the basis for the WHO (2011) and FDA (FDA, 2016; Carrington et al., 2013) inorganic arsenic assessments are used to illustrate the approach. The suitability of these Taiwanese studies for dose–response² analysis is uncertain due to questions around the ability to describe dose–response from levels of inorganic arsenic intake estimated for this population, 0.85 µg/kg-day for the reference groups and 2.0 µg/kg-day for the lowest exposure group (see Table 5) down to the below 0.1 µg/kg-day background levels of inorganic arsenic estimated for other populations such as the U.S. (see Section 2.4). The analysis we will describe uses dose–response model averaging methods to evaluate confidence in extrapolation to the lower doses such as those experienced in the U.S.

Table 5.

Estimated low-dose lifetime extra bladder and lung cancer risks versus dose and equivalent drinking water inorganic arsenic concentration (per 10,000)^a extrapolated from data in Chen et al. (2010a, b) using constrained and unconstrained model averaging.

Extra Risk	Average daily inorganic arsenic dose (µg/kg-day)
	0.064	0.071b	0.12	0.19	0.26	0.33	0.75	1.45
	Equivalent daily drinking water inorganic arsenic concentration (µg/L)
	1	1.5	5	10	15	20	50	100
Bladder Cancer
Constrained Models
Mean	−0.1	0.0	0.5	1.2	2.0	2.7	7.3	15.5
97.5th percentile	−0.2	0.0	1.7	4.1	6.6	9.0	23.6	47.9
Unconstrained Models
Mean	−0.5	0.0	2.7	4.8	7.0	9.0	17.7	29.5
97.5th percentile	−1.3	0.0	6.3	10.3	14.2	17.7	32.1	51.4
Lung Cancer
Constrained Models
Mean	−0.1	0.0	0.4	0.9	1.5	2.0	5.2	10.4
97.5th percentile	−0.2	0.0	1.5	3.6	5.6	7.7	19.8	39.0
Unconstrained Models
Mean	−1.1	0.0	5.3	7.6	10.0	11.9	19.4	28.4
97.5th percentile	−7.0	0.0	32.0	43.0	54.0	63.0	91.0	119

^aThese extra risk estimates are estimated based on model-estimated background rates for the constrained and unconstrained models of 4.2X10⁻³ and 2.4X10⁻³ respectively for bladder cancer and 2.3X10⁻² and 2.0X10⁻² respectively for lung cancer (Table 4).

^bTo illustrate model uncertainty when extrapolating from the Chen et al. (2010a, b) study data to much lower arsenic doses, the background level of exposure population, specifically 0.071 µg/kg-day (see Section 3.2.1).

1.2. Overview of the Chen et al. (2010b; 2010a) studies

The prospective cohort studies of bladder (Chen et al., 2010b) and lung cancer risk (Chen et al., 2010a) in 8,086 adult residents, aged 40 years and older, residing in four townships in northeastern Taiwan afford several advantages that have enticed risk assessors (Carrington et al., 2013; FDA, 2016; WHO, 2011) to use them as the basis for prominent dose–response analyses:

• A large cohort exposed for large proportions of their lifespan, including childhood, to a wide range of arsenic concentrations, principally from inorganic arsenic in drinking water; subjects were followed for a substantial period, specifically 12 years plus 2 more years in a follow-up study by Yang et al. (2013).

• The Northeastern Taiwanese population studied appeared to be adequately nourished in contrast to high-exposure areas in south-eastern Taiwan where nutritional insufficiency might have complicated the analysis of epidemiological data.

• Exposure ranges were well documented (Chiou et al., 2001). Water concentrations were measured from household wells serving over 85 percent of the study subjects; concentrations were measured at study enrollment (1991–1994), rather than relying on historical data.

• Outcome ascertainment was very reliable. Clinical outcomes were based on the 9th revision of the International Statistical Classification of Diseases and Related Health Problems (ICD-9) codes and histopathological review of cases identified in the Taiwan National Cancer Registry. Information on important covariates was gathered from all subjects, and relative risks were calculated with appropriate covariate adjustment.

• Both studies reported clinician-diagnosed cancer incidence, which is preferred over mortality data (generally collected from death certificates) for dose–response analyses (U.S. EPA, 2005).

• The prospective cohort design of these studies is amenable to relatively straightforward statistical analysis and dose–response modeling arising from the (assumed) random nature of the cancer incidence in the preselected populations with specified ranges of arsenic exposure. The studies are amenable to the use of standard maximum likelihood methods to fit dose–response functions for exploring model uncertainty.

The primary source of drinking water in the study area was arsenic-contaminated shallow wells. Shallow wells were first installed in the affected areas in the 1940s, and most of the study subjects reported that they drank well water either continuously from birth (63.5 percent) or began drinking well water after birth and continued until enrollment (34.3 percent). Arsenic concentration data were taken from the Chiou et al. (2001) study; well-water arsenic measurements, the principal component of which is inorganic arsenic (WHO, 2011; Mendez et al., 2017), were collected from 3,901 households (85 percent of subjects) at study enrollment in 1991–1994. The average duration of well-water consumption was reported to be 40.7 years (Chiou et al., 2001). Water arsenic concentration data were not provided for individual subjects, only the numbers of subjects in different exposure ranges. Chiou et al. (2001) reported the range of arsenic concentration was < 0.15–3,843 µg/L. Of the 6,888 subjects for whom water arsenic concentrations were available, approximately 33% were exposed to < 10 µg/L (referent group), approximately 30% were exposed to between 10 µg/L and 50 µg/L, about 27% were exposed to between 50 µg/L and 300 µg/L and about 10% were exposed to > 300 µg/L.

Outcome measures (numbers of subjects and cases of bladder and lung cancer by exposure stratum, raw and adjusted relative risks) as reported by Chen et al. (2010b) and Chen et al. (2010a) were used as inputs to the dose–response analyses. Subjects in these cohorts were followed for an average of 11.6 years after recruitment. The approximate average age of subjects at recruitment was 59 years. This age and follow up period are considered appropriate for this health outcome (though not necessarily all health outcomes) given the potential contribution of early life exposures and the 4 to 5 decade latent period for bladder cancer (Steinmaus et al., 2014) and the fact that the majority of this population was exposed for their entire lifespan (Yang et al., 2013).

2. Methods for dose-response analysis

Model averaging approaches were used to estimate the relationship between lifetime bladder and lung cancer probabilities (absolute risks) and intake dose in a large prospective cohort study of residents in northeast Taiwan (Chen et al., 2010b; Chen et al., 2010a). Both the bladder and lung cancer analyses employ a bootstrap methodology to incorporate uncertainty in the estimation of adjusted outcomes (cases of cancer) and estimated daily inorganic arsenic intake dose. The methodologies are similar to those employed by FDA (FDA, 2016; Carrington et al., 2013) for the same endpoints and study population. For our purposes, the differences of note have to do with model choice. Because our intention is to assess the impact of model selection on extrapolating low-dose risk from studies of populations with high levels of exposure, we considered a broader set of models, adding a Multistage model and unconstrained versions of four of the models considered by FDA (Weibull, log logistic, Gamma, and dichotomous Hill). The purpose and impact of these additional models are discussed further in Sections 2.3 and 4).

2.1. Bootstrap simulation approach

The dose–response estimation is built around a “bootstrap” methodology (Fig. 1), which uses reported variability in arsenic intake and in outcome measures to derive mean and 2.5th and 97.5th percentile risk estimates. The steps in the analysis include:

• Selection of outcome variables. For these studies, the outcome variables were cases of total bladder and lung cancer cases and adjusted relative risks, as reported by Chen et al. (2010b) and Chen et al. (2010a) for varying levels of reported water arsenic concentration.

• Adjustment of outcome (cases). To model lifetime bladder or lung cancer probability (absolute risk) versus dose, the reported partial lifetime outcomes (cases) must be adjusted to make them consistent with (1) the reported covariate adjusted risks (described below) and (2) a full lifetime of observation (see Supplemental Material, Section 1).

• Bootstrap outcome simulation. The distributions of adjusted lifetime cases of lung and bladder cancer in each of the exposure group were characterized by sampling 1,000 times from the derived distributions of covariate-adjusted cases.

• Water arsenic concentration. Data from Chiou et al. (2001) were used to estimate the best-fitting parametric (mixed lognormal) distribution to the grouped water arsenic data.

• Estimation of inorganic arsenic intake from water. Daily inorganic arsenic intakes from water were estimated by sampling from the derived arsenic concentration (estimated in the previous step) and distributions of daily water consumption. Daily water intake data for the Taiwanese adult population were derived from health survey data summarized by the Taiwan Department of Health (TDOH, 2007), adjusted for seasonality. Intake estimates were not adjusted for potential early life (infant) exposures. This adds uncertainty to the analysis given that a majority of the study population were exposed from birth (Yang et al., 2013).

• Estimation of dietary inorganic arsenic intake dose. Dietary inorganic arsenic intake dose for the adult study population was estimated from data on food consumption and arsenic concentrations in Taiwan, as described in the Supplemental Material, Section 2. Estimates were developed for foods consumed in substantial amounts for which arsenic concentration data were available.

• Bootstrap estimation of total inorganic arsenic intake dose. Average total inorganic arsenic intake dose (µg/kg-day) from water and diet was estimated by sampling 1,000 times from uncertainty distributions estimated for the mean water arsenic concentration, the mean water consumption, dietary intake of specific foods, arsenic concentration distributions in food, proportions of inorganic arsenic in food, bioavailability and body weight in each exposure stratum.

• Dose-response fitting of bootstrap samples. Data from each of the 1,000 bootstrap outcomes and inorganic arsenic intake samples were used as inputs to 9 dichotomous models (model selection is described below). For each run, the same “seed” was used; that is, in all runs, the same intake and outcome samples were selected for fitting in each iteration. Outputs of the bootstrap included estimates of goodness of fit (likelihoods), Bayesian Information Criteria (BIC) values, and Bayes weights used in model averaging.

• Model-averaged estimates of bladder and lung cancer risk. The average BIC weights from the bootstrap model were applied to estimate model-weighted lifetime risk predictions across the range of estimated inorganic arsenic intake doses. In this analysis, all models were assumed to have the same “prior” probability; that is, no models were excluded, and all models were weighted equally a priori.

Fig. 1.

Summary of dose–response methodology for bladder and lung cancer. Note: BIC = Bayesian Information Criterion.

Outputs from the bootstrap models consist of multiple risk estimates at specified inorganic arsenic intake values. The output distributions from the bootstrap provide nonparametric summaries of the overall uncertainty, incorporating reported variability in each input parameter. This bootstrap incorporates the effects of both dose uncertainty (by simulations using reported variability in intake measures) and estimated sampling uncertainty in the outcome (cases of cancer). As discussed in Section 3, not all key sources of uncertainty (e.g., the different contribution that early life [infant] exposure could make) could be incorporated into the bootstrap simulation. Most importantly, the model iterations are performed based on group mean dose and outcome distributions and, therefore, do not accurately capture other potentially important sources of individual variability in response to inorganic arsenic dose.

2.2. Input data and data sources

The following sections describe the approaches used to represent the uncertainty in the input variables to the bootstrap model.

Bootstrap estimation of water and dietary inorganic arsenic intake

Details regarding data sources and methods used to derive inputs for the bootstrap exposure and inorganic arsenic intake dose are provided as Supplemental Material (Section 2). To summarize:

• Average adult inorganic arsenic water concentrations were estimated by fitting a mixed lognormal distribution (Supplemental Material Section 2.3.2) to the drinking water concentration data from the Chen et al. cohort (Chiou et al., 2001). Distributions of drinking water consumption were estimated based on age-specific survey data for adults 40 years of age and older from the Taiwan Department of Health (TDOH, 2007).

• Consumption of foods identified as contributing substantially to total inorganic arsenic intake were likewise obtained from the Taiwan Department of Health survey data (TDOH, 2007). Inorganic arsenic concentration distributions (for rice and leafy vegetables) or central tendency estimates (tubers, pulses, meats and fish) were estimated from various studies of adults in Taiwan and other Asian countries.

As shown in Fig. 1, the estimated inorganic arsenic intake doses from water and diet were summed for each subject in each bootstrap iteration, and average total daily intake doses were estimated across each exposure group. The 1,000 sets of group average inorganic arsenic intake dose served as inputs, along with the outcome data sets, to the dose–response estimation. The mechanics of the bootstrap intake dose sampling are discussed in detail in the Supplemental Material, Section 2.5.

2.3. Model averaging approach for the estimation of lifetime probability (“Absolute” Risk)

For the modeling averaging, nine dose–response model forms were fit to each bootstrap data set, as shown in Table 1. These models vary in the degree of complexity, numbers of parameters, and ability to accommodate specific forms of the dose–response relationship. The intent in including this diverse set of models was to cover “model space” as much as was practical, and to explore “model uncertainty” as fully as possible. The models are all standard forms for dichotomous endpoints that are included in EPA’s Benchmark Dose Software (BMDS) package.³ In this analysis, models were estimated by maximizing binomial likelihood with varying constraints (i.e., using models with both constrained and unconstrained parameters), as discussed below; maximization was implemented using the R package for nonlinear minimizations subject to box constraints (nlminb) with default convergence criteria.

Table 1.

Models included in the dose–response analysis.

Model	Form	Parameters
Logistic	r(dose) = 1/(1 + exp(−a − b × dose))	2
Probita	r(dose) = pnorm(a + b × dose)	2
Quantal linear	r(dose) = a + (1 − a) × (1 − exp(−b × dose))	2
Log probita	r(dose) = a + (1 − a) × pnorm(c + b × log(dose))	3
Multistage 2	r(dose) = a + (1 − a) × (1 − exp(−b × dose − c × dosê2))	3
Gammaa,b	r(dose) = a + (1 − a) × pgamma(c × dosêb)	3
Log logisticb	r(dose) = a + (1 − a)/(1 + exp(−c − b × log(dose)))	3
Weibullb	r(dose) = a + (1 − a) × (1 − exp(−c × dosêb))	3
Dichotomous Hillb	r(dose) = v × g + (v − v × g)/(1 + exp(−c − b × log(dose)))	4

^aThe pnorm and pgamma terms refer to the standard normal and gamma probability density functions.

^bThe power or slope parameters of these models were restricted to be ≥ 1 in our “constrained” model averaging analysis, and were unrestricted in our “unconstrained” model averaging analysis (see discussion in Section 2.3).

Outputs from the bootstrap analysis included 1,000 sets of maximum likelihood parameter estimates derived for each input data set. Log likelihoods also were saved for each model and data set, and Bayesian Information Criteria (BIC) values were calculated in the usual fashion (Allen et al., 2020b):

$$BIC=-2\times \log (likelihood)+k\times \ln (n)$$ (1)

where k is the number of parameters estimated in the model and n is the number of observations, (in this case five, corresponding to the number of exposure groups).

The weights employed in model averaging were based on the calculated average BIC values for each model. Weighting allows multiple models to contribute to the dose–response estimates, taking into account their overall goodness of fit (log likelihood), penalized according to the number of estimated parameters. For each model (i), the Bayes weight (posterior probability) was calculated as:

$$Weigh{t}_i=\frac{e^{(-0.5\times BI{C}_i)}}{{\mathrm{\Sigma }}_{i=1}^9{e}^{(-0.5\times BI{C}_i)}}$$ (2)

This approach assigns approximate relative posterior probabilities that the individual models are “true” based on their penalized log likelihood (Neath and Cavanaugh, 2012). In all cases, the “prior” weights for all models were assumed 1/9; that is, no models were assumed a priori to be better or worse than any others were. This assumption could be changed if, for example, quantitative mechanistic data become available that indicate one or more of the models is inherently more or less biologically plausible than the others.

When applied individually to dose–response datasets, EPA generally recommends (U.S. EPA, 2012) that four of the nine model forms explored in this analysis (Weibull, log logistic, Gamma, and dichotomous Hill) have their slope or power parameters (“b” terms in the Table 1 equations) constrained to be > 1.0. These parameters are constrained because the individual unconstrained models can take on forms (e.g., supralinear at low doses or nonmonotonic) that are biologically improbable. In the context of model averaging, however, relaxing these constraints is unlikely to result in the extreme supralinearity (slopes that approach infinity as dose approaches 0) that can be observed for some individual models because the probability of multiple, diverse models predicting the same extreme supralinearity is low. Further, relaxing constraints in a model averaging analysis can improve overall model fits and benchmark dose (BMD) coverage by including more flexible curve shapes that can better represent the data (and possibly biology) (Wheeler and Bailer, 2009). Therefore, for our purposes (e.g., for evaluating model uncertainty using a broad set of reasonable model forms), model averaging was performed in two ways, using the EPA preferred constraints for all nine models (referred to as the “constrained” analysis) and using the same model suite with the power parameters of the Weibull, Log-logistic, Gamma and dichotomous Hill models unconstrained (referred to as the “unconstrained” analysis).

The effects of different assumptions regarding constraints on the slope or power parameters were investigated by calculating model-weighted risk estimate distributions with the parameters constrained (as traditionally) to be greater than or equal to 1.0 and with no constraint. Weighted estimates of lifetime bladder and lung cancer probabilities from the Chen et al. (2010a, 2010b) were calculated for a series of doses from 0 to 40 µg/kg-day, approximately corresponding to the range of mean total inorganic arsenic intakes observed in the bootstrap data set corresponding the study population (see Section 3.2).

2.4. Estimation of lifetime extra risk

As described in the Supplemental Material, Section 3, the lifetime probability of disease (“absolute” risk) was first estimated (Table 4) through model averaging of the full-life adjusted cases/subjects (Table 2) vs estimated intake dose from all sources (Table 3). Then extra risk estimates were calculated from these results using the risk estimated at an assumed U.S. background intake level of 0.071 µg/kg-day as the background risk level (Table 5). Extra risk (Table 6) is estimated as:

$$Extrarisk=(R(d)-R(bgd)/(1-R(bgd))$$ (3)

where R(d) is absolute risk at dose d and R(bgd) is the risk predicted at the background arsenic intake level. The U.S. background intake level was estimated by assuming zero arsenic intake from air exposures and summing the median U.S. background dietary inorganic arsenic intake of 0.05 µg/kg-day (Xue et al., 2010) with a background drinking water inorganic arsenic intake of 0.021 µg/kg-day, derived by assuming that a typical adult water intake of 0.014 L/kg-day (U.S. EPA, 2011) and a typical drinking water arsenic concentration of 1.5 µg/L (Mendez et al., 2017).

Table 4.

Estimated lifetime probability (absolute risks estimated from Taiwan cohort) of bladder and lung cancer versus dose from the weighted bootstrap models, with and without constraints on slope or power parameters, based on data from Chen et al. (2010a, b).

Predicted lifetime risks	Inorganic arsenic intake dose, µg/kg-day
	0	0.1	0.3	1	3	10	20	40
Bladder Cancer
Constrained Models
2.5th Percentile	3.8E-04	5.9E-04	1.0E-03	2.8E-03	5.0E-03	1.1E-02	1.5E-02	2.2E-02
Mean	4.2E-03	4.2E-03	4.5E-03	5.3E-03	7.9E-03	1.7E-02	2.4E-02	3.6E-02
97.5th Percentile	7.0E-03	7.1E-03	7.2E-03	7.7E-03	1.1E-02	2.8E-02	3.4E-02	5.1E-02
Unconstrained Models
2.5th Percentile	1.0E-04	7.0E-04	1.3E-03	3.0E-03	5.3E-03	1.1E-02	1.6E-02	2.3E-02
Mean	2.4E-03	3.0E-03	3.7E-03	5.1E-03	8.2E-03	1.7E-02	2.4E-02	3.5E-02
97.5th Percentile	6.3E-03	6.3E-03	6.5E-03	7.3E-03	1.1E-02	2.5E-02	3.3E-02	5.0E-02
Lung Cancer
Constrained Models
2.5th percentile	1.8E-02	1.9E-02	1.9E-02	2.0E-02	2.3E-02	2.6E-02	3.0E-02	3.9E-02
Mean	2.3E-02	2.3E-02	2.4E-02	2.4E-02	2.7E-02	3.3E-02	4.0E-02	5.5E-02
97.5th Percentile	2.8E-02	2.8E-02	2.8E-02	2.8E-02	3.3E-02	4.8E-02	5.4E-02	7.5E-02
Unconstrained Models
2.5th percentile	5.5E-03	1.3E-02	1.7E-02	1.9E-02	2.3E-02	2.6E-02	2.9E-02	3.9E-02
Mean	2.0E-02	2.2E-02	2.3E-02	2.4E-02	2.8E-02	3.4E-02	3.7E-02	5.5E-02
97.5th Percentile	2.7E-02	2.7E-02	2.7E-02	2.8E-02	3.4E-02	4.7E-02	5.1E-02	7.3E-02

Table 2.

Cases, adjusted relative risks, and adjusted cases used in the bladder and lung cancer bootstrap analysis based on cancer incidence data from Chen et al. (2010a,b).

Water inorganic arsenic concentration, µg/L	Subjects	Observed cases	Covariate adjusted relative risk	Covariate-adjusted cases	Full-life adjusted cases (simulated standard deviation)
Bladder Cancer
< 10	2288	5	1	5.0	9.8 (3.1)
10–49.9	2093	8	1.66	7.6	14.5 (3.8)
50–99.9	907	5	2.42	4.8	9.3 (3.0)
100–299.9	909	8	4.13	8.2	16.0 (3.9)
> 300	691	11	7.80	11.8	23.0 (4.7)
Lung Cancer
< 10	2288	48	1	48	53.4 (6.9)
10–49.9	2093	51	1.1	48.3	53.4 (7.0)
50–99.9	907	20	0.99	18.8	21.2 (4.6)
100–299.9	909	28	1.54	29.4	32.6 (5.7)
≥ 300	691	31	2.25	32.6	36.4 (5.8)

Table 3.

Bootstrap estimates of inorganic arsenic intake dose distributions from diet and drinking water.

Exposure group, µg/L in water	Daily inorganic arsenic intake dose from dietary sources, µg/daya							Waterd(µg/kg-day)	All sources (µg/kg-day)
	Rice	Vege-tables	Tubers	Pulsesb	Fish	Meatc	All Diet
< 10	0.38 (0.38)	0.21 (0.49)	0.01 (0.03)	0.06 (0.01)	0.06 (0.01)	0.03 (0.01)	0.7 (0.6)	0.09 (0.2)	0.85 (0.8–0.9)
10 > 49.9								1.3 (0.8)	2.0 (1.9–2.1)
50–99.9								3.2 (1.6)	4.1 (4.0–4.2)
100–99.9								8.3 (4.6)	8.9 (8.6–9.2)
300+								37.0 (37.3)	38.8 (35.9–42.0)

^aStandard deviations in parentheses

^blentils

^cbeef and pork

^ddirect ingestion and cooking water (1 gm/gm vegetables, 2 gm/gm rice consumption).

Table 6.

Distributions of predicted lifetime bladder cancer risk at 1.0 µg/kg–day based on modeled data from Chen et al. (2010a, b) with outcome and intake dose variability suppressed.

Simulation	Bootstrap estimate	Endpoint variance suppressed	Inorganic arsenic intake dose variance suppressed
2.5th percentile	3.6E–04	3.4E–03	3.6E–04
Mean	2.7E–03	3.6E–03	2.8E–03
97.5th percentile	5.2E–03	3.7E–03	5.2E–03

3. Results

3.1. Bootstrap modeling of outcomes and inorganic arsenic intake

The third and fourth columns of Table 2 show the outcome metrics, “Observed cases” and ”Covariate-adjusted relative risk,” reported by Chen et al. (2010b) for bladder cancer and by Chen et al. (2010a) for lung cancer. The bootstrap method considers simulated sampling uncertainty in outcomes by assuming that each subject in each exposure group represents a Bernoulli trial (Papoulis, 1984), with individual probabilities of getting cancer defined by the average adjusted lifetime probability of cancer in the group. Count data were adjusted to account for two important factors: 1) the effects of covariates (demographics, education level, smoking, and alcohol consumption) and 2) the lessthan-lifetime follow-up period reported in the study (see Supplemental Material, Section 1).

Table 3 shows estimates of the mean inorganic arsenic intakes from all sources in the five Chen et al. (2010b) exposure groups from a single bootstrap iteration. The estimates include contributions from both direct water ingestion and cooking water (for rice and vegetables) as well as dietary contributions from rice, vegetables, pulses (lentils), meat, and fish. The estimates span a large range, from approximately 0.85 µg/kg-day in the 0 to 10 µg/L group to 38.8 µg/kg-day for the > 300-µg/L group, whose estimated mean water concentration exposure is approximately 840 µg/L. As expected, total inorganic arsenic intake for the lowest exposure groups are primarily through diet, while the proportion of intake associated with water ingestion (direct and through cooking water) accounts for the bulk of inorganic arsenic intake in the high-exposure groups. In this analysis, inorganic arsenic concentrations in specific food items are assumed to be independent of water exposure levels; that is, while cooking water intake is modeled as a function of selected for calculating extra risks using the model averaging results from these studies was set to the estimated arsenic dose encountered by the general U.S. drinking water concentration, inorganic arsenic concentrations in foods do not vary with modeled inorganic arsenic concentration. It is assumed that no inorganic arsenic in the raw food is lost during cooking. Because the intake statistics in Table 3 are derived from a single bootstrap iteration, they incorporate the large variability and uncertainty to be expected when the individual intake estimates are derived through Monte Carlo sampling from multiple exposure factors. The mean total inorganic arsenic intake doses for the five exposure groups are very similar to those estimated by FDA (FDA, 2016), who used slightly different data sources and methods from this analysis (Supplemental Material Section 2).

3.2. Model averaging results

The results of model averaging analyses for the Chen et al. (2010b) bladder cancer and the Chen et al. (2010a) lung cancer data are summarized in this section. The Supplemental Material sections 3 and 4 provide additional details regarding the model averaging analyses.

3.2.1. Lifetime probability and extra risk of lung and bladder cancer

Both unconstrained and constrained model parameters were successfully fit to all 1,000 bootstrap iterations (the likelihood maximization routine successfully achieved specified convergence criteria). Model BIC weights varied slightly depending on whether the power parameters were constrained.

For bladder cancer, the relatively flexible dichotomous Hill model received the highest BIC weights, from 0.24 (constrained) to 0.42 (unconstrained). Roughly equivalent BIC weights were obtained for the quantal linear, log logistic, Weibull, Gamma and Multistage 2 models for both constrained and unconstrained runs. The probit, logistic, and log probit models received low BIC weights (< 0.05) for both constrained and unconstrained runs, perhaps because these model forms could not fit the slightly convex (upward) curve of the bladder cancer data.

For the lung cancer data, when power parameters were constrained, the dichotomous Hill model was assigned the highest BIC weight (0.19), and the weights assigned to the quantal linear, Probit, and logistic were between 0.14 and 0.17. When the power parameters were un-constrained, seven of the nine models (Hill, quantal linear, Probit, logistic, log-logistic, and Weibull) were assigned weights with a relatively narrow range (0.11–0.15). The log-Probit and Multistage 2 models received low BIC weights (< 0.1).

Weighted estimates of the lifetime probability of contracting bladder and lung cancer in the Chen et al. (2010a, 2010b) study population (northwestern Taiwanese cohort), derived from the constrained and unconstrained models, are summarized in Table 4. It can be seen that, within the range of the data (approximately 1–40 µg/kg-day), the predicted mean risks, 2.5th and 97.5th percentiles derived from the unconstrained and constrained models are similar. At lower doses (below the range of the data), the weighted risk estimates derived from the unconstrained models curve sharply downward compared to those from the constrained models (Figs. 2 and 3; lower plots).

Fig. 2.

Model average (left) and individual model (right) results for predicted lifetime probability (absolute risk) of bladder cancer vs. all doses (upper plots) and low doses (lower plots) using constrained (black) and unconstrained (U; red) versions of four models compared to adjusted incidence from adjusted relative risks reported in Chen et al. (2010b).

Fig. 3.

Model average (left) and individual model (right) results for predicted lifetime probability (absolute risk) of lung cancer vs. all doses (upper plots) and low doses (lower plots) using constrained (black) and unconstrained (U; red) versions of four models compared to adjusted incidence from adjusted relative risks reported in Chen et al. (2010a).

Table 5 presents the estimated lifetime extra risk estimated for bladder cancer and lung cancer, respectively, for various intake dose levels and equivalent drinking water concentrations. While the differences in lifetime probability (absolute risk) predicted by the constrained and unconstrained models are relatively small, the resultant differences in extra risk predicted by the constrained and unconstrained models are substantial for both bladder and lung cancer, particularly in the low-dose range. This is because “background risk”⁴ from which extra risks are calculated is lower for both health outcomes when the slope or power parameters are unconstrained.

4. Discussion

We have conducted a case study on the use of model averaging for the evaluation of model uncertainty. For illustrative purposes, we have performed dose–response analysis of inorganic arsenic intake doses associated with exposures reported in two studies (FDA, 2016; WHO, 2011) of lung and bladder cancer incidence in the northeast Taiwanese population (Chen et al., 2010b; Chen et al., 2010a). We used a model averaging approach that is similar to the approach used by FDA (2016) modified to suit our goal of examining model uncertainty. Notably, we expanded the number of models considered to include a 2nd degree Multistage model and Weibull, log logistic, Gamma, and dichotomous Hill models that are unconstrained with respect to their power parameters, and we weighted all models equally a prior. The Multistage model was included because it is viable model and is EPA’s preferred model for evaluating cancer data, particularly animal bioassay data (U.S. EPA, 2012). The use of unconstrained power models has been discouraged when using an approach that involves selecting a single model from a suite of adequate model fits to avoid the selection of models with a biologically unreasonable, infinite slope at the origin (U.S. EPA, 2012). However, the European Food safety Authority (EFSA, 2017) does not recommend constraining models, based largely on the work of Slob and Setzer (2014) who argue that there is no biological reason to reject the unrestricted models. For the purposes of our analysis, unconstrained models have been included primarily because a) it has been shown that, in a model averaging context, augmenting the model space with supra-linear dose–response models can substantially improve BMD coverage (Wheeler and Bailer, 2009) and b) because our model averaging results using unconstrained models did not result in extremely steep supra-linear dose–response curves (Figs. 2 and 3). Nevertheless, as can be seen from the plots of individual model runs (Figs. 2 and 3, right plots), the differences we observe between models are not restricted to the unconstrained models as there are substantial differences in the modeling results even within the constrained models (black plots).

Arsenic exposures from drinking water were well-documented in these studies. Measurements were obtained directly from wells providing drinking water to the subjects’ households. While water arsenic concentrations were measured at enrollment, and the exposure estimates do not take into account natural variations in arsenic exposure (including across lifestage, since the cohort was exposed from birth but estimates only reflect adult intakes) or changes due to mitigation, approximately 97 percent of the subjects, reported they had either started drinking well water at birth and still drank it or started at a later age but still obtained water from tube wells (Chen et al., 2010b). The average duration of well water consumption was estimated to be 40 years in the study cohort.

Outcome ascertainment (numbers of cases of lung and bladder cancer) was based on data from the Taiwan National Cancer Registry, linked to specific ICD-9 codes. Detailed information on exposure history and important covariates (demographics, education level, smoking, and alcohol consumption) was gathered from all subjects. Covariate-adjusted relative risks were used to estimate covariate-adjusted cases of cancer for use in the bootstrap simulation. The data used in our analysis of the Chen et al. (2010b; 2010a) studies were obtained after 12 years of follow-up, with the study by Yang et al. (2013) providing information on cancer incidence after two additional years, and reported incidence separately for smokers and nonsmokers. While the basis for the selected exposure group bounds was not clearly explained and the numbers of cancer cases were relatively low in some exposure groups, uncertainty in the outcome estimates was modeled by treating every hypothetical “subject” in the bootstrap as a Bernoulli trial that “got cancer” based on the covariate-and whole-life adjusted probability of cancer for each exposure group.

In contrast to many published analyses that assess the relationship between exposures (e.g., water concentrations) and responses, we have based this analysis on the relationship between estimated total intake dose of inorganic arsenic from water and diet and responses. Because dietary sources can account for a large proportion of total intake at low drinking water levels, incorporating dietary intake is necessary to afford accurate representation of dose–response relationships where water exposures are small. Here, we used data related to food consumption and arsenic concentration developed by the Taiwanese Department of Health (TDOH, 2007) and from other literature sources, to derive simulation estimates of inorganic arsenic intake from water and important dietary sources. The bootstrap simulation included both direct ingestion of drinking water and water used in the cooking of rice and vegetables (Supplemental Materials Section 2.5).

Two aspects of the dataset that potentially limit its use for extrapolating to doses typically encountered in U.S. populations are that the numbers of cases in the low exposure groups are small and the estimated average inorganic arsenic intake dose associated with the lowest exposure group (0.85 µg/kg-day) is considerably above estimated typical U.S. inorganic arsenic intake dose (on the order of 0.07 µg/kg-day) experienced by individuals living in areas with low drinking water concentrations; see Section 3.2. A number of other considerations beyond the scope of this article have implications for the use of the results from this analysis to estimate potential risks in other populations outside of northwestern Taiwan, including the U.S. These include differences in both the baseline disease incidence and the relationship between arsenic intake and disease that can be caused by factors such as differences in smoking patterns, dietary differences and nutritional factors, and genetic variations affecting both the pharmacokinetics and pharmacodynamics of response to inorganic arsenic exposure.

As reflected in Figs. 2–5, our model averaging analyses indicate substantial model uncertainty in extrapolating from the inorganic arsenic doses estimated for the Taiwan cohort (Table 3) to doses in the range of the estimated U.S. background dose of 0.071 µg/kg-day. The 0.85 µg/kg-day dose associated with the reference group and 2.0 µg/kg-day dose associated with the lowest exposure group of the Chen et al. (2010b; 2010a) studies (Table 5) are 12-fold and 28-fold higher, respectively, than the U.S. background estimate of 0.071 µg/kg-day. At a 0.19 µg/kg-day dose, the dose associated with the 10 µg/L U.S. drinking water standard, our model averaging analyses indicates that there is a 4-fold and 8-fold difference between constrained and unconstrained model estimates of lifetime extra risk for bladder and lung cancer, respectively, with much greater differences estimated from the individual models (see Figs. 2 and 3). The model uncertainty increases as one approaches background; at 0.12 µg/kg-day the difference between constrained and unconstrained lifetime extra risk estimates for bladder and lung cancer was roughly 5-fold and 13-fold, respectively (Tables 4 and 5).

Fig. 5.

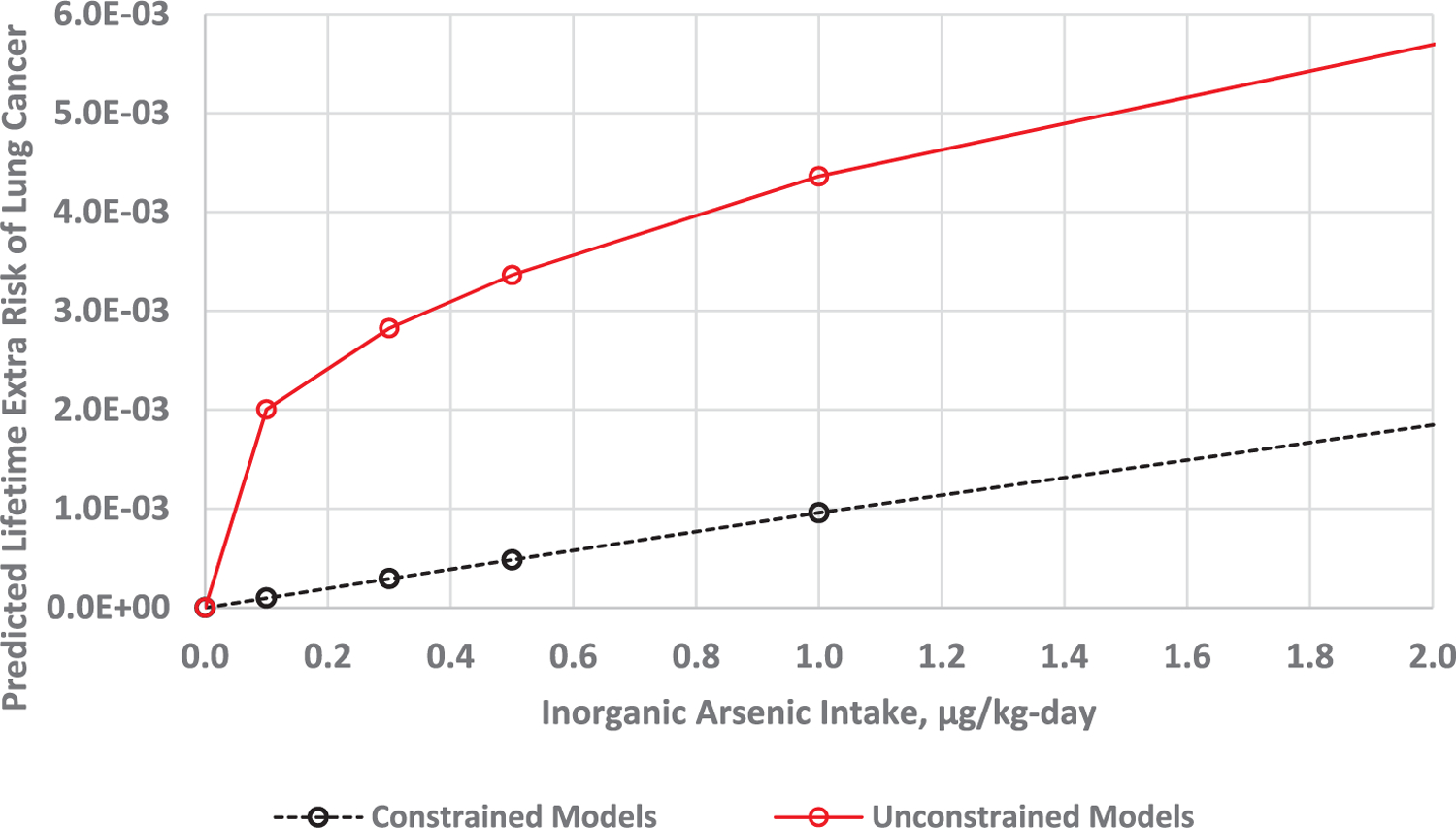
Predicted low dose extra risk of lung cancer extrapolated from Chen et al. (2010a) study data using constrained (black) and unconstrained (red) model averaging.

5. Conclusions

We have conducted a model averaging dose–response analysis using a broad range of constrained and unconstrained models. The case studies for this analysis were lung and bladder cancer risks associated with intake doses associated with inorganic arsenic exposure in the northeast Taiwanese population studied by Chen et al. (2010b; 2010a). A broad range of models was applied to investigate whether model choice would have a large impact on attempts to extrapolate risk estimates from the relatively high dose levels of Chen et al. (2010b; 2010a) to doses more relevant to countries like the U.S. that have proportionally lower arsenic exposure levels. The reported analyses further extends and refines previous analyses of the same data sets conducted by WHO (2011), and the FDA (FDA, 2016; Carrington et al., 2013) by evaluating, to the extent practical, important sources of intake and outcome variability and uncertainty in the data set. Limitation of the analysis include the lack of early life (infant) exposure information and that only aggregate (grouped) data related to individual adult exposures, outcomes, and covariate distributions were available for modeling.

The extrapolation of risk from high Taiwanese doses to doses experienced by U.S. populations involves considerable model uncertainty as indicated by the substantial model dependence in the estimation of lifetime probabilities (Table 4) and extra risk (Table 5). For these reasons, it will be important to consider alternative approaches for the estimating risk at low inorganic arsenic doses, such as those encountered in U.S. populations. One such approach that allows for the consideration of dose–response information from multiple studies is the application of Bayesian meta-regression methods (see Allen et al., 2020a, b for a case study applying such approaches to the inorganic arsenic evidence base).

This paper demonstrates the value of a model averaging approach using a broad spectrum of constrained and unconstrained models in situations where there is uncertainty in the extrapolation of risk from a study population to a different, target population. In this case, the results of such a model averaging analysis of the Chen et al. (2010b; 2010a) studies indicate that other approaches, such as Bayesian meta-regression analyses, that have the potential to better inform dose–response in the low dose region may be warranted for more reliable estimation of lung and bladder cancer risk at U.S.-relevant inorganic arsenic exposure levels.

Fig. 4.

Predicted low dose extra risk of bladder cancer extrapolated from Chen et al. (2010b) study data using constrained (black) and unconstrained (red) model averaging.