Progressive multifocal leukoencephalopathy lesion and brain parenchymal segmentation from MRI using serial deep convolutional neural networks

Highlights

• •PML has characteristic dynamic changes in brain and lesion volume on MRI.
• •JCnet is an automated method for brain atrophy and lesion segmentation in PML.
• •JCnet improves PML lesion segmentation accuracy compared to conventional methods.
• •JCnet can accurately track PML lesion changes over time.

Abstract

Progressive multifocal leukoencephalopathy (PML) is a rare opportunistic brain infection caused by the JC virus and associated with substantial morbidity and mortality. Accurate MRI assessment of PML lesion burden and brain parenchymal atrophy is of decisive value in monitoring the disease course and response to therapy. However, there are currently no validated automatic methods for quantification of PML lesion burden or associated parenchymal volume loss. Furthermore, manual brain or lesion delineations can be tedious, require the use of valuable time resources by radiologists or trained experts, and are often subjective. In this work, we introduce JCnet (named after the causative viral agent), an end-to-end, fully automated method for brain parenchymal and lesion segmentation in PML using consecutive 3D patch-based convolutional neural networks. The network architecture consists of multi-view feature pyramid networks with hierarchical residual learning blocks containing embedded batch normalization and nonlinear activation functions. The feature maps across the bottom-up and top-down pathways of the feature pyramids are merged, and an output probability membership generated through convolutional pathways, thus rendering the method fully convolutional. Our results show that this approach outperforms and improves longitudinal consistency compared to conventional, state-of-the-art methods of healthy brain and multiple sclerosis lesion segmentation, utilized here as comparators given the lack of available methods validated for use in PML. The ability to produce robust and accurate automated measures of brain atrophy and lesion segmentation in PML is not only valuable clinically but holds promise toward including standardized quantitative MRI measures in clinical trials of targeted therapies. Code is available at: https://github.com/omarallouz/JCnet.

1. Introduction

Progressive multifocal leukoencephalopathy (PML) is a rare opportunistic brain infection caused by the JC virus (JCV), a human polyoma virus. PML almost uniformly affects patients with significant immunocompromise, such as HIV/AIDS, lymphoproliferative or myeloproliferative disorders, inherited/acquired immunodeficiency, or drug-induced immunosuppression (Major et al., 2018). The estimated prevalence of PML has been reported to be between 0.07% for patients with hematologic malignancies, and up to 5% in patients with HIV/AIDS (Power et al., 2000). Magnetic resonance imaging (MRI) is considered the gold standard method for the identification and monitoring of PML lesions in vivo. On MRI, PML lesions appear as multifocal, patchy, and/or confluent areas of hyperintensity on T2-weighted sequences, often with corresponding hypointensity on T1-weighted images (Tan and Koralnik, 2010). This infection is associated with a wide range of mortality rates (dependent on the cause of the underlying immunosuppression), with substantial persistent morbidity and disability amongst PML survivors (Carson et al., 2009, Eng et al., 2006, Hadjadj et al., 2019).

There are no approved therapies for PML to-date, however recent studies employing immunomodulatory strategies have shown promising results (Cortese et al., 2019, Muftuoglu et al., 2018). The development of novel treatments for PML would be facilitated by widely available tools that can accurately track PML lesion and global/regional brain volume loss that occurs as part of this condition. This information is valuable for clinical applications and has the potential to be incorporated as an outcome measure for future investigational studies.

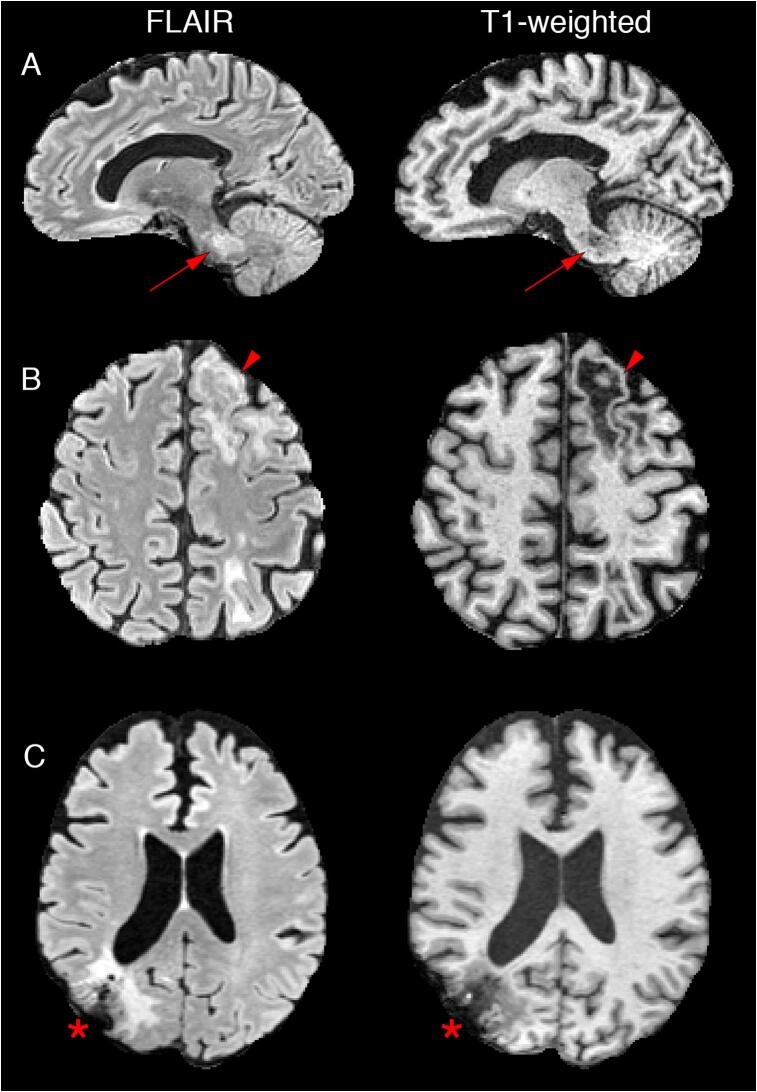
Despite the characteristic appearance of PML on MRI, a number of factors pose unique technical challenges when it comes to developing methods for automated lesion and brain volume segmentation, including the multifocal nature of PML and frequent involvement of infratentorial regions, an area prone to artifacts on commonly acquired MRI sequences (Fig. 1, Panels A and B). Many PML patients undergo brain biopsies as part of their diagnostic work-up, introducing further distortions to the cranium and outer aspects of the brain (Fig. 1, Panel C). Furthermore, the rarity of PML limits the availability of large, well-characterized imaging datasets for training and testing implementations.

Fig. 1.

Illustration of the different challenges unique to progressive multifocal leukoencephalopathy (PML) lesion and brain segmentation on fluid attenuated inversion recovery (FLAIR) and T1-weighted MRI sequences. Given the multifocal nature of PML, there is often a preponderance of infratentorial structure involvement, including the middle cerebellar peduncles (Panel A, red arrows). PML lesions are often associated with confluent areas of T1 hypointensity with overlying cortical thinning, as seen in the left anterior frontal lobe in Panel B (red arrowheads), which can be readily misclassified as cerebrospinal fluid by conventional methods. Many patients with PML undergo brain biopsies as part of their diagnostic work-up, resulting in further cranial and outer brain parenchymal distortions on imaging, as illustrated in the right parietooccipital cortex and subcortical white matter in Panel C (asterisk). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Earlier studies attempting to quantify PML lesion volume on MRI have utilized methods based on region growing and adaptive thresholding (Itti et al., 2001). These methods require manual input to set the seed point(s) and can work well with a limited number of lesions. However, this task can quickly become tedious when many discrete, non-contiguous lesions are present. This approach can also be particularly prone to image artifacts and brain- or lesion-shape irregularities, thereby limiting its generalizability to larger PML datasets. More recently, advances in supervised machine learning approaches for object detection and semantic segmentation have introduced significant improvements in segmentation accuracy on brain MRI of lesions in various neurological disorders, such as multiple sclerosis (MS) lesions (La Rosa et al., 2020, Roy et al., 2018a, Valverde et al., 2017), HIV and human T-cell leukemia virus type 1 (HTLV-1) associated brain lesions (Selvaganesan et al., 2019), brain gliomas (Pereira et al., 2016, Yi et al., 2016), and ischemic strokes (Guerrero et al., 2018), as well as of brain substructure segmentation (Wachinger et al., 2018).

Currently, no specific deep learning approaches have been tailored for PML lesion segmentation or the measurement of concomitant brain atrophy, an important paraclinical marker of disease progression and neuronal loss. Therefore, we designed a 3D deep convolutional neural network (CNN) that can be employed for robust, fully automated PML brain parenchymal and lesion segmentation on MRI scans using a serial approach that we have dubbed ‘JCnet,’ named after the causative viral agent. In PML, as well as in the segmentation of brain pathologies in general, healthy tissue can be present in greater abundance than that of the pathological target in segmentation applications, resulting in voxel-level class imbalance. An important methodological contribution of the work presented here is the serial architecture employed, whereby the first CNN performs candidate extraction of brain parenchymal voxels as foreground and the meninges as well as cerebrospinal fluid (CSF) spaces as background, followed by a second CNN trained to perform PML lesion segmentation on the extracted foreground voxels. Our design helps address the issue of class imbalance by excluding voxels corresponding to structures not relevant to the lesion segmentation task (namely the meninges and CSF spaces), while simultaneously allowing the generation of a brain parenchymal mask that can be utilized to track the degree of brain atrophy in PML, an important marker of neuronal degeneration and brain volume loss in neuroimmunological conditions (Rudick et al., 1999).

Given the lack of widely available methods specific to PML, we evaluate JCnet against several approaches designed for normal-appearing brain and MS lesion segmentation. In both cases, we show significant improvements of performance in PML with an accuracy that approaches that achieved by a trained human rater. We outline our approach in this paper in chronological order. In Section 2, we describe patient recruitment, MRI data acquisition, and preprocessing. In Section 3, we describe the method, implementation, and training specifications. Experimental evaluation and results on the testing dataset are presented in Section 4, followed by a discussion of the proposed network architecture in the context of unmet needs in PML and future directions in Section 5.

2. Materials

2.1. Study population

Scans included in this analysis were selected via retrospective review of patients with PML who were seen at the NIH Neuroimmunology Clinic and evaluated under the Natural History Study of PML (ClinicalTrials.gov number, NCT01730131). The study protocol was approved by the NIH institutional review board, and all the participants provided written informed consent prior to study enrollment. Demographics and clinical characteristics were obtained through electronic chart review. Study participants underwent clinical evaluations, including neurologic examinations and disability measurement at each study visit. PML diagnosis was confirmed by the treating neurologists in accordance with the 2013 American Academy of Neurology Neuroinfectious Disease Section diagnostic criteria (Berger et al., 2013). Scans from a total of 41 patients with PML were included in the final analysis.

2.2. Image acquisition

To improve the generalizability of the trained models, MRI scans acquired on either a Siemens Skyra 3T scanner equipped with a body transmit and a 32-channel receive coils, or a 3T Philips MRI scanner (Philips Medical Systems, Netherlands) equipped with an 8- or 32-channel receive head coils were included in the analysis. Four whole-brain MRI sequences without gaps were used for training and testing implementations: whole brain 3D T1-weighted magnetization-prepared rapid acquisition of gradient echoes (T1-MPRAGE), 3D T2-weighted fluid-attenuated inversion recovery (FLAIR), and multislice T2-weighted (T2) and proton density (PD) sequences (acquired via a dual-echo fast-spin-echo sequence). The MR acquisition parameters for these sequences per scanner are detailed in Table 1.

Table 1.

MR acquisition parameters for the sequences utilized in the study.

	3D-T1 MPRAGE*	3D-FLAIR	2D-FSE T2/PD
Siemens Skyra 3T MRI scanner (16/41 scans)*
Slice thickness (mm)	1	1	3
Inversion time (ms)	900	1800	–
Echo time (ms)	1.7	352–354	18, 82
Repetition time (ms)	3000	4800	3000 or 5000
Flip angle (deg)	9	120	150
Number of repetitions	1	1	1
Philips 3T MRI scanner (25/41 scans)
Slice thickness (mm)	0.73 or 1	0.75, 1, or 1.117	3
Inversion time (ms)	900	1600–1650	–
Echo time (ms)	3.2	276–365	15.38, 100
Repetition time (ms)	7	4800	3410–3763
Flip angle (deg)	9	90	90
Number of repetitions	1	1	1

* A total of 6 scans on the Siemens Skyra were acquired using the T1-weighted MP2RAGE protocol (repetition time = 5000 ms, echo time = 2.9 ms, inversion time = 700 ms/2500 ms, flip angle = 4˚/5˚).

Abbreviations: 3D = 3 dimensional; deg = degrees; FLAIR = fluid-attenuated inversion recovery; MPRAGE = magnetization-prepared rapid acquisition of gradient echoes; FSE = fast spin echo; ms = millisecond; PD = proton density; T = tesla; T2 = T2-weighted sequence.

2.3. Image preprocessing

MR image preprocessing was undertaken using the FMRIB Software (FSL) and Advanced Neuroimaging Tools (ANTs) open source software libraries (Avants et al., 2011, Jenkinson et al., 2012). The T1-weighted images were initially rigidly registered to the Montreal Neurological Institute (MNI)-152 and International Consortium for Brain Mapping (ICBM) nonlinear symmetric 1x1x1mm atlas template that is publicly available for download (http://nist.mni.mcgill.ca/?p=904) (Fonov et al., 2009). The skull and extracranial tissues were removed using the MONSTR algorithm (Roy et al., 2017) and corrected for any inhomogeneity using the Multiplicative Intrinsic Component Optimization (MICO) method for bias-field estimation (Li et al., 2014). Subsequently, the other contrasts, i.e. FLAIR, T2, and PD images, were rigidly co-registered to the T1-weighted image in MNI space, skull-stripped with the same binary mask, and corrected by MICO in a similar fashion.

3. Reference labeled mask creation

To generate the ground truth brain parenchymal masks, we analyzed the T1-weighted and FLAIR images using the Lesion-TOADS (Topology-preserving Anatomy-Driven Segmentation) algorithm (Shiee et al., 2010). The final brain parenchymal masks were generated by combining all the brain substructure labels into a single foreground label category and excluding the meninges, sulcal CSF, and ventricles by merging them with the background. All brain parenchymal masks were manually corrected by a single experienced rater (OA). These masks were subsequently used to train the first stage of JCnet as described in detail below in Section 3.1. Ground truth PML lesion masks were manually delineated by two raters (IO and OA) using the publicly available ITK-SNAP software (Yushkevich et al., 2006). Inter-rater reproducibility was calculated on a subset of 3 subjects delineated by both raters.

4. Methods

4.1. Network architecture

CNNs have emerged as a powerful tool in performing object detection and semantic segmentation tasks on natural images in recent years. This is due to their ability to perform feature-extracting convolutions on images that are learned through iterative training cycles, obviating the need to design hand-crafted features as in classical machine learning approaches. This capability can be easily extended to medical image analysis, object detection, and lesion segmentation, where features are extracted from either multichannel 2D slices (Roy et al., 2018b) or 3D patches (Wachinger et al., 2018) sampled from the original input images. As detailed in Guerrero et al. (2018), the network learns a mapping function that transforms voxel-level image intensities to a desired label classification or segmentation category through a series of convolutions followed by nonlinear activation functions, with each component of this series being referred to as a layer. Feature pyramid networks further exploit the hierarchical architecture of CNNs along their depth by combining low-resolution, semantically strong features (from deeper layers) with high-resolution, semantically weak features (from shallow layers) via a top-down pathway and lateral connections (Lin et al., 2016). The feature map outputs of each layer in the convolutional pathway are then concatenated to predict a voxel-wise membership function of the patch.

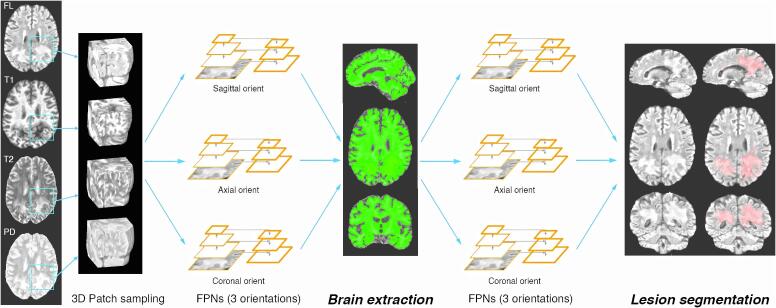
We implement feature pyramid networks in a two-staged approach, each consisting of 3D patch-based multi-view CNNs: the first stage aims at extracting the brain parenchymal voxels as foreground, while the second stage performs PML lesion segmentation. The output of the first stage can be used to exclude meningeal structures and CSF spaces, which are present in the skull-stripped input images, and allows the generation of a brain parenchymal mask to quantify parenchymal volume loss in PML. This strategy also mitigates class imbalance when used as input to the second network stage similar to the work presented by Wachinger et al. (2018). The overall structure of the stages for JCnet are illustrated in Fig. 2.

Fig. 2.

Overview of the proposed two stage approach of JCnet. Three-dimensional patch samples are extracted from input skull-stripped contrast modalities, reoriented, and used to train three multi-view feature pyramid networks (FPNs) to identify the brain parenchyma as foreground, with meninges and cerebrospinal fluid spaces as background. The second stage utilizes a similar neural network architecture to perform PML lesion segmentation, illustrated in light red. Abbreviations: FPNs = feature pyramid networks; orient = orientation. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The details of the network architecture for the CNNs used in each stage of JCnet are listed in Table 2. For each individual CNN, we adopt an FPN design with a ResNet-50 backbone as our baseline. We use deep residual learning given the improved optimization and training of deeper networks, as has been shown by He et al. (2016). We utilize a total of 4 ResNet levels with embedded residual bottleneck building blocks containing projection and identity shortcuts (He et al., 2016b). The residual blocks consist of a series of three sequential convolution operations, each followed by a batch normalization step to correct for internal covariate shift (Ioffe and Szegedy, 2015) and a rectified linear unit (ReLU) activation (Nair and Hinton, 2010), with the exception of the last convolution in each block where the ReLU activation is applied after the shortcut connection and element-wise addition. Aside from a single max pooling operation after the first ResNet layer, down-sampling in the network is otherwise achieved through strided convolutions in the 3rd and 4th layers, as has been described by Springenberg et al. (2014) and implemented by He et al. (2016a). For all the other convolutions within the network, we use zero padding in order to have uniform input and output sizes for all filters.

Table 2.

Network architecture details for the CNNs used in each stage of JCnet. The default input 3D patch size we used is 80x80x80 with 16 base filters. The network architecture is identical for the three multi-view CNNs in each stage. Given the large number of layers, we describe the aggregate of the convolution specifications across each residual block. Projection shortcut blocks contain a 1x1x1 convolution in the shortcut compared to identity shortcuts, which are empty and parameter-free.

Level name	Output size	Layer components	Specification(s)	No. of parameters
ResNet 1	80 × 80 × 80 × 16	•Input layer •Convolution •Batch normalization •ReLU activation	– 3 × 3 × 3	– 1744 64
ResNet 2	40 × 40 × 40 × 32	•Max pooling	3 × 3 × 3 pool size, stride 2	–
		•Projection shortcut block •Identity shortcut block	1 × 1 × 1 → 3 × 3 × 3 → 1 × 1 × 1 1 × 1 × 1 → 3 × 3 × 3 → 1 × 1 × 1	30,336 30,176
ResNet 3	20 × 20 × 20 × 64	•Projection shortcut block* •Identity shortcut block	1 × 1 × 1 → 3 × 3 × 3 → 1 × 1 × 1 1 × 1 × 1 → 3 × 3 × 3 → 1 × 1 × 1	120,064 119,744
ResNet 4	10 × 10 × 10 × 128	•Projection shortcut block* •Identity shortcut block  × 6	1 × 1 × 1 → 3 × 3 × 3 → 1 × 1 × 1 1 × 1 × 1 → 3 × 3 × 3 → 1 × 1 × 1	477,696 2,870,592
Fully convolutional concatenation	All levels	•Convolutional merging of bottom-up and top-down up-sampled feature maps •Convolution appended on each merged feature map to reduce aliasing effect from up-sampling •Convolutional pathway to predict membership function of the patch	1 × 1 × 1 3 × 3 × 3 3 × 3 × 3, sigmoid activation	7360 442,624 6916

* Denotes residual blocks that contain down-sampling convolutions with stride 2.

Abbreviations: No. = number; ReLU = rectified linear unit.

In contrast to the standard ResNet implementation, which uses a fully connected (FC) layer to generate label predictions, we employ a fully convolutional pathway to merge the feature maps across the bottom-up and top-down pathways in our FPN architecture, then append further convolutions to reduce aliasing effects from up-sampling, and subsequently predict the membership function across the patch (Table 2). This approach has been shown to reduce false positives in semantic lesion segmentation tasks and limit the total number of parameters in the model (Roy et al., 2018b). In addition, this also improves the prediction time of the network, as convolutions circumvent the need to perform voxel-wise predictions on each voxel of a new image during testing, which is the case with FC layers. We ensemble the outputs of the three CNNs after reorientation by averaging the voxel-wise probability memberships, which is then thresholded to obtain a hard segmentation of the brain parenchymal voxels (stage 1) and the PML lesional tissue (stage 2). The total number of parameters in our model is 4.1 M, with 7008 non-trainable parameters. This compares favorably with other types of ResNet-50 network models with preserved complexity, where the estimated number of parameters can approach ~25 M (Hu et al., 2017).

4.2. Class imbalance

Class imbalance is an important topic to consider in classification applications and refers to when the distribution of the target classes is skewed within the training dataset. The measures of voxel-level class imbalance across our entire PML dataset of 41 subjects pertaining to both stages are displayed in Table 3. When examining this data, a few trends become clear. First, class imbalance exists in the input datasets for both stages of JCnet. As expected in the first stage, this imbalance is skewed toward brain parenchymal voxels occupying a larger volume when compared to the background class (meninges and CSF spaces), whereas in the second stage the converse is true: PML lesions occupy a much smaller volume (~2–5% on average) compared to the brain parenchyma. Secondly, whereas classifying lesions on the brain parenchymal foreground (instead of the entire stripped volume) helps correct the imbalance by 0.5–1%, this still does not nearly enough result in a sufficient reconciliation toward a balanced state. Therefore, we implement other measures in our patch sampling and loss function specification to mitigate this issue, as described in more detail in the Supplement.

Table 3.

Class level voxel data for stages 1 and 2 of JCnet extracted from the manually labelled masks across both the training and testing sets.

Dataset	Training (n = 31)	Testing (n = 10)	Total (n = 41)
Proportion of brain parenchymal voxels out of all nonzero voxels; mean % across volumes (SD)	77.1 (5)	76.0 (3)	76.8 (5)
Proportion of lesion voxels out of all pre-processed voxels; mean % across volumes (SD)	4.2 (3)	2.0 (1)	3.6 (3)
Proportion of lesion voxels out of brain parenchymal voxels; mean % across volumes (SD)	5.3 (4)	2.7 (1)	4.7 (4)

4.3. Training implementation

JCnet was implemented using Python version 3.6 (https://www.python.org/) and Keras version 2.2.4 (https://keras.io/about/), with TensorFlow as backend. For training purposes, 3D image patches were extracted from the available training dataset, yielding thousands of image samples and allowing for the sample-size necessary for training effective deep learning approaches. We split the 3D patches extracted from the training dataset (n = 31) into 80% used for training and 20% used for validation purposes. Adam optimization was used for training (Kingma and Ba, 2015), with an initial learning rate of 0.0001 and a decay factor of 0.5 if learning plateaued for more than 2 epochs. In addition, we specified early stopping criteria if validation accuracy failed to improve by more than 0.0001 over 4 epochs during training. These specifications were found to produce sufficient convergence without overfitting in most of our training procedures. All experiments were conducted using the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov), using nodes equipped with 4x NVIDIA V100-SXM2 GPUs (32 GB VRAM, 5120 cores, 640 Tensor cores). Training of our primary 80x80x80 patch model with 16 minibatches took approximately 20 hours to converge for all 3 multi-view models of a single JCnet stage. Testing JCnet on a single subject takes approximately 15 min per stage. The implementation details and code for JCnet have been made available at: https://github.com/omarallouz/JCnet.

4.4. Statistical analysis and comparison metrics

Statistical analyses were performed using Stata software (version 13; StataCorp LP, College Station, TX). The Shapiro-Wilk test was used to assess the normality of distributions. Comparisons between training and testing subsets were performed using the two-sample t-test. For age, Chi-square test for sex, Wilcoxon signed-ranks test for PML duration, and Fisher’s exact test for PML risk factors and brain biopsy designation. For comparisons between the different patch size models, we used a one-way analysis of variance with repeated measures (i.e. different models applied to the same PML testing set scans repeatedly).

We evaluated the accuracy of JCnet using Dice similarity coefficients (DSC), and absolute volume differences (AVD). For a manual segmentation (M) and an automated binary segmentation (A), DSC (Dice, 1945) is defined as:

$$DSC\left(M,A\right)=\frac{2|M\cap A|}{\left|M\right|+|A|}$$ (3)

In cases where the target segmentation volume is small, DSC scores can be penalized more by absolute voxel disagreements between the manual and automated segmentations that may not necessarily be clinically significant. Therefore, we also compare AVD, defined as:

$$AVD\left(M,A\right)=|M-A|$$ (4)

All statistical tests between cross-sectional comparison metrics were performed with a non-parametric paired Wilcoxon signed-ranks test. To measure the longitudinal lesion segmentation consistency and agreement of the method with manual delineations, we calculated intraclass correlation coefficients derived from three-level random intercept models: automated and manual lesion volume measurements (level 1) nested within timepoints (level 2), which are in turn nested within PML test subjects (level 3). The intraclass correlation coefficients describe the agreement of the automated and manual delineations relative to the variability seen between different timepoints of the same subject, and between different test subjects. Statistical significance was defined as p < 0.05.

5. Results

5.1. Clinical characteristics

The cohort of 41 patients with PML included in the analysis was empirically divided into 31 training and 10 testing cases sampled at random from the entire set. The testing dataset was unseen by any of the trained networks and used solely to assess the performance of JCnet and the comparator methods. The demographics and clinical characteristics of the patient population by training/testing designation are presented in Table 4. The median number of months between PML symptom onset and image acquisition was 4.5 months (range 0.6–44.5 months), reflecting a wide spectrum of early and overt disease. The test group comprised a wide range of lesion size measurements with a mean of 29.1 cm³ (SD 17, range 7.2–62.5 cm³). Excellent inter-rater reliability of PML lesion segmentation was noted on the sample of 3 scans that were segmented by both raters (mean DSC 0.95, SD 0.02, range 0.94–0.97).

Table 4.

Demographics and clinical characteristics of study participants. Disease duration was defined as the time between PML symptom onset and the acquisition date of the MRI scan.

	Overall n = 41	Training set n = 31	Testing set n = 10	p-value
Age, years; mean (SD)	55 (13)	54 (14)	57 (12)	0.62a
Female; n (%)	18 (44)	12 (39)	6 (40)	0.24b
PML risk factor category; n (%):
•Hematological malignancy •HIV •Idiopathic CD4 lymphopenia •Medication-related •Other acquired immunodeficiency •No known immunocompromise	•15 (37) •8 (20) •4 (10) •4 (10) •8 (20) •2 (5)	•12 (39) •6 (19) •3 (10) •2 (6) •6 (19) •2 (6)	•3 (30) •2 (20) •1 (10) •2 (20) •2 (20) •–	0.88c
PML disease duration, months; median (Q1-3)	4.5 (2–10)	5.8 (2–10)	3.0 (1–8)	0.08d
Underwent brain biopsy for diagnosis; n (%)	12 (29)	10 (32)	2 (20)	0.69c

^a two-sample t-test.

^b chi-square test.

^c Fisher’s exact test.

^d Wilcoxon rank-sum test.

Abbreviations: HIV = human immunodeficiency virus; MRI = magnetic resonance imaging; PML = progressive multifocal leukoencephalopathy; Q = quartile; SD = standard deviation.

5.2. Impact of patch size selection

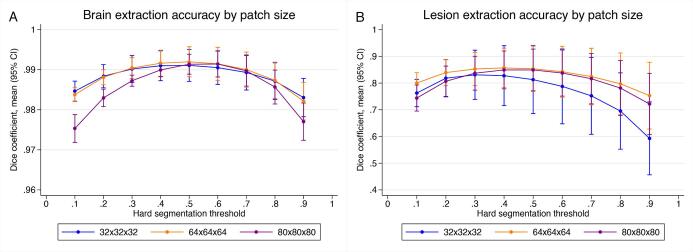
To understand whether the accuracy of brain extraction or lesion segmentation was influenced by the input patch size, we compared three JCnet models that were trained on different input patch sizes of 32x32x32, 64x64x64, and 80x80x80 voxels. As the patch size increased, the number of base filters was reduced from 64 to 32 to 16 base filters, respectively, to allow the data to fit into the available video random access memory (VRAM). Therefore, this decrement provides insight on the trade-off between patch size and the number of base filters in model hyperparameter selection. The output voxel-wise probability membership for each stage of JCnet was segmented at regular thresholds between 0.1 and 0.9 (step size of 0.1), and the mean DSC were compared across models and hard segmentation thresholds keeping all other parameters in training and testing constant (Fig. 3).

Fig. 3.

Mean Dice similarity coefficients and 95% confidence intervals of brain extraction and lesion segmentation displayed by input patch size across the PML testing set. For brain extraction, models with a variety of patch sizes performed similarly using a threshold range of 0.5–0.6, but a more rapid drop-off in accuracy at the tails of the membership distribution was noted for the 80x80x80 patch size model. For lesion segmentation at the best performing threshold for each model, the 64x64x64 model performed better than the smaller 32x32x32 patch size model (mean DSC difference 0.022; p = 0.01). Otherwise, pairwise comparisons between the lesion segmentation models at their best performing threshold were not statistically significant.

For brain extraction, there was no apparent difference in performance between different patch sized models at thresholds of 0.5–0.6, or with the best-performing threshold for each model using a one-way analysis of variance with repeated measures for all pairwise model comparisons (p > 0.05). Interestingly, for the 80x80x80 patch size, there was a drop-off in accuracy at the tails of the membership distribution (particularly for voxels at the brain-sulcal CSF boundaries) indicating that the decrement in base filters during training may have impacted the accuracy of boundary voxel classification (Fig. 3, Panel A; purple curve). On the other hand, larger patch-sized models tended to outperform the smaller 32x32x32 one for lesion segmentation on average (Fig. 3, Panel B). After selecting the best performing threshold for lesion hard segmentation models, a one-way analysis of variance with repeated measures showed an improvement of the 64x64x64 model DSC scores on the test dataset compared to the 32x32x32 model (mean DSC difference 0.022; p = 0.01), but there were no significant differences between the 80x80x80 and 32x32x32 models (p = 0.06) or the 64x64x64 and 80x80x80 models (p = 0.49).

5.3. Comparison to reference methods

We compared the performance of JCnet on PML test cases with FMRIB's Automated Segmentation Tool using FSL version 6.0.0 (FSL-FAST; Zhang et al., 2001) and FreeSurfer version 6.0.0 (Fischl et al., 2002) for global brain parenchymal segmentation. For lesion segmentation, JCnet was compared with two methods designed for general T2/FLAIR or MS lesion segmentation applied directly to the PML testing dataset: Lesion-TOADS (Shiee et al., 2010) and the lesion prediction algorithm of the Lesion Segmentation Tool version 3.0.0 (LST-LPA), which is an open source toolbox for SPM12 (Schmidt, 2017). Based on our initial testing, the LST-LPA performed better than its counterpart in the toolbox, the lesion growth algorithm (Schmidt et al., 2012), in PML lesion segmentation; therefore, LST-LPA was included for all subsequent analyses. It is important to note that the reference methods we used for comparison have not been developed or validated for use specifically in PML, but their utilization here is driven primarily by the lack of other validated methods for PML MRI analysis. The input specifications and parameter details used to apply the comparator methods on the PML testing dataset are specified in Supplementary Table 1. JCnet was also compared to another CNN-based method using U-Net architecture (Çiçek et al., 2016) trained on the same dataset as described in detail in Supplementary Fig. 1.

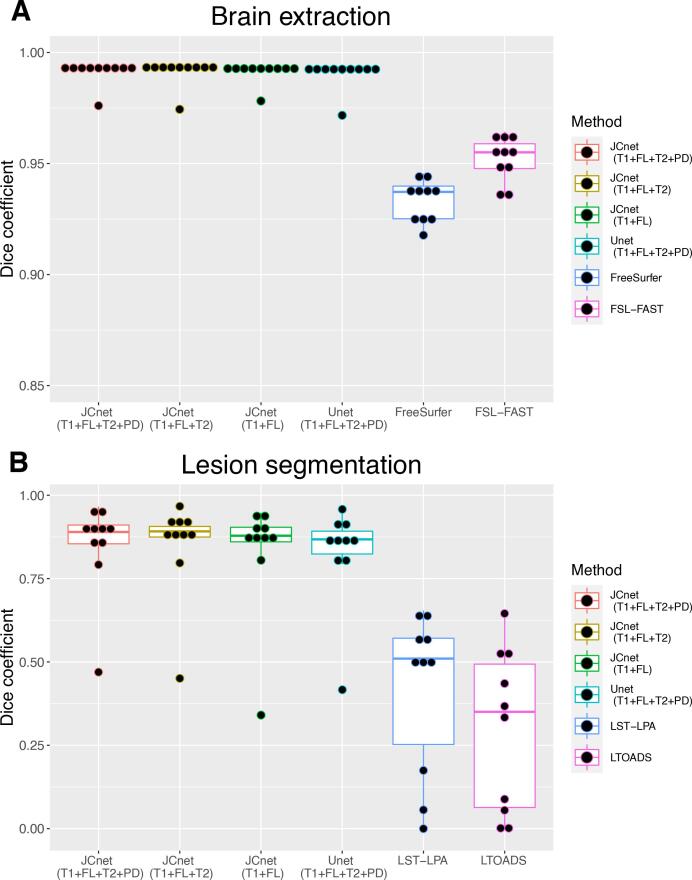
The quantitative differences in PML brain extraction accuracy for JCnet, FSL-FAST, and FreeSurfer methods are described in Table 5 and Fig. 4 (Panel A). Given that the input contrasts differ between the comparator methods, we display equivalent JCnet models where the T2- and/or PD-weighted input contrasts were omitted during both training and testing. JCnet was associated with improvement in voxel-wise classification as measured by DSC and AVD compared to both FSL-FAST and FreeSurfer (Table 5). Qualitatively, this was in part driven by improved performance in areas of significant T1-hypointesity within PML lesions (particularly near the cortical mantle), as well as in regions of biopsy-related changes (Fig. 5, Rows A-B).

Table 5.

Brain extraction and lesion segmentation accuracy metrics between JCnet, FSL-FAST, FreeSurfer, Lesion-TOADS, and LST-LPA methods applied on the PML test dataset. The DSC and AVD scores were measured relative to the gold-standard manual delineations separately for each automated method. The DSC scores reflect the degree of overlap of each of the automated methods to that of the manual delineations, where 0 indicates no overlap whatsoever and 1 indicates exact voxel-wise agreement between both. Comparisons were conducted using methods with the same number and type of input contrasts using Wilcoxon signed-ranks test.

Brain Extraction
Comparison metric	JCnet (T1 + FL + T2 + PD)	JCnet (T1 + FL + T2)	JCnet (T1 + FL)	U-Net (T1 + FL + T2 + PD)	FSL-FAST	FreeSurfer	p-value, JCnet vs U-Net	p-value, JCnet (T1 + FL + T2 + PD) vs FSL-FAST	p-value, JCnet2 (T1 + FL) vs FreeSurfer
Brain parenchymal volume, cm3, mean (SD)	1080 (100)	1079 (99)	1080 (98)	1081 (100)	1159 (108)	1129 (91)	0.33	0.005*	0.009*
DSC scores, mean (SD)	0.992 (0.005)	0.991 (0.006)	0.991 (0.005)	0.991 (0.007)	0.952 (0.010)	0.933 (0.010)	0.07	0.005*	0.005*
AVD, cm3, mean (SD)	8.5 (15)	8.2 (16)	8.0 (13)	9.7 (17)	72.8 (36)	48.9 (27)	0.33	0.01*	0.02*
Lesion segmentation
Comparison metric	JCnet (T1 + FL + T2 + PD)	JCnet (T1 + FL + T2)	JCnet (T1 + FL)	U-Net (T1 + FL + T2 + PD)	LTOADS	LST-LPA	p-value, JCnet vs U-Net	p-value, JCnet (T1 + FL) vs LTOADS	p-value, JCnet (T1 + FL) vs LST-LPA
Lesion volume, cm3, mean (SD)	29 (17)	29 (17)	31 (20)	30 (17)	7 (6)	12 (9)	0.037*	0.005*	0.005*
DSC scores, mean (SD)	0.848 (0.14)	0.850 (0.15)	0.830 (0.18)	0.827 (0.15)	0.300 (0.24)	0.415 (0.24)	0.007*	0.005*	0.005*
AVD, cm3, mean (SD)	2.4 (2)	1.8 (2)	3.1 (3)	3.0 (3)	21.7 (14)	17.1 (12)	0.3	0.005*	0.005*

* p < 0.05.

Abbreviations: AVD = absolute volume difference; DSC = Dice Similarity coefficient; FL = fluid-attenuated inversion recovery image; FN = false negative; FP = false positive; FSL-FAST = FMRIB's Automated Segmentation Tool; LTOADS = Lesion-TOpology-preserving Anatomical Segmentation; LST-LPA = Lesion Segmentation Tool - Lesion prediction algorithm; PD = proton density image; T1 = T1-weighted image; T2 = T2-weighted image.

Fig. 4.

Box plots of Dice similarity coefficients (DSC) between JCnet with different input contrast specifications and the comparator methods for brain extraction (Panel A) and lesion segmentation (Panel B) across 10 PML subject test cases. The single outlier subject with a DSC < 0.5 using JCnet, and DSC < 0.05 on LST-LPA and LTOADS, had the smallest lesion size of all the test subjects (7.2 cm³). Abbreviations: FL = fluid-attenuated inversion recovery image; FSL-FAST = FMRIB's Automated Segmentation Tool; Lesion-TOADS = Lesion-TOpology-preserving Anatomical Segmentation; LST-LPA = Lesion Segmentation Tool - Lesion prediction algorithm; PD = proton density image; T1 = T1-weighted image; T2 = T2-weighted image.

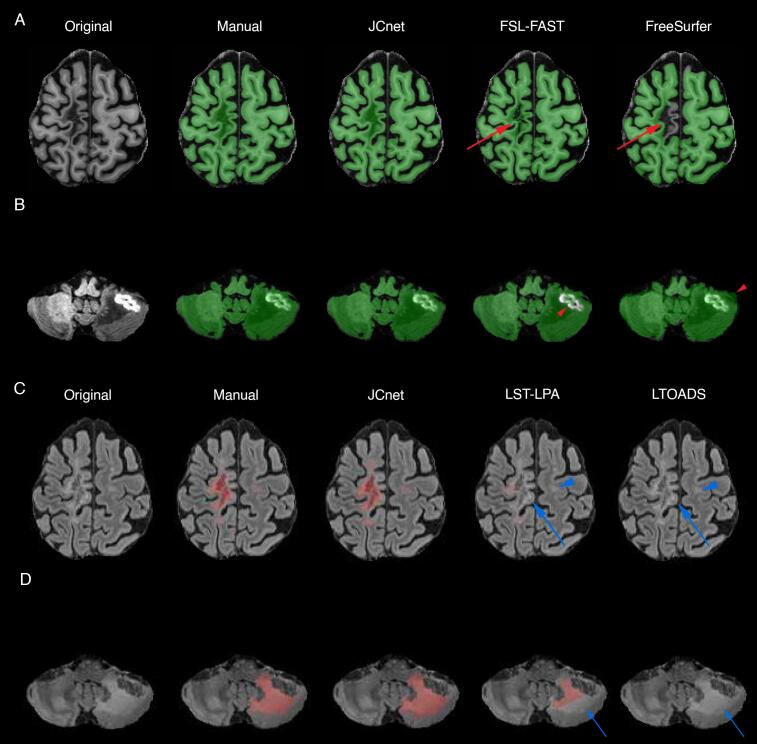
Fig. 5.

Visual depictions of the performance of the proposed and comparator methods on 2 PML test subjects. Rows A and B demonstrate T1-weighted images with binary brain parenchymal masks overlaid in green, whereas Rows C and D demonstrate FLAIR images with lesion segmentation results overlaid in light red. JCnet displayed improved brain extraction results in areas of underlying T1-hypointensity, particularly near the cortical mantle (Row A, red arrows). Similarly, regions of post-biopsy related signal changes, as seen in the left cerebellum in Row B, showed a reduction of false negative voxels within the biopsy bed compared to FSL-FAST and false positive voxels outside the meningeal folds compared to FreeSurfer (red arrowheads). An improvement in PML lesion delineation was seen across the spectrum of supratentorial and infratentorial lesions (Rows C and D, blue arrows). There was also a concomitant improvement in the detection of lesions that were entirely missed by the other methods (blue arrowheads). Abbreviations: FLAIR = fluid-attenuated inversion recovery; PML = progressive multifocal leukoencephalopathy. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

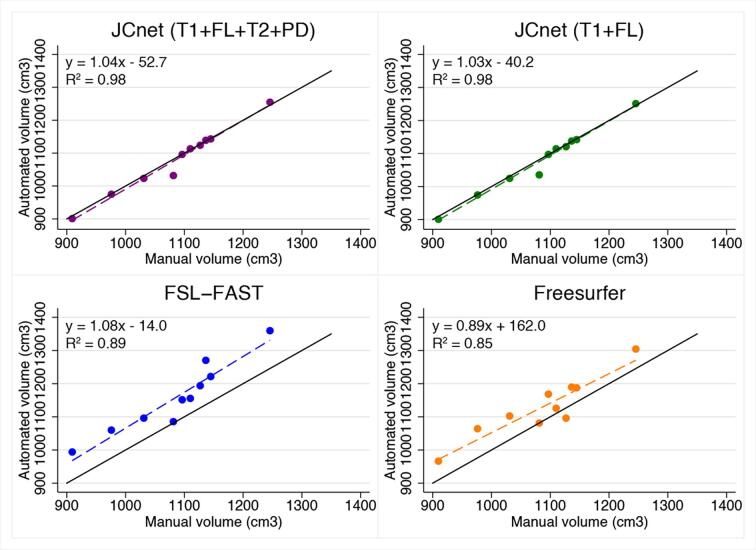
Fig. 6 shows the correlation between the manual PML brain parenchymal masks and automatically generated ones using JCnet models with an equivalent number and type of input contrasts to FSL-FAST and FreeSurfer. In both cases, an improvement of 9–13% was noted in the R² values, reflecting the strength of linear association between automated and manual measurements. We further inspected the regions of voxel mismatch between the manual brain parenchymal masks and FSL-FAST/FreeSurfer automated masks using binary mask subtraction, which showed that most voxel misclassifications occurred due to false positive voxels within sulcal CSF spaces near brain boundaries (Supplementary Fig. 2).

Fig. 6.

Scatter plots of automated versus manual brain parenchymal volumes for JCnet with 4 input contrasts compared to FSL-FAST, and JCnet with 2 input contrasts compared to FreeSurfer. Solid black lines represent the identity lines. Dashed lines represent the linear regression fit for each method. Abbreviations: FL = fluid-attenuated inversion recovery image; FSL-FAST = FMRIB's Automated Segmentation Tool; PD = proton density image; T1 = T1-weighted image; T2 = T2-weighted image.

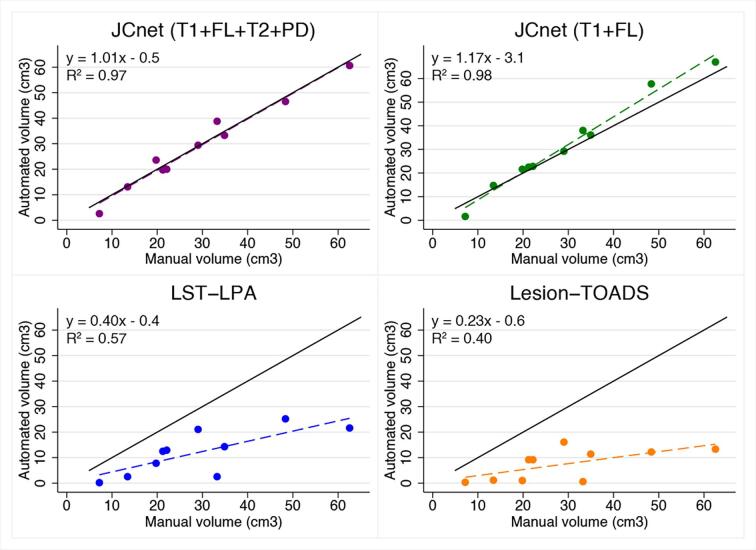
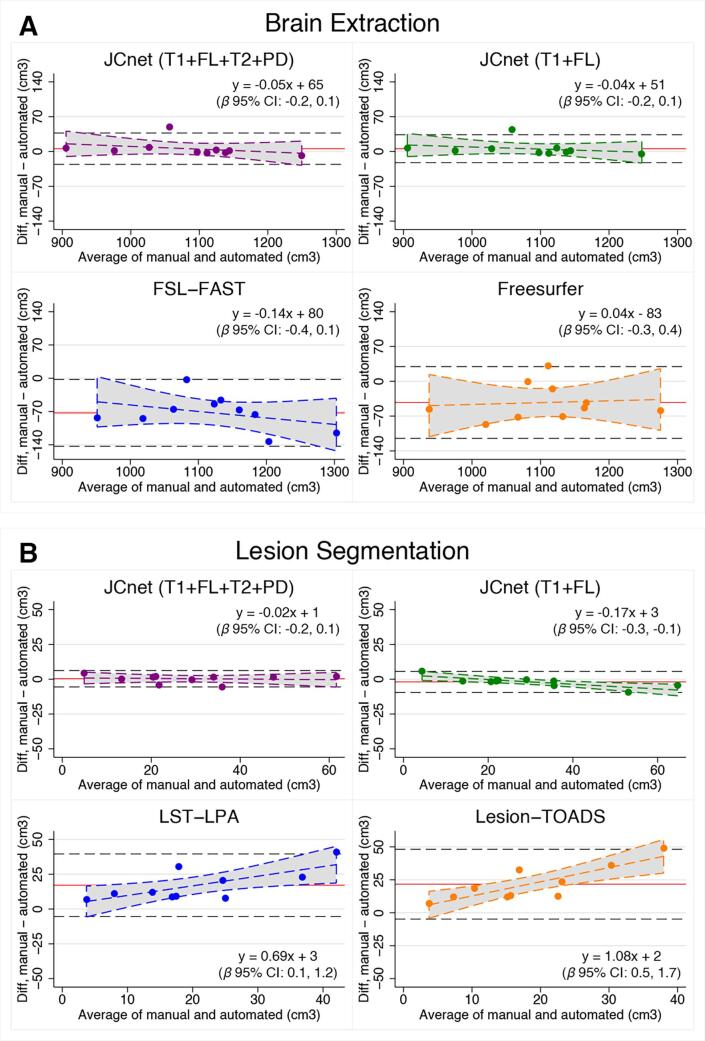
Lesion segmentation comparisons in the unseen PML testing set were undertaken with both Lesion-TOADS and the LST-LPA algorithms, as presented in Fig. 4 (Panel B) and Table 6. JCnet achieved a 42–55% absolute improvement in DSC scores compared to either method, which was driven by an increased sensitivity in PML lesion detection and boundary segmentation (Fig. 5, Rows C and D). This is also illustrated in Fig. 7, which shows volume comparisons between manually delineated lesion masks and automated ones from JCnet, Lesion-TOADS, and LST-LPA. Bland-Altman plots comparing manual and automated values for each method included in the brain extraction and lesion segmentation analyses are displayed in Fig. 8 (Panels A and B respectively).

Table 6.

Intraclass correlation coefficients (ICCs) of longitudinal lesion segmentation for 17 timepoints of a subset of 4 PML test cases. Given a three-level nested model of two lesion measurements (manual and automated) nested within timepoints, nested within subjects, we can calculate the ICCs at the subject (level-3) and timepoints-within-subjects (level-2) parts of the model. The subject level ICC (level-3) estimates the total residual variance explained by between-subject differences (ignoring the nested timepoint structure), whereas the timepoints-within-subjects ICC (level-2) describes the total residual variance explained by differences between timepoints within the subjects. Any residual variance not explained by the level-2 part of the model (1- level 2 ICC) reflects the degree of disagreement between the manual and automated measures relative to the total residual variance.

Automated method	Subject level ICC (Level-3)	Subject level ICC95% CI	Timepoints-within-subjects ICC (Level-2)	Timepoint level ICC 95% CI
JCnet	0.64	0.21, 0.92	0.99	0.98, 0.99
LST-LPA	0.58	0.20, 0.88	0.64	0.25, 0.90
LTOADS	0.60	0.22, 0.89	0.60	0.22, 0.89

Abbreviations: CI = confidence interval; ICCs = intraclass correlation coefficient; LTOADS = Lesion-TOpology-preserving Anatomical Segmentation; LST-LPA = Lesion Segmentation Tool - Lesion prediction algorithm; MS = multiple sclerosis.

Fig. 7.

Scatter plots of automated versus manual lesion masks comparing JCnet, LST-LPA, and Lesion-TOADS . Solid black lines represent y = x identity lines. Dashed lines represent linear regression fit for each method. Abbreviations: FL = fluid-attenuated inversion recovery image; Lesion-TOADS = Lesion-TOpology-preserving Anatomical Segmentation; LST-LPA = Lesion Segmentation Tool - Lesion prediction algorithm; PD = proton density image; T1 = T1-weighted image; T2 = T2-weighted image.

Fig. 8.

Bland-Altman plots comparing manual delineations with all other methods included in our analysis for brain extraction (Panel A) and lesion segmentation (Panel B). The red horizontal line represents the mean of the differences and the black dashed horizontal lines represent the upper and lower limits of agreement, calculated as the mean ± 1.96SD. The dashed colored lines for each method represent the linear regression fit and 95% confidence intervals (shaded gray region), with the regression parameters and 95% confidence interval of the slope (i.e. β coefficient) included in the inset for each method. Abbreviations: FL = fluid-attenuated inversion recovery image; FSL-FAST = FMRIB's Automated Segmentation Tool; Lesion-TOADS = Lesion-TOpology-preserving Anatomical Segmentation; LST-LPA = Lesion Segmentation Tool - Lesion prediction algorithm; PD = proton density image; T1 = T1-weighted image; T2 = T2-weighted image. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

When compared to a U-Net based model architecture with an equivalent number of input contrasts, base filters, and focal loss function (Table 5 and Supplementary Fig. 1), there were no statistically significant differences in brain extraction DSC and AVD results using JCnet’s FPN architecture (mean DSC difference 0.001, p = 0.07; mean AVD difference 1.2 cm³, p = 0.33). However, a significant improvement in lesion segmentation DSC scores was noted utilizing the FPN design (mean DSC difference 0.02, p = 0.007).

5.4. Longitudinal lesion segmentation performance

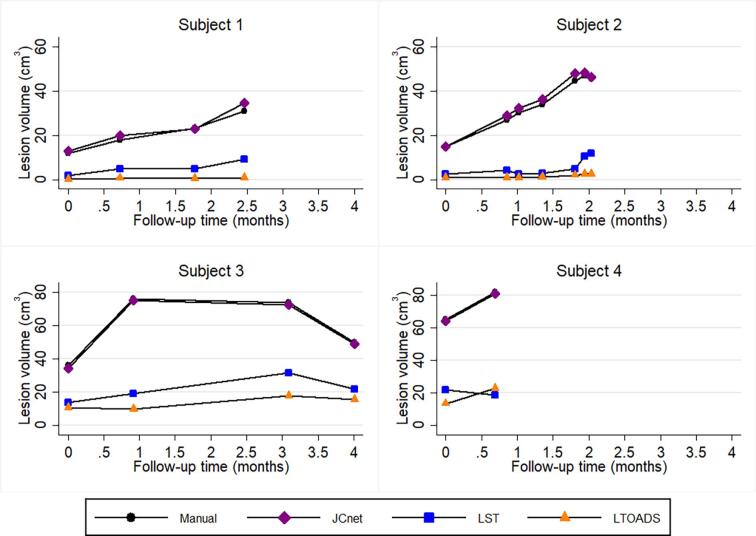
Longitudinal lesion segmentation assessment across follow-up scans was performed on a total of 17 timepoints from a subset of 4 PML test subjects. Median number of timepoints per subject was 4 (range 2–7), spanning a median of 2.3 months (range 0.7 – 4.0). Manual lesion delineations were performed on all 17 timepoints, and the consistency of the automated methods was compared to the manual delineations at each timepoint, as discussed in sections 3.4 and 4.3 (Fig. 9).

Fig. 9.

Longitudinal lesion profile plots of 4 PML test subjects comparing the consistency of JCnet (purple), LST-LPA (blue), and LTOADS (orange) with those of manual delineations (black). Dynamic lesion volume changes over time were better captured using convolutional neural networks trained on PML cases (JCnet), compared to other methods developed for multiple sclerosis lesion segmentation (LST-LPA and LTOADS) which did not fully reflect the extent of lesion accumulation over time in Subjects 1, 2, and 4. Abbreviations: LTOADS = Lesion-TOpology-preserving Anatomical Segmentation; LST-LPA = Lesion Segmentation Tool - Lesion prediction algorithm; PML = progressive multifocal leukoencephalopathy. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The intraclass correlation coefficients (ICCs) comparing the consistency of lesion segmentation between the manual delineations and different automated methods for the longitudinal PML subset are presented in Table 6. Interestingly, between-subject variability in PML lesion volume accounts for only 58–64% of the total residual variance across the different methods, indicating that considerable variation in lesion volume occurs between different timepoints within subjects, highlighting the dynamic nature of PML lesions across time. JCnet showed an improved ability to track within-subject, between-timepoint variations in lesion volume segmentation, with 1% of the total residual variance being related to differences between manual and JCnet lesion volume measurements over time, compared to 36–40% for methods developed for general T2/FLAIR or MS lesion segmentation.

5.5. Visualizing JCnet filter activation patterns

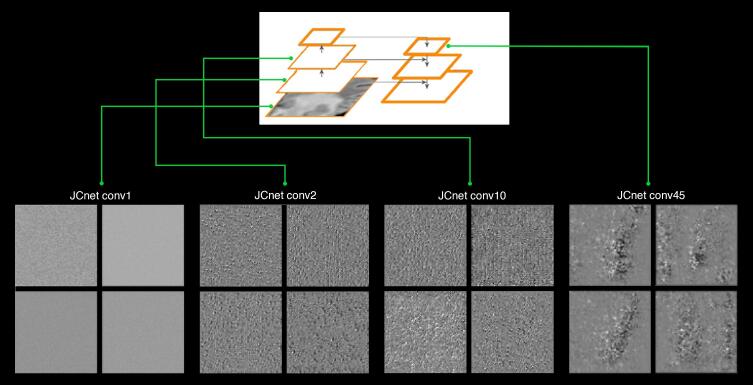
To gain a better understanding of the classification process taking place within JCnet, we inspected the filter activation patterns using the gradient ascent in input space method (Chollet, 2017). This method enables the visualization of simulated patterns in input images to which filters in selected convolutional layers in the network respond maximally (Fig. 10). At shallow layers, the simulated FLAIR input of the lesion segmentation network consisted of hyperfine texture patterns, which evolved into checker-like and polka dot patterns in intermediate layers, and finally more abstract patterns in deeper, more semantically rich layers. Such patterns bear some resemblance to confluent PML lesions, meaning that the corresponding filters of these layers would respond maximally to signs of confluency in the input FLAIR volume.

Fig. 10.

Examples of filter activation patterns within successive layers of increasing depth within the JCnet lesion segmentation convolutional neural network extracted from the midpoint slice of the 3D FLAIR input channel. Only 4 representative filters are displayed per layer from the entire set of available filters. In shallow layers, these resemble hyperfine texture patterns and then evolve to checker-like or polka-dot patterns in intermediate layers. In deeper layers (far right), more abstract visual patterns start to emerge, which arguably bear some resemblance to discrete or confluent PML lesions. Abbreviations: conv = convolutional layer.

6. Discussion

We describe a 3D patch-based, fully convolutional framework for brain extraction and lesion segmentation in PML. Accurate assessment of PML lesion burden and associated brain parenchymal atrophy is of critical importance for PML disease monitoring, assessing response to therapeutic measures, and obtaining a reliable MRI outcome measure for clinical trials of targeted therapies (Cortese et al., 2019). One of the important findings of the work presented is that the application of standard methods of healthy brain extraction in the context of PML may not be optimal and should be approached with caution, given the increased incidence of brain parenchymal classification errors within T1 hypointense PML lesions and in the vicinity of biopsy-related changes. Similarly, we show that methods designed for lesion segmentation in MS are associated with an underestimation of PML lesion volume, particularly in patients with significant infratentorial disease burden (Figure, Row D). Collectively, these findings underscore the need for developing methods tailored to PML and capable of handling the unique morphological and intensity-based changes occurring in the PML brain on standard MRI sequences.

Generally speaking, CNNs have been implemented with varying degrees of success in a number of medical and neuroimaging applications, including automated motion detection (Fantini et al., 2018), anatomical brain segmentation (Wachinger et al., 2018), and accurate identification of pathologies such as ischemic strokes (Guerrero et al., 2018) or MS lesions (La Rosa et al., 2020, Roy et al., 2018a, Valverde et al., 2017). In the context of PML, CNNs offer several unique advantages suited to the task of brain extraction and lesion segmentation. CNNs can be viewed as powerful feature extractors able to learn local, translation-invariant features, which makes them highly data-efficient at solving perceptual problems and ideal for the task of multifocal lesion detection, which is seminal for PML analysis. Additionally, the hierarchical spatial representation of the feature maps within CNNs allows for combining local or hyperlocal patterns into higher level conceptual views (Fig. 10). FPNs, in particular, exploit this hierarchy by merging higher-level semantic features at different scales (Lin et al., 2016), therefore their implementation in PML can help the network address the combination of larger confluent or more complex PML lesions as well as the smaller satellite lesions often encountered in practice, sometimes even in the same scan (Fig. 5, Row C). In addition to the FPN architecture, we utilize residual learning blocks in our network in order to improve the training convergence speed while, at the same time, allowing the training of networks with increasing depth and resultant accuracy gains (He et al., 2016a).

Class imbalance is a prevalent issue in medical image segmentation (Zhou et al., 2019), and we show in this work that PML datasets are no exception. Despite the larger size of PML lesions on average compared to those observed in MS, for example, there remains a significant voxel-wise imbalance, with PML lesions constituting only approximately 3.6% of the total nonzero voxels in a skull-stripped volume (Table 3). This has important ramifications when it comes to network design, parameter selection, and data sampling. Prior studies have addressed this issue by proposing the use of specific loss functions, such as weighted or bootstrapped cross-entropy (Guerrero et al., 2018), or by modifying the data sampling process such that all labels are equiprobable during sample (Kamnitsas et al., 2017). In our implementation, we utilized a comparable strategy for data sampling, but opted to use the recently described focal loss function, which downscales the loss values for easily classified observations and allows the network to focus on poorly classified examples, which are arguably more pertinent for training (Lin et al., 2017). Systematic comparisons between the use of different loss functions for PML lesion segmentation are out of the scope of the work presented but should be explored in future work to further assess which loss functions are better suited for lesion segmentation tasks.

The collective application of these specifications in our network design resulted in a significant improvement of voxel-wise classification accuracy of 4–6% and 42–55% for PML brain extraction and lesion segmentation, respectively, compared to reference comparator methods. Furthermore, we show that CNNs trained on PML data are able to capture the dynamic changes in PML lesions over time (using manual delineations as reference), and in a more consistent fashion compared to the comparator methods used in this study, with a level-2 ICC of 0.99. This is particularly important from the perspective of monitoring and clinical trials, where detection of change in lesion volume over time is of critical value. However, it is important to note that the comparator methods utilized here were not developed or validated for use in PML, but rather for segmentation of either normal-appearing brain tissue (FSL-FAST and Freesurfer) or T2-FLAIR hyperintense lesions in MS (LST-LPA and Lesion-TOADS). Their use in this context is primarily driven by the paucity of publicly available methods specific for PML.

One of the limitations of the work presented is that we have limited our analysis to a single label for the foreground brain parenchymal voxels in order to preserve simplicity and a focus on achieving accurate PML lesion segmentation when used as the input for the second stage of the method. With better availability of PML ground truth datasets, including those with manual brain substructure delineations, future work could investigate the possibility of extending our framework to include deep learning-based segmentation of brain substructures. The ability to discriminate PML lesions from those seen with concomitant or other neurological disorders is outside the scope of the current study given our primary focus on quantifying and tracking lesions in PML patients who have already been diagnosed. In patients with longitudinal imaging available prior to PML onset, this can be accomplished by masking out pre-existing lesions on imaging obtained prior to PML onset. However, in patients where this imaging is lacking, this remains a challenging task and would be an interesting target for future studies to investigate. It is also important to keep in mind that, although we have included MRI data from several different protocols acquired on two scanners, this analysis does not encompass the vast spectrum of available MRI scanners and protocols used in different medical centers. As a result, pretrained models should be applied with caution and rigorous quality control for imaging data acquired with different protocols or on different devices than those used in this study; alternatively, the models should be retrained.

In summary, we present an end-to-end framework capable of performing robust brain extraction and lesion segmentation in PML using a consecutive CNN strategy. We demonstrate significant improvements over current state-of-the-art comparator methods designed for normal-appearing brain and MS lesion segmentation. By tracking quantitative measures of PML-related brain and lesional changes, this approach can provide a window for clinicians and scientists to more accurately monitor PML in vivo, track its response to therapeutic strategies, and introduce standardized, quantitative MRI markers for use as outcome measures in clinical trials.

Study funding

O.A. is supported by a National Multiple Sclerosis Society-American Brain Foundation Clinician Scientist Development Award (FAN-1807-32163). This work was also supported by the Intramural Research Program of the National Institute of Neurological Disorders and Stroke of the National Institutes of Health.

Role of the funding source

The sponsors of this study had no role in study conceptualization, study design, data acquisition, analysis or interpretation, manuscript drafting or critical revision. The corresponding authors had full access to all data and accept responsibility for the decision to submit for publication.

Disclosures

Drs. Omar Al-Louzi, Snehashis Roy, Ikesinachi Osuorah, Prasanna Parvathaneni, Bryan Smith, Joan Ohayon, Pascal Sati, Dzung L. Pham, Steven Jacobson, Avindra Nath, and Irene Cortese have no disclosures pertaining to the work presented. Dr. Daniel S. Reich received research funding from Vertex Pharmaceuticals, unrelated to the current project.

CRediT authorship contribution statement

Omar Al-Louzi: Conceptualization, Methodology, Software, Validation, Data curation, Formal analysis, Writing - original draft. Snehashis Roy: Methodology, Software, Validation, Formal analysis. Ikesinachi Osuorah: Methodology, Data curation, Validation. Prasanna Parvathaneni: Methodology, Software. Bryan R. Smith: Investigation, Resources, Data curation. Joan Ohayon: Investigation, Resources, Data curation. Pascal Sati: Methodology, Investigation, Resources, Data curation, Supervision. Dzung L. Pham: Methodology, Software, Validation, Supervision. Steven Jacobson: Investigation, Resources, Data curation, Supervision. Avindra Nath: Investigation, Resources, Data curation, Project administration, Supervision. Daniel S. Reich: Conceptualization, Methodology, Investigation, Resources, Data curation, Formal analysis, Writing - review & editing. Irene Cortese: Conceptualization, Methodology, Investigation, Resources, Data curation, Formal analysis, Writing - review & editing, Project administration.

Appendix A. Supplementary data

The following are the Supplementary data to this article: